1. Introduction
The international political response to climate change began at the Rio Earth Summit in 1992. The adoption of the UN Framework on Climate Change (UNFCCC) was included in this convention, with the aim of stabilizing atmospheric concentrations of greenhouse gases (GHGs) to avoid dangerous interference with the climate. The UNFCCC, which entered into force in 1994, has been reviewed in the annual Conference of Parties (COP). Thus, the Kyoto Protocol was adopted in the COP3 and the Green Climate Fund was created in the COP17. In the COP21 (Paris Climate Conference), an action plan was set out in order to avoid climate change, by keeping the increase in global average temperature to well below 2 ℃ [1].
The COP21 [2] contains the steps all countries have the responsibility to make before 2020. Thus, each country shall prepare and communicate its nationally determined contributions (NDCs) every five years. Much work is to be done in this respect because, as stated in Climate Action Tracker [3], only five intended NDCs are already considered sufficient. Hence, as stated in Brauers and Richter [4], almost all countries have to scale-up their 2025-2030 contributions. Therefore, to achieve this target, energy and GHG emission must be reduced in all economic sectors.
In order to reduce these emissions, action on energy policy is essential, as emissions from the energy sector represent roughly two-thirds of all GHG emissions [5]. Therefore, these policies are essential for tackling the climate change problem. The main origin of emissions in the energy sector is the use of fossil fuels, as over 90% of energy-related emissions are CO2 from fossil-fuel combustion. By sector, as stated in IEA [6], the largest emitting sector is power generation (40% in the world in 2014), mainly due to the use of fossil fuels. Therefore, reducing the use of fossil fuels is especially relevant within the power generation sector. In that regard, the use of renewable energies is one of the main measures to be applied and, over recent years, many countries have started to produce electricity and heat from renewable energies. Among renewable energies, wind energy is believed to have the least adverse environmental impact and is one of the renewable energies that has become economically affordable long before several others [7]. As a result, it is worth noting the substantial additions of wind capacity between 2000 and 2014, although many differences can be observed between countries [8].
Despite the importance of the increase in electricity consumption and wind capacity, there are few studies focusing on its heterogeneity across the world. Some studies refer to a specific part of the world. Thus, the study by Scarlat et al. [9] analyzes the bioenergy contribution in the European Union, the study by Dent [10] analyzes the wind energy development in East Asia and Europe, and the study by Mohammed et al. [11] presents the status of renewable energy consumption, including wind, in Sub-Saharan Africa. Likewise, some studies refer to specific countries, for example, the study by Chingulpitak and Wongwises [12] refers to wind energy in Taiwan, the study by Ho [13] refers to wind energy in Malaysia and the study by Kaplan [14] refers to Turkey. From a more general perspective, Leung and Yang [15] provide an overview of wind turbine development and development trends of offshore wind farms in some countries, such as China, the USA, Germany, Spain and India. However, very little consideration has been given to some regions such as Africa, Transition economies, Latin America and the Middle East. However, as stated in Mundaca et al. [16], the causes and impacts of climate change are mostly couched in regional terms.
In addition, although some studies, such as those by IEA [8,17], refer to the electricity trends, these studies do not provide a detailed regional vision. Although there are some previous studies referring to renewable energy trends [18,19], they also do not offer a detailed regional vision in terms of the main world regions or of income groups, nor do they specifically focus on wind energy. In addition, these studies do not analyze the electricity or wind electricity consumption related to economic and population growth. In that sense, few data have been previously provided about wind regional trends and its main economic indicators. Therefore, it is appropriate to develop much more research on these geographical differences [20,21].
Following these previous studies, the aim of this short paper is to provide a concise analysis of electricity and wind energy consumption trends for the period 1990-2014 in a dual perspective, by principal world regions, covering 11 regions, and by per capita gross national income (GNI) levels in 2014, covering 4 groups. Thus, the study focused on electricity and wind energy trends from a worldwide regional perspective in total consumption and per inhabitants and by GDP terms, for which, to our knowledge, there are no previous specific studies. Considering world regions by geographic and income groups allows an illustration as to what extent the electricity and wind energy consumption evolution is a geo-economic process. In that regard, the choice of the 11 regions and four groups of GNI levels are related to geographical and economic issues, in line with the main classifications provided by the World Bank [22] and the United Nations [23]. Alternative factors, such as atmospheric pressure and temperature, may also be adopted as criteria to categorize regions consuming electricity and wind energy, however this analysis goes beyond the objective of this work. The results of the paper may be taken as a starting point for additional and deeper analyses regarding regional economies.
2. Methodology
Wind electricity is analyzed by comparing its main indicators with respect to other general electricity sources. Therefore, electricity consumption (E) world data are analyzed and presented by world regions and by GNI levels. The E has been divided into three types of electricity sources: non-renewable electricity (NRE), renewable electricity excluding wind electricity (RE) and wind electricity (WE). These variables were analyzed by comparing annual changes, energy intensity (ratio of energy consumption to GDP in PPP) and energy in per capita terms. Additionally, the trend of the following ratios has been studied: total electricity consumption to total energy consumption, total renewable electricity to total electricity consumption and wind electricity to total renewable electricity consumption.
NRE is the electricity consumed which has been generated by using non-renewable energies. It is calculated as follows:
|
NRE=nre∗Electricityconsumption
|
|
nre=NRREEusedintheElecproductionElecproduction+Elecimports
|
where NRREE refers to non-renewables energies and Elec to electricity. NRREE is calculated as the sum of coal, oil, gas, nuclear and other sources used in the electricity generation.
RE is the electricity consumed which has been generated by using renewable energies, with the exception of wind. It is calculated as follows:
|
RE=re∗Electricityconsumption
|
|
re=RREEusedintheElecproductionElecproduction+Elecimports
|
where RREE refers to renewable energies and Elec to electricity. The RREE used in the electricity production is calculated as the sum of biofuels, waste, hydro, geothermal and solar PV, solar thermal and tide used in the electricity generation.
Finally, WE is the electricity consumed which has been generated by using wind energy. It is calculated as follows:
|
WE=w∗Electricityconsumption
|
|
w=windenergyusedintheElecproductionElecproduction+Elecimports
|
The world has been divided into the following regions: the first 15 members European Union (EU15), new European Union members (EU+), other developed countries (ODC), economies in transition (ET), Middle East and North African (MENA), East Asian (EAS), South Asian (SAS), Central African (CA), Southern African (SA), Latin American (LAC) and The Caribbean (CAR) countries. In addition, four groups have been considered by dividing the world according to GNI per capita in 2014: High income (HI), upper medium income (UMI), lower medium income (LMI), and, lower income (LI) countries (See Appendix).
The time period analyzed is 1990-2014, for which there are enough available data for all sample countries. Although the IEA [24] provide monthly electricity statistics, the last being for February 2017, this database only provides data on electricity production and not on its consumption. Also, it does not detail data on wind energy, but only on renewable energies as a whole. Therefore, data based on energy balances and heat and electricity production provided by IEA [25] have been used, the latest data for which refers to 2014.
3. Results
3.1. Total energy, electricity and wind electricity consumption trend in the period 1990-2014
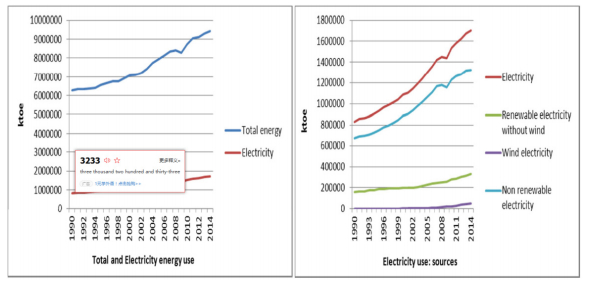
Figure 1 shows world total energy and total and wind electricity consumption trends during the 1990-2014 period. It is worth noting the notable lower growth trend for electricity with respect to total energy consumption during the whole period. Likewise, it is noticed that total consumed electricity was mostly generated by non-renewable sources, although in recent years, the share of renewable sources has increased slightly. Thus, the non-renewable electricity consumption shows a similar growth trend with respect to that of electricity. It is also worth noting that wind electricity consumption shows growth from 2005, but it represents a small share of electricity consumption.
By regions, Table 1 shows that the electricity growth rate is nearly double the total energy growth rate, being 101% and 48%, respectively. Additionally, all regions have electricity growth rates higher than that of total energy, except for Southern Africa. The regions with highest electricity growth rates are East Asia (668%), South Asia (311%) and MENA (310%), while Central African, Latin American and The Caribbean regions show electricity growth rates higher than 100%. In absolute terms, East Asian and the other developed countries have the highest values. The East Asian region electricity consumption increase is 52% of the world electricity increase, while the other developed countries increase is 16%. The electricity consumption growth may be related to the economic growth in the world regions. Several studies have previously related electricity consumption to economic growth in a double sense [26]. Firstly, electricity consumption is considered necessary to generate growth, as are other energy sources such as fuels. Secondly, it is also seen as a consequence of this economic growth. In this latter sense, electricity consumption especially grows in the residential sector which may be linked to urbanization, lifestyle changes and the development of modern society. Thus, Ferguson et al. [27,28] show that while a well correlated relationship is observed between electricity use and wealth creation, there is no correlation between total energy use and wealth, indicating the essential role that electricity, rather than energy in general, plays in the development of modern society. Therefore, as regions grow, the electricity consumption may grow by a higher percentage than does total energy.
Table 1. Growth rates and electricity consumption increase during 1990-2014. Source: Own production from IEA [25].
|
Total energy growth rate percentage |
Electricity growth rate percentage |
Electricit increase (ktoe) |
RE contribution to electricity increase percentage |
WE contribution to electricity increase percentage |
NRE contribution to electricity increase percentage |
| World |
48.08 |
101.15 |
843384 |
18.65 |
5.22 |
76.13 |
| EU15 |
6.34 |
32.07 |
50255 |
40.71 |
29.45 |
29.84 |
| EU+ |
-21.37 |
6.85 |
2011 |
53.62 |
24.11 |
22.28 |
| ET |
-33.94 |
-14.96 |
-17239 |
10.81 |
0.18 |
89.00 |
| ODC |
15.61 |
37.53 |
132522 |
8.49 |
10.81 |
80.70 |
| CA |
102.12 |
199.33 |
4461 |
36.20 |
0.51 |
63.29 |
| SA |
60.10 |
54.30 |
7284 |
19.64 |
0.04 |
80.32 |
| MENA |
160.31 |
310.26 |
70187 |
5.39 |
1.06 |
93.55 |
| EAS |
177.29 |
668.51 |
437650 |
16.06 |
2.34 |
81.60 |
| SAS |
127.26 |
311.25 |
80576 |
10.38 |
2.70 |
86.92 |
| LAC |
81.43 |
150.30 |
61388 |
41.50 |
1.51 |
56.99 |
| CAR |
29.32 |
110.59 |
1922 |
4.75 |
0.44 |
94.81 |
Columns 5-7 in Table 1 show the participation in the total electricity consumption increase of renewable, wind and non-renewable electricity consumption. Globally, 18.65% of the electricity consumption increase was generated by using renewable electricity, while 5.2% was generated by using wind energy. It is worth noting that the highest renewable electricity consumption participations are observed in new European Union members, Latin American and EU15 countries, while the highest participation of wind electricity consumption is observed in the EU15 and new European Union members, with 29% and 24%, respectively. Likewise, the other developed countries region has a notable wind electricity participation in the electricity consumption increase, as 11% of this increase is generated by using wind energy. It can also be highlighted that the participation of wind in the electricity consumption increase in some regions has been very small, such as, for example, in Southern African, economies in transition, Central African and The Caribbean regions. In these regions, this participation is less than 1%. In line with these findings, the European Commission [29] already included the suggestion for a target share of renewable energy in 1997, with Denmark (1979), Portugal (1988), Germany (1989) and the United Kingdom (1989/90) being the first countries to introduce policy supports to promote renewable energy to produce electricity. Thus, prior to 2000, 15 countries in the EU had introduced policy measures to promote electricity from renewables and all of them have had policy support schemes since 2007 [30]. Regarding wind energy, it is worth noting that its growth has also been directly linked to policy supports, at least until recently. In this regard, the implementation of various support mechanisms, such as feed-in-tariffs, tax incentives or tradable green certificates, led to the remarkable growth of wind energy generation over the period in some European countries such as Germany and Spain, and later in others such as the USA, China and India [31].
The different growth rates by world regions makes the changes that took place evident, with regard to the weight of each of the sources used to generate the electricity used, in the period 1990-2014, especially for wind electricity. Firstly, the notable increase in the participation of the East Asian region in world electricity consumption, from 8% to 33%, may be highlighted. Likewise, South Asian and MENA regions also increased their participation significantly.
Secondly, only the East Asian region increased the renewable electricity world participation in a relevant manner, from 7% to 30%. The increases of renewable energy in electricity production in China may be related, according to Lo [32], to several factors, such as energy security (in order to reduce fossil fuel dependence), pollution and the increasing international pressure to control its carbon emissions, the growth of the manufacturing of renewable energy products (which are making China a global leader and exporter of green technologies) and finally, the consideration that renewable energies may be the appropriate way to bring electricity to underdeveloped rural areas.
Thirdly, the participation in wind electricity has changed remarkably. Thus, while in 1990, only three regions used wind electricity significantly (ODC: 80%, EU15: 19% and SAS: 1%), at the end of the studied period, many more regions use this energy. It is worth noting that the EU15 especially increased its participation, reaching 32%, which reflects the notable expansion of wind energy in the region, which, as mentioned before, may be related to wind energy support in the EU countries. Likewise, the East Asian region emerges strongly, representing 23% of total wind electricity used in the world, and other regions have started using wind electricity, although still with small percentages (EU+, MENA and LAC). The Chinese Renewable Energy Law, which came in force in 2006, prompted a large increase in renewable energy, particularly wind and photovoltaic power [33]. These renewable energy increases were made possible by renewable portfolio standards, feed-in tariff, and direct subsidies [32]. Also, it is worth noting that the growing participation of other world regions in worldwide wind energy may be related to their increasing demand for electrical energy, the continuous reduction of wind energy production costs, especially in recent years, which is placing it at competitive levels with respect to fossil fuels [34,35], and the allowance of new wind power plants through auctions involving companies with foreign capital and resulting in low bid prices [36].
Finally, it is also worth noting that only two regions increased their participation in non-renewable electricity consumption use, being the other developed countries and MENA regions which varied from 1% to 6%. These increases reflect that these regions have made less effort in the use of renewable energies to produce electricity. The OECD [37] reports indicate that there are three main barriers that slow investment in renewable energy in MENA countries. Firstly, the lack of profitability of renewable energy projects, which may also be related to the fact that many of these countries have fuel or gas energy resources. Secondly, insufficient cash flow to recover the high investment costs, and thirdly, difficulties in accessing financing. As stated in Kahia et al. [38], the MENA countries have high energy costs, which are related to MENA governments that typically sustain the energy market by subsidizing energy prices, creating barriers for new investors, thereby continuing to favor fossil fuels.
On the other hand, the other developed countries have also increased the non-renewable energies to produce electricity, which may be related not only to the fact that the USA did not commit itself to a reduction of carbon emissions or ratify the Kyoto Protocol [39], but also to the expansion of shale gas in its territory. As stated in Wang et al. [40], since 2000 the main oil and gas companies aggressively entered the shale gas business due to the increasing profitability of natural gas in shale formations production. Thus, lower natural gas prices have not only encouraged substitution away from sources such as coal and nuclear but also from renewable energies [41].
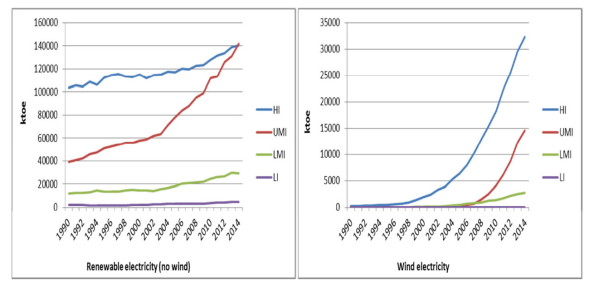
Figure 2 shows the renewable and wind electricity consumption trends by per capita GNI levels. Renewable electricity consumption is only proved a practically stable consumption in lower income countries, also having a very low level. The rest of the regions presented a growing trend. This is especially notable for upper medium income countries, which reached the high income countries level in 2014. Wind electricity consumption showed an exponential rate of growth, as much as in high as in upper medium income countries, although in the latter countries this growth started later, around 2005, also reaching lesser values than the first. Likewise, lower medium income countries also grew, but in this case, the trend is linear. Additionally, its values are much smaller. Finally, lower income countries practically do not have wind electricity. Therefore, wind electricity use is growing especially in the more developed countries, probably due to the high investment costs of the technologies, which implies the need of some kind of state aid or subsides to promote it. It is worth noting that although the wind costs are declining as stated before, the project startup cost of a wind turbine is high [34].
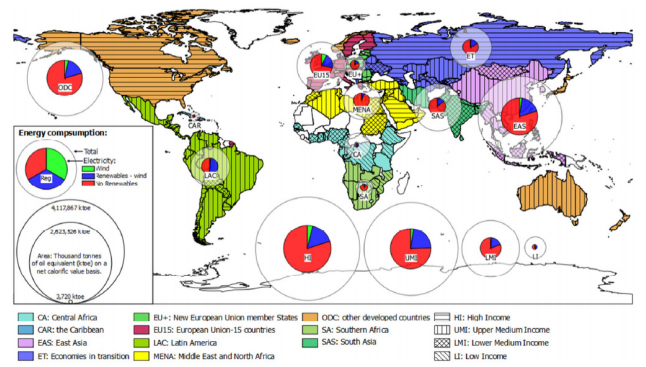
In spite the growing trend in wind energy use over recent years, it is worth noting that it still represents a small percentage of total electricity consumption and therefore of total energy use. These values are represented in Figure 3, which shows the total energy, electricity and wind consumption in 2014 by world regions (colors) and by per capita GNI levels (plots). The area of the outer pie shows the total energy consumption in the region, while the area of the inner pie shows the electricity consumption, the latter being divided into non-renewable, renewable and wind electricity. Thus, by electricity sources, it can be clearly seen that most of the electricity has its origin in non-renewable energies. Only the Latin American and EU15 regions have more than a quarter of their electricity produced by renewable energies. With respect to wind electricity, only three regions (EU15, ODC and EAS) show appreciable electricity percentages, of which the EU15 has the highest. Additionally, Figure 3 shows that the ratio of electricity consumption to total energy decreases with a decrease in GNI. Likewise, wind electricity consumption decrease with a decrease in GNI.
3.2. Total and wind electricity consumption per inhabitants during 1990-2014
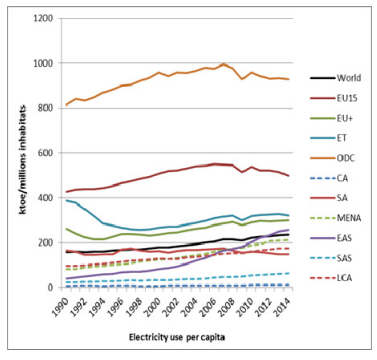
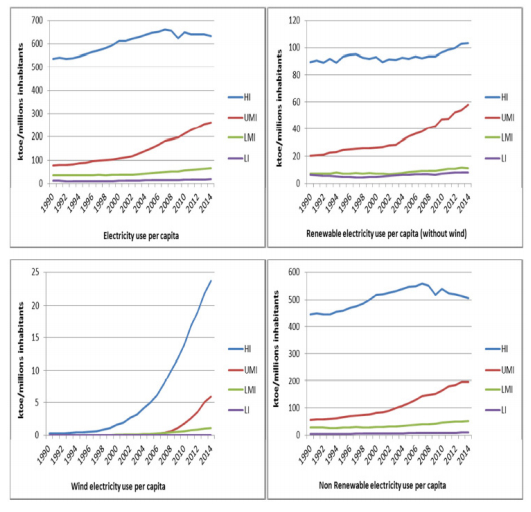
Figure 4 shows the evolution of electricity consumption per inhabitants, by world regions in the period 1990-2014. During the period, the total electricity consumption per inhabitants was around 200 Ktoe/million inhabitants, showing a slightly positive trend. Above the world trend is highlighted the other developed countries region, with a 930 Ktoe/million inhabitants electricity consumption in 2014. During the period, its trend has been positive, although a negative trend since 2005 is observed. Likewise, EU15 also shows values notably higher than the world, with a trend similar to the other developed countries region. The economies in transition and new EU members regions can also be seen to be above the world trend. Both began the period with decreasing electricity consumption, but started growing from 1995 with the world trend. Below world trend, it is worth mentioning the high growth in the East Asian region, which surpassed the world value at the end of the period. Likewise, MENA, Latin American and South Asian regions also show positive trends.
It is again worth noting that urbanization and economic development are strictly linked to the variations in electricity consumption [42]. Urbanization and economic growth may be two of the main causes of the electricity consumption in East Asian countries, while the declining trend observed in other developed countries and the EU region since 2008, may be related to the decrease of economic growth linked to the financial crisis. Nevertheless, in spite of this electricity consumption decrease, it is observed that other developed countries and the EU countries have higher electricity per capita consumption, which is in line with the conclusions of Ferguson et al. [28]. These authors state that, for the global economy as a whole, there is a stronger correlation between electricity use and wealth creation for richer countries, therefore implying that these countries will have higher electricity consumption in per capita terms.
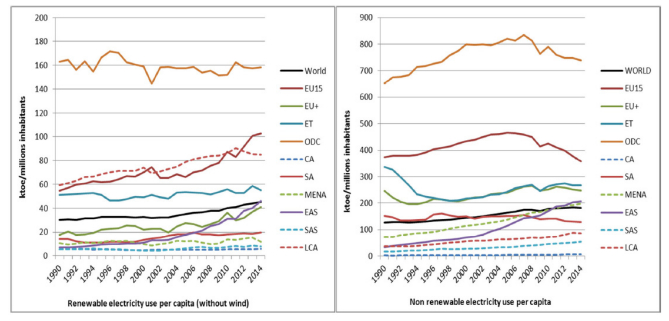
Figure 5 shows the evolution of renewable and non-renewable electricity consumption per inhabitants, by world regions along the studied period. As can be observed, the renewable electricity consumption trend is positive globally, although, it did not start growing until 2002. Once again, below the world trend, the other developed countries region is highlighted, which shows a quite constant trend during the period. Additionally, it may be pointed out the growing trend of EU15 and Latin American regions (below the world trend). Likewise, the East Asian and new EU members regions also have a positive trend. Although their values are smaller than world figures, at the end of the period both regions presented similar values to the world region. Nevertheless, these increasing trends may have different explanations. The increasing trend observed for all EU countries may be explained by the European energy and climate policies aimed at promoting renewable energies. As stated before, the EU has been playing a leading role in setting ambitious targets for renewable energy and establishing appropriate policies and instruments to support it, especially oriented to electricity production. Therefore, the decreasing trend in non-renewable energy consumption is partially due to its substitution by renewable energies. These changes in the electrical energy mix are proved to be the main factor driving down CO2 emissions in the EU countries, at least since 2000 [43]. However, in the East Asian region, the renewable energy increase may be related more to increased electricity demand than to changes in the energy mix. Both graphs in Figure 5 show increasing trends for Asian regions, implying that all fuels have been growing to satisfy the electricity demand. In this regard, it is worth noting that renewable energy, especially solar and wind energy, can be installed in rural regions where it is difficult to bring electricity. Additionally, some renewable plants can be in operation in a few months instead of some years [35]. Finally, the renewable energy growth in the Latin American region is also due to economic growth and urbanization and the rise of the middle class, but is especially linked to hydropower electricity [44]. The study by Al-Mulali et al. [45] indicated that renewable electricity consumption is more significant than non-renewable electricity consumption in promoting economic growth in the Latin American region.
On the other hand, it is worth noting that the regional trends for non-renewable electricity use are quite similar to those for electricity, was showed in Figure 4. Nevertheless, it may be pointed out that the MENA region ended the period with more non-renewable electricity consumption per capita than the world region. The MENA countries are using non-renewable energies to produce electricity in order to satisfy their increasing demand, which are mainly related to urbanization and economic growth. Thus, in spite of having high solar irradiation and strong winds, offering excellent potential for generating electricity from renewable sources, the use of renewable energy for generating electricity still remains low [46].
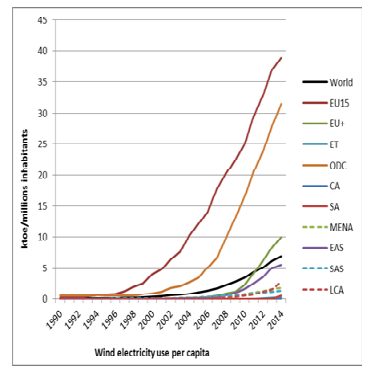
Finally, Figure 6 shows a very different behavior with respect to wind electricity use. At the beginning of the period, hardly any region used wind electricity to produce electricity. However, some of them started producing this energy during the period. The first region, which started increasing wind electricity consumption, was the EU15, around 1995. From this year, the region showed exponential growth. The second region increasing its wind electricity use was other developed countries, at the end of the nineties (also with an exponential growth). Its growth was very similar to that of the EU15, but always with lower values. Later, around 2006, two regions also started increasing their wind electricity production with an exponential growth: the new EU members and East Asian regions. Nevertheless, the first reached higher growth. Additionally, Latin American and South Asian countries have also increased their wind electricity consumption since 2006, but with a linear trend. Finally, the strongest growth in wind energy in the MENA region occurred between 2005 and 2010. Nevertheless, the socio-political events linked to the Arab Spring in some parts of the MENA region have slowed the incipient development of wind energy [46]. Therefore, it is worth noting the leading role of the EU during the studied period. Nevertheless, Figure 6 also shows the rise of the other developed countries and the growth of the wind energy industry in the East Asian region, especially since 2005. In addition, the gradual adoption of wind energy by several countries of the developing world is of special interest, and demonstrates the ability to largely substitute fossil-fueled power generation [31]. Along this line, wind energy has achieved remarkable advances and nowadays most studies show that it is an economically efficient and accessible energy resource for large scale utilization because of the decreasing energy cost [34]. Thus, according to the REN21 [36] report, the weighted average investment cost for onshore wind fell by slightly more than two-thirds between 1983 and 2015. Therefore, this decreasing cost, the growing interest of developing countries in promoting cleaner energy sources and greater energy security to meet the growing demand for energy, are factors that may be behind the growing development of wind energy in the developing regions of the world.
Notable electricity consumption differences are also shown when countries are grouped by per capita GNI levels. Figure 7 shows that the highest electricity per capita consumption is conducted, with an outstanding difference, by high income countries. Likewise, it is observed that the electricity consumption in per capita terms is lower as income decreases. Therefore, as observed by Kim [47], groups with relatively high per capita income tend to exhibit high electricity consumption. In addition, the lack of overall convergence in per capita income is observed to be an important source of per capita electricity consumption divergence.
Figure 7 also shows that the high income group electricity consumption trend is positive until 2006 and then slightly decreasing. These countries also show a similar trend for non-renewable electricity consumption, being constant until 2008 and positive since then for renewable one. The total electricity consumption decreasing trend may be explained not only by GDP decline, but also by energy efficiency gains. It is worth noting that the electricity consumption decrease is linked to non-renewable energies, as renewable energies are still having a positive trend, even after 2006. Figure 7 shows that upper middle-income countries have a positive trend for non-renewable and renewable electricity consumption per capita. In this regard, Apergis and Payne [26] found that the factor that affects electricity consumption in these countries is mainly urbanization. It is also relevant to note that the lowest income countries have low electricity consumption in per capita terms, without growth. In these countries, as stated by Apergis and Payne [26], the variations in electricity consumption may have an impact on both GDP and urbanization levels, with the electricity shortages which make these countries very vulnerable being one of the most relevant problems observed.
Finally, it is worth noting the special growth of wind electricity consumption presented by the groups. Once again, the high income countries stand out in the graph, but this time with a clear exponential trend. Later, around 2006, the upper middle income countries also started growing with an exponential trend. The lower middle income countries also started growing from 2006, but with a linear trend. Finally, no growth is observed for the lowest income countries.
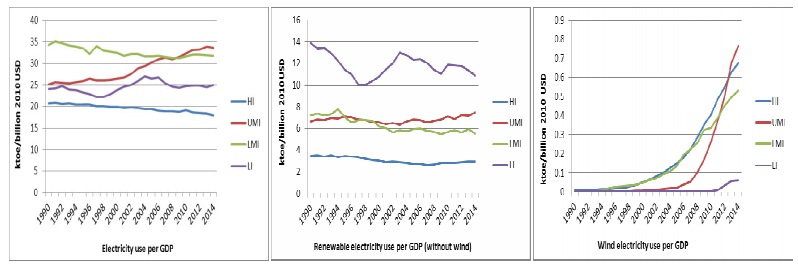
3.3. Total and wind electricity consumption per GDP during 1990-2014
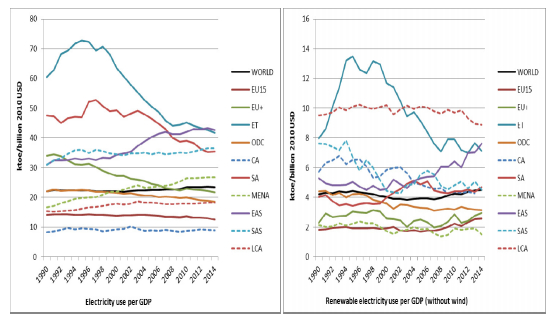
Figure 8 shows the evolution of electricity and renewable electricity consumption in terms of GDP, by world regions in the period 1990-2014. The world trend is quite constant for the electricity and renewable energy consumption per GDP. Nevertheless, those regions with higher electricity consumption per GDP (ET and SA) had notable decreasing trends since 1995. In this regard, Brizga et al. [48] find a significant correlation between the reindustrialization process and the energy intensity decrease in the economies in transition. Likewise, the industrial efficiency gains may be related to the South African countries, as in the first stage of development the industrial improvement may not be compensated by household energy demand growth [49]. On the other hand, the East Asian region presents a positive trend, its values being the highest at the end of the period. The rapid industrialization of this region, especially in energy intensive industries, and the rapid household electricity demand growth, due to notable urbanization and changes in lifestyle, may be the cause of the growing trend. Finally, it is also worth noting the decreasing trend for the developing countries group. The electricity intensity decrease may be related not only to energy efficiency policies, but also to an economy dematerialization and to industry displacement to developing countries [49,50].
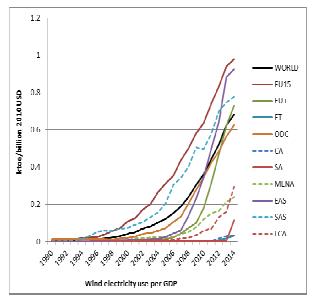
In terms of renewable energies, transition and East Asian countries show a similar trend, which may be explained in the same way. However, South African countries show a quite constant trend during the whole period, which implies no main changes in the energy mix. More remarkable is the trend for wind electricity showed in Figure 9. An exponential growth is observed in almost all regions. Above the world trend, are highlighted the EU15 and the Asian countries groups, with the East Asian group showing later, but more intense, growth. In this regard, it is worth noting the rapid incorporation of wind energy into the economy.
Finally, Figure 10 shows that electricity and renewable electricity consumption per GDP tend to be decreasing in all regions when considering the economies of the groups by per capita GNI, except for upper medium income region which presents a remarkable increasing trend for electricity and a slightly increasing trend for renewable electricity, which may be related to the increasing electricity consumption by households. Again, it is worth noting the exponential growth of wind energy. The upper medium income region shows a later and more intense growth, while the lower income countries only start to grow slightly at the end of the period. Additionally, it is worth noting that while renewable energy with respect to GDP is lower for high income countries, the wind energy is almost higher for them through the whole period, which may be related to the high biomass use in developing countries. Therefore, it may be highlighted that over recent years, renewable energy has become more and more dominated by wind and solar [35].
3.4. Electricity and wind consumption ratios during 1990-2014
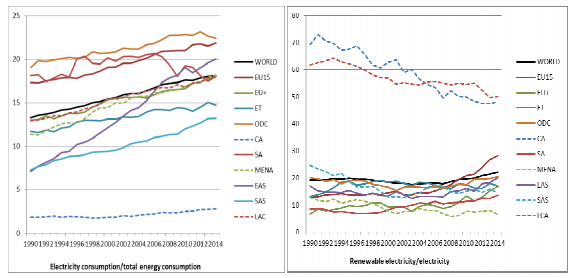
Figure 11 shows the ratio of electricity to total energy consumption and total renewable electricity to total electricity consumption by the world. World electricity consumption represents around 18% of total energy consumption at the end of the period. During the period, the world trend of the electricity to total energy consumption ratio has been positive. All regions show a positive trend, except Southern African countries which shows a decreasing trend from 2008. It is worth noting the high growth of this ratio, in the case of the East Asian region, whose rate grew from 5% to 20%. It is also worth noting that the EU15 and other developed countries regions show the highest rate value (around 23%), while the Central African shows 3%.
The ratio of renewable electricity to total electricity consumption grew slightly in the world from 2002, being around 23% in 2014. Most regions also showed a similar growth trend from 2002, although three regions showed negative trends. On the one hand, Latin American and Central African regions showed a notable negative growth, but still had very high ratio values at the end of the period, of around 50%. On the other hand, the MENA countries presented a softer negative trend but with only an 8% ratio value at the end the period, being the lowest. In addition, it is worth noting that the Southern African region had a more pronounced positive trend.
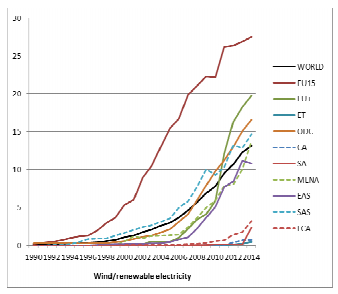
Figure 12 shows the ratio of wind electricity to renewable electricity consumption. An exponential growth is shown in the world, starting from almost 0% to 13%. The EU15 is the region with the highest growth, ending the period with 28%. A remarkable growth is also observed in the new European countries region, especially from 2010 to 2012. Asian, MENA and other developed countries had similar trends, although East Asian and other developed countries started growing earlier. At the end of the period, their ratio ranged from between 12% to 16%. The other regions only showed a slight growth in the latter years.
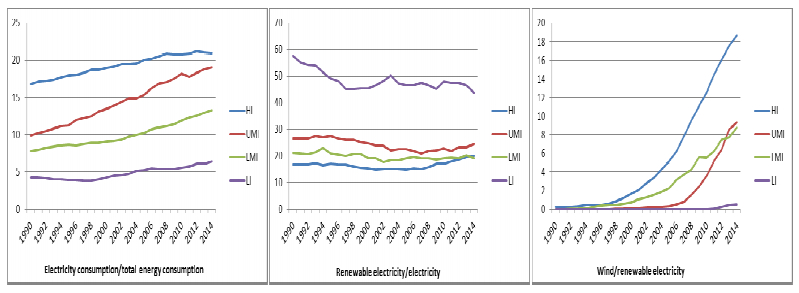
Figure 13 shows notable differences in these ratios when considering the world regions by per capita GNI level. Electricity consumption with respect to total energy is around 21%, 19%, 14% and 6% in high, upper medium, lower medium and lower income countries, respectively, in 2014, increasing in all cases during the period. The renewable electricity with respect to electricity ratio is quite constant in lower medium income countries, slightly increasing in high income countries from 2005 and slightly decreasing in upper medium income countries, but all of them ended the period with a ratio ranging from 20% to 22%. Lower income countries presented a higher ratio in 2014 (45%). Finally, wind electricity to renewable electricity consumption had an exponential growth in high and upper medium income countries, the second starting to grow around 2005. Lower medium income countries show a constant linear growth and lower income countries have only a very slight growth from 2012. In 2014, the ratio values are equal to 19% in high income countries, 9% in upper medium and lower medium income countries and less than 1% in lower income ones. It is worth noting that the lower percentage of wind with respect to other renewable energies in non-high-income countries, at the end of the period, is due to the relevance of biomass and hydropower. Nevertheless, once again it is observed that wind energy, along with solar, is becoming one of the most important renewable energy sources to generate electricity [35].
4. Wind Electricity Trends Explaining Factors
Economic growth is one of the main causes of increased energy use and especially of electricity consumption increases over recent times, as has been noted in several previous papers, such as in Apergis and Payne [26]. Nevertheless, urbanization, changes in lifestyles and improvements in electricity access are also relevant factors, especially for developing countries. Thus, the economic growth and these other factors have been increasing the electricity consumption worldwide, being particularly relevant in those regions in which these changes have happened in a more intensive way. The increasing electricity demand has provoked the growth of electricity production, both from non-renewable and renewable energies.
Nevertheless, these changes have also been accompanied by a growing interest in climate change and environmental issues, which has led governments to have more interest in the use of renewable energy as a source of energy generation in general, and electricity in particular. At first, attention was focused on the most developed countries, as they were considered the main causes of pollution and climate change. Thus, the Kyoto Protocol [51] set binding emission reduction targets only for 37 industrialized countries and the European community over the five-year period, 2008 to 2012, which led those countries to promote renewable energies and energy efficiency even before the Kyoto protocol entered into force. Hence, during the period 2005-2012, Europe recorded the highest share in total new global investments in renewable energies, with wind, solar and biomass industries being especially supported [52]. Developing countries, including China, India, Brazil and South Africa, did not have to reduce their emissions, but were encouraged to also adopt policies to promote renewable energies. Thus, for example, China approved the Chinese Renewable Energy Law in 2006, mainly boosting wind and photovoltaic energy [33]. Over time, the role of the developing countries in the fight against climate change and in the promotion of renewable energies has been increasing, which can be highlighted with the signing of the Paris agreement at COP21. Thus, many countries worldwide have begun to develop energy plans to combat climate change, which has given a significant boost to the growth of renewable energy, especially solar and wind [35].
However, the exponential growth of wind energy cannot be explained solely by increasing concern about climate change worldwide. Firstly, it is worth noting that wind energy has grown notably in those countries with high or increasing electricity consumption and without their own fuel or gas resources. Security motivations and energy independence gains have also motivated the renewable energy investments. Thus, energy security is especially relevant for those countries where growing dependence on imported gas is a significant energy security issue. In this regard, renewable energy can provide alternative sources of electric power [53]. It may also be an appropriate way to bring electricity to rural areas which have difficulty integrating into the distribution network [32]. Nevertheless, it is worth noting that some renewable energy technologies, such as wind, depend on different natural cycles, and are therefore subject to variability on differing timescales. Thus, it is important to have alternative electricity plants, and to encourage inter-connections between grids and across national borders to balance supply and demand. Some interconnectors have been built, such as Skagerrak 4, which helps to balance Denmark's wind and thermal power and Norway's hydropower. Likewise, innovative hybrid systems linking hydropower and renewable plants have also emerged [54]. Moreover, stationary battery storage continues to advance, and costs are decreasing, although most of the capacity has been installed in the developed world. However some storage projects are also being undertaken in developing countries, particularly in conjunction with mini-grids [36].
Additionally, wind deployment was also driven by wind power's cost-competitiveness. The continuously decreasing cost has determined that wind energy is becoming the least-cost option for new power generating capacity in an increasing number of markets [36]. However, as stated by Kumar et al. [34], wind energy systems have very high start-up costs, needing a large scale investment. Therefore, support measures have been adopted by governments to promote wind energy, usually being performed by the combination of several measures such as Feed-in-Tariff (FIT), Fit-in-Premiums (FIP), tenders, quota obligations or contracts for difference. FIT systems are the most used worldwide because of their better dynamic efficiency, low transaction cost, diversity, and high investing securities. Nevertheless, it may not be able to respond quickly to falls in production costs, generating overcompensation and excessive demand for new installations [55]. Therefore, authors such as Hiroux and Saguan [56] consider that wind energy producers should be exposed to market signals, FIP therefore being a more appropriate choice. Alternatively, auctions are emerging as a popular alternative because of their potential to achieve deployment in a cost-efficient and regulated manner, nevertheless they have to be adequately defined [57]. Also, the degree of effectiveness of these policies may vary among countries and regions, even though establishing a stable legal framework can be considered the best way to promote investments in renewable energies. Issues related to the political and economic framework are the most relevant barriers for wind energy diffusion [58].
Finally, it is worth noting that support measures may be difficult to implement in the poorest countries due to their low budgets. International aid is needed in order to establish adequate promotion. Alternatively, these countries may also consider the opportunity to promote foreign investments to enhance renewable energy projects, which could improve the electricity supply in their country, boosting their economic development
5. Conclusions and Policy Implications
Wind energy is crucial to achieve CO2 emission reductions related to electricity production as it is believed to have the least adverse environmental impact and is one of the renewable energies that has become economically affordable long before several others. Nevertheless, although wind power has begun to grow, especially from 2005, it still represents a small share of electricity consumption.
At regional level, remarkable differences are observed between the world regions. Therefore, diverse global energy policy should be applied. All regions, except Southern African, have electricity growth rates higher than that of total energy in the analyzed period, the regions with the highest growth rates being in Asian and MENA regions. The electricity growth was mostly produced by non-renewable energies, with 18.65% generated by using RE and 5.2% by using wind energy, with the highest renewable electricity consumption participation being observed in new European Union members, Latin American and EU15 countries, and the highest participation of wind electricity in EU15, new European Union members, and the other developed countries. Very little wind electricity was used in Southern African, economies in transition, Central African and The Caribbean regions. In these regions, this participation is less than 1%. Therefore, all regions should make greater effort if they want to increase renewable energies in order to reduce emissions, especially those with the highest electricity consumption and not much renewable use, for example, the South Asian and MENA regions. It is convenient to make efforts to change the electricity mix by discouraging fossil fuel use and promoting renewable and also wind energy use. The EU regions are the only ones with a notable use of renewable energies, and wind, which may be related to their current energy policy, nevertheless, it is also desirable to take a closer look at their energy policies.
The different evolution in the electricity consumption and in the main generation sources between 1990 and 2014 have changed their distribution in the world. In electricity consumption, it is worth noting the notable participation increase in East Asian region, and to a lesser value, in South Asian and MENA countries. However, renewable electricity consumption also increased in East Asian countries, but not in the other regions, which means they need to make special efforts to promote their renewable energies for electricity generation. On the other hand, the participation in wind electricity has changed remarkably while, as in 1990, only three regions used wind electricity (ODC, EU15 and SAS), in 2014, East Asian, new EU members, MENA and Latin American countries also used it. Likewise, it is worth noting that a notable expansion of wind electricity use is observed in EU15 and also in East Asia (23% of total wind electricity). Therefore, countries should focus on the behavior of these regions if they want to impulse their wind power usage.
In per capita terms, the renewable electricity consumption trend is positive in the world, starting from 2002. EU15, Latin American, East Asian and new EU members countries have positive trends, while MENA countries end the period with more non-renewable electricity use per capita than the world region. Referring to wind electricity, at the beginning of the period, hardly any region used wind electricity to produce electricity. The first regions which started increasing it were EU15 and other developed countries which showed exponential growth. Later, around 2006, new EU members and East Asian region also started to grow exponentially. Finally, Latina American and South Asian countries have also increased their wind electricity consumption from 2006, but with a linear trend. By per capita GNI levels, high income countries stand out in the use of wind electricity, with a clear exponential trend. Later, upper medium income countries also started growing, also with an exponential trend, while lower medium income countries had a linear trend. Finally, no growth is observed for lower income countries. More effort is especially needed in lower medium and lower income countries. Nevertheless, as the exponential growth observed in more developed countries has been promoted with important support measures, international aid will be required in the less developed countries in order to increase renewable and wind electricity to produce electricity.
In GDP terms, the world trend is quite constant for electricity and renewable electricity consumption per GDP. Nevertheless, those regions with higher electricity consumption per GDP (ET and SA) have had notable decreasing trends since 1995, while East Asian region presents a positive trend, its values being the highest at the end of the period. The trend for wind electricity is exponential in almost all regions, highlighting EU15 and Asian regions. By per capita GNI groups, electricity and RE per GDP tend to be decreasing in all regions except for the upper medium income countries which present a remarkable increasing trend for electricity and a slightly increasing trend for renewable electricity use.
Acknowledgments
The first author acknowledges the funding received from the Project SEJ 132 project by the Andalusian Regional Government, the funding received from the Project ECO2014-56399-R by Spain's Ministry of Economy and Competitiveness, from the "Cátedra de Economía de la Energía y del Medio Ambiente" (Department for Energy Economics and the Environment) at the University of Seville (Reference: 1394/0103) and the "Fundación Roger Torné", and the funding received from the Project FONDECYT Regular 1150025 of Chile's Ministry of Education. The standard disclaimer applies.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: