1. Introduction
Atmospheric particulate matter (PM) has several adverse effects on human health [1,2]. PM is considered one of the main air pollutants in urban areas as it reflects a complex mixture of anthropogenic emission sources and atmospheric processes [3,4]. Moreover, the habitants of the densely populated urban areas are often living in the vicinity of these sources, increasing the exposure to PM. Submicron particulate matter (PM1: particles with an aerodynamic diameter less than 1 micrometer), in contrast to larger particle fractions, is able to penetrate into the lung alveoli and pass the lung-blood membrane, being transferrable to organs [5]. Moreover, this submicron PM contains a significant and variable fraction of organic material, ranging from 20% to 90% of the mass [4,6]. The presence of organic pollutants in atmospheric PM depends on the physico-chemical properties of organic compounds and environmental conditions [7,8].
Among other contaminants, special attention has lately been devoted to organophosphorus flame retardants (OPFR) because they are used in large quantities globally and are considered neurotoxic, cause haemolysis and chlorinated OPFR are carcinogenic [9,10]. These chemicals are currently widely employed as flame retardants and plasticizers in many industrial applications and household products [11] and have been detected in waters and sediments [12]. OPFR have low to high solubility in water (0.0003 to 6.5 g/L) and their medium to high log Kow (between 1.9 to 9.5) and medium to low vapor pressures (Pvap; between 0.02 and 3.5 × 10–8 mmHg) (Table 1) makes that the majority of these compounds are semi-volatile with a tendency to bind to particulate matter [7]. Recently it has been reported the human risks when associated to dust [13] or atmospheric PM [14]. They have also been detected in office air particulate matter [17,19] and in indoor dust of different environments [20] at levels of pg to ng per cubic meter. In outdoor air, OPFR have been detected in PM in the Great Lakes region of North America [7], the Mediterranean and Black Sea [15], polar areas [16] and with specifically high levels in urban areas [14,17]. The association of OPFR to ambient air PM and the relatively high concentrations compared to other flame retardants, such as brominated FR, indicates that OPFR are intrinsic to long-range atmospheric transport [21].
Table 1. Studied compounds and physico-chemical properties (order based on vapor pressure Pvap).
| Compound |
Log Kow |
Pvap (mmHg). 25 ℃ (MGM)* |
Water solubility (mg/L). 25 ℃ |
H (atm m–3 mol–1) |
t1/2 (25 ℃. 1.5e6 OH/cm3) |
| TPrP |
1.87 [23] |
0.0231 |
6450 [24] |
6.80e-7 |
1.721 h |
| TBP |
4.00 [23) |
0.00349 |
280 [25] |
1.5e-7 |
1.628 h |
| TCPP |
2.89 (calc) |
5.26e-5 |
740 (calc) |
7.834e-7 (calc) |
5.451 h |
| EHDPP |
5.73 [23] |
3.34e-5 |
1.9 [25] |
1.58e-5 |
3.221 h |
| TBEP |
3.75 [24] |
1.23e-6 |
1100 [24] |
3.285e-7 (calc) |
0.997 h |
| TEHP |
9.49 (calc) |
6.07e-7 |
0.6 [26] |
7.86e-8 |
1.312 h |
| TPhP |
4.59 [23] |
4.72e-7 |
1.9 [25] |
3.31e-6 |
11.838 h |
| TCP |
6.34 (calc) |
3.49e-8 |
0.3 |
9.208e-7 |
9.369 h |
a.
*MGM (Modified Grain Method)
b. (calc): EPI Suite Software |
This study focusses on PM1, which can represent a major route in human's exposure to OPFR. Thus, the aim of this study was to develop an analytical methodology to determine the occurrence of OPFRs in outdoor atmospheric PM1. In order to gain insight on the levels of OPFRs in urban areas, PM1 samples were collected at a 24-hour time resolution in spring 2014 at an urban background site in Barcelona. Here, the outcome of these analyses is presented and the results of ambient air OPFRs are discussed in terms of meteorological changes and PM loadings.
2. Materials and methods
2.1. Chemicals and reagents
Eight OPFRs were studied for their occurrence in PM1 loaded filters. Table 1 shows the compounds that were studied here and ordered by their vapor pressure. These compounds were tripropylphosphate (TPrP), tributylphosphate (TBP), tris(1-chloro-2-propyl) phosphate (TCPP), triphenylphosphate (TPhP), and 2-ethylhexyl diphenylphosphate (EHDPP) (Sigma Aldrich (Germany)), and Tris(2-butoxyethyl) phosphate (TBEP), tris(2-ethylhexyl) phosphate (TEHP) and tricresylphosphate (TCP) (Dr. Ehrenstorfer (Augsburg, Germany)). Labeled TBP-d27 was purchased from Cambridge Isotope Laboratories (Andover, USA) and TPhP-d15 (Sigma Aldrich) were used as surrogate standards in the OPFR analysis in filter samples. PCB-65 and PCB-209 were acquired from Dr. Ehrenstorfer and were used as internal standards to correct for instrumental instability. GC grade solvents acetone, hexane, methanol, dichloromethane, ethyl acetate and toluene were acquired from Merck (Darmstadt, Germany).
2.2. Sampling
Sampling of PM1 was performed with a high volume air sampler (DIGITEL DHA-80) for 24 hour collecting 1200 m3 on quartz filters (Pall). The sampler was equipped with a head that pre-separated the PM1 particles from larger aerodynamic particle sizes. This method is technically equivalent to PM2.5, or PM10 sampling. Before sampling, filters were baked at 450 ℃ in order to remove any organic compounds or interferences, and stored in aluminum foil to keep them away from potential sources of contamination like dust. The sampling was performed at an urban background site (41°23.232'N; 2°6.943'E) in Barcelona. This site forms part of the Air Quality network of the local government, which is operated in collaboration with the Institute of Environmental Assessment and Water Research (IDAEA-CSIC). During the sampling period between 18th and 25th of March 2014, meteorological parameters, such as temperature, relative humidity, wind speed, atmospheric pressure, and precipitation were registered, as well as air quality data on PM1 and black carbon (BC) concentrations using optical methods. Within the sampling week the weather conditions shifted from stagnant atmospheric conditions to unstable conditions, allowing study of the influence of these scenarios on the fate and distribution of OPFRs in the urban atmosphere particulate matter. During the whole campaign one filter was placed inside the high volume sampler to act as field blank and to evaluate possible contributions of OPFRs from the sampling device.
2.3. Extraction and analysis
After sampling the filters were spiked with 25 ng of each surrogate standard and then were Soxhlet extracted during 6 h in a 70 mL solvent mixture of ethyl acetate/cyclohexane (5:2, v/v). Extracts were transferred into conical balloons and they were evaporated in a rotary evaporator at 33 ℃ to a volume of 0.5 mL. The clean-up was made on Florisil SPE cartridges from Waters (Sep-Pak Vac 20 cc, 5 g). Conditioning was made with 10 mL of ethyl acetate/cyclohexane 5:2 (v/v), and then the extract was eluted with 20 mL (2 × 10 mL) of ethyl acetate/cyclohexane 5:2 (v/v). Then, the collected fraction was rotovaporated until almost dryness and transferred into amber chromatography vials with a 300 µL insert and extracts were evaporated under N2 flow and reconstituted in toluene to a final volume of 250 µL. At this step, 25 ng of each internal standard (IS) PCB-65 and PCB-209 were added.
GC-EI-MS/MS analysis was performed in a GC Agilent 7890A equipped with a 7000A GC-MS triple quadrupole equipped with a DB-5MS 15 m column. The oven temperature ramp was set at 60–220 ℃ at 10 ℃/min and to 315 ℃ at 15 ℃/min (8 min), using helium as carrier gas with a flow of 1.5 mL/min. Injection volume was 2 µL in splitless mode. Acquisition was performed in Multiple Reaction Monitoring according to the method of Cristale et al.
[20]. Internal standard quantification was used. A calibration curve with 9 levels ranging from 0.001 to 1 ng/ µL was prepared.
2.4. Quality control analysis
For quality control analysis, different procedural steps were performed in triplicate in order to study the influence blank contribution of these steps on the OPFR concentrations. Table 2 describes the analysis of different components of the laboratory procedure and the text below describes these entries: Laboratory blanks consisted in the analysis of OPFR in the (1) solvents used for extraction, (2) rotary evaporation (RotoVap), (3) Soxhlet extraction, and (4) Absorbent (Florisil SPE) used for clean-up. For each step 70 mL of solvent mixture of ethyl acetate/cyclohexane (5:2 v/v) was used, while 20 mL was used to determine the blank contributions of 'absorbent'. All volumes were concentrated by rotary evaporation to 0.5 mL, except (1)
'Solvents' that was concentrated under a nitrogen gas stream. Then, the volumes were further concentrated to almost dryness and dissolved in 250 µL toluene containing the internal standards. The (5) 'method' consists of the all aforementioned steps, without extracting a filter. The (6) 'Filter' includes a blank filter that was exposed for one day in the sampling devices, while the (7) 'Field Blank' consists of the filter that was exposed in the sampling device for eight days. Method detection limits (MDL) were calculated as the mean concentrations of the blank levels plus three times the standard deviation of methodological blanks (n = 3). All blank levels were divided by the sampling volume of 1200 m3, and contribution percentages were relative to the MDL values.
Table 2. Blank concentrations in pg/m3 (24-h sample volumes of 1200 m3). Method detection limit (MDL in pg/m3 calculated as the mean plus 3 times the standard deviation of the laboratory blanks), and recoveries % of spiked filters with 20 ng and 200 ng.
| Compound |
1)Solvent |
2)RotoVap |
3)Soxhlet |
4)Absorbent |
5)Method |
6)Filter |
7)Field Filter |
MDL |
Recovery% |
|
|
|
|
|
|
|
|
|
20 ng |
200 ng |
| TBP-d27 |
|
|
|
|
|
|
|
|
100 ± 2 |
106 ± 1 |
| TPhP-d15 |
|
|
|
|
|
|
|
|
102 ± 1 |
93 ± 2 |
| TPrP |
2.4 |
3.3 ± 0.3 |
4.3 ± 1.9 |
0.4 ± 0.1 |
2.6 |
12.1 |
22.7 |
42.8 |
114 ± 4 |
98 ± 2 |
| TBP |
2.0 |
2.2 ± 0.2 |
2.9 ± 1.2 |
0.3 ± 0.1 |
1.3 |
8.6 |
25.5 |
48.5 |
92 ± 3 |
99 ± 5 |
| TCPP |
4.2 |
3.6 ± 0.5 |
3.4 ± 1.3 |
5.8 ± 2.4 |
7.7 |
48.1 |
124.0 |
240.3 |
93 ± 9 |
104 ± 7 |
| EHDPP |
3.0 |
6.7 ± 0.7 |
5.8 ± 0.5 |
0.2 ± 0.02 |
5.0 |
27.3 |
50.0 |
97.0 |
265 ± 26* |
185 ± 32* |
| TBEP |
< 1 |
< 1 |
< 1 |
2.2 ± 0.4 |
5.8 |
7.7 |
11.2 |
23.5 |
69 ± 6 |
13 ± 1 |
| TEHP |
0.07 |
0.09 ± 0.01 |
0.11 ± 0.03 |
< 0.05 |
0.1 |
1.3 |
0.6 |
2.5 |
113 ± 11 |
127 ± 17 |
| TPhP |
0.4 |
0.8 ± 0.1 |
0.8 ± 0.1 |
< 0.3 |
0.6 |
4.3 |
4.6 |
10.1 |
109 ± 4 |
96 ± 6 |
| TCP |
< 1 |
< 1 |
< 1 |
< 1 |
< 1 |
< 1 |
< 1 |
1 |
119 ± 6 |
158 ± 4 |
| * EHDPP has high recoveries due possibly to external contribution and this compound was not quantified in samples. |
Moreover, pre-cleaned filters were spiked in triplicates with 20 and 200 ng OPFR mixtures and were used to determine method efficiency.
3. Results and discussion
3.1. Method performance
One of the main challenges in the trace analysis of OPFR is the control of low blank values, due to possible presence of these compounds in laboratory material, indoor ambient air, and sampling device. Therefore, emphasis was given to the determination of the OPFR contribution during the analytical process. Table 2 shows the blank concentrations of the detected compounds in the different steps of the analytical procedure. All compounds, except TCP, were detected in one or more analytical steps. The blank levels were relatively low in the different analytical steps representing the chemical procedure in the laboratory, with contribution percentages compared to the 'Filter' (one day in sampling device) between 41 and 22%. The solvent mixture contributed to most of the blank values, especially in the case of TPrP and TBP, with levels of 2.4 and 2.0 pg/m3 (normalized to 24 hour HiVol-sample of 1200 m3), which can be related to their higher vapor pressure compared to the other compounds and rapid absorption into solvents. Considering the 'solvent' blank contributions, the additional contributions of the RotoVap and Soxhlet apparatus was < 13% for all compounds. The adsorbent showed contribution between 0.6 and 28%, with the highest contribution observed for TCPP (5.8 pg/m3). In fact, TCPP also showed the highest blank values in the blank filter that was left for one day in the sampling device (48 pg/m3), followed by TPrP (12 pg/m3), which is related to their general higher ambient concentrations in comparison to other compounds. Nevertheless, the highest blank contributions were observed in the ‘Field Filter’, with levels up to 124 pg/m3. It is interesting to note that the blank levels increase for all compounds when the blank filter was left inside the high volume sampler during the eight days. Although the sampling device allows the accumulation of serial sample filters in the device, the blank results show that the device is an important contributor to the blanks. In order to reduce the contribution of the device on the field blank (and sample filters) it is best to collect each filter sample right after sampling. This procedure was followed in the present study. For the determination of the concentrations in PM1 subtraction of the blank concentrations was applied. The methodology detection limit (MDL) is based on the triplicate blank levels in the complete procedure, including filter, solvents, and analytical steps. MDL are indicated in Table 2 and are below 340 pg/m3, indicating the suitability of the method for the trace analysis of OPFR in PM1.
Regarding extraction efficiency, TPrP, TBP, TCPP, TEHP, TPhP and TCP (Table 2) were efficiently recovered and triplicate analysis had a low variation. TBEP was weakly recovered in the analysis, which could be related to degradation of this compound during the analytical procedure, due to its short atmospheric lifetime (Table 1) in comparison to the other compounds. Another explanation could be the poor elution of the compound in the clean-up step with silica gel. On the other hand, EHDPP presented higher recoveries (>200%), which could be caused by its relatively high blank contribution in the procedure. Nevertheless, TCPP showed also relatively high blank levels, showed good recoveries, so there should be other reasons for the high recoveries of EHDPP in these tests. Acceptable recoveries were obtained in previous analysis using dust sample [12]. Due to the high recoveries in the present study, quantified levels of EHDP in the samples will not be taken into account for further discussion. Finally, extraction efficiency was also evaluated by determining the recovery of the surrogate standards. Both TBP-d27 and TPhP-d15 presented good recoveries in 20 ng and 200 ng levels (Table 2). These findings indicate that the developed analytical method is suitable for the determination of OPFRs in low PM loadings.
3.2. Application of analytical method for OPFRs in urban outdoor PM1
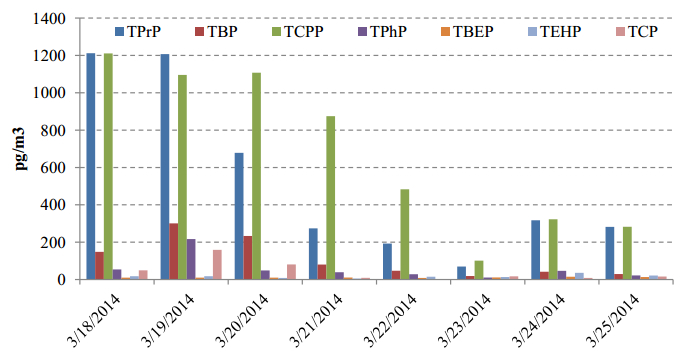
After each 24-h sampling the filters were collected immediately and analyzed. The concentrations of the eight OPFRs could be determined in outdoor PM1 in an urban background site, using the current sampling and analytical method (Figure 1). The concentrations of all studied compounds were above the MDL, except for TBEP, and the sample collected on 23 March. TBEP showed generally concentrations below the MDL (24 pg/m3) and was not detectable in the PM1 samples with the current method. The highest concentrations in all samples were observed for TPrP (range 70 to 1200 pg/m3) and TCPP (range MDL to 1200 pg/m3), followed by TBP (range MDL to 300 pg/m3), TPhP (range MDL to 200 pg/m3), TCP (range MDL to 160 pg/m3), and TEHP (range 5 to 40 pg/m3).
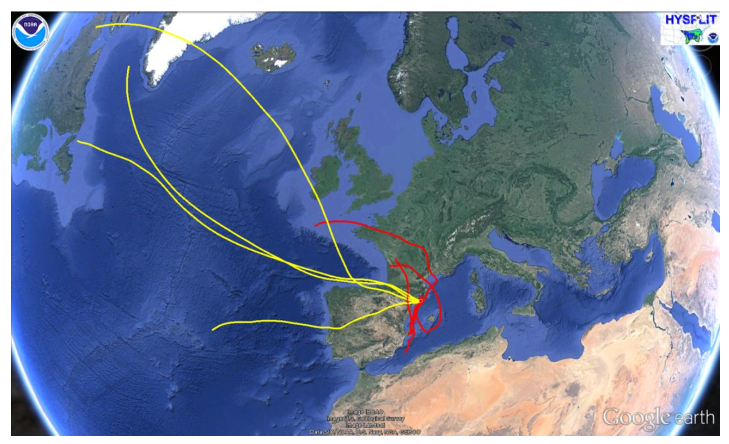
The relative composition of OPFRs in this study is rather constant among the sampled week, despite the large concentration variations of the individual compounds among the sampling days (Figure 1). Overall, the highest daily concentrations were observed in the first half of the sampling campaign (18th to 21st of March 2014) in comparison to the second half (22nd to 25th of March 2014). The first period was characterized by stagnant weather conditions with relatively high PM1 loadings (PM1 = 21 ± 3 µg/m3) and air mass trajectories from the European continent and Mediterranean Sea (Figure 2). On the other hand, the FR concentrations decreased in the weekend (22nd and 23rd of March), which coincides with a depression causing some precipitation and was also related to air masses that came from the Atlantic Ocean (Figure 2). During this second period (22nd to 25th of March), the FR concentrations were 3 to 7 times lower than under stagnant conditions, coinciding with 5 times lower PM1 loadings (PM1 = 4 ± 1 µg/m3). The OPFR concentrations in PM1 observed in the present study are similarly high as those observed in outdoor air PM in urban areas in Germany [17], USA [7], and China [14]. In these studies, TCPP was also the predominant compound, although TPrP levels were lower. In these former studies PM2.5 or larger atmospheric particles were sampled, and it is unclear whether the influence of particle size affects the abundance and composition of OPFR in atmospheric particles. On the other hand, dust samples from indoor and outdoor urban environments showed that the finest particles in that study (~7 to 12 µm) represented a dominant fraction for OPFRs together with much larger particles (>70 µm) [13]. The higher concentration of OPFR in the later was probably related to abrasion and weathering of OPFR containing materials, while the former was probably originated from gas-particle transfer after volatilization of OPFR from material which is highly controlled by the organic content of the particles [13]. The finer fraction is more relevant for the ambient air PM and atmospheric transport. PM1 has a high organic matter content and large surface area compared to larger particles in the studied urban area [4]. The relatively high concentrations of OPFRs in the submicron particles in the present study suggest that the submicron fraction plays an important role in the atmospheric fate of OPFR, and consequently exposure of these compounds to humans. It is also interesting to note that the relatively high concentrations in the air masses related to the Mediterranean Sea (first period) are comparable to those observed by Castro et al. [15] in PM samples collected off-shore in the Mediterranean Sea, suggesting that the occurrence of the OPFRs in ambient air could be regional and not necessarily related to local sources in the urban area of Barcelona. In fact, analysis of atmospheric PM on OPFR in the Pacific Ocean shows also considerably high levels [16], indicating a ubiquitous presence of these compounds in the atmosphere.
In order to observe any relation with locally measured air quality parameter, the concentrations of the most abundant individual OPFRs (i.e. TPrP, TBP, and TCPP) were compared with the mass concentrations of PM1 and black carbon (BC) (Table 3). In all cases these compounds showed significant positive correlations (p < 0.05) with BC and with PM1, except for TPrP (p = 0.07). In the studied urban area, PM1 and BC correlate well between each other, due to the high traffic density [4]. However, the findings in the present study does not necessarily relate the presence of OPFRs to traffic emissions or other local anthropogenic sources, but also to the presence of stagnant atmospheric conditions that favor the recirculation of regional air masses and the accumulation of aerosols as well as related organic pollutants as seen in other studies [8,22]. The relative composition of OPFRs in PM1 is very similar among all samples, despite changes in air mass origin and meteorological conditions, and despite the wide range of physico-chemical properties of the studies OPFRs. This is the case of TPrP, which is relatively more volatile as well as more soluble in water, compared to the other OPFRs. These differences could play a role in the fact that TPrP was not significantly correlated to PM1. On the other hand, TPrP is one of the dominating compounds, even in samples with air mass origins on the Atlantic Ocean (second period). Therefore, the OPFR composition in these samples may be a reflection of local emissions, whether or not diluted with cleaner air, or it may be a reflection of generally stable composition of OPFR in atmospheric particles. The OPFRs that are bound to PM may be more protected from atmospheric degradation, as observed for other organic compounds, such as PAH [27]. Nevertheless, longer term analysis and the study of OPFR in different PM fractions and in remote sites would be necessary to confirm these hypotheses.
Table 3. Spearman correlation (r) and p-values (p) of TPrP, TBP, TCPP and TPhP concentrations versus BC and PM1 levels.
|
|
BC (μg/m3) |
PM1 (μg/m3) |
TPrP |
TBP |
TCPP |
| PM1 |
r |
0.88 |
|
|
|
|
|
p |
0.004 |
|
|
|
|
| TPrP |
r |
0.79 |
0.67 |
|
|
|
|
p |
0.021 |
0.071 |
|
|
|
| TBP |
r |
0.91 |
0.93 |
0.74 |
|
|
|
p |
0.002 |
0.001 |
0.037 |
|
|
| TCPP |
r |
1.00 |
0.88 |
0.79 |
0.91 |
|
|
p |
0.001 |
0.004 |
0.021 |
0.002 |
|
| TPhP |
r |
0.86 |
0.76 |
0.91 |
0.91 |
0.86 |
|
p |
0.007 |
0.028 |
0.002 |
0.002 |
0.007 |
4. Conclusions
In this study we highlight the importance of PM1 as a vehicle for the atmospheric distribution of OPFRs. We have developed a reliable and efficient analytical procedure to determine 7 OPFRs in PM1. GC-EI-MS/MS gives good specificity and substantially reduces the background noise, resulting in low LODs. Among different blank tests, the highest contribution was observed in filter blanks that were placed in the sampling device for the whole sampling campaign, suggesting that the filter samples should be collected immediately after sampling to avoid external contamination from the sampling device. OPFRs were detected at concentrations ranging from a few pg/m3 to more than 1000 pg/m3. The most abundant OPFRs were TCPP, TPrP and TBP. Although in the present study substantial concentrations were observed in the urban background in Barcelona, the levels are comparable to those observed off-shore in the Mediterranean Sea. The detected OPFRs were strongly related to ambient air PM1 mass concentrations, and tend to accumulate in the urban air shed under stagnant atmospheric conditions that favor regional recirculation of air masses. Overall, this study suggests the importance to control OPFR in PM1 samples as this might represent an important human exposure route.
Conflict of interest
The authors declare there is no conflict of interest.
Acknowledgements
Technical assistance from R. Chaler and D. Fanjul is acknowledged. We thank the Department of Geosciences for the supply of air quality data. This work was financially supported by the scientific research projects CTM2008-03263/TECNO and TEAPARTICLE (CGL2011-29621) granted by the Spanish Ministry of Economy and Competitiveness.









 DownLoad:
DownLoad: