In the present paper, renormalization group methods are used to develop a macroscopic turbulence model for thermal diffusivity in turbulent fluid flow under conditions of endothermic and exothermic chemical reactions in flow. The temperature field is divided into slow (large-scale) and fast (small-scale) modes. With the help of the renormalization procedure, energy equations for the large-scale modes and relations for effective turbulent thermal diffusivity were obtained. It was shown how the type of the chemical reaction affects turbulent thermal diffusivity. In addition, the conditions were identified where effective thermal diffusivity undergoes a sharp growth.
1.
Introduction
According to the World Malaria Report 2017 [1], an estimated 216 million cases of malaria occurred worldwide, and an estimated 445, 000 deaths resulted from malaria globally. Reducing mortality and morbidity rates is a great challenge in malaria control. Currently, the principle tools for malaria eradication are antimalarial drugs and their combinations. Chloroquine and pyrimethamine, the two key roles of antimalarial drugs, have become less effective with monotherapy treatment during the last few decades in many countries. Artemisinin, an alternative antimalarial drug, shows a high eliminate rate of malaria parasites, based on its strong ability to kill almost all of the asexual stages of parasite development in the blood. However, drug resistance is still inescapable. Therefore, it is critical to balance the relationship between the drug use and the evolution of resistance effectively, thereby extending the useful lifespan of antimalarial drugs.
The effective lifespan of antimalarial drugs relies not only on the probability of the emergence of drug resistance from the very beginning, but also on the spread rate of drug resistant parasites in the population [2]. High-dose of antimalarial chemotherapy, which aims at cleaning the whole sensitive parasites as soon as possible, is a clearly feasible regimen [3]. However, it may be a risky strategy once some resistant parasites survive, because the antimalarial drugs could help drug resistant parasites to remove drug sensitive competitors [4]. This may result in competitive release of drug resistant parasites [5,6]. Competition between drug sensitive and drug resistant parasites, if it occurs, would be a pivotal factor affecting the spread of drug resistance. The reason is that the fitness cost of resistance in untreated hosts and benefits of resistance in treated hosts increase significantly by competitive interaction [7,8]. Low-dose of antimalarial chemotherapy, allowing several drug sensitive parasites alive to compete with resistant ones for suppressing the rise of them, may be a viable treatment to better manage the drug resistance. The hardest part of the treatment is to find a critical point that could keep a balance between felicitously alleviating symptoms and suppressing resistant parasites [3].
Additionally, it is worthwhile to focus on the host immunity that contributes to the process of parasites clearance and resistance management [9]. Immune response may work on narrowing down the mutant-selection window and cleaning resistant parasites [10]. As a vital part of immunity, antibodies can target the sporozoite stage, decrease the infection rate and parasite proliferation rate as well as the number of blood-stage parasites [9]. In the absence of the immune response, the selection of resistant mutants may increase to a higher level [11]. Yet, a quantitative understanding which treats host immunity as a player in optimal treatment of resistant infections remains under-developed [12].
Mathematical models often show their convenience and flexibility as a way to characterize interactions between different state variables. In [13], Mackinnon et al. presented an epidemiological model to explore the drug resistance in malaria sexual cycle(i.e. from one host to the next) by tracking the relative size of host population infected with resistant parasites. The model not only incorporated two types of parasites (drug sensitive and drug resistant), but also considered the effect of drug treatment.The influence of treatment on drug resistance was further analyzed in [14]. Moreover, in order to explore whether the competitive release could contribute to the spread of resistance, Hansen et al. [15] presented a general, between-host epidemiological model that explicitly took into account the effect of coinfection and competitive release. For the sake of studying the effect of immunity, Chiyaka et al. [16] considered two intra-host models of malaria: with and without immune response, and extended the two models incorporating the antimalarial drug treatment to analyze the relationship between the drug efficacy level and infection elimination. And Li et al. [17] studied the blood-stage dynamics of malaria in an infected host by considering the immune effector. Plenty of theoretical analysis and numerical simulations were made to reveal how immune cells interacted with infected red blood cells and merozoites. In addition, Bushman et al. [18] modeled immune responses by developing a nested individual-based model consisted of a population of human hosts. They concluded that within-host competition was a key factor in shaping the evolution of drug resistance in P. falciparum.
In this paper, we develop mathematical models to understand the evolution of drug resistance within an infected host by considering competition (which is between drug sensitive parasites and drug resistant parasites), drug treatment, and immune response. In order to explicit the effect of immunity, we construct two models with and without considering the immune response, and make a detailed theoretical analysis of the two systems, including the existence of equilibrium and their stability as well as Hopf bifurcation for the system with immunity. Later, these results are verified by numerical simulations, indicating that competition could inhibit the evolution of drug resistant parasites to some extent. Therefore, appropriate treatment, which allows some sensitive parasites to remain to suppress resistant ones, would delay the emergence of resistance. If the agammaessive drug treatment is adopted, a completely opposite result that the competitive release of drug resistant parasites is obtained. These results are in line with the experimental outcomes from [8]. However, when the immune response is considered, periodic solution, caused by Hopf bifurcation, are observed for relatively small treatment rates. Moreover, numerical simulations indicate that the direction of Hopf bifurcation is backward and the Hopf branch can be extended for all the parameter values less than the critical bifurcation value. This implies that the recurrence of resistance may happen for the chronic control strategy, even though it could delay the spread of resistance. Hence, a reasonable and appropriate level of the adjustment of drug dose is of great importance in practice. Finally, sensitivity analysis is performed to identify the relative significant parameters on outcome variables, which can provide a reference to make an optimal policy on resistance management and disease control.
The paper is organized as follows. Two mathematical models are formulated and analyzed in section 2. In particular, we perform detailed analysis for the system with immunity, finding out that Hopf bifurcation could occur under appropriate conditions. Theoretical results are numerically verified in section 3. Other than this, global sensitivity analysis, the global extension of Hopf bifurcation branch are also carried out. The main results of this paper and the potential application are discussed in section 4. In section 5, we list some long but tedious formulas for the coefficients that are used in the stability analysis.
2.
Model formulation
We construct two within-host dynamical models of malaria parasite infection. The first model aims to study issues related to the evolution of drug resistance in the absence of immunity. The second model explores the effect of the immune response on the spread of drug resistance completely based on the first model. It is normally supposed that the parasites population consists of diversiform of strains, which are classified as sensitive and resistant from the phenotype. An individual host could have different types of infections, for instance, a single strain is comprised of all the same types of parasites, hence, infection with one identical type is regarded as a single strain infection, while two identical types are regarded as mixed strain infection.
2.1. Within-host model in the absence of immune response
The ODEs system is employed to describe the dynamics of within-host infection, including three cell populations: uninfected red blood cells, S(t); drug sensitive malaria parasites, Is(t); drug resistant malaria parasites, Ir(t). The ODEs for the within-host model is as follows:
The model (2.1) assumes that new RBCs have a production rate is Λ with a natural life expectancy of 1/d1 days. The uninfected RBCs become infected by drug sensitive parasites and drug resistant parasites with rates of β1 and β2 respectively. Merozoites released from the liver cells invade RBCs to intake nutrients for fissure reproduction, eventually growing up to a mature schizont to burst RBCs and releasing a number of merozoties by a single infected red blood cell. The burst size is measured by α. Unlike the bacteria, the parasite is genetically unstable from one generation to the next so that a red blood cell infected by resistant stain may produce offspring which are drug sensitive [6]. The parameter p is the proportion of drug sensitive parasites released from the red blood cell infected by resistant parasites. Since resources and ecology space are limited within a host, hence, strains in a mixed infection have to compete with each other. Our model also depicts the influence of competition by using γ1Is(t)Is(t) and γ1Is(t)Is(t), which is convenient for us to explore how the competition influences the evolution of drug resistance. The drug resistant parasites and sensitive parasites die at a rate of d2 and d3. When malaria is treated by antimalarial drugs, the intensity of antimalarial drug use is measured by μ. Parameters and their biological interpretations are given in Table 1. Moreover, it is worthwhile to note that most within-host dynamical models take infected red blood cells into account [17,19], and the dynamic behavior of the within-host system can be described in more detail in this way. However, our paper mainly focuses on the interaction between the drug resistant parasites and drug sensitive parasites, hence for the simplification, the infected red blood cells are not involved in our model.
To determine the interior equilibrium P∗=(S∗,I∗s,I∗r) of system (2.1), we set the right hand side of (2.1) be zero. It then follows from the last two equation of (2.1) that
and
Substituting I∗r and I∗s into the first equation of (2.1), we get that S∗ satisfies
where
2.2. Within-host model in the presence of immune response
Host immunity against malaria parasite is complicated and stage-specific. Many interdependent players, such as different cell types and cytokines, participate at varying degrees [10]. For the sake of simplicity, pathogen-immune interactions are typically treated as predator-prey interactions, which has been studied in many literatures [22,23]. The two types of parasites played the prey role against a shared predator species (immune cells). Then the dynamics of the host immunity can be described as follows:
From the above dynamical model, the function of b1IsE1+θIs and b2IrE1+δIr represent the elimination of drug sensitive parasites Is and drug resistant parasites Ir by immune cells E respectively, where b1 and b2 are the removal rate of drug sensitive parasites and resistant ones, 1/θ and 1/δ are saturation constants that simulate immune cells to grow at half their maximum rate [17]. We assume that the net multiplication rate of immune cells stimulated by the drug sensitive parasites and sensitive ones are c1IsE1+θIs and c2IrE1+δIr, where k1 and k2 are the multiplication rate of lymphocytes due to the interactions between immune cells and drug sensitive parasites and drug resistant parasites respectively. The immune cells have a death rate of d4. In addition, the meaning of other terms in this model can refer to the Eq (2.1). Parameters and their biological interpretations are given in Table 1. In this case, to compute the specific expression of the interior equilibrium is extremely difficult, hence we mainly utilize the numerical method to analyze it.
2.3. Dynamical behavior of the system
In order to observe the dynamical behavior of system (2.5), we first study the existence of equilibrium of system (2.5) in R4+, where R4+={(S,Is,Ir,E):S≥0,Is≥0,Ir≥0,E≥0}. Note that the equilibrium of system (2.5) must satisfy the following equations.
Following the references[24] and [25], we obtain the basic reproduction number of our system, which is
Then we can have the following Lemma.
Lemma 2.1. System (2.5) has a unique non-negative equilibrium which is the malaria-free equilibrium P0=(Λ/d1,0,0,0), if R0≤1 and at least two equilibria if R0>1. More precisely,
(A) system (2.5) has two equilibria: P0=(Λ/d1,0,0,0) and P1=(S1,Is1,0,0) if R1>1, where S1=Λd1R1, Is1=(R1−1)d1β1;
(B) system (2.5) has three equilibria: P0=(Λ/d1,0,0,0), P1=(S1,Is1,0,0) and P3=(S3,Is3,0,E3) if R1>max{L,1}, where L=β1d1(c1−d4θ)+d4, S3=Λβ1(c1−d4θ)+d1d4, Is3=c1−d4θd4, E3=1b1(αβ1S3−(d2+μ))(1+θIs3);
(C) system (2.5) has four equilibria: P0=(Λ/d1,0,0,0), P1=(S1,Is1,0,0), P2=(S2,Is2,Ir2,0) and P3=(S3,Is3,0,E3) if R1>max{L,1}, R2>1 and k1S23+k2S22+k3S2+k4=0 has a positive solution S2 with
(H1) d3(1−p)αβ2<S2<min{d2+μαβ1,γ1d3αβ2(γ1(1−p)−γ2p)}; or
(H2) max{d2+μαβ1,d3(1−p)αβ2}<S2<γ1d3αβ2(γ1(1−p)−γ2p)
where Is2=(1−p)αβ2S2−d3γ2, Ir2=(αβ1S2−d2−μ)((1−p)αβ2S2−d3)γ1((1−p)αβ2S2−d3)−pαβ2γ2S2;
(D) system (2.5) has five equilibria: P0=(Λ/d1,0,0,0), P1=(S1,Is1,0,0), P2=(S2,Is2,Ir2,0), P3=(S3,Is3,0,E3) and P4=(S4,Is4,Ir4,E4), if R1>max{L,1}, R2>1 and k1S23+k2S22+k3S2+k4=0 has a positive solution S2 satisfying (H1) or (H2), moreover, l1Ir45+l2Ir44+l3Ir43+l4Ir42+l5Ir4+l6=0 has a positive solution Ir4 satisfying
(H3) c2−d4δ>0, Δ<0 and S4>γ2Ir4+d3(1−p)αβ2; or
(H4) c2−d4δ>0, Δ≥0, Ir4(1,2)=−(β2e2−β1e3+d1)±√Δ2β2, and without loss of generality, let Ir4(1)>Ir4(2), if Ir4>Ir4(1) or Ir4<Ir4(2), and S4>γ2Ir4+d3(1−p)αβ2;
where
and the expressions of l1 to l6 are shown in (2.20).
Proof. The existence of P0 can be obtained directly from (2.6) by setting Is=Ir=E=0, the existence of P1 can be obtained from (2.6) by setting Ir=E=0, and the existence of P3 can be obtained from (2.6) by setting Ir=0. Then we would seek conditions for the existence of P2 and P4 of (2.6). For the existence of P2, we have P2=(S2,Is2,Ir2,0) as setting E2=0. The following formulations of Is2 and Ir2 are obtained from (2.6), where
It is clear that Is2>0 and Ir2>0 if the following conditions hold:
From (2.9), we have
Now, we discuss the existence of S2. Substituting (2.7) and (2.8) into the first equation of (2.6), we obtain that
where
To sum up, if R1>max{L,1}, R2>1 and (2.4) has a positive solution S2 with condition (2.9), then P2=(S2,Is2,Ir2,0) is the equilibrium of (2.6), which implies statement (C) holding. Next, we discuss the existence of the positive equilibrium P4=(S4,Is4,Ir4,E4) of system (2.5). Suppose that (S4,Is4,Ir4,E4) is a positive solution of (2.6). From (2.6), we have
It is clear that S4>0, Is4>0 and E4>0 if the following conditions hold:
From (2.13), we obtain that
and hence, from (2.16), we infer that
Based from (2.14), we obtain that
The (2.15) can be held in the following two cases, we first let
Then we analyze the roots of F(Ir4)=0, set Δ=(β2e2−β1e3+d1)2−4β2(β1e1+d1e2),
(I) Note that F(Ir4)=0 has two real roots Ir4(1,2) if Δ>0, where
when β2e2−β1e3+d1>0, the two roots of F(Ir4)=0 are negative, then P4 exists if Ir4>0 and both (2.17) and (2.18) hold. When β2e2−β1e3+d1<0, the two roots of F(Ir4)=0 are positive, we assume that Ir4(1)>Ir4(2), then P4 exists if Ir4>Ir4(1) or Ir4<Ir4(1) and both (2.17) and (2.18) hold.
(II) Note that F(Ir4)=0 has no roots if Δ<0, then P4 exists if both (2.17) and (2.18) hold.
Substituting (2.12) into the third equation of (2.6), we have the following equation
where
Therefore, according to the above analysis and inference, system (2.6) have a positive solution, which implies statement (D) holds. This completes the proof.
Then we begin to analyze the stability of these equilibria of system (2.5). Computing the Jacobian matrix of system (2.5) at point P=(S,Is,Ir,E), we have
where A1=αβ1S−γ1Ir−d2−μ−b1E(1+θIs)2.
2.3.1. Local stability of the malaria-free equilibrium P0
At the malaria-free equilibrium P0=(Λ/d1,0,0,0), the Jacobian matrix is
and the characteristic equation is
According to (2.21), all eigenvalues could be negative if R0<1, and one of the eigenvalues is positive if R0>1. Then we can get the following lemma.
Lemma 2.2. The malaria-free equilibrium P0 of system (2.5) is locally asymptotically stable if R0<1 and unstable if R0>1.
2.3.2. Local stability of the malaria infection equilibrium P1
If R1>1, the system (2.5) has a malaria infection equilibrium P1=(S1,Is1,0,0) with
The Jacobian matrix at P1 is
and the characteristic equation is
where m1=β1Is1+d1−αβ1S1+d2+μ,m2=αβ21S1Is1−(β1Is1+d1)(αβ1S1−(d2+μ)).
By the Routh-Hurwitz criterion, the roots of (2.22) have negative real parts if and only if
On the basis of above analysis and combining with the Lemma 2.1 and 2.2, we have the following theorem.
Theorem 2.1. If R1>1, then system (2.5) has two equilibria: P0=(Λ/d1,0,0,0) and P1=(S1,Is1,0,0). Moreover, the malaria-free equilibrium P_0 is unstable, and the malaria infection equilibrium P_1 is locally asymptotically stable if the inequalities in (2.23) hold.
2.3.3. Local stability of the malaria infection equilibrium P_2
From lemma 1, we know that system (2.5) has four equilibria: P_0 = (\Lambda / d_1, 0, 0, 0) , P_1 = (S_1, I_{s_1}, 0, 0) , P_2 = (S_2, I_{s_2}, I_{r_2}, 0) and P_3 = (S_3, I_{s_3}, 0, E_3) .
The local stability of P_2 is established from the Jacobian matrix at P_2 , which is given by
and the characteristic equation is
where the expressions of r_1 , r_2 , r_3 and r_4 are shown in Appendix due to their complexity.
By using the Routh-Hurwitz criterion, the roots of (2.24) have negative real parts if and only if
Hence, we obtain the following theorem based on above analysis and Lemma 2.1 and 2.2.
Theorem 2.2. If R_1 > \max\left\{\frac{\beta_1}{d_1}(c_1 - d_4 \theta) +d_4, 1\right\} , R_2 > 1 and k_1 {S_2}^3+k_2 {S_2}^2+k_3 {S_2}+k_4 = 0 has a positive solution S_2 with \frac{d_3}{(1-p) \alpha \beta_2} < S_2 < \min\left\{\frac{d_2+\mu}{\alpha\beta_1}, \frac{\gamma_1 d_3}{\alpha \beta_2 (\gamma_1 (1-p)-\gamma_2 p)}\right\} or \max\left\{\frac{d_2+\mu}{\alpha\beta_1}, \frac{d_3}{(1-p) \alpha \beta_2}\right\} < S_2 < \frac{\gamma_1 d_3}{\alpha \beta_2 (\gamma_1 (1-p)-\gamma_2 p)} . Then system (2.5) has four equilibria P_0 , P_1 , P_2 and P_3 , where P_0 is always unstable, P_1 is locally asymptotically stable if the inequalities in (2.23) hold, P_2 is locally asymptotically stable if the inequalities in (2.25) hold and P_3 is locally asymptotically stable if the inequalities in (2.27) hold.
2.3.4. Local stability of the malaria infection equilibrium P_3
From lemma 1, we know that system (2.5) has three equilibria: P_0 = (\Lambda / d_1, 0, 0, 0) , P_1 = (S_1, I_{s_1}, 0, 0) and P_3 = (S_3, I_{s_3}, 0, E_3) .
The local stability of P_3 is established from the Jacobian matrix at P_3 , which is given by
and the characteristic equation is
where the expressions of s_1 , s_2 , s_3 and s_4 are shown in Appendix.
By employing the Routh-Hurwitz criterion, the roots of (2.26) have negative real parts if and only if
Hence, we obtain the following theorem based on above analysis and Lemma 2.1 and 2.2.
Theorem 2.3. If R_1 > \max\left\{\frac{\beta_1}{d_1}(c_1 - d_4 \theta) +d_4, 1\right\} , then system (2.5) has three equilibria P_0 , P_1 and P_3 , where P_0 is unstable, P_1 is locally asymptotically stable if the inequalities in (2.23) hold, and P_3 is locally asymptotically stable if the inequalities in (2.27) hold.
2.3.5. Local stability of the malaria infection equilibrium P_4
From Lemma 2.1, we know tha system (2.5) has five equilibria: P_0 = (\Lambda / d_1, 0, 0, 0) , P_1 = (S_1, I_{s_1}, 0, 0) , P_2 = (S_2, I_{s_2}, I_{r_2}, 0) and P_3 = (S_3, I_{s_3}, 0, E_3) , P_4 = (S_4, I_{s_4}, I_{r_4}, E_4) .
The local stability of P_4 is established from the Jacobian matrix at P_4 , which is given by
where A_1 = \alpha \beta_1 S_4 -\gamma_1 I_{r_4} -d_2-\mu - \frac{b_1 E_4}{(1+\theta I_{s_4})^2} . The characteristic equation is
where the expressions of t_1 , t_2 , t_3 and t_4 are shown in Appendix.
By employing the Routh-Hurwitz criterion, the roots of (2.26) have negative real parts if and only if
Hence, we obtain the following theorem on the existence and stability of positive equilibrium based on above analysis and Lemma 2.1 and 2.2.
Theorem 2.4. If R_1 > \max\left\{\frac{\beta_1}{d_1}(c_1 - d_4 \theta) +d_4, 1\right\} , R_2 > 1 , and k_1 {S_2}^3+k_2 {S_2}^2+k_3 {S_2}+k_4 = 0 has a positive solution S_2 satisfying (H1) or (H2), and l_1 {I_{r_4}}^5 + l_2 {I_{r_4}}^4 + l_3 {I_{r_4}}^3 + l_4 {I_{r_4}}^2 + l_5 {I_{r_4}} + l_6 = 0 has a positive solution I_{r_4} satisfying either (H3) or (H4) or (H5). Then system (2.5) has five equilibria P_0 , P_1 , P_2 , P_3 and P_4 , where P_0 is unstable, P_1 is locally asymptotically stable if the inequalities in (2.23) hold, P_2 is locally asymptotically stable if the inequalities in (2.25) hold, P_3 is locally asymptotically stable if the inequalities in (2.27) hold, P_4 is locally asymptotically stable if the inequalities in (2.29) hold.
According to the previous analysis, we know that P_4 is an interior positive equilibrium. For this equilibrium, we are interested in when it becomes unstable and Hopf bifurcation occurs. Following the analysis of a fourth-order characteristic equation in Ruan and Wolkowicz [26], we need to satisfy conditions, which make characteristic equation (2.28) having two roots with a negative real part and a pair of conjugate purely imaginary roots, which are
Next, we would verify the transversal condition to prove the occurrence of Hopf bifurcation at the positive equilibrium P_4 . We choose \mu as a bifurcation parameter. Define
Suppose that there exists a \mu^* > 0 so that t_1(\mu^*) > 0 , t_4(\mu^*) > 0 , t_1(\mu^*) t_2(\mu^*) - t_3(\mu^*) > 0 and \psi(\mu^*) = 0 . Then equation (2.28) has four roots, \pm \omega i , \lambda_1 and \lambda_2 , where \omega = \sqrt {\frac{t_3(\mu^*)}{t_1(\mu^*)}} , Re(\lambda_1) < 0 and Re(\lambda_2) < 0 . When 0 < |\mu-\mu^*|\ll 1 , we assume that equation (2.28) has four roots, \xi(\mu)\pm \omega (\mu) i , \lambda_1(\mu) and \lambda_2(\mu) , where \xi(\mu^*) = 0 , \omega(\mu^*) = \omega , \lambda_1(\mu^*) = \lambda_1 and \lambda_2(\mu^*) = \lambda_2 . Then we compute the derivative of \xi(\mu) with respect to \mu at \mu^* . Note that
We obtain the following result by (2.31)
Hence, the transversal condition holds under some conditions. According to the Hopf bifurcation theorem, we have the following theorem about bifurcation at the positive equilibrium P_4 .
Theorem 2.5. Assume that system (2.5) has a positive equilibrium at P_4 . If there exists a \mu^* > 0 so that t_1(\mu^*) > 0 , t_4(\mu^*) > 0 , t_1(\mu^*) t_2(\mu^*) - t_3(\mu^*) > 0 , \psi(\mu^*) = 0 , and {\frac{d\xi(\mu)}{d\mu}}\big|_{\mu = \mu^*} \neq 0 , then Hopf bifurcation occurs at \mu = \mu^* , and a periodic solution appears near P_4 when \mu passes through \mu^* .
2.4. Sobol' sensitivity analysis method
Sobol' sensitivity analysis method is one of the global sensitivity methods, which is performed over the entire parameter space, and all parameters could vary simultaneously. The core of this method is variance decomposition to measure the sensitivity of parameters [27,28]. Assuming a mathematical model is described by a function
where \textbf{x} = (x_1, x_2, ..., x_n) represent the input parameters, which defined on a n -dimensional unit cube H^n = \left\{\textbf{x} | 0 \leq x_i \leq 1, i = 1, 2, ..., n\right\} , and y = f(x) is the model output variable. According to the Sobol' method, y = f(x) can be decomposed into single model parameters and subitem functions of parameter interaction:
The number of all subitems is 2^n , and the subitem function is obtained by calculating the following multiple integrals:
Similarly, other subitem functions of a high order can be achieved. f_0 is a constant, and the integral of every summand over any of its own variables is zero:
The subitem functions in equation (2.35) satisfy equation (2.36), it can be inferred that every subitem functions in equation (2.34) is orthogonal, that is:
Based on the above properties, the variance of output variable V(y) can be decomposed as follows:
where V_{i_1, ..., i_s} = \int_{0}^{1}f_{i_1, ..., i_s}^2(x_{i_1}, ..., x_{i_s})dx_{i_1}, ..., x_{i_s} is the partial variance corresponding to the subitem function of equation (2.34). The Sobol global sensitivity indices are defined by
For instance, S_i = \frac{V_i}{V(y)} is the first order Sobol' index, and S_{ij} = \frac{V_{ij}}{V(y)} is the second order Sobol' index. And the total effect sensitivity index as an extension of the Sobol sensitivity indices, which is defined as the ratio of the sum of the related sensitivity indices:
Total effect indices have great significance. Parameter x_i has no impact on the outcome variable in the case S_{T_i} = 0 and vice versa, which indicates that the condition S_{T_i} = 0 is necessary and sufficient for x_i to be a noninfluential factor. Hence, the total Sobol' indices not only characterized the contribution of the concerned parameters but also their interactions. The calculation of Sobol' sensitivity indices involves the computation of multiple integrals, which are very complicated and difficult especially for the complex nonlinear models. Therefore, the Monte Carlo method is employed to approximate the multiple integral solutions.
3.
Numerical results
The paper illustrates some numerical results on the within-host dynamical models with and without considering the immune response.
3.1. Within-host model in the absence of immune response
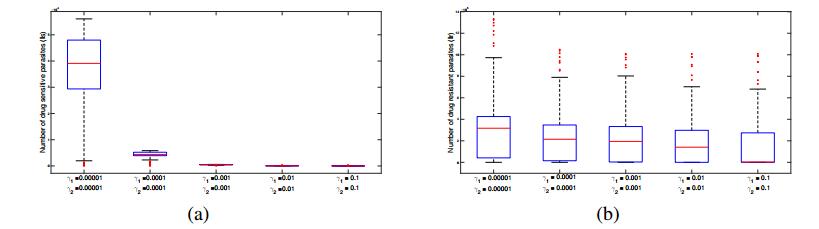
Initially, we take into account the within-host dynamical model without involving the immune response. In order to examine the influence of competition, we observe the solution of I_r by varying the competitive coefficients and fixing the remaining parameters as in Table 1 (here we set \mu = 0.1 , because it is not given in Table 1). The function of " ode45 " provided by MATLAB software is employed to calculate the solution of I_r , where the time (days) ranges from 0 to 1500. Five different groups of competitive coefficients are chosen and sorted in ascending order. (First group : \gamma_1 = \gamma_2 = 0.00001 , second group : \gamma_1 = \gamma_2 = 0.0001 , third group : \gamma_1 = \gamma_2 = 0.001 , fourth group : \gamma_1 = \gamma_2 = 0.01 , fifth group : \gamma_1 = \gamma_2 = 0.1 ). We illustrate the results in the box-and-whisker plot, and each box-and-whisker corresponds to a set of solutions of I_r for a given group of competitive coefficients. Figure 1 displays that the number of both drug sensitive parasites and drug resistant parasites decreases with the increasing intensity of competition. However, comparing Figure 1(a) with Figure 1(b), it is observed that the descending rate of the number of sensitive parasites is much faster than resistant ones. Moreover, the number of drug resistant parasites is roughly one order of magnitude larger than that of sensitive parasites. This phenomenon may imply that drug sensitive parasites are more susceptible to competition than resistant ones with the same competitive coefficients in each circumstance.
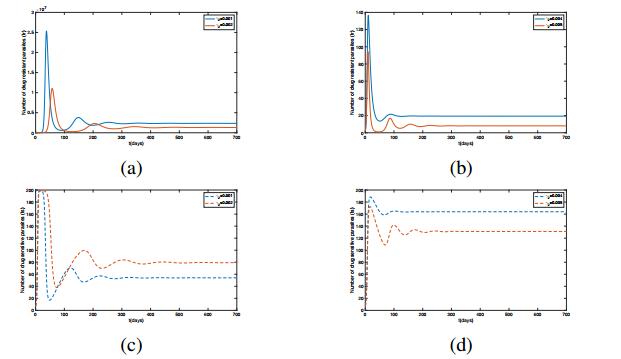
Now, fix one of the competitive coefficients \gamma_1 and vary another one \gamma_2 to observe the number of two types of parasites, and the remaining parameters are as in Table 1 (here we set \mu = 0.1 , because it is not given in Table 1). Figure 2 (a) and (b) illustrate that the number of resistant parasites constantly declines with the reduction of competitive ability. Especially, when the competitive ability of resistant parasites is under sensitive ones, the number of resistant parasites will decline sharply by about five orders of magnitude. The number of sensitive parasites is precious few comparing with resistant ones as their competitive ability is lower than resistant ones (Figure 2 (c)). But they would exceed resistant parasites once they develop a higher competitive ability (Figure 2 (d)). It can be deduced that sensitive parasites are able to competitively suppress resistant parasites when the sensitive population achieves a higher competitive ability. Especially, the higher the competitive ability of sensitive parasites are, the more the competitive suppression on resistant parasites are, and the fewer the number of resistant population is. Wale et al. demonstrated that a parasite nutrient could mediate competition between a drug resistant and drug sensitive strain of the malaria parasite. Hence, they tried to intensify the competitive suppression on drug resistant parasites by reducing the availability of the nutrient in a host environment, and results show that with resistant parasites struggling to replicate, susceptible parasites outcompeted them before they can emerge [29]. These experimental findings are consistent with our numerical results.
The model also reproduces the relationship between drug treatment and the spread of drug resistance. Figure 3 depicts the trend of the number of drug resistant parasites with the ranging treatment level. We mainly vary the parameter \mu ( \mu = 0, 1, 5 ) and fix the remaining parameters as in Table 1 (here we set \gamma_1 = \gamma_2 = 0.001 , because they are not given in Table 1). High level chemotherapy leads to a large production of drug resistant parasites. The more agammaessive the chemotherapy is, the more the drug sensitive population will be reduced, which accordingly will promote the competitive release of resistant parasites, leading them to maintain at a high level ultimately. The results are also in line with experimental findings of [4,30]. In particular, it can be discovered that high level chemotherapy also accelerates the evolution of drug resistance. Both the peak and equilibrium of the number of drug resistant parasites appear much earlier than low level chemotherapy.
3.2. Within-host model in the presence of immune response
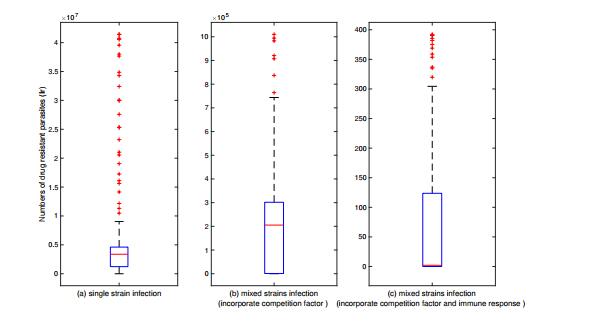
Now, the role of immune response is added into the mathematical model. Three cases are studied in our paper, including the single strain infection, mixed strains infection (incorporate the competition) and mixed strains infection (incorporate the competition and the immune response). They are set to have same parameters as in Table 1 (here we set \gamma_1 = \gamma_2 = 0.001 and \mu = 0.1 ). Figure 4 (a) plots that, in single infections with drug resistant parasites, the number of drug resistant parasites stands at a quite high level. Whereas in mixed strains infection (Figure 4 (b)), the number of resistant populations drops roughly by two orders of magnitude. The influence of both competition and immune response on drug resistance is shown in Figure 4 (c). The result reveals that the number of resistant population downs unceasingly to two orders of magnitude, indicating that the immune response could inhibit the spread of drug resistance to some extent. This is in accord with the experimental result of Ataide in [9] that immunity may play an important role in the emergence and transmission potential of artemisinin-resistant parasites.
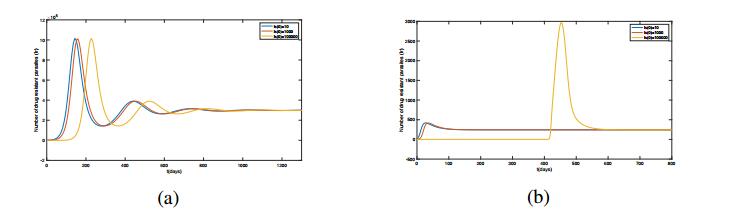
The impact of the ratio of initial drug sensitive and resistant parasites is also examined on the prevalence of drug resistant strains. We take all parameters as in Table 1 (here we set \gamma_1 = \gamma_2 = 0.001 and \mu = 0.1 ). Figure 5 (a) presents the effect of different initial values of drug sensitive parasites on drug resistant parasites without considering the immune response. As the initial value of drug sensitive parasites I_s(0) = 10 , I_s(0) = 1000 and I_s(0) = 100000 , the number of drug resistant parasites peaked on the 140th, 160th and 220th day, respectively. The case I_s(0) = 100000 is the latest among the three cases. It can be deduced that a large initial number of drug sensitive parasites could delay the emergence of the peak. This phenomenon may result from the competition between the two parasites, and drug resistant parasites can be suppressed by sensitive ones when they have a large initial number.
If the effect of the immune response is incorporated, Figure 5 (b) shows that the number of drug resistant parasites reduces by around 3 to 4 orders of magnitude. As the initial value of drug sensitive parasites I_s(0) = 10 , I_s(0) = 1000 and I_s(0) = 100000 , the number of drug resistant parasites peaked on the 40th, 50th and 460th day, respectively. Compared with Figure 5 (a), the peak of drug resistant parasites comes about 100 days earlier in the case of I_s(0) = 10 and I_s(0) = 1000 . This may be explained by immunosuppression. On this account, parasites would be eliminated in large quantities, especially, only a few parasites could survive when the given initial number of drug sensitive parasites is relatively small. Hence, the number of two types of parasites may remain the same order of magnitude, thereby leading to the failure of competitive suppression on drug resistant parasites. However, the peak of drug resistant parasites in the case of I_s(0) = 100000 appears around 240 days later than the same case without considering the immune response. This may be because the initial number of drug sensitive parasites is much larger, hence immune cells are unable to kill these parasites as fast as possible, so that there are enough sensitive parasites left to play a role in suppressing resistant ones. Nevertheless, the values of both the peak and equilibrium of drug resistant parasites remain at low levels since the total cardinal number of two types of parasites is relatively small, which is reduced by immune cells. Wale et al. [29] had an analogous experiment to investigate the intensity of competition between strains of P. chabaudi in the period before they were cleared by the immune system. They discovered that immunity could be responsible for the clearance and the post-peak control of malaria infections, which also explained Figure 5 (b) to some extent.
The above analysis has shown that within-host competition and immune mechanisms are able to inhibit the spread of drug resistance. The following step is measuring how the drug treatment level influences the number of drug resistant parasites. Figure 6 illustrates the simulation results with three different levels of antimalarial drug treatment (one of which equals zero, in order to examine the effect from competition alone) combined with three different competitive intensities. Equilibrium values of two parasites gradually fall with the rise of the immunity level in every case. And the number of two parasites moves in a similar trend, but the sensitive type always goes below the resistant one.
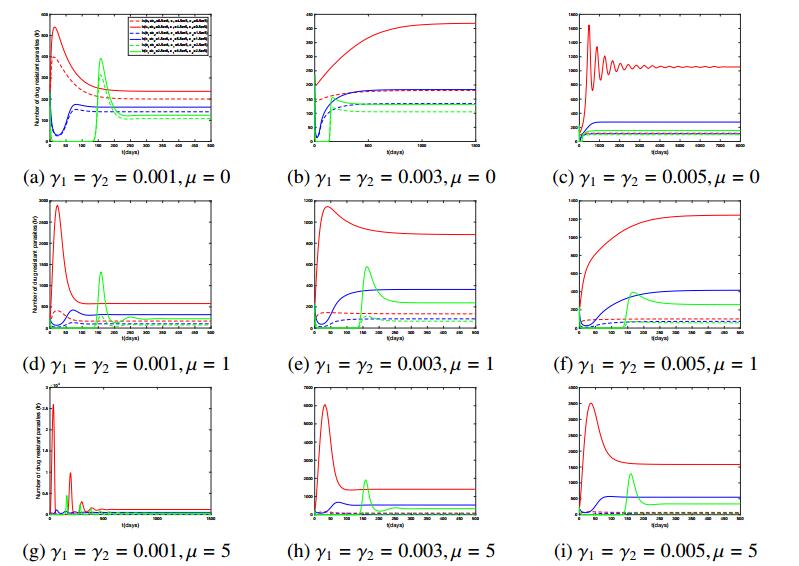
Figure 6 (a)-(c) depict the simulation results with no drug use and different levels of competitive intensity. It is observed that resistant parasites take more time to reach equilibrium with the increasingly fierce competition. Under the lowest level of competitive intensity ( \gamma_1 = \gamma_2 = 0.001 ) (Figure 6 (a)), the gap of the number between the two parasites is also the lowest. This may indicate that drug sensitive parasites can survive more equally with resistant parasites in a loose competitive environment. The resistant population has not shown its strong agammaessiveness yet. However, the gap would be significantly widened once the competition is intensified(Figure 6 (b) (c)), indicating that drug resistant parasites are able to survive in all settings, moreover, the number of drug resistant parasites is larger in a highly fierce competition setting. In addition, the immune response also plays an important role in controlling the number of parasites. The aforementioned gap is narrowed due to the immune effect in each case(Figure 6 (a)-(c)). Especially, in the case of high level competition and low level immune response (Figure 6 (c)), drug resistant parasites exhibit a tendency of decaying oscillation until they reach equilibrium eventually. It also spends the longest time among these three cases. In conclusion, the results demonstrate that in highly immunity settings and competition is light, drug resistant parasites are inclined to remain at a low level. But if the competition is strengthened, the death rate of drug sensitive parasites keeps increasing to leave more ecological space for resistant ones, which may actually ascend their survival rate.
Figure 6 (d)-(i) present simulation results including drug treatment and competition, which mainly yield several observations. First of all, with the increase of drug treatment level, accordingly, drug resistance expands rapidly without exception. This can be observed from Figure 6 (d) (g), Figure 6 (e) (h), and Figure 6 (f) (i), respectively, which provide a clear comparison between low- and high- drug dose. This may arise from the competitive release. Agammaessive chemotherapy aims to kill sensitive parasites such that resistant parasites could benefit from this behavior in a resource-limited environment. Secondly, the number of resistant parasites stands at a low level with light treatment and a low level of competitive intensity (Figure 6 (d)). Moreover, the spread of drug resistance is again depressed by enhanced immunity. Thirdly, the case of agammaessive drug treatment and a low level of competitive intensity(Figure 6 (g)) describes the process of oscillation attenuation of drug resistant parasites and reach the equilibrium ultimately, which is fairly similar to the case with high level of competitive intensity and zero-dose of antimalarial drug(Figure 6 (c)). Immunity effectively diminishes the value of peak and equilibrium, thereby highlighting its importance. Fourthly, with the ascending level of both competitive intensity and antimalarial drug dose, the gap between the amount of two parasites is getting wide. It is clear that case Figure 6 (i) ( \gamma_1 = \gamma_2 = 0.005, \mu = 5 ) presents the widest gap of all cases, particular for a relatively low level of the immune response. Lastly, when the competition is relatively moderate(Figure 6 (e) (h)), the tendency of two parasites varies between the case of high level and low level of competitive intensity(Figure 6 (d) (f) and Figure 6 (g) (i)).
To summarize, the results of these simulations could boil down to a fact that immune response is a real threat to resistant parasites. If equal proportions of infections are treated in low- and high-level of immune response settings, a higher proportion of hosts will be treated in a high-level of immune response settings. Similarly, Ataide et al. also studied the effect of both low- and high- level of immunity on the emergence of drug resistant mutant parasites. Results suggest that low levels of immunity may facilitate the transmission of resistant parasites, and resistant parasites may be better able to persist compared with the case of high immunity [9]. Moreover, the number of drug resistant parasites would be increased by employing antimalarial drug treatment, especially the agammaessive regimen, which refers to the accelerated spread of drug resistance in a host accompanying with the elimination of drug sensitive competitors.
Many studies have suggested that oscillations are frequently observed in the immune system [17,31]. Figure 6 (c) and Figure 6 (g) exactly describe this phenomenon of "decaying oscillation"[31]. On the basis of the above analysis, if the dissipation of energy could be controlled, the regular periodic oscillation is possible to appear. In the case of Figure 6 (c), when the level of immune response is at a high level, the curve depicts a tendency of decaying oscillation of the drug resistant parasites, but there is no analogous phenomenon when the competitive intensity is much lower(Figure 6 (a) and (b)). Similarly, in terms of the Figure 6 (g), the phenomenon of decaying oscillation shows again when the competitive intensity is light and the level of immune response is high with agammaessive drug treatment. Nonetheless, decaying oscillation disappears with the increasing competitive intensity (Figure 6 (h) and (i)).
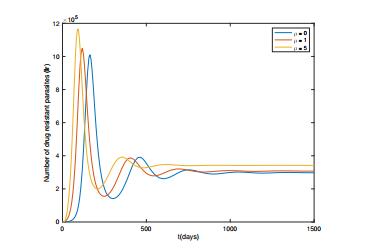
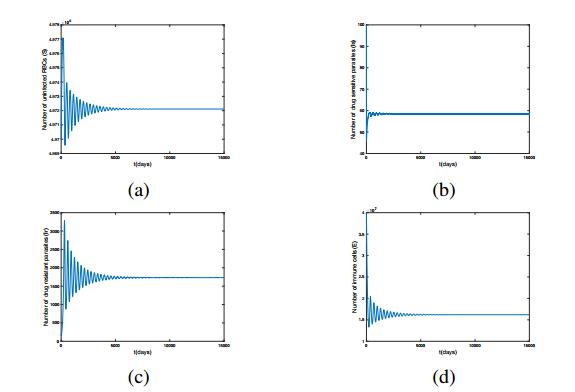
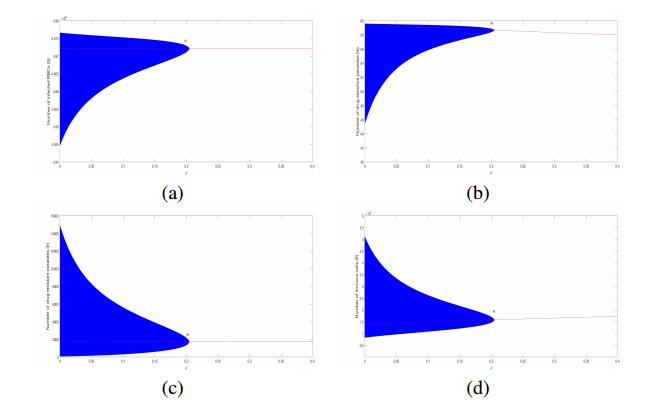
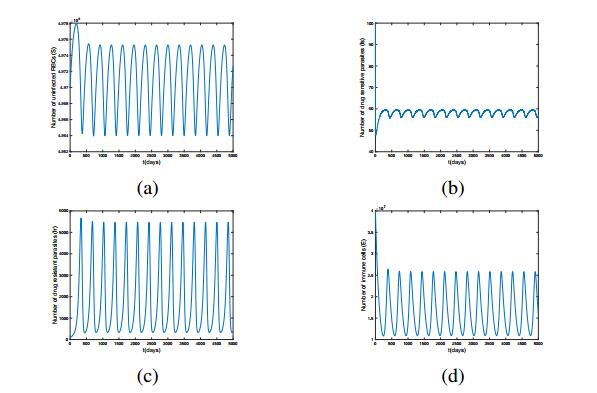
In order to explore the interior equilibrium P_4 of system (2.5), we choose \gamma_1 = \gamma_2 = 0.01 , \mu = 0.26408 and take all other parameters as in Table 1. Then, P_4 = (4972109.16, 58.46, 1732.77, 16284461.14) , which is stable by checking the stability conditions (2.29), see Figure 7. Furthermore, using the software Matcont (a Matlab package for numerical bifurcation analysis of ODEs), we also detect that the system (2.5) undergoes a Hopf bifurcation at P_4 as \mu passes through a critical value \mu = 0.20408 . In addition, the transversality condition \xi'(\mu^*)\neq 0 holds, the first Lyapunov coefficient equals -8.076492 \times 10^{-3} , indicating a supercritical bifurcation, see Figure 8. For instance, if we set \mu = 0.10408 , then P_4 is unstable and a stable periodic solution can be observed, see Figure 9.
3.3. Sensitivity analysis
The value of sensitivity analysis can be reflected in the natural level of variation in several aspects of the model, including epidemiological and immunological [19]. Generally, global sensitivity analysis is rather complicated in dealing with high-dimensional models from the point of methodology. However, it is still worthwhile to perform for providing further insights on the dynamical infection process of within-host as well as resistance management.
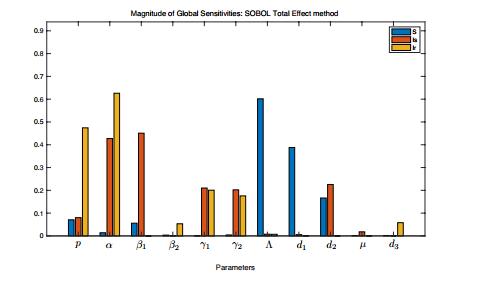
In this paper, a uniform distribution within 20% of nominal values was used for sampling with a base sample size of 2, 000 simulations. Sobol' sensitivity analysis was conducted in two cases, with and without considering the immunity of the within-host dynamical system, respectively. Sobol' results are shown in Figure 10 and Figure 11. As for the first case (Figure 10), parameter \Lambda and d_1 are significant for uninfected RBCs ( S ). It is clear to figure out that parameters \alpha, \beta_1, d_2, \gamma_1, \gamma_2 can be labeled as significant for drug sensitive parasites ( I_s ). Notice that \alpha, p, \gamma_1, \gamma_2, d_3 have a significant influence on drug resistant parasites( I_r ).
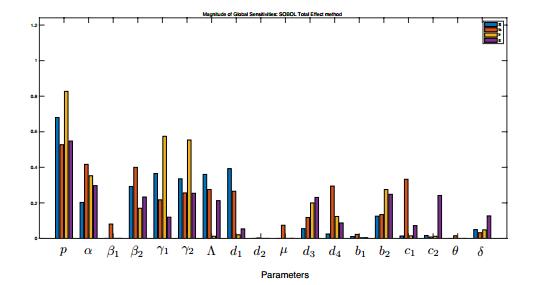
For another case (Figure 11), the immune effect is added to the dynamical system, therefore, our interest is to observe the variation of the sensitivity of all parameters after the immune response is involved. Parameters p, d_1, \Lambda, \gamma_1, \gamma_2 rank the top five in the sensitivity ranking of uninfected RBCs ( S ). It seems that competition has a relatively significant influence on uninfected RBCs ( S ) in the current system. Parameters p, \alpha, \beta_2, c_1, d_4 can be labeled as significant for drug sensitive parasites ( I_s ), where the proliferation rate of immunity effectors ( c_1 ) plays an important role after incorporating the immune response. Values of Sobol' index of parameters p, \gamma_1, \gamma_2, \alpha, b_2 are much higher than other parameters. Similarly, the removal rate of drug resistant parasites by immune system ( b_2 ) could affect I_r more, indicating that parameters related to immunity act actually on state variables, in particular for I_s and I_r . For the immunity effectors ( E ), parameters p, \alpha, \gamma_2, \beta_2, c_2 have a critical influence.
4.
Disscussion and conclusion
Within-host competition is a real major hurdle in the evolution of drug resistance when the immune response is not considered. Results of the dynamical analysis indicate that, if sensitive parasites achieve a higher ability of competition than resistant ones, such that resistant parasites will be in a competitive disadvantage, and sensitive parasites could suppress their competitors. Wale et al. [29] showed that intensifying competitive interactions between sensitive and resistant parasites by limiting a resource could retard the evolution of drug resistance. Hence, if it is possible to improve the competitive ability of sensitive parasites, it will be a good way to manage drug resistance.
As the immune response is considered in the dynamical system, the interactions between malaria parasites and immune cells can be modeled in analogy to ecological interactions, where two prey species (drug sensitive and resistant parasites) are mediated by a shared predator species (immune cells) [32]. Figure 5 presents the influence of different initial values of drug sensitive parasites on resistant ones in two cases (with and without immunity). Essentially, it is mainly about the different ratios between the two parasites. Hence, the infection can be divided into different types according to the ratio \frac{I_r}{I_s} . If the ratio \frac{I_r}{I_s} is large, the type will be regarded as a host infected with resistant parasites from the very beginning. In contrast, if the ratio \frac{I_r}{I_s} is small, the type will be regarded as resistant mutants of parasites produced directly within a host. The infection with a small \frac{I_r}{I_s} exhibits a delay of drug resistance. This may be due to the competitive inhibition of the replication of resistant parasites by the numerically predominant sensitive parasites. Another interesting fact is detected when the immune effect is involved in this process, which resistant parasites can either be suppressed for a much longer time than before or reach equilibrium rapidly. The inferences are as follows: when the initial value of I_r is fixed and I_s is large enough ( \frac{I_r}{I_s} is small), immune cells are insufficient to completely clear parasites as fast as possible, hence the remaining sensitive parasites still can competitive suppress resistant ones, thereby delaying the spread of drug resistance. On the other hand, when I_s is much smaller( \frac{I_r}{I_s} is large), immune cells have the ability to eliminate most parasites rapidly to reach equilibrium accordingly.
Simulations with drug treatment show that high dose antimalarial chemotherapy will actually contribute to the spread of drug resistance in both situations. Motivated by studies of [30,33], we explore the influence of immune response in the treatment process. The results show that the reality of the dynamics of within-host infection is non-linear, even the oscillation occurs in some cases. This mainly results from the role of the immune response, acting in conjunction to produce diverse outcomes, which coincide with the analysis in [12]. From both Figure 8 and 6(c), an interesting fact is observed that the malaria infection exhibits a periodic phenomenon as the drug treatment remains at a lower level and competition stays at a high level. This may illustrate that light drug treatment is ineffective because of the fierce competition between the two parasites. But we also find that resistant parasites still can benefit from the agammaessive therapy with a similar tendency of the immunodeficient dynamical system, which is consistent with experimental results of [4,30]. Hence, it is very necessary to control the drug dose at an appropriate level that not only alleviate the symptoms but also manage the spread of drug resistance effectively [3].
Our models involve a variety of parameters, especially when the immune effect is involved in the system. In order to identify the importance of these parameters, sensitivity analysis is conducted in two models. In particular, we mainly focus on the sensitivity of parameters related to competition, immunity and drug treatment. Results imply that competition remains a critical factor in both cases(with and without immune response) for resistant parasites ( I_r ), and the immune effect also plays an important role in the immune system. In addition, the significance of drug treatment to drug sensitive parasites ( I_s ) and drug resistant parasites ( I_r ) is lower in both cases (with or without immune response), where the sensitivity index of I_s is much higher than I_r , which is obvious and reasonable, because antimalarial drugs have a direct effect on drug sensitive parasites, but pose indirect impact on drug resistant parasites, such as competition.
The within-host dynamical model of malaria infection is extended to consider competition and host immunity. Our goal is mainly to explore the evolution of drug resistance, which is obviously complex due to involving interacting processes, such as immunity, within-host competition and the patterns of drug use. Our model also appropriately embodies the effects of these interacting processes on the spread of resistance to some extent. However, we have to emphasize that this model cannot rule out the possibility, that intraspecific competition, immune-mediated competition and the fitness costs of resistance may have an influence on the evolution of drug resistance. Hence, it is worth continuously studying these aspects of resistance management.
Acknowledgments
This research is supported by Chinese NSF (grant 11671110) and Heilongjiang NSF (grant LH2019A010).
Conflict of interest
All authors declare that there are no conflicts of interest in this paper.
Appendix
Coefficients to polynomial Equation (2.24)
Coefficients to polynomial Equation (2.26)
Coefficients to polynomial Equation (2.28)









 DownLoad:
DownLoad: