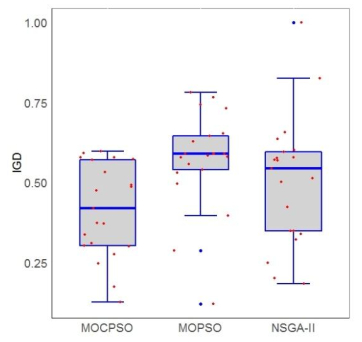
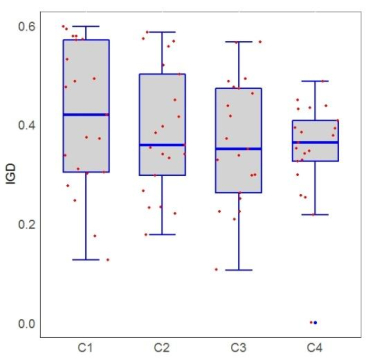
Wellbore drilling parameters optimization is one of the most important issue in drilling engineering. Rate of penetration or mechanical specific energy was usually utilized as the optimization objective. The rate of penetration directly relates to the drilling cycle, while mechanical specific energy reflects the drilling efficiency. In this paper, except for rate of penetration and mechanical specific energy, the drilling life of bit is also summarized as a comprehensive assessment indicator in wellbore drilling parameters optimization problem. The drilling life of bit is taken into consideration for the design and manufacturing cost of bit compose a significant part of the drilling cost and the bit drilling life greatly influences the drilling efficiency. However, those objectives are usually related in a highly nonlinear relationship and in conflict with each other. Thus, a multi-objective cellular particle swarm optimization (MOCPSO) is developed to solve the three-objective drilling parameters optimization problem. Moreover, the radius basis function (RBF) method is employed into the formation parameters identification for rate of penetration model. Performance of MOCPSO is investigated by taken a comparison with multi-objective PSO and non-dominated sorting genetic algorithm-Ⅱ (NSGA-Ⅱ). Effect of the four commonly used neighborhood function is also investigated by making contrasts with each other. It can be inferred that MOCPSO is statistically superior to both multi-objective PSO, NSGA-Ⅱ at the 0.05 level of significance on the wellbore drilling parameters optimization problem. And the four commonly used neighborhood templates perform comparable with each other, and are not statistically different for the drilling parameters optimization problem.
1.
Introduction
In 2017 over 10 million new infections of tuberculosis (TB) occurred mostly in developing countries. TB caused more deaths worldwide than HIV/AIDS. In the same year in Germany, a total of 5,486 cases of TB were notified, which corresponds to an annual cumulative TB incidence of 6.7 cases per 100,000 population. TB incidence in foreign nationals residing in Germany was 18 times higher than the incidence in German citizens [1]. The Bacille Calmette-Guérin (BCG) vaccine is the only available vaccine for prevention of TB. A previous decline in the incidence of TB over several decades in Germany as well as the limited effectiveness of the vaccine led in 1998 to the decision of German officials to discontinue the recommendation for BCG-administration. However, new epidemiological aspects, e.g. the immigration of persons from countries with a higher prevalence of TB [2,3,4,5,6] and the even more challenging view that BCG-vaccination could possibly induce a clinically relevant degree of protection against infections other than TB, could finally result in the conclusion to consider a relaunch of the BCG vaccination in low-prevalence countries like Germany [7]. For other low-prevalence countries we refer the interested reader to [8,9,10,11,12,13,14,15].
The hypothesis that BCG has nonspecific (or: heterologous) effects like induction of protection against other pathogens than M. tuberculosis or M. bovis has emerged from recent findings that the innate host defense system develops immunologic memory similar to the adaptive immune system. The basis of this secondary exaggerated response of the innate immune system is thought to rely on epigenetic programming of macrophages and subclasses of lymphocytes. This phenomenon has been called trained immunity. Several pieces of good evidence culminated in the suggestion that live attenuated vaccines, especially BCG, could be able to enhance trained immunity. In addition, trained immunity might be a target for new approaches to drug development.
The first objective of this paper is to analyse the non-specific effects of a vaccination with the Bacille Calmette-Guérin (BCG) vaccine for limitations of other diseases. The second objective is a determination of conditions and parameters for a model-specific forecast concerning prevalence of tuberculosis afflictions, as well as an evaluation of the used mathematical model.
The relevance of the associated elaborations arises from the current increase in the incidence rate of tuberculosis infection in Germany, which is particularly accounted for by cross-border refugee movements, high rates of infection in at-risk groups. Identifications of an outbreak of tuberculosis often need a considerable amount of time because hardly any specialised centres exist due to the rare occurrence of this disease over several decades. Nonetheless, a target of the World Health Organisation (WHO) is the eradication of the disease by 2050 [27].
Therefore country-specific forecasts are desirable and reasonable. Especially in Germany, where the number of infections is low compared to other countries, tuberculosis is a rather rarely addressed subject. E.g. tuberculosis is contracted by ten times as many humans in London as in Berlin every year. Very high rates of infection are registered in Eastern Europe, where moreover a rise in antibiotic resistances is detected [27].
There are different, hereinafter listed tuberculostatics, which can be prescribed after a diagnosis. The vaccine Bacille Calmette-Guérin (BCG) was developed at the beginning of the twentieth century and protects especially against severe disease progression [16]. However, a BCG-vaccine does not offer sufficient protection against the most frequent form of tuberculosis, which affects the lungs [17,18].
In addition, the significance of this composition is implied by the fact that the Max-Planck-Institute generated a new vaccine on the basis of gene technology at the beginning of this decade. It has already been precisely inspected for safety and effectiveness in clinical testing procedures. The so-called clinical phase-Ⅱ-study will furthermore be carried out with children exposed to HIV. Thus the influence of the vaccine on disease outbreaks and processes as well as side effects on HIV-infected humans, a main group at risk for tuberculosis, are going to be examined.
The outline of this paper reads as follows. First, medical aspects of tuberculosis, specific and innate immune defence and the BCG-vaccine are explained. Next, the elaboration of transitions into mathematical models and evaluations, that are characterised in Sections 4 and 5 are described in a more detailed way and applied with help of the software MATLAB. For this purpose, parameters necessary for a compartment model are calibrated in order to optimally predict sizes of country-specific susceptible, infected, infectious and recovered population groups for future years. Apart from this, child mortality rates of the two African countries Guinea-Bissau and South Sudan, which are comparable regarding their gross domestic product, are considered for their dependence on local BCG-coverages of years starting in 2005 in a second model. The so-called non-specific effects of BCG-vaccinations on respective morbidities are subsequently elucidated.
Selected topics of bacteriology and immunology are presented in this paper in order to enable a deeper understanding of the performed calculations. All used types of compartment models as well as the considered ordinary differential equations (ODEs) are numerically solved using the programming language MATLAB.
2.
Medical background
The medical background of this work includes sections on the epidemiology, the transmission, clinical aspects, diagnosis and therapy, reporting obligations of tuberculosis as well as the development of the specific and the non-specific host defense after BCG-vaccination. In addition, differences and similarities between the adaptive and the innate immune response are outlined. In particular, the concept of trained immunity will be elaborated in detail.
2.1. Tuberculosis
Tuberculosis (TB) caused by Mycobacterium tuberculosis (MTB) can involve all organs of the body but primarily affects the lungs, because the bacteria are most frequently transmitted by aerosol. Ninety percent of the infections do not result in clinical symptoms (latent tuberculosis, LTB). If they are not treated adequately, approximately 50% of the patients suffering from active disease die, in most cases after a prolonged, chronic course lasting months or years. The slow often undetected progress of TB facilitates the transmission of the etiologic agent to susceptible persons, who come in close contact to an index case (22% infection rate).
The most important risk factors for enhanced acquisition of TB are HIV/AIDS, malnutrition, crowding, diabetes, alcoholism and iv-drug abuse, because host defense mechanisms are hampered or overstressed under these conditions. In addition, infants, children and patients with chronic lung disorders, e.g. silicosis, and smokers are more susceptible to TB. Silicosis increases the risk about 30-fold and cigarette smokers have nearly twice the risk of TB as compared to nonsmokers. Certain medications, e.g. corticosteroids or infliximab (an anti-TNFα monoclonal antibody) increases the susceptibility for TB. Persons with LTB do not spread the disease.
Subsequently we outline the epidemiology and the prevention of TB in detail, because they are fundamental for the understanding of our mathematical model. Clinical aspects, diagnostic procedures and the therapy of TB are only briefly presented, whereas the specific and especially the nonspecific host response after Bacille Calmette Guérin (BCG)-vaccination are again discussed extensively with emphasis on differences between adoptive and innate host defense. In this context we will explicitly elucidate the rather recently discovered important issue of trained innate immunity [19,20,21,22,23,24,25,26].
2.2. Epidemiology
Patients with active pulmonary TB expel infectious aerosol droplets 0.5 to 5.0 micrometer in diameter. A single sneeze can release up to 40,000 droplets, of which each one may transmit the disease, since the infectious dose of tuberculosis is small. The inhalation of fewer than 10 bacteria may cause the disease. A person with active but untreated tuberculosis may infect 10–15 other people per year. The probability of transmission from one person to another depends on the number of infectious droplets expelled by the carrier, the effectiveness of ventilation, the duration of exposure, the virulence of the strain of M. tuberculosis, the level of immunity and other risk factors of the uninfected person. The cascade of person-to-person spread can be circumvented by segregating those with active ("overt") TB and by administration of tuberculostatic medication. After about two weeks of effective treatment, subjects infected with nonresistant MTB generally do not remain contagious. If someone does become infected, it typically takes three to four weeks before the newly infected person becomes infectious enough to transmit the disease to others.
Despite considerable achievements in prophylaxis, diagnostic procedures and therapy, TB is still (2016) among the 10 leading causes of death worldwide and the leading cause of death from a single infectious agent, ranking above HIV/AIDS [27,28]. Globally, the TB mortality rate is falling at about 3% per year. This figure needs to improve to 4–5% per year in order to reach the first (2020) milestone of the WHO End TB Strategy [29]. It is estimated that 25 to 30% of the world population is infected with M. tuberculosis without exhibiting overt disease symptoms, and that 67 million children are latently infected [27,28]. More than 95% of deaths occur in developing countries.
In 2016, 6.3 million new cases of TB were reported (up from 6.1 million in 2015), equivalent to 61% of the estimated incidence of 10.4 million. The latest outcome data show a global treatment success rate of 83% similar to previous years. There were 476 774 reported cases of HIV-positive TB (46% of the estimated incidence), of whom 85% were on antiretroviral therapy. Of the estimated 10.4 million new cases of TB in 2016 approximately 90% were adults, 65% were male, 10% were people living with HIV (74% in Africa) [27].
Approximately 5–10% of people without HIV who are infected with MTB develop active disease during their lifetimes. In contrast, 30% of those coinfected with HIV and MTB develop overt tuberculosis. Active TB is closely linked to both overcrowding and malnutrition, making it one of the principal diseases of poverty. Regions with universal access to high quality diagnostic and therapeutic interventions, adequate nutrition, good housing, working and other socio-economic conditions exhibit low incidence rates for TB, low prevalence countries.
Children develop disease symptoms approximately one year after infection. Without adequate therapy 45% of HIV-negative and almost all HIV-positive patients with overt TB will succumb to the disease. In Africa in 2015 81% of TB-patients were co-infected with HIV, emphasizing the strong correlation between both infections.
Drug-resistant TB is a continuing threat. In 2016, there were 600 000 new cases with resistance to rifampicin (RR-TB), the most effective first-line drug, of which 490 000 had multidrug-resistant TB (MDR-TB). Almost half (47%) of these cases occurred in India, China and the Russian Federation. Extended Dug Resistant TB (XDR-TB) is also of special concern. In 2015 it has been estimated that 4.3 million cases with resistant MTB were not reported to health officials.
In Germany a total of 5915 new TB-cases were notified in 2016, and 5486 cases in 2017 [30,31]. This corresponds in 2016 to an annual TB incidence of 7.2 cases per 100,000 of the total population, 1.332 (29%) more than 2014, which has been the largest increase within the last nine years, see Figure 1.
The total number of TB-cases between 2016 and 2017 remained almost unchanged in comparison to 2015 with 5,828 patients, incidence 7.1 per 100,000 [30]. The incidence of tuberculosis was 9.9 cases per 100,000 population in men and 4.6 in women (male to female ratio of 2.2). The age-specific incidence was highest in the age-group 20–24 years (18.3 cases per 100,000 population; 25.9 in men and 9.7 in women). TB-incidence in persons of foreign nationality residing in Germany was 19 times higher than the incidence in German citizens (42.6 vs. 2.2 cases per 100,000 population). This difference between the two groups increased in comparison to the previous year (16.6 times higher). The greatest increase was seen in young adults. German citizen comprised 30.9% of all tuberculosis cases, whereas the remaining 69.1% were of foreign nationality. Foreign nationals with tuberculosis were younger than German nationals (median age: 28 vs. 58 years) [30,31]. The incidence of TB decreased in 2017 (6.7 cases per 100,000 inhabitants) but was still higher than during the years 2008 to 2014 before the influx of migrants from high prevalence countries [1,32].
In children younger than 15 years 233 cases were reported in 2016 (incidence 2.1 cases per 100,000 children). The number of cases increased compared to 2015 (196 cases; incidence 1.8 per 100,000 children). Tuberculosis incidence was highest in the youngest age group below five years (104 cases; incidence 2.9 per 100,000). In children aged 5 to 9 years, the incidence of TB was 1.5 per 100,000 (53 cases), while in children of 10 to 14 years, it was 2.1 per 100,000 (76 cases). The number of children with resistant TB (RR-TB, MDR-TB and XDR-TB) increased (18 of 89 children, 30.5%).
In 2016 a total of 100 patients died of tuberculosis (2015: 110 deaths), mortality rate 0.12 cases per 100,000 population. The case fatality rate in 2016 was 1.7% (1.9% in 2015). The proportion of MDR-TB 2016 in Germany (104 cases; 2.7%) was lower as compared to 2015 (123 cases, 3.1%), but still higher than in 2014 (94 cases; 2.1%). The proportion of MDR-TB was highest in patients born in one of the newly independent states (NIS) of the former Soviet Union (15.3% compared to 1.0% in German born patients). Five XDR-TB cases were reported to the Robert Koch Institute (RKI) in 2016. The overall proportion of TB cases resistant to at least one of five standard anti-TB drugs (isoniazid, rifampicin, ethambutol, pyrazinamide and streptomycin) was 12.8% in 2016 (2015: 13.0%). Primary resistance occurs when a person becomes infected with a resistant strain of TB. A person with fully susceptible primary infection may develop secondary (acquired) resistance during therapy because of inadequate treatment, not taking the prescribed regimen appropriately (lack of compliance) or using low-quality medication.
Drug-resistant TB is a serious public health issue in many developing countries, as its treatment lasts longer and requires more expensive drugs. MDR-TB is defined as resistance to the two most effective first-line TB drugs: rifampicin and isoniazid. Extensively drug-resistant MTB XDR-TB is a term sometimes used to define extensively resistant TB and constitutes one in ten cases of MDR-TB. Cases of XDR-TB have been identified in more than 90% of all countries. Totally drug-resistant TB is resistant to all currently used drugs. It was first observed in 2003 in Italy, but not widely reported until 2012.
2.3. Pathogenesis and immunity
Macrophages usually residing in the alveoli recognize the infecting bacterium as foreign and attempt to eliminate it by phagocytosis. During this process, the bacterium is enveloped by the macrophage and stored temporarily in a membrane-bound vesicle called a phagosome. The phagosome fuses with a lysosome to create a phagolysosome. In the phagolysosome, the host cell attempts to use reactive oxygen species and acid to kill the bacterium. However, the thick, waxy mycolic acid capsule protects M. tuberculosis from these toxic substances and enables the bacterium to multiply inside the macrophage. This might kill the macrophages resulting in caseous necrosis and caverns in the lung of the infected patient.
Tuberculosis is classified as a granulomatous inflammatory disease. Macrophages, T-lymphocytes, B-lymphocytes, and fibroblasts agammaegate to form granulomas, with lymphocytes surrounding the infected macrophages. When other macrophages attack the infected macrophage, they fuse together to form a giant multinucleated cell in the alveolar lumen. The granuloma may prevent dissemination of the mycobacteria and provide a local environment for interaction of cells of the immune system. In addition, the bacteria use the granulomas to avoid destruction by the host's immune system. Macrophages and dendritic cells in the granulomas are unable to present antigen to lymphocytes, i.e. the immune response is suppressed. Bacteria inside the granuloma can become dormant sometimes for years, resulting in latent infection. Miliary tuberculosis and tuberculous meningitis, the most severe forms of the disease, are most common in young children and those with HIV infection.
2.4. Diagnosis
Diagnosis of active TB is based on chest x-ray, as well as microscopy of smears and culture of body fluids. Furthermore, diagnosis of latent TB relies on the tuberculin skin test (TST) or tests for antibodies in serum. About 80% of people in many Asian and African countries but only 5–10% of people in the United States population test positive by the tuberculin test. In Germany refugees accounted for 74.3% of cases detected by active case finding. Pulmonary tuberculosis was diagnosed in 74% of cases (4397 of 5915 cases; incidence 5.4 per 100,000). Sputum-smears or cultures were positive in most cases (3362 cases, incidence 4.1) rendering these patients potentially contagious in comparison to non-infectious pulmonary tuberculosis (1035 cases; incidence 1.3). Of the patients with pulmonary TB, 40.3% (1774 of 4397) were smear - positive and, thus, the most infectious cases [30,31].
2.5. Therapy
The recommended treatment of new-onset pulmonary tuberculosis is six months of a combination of antibiotics. If MTB recurs, antibiotic sensitivity testing is important before treatment is initiated. If MDR-TB is detected, treatment with at least four effective antibiotics for 18 to 24 months is recommended. Treatment outcome can only be assessed after at least 12 months of follow-up. People with latent infections are also treated to prevent them from progressing to active TB disease later in life.
2.6. Prevention
Prevention of TB involves screening persons at high risk with early detection, and vaccination with Bacille Calmette-Guérin (BCG). Tuberculosis prevention and control efforts rely primarily on the vaccination of infants and the detection and appropriate treatment of active cases. The US Preventive Services Task Force (USPSTF) recommends screening people who are at high risk for latent tuberculosis with either tuberculin skin tests or interferon-gamma release assays.
Bacille Calmette Guérin (BCG) vaccine consists of an attenuated live bovine tuberculosis strain and is at present the only available vaccine for routine use. The BCG-vaccine introduced in 1921 is on the WHO-List of Essential Medicines, the most effective and safe medicines needed. Between 2011 and 2014 the wholesale price was 0.16 to 1.11 USD a dose in the developing world. In the United States it costs 100 to 200 USD. The vaccine is given to about 100 million children per year globally.
Good protection is provided by BCG-vaccination against meningitis and miliary tuberculosis, whereas rates of protection against pulmonary tuberculosis infection vary widely [33]. This variable efficacy found in different clinical trials appears to depend on geography. Trials conducted in the UK have consistently shown a protective effect of 60 to 80%, but those conducted elsewhere have shown little to no protective effect. Genetic differences in the populations, changes in environment, exposure to other bacterial infections, and conditions in the laboratory where the vaccine is grown might be responsible for the differences in vaccine efficacy. A systematic review and meta-analysis conducted in 2014 demonstrated that the BCG-vaccine reduced infections by 19–27% and reduced progression to active TB by 71% [33].
BCG-vaccine is primarily used in countries where tuberculosis is common. One dose is administered in healthy infants by intradermal injection close to the time of birth. Serious side effects of the BCG-vaccination are rare, but it is not safe for use during pregnancy. Vaccinated persons can be infected and become infectious. Because the BCG vaccine has efficacy-limitations, investigations to develop new TB vaccines are ongoing [34,35]. Its preventive effect against pulmonary TB varies from person to person. Therefore, there arises a need for a new TB vaccine to replace or supplement BCG. Several potential candidates are currently in clinical trials of phase Ⅰ and phase Ⅱ. Two main approaches are being used to attempt to improve the efficacy of available vaccines. One approach involves adding a subunit vaccine to BCG, while the other strategy is attempting to create new and better live vaccines. Additional doses are not supported by evidence. In low prevalence areas, only children at high risk are immunized. Adults who do not have tuberculosis and have not been previously immunized but are frequently exposed to drug-resistant tuberculosis may be immunized as well. Further, BCG does not protect from the reactivation of latent tuberculosis.
In low prevalence regions like the United Kingdom, the United States, and most European countries BCG is only administered to people at high risk, because the vaccination can induce a false-positive reaction of the tuberculin skin test (Mendel-Mantoux test). The duration of protection of BCG is not clearly known. The MRC study showed protection waned to 59% after 15 years and to zero after 20 years [33].
BCG has a protective effect against leprosy in the range of 26 to 41% based on controlled trials [36]. The authors argue for more emphasis on the role of BCG vaccination in leprosy control. Furthermore, BCG has been one of the most successful immunotherapies of non–muscle-invasive bladder cancer (NMIBC) [37].
Except in neonates, a tuberculin skin test should always be done before administering BCG. A person with a positive tuberculin reaction is not given BCG, because the risk of severe local inflammation and scarring is high. BCG is also contraindicated in certain people who have IL-12 receptor pathway defects. If BCG is accidentally given to an immunocompromised patient (e.g. an infant with Severe Combined Immuno-Deficiency, SCID), it can cause disseminated or life-threatening infection. WHO stopped recommending BCG for infants with HIV, even if there is a high risk of exposure to TB because of the risk of disseminated BCG infection, which is approximately 400 per 100,000 in this higher risk context. BCG is administered only once during an individual's lifetime, because there is no evidence of additional protection from more than one vaccination. BCG was also given to protect people who had been exposed to tuberculosis. Routine immunization with BCG for all school children was discontinued in low prevalence countries because of falling cost-effectiveness. Whereas in 1953, the number needed to vaccinate was 94 by 1988 the annual incidence of TB in the UK had so significantly decreased that 12,000 children would have to be immunized to prevent one case of TB [33]. The vaccine is still given to certain healthcare professionals, however.
After the Second World War several European countries including the former German Democratic Republic have practiced mandatory BCG-vaccinations, whereas in the United States it has never been necessary to practice mass immunization of BCG, relying instead on the detection and treatment of latent tuberculosis.
2.7. Nonspecific effect
Host immune responses are classically divided into innate immune responses, which react rapidly and nonspecifically upon encountering a pathogen, and adaptive immune responses, which are slower to develop but are specific and build up immunological memory with augmented host response. The dogma that only adaptive immunity can build immunological memory has been challenged by studies showing that innate immune response in organisms lacking adaptive immunity can develop increased resistance to reinfection. Furthermore, in certain mammalian models of vaccination, protection from reinfection has been shown to occur independently of T and B lymphocytes. These observations led to the hypothesis that innate immunity can display adaptive characteristics after challenge with pathogens or their products. This de facto immunological memory has been termed "trained immunity" or "innate immune memory" [22,38,39,40].
Non-specific, also called "heterologous" or "off-target" effects of vaccines, are effects which go beyond the specific protective activities against the targeted diseases. All live attenuated vaccines like BCG, measles (MV), polio (OPV) and smallpox have been shown to reduce mortality more than explained by target-disease prevention [18,25,41,42,43,44,45,46,47]. The internal validity of studies on the effects of BCG, whole cell DTP, and standard titre MCV in children under 5 years revealed that BCG and MCV reduce overall mortality by more than would be expected through their effects on the diseases they prevent, whereas receipt of DTP may be associated with an increase in all cause mortality [18]. In a situation with herd immunity to the target disease, the non-specific effects (NSE) [48,49] could be more important for overall health than the specific vaccine effects. The non-specific effects represent a form of general immunomodulation, with important consequences for the ability of the immune system to handle subsequent challenges. It is estimated that a considerable number of child deaths in low income countries could be prevented every year if the non-specific effects of vaccines were taken into consideration in immunization programs [42,47,50].
It has also been shown in epidemiological studies that BCG administration may reduce sepsis and respiratory tract infections [51]. Before the reunion of the two parts of Germany in 1990 different vaccination policies were practiced. In the former German Democratic Republic (GDR) BCG was part of the mandatory vaccination program, whereas in the Federal Republic of Germany (FRG) BCG has been administered to persons under increased risk for TB only. By comparing these two populations, GDR and FRG, we could recently provide some evidence that BCG might induced beneficial effects against other diseases than tuberculosis, e.g. decreased hospitalization for sepsis, HIV and pneumoia [52]. This issue is addressed by our mathematical model. The non-specific effects do not only affect bacterial but also viral infections [53]. Non-specific effects can be strongly beneficial, increasing protection against non-targeted infections, but also at times negative, increasing susceptibility to non-targeted infections. This depends on both the vaccine and the sex of the infant [20,54]. The marked reduction in mortality in the days after BCG vaccination in boys emphasizes the importance of providing BCG soon after birth.
These observations encouraged randomized controlled trials in low prevalence countries to examine BCG vaccination's beneficial non-specific effects on overall health [55,56]. In Denmark BCG vaccination did not affect the rate of hospitalization for infection up to the age of 15 months in this high income low prevalence study population. Of considerable importance would be the extension of the non-specific effect of BCG or other live vaccines on the prevention of HIV/AIDS [57]. BCG vaccination later in infancy may modify immune responses to non-TB antigens and potentially enhance immunity also against tuberculosis (TB). It is unclear whether BCG vaccination very early in life offers adequate protection against TB and other infections among HIV-1-exposed children. Further studies on this aspect of non-specific protection are ongoing in Uganda [21,58]. Revaccination with live vaccines led to substantial reductions in overall mortality. These findings challenge current understanding of vaccines and may explain the beneficial effects of campaigns with live vaccines. Non-specific effects of vaccines could be boosted or diminished when other immunomodulating health interventions such as other vaccines are provided [59].
The results of clinical trials have stimulated interest in understanding the immunological mechanisms underlying the effects on nonspecific protection in the hope of harnessing them to reduce all-cause mortality. This line of investigation is especially important in light of BCG being discontinued in some countries as the prevalence of TB falls. Stopping routine BCG in this situation may have the unintended consequence of depriving children of the beneficial immune modulating effects of this vaccine. BCG has been recognized as a potent immunomodulator for decades. The lines of immunological enquiry can be seen to mirror the evolution of our understanding of cell-mediated immunity and its components. BCG-induced immunity against heterologous antigens may provide information on immunological pathways worthy of further interrogation using modern immunological methods.
BCG increased proportions of effector memory cells at 3 months. However, limited overall impact of neonatal BCG vaccination on lymphocyte subsets was found in healthy Danish infants within the first 13 months of life [60]. The findings from the epidemiological studies on the non-specific effects of vaccines pose a challenge to the current understanding how vaccines affect the immune system. They also question whether boys and girls have identical immune systems and should receive the same treatment. The mechanisms for these effects are not fully understood [22,61]. Heterologous T-cell immunity can lead to improved clearance of a subsequent cross-reactive challenge. However, induction of heterologous immunity would not explain effects occurring shortly after vaccination, as for instance the rapidly occurring beneficial effects of BCG, because adoptive immunity needs some weeks to develop. It would also be difficult to explain why the effect would vanish once a child receives a new vaccine. The recently evolving concept that mammals including humans have innate immune memory may provide new clues to the argument that live vaccines have non-specific effects. Studies into BCG have recently revealed that BCG induces epigenetic changes in the monocytes in adults, leading to increased pro-inflammatory cytokine production upon challenges with unrelated mitogens and pathogens [62].
In SCID mice that have no adaptive immune system, BCG reduced mortality from an otherwise lethal candida infection. The effects of BCG presented when tested after 2 weeks, but would be expected to occur rapidly after vaccination, and hence might be able to explain the very rapid protection against neonatal septicaemia seen after BCG vaccine administration. Trained innate immunity may also explain the generally increased resistance against broad disease categories, such as lower respiratory tract infections [53,63]. Such effects would be difficult to explain merely by shared epitopes, unless such epitopes were almost universally common on pathogens.
Lastly, it is plausible that the effects are reversible by a different vaccine. Hence, trained innate immunity [64] may provide a biological mechanism for the observed non-specific effects of vaccines. It would have major consequences for child survival if the non-specific effects of vaccines were taken into consideration in immunization programs.
A positive association between thymic output, lymphocytes and a reduced risk of infections has been found. Recent studies suggest that "trained immunity" mediated via functional reprogramming of the monocytes may play an important role [62]. Effects on the adaptive immune system are also a possibility. The thymus is essential in the generation and maturation of T cells and therefore, also in generating a normally functioning immune system [60]. The size of the thymus has been shown to be important for infant survival in low-income countries. In Guinea-Bissau thymic size at birth, was found to have a stronger association with survival than body weight and among 6-mo-old children, a doubling of the thymic size was associated with a 72% reduction in mortality up to 3 years of age. Based on the facts that both BCG vaccination and a large thymus have been associated with increased infant survival, it has been hypothesized that the BCG-induced beneficial nonspecific effects were mediated by increasing thymic size.
It has also been shown that BCG vaccination in healthy volunteers led to NOD2-dependent epigenetic reprogramming of monocytes, which resulted in an increased expression of cellular receptors on the monocytes, accompanied by higher cytokine production in response to non-related pathogens [62]. This newly described mechanism might represent the explanation for the rapid non-specific protective effects induced by BCG vaccination. However, it is not known how long trained immunity and/or heterologous immunity persist after BCG vaccination. The heterologous production of Th1 (IFN-γ) and Th17 (interleukin (IL)-17 and IL-22) immune responses to non-mycobacterial stimulation remained strongly elevated even one year after BCG vaccination. In conclusion, BCG induces sustained changes in the immune system associated with non-specific response to infections both at the level of innate trained immunity, as well as at the level of heterologous Th1/ Th17 responses [62]. BCG-vaccinated infants had increased production of interleukin 6 (IL-6) in unstimulated samples and decreased production of interleukin 1 receptor antagonist, IL-6, and IL-10 and the chemokines macrophage inflammatory protein 1α (MIP-1α), MIP-1β, and monocyte chemoattractant protein 1 (MCP-1) following stimulation with peptidoglycan (TLR2) and R848 (TLR7/8). BCG-vaccinated infants also had decreased MCP-1 responses following stimulation with heterologous pathogens. Sex and maternal BCG vaccination status interacted with neonatal BCG vaccination, [65]. Neonatal BCG vaccination influences cytokine responses to TLR ligands and heterologous pathogens. This effect is characterized by decreased antiinflammatory cytokine and chemokine responses in the context of higher levels of IL-6 in unstimulated samples. This supports the hypothesis that BCG vaccination modulates the innate immune system. Further research is warranted to determine whether there is an association between these findings and the beneficial nonspecific (heterologous) effects of BCG vaccine on all-cause mortality.
3.
Vaccine effectiveness
In this section we distinguish between vaccine efficacy and vaccine effectiveness. Moreover, differences between direct, indirect, total and overall vaccine effectiveness are shown and explained using a graphic. This section therefore serves to understand the terms "vaccine efficacy" and "vaccine effectiveness", which will be used in later subsections.
3.1. Calculation of vaccine efficacy and vaccine effectiveness
When calculating how well disease outbreaks are prevented by the vaccine developed for this purpose, a distinction between vaccine efficacy and vaccine effectiveness is necessary. Vaccine efficacy defines how helpful a vaccine is if 100% of those who could be vaccinated are vaccinated. Thus the environment in the population is assumed to be controlled. Studies that analyse vaccine efficacy yield most accurate results as prospective, randomized, double-blind, controlled clinical trial.
Vaccine effectiveness determines how helpful a vaccine is under normal circumstances. This means that access to the respective health care system, vaccination costs, storage time of the vaccine as well as other facts that may influence the vaccination status of individuals are included in the calculation [66]. It follows that certain regions within a population can be regarded as completely unvaccinated due to lacking vaccination practice. The vaccine effectiveness (VEeffective) is calculated as follows [66]:
The odds ratio OR is a risk identifiable in the following way [67]:
The variables Ni,j with i,j=1,2 denote the number of individuals with the expression i respectively j of the characteristic "Disease" respectively "Vaccination". The odds ratio is determined as
The vaccine efficacy is calculated by the formula
Here, RR denotes the relative risk of falling ill as an uninoculated person in relation to the diseased inoculated. It is also called the cumulative incidence of the group that is not exposed to the risk compared with the cumulative incidence of the group exposed with a risk factor. Based on the explanations for Eq (3.2), the relative risk RR can be calculated as:
The OR, however, describes the risk of falling ill as an unvaccinated person, compared with the probability of not falling ill as a vaccinated person. It reveals how much likelier it is to sicken with the risk factor than without it.
It is always greater than 0 and, unlike relative risks, does not directly relate to probabilities. The so-called indirect, direct, total as well as overall vaccine effectiveness explained in Section 3.2 can be analysed with the help of infection rates (attack rates, AR) of the members of the population. These AR describe the incidence rates for infected people of certain groups: AR0 defines the AR of individuals before the introduction of the respective vaccination program (pre-vaccination rate), ARu and ARv equal the attack rate of the unvaccinated respectively vaccinated after the introduction of the program [66]. This leads to the following formulas, where f denotes the vaccination coverage [43]:
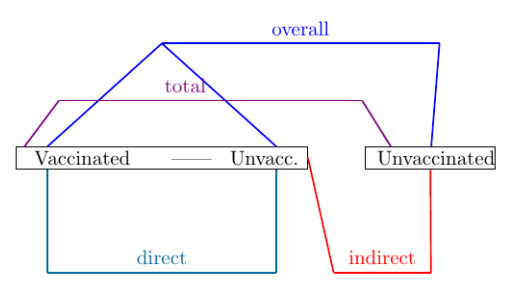
3.2. Indirect, direct, total and overall vaccination effect
Vaccine effectiveness can be divided into the direct, indirect, total and overall effect. The three last ones increase as part of a rising vaccination coverage.
● The direct effect corresponds to the direct risk of a randomly selected vaccinated individual compared with an unvaccinated person.
● The indirect effect is defined as the protection which unvaccinated individuals obtain due to a vaccination program available to the population. The basis for comparison is the same population in which this vaccination program is not carried out.
● The total effectiveness compares the relative risk of infection of vaccinated individuals with the risk of unvaccinated individuals before the introduction of the vaccination program.
● The overall effectiveness of a vaccination program is defined by its reduction of the transmission rate for an average individual in a society compared with a society without such a vaccination program. For that reason it represents a combination of direct and indirect effectiveness.
The indirect and the total effect thus compare the cumulative incidence of a population in which a vaccination is or respectively is not possible with each other [43]. The four types of vaccine effectiveness are illustrated in Figure 2.
4.
Vaccine efficacy in the SEIR model
We now consider the so-called SEIR model, in particular by reference to the variable α representing the vaccine efficacy. The term SEIR stands for the groups of "susceptibles", "exposed", "infectious" and "recovered" individuals. The context of these terms is explained in more detail in this section. The model is applied in epidemiology in order to describe the spread of diseases. Accruals and decreases of individual population groups are described in a disease-related manner. The SEIR model is mathematically expressed by a system of ODEs, which is set up in Section 4.3. All required variables are furthermore introduced in Section 4.2, whereby assumed values are discussed in line with their consequences. As a result, the differences between so-called all-or-nothing (AoN) and leaky vaccinations are described. They are mathematically explained in Section 4.1, which has the two purposes of being able to use the variable α in Sections 4.2 and 4.3, and to show impacts of variable changes and the inclusion of vaccine-administered individuals in the model in Section 4.4. Finally, in Section 4.5, possibilities of predicting vaccine effects are presented by using MATLAB programs. Possible extensions of the existing SEIR model are also described.
4.1. Leaky and all-or-nothing vaccinations
The effectiveness of a vaccination mechanism can be demonstrated by describing it as an all-or-nothing (AoN) or leaky vaccination. In AoN vaccinations, a proportion i of all vaccinees is immunized with respect to the considered infection. The proportion 1−i of unimmunized vaccinees is not included. In the case of a leaky vaccine, by contrast, unimmunized individuals are included as well. The following equation targets to calculate the vaccine efficacy α, where ˜α represents a reduction of the risk of infection:
If a vaccine is completely (entirely) leaky, complete protection against the respective infection is not provided for anybody. Every individual can be re-infected. The following applies:
Here α is equivalent to the risk of re-infection ˜α. In the case of an AoN vaccination, only the proportion of vaccinees who receive complete protection is considered. Then ˜α=0 and α=i. Here α corresponds to the proportion of individuals who are immunized against the particular infection by vaccination. However, a vaccine can also be considered as not completely leaky. For example, i may be in the range of [0, 0.7] so that 70% of the population receives complete protection, but the remaining vaccinated can be included too. The following applies:
We deduce that the vaccine efficacy equates to the relative reduction of the transmission rate of vaccinated individuals. AoN vaccinations are generally more effective than entirely-leaky vaccines. For instance, in scenarios with a high risk of re-infection or transmission, a vaccine that immunizes a certain amount of the population is more efficient [43].
Total effectiveness is greater than direct effectiveness of leaky vaccines at each percentage of vaccination coverage. If this proportion increases, overall effectiveness increases faster than the indirect effect. In addition, vaccine protection can be underestimated here. This underestimation tends to increase as soon as the vaccination rate or the reduction of infectiousness among vaccinated decreases. In leaky and AoN vaccinations total effectiveness is greater than indirect as well as overall effectiveness for any proportions of inoculum quota. The reason for this is the fact that overall and indirect effectiveness provided by herd immunity warrant partial protection for unvaccinated individuals, but direct in the course of total protection for vaccinated people is often more beneficial.
4.2. Meaning of variables in the SEIR model
For infectious diseases, a dynamic model can be established. A basic model is the SIR model composed of healthy but not immunized individuals ("susceptibles"), infectious individuals as well as immunized individuals ("recovereds"). It can be expressed by the following system of ODEs, provided that birth and mortality rate of the respective population are not considered [68,p. 1]:
Here β denotes the transmission rate at which individuals are exposed to infection, and 1/γ is the mean duration of infectiousness. Meanings of the variables β and γ will be explained in more detail. When modeling the rate of infection, the law of mass action can be invoked. In the context of tuberculosis it describes that the infection rate is proportional to the prevalence or depends on the product of members of certain compartments (reactors). This yields β⋅S⋅I. The form β⋅S⋅I/N is used in most epidemiological models today. It means that if the population size N remains constant or asymptotically approaches a certain value, the use of an infection rate proportional to S⋅I does not cause any qualitative changes in the model [69]. The present SIR model can be extended to a SEIR model. This extension is especially useful concerning a longer incubation period of a disease, as individuals have usually been ill for a certain period but are not infectious in this case. They are then called 'exposed'. Using the example of tuberculosis, 'exposed' individuals are those who are infected but not contagious. Because the model can be used to assess the effects of a vaccination program, a distinction between vaccinated and unvaccinated individuals can be made. Consequently, the N members of an existing population are divided into the following subetaoups:
Sv: vaccinated susceptibles
(vaccinated healthy individuals who are not immunized)
Su:unvaccinated susceptibles
(unvaccinated healthy individuals who are not immunized)
Ev: vaccinated exposed
(vaccinated diseased individuals)
Eu: unvaccinated exposed
(unvaccinated diseased individuals)
Iv: vaccinated infectious
(vaccinated infectious/infectious individuals)
Iu: unvaccinated infectious
(unvaccinated infectious/infectious individuals)
Sv2: vaccinated recovered susceptibles
(vaccinated individuals who can get sick again)
Su2: unvaccinated recovered susceptibles
(unvaccinated individuals who may become ill again)
R: recovereds
(immunized individuals by vaccination)
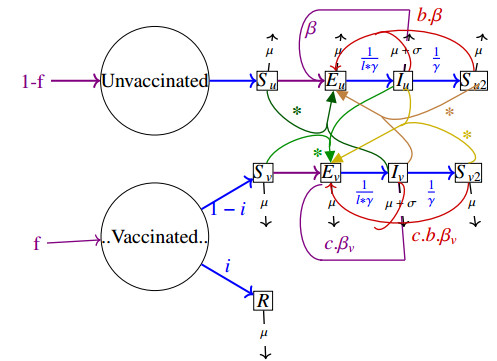
Diseased individuals Ev and Eu also comprise infected people without active disease. Consequently, infectious people and infected people with latent tuberculosis are in the same compartment. Individuals enter the given system by birth. A proportion f of the newborn is vaccinated and 1−f individuals are not vaccinated. The variable f therefore represents the percentage proportion of vaccinated people of the considered population and is referred to as vaccination coverage. In each of the segments S, E, I, S2 and R the mortality rate for non-disease deaths is given by a variable μ. Furthermore, there is a specific mortality rate for death due to disease called σ. The duration of infectiousness is γ and the rate at which individuals recover is defined by 1/γ. The variable l describes a latency multiplier. In addition, the variable b represents the risk of re-infection. β is the transmission rate at which unvaccinated healthy individuals Su are exposed to an infection. For individuals Su2 this rate is replaced by b⋅β, for Sv it is replaced by βvacc, and for Sv2 is replaced by b⋅βvacc. βvacc is defined as transmission rate for unvaccinated individuals who have incomplete immunisation coverage:
Because (1−˜α) equals a reduced risk of infection, which is displayed by incoulated as opposed to unvaccinated individuals. Apart from that, the variable c is the relative infectiousness of vaccinated infectious individuals [43]. In Table 1, all variables are listed along with values they can take.
The baseline values refer to leaky vaccinations as well as overall and a direct effectiveness of 63% each. The parameter β has to be derived from the other values. The equation
can be rewritten as
cf. [43,p. 9]. R0 can be calculated using the equilibrium condition [70]:
4.3. System of differential equations for the SEIR model
In epidemiology populations are divided into so-called compartments for the purpose of modeling the occurrence and spread of diseases and infections. Different compartments are distinguished by the health status of their members regarding the respective pathogen. The described SEIR model is such a compartment model. Our first aim is the derivation of a system of differential equations from the given compartments. Iv is generally multiplied by the parameter c because vaccinated are less infectious than unvaccinated individuals with respect to a large number of diseases. Furthermore, Su2 and Su are multiplied by β, and Sv2 as well as Sv are multiplied by βvacc as β and βvacc are the transmission rates of the respective infection. Additionally, a multiplication of Su2 and Sv2 by b is essential because these compartments describe individuals with a risk of relapse. In this context, a relapse is either a re-infection or a repeated "flare-up" (or recurrence) of the respective disease. Individuals Eu result from pairwise contact of individuals Su, Su2, Iu and Iv, and individuals Ev result from pairwise contact of individuals Sv, Sv2, Iu and Iv. This leads to the two contact terms
It firstly means that both vaccinated and unvaccinated healthy people are infected by contact with unvaccinated or vaccinated individuals. A multiplication of any two compartments is called a contact term. In Figure 3, this is indicated by the dark green and upper purple arrow for Eu, and by the light green and the lower purple arrow for Ev. Secondly, those having suffered from tuberculosis and still carrying the infection but are not infectious can fall ill again. They are part of the compartments Su2 or Sv2 and called carrier. In Figure 3, this is expressed by the red arrows, the brown and the orange arrow. In period t, the numbers Eu and Ev are reduced by the sum of those who die and the ones who become infectious after a certain time. The model is based on the fact that only infectious (not infected) individuals die due to infection. This leads to the two ODEs
The number Su reduces by the numbers of individuals coming in contact with infectious Iu or Iv and contracting the infection by rate β during a time t. This is β⋅Su⋅(Iu+Iv⋅c). Furthermore, Su reduces by the number of healthy unvaccinated dying at rate μ. The number of new births in period t is identified with the number B of all deaths. Su increases by the number (1−f)⋅B of all unvaccinated newborns. Changes in the number Sv behave analogously except for the fact that Sv increases by the number of vaccinated non-immunised newborns per unit of time. We derive the two ODEs
and
Numbers of infectious Iu and Iv increase by the numbers of exposed individuals Eu or Ev who become infectious during period t, and reduce by the number of those who recover after a certain period 1/γ and by the number of infectious dying at rates μ and σ. Therefore we obtain the ODEs
and
The numbers of vaccinated or unvaccinated who have recovered is decreased by the proportion of dying or re-infected individuals per time t. These newly infected are
In contrast, the numbers increase by the sum of vaccinated and unvaccinated infectious recovering by rate 1/γ. 1/γ denotes the rate at which infectious recover. The complete differential equations read
The number of immunised individuals R increases by the sum of people immunised by vaccination. It reduces by the number of dying immunised per time unit t.
Figure 3 illustrates the structure of the compartment model used here. Coloured arrows represent the transitions between the compartments.
The course of health behaviour of the members of the compartments over time can be explained by the derived ODEs. The following system of ODEs in the SEIR-Model (cf. [43]) can be established:
Note that the sum of these nine ODEs equals zero, i.e. the total population is assumed to be constant.
4.4. Influence of Variables in the Differential Equations System
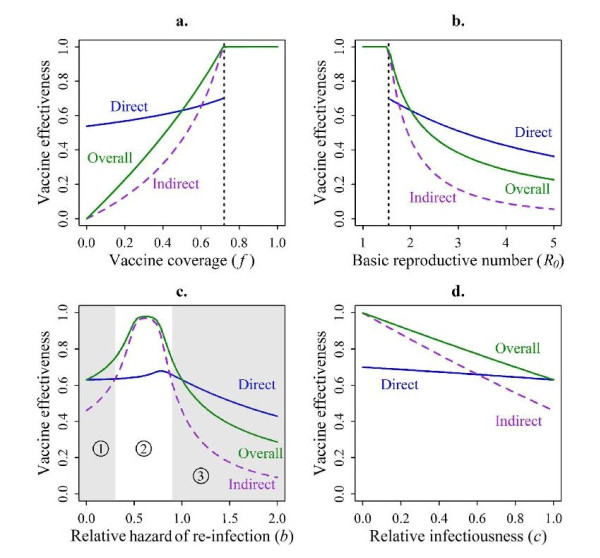
The parameters with greatest impact on vaccine effectiveness are vaccine efficacy α as well as vaccination coverage f.
α At low vaccine efficacy (α=0.2), an AoN vaccination provides 20% and a leaky vaccination 12% effectiveness, whereas at high vaccine efficacy (α=0.9) both vaccination mechanisms are equally effective.
f Changing the vaccinated population share total and direct effectiveness vary in different ways. For example, an increase in vaccination rate increases overall effectiveness much more than direct effectiveness. At f=0.2 the direct effectiveness is 57% and the overall effectiveness is only 23%. At f=0.72 a vaccination is most effective, cf. Figure 4a).
R0 Vaccine effectiveness is sharply influenced by the basic reproduction number R0 [71], which affects direct effectiveness less than overall effectiveness. For less transmissible infections, effectiveness of a vaccination program can be underestimated due to higher overall than direct vaccine effectiveness. For easily transmissible infections, on the other hand, effectiveness of a vaccination program can be overestimated. At R0<2 an infection is said to be less transmissible, and at R0>2 it is easily transferable. At R0=5, an overall effectiveness of 44% is reached for AoN vaccinations, which is more than for leaky vaccines. At lower infectiousness both vaccination mechanisms are equally effective, cf. Figure 4b).
b The re-infection risk b also has major impact on vaccine effectiveness. b lies in the interval [0, 1]. A value of zero is indicative of total natural immunity. A value of 1 argues an unchanged risk of infection after a first infection. Partial natural immunity is given at values 0<b<1. In this case, overall effectiveness increases, while direct effectiveness remains constant. The effect of a vaccination is thus underestimated. At b=0.6 partial natural immunity is 40%, overall effectiveness is 98% and direct effectiveness at 65%. Values of b>1 overestimate the effect of each vaccination program. This holds true for sexually transmitted diseases. Total effectiveness is highest at a value of b=0.7 because prevalence is moderate in unvaccinated individuals and very low in vaccinated ones. At b>2, an AoN vaccination provides 47% overall effectiveness. It is much more effective than a leaky vaccination providing 29% effectiveness. This also holds true for b≈0, but the difference is smaller. For b≠1 the introduction of a latency parameter l has influence on overall effectiveness.
b<1 leads to a reduction and b>1 to an increase in overall effectiveness, cf. Figure 4c).
c The relative infectiousness c is a parameter to which direct effectiveness is less sensitive than overall effectiveness. However, both increase in the course of a reduction in infectiousness (c<1, underestimation of the effect of the vaccination program). At c=1 an AoN vaccination has greater impact on overall effectiveness than a leaky vaccination. For low values such as c=0.25, AoN and leaky vaccination are equally effective, cf. Figure 4d).
Only two parameters are not variable. These are the natural death rate μ and the duration of an infectiousness γ. Concerning the latency parameter l, the absence of latency is symbolized by a very low value of around l=10−10. All other parameters are variable and in every simulation non-analysed parameters are set as fixed (baseline values). The dashed lines in Figure 4a and 4b) mark the threshold value of f respectively R0, from or to which the vaccination program is totally effective. Direct effectiveness is not measurable since morbidity is zero from or until then.
4.5. Implementation in MATLAB
In this subsection we introduce the MATLAB programs for the calculation of tuberculosis-related developments of populations. Furthermore, data sets of an Eastern European country are evaluated.
4.5.1. Benefits of the implementation
In order to be able to calculate vaccine effectiveness, values of the sizes of certain population groups are needed. Therefore the differential equations (4.22)–(4.30) can be solved at individual points in a selected period of time. For this elaboration MATLAB is used. The forms of vaccine effectiveness introduced in Section 3.1 are VEdirect, VEindirect, VEoverall and VEtotal. They depend on the incidence numbers (attack rates, AR) ARu, ARv and AR0, which are defined by the following formulas:
These equations can be rewritten by substituting the compartment variables as follows:
It is possible to develop the country-specific dataset of a starting year over multiple points of time. Varied settings of the parameters i, β, σ, γ, μ, b, L, f and c in the MATLAB program lead to different values of the compartment variables Su, Sv, Eu, Ev, Iu, Iv, Su2, Sv2 and R. Depending on the definition of these parameters, one obtains divergent results regarding the different types of vaccine effectiveness. Provided an optimization of starting parameters in order to being able to finally use the best possible calibrated parameters future developments can be predicted using data sets of the current year. A significant aspect is the introduction of possible new tuberculostatics, vaccines or vaccination programs. Consequently, a comparison can be made between the data set predicted and the one in which individual parameters are changed. Preconditioned exact starting values, it can be estimated how effectively such an introduction would combat a disease.
4.5.2. Data Sources and Target Variables
Data of a country in which the BCG vaccination is recommended and carried out as widely as possible should be taken as a basis. Certain data sources need to be accessible, as the variables i, β, σ, γ, μ, b, L, f and c are to be set. For these reasons records of Hungary are referred to in the following implementations. Some data must be calculated from given values. Thus it is clear that they are not exact. No data for the year 2013 were available in the indicated sources. Calculations result in the two Tables 2 and 3, where # stands for the word number. Concerning vaccinated (unvaccinated) compartments, starting values are multiplied with f=0.99(0.01).
The values in Table 3 are expected to lie in the intervals given in Table 1, which is why σ is rounded off from 0.1246 to 0.1. Relapses are again "flare-ups" (recurrences) and re-infections. β is rounded up to the very low value of 0.0001 because this represents the smallest usable value >0. The entire implementation consists of four MATLAB programs. The first program ode_sirmodell.m sets up the ODE system from Section 4.3. In the second program error_sir.m differential equations are derived from the dataset of S, E, I, S2 and R of the year 2010. This works by using the MATLAB function ode45. The development takes place over 4 points of time corresponding to the years 2011, 2012, 2014 and 2015. In order to capture those, a variable years=1,2,3,4,5,6 is set. Finally, the difference between the levels of development and the known data sets of the said 5 years are calculated. Herefrom the middle quadratic error, which is subsequently to be minimized, is calculated. The program error_sir.m outputs the error corresponding to the parameter values of Tables 2 and 3 and the ODE system (4.22)–(4.30). Using the data of Table 2, which are multiplied by 0.000001 for simplicity, and of Table 3, this value is 0.0028. The error is minimized by calibrating some of the parameters that are used to solve the differential equations (4.22)–(4.30). In the case of the BCG vaccine effectiveness of Hungary, it is β, σ, b and c because these are the transmission rate, disease-related mortality rate, risk of re-infection and relative infectiousness, of which values are changeable in the course of the introduction of a new vaccination program. It is assumed that full immunity cannot be achieved by vaccination and thus i is set zero. The four parameters are thus kept variable in contrast to i, f, γ, μ and L. In another scenario, for example when considering a country with high tuberculosis incidence but low vaccine coverage, a new program could lead to higher numbers of vaccinations. Here it would make sense to keep f variable. In Hungary a (significant) change in the value of f, which has been 99% for years, is unlikely. Error minimization is implemented in the program Fehlerminimierung.m. By n-fold call of the function fminsearch the function calculating the error is executed several times with random start values from a limited area. In general, this MATLAB function calculates the minimum of an unlimited function which uses several variables as input parameters. This means that the function is called m times. Meanwhile, the parameters β,σ,b and c are calibrated using the Nelder-Mead method. The variable m defines the number of iterations of the Nelder-Mead procedure per call of fminsearch. It can be set before calling fminsearch in the algorithm by using the statement options = optimset ('MaxIter', m). Parameter values which are assigned in this way vary for different n and m and are generally different in each implementation of the program.
4.5.3. Results of the calculations
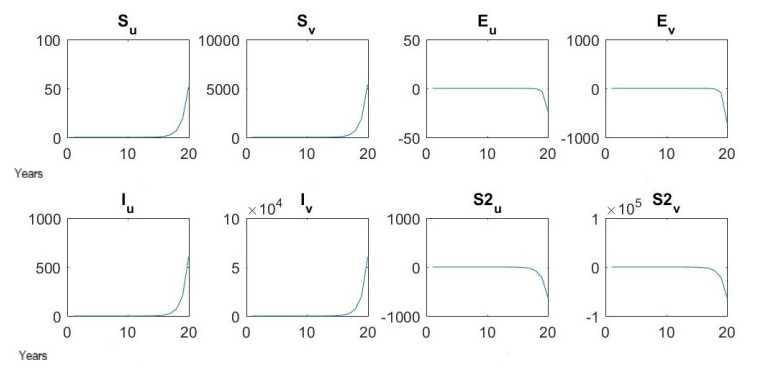
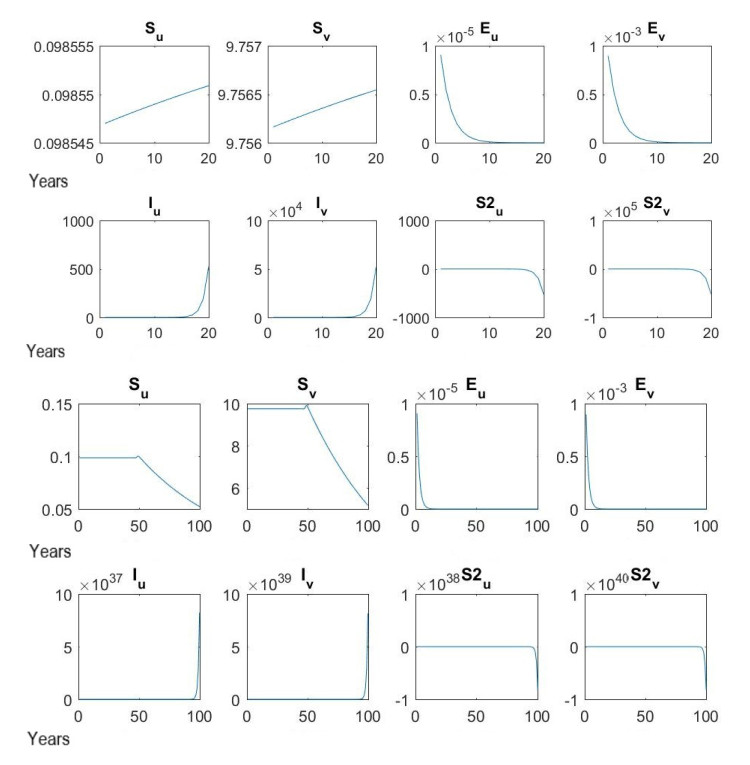
The main problem is to generate an output in which the four parameter values lie in the intervals of Table 1. Since this is realised in only a few cases, the search for a minimum error for certain m and n is performed until parameter values meet special conditions (e.g. all are less than 1). In the program fehlerminimierung.m a while loop is used for this purpose. The more constrained a search under such conditions is, the less often the program delivers a sharply reduced error. A value of 0.0000 means <0.0001 in the upcoming presentations. The following are exemplary predictions for several years starting from 2015 with output values for parameters set according to Table 3, with parameter values of zero and with greater transmission. Predictions are enabled by outputs of the program testprogram_sir.m. Thus err_sir.m is called with the respective changed and / or optimized parameter values, whereby the error is recalculated and changes of the compartments over time are depicted. Figures 10, 11 and 7 are compared for progressions in compartments. Values on the y axes are to be multiplied with 1,000,000 and bear relation to the maximum achievable value of the axis. At first, the output of testprogram_sir.m concerning the values of Table 3 is depicted. The axes are generally short and thus do not allow relatively small intervals in relation to the maximum value of the respective y-axis. Additionally, the maximum value of the compartment Sv on the y-axis is set 10,000,000,000⋅0.000001=10,000, which is why the starting value of around 10,000,000⋅0.000001=10 at x=0 is seemingly zero. The same applies for the compartments Su, Ev and Eu in Figure 10.
Figure 6 shows the generated profiles of the compartment variables.
At last the two programs error-minimization.m and test-program_sir.m are applied with regard to a greatly increased transmission rate and a high risk of re-infection:
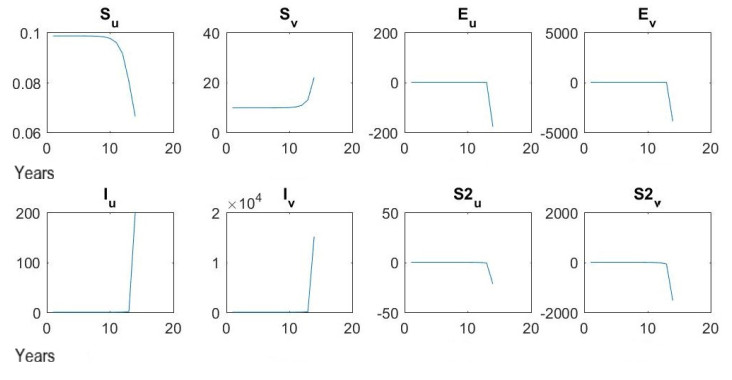
The profiles of the considered population groups for β=0.5 and b=0.9 are shown in Figure 7.
It can be seen that different courses of compartments are predicted by using different parameter values. The best case is an error as minimal as possible for parameter values smaller than those in Table 3. It must be stressed that the prediction made here is not exact since no exact starting values are given and the ODE model could be specifically extended for tuberculosis. Looking at Figure 5, it is noticeable that the numbers of susceptibles S and infectious I are predicted to rise and the sizes of the populations of exposed E and relapse-endangered S2 are predicted to fall sharply after nearly 20 years. The reason for the rise in the number of susceptibles is an only small transmission due to which few individuals pass into E. Additionally, a part of infectious I die at an early stage at rate σ, so in place of these prematurely dying individuals new ones enter the system (i.e. entering S) in the following time unit. The number of infectious increases due to transmission, a re-infection risk of 65% and a disease-related mortality rate of only 10%. The increase of Iu or Iv is given as approximately 500,000,000 or 50,000,000,000 within 20 years. Because our system of differential equations is not exactly adapted to tuberculosis and expandable, this increase should be considered too drastic. With parameter values of 0 and a hardly divergent error however, the numbers of susceptibles are predicted as slightly growing, climbing by around 1000 (Su) or 200,000 (Su) within 5 years after about 50 years, and falling to zero after 50 years. The sharp reduction of the size of the exposed population stems from the suggested lack of ill people after 10 years. Courses of infectious and individuals in danger of recurrence at Figure 6 are similar to those in Figure 5. The radical decrease in exposed can be explained by a lack of transmission. Owing to the average shifted deadlines of the members of the population, the latter enter the system (thus the compartment S) in a more constant way. In our example, sizes of Su and Sv grow in the first few years, because no transmission happens compared to the previous situation with transferred infections. The number of susceptible subjects could exclusively be given for β=0, σ=0, b=0, c=0 for more than 20 years by MATLAB. Susceptibles who do not fall ill due to lacking transmission die on average later and at rate μ. Every year, as many individuals enter the system as have died in the precious year. Moreover, there are ill, infectious and relapse-endangered individuals from previous years. The exposed may still become infectious and later be at risk of relapse, and because σ is zero (for instance due to excellent therapy) infectious do not die because of illness, but on average later at rate μ. Even after 100 years, if μ is set to 0.01296, not all members of the compartments E, I, and S2 have died. As a result, they have not yet left the system and no new individuals have replaced them. For these reasons, in our example, sizes of Su and Sv decrease after just over 50 years.
Furthermore, the rise in infectious can be justified by the possibility that exposed people can become contagious. Certainly, the increase in Figure 7 is accounted for by the too drastically presented non-exact ODE system.
Figure 7 implies that the number of infectious seriously grows after about 15 years if β and b are unrealistically increased. Apart from the increased transmission rate this results from the very high risk of re-infection combined with the fact that stage of relapse risk is reached as last compartment. The number of susceptibles who are not vaccinated sharply decreases, as 50% of susceptibles proceed to the compartment of exposed. The size of E does not decrease as clearly as in Figure 6, but rather as in Figure 5. Since the fluctuation in this scenario is extremely high and the number of unvaccinated susceptibles drops to almost zero, the small increase in vaccinated susceptible people is understandable. On the whole, the ODE system in Table 2 can be helpful in interpreting predictions because they can explain entries and exits into / from compartments, which are represented by the MATLAB program testprogram_sir.m. The above short analysis of the given three Figures 5, 6 and 7 serves as an example. It needs to be stressed that the four described programs can be used to predict the impact on a population affected by an infection, and that this can be improved by using exact starting values, a reduced model error and an extension of the ODE system. Detailed explanations of such model enhancements can be found in the outlook in Section 6. A significant extension is the inclusion of time delay.
4.6. Time-Delayed SIR model
The number of transitions of susceptibles S into infectious I can also be considered. Thus the term β⋅S(t)⋅I(t) must be replaced. Let s be the time to infectiousness and h the maximal length of an infectious period. Consider f:[0,h]↦R+0 with the normalization ∫h0f(s)ds=1.
Every point of time s between 0 and h, when infectiousness can be reached, is assigned a part of the population by the variable f. Let
be the average incubation time for infectiousness. The number of deaths of individuals having transitioned into I at rate β after a period s is given by
The time s to infectiousness is limited by an upper bound. For this reason we consider transfers to the compartment I in a period from the current time point t−0 until the time point t−h at which infectiousness can be reached earliest. Considering time delay, the transmission strength hence behaves according to [68]
This term represents the number of susceptibles at t including the accesses to the compartment S as well as the susceptibles dying or passing into I. Then the SIR model looks like [68,p. 2]:
In the case of an SEIR model (without compartment S2), the word infectious / infectious in the above descriptions has to be replaced by the word infected / infection. Then the ODE system looks as follows:
Again, it is assumed that as many individuals as have died in the previous year at μ>0 and N=constant are born, and that all newborns are susceptible. Similarly, the number of deaths of infectious (I) who recover during the time ˜s can be taken into account. Then, instead of β⋅S(t)⋅I(t), we would have the term 1/γ⋅I(t). ˜s is the time to recovery, which means the transition to recovered individuals. f would then assign every ˜s between 0 and h, at which one can recover, a part of the population.
The considerable number of deaths of those transitioning to I at rate β and recovering after a time ˜s would then be defined by the following term:
Any other transitions can be described equally, i.e. by substituting a term. In the following, however, the ODE system represented by terms (4.37) to (4.43) is referred to. The basic reproduction number [71] of the SIR model is R0=β/(μ+1γ) [68], unless any time delay is included.
Apart from this, it is possible that a (pulse vaccination strategy, PVS) is applied instead of constant vaccination. For instance, a PVS has turned out to be highly successful in the fight against measles [68,p. 3]. In order to create an ODE system for a PVS a variable τ>0 and a variable θ with 0<θ<1 have to be set as the pulsing period and the share of successfully vaccinated people must be considered. Moreover, let ˉt=(μ+1γ)⋅t,ˉμ=μ/(μ+1γ), ˉγ=γ/(μ+γ) and ˉh=(μ+1γ)⋅h [68,p. 2]. With an additional time delay and omitted overlines, the following ODE system results:
This system is valid for a PVS which is applied every τ years for t≠k⋅τ, k∈N. For t=k⋅τ it looks like [68]:
At every point of time k⋅τ a share θ of successfully vaccinated transitions into the compartment of immunised. Because dS(t)/dt and dI(t)/dt are independent of the variable R, they can be viewed in their own system. Setting I(t)=0 it follows:
In this case, dynamics of the compartment S are given by:
with k⋅τ<t≤(k+1)⋅τ.
Let us note that infectiousness does not exist here. The condition for the elimination of a disease reads
The derivation of (4.54) can be found in [68,p. 5–6].
5.
Non-Specific effects of BCG vaccination
This section discusses effects of BCG vaccinations other than prevention or control of tuberculosis. In each case they are briefly explained on the basis of numerous studies and mathematically evaluated using data sets of the two African countries Guinea Bissau and South Sudan. In particular, correlations between vaccination rates and mortality rates of these countries, which may be diminished by non-specific effects, are discussed.
5.1. Detectability of non-specific effects
The BCG vaccine has been investigated for non-specific effects in numerous studies. An average 25% lower mortality risk in BCG vaccinated subjects, which is not solely due to avoided tuberculosis cases according to [17,25], was assessed in studies with over 46,500 infants in the United States and United Kingdom during the 1940s and 1950s. Furthermore, in a blind study published in 2015, immune system-related parameters of infants from Uganda who had been vaccinated at birth or 6 weeks after birth were compared. IL-1β-, IL-6, IL-10, TNF-α and IFN-γ-cytokine levels that were in-vitro stimulated with S. aureus, S. pneumoniae, E. coli, C. albicans and poly Ⅰ: C / CPG, H3K4 trimethylation, transferring saturation and hepatitis levels as well as forms of infectious diseases and deaths were checked and results were evaluated using the Pearsons chi square and the t test. The result was that the six-week delay of vaccination could be more advantageous due to a detected reduction of lymphadenitis, osteomyelitis and abscesses by about a third [58]. In an international study in Guinea Bissau, India, Malawi, Burkina Faso, Papua New Guinea and other countries over the years 1985 to 2011 the non-specific effect of BCG vaccinations on childhood mortality was tested by sex and the condition if vitamin A was supplemented.
In a study published in 2014, blood was extracted from 20 healthy people before, 2 weeks after, 3 months after and one year after their respective BCG vaccination. PBMC Stimulation Assays which are stimulations with M. tuberculosis, C. albicans, S. aureus and E. coli and an application of the ELISA method, cytokine measurements, fluorescence-activated cell sorting analyses as well as statistical analyses were performed [75]. 2 to 3 weeks after vaccination M. tuberculosis-induced interferon-γ production was seven times higher than before it and this effect lasted up to one year. Cytokine increases caused by S. aureus and C. albicans were reported too. Likewise, IL-17 production was increased after vaccination. Other effects that indicate an effect of the BCG vaccination on trained immunity were listed [75]. These examples of studies on non-specific effects of BCG vaccination are intended to emphasize the significance and meaningfulness of this research and the calculations listed in the following subsections.
5.2. Correlation
In general, correlations describe relationships between at least two events, functions or features. There are different ways of presenting these relationships. There does not have to exist any correlation between two events, functions or features of a system. For our purposes, it is relevant that correlations between changes in BCG vaccination rates and mortality or disease incidence can be calculated in order to assess whether a non-specific effect on the health status of individuals is probable. In this section, we make use of the Pearson correlation. The Pearson correlation coefficient rA,B is a measure of strength of the linear relationship between events or features A and B, which data is available on shapes at i=1,…,n points of time. rA,B lies either in the interval [-1, 0[ or in the interval ]0, 1] or equals zero. The closer the coefficient is to zero, the lower the linear relationship. At rA,B=0 the latter one does not exist. At rA,B<0 a negative and atrA,B>0 a positive relationship between A and B is given. If the coefficient takes the value 1 or -1, a functional linear relationship is implied.
5.3. Correlation between child mortality and BCG vaccination rates in Guinea-Bissau and South Sudan
The BCG vaccine could have a non-specific effect on child mortality. This has already been demonstrated in various studies. In this section, child mortality in the two African countries South Sudan (SSD) and Guinea Bissau (GNB) are tested for their dependence on BCG vaccination quotas of different years. Our calculations are based on data of under-five mortality rates (under-five-mortality rate, U5MR), under-1-year-olds (infant mortality rate, IMR) as well as infants (neonatal mortality rate, NMR). The two countries are analysed separately. Life expectancy is less than 60 years in both countries. The main causes of death are respiratory infections, AIDS, malaria, tuberculosis, malnutrition and coronary heart disease [76,77]. This proves that many other diseases than tuberculosis often cause death in both countries. Therefore, a dependence on the extent of infant mortality cannot be attributed to only the tuberculosis-reducing effect of the BCG vaccine. In the end, both countries can be compared with regard to the results of these tests. A special feature is that in South Sudan, unlike Guinea-Bissau, never more than 75% of the population has been vaccinated. The two African states mentioned above are comparable since they display similar per capita gross domestic products [78].
The considered sections of vaccination coverages originate from the estimates of the WHO and UNICEF of 2017 [79,80]. The estimates are listed in Table 4. Data on mortality rates refer to 1000 live births each and are shown in Tables 5, 6 and 7. In the following, the terms Vj and Ni,j are used. V stands for the respective vaccination coverage. N stands for the possible non-specific effect on the respective mortality rate. The index j determines the country. The index i defines the type of mortality rate (U5MR, IMR or NMR). There were no data for 2014 in the indicated sources.
Based on these records, the correlation coefficients between V1 and V2 and Ni,j, i=1,2,3, j=1,2 are calculated.
ˉV and ˉN define [∑nk=2005Vjk]n−2005+1 or [∑nk=2005Ni,jk]n−2005+1. Creating the table it is noticeable that a BCG vaccine may have effects on several subsequent years. This means in this context, when using data of the U5MR, effects for up to 5 subsequent years should be included. For the IMR consequences of the vaccination for the respective following year should be considered. For example, it is assumed that a BCG vaccine in Guinea-Bissau in 2009 gives a mortality rate of under-fives of
or in 2006 a mortality of
As there are no data of mortality rates of years earlier than 2009, these cannot be included in the calculations. A sole consideration of the vaccination impact on the respective vaccination year would be inaccurate. Our calculations of the Pearson correlation coefficients result in different tables, which are listed as Tables 8 to 13.
It follows from Table 8:
It follows:
ˉV and ˉN are defined as average of entries in the column with the heading V1k resp. N1,1k.
with ˉV=42.6,ˉN=103.884.
It follows from Table 9:
It follows:
ˉV and ˉN are defined as average of entries in the column with the heading V2k resp. N1,2k.
with ˉV=93.43,ˉN=88.64.
It follows from Table 10:
It follows:
ˉV and ˉN are defined as average of entries in the column with the heading V1k resp. N2,1k.
with ˉV=52.14,ˉN=66.64.
It follows from Table 11:
It follows:
ˉV and ˉN are defined as average of entries in the column with the heading V2k resp. N2,2k.
It follows from Table 12:
with ˉV=93.4,ˉN=42.8.
It follows:
ˉV and ˉN are defined as average of entries in the column with the heading V1k resp. N3,1k.
with ˉV=57,ˉN=37.4.
It follows from Table 13:
It follows:
ˉV and ˉN are defined as average of entries in the column with the heading V2k resp. N3,2k.
In order to control the six calculated correlation coefficients the MATLAB function corrcoef is used. It calculates the respective coefficients rVj,Ni,j from the input corrcoef(Vj,Ni,j).
Table 14 shows the program outputs. For example, r11 stands for rV1,N1,1, so it refers to the indices of N.
The results using MATLAB and the results calculated by hand correspond with a standard deviation of differences of 0.0152 using the formula √1n⋅∑ni=1(ri−ˉr)2 and of 0.01665 using the formula √1n−1⋅∑ni=1(ri−ˉr)2. Five of the six correlation coefficients lie in the interval [-1, 0]. This implies a negative linear correlation between the respective vaccination rate Vj and the respective mortality rate Ni,j. Exclusively rV1,N3,1 is calculated as greater than zero. But 0.0417 is only slightly above zero in relation to the length of the interval [0, 1]. The time span used for the calculation is small, whereby a deviation is less meaningful than with larger periods of time, where the deviation could be larger or negative. Overall, it is implied that an increase in BCG vaccine coverage actually causes a reduction in the rate of childhood mortality.
This statement is additionally supported by the high extent of changes in BCG vaccination rates in Guinea Bissau. Numerous studies on the effects of BCG vaccinations there have already been carried out. Among other things, significantly increased cytokine responses in BCG vaccinated neonates on M. tuberculosis derivatives were found. Thus it has been shown that neonatal mortality due to prevention of pneumonia and sepsis could be reduced by over 40% if BCG-vaccinated infants display a substandard bodyweight [75].
It is noticeable that vaccination coverages of South Sudan clearly correlate with the rates of child mortality, although these are overall much lower than those of Guinea Bissau. This suggests that increases in the number of BCG vaccines in ranges between 30% and 75% already lead to of less fatalities and / or less agammaessive diseases in childhood. In Guinea Bissau, on the other hand, mortality rates have fallen faster and more pronounced. This most likely results from very high vaccination coverages in the range between 89% and 94%.
5.4. Dependence between pneumonia and BCG vaccination rates in Gui-nea-Bissau
Drawing upon data on childhood pneumonia rates in Guinea Bissau a stochastic dependence on BCG vaccination coverages of this country can be ascertained. Based on the data set on pro-rata pneumonia symptoms of the population we now examine stochastic dependence on BCG vaccination quotas. Because only average percentages, which were collected over several years, are available, average BCG vaccination rates are calculated at first. Table 15 below shows the rates of "under-five-year-olds" (U5J) from Guinea Bissau, whose guardians / carers did not visit any treatment center with them due to pneumonia symptoms in years between 1999 and 2015. Exactly these under-five-year-olds are described below as such without pneumonia symptoms.
The correlation coefficient calculated by MATLAB is 0.6792 here, as can be seen in Table 16.
Since the coefficient is 0.6792, we find a relatively strong positive linear relationship between vaccination rate (I)-change and non-occurrence of those in need of treatment to pass pneumonia symptoms (S). In addition, stochastic dependence can be verified. The Bayes theorem is helpful here:
P(S|I) defines the probability that S occurs on the condition that I has occurred. The following holds:
Stochastic independence exists, if:
It must therefore apply:
A probability P(S|I) that an individual does not suffer from pneumonia in need of treatment, assuming that he/she was vaccinated, would very likely differ between various Earth regions and is unknown for GNB. It follows that the Bayes theorem cannot directly be applied here.
Instead, we show which values of P(S|I) would hint at stochastic dependence. Because there is a relatively strong positive linear relationship between changes of vaccination coverages and the number of U5J patients who are not in need of treatment for pneumonia, it can be assumed that P(I)⋅P(S)<P(S∩I) holds. Thus, we have
and stochastic dependence is given for values P(S|I)>P(S) or P(I|S)>P(I). In our considerations so far it has been assumed that P(S|I) and P(I|S) are equal for all t as among others the effectiveness of a BCG vaccination on the prevention of pneumonia among under-five-year-olds has been assumed to be constant over several years. Stochastic dependence can be obtained by using the values for P(S|I) and P(I|S) for certain P(I) and P(S). It is shown below how difficult a determination of stochastic dependence is if we use values Pt(I) and Pt(S) over different years. Following the above conditions we have:
Using constant P(I|S) and P(S|I) this cannot apply to all t, which is why average values for Pt(S) and Pt(I) are taken as a basis. The values Pt(S)/Pt(I) are 52.067% on average, which is why for a U5J the probability of being BCG vaccinated, provided that he / she does not fall ill (=Pt(I|S):=WK1), is on average about twice as high as the probability of not falling ill, provided that he/she was BCG-vaccinated (=Pt(S|I):=WK2). Based on this knowledge estimates are invoked. As an average 46.89% of vaccinated and unvaccinated are not in need of treatment but ill, it should be assumed that WK2 is at least as large. Then WK1 could be set 0.4689/0.52067≈0.90=90%. But only a high value WK1>93.5% would eventually lead to the inequality
It is therefore P(I|S):=0.936. In this case Pt(S|I):=Pt(S)/Pt(I)⋅0.936 would hold, in order that (5.6) would apply. But then no constancy of P(S|I) would be given any more.
6.
Conclusion and outlook
The first objective, analysing non-specific effects of BCG vaccinations on limitations of other diseases, has been achieved. We showed a negative linear relationship between BCG vaccination rates and child mortality rates of two comparable African countries, whereby non-specific effects of BCG vaccinations have already been demonstrated in various studies in one of them (Guinea-Bissau). The second objective, setting framework conditions for a model-specific prediction of the emergence of tuberculosis diseases and evaluating the used mathematical model, was also fulfilled. This results from the fact that the SEIR model was explained and applied to the nationwide BCG-vaccinating country Hungary with help of MATLAB. Compartment gradients were modelled and emphasis was put on the fact that the present SEIR model provides more accurate results with exact starting values and that it could be changed and expanded.
In the outlook, in particular, expansion possibilities of our system of differential equations are discussed. In addition, a framework for further elaborations is given with regard to current research findings. Further studies should be carried out so as to prove the negative linear relationship between BCG vaccination rates and child mortality rates in Guinea Bissau and South Sudan, which was implied in Section 5. Here data which should affect different diseases would have to be evaluated using other tests. It is recommended to carry out a detailed analysis of studies.
Nonetheless, examples of extensions of the SEIR model are mentioned at this point. For instance, a compartment L could be added for vaccinated (Lv) and unvaccinated (Lu) individuals. This would serve as a transition between susceptibles S and exposed E. Accordingly, this compartment would include latently affected, which means infected, but not actively diseased individuals, who are embraced by the compartment E in the SEIR model. Individuals would emerge from E to L at rate σ. The transmission rates β and βvacc introduced in Section 4.2 would be the rates at which individuals would pass into Lu or Lv. There would have to be another variable describing the transition from L to E. A direct transfer from E to S2 could also be added to the existing ODE system.
Finally, it is possible that individuals who are ill but not infectious recover and are at risk of relapse. Similarly, a direct transition from S to I may be considered since individuals could develop an open tuberculosis directly or very soon after their infection. In reality, not as many individuals as have emerged from the system in the previous year enter it each year. In the described model individuals enter the system by birth, which is shown in Figure 3. But actually, not exactly as many individuals are born as have died in the previous year. Another noteworthy but non-tuberculosis-related aspect is that some immunised individuals could lose their immunity after a while. In this case, individuals would pass from the compartment R into S at rate α.
The mentioned expansion possibilities, which concern the topic of non-specific effects of BCG vaccinations, have not been mathematically realised in this paper because it does not aim at providing exact results proving effectiveness of the BCG vaccination against certain diseases or even child mortality. This is difficult to achieve regarding only a single country or region of this world, and would be connected to several study conducts. The fifth section of this paper is rather intended to provide a broad view over and insight into the various possible / probable effects of a BCG vaccination at birth on the health status of individuals. Due to partially calculated strong correlations and successfully carried out studies this elaboration is to imply an extension of statistics on non-specific effects of BCG vaccinations and especially in-depth research in this direction.
Section 3 explains that an introduction of a new vaccination program or development of a new vaccine or improved therapies would influence predictions on the spread of tuberculosis. Such new developments would necessarily lead to the change of one or more parameters of the model (e.g. to a reduced disease-related death rate σ). Their values could be set and model-specific forecasts could be made. On the basis of such predictions an SEIR model, which would be precisely adjusted to tuberculosis, decisions on the practical change of further model parameters (e.g. the vaccination rate f) could be facilitated. Apart from this, the model could influence decisions to increase the vaccination quota within frame of a vaccination program in countries with low prevalence and without a vaccination recommendation. Likewise, a model prediction could imply that a change in a certain parameter would lead to a much lower mortality rate. Subsequently, especially countries with high prevalence and a nationwide vaccination program could be hinted at financial investment in reducing the median duration of infectiousness or the risk of re-infection.
There will be future research for the purpose of containing and preventing tuberculosis cases. Two new drugs treating multidrug-resistant strains were approved in 2014, and other combinations of drugs will undergo clinical trials over time. With regard to diagnostics, the so-called biomarker test can be applied. With help of blood cells and biomarkers tuberculosis diseases could even be predicted. This means that it is not only possible to differentiate between ill and healthy persons. Instead, an additional opportunity of differentiating between infected individuals with a high-risk and those with a low risk of getting active tuberculosis is given. As a result, the spread of tuberculosis could be limited by preventive measures.
The fact that the BCG vaccine does not induce sufficient protection against lung infection has been mentioned in the introduction. However, the previous assumption, that children are not protected longer than 10 to 15 years, was proved in a British case-control study [83]. An effectiveness of 51% for the first 10 to 15 years with a significant 95%- confidence interval from 21% to 69% was determined. After 15 to 20 years, an effectiveness of 57% (33–72%) implied no reduction. Only after 20 to 25 years no significant protective effect was detectable any more because effectiveness was determined at 25% (14–51%). Eventually, it is accentuated that a new vaccine against tuberculosis disease is developed, which could offer protection against infection. It has been genetically engineered by the Max Planck Institute for Infection Biology on the basis of the BCG vaccine by incorporating a gene into altered M. bovis bacteria. Because of this modification, the latter can be released from digestive vesicles, into which they are absorbed by phagocytes of the human immune system. The vaccine VPM002 is intended for protection against active tuberculosis. The main reason for its development is the fact that BCG often has lost efficacy especially in the context of increasing antibiotic resistance. In addition to this, other vaccines against tuberculosis are repeatedly under investigation. In animal tests, the vaccine was determined to be effective and safe. In order to go through the necessary testing for efficacy and safety in humans, a full range of tests must be undergone. This is expected to last at least ten years.
The results of this work imply that the above extensions of the differential equation system of the here established SEIR model or other tuberculosis-specific model changes should be applied in further elaborations. In addition, one or more initial parameters could be set so that they more closely match effects of the vaccine developed by the Max Planck Institute. Potentially positive effects on the elimination of tuberculosis with help of the new vaccine could be detected by accompanying predictions. Ultimately, it would be equally useful to carry out analyses on non-specific effects of tuberculosis and on correlations between HIV / AIDS and tuberculosis.
Finally, in future work, we will design a nonstandard finite difference scheme (NSFD) for solving the proposed ODE system that is capable to preserve the positivity of the numerical solution. Next, we will prove the (global) stability of the newly designed scheme following the ideas of [84,85,86,87,88,89,90]. Moreover, we may consider fractional-order models [91] that take care of the memory effects or regard the mathematical technique of optimal control [92] or extend the complexity by regarding uncertainty using stochastic SEIR models [93,94,95,96,97,98,99], or consider multiscale models of different contact levels [100], or regard more structures in the compartments [101,102], effects of seasonality [103,104], health education and early therapy [105], age groups of infection [106,107], immigration of infected individuals [108], exogenous reinfections and endogenous reactivation [109,110], treatment at home and treatment in hospital [111], incomplete treatment and vaccination [87] or investigate the transmission of tuberculosis by the world-wide air traffic [112,113].
Conflict of interest
The authors declare no conflict of interest.
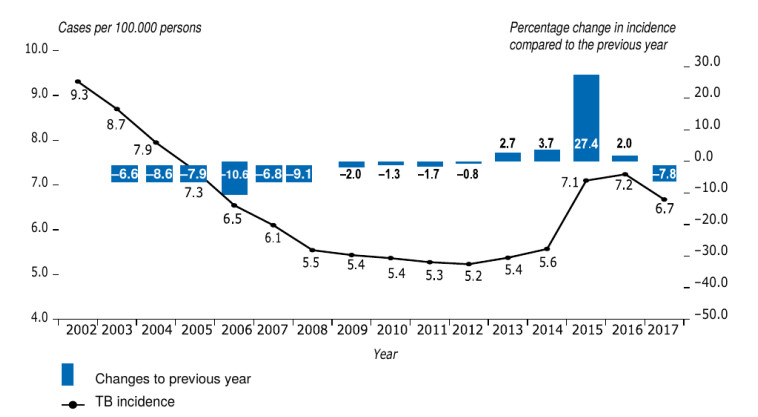









 DownLoad:
DownLoad: