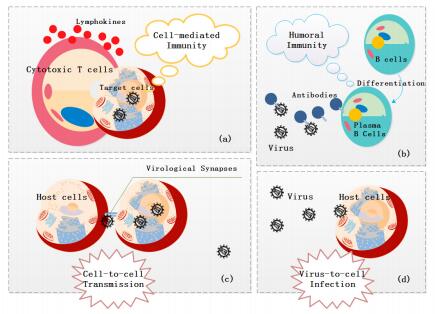
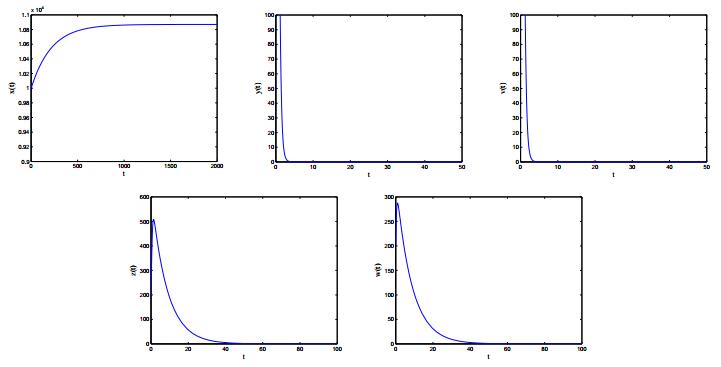
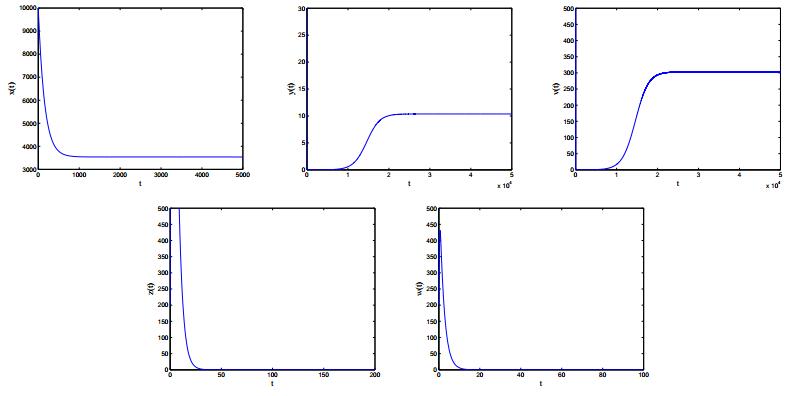
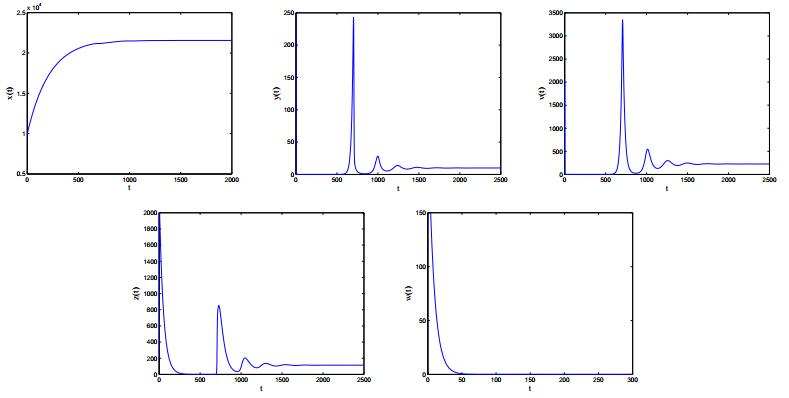
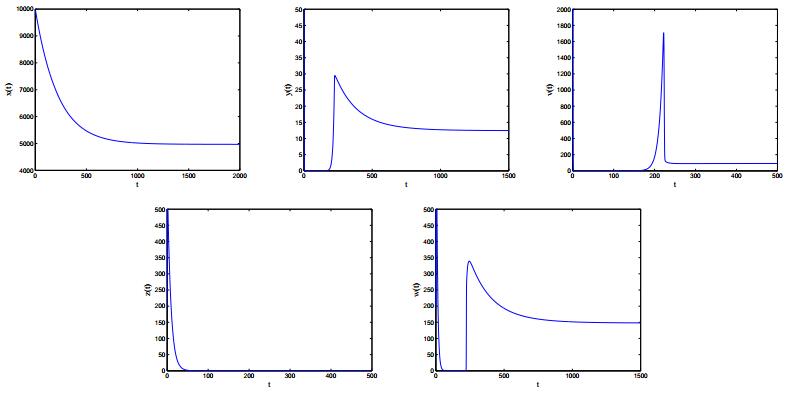
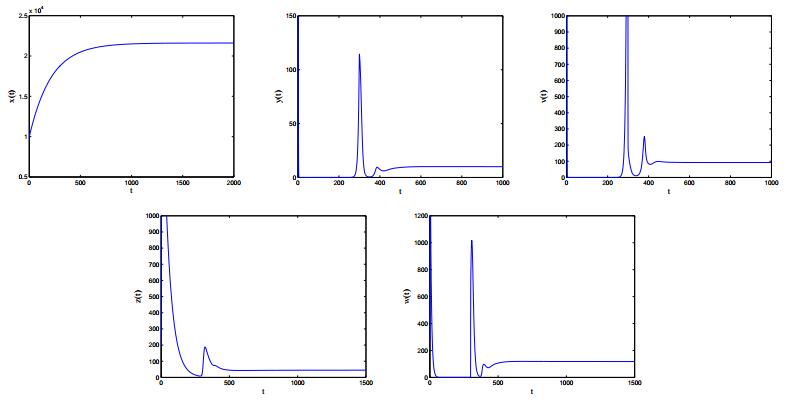
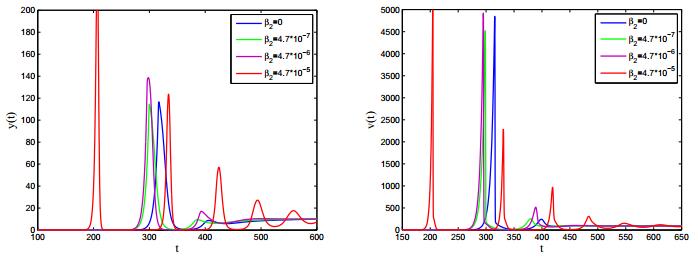
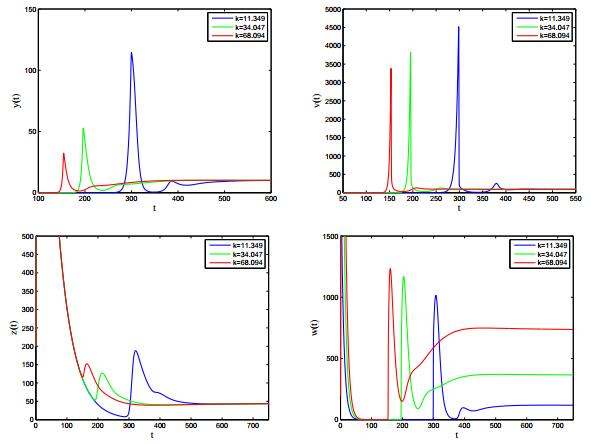
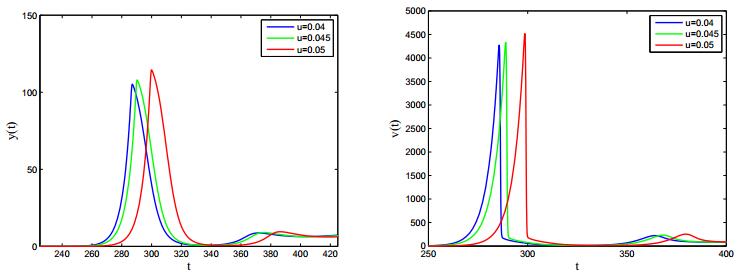
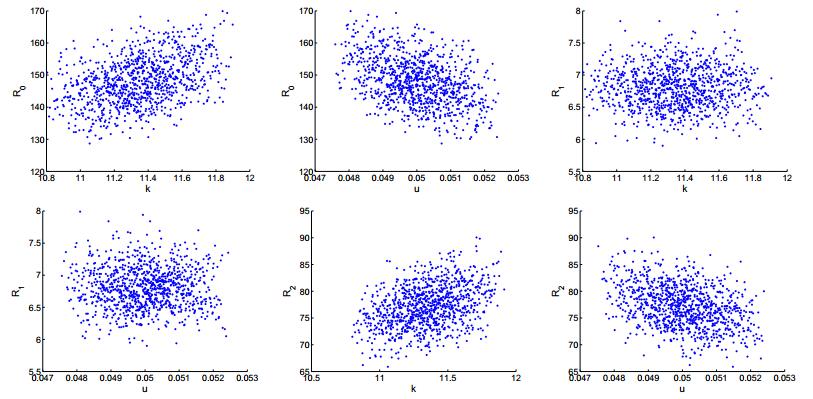
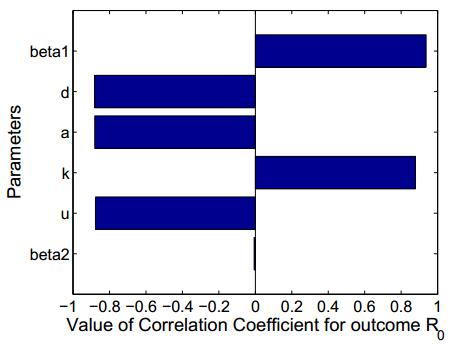
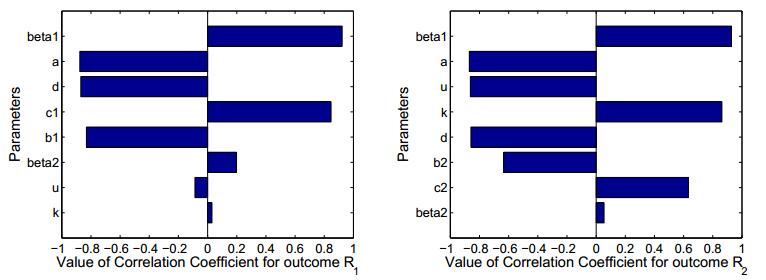
Human specific immunity consists of two branches: humoral immunity and cellular immunity. To protect us from pathogens, cell-mediated and humoral immune responses work together to provide the strongest degree of efficacy. In this paper, we propose an HIV-1 model with cell-mediated and humoral immune responses, in which both virus-to-cell infection and cell-to-cell transmission are considered. Five reproduction ratios, namely, immunity-inactivated reproduction ratio, cell-mediated immunity-activated reproduction ratio, humoral immunity-activated reproduction ratio, cell-mediated immunity-competed reproduction ratio and humoral immunity-competed reproduction ratio, are calculated and verified to be sharp thresholds determining the local and global properties of the virus model. Numerical simulations are carried out to illustrate the corresponding theoretical results and reveal the effects of some key parameters on viral dynamics.
1.
Introduction
Following their good strength/ductility combination coupled with their excellent corrosion resistance [1], stainless steels are adopted in many applications including automotive [2], construction and building [3,4], energy [5,6,7], aeronautical [8], medical [9] and food [10,11,12,13]. Following nickel and molybdenum significant price increase, nowadays the stainless steel market is moving toward an increasing use of ferritic stainless steel instead of austenitic stainless. Following to that, advanced ferritic stainless steels are being developed by many companies. Such steels are expected to substitute austenitic steels in many applications. Based on those considerations, two new stainless steel grades characterized by a medium-high Cr content (≥20%), a very low content of interstitial and stabilizing elements (Ti/Nb/Ta) and without Mo addition are here considered. Cr content increase is here due to compensate Mo absence. In fact, Mo is usually present in lower Cr (<20%) alloys and austenitic stainless steels with the aim to increase corrosion resistance as predicted by Pitting Resistance Equivalent Number (PREN), according to:
Moreover, the necessity to add stabilizing elements and low interstitial elements content comes from the need to guarantee intergranular corrosion resistance and stabilize ferritic matrix, especially during welding processes [14,15,16]. In particular, stainless steels are here stabilized by titanium and niobium addition, following the criteria of mix stabilization: titanium stabilizes nitrogen at the solidus temperature, niobium stabilizes carbon. The presence of Ti and Nb carbides and nitrides is foreseen aimed to avoid Cr carbides precipitation with consequent intergranular resistance loss. It also allows to controlling grains growth during heath treatments and welding processes [1]. In addition, carbon and nitrogen reduction improve formability and toughness [17].
Nickel reduction targets a stress corrosion resistance improvement. Nonetheless, it limits interstitial corrosion resistance or crevice corrosion [18]. This corrosive attack can rise between two metallic junctions or between metallic components and not a conductive material. It is well known that crevice corrosion resistance is promoted by nickel alloying. Copper and molybdenum show a strong effect [18]. In particular, molybdenum addition is really effective versus crevice corrosion [19]. No many data are anyway available on such new ferritic steels, especially concerning corrosion resistance. In particular, a corrosion ranking including the most common austenitic stainless steels is required to understand which applications/environments they can be devoted to. Aim of this paper is to evaluate the corrosion resistance of 460LI and 470LI steels aimed to face the materials selection criteria for stainless steels in specific applications.
2.
Materials and methods
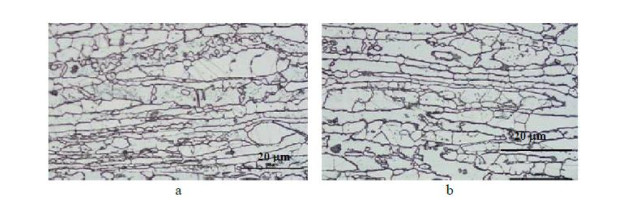
Four different types of stainless steels are considered: two super-ferritic stainless steels (AISI 460LI and AISI 470LI) and two austenitic grades, AISI 304 and AISI 316L, chosen as reference materials. The chemical composition of the analyzed steels is reported in Table 1. In Figure 1, typical microstructures of AISI 460LI and AISI 470LI as detected by means of optical microscopy are reported.
2.1. General corrosion resistance
General corrosion resistance has been tests in a salt spray chamber (WEISS system model SSC 450). Testing temperature was 35 ℃ with a nebulized 5 wt% of NaCl solution according to UNI EN ISO 9227. Samples were 100 mm × 200 mm. Samples were cleaned with acetone before testing; edges were protected with wax and pix. Then, samples were placed into the chamber hunged on a plastic rack to maintain them at 20 ℃ respect to the vertical position. This arrangement was essential to avoid mutual contact between samples or with other parts of the chamber. Total duration of this test was 1000 h.
Generalized corrosion resistance from chemical agents and conditions typical for stainless steels was tested dipping samples of 20 mm × 50 mm dimensions (polished until to 120 mesh) in 8 solutions at different temperatures as reported in Table 2 according to ASTM G157. Before the beginning of the test and after every exposure cycle, samples were weighted and measured to determine the corrosion rate expressed in mm/year.
2.2. Confined corrosion resistance according to UNI EN ISO 17475
Potentio-dynamic polarization curves were measured using an electrochemical cell with three electrodes. A calomel reference electrode (SCE) and a platinum counter-electrode, immersed in a 3% NaCl solution at room temperature were used. To realize the potentio-dynamic curves, a Solatron 1287 was used connected to a PC for setting the beginning value of the potential scan. The power value and the surface (1 cm2) of metal exposed to the corrosive agent. Starting from a potential of 1 V (lower than the open circuit potential), a scan rate of 1 mV/s was set and an intensity of the inversion current equal to 5 mA/cm2. Samples before the beginning of the test were polished adopted 600 mesh.
Moreover, critical pitting temperature (CPT) has been determined by immersing different samples in a solution of 6% FeCl3 for 24 h at a fixed temperature. This scheme was repeated increasing each time the solution's temperature of 5 ℃ until it was possible to observe the onset of pitting phenomena. Samples had dimensions of 30 mm × 40 mm with rounded corners. Moreover, both samples' surfaces were polished at 120 mesh.
Crevice critical temperature (CCT) determination was realized with the same test procedure used to detect the critical pitting temperature (CPT). 20 embossed sectors were made on the cylinders and held together by a nickel-based alloy screw (shielded with Teflon). Test in salt spray chamber was performed applying on the samples two cylinders made in Teflon with a diameter of 50 mm. Twelve embossed sectors were obtained on the surfaces. Test duration was 260 h and the spray solution had a content of 5% NaCl as reported in UNI EN ISO 9227. At the end of the cycle, samples were visually analyzed. In particular, the sectors number on samples was evaluated. Corrosion resistance was related to the above number.
2.3. Intergranular corrosion resistance
Intergranular corrosion was measured by Huey and Strauss tests. In both cases 20 mm × 30 mm samples were used. Both surfaces were mechanically polished at 120 mesh. The Huey test allowed the measure of the corrosion rate and in the morphologic observation of the corrosive attack endured by the samples, tested in a hot solution of HNO3 (65%) for five period of 48 h each. In the Strauss test procedure, samples were maintained in a solution at 16% of copper sulfate and sulfuric acid with copper turnings after boiling 72 h. The evaluation consisted of visually looking for cracks originated from intergranular corrosion's attacks. Samples were bent as usual before the examination. If cracks were suspected to arise from poor ductility, even in unsensitized samples, a similar but unexposed sample should be used for reference. This test method can detect chromium-depleted regions in the material, but cannot detect other possibly detrimental homogeneities, like precipitations of sigma phase. This test is based on a visual examination of the bent specimen.
2.4. Stress corrosion resistance
Stress corrosion susceptibility was measured immerging U-bended samples in a boiling solution. MgCl2 (42%) solution was adopted according to ASTM G30-97 standard. At the end of the test, samples were observed with a low magnification microscope to identify the presence of cracks.
3.
Results and discussion
3.1. Generalized corrosion resistance
Photos of the four samples of AISI 304, AISI 316L, AISI 460LI and AISI 470LI exposure to the cycle in the salt spray chamber are reported in Figure 2. Super-ferritic stainless steel performances after 1000 h exposure are similar to those of austenitic stainless steel.
Results of general corrosion resistance tests are reported in Tables 3 and 4. This kind of test was just performed on the super-ferritic stainless steel, and the corrosive agents were chosen aimed to evaluate the possibility to use this type of steels in the chemical sector and in the food industry. In every case, the result of the test was positive and the corrosion rate was widely within the ASTM G157 limit (0.13 mm/year).
3.2. Confined corrosion resistance
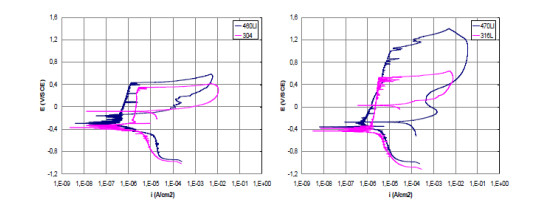
Potentio-dynamic polarization curves for all the analyzed steels are reported in Figure 3. It can be observed that it is not possible to recognize the activity peak of the material namely the current critical value that is linked to the active-passive transition.
The passivation current detected values were in the order of 10−6 A/cm2 even if there are some differences between the four different steels. In fact, the AISI 304 showed the highest passivation current value. On the contrary, AISI 470LI showed the lowest one. Moreover, a different behavior of AISI 470LI steel has been recognized with respect to other steels. In fact, the pitting phenomena started for all the other materials in the range 400–500 mV/SCE while AISI 470LI steel remained passive until 1 V/SCE. In this case, the breakage of the passive film didn't happen following a pitting phenomenon but it was caused by crevice. When the inversion current was reached, AISI 470LI showed more difficulties to passivate because the damage at the passivation film caused by crevice phenomena was more significant compared to the damage caused by pitting. The values of the passivation current density, pitting potential and the passivation potential, determined by the cyclic potentio-dynamic polarization curves, are reported in Table 5.
The critical pitting and crevice temperatures calculated according to ASTM G48 are reported in Table 6. The critical pitting temperature of the super-ferritic stainless steel is higher than the austenitic stainless steel while the pitting critical temperature is comparable.
Photos of samples after crevice test in salt spray chamber for 260 h are reported in Figure 4. The number of sectors imprinted on the sample and their severity are reported in Table 7. Results show similar behavior in the AISI 460LI and AISI 304 steels. On the contrary, the AISI 470LI steel shows a different behavior if compared to AISI 316L material: on the first steel only one sector was imprinted; on the second steel two sectors are visible. The severity on the AISI 470LI is greater than that of the multiple sector embossed in the AISI 316L. It can be assumed that AISI 470LI is characterized by a more resistant passive film layer but when this film is damaged, the propagation of the corrosion rate is higher, as reported by the electrochemical test. This behavior can be explained in terms of material's chemical composition since AISI 470LI steel does not contain alloy elements such as nickel and molybdenum. Such elements are present in the AISI 316L allowing to slow down the propagation of the crevice corrosive attack.
3.3. Intergranular corrosion resistance
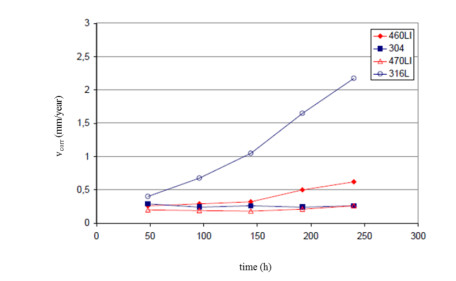
Even as far as concerns intergranular corrosion resistance, super-ferritic stainless steels behavior is comparable with the one shown by austenitic materials and both tests have successful outcome. The corrosion rate as a function of the immersion time in HNO3 according to the Huey test is reported in Figure 5.
The AISI 470LI shows the slowest corrosion rate while the AISI 460LI reported a little bit worse behavior than AISI 304. The AISI 316L steel shows the higher corrosion rate. Such phenomenon, well known in literature, can be attributed to the presence of molybdenum that promotes the precipitation of the sub-microscopic σ phase that dissolves rapidly in HNO3 [1]. Test executed after the immersion for 72 h in a solution of Cu-CuSO4-H2SO4 has a positive outcome; in this case not visible formations of cracks were detected.
3.4. Stress corrosion resistance
Photos of U-bend samples immerged in a boiling solution of MgCl2 for 500 h are reported in Figure 6. At the end of the test, samples were observed with a low magnification microscope to identify the presence of cracks and by Electron Scanning Microscope. Analyses reported that the super-ferritic samples are not susceptible to stress corrosion cracking while the tested samples of 316L achieves break, as expected for austenitic stainless steels.
4.
Conclusions
The behavior of two innovative super-ferritic stainless steels grades with high performances against local and intergranular corrosion resistance characterized by a medium-high content of chromium (≥20%), a really low content of interstitial elements and the mix stabilization with Ti/Nb/Ta, without the addition of molybdenum has been reported.
Results show that:
● As regards the general corrosion resistance, super-ferritic grades guarantee performances comparable with the ones typical of austenitic stainless steels. Corrosion resistance tests through immersion in different environments detected low corrosion rates.
● The localized resistance corrosion for pitting, in term of critical pitting potential and critical pitting temperature, resulted a little higher with respect to that of the austenitic stainless steels taken as a reference point.
● The super-ferritic stainless steels are affected neither by intergranular corrosion nor by stress corrosion.
Conflicts of interest
There are no conflicts to declare.









 DownLoad:
DownLoad: