1. Introduction
1.1. Scope
Hantavirus (family Bunyaviridae) is a rodent-borne infectious disease of significant concern as it can generate high case fatality rates in the human population [55]. Transmission of hantavirus from infected rodents, the main known reservoir of the virus, to humans, typically occurs via inhalation of aerosols contaminated by virus shed in excreta, saliva, and urine [36]. Risk of infection with hantavirus in the human population is facilitated by crowding conditions and close proximity to rodent populations. Not surprisingly, the total population at risk for hantavirus infection has increased with urbanization rates. In the Americas, hantavirus represents a public health issue particularly in South American countries including Chile [48]. The great majority of hantavirus cases have been reported in China, however [64,65]. A better understanding of the transmission dynamics of hantavirus in rodent populations has the potential to improve interventions strategies aimed at minimizing the number of infections in the human population.
It is the purpose of this contribution to advance a spatio-temporal compartmental model of hantavirus infection in rodents with a focus on its efficient numerical solution. The total population of rodents is subdivided into males and females (indices m and f), and for each of both subpopulations a variant of the well-known susceptible-exposed-infective-recovered (SEIR) compartmental model [33] is formulated. The compartments of male and female individuals are Cm:={Sm,Em,Im,Rm} and Cf:={Sf,Ef,If,Rf}, respectively, and the final model for
|
u=(u1,…,u8)T=(Sm,Em,Im,Rm,Sf,Ef,If,Rf)T
|
as a function of position x∈Ω and time t∈T:=[0,T] on a bounded domain Ω⊂R2 is given by a convection-diffusion-reaction system of the type
|
∂u∂t+∇⋅Fc(u)=DΔu+s(u),
|
(1.1)
|
supplied with initial and boundary conditions, where the convective fluxes Fc(u), the diffusion matrix D and the vector of reaction terms s(u) are specified in later parts of the paper. It is proposed to describe the movement of the male individuals in a particular way that depends non-locally on the density Nf=Sf+Ef+If+Rf of female individuals, in combination with several alternative local or non-local dependences on the density Nm=Sm+Em+Im+Rm of male individuals. These alternatives give rise to three models that will be discussed in parallel, and that are expressed by the respective choice of Fc(u). In any case the movement of the male individuals is assumed to depend non-locally on Nf. All variants of (1.1) call for numerical methods that on one hand avoid the severe time step restriction incurred by explicit time discretizations of the diffusion term DΔu, and on the other hand allow the efficient computation of numerical fluxes based on the non-local evaluation of data. As we outline in this paper, the first goal can be achieved by an implicit-explicit (IMEX) discretization in combination with a technique based on Fast Fourier Transform (FFT) to handle the second. The simulator constructed in this way is applied to provide numerical results of several scenarios that allow comparing the model variants.
1.2. Related work
First of all, it worth mentioning that general references to the spatial spread of infectious diseases include [5,22,38,41,52,60]. The basic assumption of our treatment, namely that all epidemiological compartments are distributed over the whole spatial domain, is opposed to the alternative metapopulation approach that describes spatial structure through the relations between a number of well-identified sub-populations or "patches" (cf., e.g., [3,6,7,18,35,57,58]).
In fact, the description of spatial structure by explicitly specifying the mobilities between "patches" is typical for characterizing the behavior of humans, who usually do not "disperse" in response to environmental stimuli (at least not in the relatively short time scales involved in epidemiological modelling) but undertake directed travels, while a description through a convection-diffusion-reaction mechanism is more suitable for non-human infectious agents such as spores, insects, and bacteria that would disperse. The diffusion mechanism is mostly associated with non-human beings is also supported by the fact that classical treatments of diffusion in ecology only include non-human populations (cf. [41,Ch. 13], [43]). This viewpoint is also assumed, for instance, in [22,Ch. 10]. Other references to the movement of animals and spread of diseases by reaction-diffusion equations include [38,44,51]. Furthermore, the distinction between metapopulation models and continuous in space models is also made in the alternative treatments in Sections 4.3 and 4.4 of Sattenspiel [52] and those by van den Driessche [58] and Wu [61] in the same volume. In the latter, a decisive advantage of the spatially continuous approach, namely its amenability to mathematical analysis is emphasized. Furthermore, a reaction-diffusion system based on the well-known non-spatial SIR model [33] is proposed as a prototype spatio-temporal epidemic model, and the underlying assumptions of variants of reaction-diffusion models are broadly discussed, with particular reference to a seminal case study [29,30,42].
A less common ingredient in mathematical epidemiology is the convective term ∇⋅Fc(u). Related advection terms, for which the essential functional dependence for one compartment is Fc=Fc(x,u)=b(x)u with a given velocity b(x), arise if the population under study is transported (as is the case with wind-borne infectious agents, plankton, etc.). A slightly different motivation of convective terms was advanced in [41,Ch. 14] in the context of a wolf territoriality model that describes directed movement of individuals towards a "den". Surprisingly, however, nonlinear convective models are less common in epidemiological applications (although they are widespread used to describe human behavior of, say, traffic and pedestrian flows [26,28,56]). Let us emphasize here that the main role of the convective term in our model is similar to that of [41,Ch. 14] in that it imposes a preferred direction of movement of (the male) individuals, where the global dependence of the direction is determined by convolution with population data within a certain horizon of current position. This idea of non-local dependence of biological fluxes goes back to a non-local predator-prey model introduced and analyzed by Colombo and Rossi [20], and for which a numerical scheme is analyzed in [50]. The scheme proposed in that paper is based on the Lax-Friedrichs scheme for the (hyperbolic) equation (2.11a) for the ease of demonstrating convergence properties; we here employ higher-order weighted essentially non-oscillatory (WENO) reconstructions (initially proposed in [27,37]) to achieve high-order spatial accuracy. (We will further relate our model to that of [20] in Section 2.3.)
Still within the framework of reaction-diffusion systems (but in simpler versions than considered here), a number of qualitative analyses of hantavirus models are available. For instance, Abramson and Kenkre [1] advance a two-equation reaction-diffusion model that is a spatial equation of the well-known susceptible-infectious-susceptible (SIS) model (the assumed population of mice is not structured in any other way), and demonstrate that one single lumped parameter, the carrying capacity, essentially controls the dynamics of the system; moreover a spatial distribution of its value explains the formation and disappearance of "refugia", that is of habitat regions with favorable conditions that influence the spatio-temporal patterns of hantavirus [2,34]. Furthermore, based on the Abramson and Kenkre model [1], Buceta et al. [17] study the the impact of seasonality on hantavirus, with the remarkable result that the alternation of seasons, each of which associated with a constant set of epidemiological parameters, may induce the outbreak of Hantavirus infection even if neither season by itself satisfies the environmental requirements for propagation of the disease [17]. The same group also investigated the effects of intrinsic noise on hantavirus spread [24]. Finally, we mention that more recently the Abramson and Kenkre model was refined to give a stage-dependent model with delay [46], where a new compartment corresponds to virus-free young mice, and the new model consists of three ordinary differential equations with delay, or in its recent spatial version presented in [47], in a reaction-diffusion system with delay (where the diffusion operator is expressed in radial variables).
From a computational point of view, and coming back to our own model (1.1), we mention that IMEX Runge-Kutta (IMEX-RK) schemes play an important role. We therefore briefly provide some background on these methods. Roughly speaking, an IMEX-RK method for a convection-diffusion-reaction equation of the type (1.1) consists of a Runge-Kutta scheme with an implicit discretization of the diffusive term combined with an explicit one for the convective and reactive terms. To introduce the main idea, we consider the problem
which is assumed to represent a method-of-lines semi-discretization of (1.1), where Φ∗(v) and Φ(v) are spatial discretizations of the convective and reactive terms and of the diffusive term, respectively. Assume, for simplicity, that the spatial mesh width is h>0 in both the x-and y-direction. Then the stability restriction on the time step Δt that explicit schemes impose when applied to (1.2) is very severe (Δt must be proportional to the square h2 of the grid spacing), due to the presence of Φ(v). The implicit treatment of both Φ∗(v) and Φ(v) would remove any stability restriction on Δt. However, the upwind nonlinear discretization of the convective terms contained in Φ∗(v) that is needed for stability, makes its implicit treatment extremely involved. This situation becomes even more complicated due to the WENO reconstructions. In fact, after the pioneering work of Crouzeix [21], numerical integrators that deal implicitly with Φ(v) and explicitly with Φ∗(v) can be used with a time step restriction dictated by the convective-reactive term alone. These schemes, apart from having been profusely used in convection-diffusion problems and convection problems with stiff reaction terms [8,23], have been recently used to deal with stiff terms in hyperbolic systems with relaxation (see [11,12,13,14,45]). Finally, we mention that many authors have proposed IMEX-RK schemes for the solution of semi-discretized PDEs [8,32,45,66].
1.3. Outline of the paper
The remainder of this work is organized as follows. The mathematical model is introduced in Section 2, starting from the spatiotemporal balance equations of a gender-structured SEIR model (in Section 2.1). The three variants of convective fluxes Fc(u) and the diffusion matrix D arising in (1.1) are specified in Section 2.2, and it is shown in Section 2.3 that the model arising from ours for Nm and Nf by summing over all compartments in Cm and Cf, respectively, can be compared with the non-local predator-prey model studied in [20]. In Section 3 we introduce the numerical scheme. We will use the method of lines to obtain a spatial semi-discretization of the initial-boundary value problem of (1.1) in the form of a system of ordinary differential equations (ODEs), to which a time-stepping procedure will be applied to obtain the final numerical scheme. To this end we introduce in Section 3.1 the Cartesian grid and discrete unknowns, and describe in Section 3.2 the discretization of non-local terms as in (2.6) that appear in the male convective fluxes. Then, in Section 3.3, we introduce the discretization of the the complete convective flux for the male species. This is essentially done by WENO reconstruction. The corresponding discretization for the female species is similar, and is omitted. Next, in Section 3.4 we describe the IMEX-RK time integrators used to solve the system of ODEs that represents the spatial discretization. Section 4 is devoted to the presentation of numerical results. Preliminaries are introduced in Section 4.1, including a definition of the constants arising in the model and of the initial scenarios. To make our results comparable with those of [4] (based on ordinary and stochastic differential equations), we adopt the parameters corresponding to the epizoology of the rice rat and the Bayou virus utilized in that paper. On the other hand, Scenario 1 is based on the hypothesis that the initial population occupies a well-identified subdomain of Ω and therefore the numerical results also address the phenomenon of biological invasion (besides that of the progression of epidemic states), while Scenario 2 aims at studying the effect of a random perturbation of a constant initial state. The corresponding numerical examples are presented in Sections 4.2 and 4.3, respectively. Furthermore, we provide in Section 4.4 an example that shows that the numerical scheme exhibits experimental second-order convergence when the solution is smooth, and in Section 4.5 present a test case that addresses the effect of seasonal variability of some of the model parameters. Conclusions are collected in Section 5.
2. Mathematical model
2.1. Gender-structured spatio-temporal SEIR model
The model for the eight unknowns in C:=Cm∪Cf, as functions of x and t, is given as follows:
|
∂Sm∂t+∇⋅FSm(Sm,Nf,Nm)=B(Nm,Nf)2−Smd(N)−Sm(βfIf+βmIm),
|
(2.1a)
|
|
∂Em∂t+∇⋅FEm(Em,Nf,Nm)=−Emd(N)+Sm(βfIf+βmIm)−δEm,
|
(2.1b)
|
|
∂Im∂t+∇⋅FIm(Im,Nf,Nm)=δEm−Imd(N)−γmIm,
|
(2.1c)
|
|
∂Rm∂t+∇⋅FRm(Rm,Nf,Nm)=γmIm−Rmd(N),
|
(2.1d)
|
|
∂Sf∂t−∇⋅(μSf∇Sf)=B(Nm,Nf)2−Sfd(N)−Sf(βfIf+βm,fIm),
|
(2.1e)
|
|
∂Ef∂t−∇⋅(μEf∇Ef)=−Efd(N)+Sf(βfIf+βm,fIm)−δEf,
|
(2.1f)
|
|
∂If∂t−∇⋅(μIf∇If)=δEf−Ifd(N)−γfIf,
|
(2.1g)
|
|
∂Rf∂t−∇⋅(μRf∇Rf)=γfIf−Rfd(N),
|
(2.1h)
|
where ∇⋅ denotes the (spatial) divergence operator. The right-hand sides of (2.1) are identical to that of the non-spatial model proposed in [4], i.e., this model, to which we refer as Model 0 for ease of reference, is recovered if all divergence terms on the left-hand sides are set to zero and variables are considered to depend on t only, and the unknowns represent suitably scaled densities. In particular d(N) is the density-dependent death rate, βf is the contact rate of an infective female with either a susceptible female or a susceptible male, βm,f is the contact rate of an infective male with a susceptible female, βm is the contact rate of an infective male with a susceptible male, δ is the inverse of the average length of the incubation period (assumed to be the same for males and females), and γm and γf are the inverse of average length of the infectious periods for males and females, respectively. Following [4], we assume a harmonic birth function,
where b is the average litter size, and regarding the contact rates and infectious periods, we assume βm≥βm,f≥βf and γf>γm. The incubation period is the same for males and females (namely 1/δ), as is the density-dependent death rate
where 0<a<b/2 and c>0.
2.2. Convective fluxes and diffusion matrix
The fluxes appearing in the lefthand sides of the full spatio-temporal model (2.1) have two components for the male compartments, and one for the female compartments. Several alternative choices of FX for the males in compartment X∈Cm will be considered in parallel and compared. Model 1 is given by (2.1) along with
|
FX(X,Nf,Nm)=X(κXV(Nf)−μXV(Nm)),
|
(2.2)
|
where κX≥0 and μX≥0 are constants and V is a non-local velocity function that will be specified below. Model 2 is given by (2.1) in combination with
|
FX(X,Nf,Nm)=Xφ(Nm+Nf)(κXV(Nf)−μXV(Nm)),
|
(2.3)
|
where the function φ is given by
|
φ(u)={1−u/Kfor 0≤u≤K,0for u<0 or u>K,
|
(2.4)
|
where K is a maximum value (carrying capacity) of the total density. Finally, we consider Model 3 that is given by
|
FX(X,Nf,Nm)=XκXV(Nf)−μX∇X,
|
(2.5)
|
where ∇X is the spatial gradient of X.
The non-local unscaled velocity V is defined as
|
V(w)=∇(w∗η)√1+‖∇(w∗η)‖2,
|
(2.6)
|
where η denotes a radial convolution kernel with radius ε, i.e., η is a piecewise smooth function such that η(x)=η(‖x‖2), η(x)≥0, η(x)=0 for ‖x‖>ε, and ∫R2η(x)dx=1, i.e., for any function w defined on Ω×T and x∈Ω such that Bε(x):={y∈R2:‖y−x‖<ε}⊂Ω, we have
|
(w(⋅,t)∗η)(x)=∫Bε(x)w(y,t)η(x−y)dy=∫R2w(y,t)η(x−y)dy.
|
(This definition will be modified slightly for points x with dist(x,∂Ω)<ε.) It is worth recalling that
so that V(w) indeed depends (non-locally) on w and not on its gradient.
The non-local velocity function (2.6) was introduced recently in a two-species predator-prey model by Colombo and Rossi [20], for which convergence of a numerical scheme was proved by Rossi and Schleper [50]. The evaluation of this velocity function at w=Nf in the equations for male individuals describes that males are attracted by females since the corresponding biological fluxes κCV(Nf), C∈Cm, are directed toward increasing densities of females. The movement of male individuals to females is balanced by a term that describes that males avoid groups of their own gender. This is achieved in Models 1 and 2 by another evaluation of the nonlocal function but this time at w=Nm, and with a coefficient, namely −μX, of opposite sign (see (2.2) and (2.3)), while in Model 3 the movement of males away from regions of large densities of their group is described by diffusive movement through the term −μX∇X (see (2.5)). The biological movement of females is standard diffusion.
Summarizing, we obtain that the convective fluxes Fc(u) and the diffusion matrix D arising in (1.1) are given by the respective expressions
|
Fc(u)=(FSm(Sm,Nf,Nm),FEm(Em,Nf,Nm),FIm(Im,Nf,Nm),FRm(Rm,Nf,Nm),0,0,0,0)T,D=diag(0,0,0,0,μSf,μEf,μIf,μRf),
|
when the definition of the fluxes is (2.2) (Model 1) or (2.3), (2.4) (Model 2), and
|
Fc(u)=(SmκSmV(Nf),EmκEmV(Nf),ImκImV(Nf),RmκRmV(Nf),0,0,0,0)T,D=diag(μSm,μEm,μIm,μRm,μSf,μEf,μIf,μRf),
|
(2.8)
|
for the definition of the fluxes (2.5) (Model 3). In all cases, the vector of reaction terms s(u)=(s1(u),…,s8(u))T is given by the right-hand sides of (2.1), i.e.,
|
s1(u)=B(Nm,Nf)2−Smd(N)−Sm(βfIf+βmIm),…,s8(u)=γfIf−Rfd(N).
|
The system (2.1) is considered on Ω×T together with the initial condition
where u0 is a given function, and zero-flux boundary conditions
|
(Fc(u)−D∇u)⋅n=0,x∈∂Ω,t∈(0,T],
|
(2.10)
|
where n is the unit exterior normal vector to the boundary ∂Ω of Ω.
2.3. Comparison with the model by Colombo and Rossi [20]
Assume that the convective fluxes Fc(u) and the diffusion matrix D are given by (2.8) according to Model 3, and that κC=κm and μC=μm for all C∈Cm and μC=μf for all C∈Cf. Then, summing (2.1a)-(2.1d) and (2.1e)-(2.1h), respectively, we get the two equations
|
∂Nm∂t+∇⋅(κmNmV(Nf)−μm∇Nm)=B(Nm,Nf)2−Nmd(Nm+Nf),
|
(2.11a)
|
|
∂Nf∂t−μfΔNf=B(Nm,Nf)2−Nfd(Nm+Nf).
|
(2.11b)
|
This model is similar to the non-local predator-prey model recently analyzed by Colombo and Rossi [20]. In fact, their model is precisely recovered if we identify Nm as the density of "predators", Nf as that of "prey", set κm=1 and μm=0, and replace the right-hand sides of (2.11a) and (2.11b) by the respective expressions (αNf−β)Nm and (γ−δNm)Nf, with positive constants α,β,γ,δ, of the well-known Lotka-Volterra predator-prey kinetics [15].
3. Numerical scheme
3.1. Discretization of local convection and diffusion terms
We take Ω=[0,L]×[0,L] and use a Cartesian grid with nodes (xi,yj), i,j=1,…,M, with xi=yi=(i−1/2)h, h=L/M.
We discretize ∇⋅Fc(u) on this grid by weighted essentially non-oscillatory (WENO) finite differences and Δu by the standard second-order scheme with a five-point stencil to get a spatial semi-discretization of (1.1) for an 8×M×M-matrix v(t) of unknown approximations
|
vℓ,i,j(t)≈uℓ(xi,yj,t),i,j=1,…,M,ℓ=1,…,8
|
given by
|
v′=−∇h⋅˜Fc(v)+Bv+S(v),
|
(3.1)
|
to which suitable implicit-explicit Runge-Kutta (IMEX-RK) schemes will be applied for obtaining the final fully-discrete scheme (see Section 3.4). In this equation ∇h⋅˜Fc(v) is the discretization of ∇⋅Fc(u), to be defined in Section 3.3, and
|
(Bv)ℓ,i,j=μℓ(Δhvℓ)i,j,i,j=1,…,M,ℓ=1,…,8
|
(3.2)
|
is the discretization of the diffusion terms. Notice that we take μℓ=0 for ℓ∈{1,2,3,4} and models (2.2) or (2.3), for these models do not have diffusion for male species. Here we have used the notation vℓ for the M×M submatrix given by (vℓ)i,j=vℓ,i,j and Δh for the standard two-dimensional Laplacian operator with Neumann boundary conditions. Furthermore, S(v) is the 8×M×M-matrix with components
|
S(v)ℓ,i,j=sℓ(vℓ,i,j),i,j=1,…,M,ℓ=1,…,8,
|
with corresponding submatrices Sℓ(v), given by
|
Sℓ(v)i,j=sℓ(vℓ,i,j).
|
(3.3)
|
We explain the discretization of the convective term appearing in (3.1) in the next two subsections.
3.2. Discretization of the convolutions
We will use the following identity for the implementation that arises from (2.6) if we take into account (2.7):
|
V(w)=w∗ν√1+‖w∗ν‖2,ν=(∂η∂x,∂η∂y).
|
(3.4)
|
The convolutions w∗χ, χ=∂η/∂x or χ=∂η/∂y, namely
|
(w∗χ)(x)=∫Bε(0)w(x−y)χ(y)dy,
|
are calculated approximately on the discrete grid via a composite Newton-Cotes quadrature formula, such as the composite Simpson rule.
Since Bε(0)⊆[−rh,rh]2, r=⌈ε/h⌉<M, and considering that, according to boundary conditions, w is extended to the exterior of Ω by reflection, e.g. by setting w(−x,y)=w(x,y), (x,y)∈Ω, we obtain
|
(w∗χ)(xi,yj)=∫rh−rh∫rh−rhw(xi−x,yj−y)χ(x,y)dxdy≈h2r∑p=−rr∑q=−rαpαqw(xi−xp,yj−yq)χ(xp,yq),
|
where αp and αq are the coefficients in the quadrature rule (e.g., for the composite Simpson rule, α=(1,4,2,4,…,2,4,1)). This can be written as
|
(w∗χ)(xi,yj)≈r∑p=−rr∑q=−rβp,qw(xi−p,yj−q),βp,q=h2αpαqχ(xp,yq).
|
(3.5)
|
The accuracy order of this approximation is given by that of the quadrature rule, e.g., it is fourth-order accurate for the composite Simpson rule. Consequently, the approximation (3.5) for W=(wi,j)∈RM×M, wi,j≈w(xi,yj), is given by
|
(w∗χ)(xi,yj)≈(W∗hβ)i,j:=r∑p=−rr∑q=−rβp,qw[i−p]M,[j−q]M,
|
(3.6)
|
where we define
|
[i]M:={−i+1for −r+1≤i≤0,ifor 1≤i≤M,2M+1−ifor M+1≤i≤M+r.
|
The discrete approximation of V(w) in (3.4) obtained from the approximation W≈w is given by
|
Vh(W)=W∗hν√1+‖W∗hν‖2,ν=(∂η∂x,∂η∂y).
|
Since r≈ε/h=εM/L, the computational cost of this discrete convolution is M2(2r+1)2≈4ε2M4/L2, which can be very high for large M. This cost can be substantially reduced to O(M2logM) by performing a convolution with periodic data by Fast Fourier Transforms (FFTs) (see [31,54]). To achieve this goal, we define from W=(wi,j)∈RM×M a matrix ˜W=(˜wi,j)∈R2M×2M such that
|
˜wi,j=w[i]M,[j]M,i,j=1,…,2M
|
and use the notation [i]′2M=mod(i−1,2M)+1, i.e., [i]′2M=i+2kM, with k being the integer such that 1≤[i]′2M≤2M. With this notation it is readily checked that
|
w[i]M,[j]M=˜w[i]′2M,[j]′2M,i,j=−r+1,…,M+r.
|
Therefore (3.6) for i,j=1,…,M can be rewritten as
|
(W∗hβ)i,j=r∑p=−rr∑q=−rβp,q˜w[i−p]′2M,[j−q]′2M.
|
(3.7)
|
The convolution on the right-hand side of (3.7) can be performed by FFTs applied to the (2M)×(2M) matrix ˜W. To save further computational costs, the FFT of the kernel βp,q is performed only once, son each convolution entails two two-dimensional FFT of (2M)×(2M) matrices and a product of 4M2 numbers, with an overall computational cost of O(M2logM).
3.3. Discretization of the convective term
The convective flux for the ℓ (female) species, ℓ∈{5,6,7,8}, is zero and the convective flux for the ℓ (male) species, ℓ∈{1,2,3,4}, in e.g., model (2.2) is given by
|
Fcℓ(u)=uℓ(κℓV(u5+u6+u7+u8)−μℓV(u1+u2+u3+u4)).
|
To discretize its divergence ∇⋅Fcℓ(u), for the approximation v, we first approximate the convolution terms as expounded in Section 3.2 to obtain
|
˜Fcℓ(v)i,j=vℓ,i,j(κℓVh(v5+v6+v7+v8)i,j−μℓVh(v1+v2+v3+v4)i,j)∈R2.
|
Similar arguments are carried out for the other models (2.3) and (2.5).
We introduce the following notation:
|
(fxi,j,fyi,j):=˜Fcℓ(v)i,j,
|
where we have dropped the ℓ index for obtaining clearer expressions.
Our purpose is to use a fifth-order WENO finite difference discretization [27,37,53] of ∇⋅Fcℓ(u) for which
|
∇⋅Fcℓ(u)(xi,yj)≈∇h⋅˜Fc(v)ℓ,i,j:=ˆfxi+1/2,j−ˆfxi−1/2,jh+ˆfyi,j+1/2−ˆfyi,j−1/2h,
|
(3.8)
|
for suitable numerical fluxes ˆfxi+1/2,j,ˆfyi,j+1/2 obtained by WENO reconstructions of split fluxes. For the numerical flux in the x-direction, the Lax-Friedrichs-type flux splitting fx,± is given by
|
fx,±i,j=12(fxi,j±αxvℓ,i,j),αx=max
|
Likewise, the numerical flux \smash{\hat f^{y}_{i, j+1/2}} is obtained by WENO reconstructions of split fluxes given by
|
\begin{align*}
f^{y, \pm}_{i, j}=\frac12\big(f^{y}_{i, j}\pm \alpha^{y} v_{\ell, i, j}
\big),\;\; \alpha^{y}=\max\limits_{i, j} |{\boldsymbol{V}}_{h}^y(\boldsymbol{v})_{i, j}|.
\end{align*}
|
If \mathcal{R}^{\pm} denotes fifth-order WENO upwind biased reconstructions, then
|
\begin{align*}
\hat f^{x}_{i+1/2, j}&=\mathcal{R}^{+} \bigl(
f^{x, +}_{i-2:i+2, j} \bigr)
+\mathcal{R}^{-} \bigl( f^{x, -}_{i-1:i+3, j}\bigr), \\
\hat f^{y}_{i, j+1/2}&=\mathcal{R}^{+} \bigl(
f^{y, +}_{i, j-2:j+2} \bigr)
+\mathcal{R}^{-} \bigl( f^{y, -}_{i, j-1:j+3} \bigr),
\end{align*}
|
where we have used matlab-type notation for submatrices.
3.4. Implicit-explicit Runge-Kutta schemes
We will use IMEX-RK integrators for ODEs, for which only the diffusion term will be treated implicitly, so we rewrite (3.1) as (1.2), where
|
\Phi^*(\boldsymbol{v}) := -\nabla_{h}\cdot \widetilde{\boldsymbol{F}}^{\rm{c}}( \boldsymbol{v})+ \boldsymbol{S}(\boldsymbol{v}), \;\;\Phi(\boldsymbol{v}) := \boldsymbol{\mathcal{B}} \boldsymbol{v}.
|
(3.9)
|
For the diffusive part \Phi(\boldsymbol{v}) we utilize an implicit s-stage diagonally implicit (DIRK) scheme with coefficients \boldsymbol{A}\in\mathbb{R}^{s\times s}, \boldsymbol{b}, \boldsymbol{c}\in \mathbb{R}^s, in the common Butcher notation, where \boldsymbol{A}=(a_{ij}) with a_{ij}=0 for j>i. For the term \Phi^*(\boldsymbol{v}) containing the convective and reactive parts we employ an s-stage explicit scheme with coefficients \smash{\hat{\boldsymbol{A}}\in\mathbb{R}^{s\times s}}, \hat{\boldsymbol{b}}, \hat{\boldsymbol{c}}\in\mathbb{R}^{s} and \smash{\hat{\boldsymbol{A}}=(\hat{a}_{ij})} with \hat{a}_{ij}=0 for j\geq i. We will denote the corresponding Butcher arrays by
|
\begin{align*}
\boldsymbol{D} := \begin{array}{c|c}
\boldsymbol{c}&\boldsymbol{A} \\
&\boldsymbol{b}^{\rm{T}} \vphantom{X_X^{X^X}}
\end{array},\;\; \hat{\boldsymbol{D}} := \begin{array}{c|c} \hat{\boldsymbol{c}}&\hat{\boldsymbol{A}} \\
& \hat{\boldsymbol{b}}^{\rm{T}} \vphantom{X_{X^X_X}^{X^{X^X}_X}}
\end{array}.
\end{align*}
|
In our simulations, we limit ourselves to the second-order IMEX-RK scheme H-DIRK2(2, 2, 2) that corresponds to
|
\begin{align*} \boldsymbol{D} =
\begin{array}{c|cc}
1/2&1/2 &0\\
1/2&0&1/2 \\
&1/2&1/2 \vphantom{\int\limits^.}
\end{array},
\;\; \hat{\boldsymbol{D}} =
\begin{array}{c|cc}
0&0&0 \\
1&1&0\\
&1/2&1/2 \vphantom{\int\limits^.}
\end{array} \, .
\end{align*}
|
Alternative choices are provided and discussed in [10,11,45]. If applied to the equation (1.2), the IMEX-RK scheme gives rise to the following algorithm (see [45]).
Algorithm 3.1.
Input: approximate solution vector \boldsymbol{v}^n of (1.2) for t=t^n
for p=1, \dots, s
if p=1 then
{\displaystyle \hat{ \boldsymbol{v}}^{(1)} \leftarrow \boldsymbol{v}^n,
\bar{\boldsymbol{v}}^{(1)} \leftarrow \boldsymbol{v}^n }
else compute \hat{\boldsymbol{v}}^{(p)} and \bar{\boldsymbol{v}}^{(p)} from the known values \boldsymbol{K}_1, \dots,
\boldsymbol{K}_{p-1}:
{\displaystyle \hat{ \boldsymbol{v}}^{(p)} \leftarrow \boldsymbol{v}^n + \Delta t\sum_{j = 1}^{p-1}\hat{a}_{pj} \boldsymbol{K}_j},
{\displaystyle \bar{\boldsymbol{v}}^{(p)} \leftarrow \boldsymbol{v}^n + \Delta t\sum_{j = 1}^{p-1} a_{pj}
\boldsymbol{K}_j}
endif
solve for \boldsymbol{K}_p the linear system
|
{{\boldsymbol{K}_p} = \Phi^*\bigl(\hat{\boldsymbol{v}}^{(p)}\bigr) +
\Phi\bigl( \bar{\boldsymbol{v}}^{(p)} + \Delta t a_{pp} \boldsymbol{K}_p
\bigr)}
|
(3.10)
|
endfor
{\displaystyle \boldsymbol{v}^{n+1} \leftarrow \boldsymbol{v}^n+\Delta t \sum_{j=1}^sb_j\boldsymbol{K}_j}
Output: approximate solution vector \boldsymbol{v}^{n+1} of (1.2) for t=t^{n+1}=t^n+\Delta t.
To solve the linear equation (3.10) that arises in Algorithm 3.1 for \boldsymbol{K}_{p} , in view of (3.9), we rewrite it as
|
\bigl( \boldsymbol{I}-\Delta t a_{pp} \boldsymbol{\mathcal{B}}\bigr) \boldsymbol{K}_{p} =\boldsymbol{b}^{(p)}, \;\;\boldsymbol{b}^{(p)}:= \Phi^*\bigl(\hat{\boldsymbol{v}}^{(p)}\bigr) + \boldsymbol{\mathcal{B}}\bar{\boldsymbol{v}}^{(p)},
|
(3.11)
|
where \boldsymbol{I} denotes the identity operator for 8 \times M \times M matrices. From the definition of the matrix \boldsymbol{\mathcal{B}} in (3.2) and from the definition of \Phi^* in (3.9), if we equate the \ell submatrices along the first dimension of both sides of (3.11) we get
|
\begin{split}& \bigl( \boldsymbol{I}_{M\times M}-\Delta t a_{pp} \mu_{\ell}\boldsymbol{\Delta}_h\bigr) (\boldsymbol{K}_{p})_{\ell}\\& = -\nabla_{h}\cdot \tilde{\boldsymbol{F}}_{\ell}^{\rm{c}}( \hat{\boldsymbol{v}}^{(p)})+ \boldsymbol{S}_{\ell}(\hat{\boldsymbol{v}}^{(p)}) + \mu_{\ell}\boldsymbol{\Delta}_h\bar{\boldsymbol{v}}^{(p)}_{\ell}, \;\;\ell=1, \dots, 8, \end{split}
|
(3.12)
|
where \boldsymbol{I}_{M\times M} is the identity operator on M\times M matrices and, e.g., (\boldsymbol{K}_{p})_{\ell} is the \ell submatrix of \boldsymbol{K}_p along the first dimension, i.e., ((\boldsymbol{K}_{p})_{\ell})_{i, j}=(\boldsymbol{K}_{p})_{\ell, i, j}. Some remarks are due here to detail the final implementation: for \ell=1, \dots, 8, the right-hand side of (3.12) is computed from (3.3), (3.2) and (3.8), taking into account that
|
\begin{align*}
\nabla_{h}\cdot \tilde{\boldsymbol{F}}_{\ell}^{\rm{c}}( \hat{\boldsymbol{v}}^{(p)})=0 \;\; \text{for }\;\;\ell\in\{5, 6, 7, 8\}
\end{align*}
|
(i.e., there is no convection in the models for females); if \mu_{\ell}=0 (for \ell\in\{1, 2, 3, 4\} and models (2.2) and (2.3) there is no diffusion term for males), then
|
\begin{align*}
(\boldsymbol{K}_{p})_{\ell} =
-\bigl(\nabla_{h}\cdot \tilde{\boldsymbol{F}}^{\rm{c}}(
\hat{\boldsymbol{v}} ^{(p)})\bigr)_{\ell}+
\boldsymbol{S}_{\ell}(\boldsymbol{v}),
\end{align*}
|
otherwise the solution of (3.12) is performed by Fast Cosine Transforms (due to boundary conditions), which entails a nearly optimal computational cost of \mathcal{O}(M^2\log
M).
4. Numerical examples
4.1. Preliminaries
According to [4], we assume that two months (60 days) is the basic time unit, \delta = 4 (1/\delta = 15 \, \rm{days}), b=4 (average litter size), \beta_{\rm{m}} = 5 \beta_{\rm{f}}, and \beta_{\rm{m}, \rm{f}}=
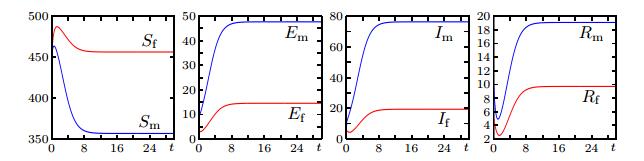
\beta_{\rm{f}}. Moreover, the infectious period for males is assumed to be twice that of females (1/\gamma_{\rm{m}} = 2/ \gamma_{\rm{f}}), and the carrying capacity is K=1000 animals. Furthermore, we set \beta_{\rm{m}} =0.01, \gamma_{\rm{m}} =0.5, a=0.01 and c=1.99 \times 10^{-3}. For these values, the next-generation-matrix method [59] employed in [4] yields a basic reproductive ratio \mathcal{R}_0 =1.38.
We wish to present numerical solutions of the different versions of the spatio-temporal model, Models 1 to 3, that can be compared with the example simulated in [4] (that is, by Model 0), and that corresponds to
|
(S_{\rm{m}}, E_{\rm{m}}, I_{\rm{m}}, R_{\rm{m}}, S_{\rm{f}}, E_{\rm{f}}, I_{\rm{f}}, R_{\rm{f}})(0) = (450, 10, 10, 10,450, 5, 5, 5) =: \boldsymbol{U}_0^{\rm{T}}.
|
(4.1)
|
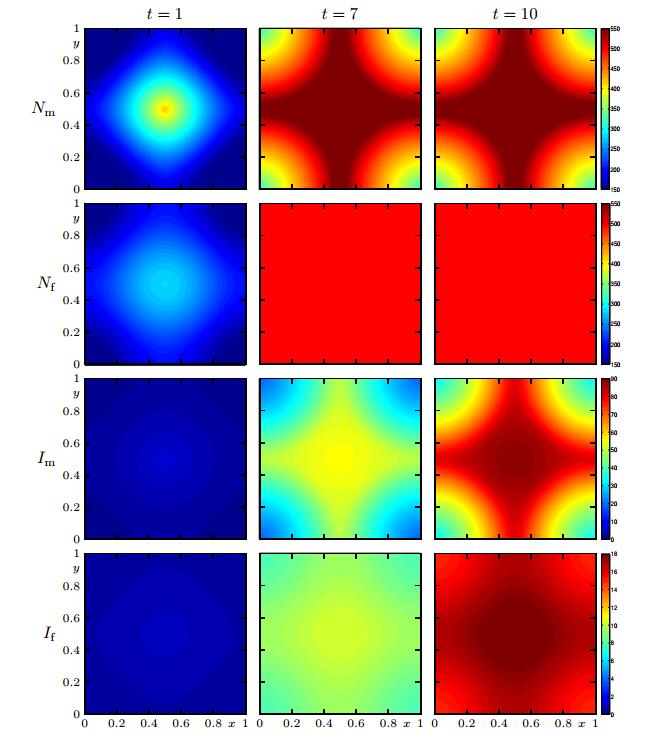
(Figure 1 shows the solution of Model 0 for this case.) To this end, we assume that the spatial domain is \Omega = [0,1]^2 (i.e., L=1 in a scale not specified) and that K=1000 is the maximum density feasible on a unit square. For the simulation, we consider Scenario 1, which corresponds to identifying a subdomain \Omega_0 \subseteq \Omega with \Omega_0 =\{(x, y)\in\Omega:|x-0.5|+|y-0.5|\leq0.2\} in which the initial population is uniformly distributed and setting
|
\begin{align*}
\boldsymbol{u} (\boldsymbol{x}, 0) =
\chi_{\Omega_0} (\boldsymbol{x}) \boldsymbol{U}_0,
\text{where} \chi_{\Omega_0} (\boldsymbol{x}) = \begin{cases}
1&\text{if }\boldsymbol{x} \in \Omega_0, \\ 0&\text{otherwise, } \end{cases}
\end{align*}
|
and alternatively Scenario 2, in which we stipulate a "random" distribution by setting
|
\boldsymbol{u} (\boldsymbol{x}, 0) = \frac{1}{|\Omega|} \bigl( 1+ r(\boldsymbol{x})\bigr) \boldsymbol{U}_0,\;\; \text{where} \;\; \int_{\Omega} r (\boldsymbol{x}) \, \rm{d} \boldsymbol{x} =0
|
(4.2)
|
and r is a given oscillatory function assuming values in (-1, 1). (The idea is not to impose any initial "pattern" in Scenario 2.)
A total number of six cases is considered by combining Scenarios 1 and 2 with Models 1, 2 and 3. We always choose \mu_X = 0.05 for all species X, \kappa_X =0.1 and h=1/200. Furthermore, we wish to compare the numerical results with the predictions made by the non-spatial ODE model, Model 0 (Figure 1). To this end we determine for each compartment X \in \mathcal{C} and time instants t^n = n \Delta t the following quantity:
|
\mathcal{I} (X) = \mathcal{I} (X, t^n) := h^2 \sum\limits_{i, j=1}^{\rm{N}} X^n_{i, j} \approx \int_{\Omega} X(\boldsymbol{x}, t^n) \, \rm{d} \boldsymbol{x},
|
(4.3)
|
which represents the approximate total number in \Omega of individuals of compartment X at time t^n. We recall that in the PDE model (2.1), the unknowns X \in \mathcal{C} are densities, and so an integration over \Omega is necessary to make results comparable to those of a model that predicts the total number of individuals in each compartment (as does Model 0). Similar "integrals" of the numerical solution are utilized by Colombo and Rossi [20,Fig. 3.2] to study the global behaviour of their predator-prey model.
4.2. Cases 1 to 3: simulations with a structured initial datum
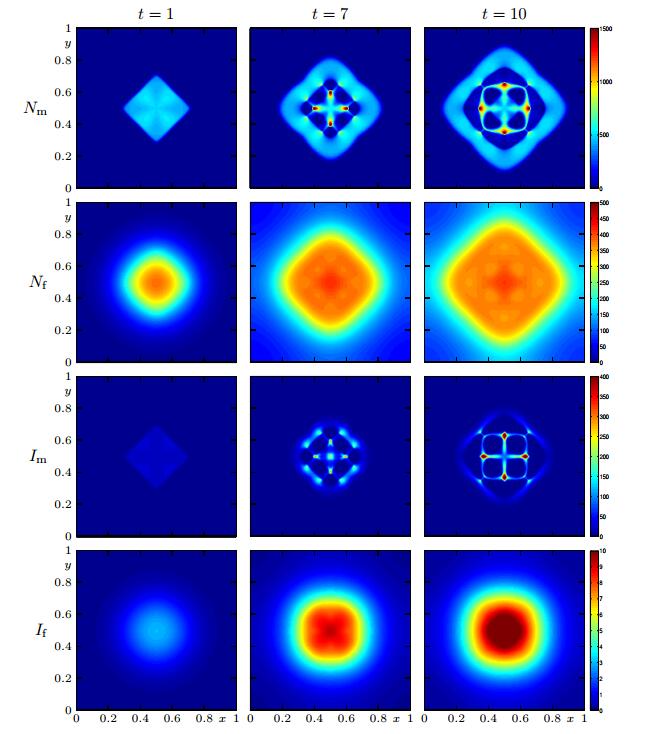
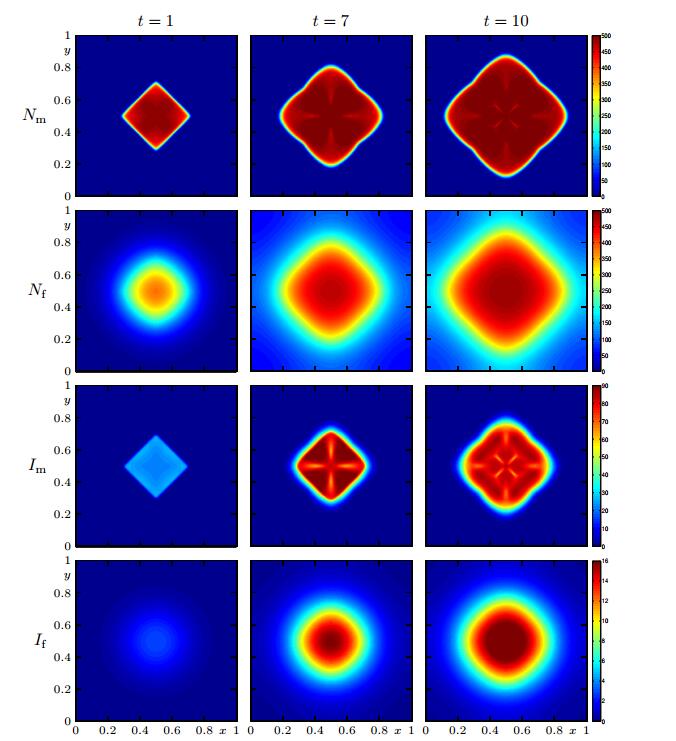
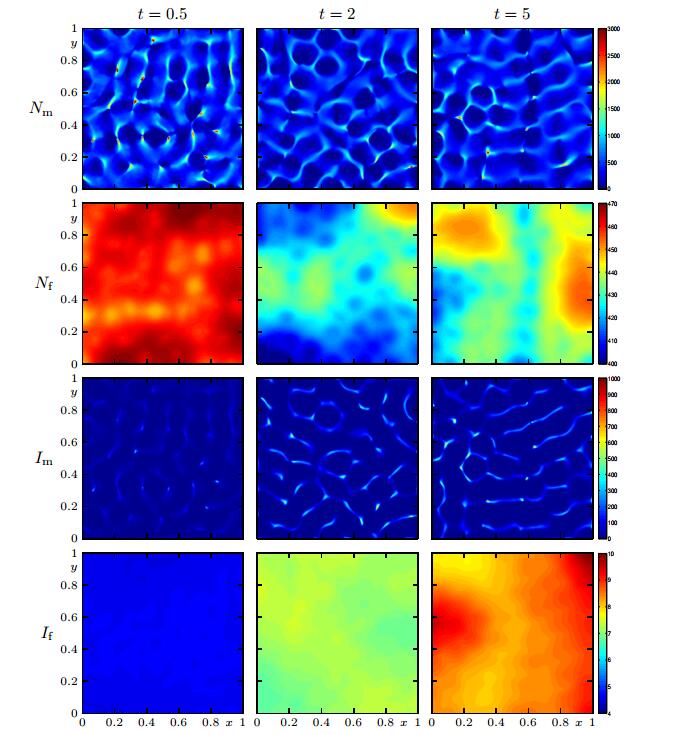
In Figures 2 to 4 we show the numerical solution for N_{\rm{m}}, N_{\rm{f}}, I_{\rm{m}} and I_{\rm{f}}, in each case at three different times, for Cases 1 to 3 that arise for Scenario 1 with Model 1, Model 2 with K=1000, and Model 3. First of all, we observe that according to the results for N_{\rm{m}} and I_{\rm{m}}, within Models 1 and 2 the male individuals keep confined to a growing but sharply limited region, with zero values outside that region. Model 3, with its linear diffusive term -\mu_X \nabla X for X \in \mathcal{C}_{\rm{m}} (instead of the expressions -\mu_X X \boldsymbol{V} (N_{\rm{m}}) or -\mu_X X \varphi(N_{\rm{m}} + N_{\rm{f}}) \boldsymbol{V} (N_{\rm{m}}) in Models 1 or 2), produces a solution that fills the entire domain. Numerical results obtained for larger times than those shown in Figure 4 indicate that the solutions of all variables become constant on the entire computational domain, and the integral quantities assume a stationary state similar (but not identical) to that of Model 0 (see Figure 1). Furthermore, comparing the results between Models 1 and Models 2 (Figures 2 and 3), we observe that Model 1 gives rise to a distinct spatial structure, including regions that are nearly void of males combined with "peaks" of the solution where N_{\rm{m}} \approx 1500. Clearly, this feature is expected since Model 1 has no mechanism that would limit the value of the total density of males N_{\rm{m}}. (We recall that although the total numbers of male or female individuals, \mathcal{I}
(N_{\rm{m}}) and \mathcal{I}(N_{\rm{f}}), are bounded by the terms with the death rates in all models, it may well happen that the densities N_{\rm{m}} or N_{\rm{f}} become locally unbounded.)
The results obtained for Case 1 are in marked contrast to those for Case 2, especially those for N_{\rm{m}}, produced by Model 2 shown in Figure 3, where we observe that N_{\rm{m}} does not exceed a value of about 500, and stays close to that value within a region of approximately the same shape as for Model 1. A similar observation is true for the compartment I_{\rm{m}}: Model 1 (Figure 2) predicts a structure with "peaks" that roughly mirrors that of N_{\rm{m}}, while Model 2 (Figure 3¿) predicts a more uniform distribution (with I_{\rm{m}} assuming values between 70 and 90) in the interior of the domain. Furthermore, we recall that for all models the flux for the female compartments is always given by -\mu_X \nabla X for X \in \mathcal{C}_{\rm{f}}, so differences in solution behavior of the female individuals are exclusively due to those in describing the male behavior. In general, this diffusive behavior tends to produce less sharp, smooth spatial structures.
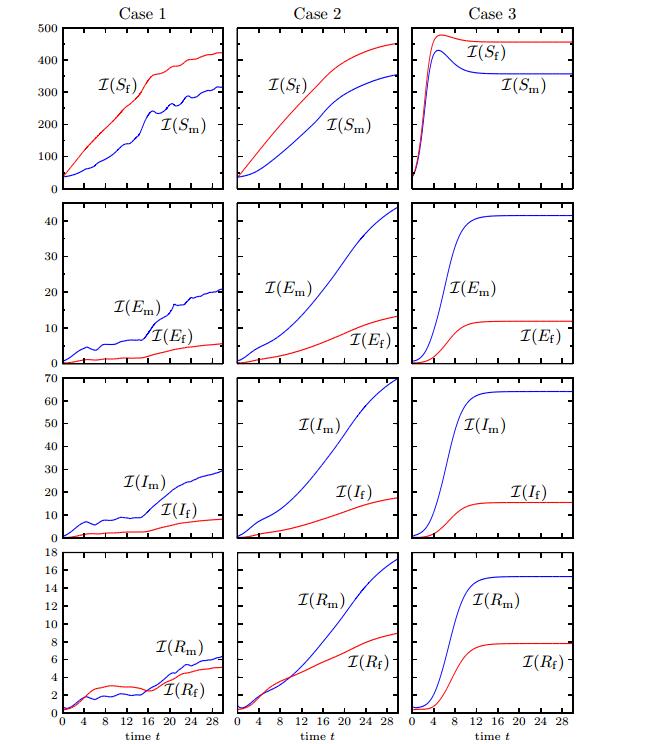
Finally, Figure 5 indicates that Models 1, 2 and 3 lead to quite different numerical results in terms of the integrated quantities (4.3). As mentioned above, the results of Model 3 are similar to those of Model 0. On the other hand, while Models 1 and 2 produce integral results whose order of magnitude for each compartment is similar to that of Model 3, it can be noted that no stationary state is attained at t=30; as the discussion of Cases 4 to 6, and in particular comparing Figures 5 and 9 show, this is a consequence of the respective model structure in combination with the choice of initial data. In any case, it is calling to attention that while Models 2 and 3 predict a smooth variation of the integrated quantity in time, the curves generated by Model 1 are somewhat oscillatory. This behavior is consistent with our observation that Model 1 does not only generate a spatial solution structure with strong variations, "peaks" and sharp gradients, but also produces rapid transitions within time. This unsteady and unstable behavior is due to the strong competence of advective and repulsive mechanisms inherent in the definition (2.2).
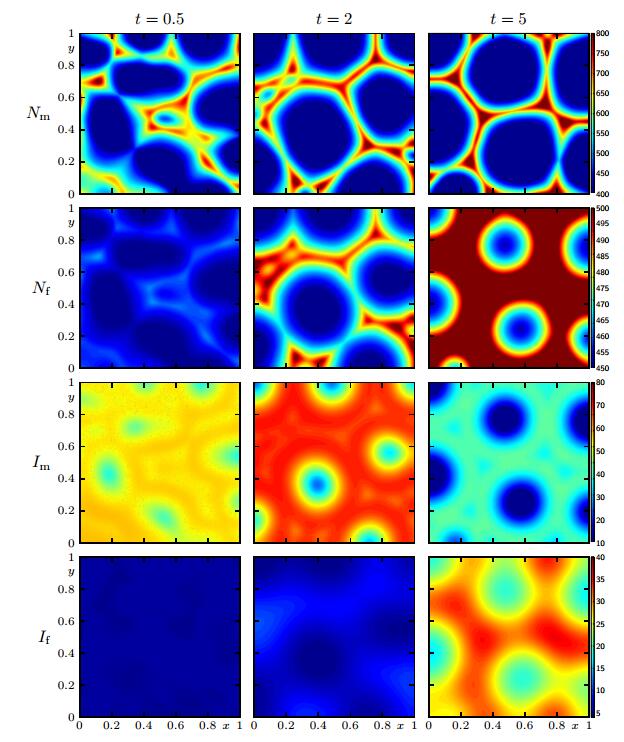
4.3. Cases 4 to 6: simulations with a randomly fluctuating initial datum
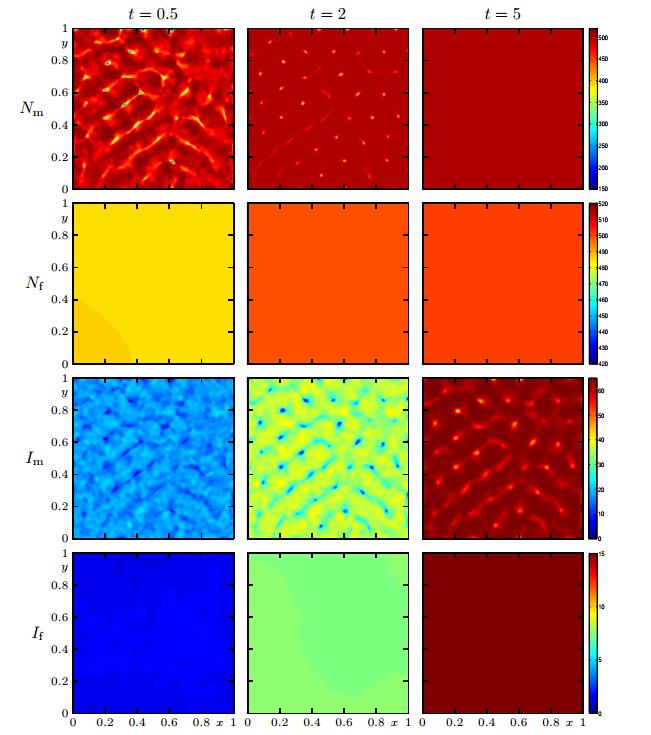
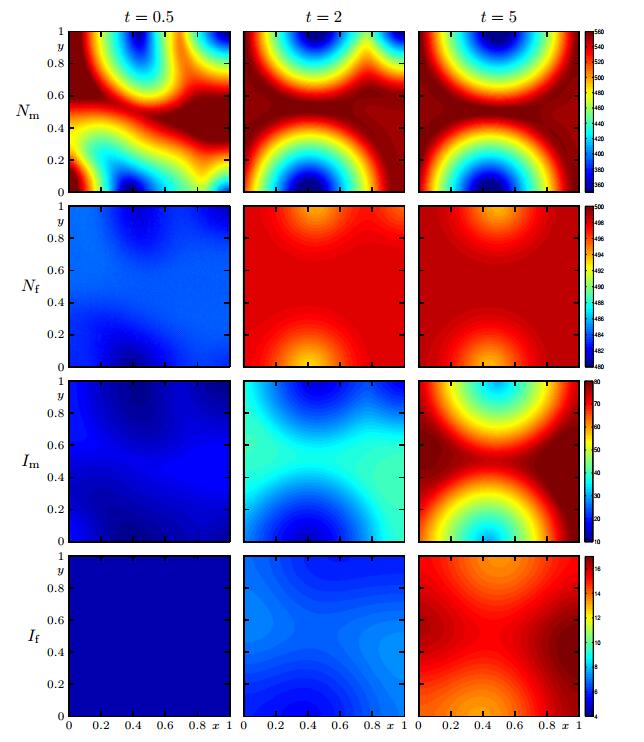
Figures 6 to 9 provide numerical solutions for Scenario 2. The "random" initial datum (4.2) has been chosen to test whether small perturbations would give rise to large-scale regular structures akin to the well-known mechanism of pattern formation (cf., e.g., [38,41]), or rather, the small fluctuations in the initial datum would simply be smoothed out. Figure 6, corresponding to Model 1, illustrates that male individuals aggregate in a kind of filamentous structure, including some marked peaks with N_{\rm{m}} reaching values close to 3000. On the other hand, we observe the formation of areas of roughly the same shape and size that are nearly void of male individuals. This behavior is similar to that observed by Colombo and Rossi for the predator density in their predator-prey model (cf., e.g., [20,Figs. 3.3-3.5]). In our cases, the densities of the female populations N_{\rm{f}} and I_{\rm{f}} do not vary much over the computational domain, and do so smoothly. For the same scenario with Model 2 and K=1000, Figure 7 indicates that while for small times we observe the formation of spatial structures similar those of Figure 6, eventually all variables become nearly constant on the whole domain. Figure 8 for Model 3 illustrates that marked circular spatial structures persist over long times. Similar results (not shown here) were obtained in other numerical experiments for times up to t=87. We also comment that Figure 9 illustrates that Model 2 leads to a nearly stationary behavior of the integral quantities within shorter time than for Scenario 1, and results for Models 2 and 3 are quite similar. The curves observed in Figure 9 for Model 1 are, again, oscillatory, which lends further support to the conjecture that this model (at least with the parameters chosen) exhibits spatial-temporal oscillatory behavior.
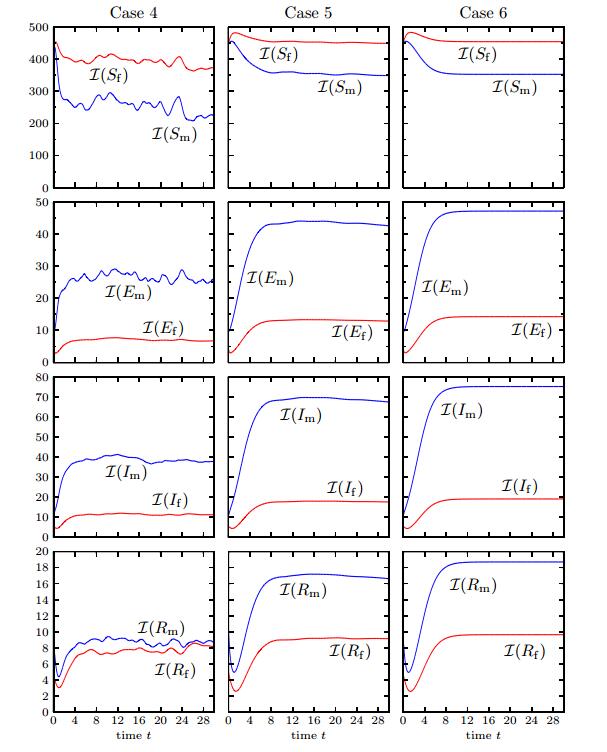
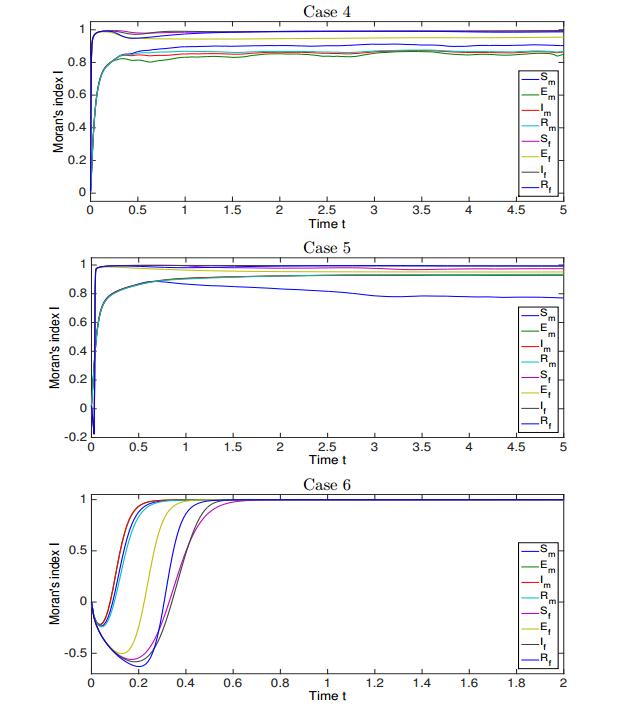
For Cases 4 to 6, we calculate the evolution of Moran's index [25,40,49], denoted here \mathsf{I}, for each species at each time step, and which is here computed by
|
\mathsf{I}=\mathsf{I}(X) := \sum\limits_{i, j=1}^{M} \frac{1}{4}Y_{i, j}(Y_{i-1, j}+Y_{i+1, j}+Y_{i, j-1}+Y_{i, j+1}) \biggl/ \sum\limits_{i, j=1}^{M} Y_{i, j}^2,
|
(4.4)
|
where X is the numerical data obtained for some species at a certain time step and
|
Y_{i, j}=X_{i, j}-\frac{1}{M^2}\sum\limits_{p, q=1}^{M}X_{p, q}.
|
(4.5)
|
Overall, the results shown in Figure 10 indicate that a strong spatial autocorrelation (\mathsf{I}\approx 1) is developed through the simulation from initial random data (\mathsf{I}\approx 0). It is, however, interesting to note for that for Cases 4 and 5 the values of \mathsf{I} for the female compartments remain consistently below those of the male compartments, while for Case 6 the limit value \mathsf{I} = 1 is closely approximated by all species. This confirms the trend evident already from the results of Figure 8 compared with those of Figures 6 and 7, namely that the presence of diffusive movement in the male species significantly contributes to generating smoothly varying solution patterns, that is, to creating a high degree of spatial autocorrelation.
4.4. Case 7: order test with smooth solution
The purpose of this test is to show that the numerical scheme exhibits experimental second order convergence when the solution is smooth. For this purpose, we choose a smooth initial configuration given by
|
\begin{align*}
X_\rm{m}(x, y, t=0)&=c_X \exp\left(-\frac{1}{2} \bigl((x-3)^6+(y-3)^6 \bigr)\right), \\
X_\rm{f}(x, y, t=0)&=c_X \exp\left(-\frac{1}{2}\bigl((x-7)^6+(y-7)^6\bigr)\right)
\end{align*}
|
for X\in\{S, E, I, R\}, constants c_S=1000, c_E=1, c_I=10 and c_R= 1, and a sufficiently small final time T=0.1 to ensure that no singularities are formed during the simulation. We choose \mu_X = 10^{-4} for X\in \mathcal{C}_{\rm{m}} and \mu_X=10^{-3} and \kappa_X =10^{-2} for X \in \mathcal{C}_{\rm{f}}.
We compute approximate L^1 errors for approximate solutions obtained with M\times M meshes, M=2^s, s=3, \dots, 8, using a reference solution with a resolution of \smash{M_{\rm{ref}}\times M_{\rm{ref}}} cells, for \smash{M_{\rm{ref}}}=2048, as follows. We denote by \smash{(v_{\ell, j, k}^M)_{j, k=1}^{M}} and \smash{(v_{\ell, j, k}^{\rm{ref}})_{j, k=1}^{M_{\rm{ref}}}} the numerical solution for the \ell-th component (\ell = 1, \dots, 8, see Section 3.3) at time T calculated with M and M_{\rm{ref}}, respectively. We project the reference solution to the coarser grids by bicubic interpolation, since the numerical scheme is designed to compute second-order approximations to the exact solutions at the nodes (x_i, y_j), with x_i=y_i=(i-1/2)L/M, for the coarse mesh, and (\bar x_i, \bar y_j), with \bar x_i=\bar y_i=(i-1/2)L/M_{\rm{ref}} for the fine mesh and these points do not coincide. Specifically, this projection \smash{\tilde{v}_{\ell, j, k}^{M}} for j, k=1, \dots, M is computed by
|
\tilde{v}^{M}_{\ell, j, k}=
\sum\limits_{j_1, k_1=-2}^1 \xi_{j_1}\xi_{k_1}v^{\text{ref}}_{\ell, \bar
j-j_1, \bar k - k_1},\;\; \bar
j= \left(j-\frac{1}{2}\right)\frac{M_{\text{ref}}}{M}, \;\;\bar k=\left(k-\frac{1}{2}\right)\frac{M_{\text{ref}}}{M},
|
where \xi_{-2}=\xi_{1}=-1/16 and \xi_{0}=\xi_{-1}=9/16. Notice that \smash{M_{\rm{ref}}/M=2^{11-s}\geq 8} in this test and the previous formula is therefore computable.
The total approximate L^1 error of the numerical solution \smash{(v_{\ell, j, k}^M)_{j=1}^{M}} at time T is then given by
|
e_M^{\rm{tot}} :=\frac{1}{M^2} \sum\limits_{\ell=1}^8 \sum\limits_{j, k=1}^{M} \bigl|\tilde{v}_{\ell, j, k}^{M}-v_{\ell, j, k}^{M}\bigr|.
|
(4.6)
|
Based on the approximate errors defined by (4.6), we may calculate a numerical order of convergence from pairs of total approximate L^1 errors \smash{e_{M}^{\rm{tot}}} and \smash{e_{2M}^{\rm{tot}}} by
|
\begin{align*}
\theta_M := \log_2 \bigl( e_{M}^{\rm{tot}}/ e_{2M}^{\rm{tot}} \bigr).
\end{align*}
|
These data are displayed in Table 1. It can be deduced that the errors start diminishing for M=64 and do so roughly at a second-order rate.
Table 1. Case 7 (Model 1, order test with smooth solution): approximate total
L^1
errors
\smash{e_M^{\smash{tot}}}
and observed convergence rates
\theta_M
.
|
M
|
8 |
16 |
32 |
64 |
128 |
256 |
|
e_M^{\smash{tot}}\times 10^{3}
|
368.90 |
383.19 |
379.01 |
153.73 |
34.70 |
9.14 |
|
\theta_M
|
-0.05 |
0.02 |
1.30 |
2.15 |
1.92 |
- |
4.5. Case 8: seasonal alternation for Models 0 and 3
Climatic changes, e.g.,
due to large periods of rain or of drought, can lead to variation in some parameters,
for example those that influence death and birth rates of the rodent population. To
study the effect of seasonal variability, in this example we identify two different sets
of parameters that can represent two different seasons, \{a_{i}, b_{i}, c_{i}\} for i=1, 2. We wish to explore the transmission dynamics of hantavirus due to an alternation in time of the parameters between these two seasons. We implement square-periodic season alternation where the duration of each season is T/2, where T units is a year. Any given quantity u(t) alternating in this way can be expressed as u(t)=u_{+}+u_{-}\mu(t), where u_{\pm}=\frac12(u_{1}\pm u_{2}) and \mu(t) is a periodic square wave \mu(t)=1 if t\in(0, T/2) and \mu(t)=-1 if t\in(T/2, T).
We consider a_{1}=0.01, b_{1}=4, c_{1}=1.99\times 10^{-3} and a_{2}=0.05, b_{2}=3, c_{2}=0.0015 in order for the carrying capacity to be K_{1}=K_{2}=1000 for both choices, so R_{0, 1}=1.38 and R_{0, 2}=2.26 are obtained. The remaining parameters and initial conditions are the same as in Cases 4 to 6 (Scenario 2).
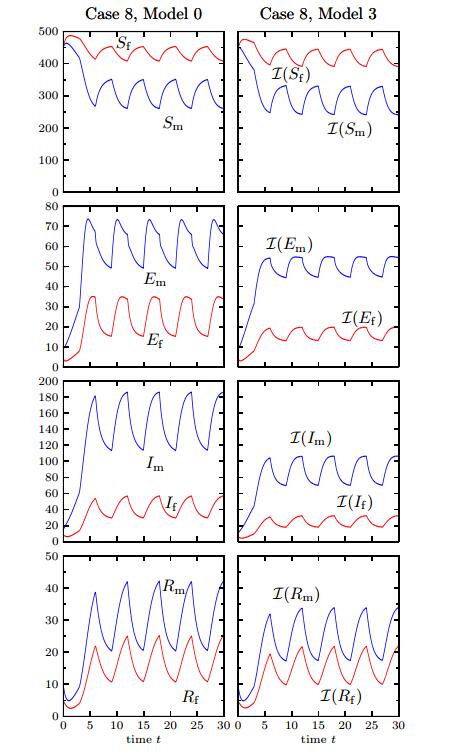
In Figure 11 we display the numerical solution for Model 3. Roughly speaking we observe that the seasonal alternation in the parameters produces a solution similar to that provided by Model 3 also with a randomly fluctuating initial datum. In Figure 12 we display the solutions for (the ODE) Model 0 and for Model 3. We observe that the seasonal alternation in the parameters generates an oscillatory and bounded solution for each case, and Model 3 displays a smaller amplitude.
5. Conclusions
We have shown that a relatively simple gender-structured spatialtemporal model (2.1) of Hantavirus transmission among rodents with a non-local velocity term (2.6), which arises in each of the Models 1, 2 and 3 defined by (2.2), (2.3) and (2.5), respectively, can yield complex spatial-temporal profiles of disease prevalence (Figures 2 to 8). However, in reality, a number of additional factors can affect the transmission dynamics of Hantavirus infections among rodents. Specifically, the transmission of hantavirus has been associated with land use patterns, elevation, vegetation types [9], as well as variations in temperature, humidity, and rainfall [64]. Moreover, rodent habitat and rodent behavior can be influenced by temperature, precipitation and land use [16]. The growth of rodent populations may also be associated with local temperature, as temperature may affect the pregnancy rate, litter size, birth rate and the survival rate of rodent populations [62]. Further, rodents tend to inhabit highly covered and less disturbed habitats, which are commonly found in agricultural habitats and pastureland habitats [39,63] in order to enhance their reproduction and survival capacity [39].
We plan to conduct further research on the qualitative analysis of the proposed models, or suitable simplifications of them, using analogous techniques to those utilized in [20]. The accuracy of the numerical method proposed in this work is worth to be studied in subsequent works, specially to establish that its order of convergence corresponds to its design order. Although in this work we use a second-order spatial discretization of the Laplacian and a second-order time-stepping, which limit the high-order accuracy of the fifth-order WENO spatial semidiscretization, we plan to perform comparisons with higher-order discretizations of the diffusion operator and time-stepping scheme. More scenarios (initial configuration, parameter calibration) should be explored with these numerical tools in order to obtain and study further spatio-temporal patterns in the simulations. In this sense, among our proposed models, we consider that Model 1 is the most promising one giving rise to interesting spatio-temporal patterns and is worth to be analyzed as in [19,38]. Finally, we wish to expand on the conclusions that can be inferred from \mathsf{I} applied to numerical solutions of a local or non-local PDEs, which to our knowledge still needs to be addressed. We leave an in-depth analysis of the behaviour of \mathsf{I} and related quantities, such as the bivariate Moran index [25,49] that could, for example, elucidate the mutual spatial correlation of the male and female patterns, as a topic of future research for the present class of models.
Acknowledgments
RB is supported by Fondecyt project 1130154; BASAL project CMM, Universidad de Chile and Centro de Investigación en Ingeniería Matemática (CI^{\rm{2}}MA), Universidad de Concepción; and Centro CRHIAM Proyecto Conicyt Fondap 15130015. PM is supported by Spanish MINECO project MTM2014-54388-P and Conicyt (Chile), project PAI-MEC, folio 80150006. LMV is supported by Fondecyt project 11140708. EG is supported by CONICYT scholarship. GC acknowledges financial support from grants NSF-IIS RAPID award #1518939, and NSF grant 1318788 Ⅲ: Small: Data Management for Real-Time Data Driven Epidemic simulation.









 DownLoad:
DownLoad: