"Intelligence is the wife, imagination is the mistress, memory is the servant."
—
Victor Hugo, a writer
"There is no such thing as Intelligence; one has intelligence of this or that. One must have intelligence only for what one is doing."
—
Edgar Degas, a painter
"Nature is immense and complex, but it is not impermeable to the intelligence; we must circle around it, pierce and probe it, looking for an opening or make it."
—
Primo Levi, A Chemist And Writer
1. Background
The overwhelming quest in cognitive science has been (and still is) to scientifically describe mental processes, notably memory, emotions and intelligence. Is it possible to chart the complex terrain of the emotive mind and to build a device or algorithm to mimic such?
Memory is the key to "mind", manifest as intelligence and emotions. In that ubiquitous artifacts (iPhones, iPads, computers) operate with a function called "memory", the popular consensus is that these artifacts emulate the processes whereby biologic neural nets memorize and learn [1,2,3,4,5,6,7,8,9,10,11]. The founders of computation [12,13,14,15], the latter presenting with neurobiologist McCullogh at the Hixon Symposium lectures [16], believed that their algorithms mimicked the mentation talents of neural brains; that computation and mentation are equivalent processes. The field of Artificial Intelligence (AI) is rife with such an assumption [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35].
What is desired and needed is a compelling thesis that comports with the material basis of all living tissue, but also offers insight into the unique talent of the biologic neural net to achieve psychic states, to experience memory and emotions, manifest as intelligence. To fashion such a thesis, one must be guided by certain principles and rationalize experimental "facts".
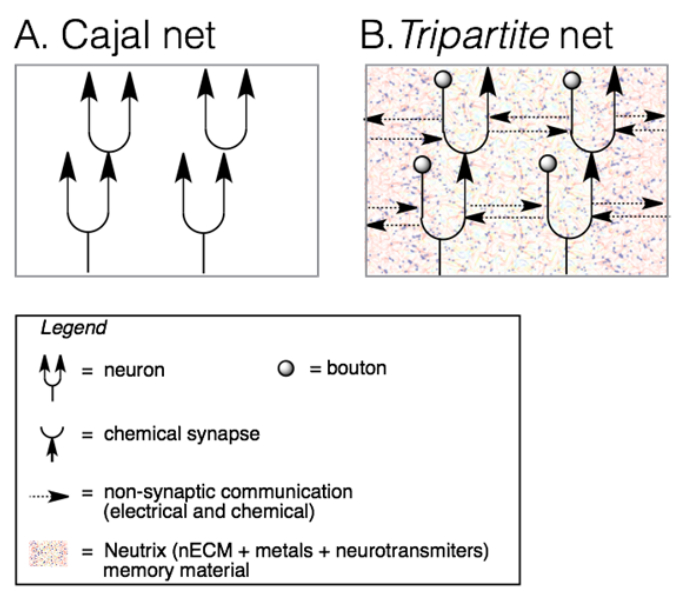
For example, if "form follows function", one could consider that the neural shape implies something about its interactions with its physical surroundings. From the time of Cajal, all considered that synaptic electrodynamic signals between neurons served as the core of neural mentation [36,37]. The Hebb concept of "synaptic plasticity" based on such, has become the modern mantra [37,38]. But reservations have been voiced [40,41,42,43]. In particular, it was noted that there are many non-synaptic neural signaling possibilities [44,45] through the ubiquitous extracellular matrix (nECM) around all neurons [44,45,46,47,48,49]. The nECM may well have a function related to signaling between neurons (including astrocytes [50]), that are not suspended in space, not "naked". This suggests that one cannot remain anchored to the Cajal-Hebb concept of synaptic contacts as the exclusive signaling modality between neurons, discussed further along our narrative.
Many attempts have been made to pierce the mystery of neural intelligence and memory, with a literature too vast to cite here (but see [51]). All manner of experiments have been designed to illuminate one or another aspect of this neural talent, including biochemical analysis, electrodynamic measurements, and in recent times, fMRI (functional Magnetic Resonance Imaging). Simulations with computers have also been used to construct and evaluate possible models of brain processes.
2. Paradigm Shift
But as in any field, phenomena or observations that do not fit a consensus model are simply not recognized as "facts" to be considered. Rather, it requires a paradigm shift for 'facts' to be recognized and a new model accepted [52]. In neurobiology for example, most research is directed to articulate the Cajal-Hebbs model of learning and memory, based on 'synaptic plasticity', the increased functionality of synaptic signaling between neurons. But objections have been raised to the idea that synaptic plasticity can encode/decode memory. Active electronic circuits do not store information, but process and transmit it between microprocessors with memory storage capability. In that information is physical [53], it requires a place wherein it can be stored for short or long periods (i.e., RAM). Electronic memory is not stored in reverberating circuits, but is physically embodied in dopants, spins, holes, pits, etc. distributed in a synthetic matrix a "memory material". Thus, as the information technology races to ever increase the memory capacity of computer chips, it develops new "memory materials" [54,55,56,57,58,59,60] and decreases the size of microprocessing circuits.
From a biologic perspective, the evidence of neural shape and the non-synaptic signaling modality (volume transmission) [61,62,63] though the nECM, is generally overlooked, ignored as irrelevant to the neurons' unique mentation talent. So too is the fact that neural nets are emotive systems that cannot be simply mimicked by electronic devices.
3. Emotions
Emotions are the bedrock of neural mind states. But in spite of many attempts to compute emotions [16,64,65,66,67,68,69,70,71,72,73,74,75,76,77], it is inescapable that electronic artifacts lack an affective mode of processing information, are 'demotive', totally lacking in emotive quality. A mathematical equation [16,64] or unary algorithm [28,29] cannot conjure a psychic state called 'emotion'. Though we know how artifact memory works and can fabricate chips constructed with "memory materials", this does not clarify the memory process of biologic neural nets resulting in psychological states. Likewise, quantum or optical effects do not serve to explain the combination of physiologic reactions and psychic states associated with emotive memory.
We suggest that one needs to couch the rationalization of neural memory in terms appropriate to biologic systems and not simply to appropriate terms i.e.,
"neural net". It is a pharmacologic fact that many legal and illegal drugs which affect memory, simultaneously elicit psychic as well as physiologic reactions. But this chemical fact has not been considered as cogent to the encoding of emotions in neural memory. Thus, we have remained dissatisfied and continued to search for a chemical rationale to describe the coding of neural memory and emotions, the pillars of intelligence.
4. Intelligence Defined
"Intelligence" is a talent that has been defined in many different ways, including capacity for logic, abstract thought, understanding, self-awareness, learning, emotions, creativity and problem solving.
"The faculty for adapting oneself is the property of intelligence and that the power of adaptation is the measure of it"
— Binet and Simon, 1916, authors of the IQ test [78].
The link of memory to abstract thought described as 'intelligence', is incontestable. Biologists have deployed convincing tests that demonstrate that animals (ducks, rats, primates) exhibit intelligence through non-verbal mentation [79,80,81,82,83,84,85,86]. In man, there may be special classes of talents described as "intelligence" for music, math, language which spring from homo sapien's talent for language.
Types of Intelligence
From our perspective, one can divide intelligence into two categories with key characteristics:
1. Logical-Intelligence expressed by an electronic artifact programmed with logical, binary algorithms. Artificial intelligence (AI) is synthetic example though it may be misnamed, as discussed later. AI algorithms can map places in space, land and sea (navigation), interpret facial features of humans, recognize the pattern of fingerprints, mimic the grouping behavior of virtual creatures ("vants", "boids", 87 Levy, 1992), fly drones, monitor credit card usage, affect the walking pace of a robot, and learn from previous efforts.
The development of machines that learn from experience lies at the basis for what is called AI. Generally, a 'goal' is imposed by the programmer so that the learning algorithm can optimize the achievement of this goal. AI computers can play board and word games and learn moves. Recent examples of such are the championship wins of computer systems in chess (IMB's Deep Blue beat Kasparov, 1997), Go (Googles Deep Mind won over Lee Se Dol in 2016; 35) and in the verbal recall game Jeopardy (IBM's Deep Blue beat human champions Ken Jennings and Brad Rutter, 1997). A listing of AI talents would include: counting, pattern recognition, game playing, objective manipulation of symbols.
But the computer's goal lacks an empathic facet. Recognizing emotions in the voice or face of humans, or remembering lists and game patterns is not the same as experiencing emotions psychically as well as physically. Quite to the contrary, the artifacts of inorganic circuit boards, which operate with binary-based algorithms in electronic mode, are bereft of emotive context ('demotive').
2. Emotive neural intelligence (NI) is a talent ascribed to living organisms which experience emotive states and learn to adapt to an everchangeing environment to obtain food, survive and reproduce.
'feelings' are perceptions from our sense; 'emotions' are psychic experiences of temporally past physiologic states (recalled feelings).
Thus,
'feelings' only require physical stimuli and can be mimicked by electronic sensors (i.e., video camera, pressure sensor, thermometer). But emotions cannot be electronically mimed and operate through memory. What other signaling modality is available to the neuron?
A listing of recalled emotive states includes: Feelings, sensations (hunger, pain, etc.), goals, desires, sociability, drive to survive. All these states require memory; each ultimately rated/judged/valued by emotive aspects, remembered to survive. Of course, non-verbal animals also experience emotions and memory [79,80,81,82,83,84,85,86]. The crux of neural mentation and intelligence lies in emotive states. One cannot grasp the essence of neural intelligence by ignoring emotions. Rather, one wants to develop a "universal" model of emotions and memory that applies to all neural creatures.
5. Hypothesis: Tripartite Mechanism of Neural Memory
As far as we know, no-one has ever addressed the potential for neurons to employ a chemodynamic signaling molecules for encoding and recalling emotive states. We have proposed [86,87,88,89,90,91,92,93] that memory involves the interactions of 3 brain compartments, as listed:
1. Neurons — sets of highly extended cells employing both electrodynamic and chemodynamic signaling modes.
2. nECM — comprising a heterogeneous collection neural extracellular matrix of biopolymers (chondroitins, hyaluronates, heparans and proteins) entangling the neurons.
3. Dopants — comprising diffusible metals and neuro-transmitters (NTs) released into the nECM.
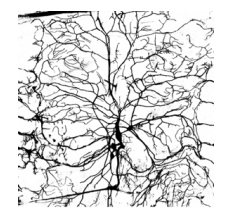
The brain is an assembly of neurons whose mentation performance, manifest as an emerging talent must be ultimately governed by the laws of chemistry and rules of biology [94]. It achieves a conscious state under metabolic conditions similar to those of an aggregate of bacteria, from which they evolved. In fact, both employ identical bio-modulating molecules (Table 1). Moreover, the shape of the neuron suggests signaling to other cells via synaptic contacts as well as non-synaptic signaling through the surrounding nECM (Figure 2).
Table 1. Bio-modulators of physiologic responses, which elicit both physiologic (feelings) and psychic (emotions) responses.
| Neuro-transmitters (NTs) |
Physiologic effects |
Phsycic effects |
|
(Feelings) |
(Emotions) |
| Biogenic amines |
Breathing |
Anxiety |
| > 10 Amino acids |
Blinking |
Aggretion |
| > 75 Neuropeptides |
Blood pressure |
Awareness |
| > 10 others (endocannabanois, NO, Achol |
Counghing |
Depression |
|
Crying |
Dreams |
| NEURO-METALS |
Dilation of pupil |
Fear |
| K, Li, Ce, Ca, Co, Cu, Mg, Fe, Ni, Mn, Sr, Zn |
Drooling |
Hate |
|
Erection |
Joy |
|
Evacuation |
Love |
|
Fever |
Pain |
|
Goose bumps |
Sadness |
|
Hunger |
Sex drive |
|
Itching |
Sociability |
|
Laughing |
|
|
Orgasm |
|
|
Pulse |
|
|
Salivation |
|
|
Secretion |
|
|
Spasms |
|
|
Sweating |
|
|
Thirst |
|
|
Trembling |
|
|
Tremors |
|
|
Urination |
|
|
Vasodilation |
|
|
Vomiting |
|
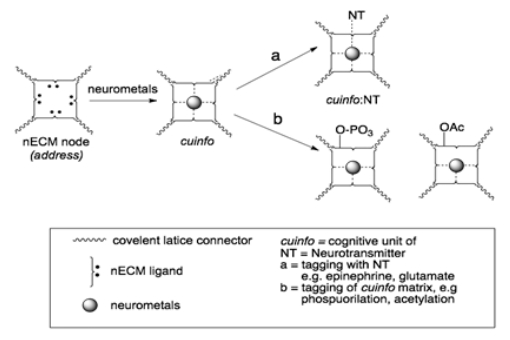
| The dopants (NT and metals) ejected by the neuron from its vesicle stores, form metal-centered complexes within the nECM, encoding cognitive units of information (cuinfo) (singular/plural). In effect, the nECM functions effectively as a 'memory material' matrix, wherein logical cuinfo are encoded with metals and possibly modified by derivatization (tagging) reactions (Figure 3 route b), none of which are inherently emotive. |
The cuinfo are not necessarily contiguous, but may be dispersed in various anatomic compartments of the brain. Emotive states with corresponding cuinfo (Figure 3 route a, Figure 4), are chemically encoded with > 100 NTs that can bind to the central metal of each cuinfo. The NTs elicit physiologic and psychic responses (feelings) (Table 1).
6. Recap
Artifact processing of information with binary-coded algorithms can only achieve logical operations, a type of 'demotive intelligence' bereft of the dimensions that feelings and emotions brings to neural intelligence. One could pen a haiku:
"Haiku" to Emotions
Emotions have no logic.
Are affective, rather than "demotive".
Circumscribed not by binary algorithms, but by Passion, Desire and Mood.
There is no room between 0 and 1 for Emotions.
For example, the movie Ex Machina reflects on the possible emotional involvement of a robot with a human [23]. The movie plot turned on a 'Turing test' that actually illustrated the "demotive" quality of the robot (compared to the emotive state of the human…an inherent distinction). But the plot had a built-in problem that was not addressed: Why did the robot desire freedom, encouraging the young programmer to an emotional relationship? Lacking Asimov's 3 Laws of Robotics [94], this robot could kill a human…and bring it to harm…and desire freedom. Others have tried to program an emotive quality to robots, but were not convincing [29,70,71,72,73,74,75,76,77,95].
7. Note on neural intelligence
Desires and goals are based on emotive valuations. Even for supposedly rational economic models, the value or worth of any commodity or act is based on desirability, a totally emotive quality. Unlike "demotive" robots, the totality of NI, as experienced by a living creature, involves emotive components which ultimately gives worth/value to all stimuli mentated by the biologic neural net.
Logical operations could be described quite apart from the particular 'hardware' on which they happened to be implemented in binary code. AI is essentially a series of advanced statistic-based algorithms which review the past, to project future trends. It is "demotive".
Not so the biologic neural nets, which achieve emotive states integral to the particular body in which they occur. Unlike "demotive" binary (n = 0 or 1) or quadro-triplet info of DNA (i.e., triplets of 4 bases), cog-info is multinary (n > 100) and combinatorial, inherent to its associated neurons. It cannot be transferred and is lost by the host's death.
The link of Memory to Intelligence is incontestable. Reflection suggests that the computer metaphor is a flawed model for neural memory and intelligence. By the same token, the idea that emotions are divorced from intelligence is not tenable, as emotions suffuse all aspects of valuation and meaning by man and animals. Is there an alternative?
Rational (abstract) thought is ultimately driven by emotive motivation. While language is integrally tied to human intelligence, not so for animals, which have demonstrated ability for abstract thought coupled to memory (cited above), but are wordless. Nonetheless, animals also experience emotions, memory and intelligence, as well as logical mentation, exemplified by objective criteria such as: use of tools, navigation, remembrance of places, group hunting, group communication, manifestations of curiosity.
For NI, time, distance and causality are interwoven with feelings, recalled as emotive memory. Learning by reward and punishment (conditioning) is enabled by affective signals and valuations (i.e., pain, food) [6,7]. Even for the logic-content activities of humans, the underlying motivation is ultimately emotive. Goals, desires, motivation and meaning are all set by emotive signals and valuations.
The perceptive mechanism of neurons is inherently coupled to emotive reality. Unlike the electronic artifact, the living neural creature is immersed in a continuum of emotive states, some which must be remembered to survive, manifest as learning and intelligence. There may be a particular talent of some individuals for mathematics, logic, games or abstract thinking. It is this particular talent of humans, tied to language, that the computer can perform. But the basis of intelligence of any neural creature (i.e., NI) relies on a memory 'colored' with a rich palette of emotive factors, which establish meaning to recalled stimuli.
A consummate test of AI has been considered to be the ability to translate human languages. Much effort has been expended to enable translation programs to parse sentences, to extract meaning from verbs and nouns, to render translated text "natural" [95,96,97,98,99]. But linguistic reference to emotive states is quite different from the existential states achieved by sets of biological neurons. Mentation and memory are not expressions of linguistic, logical or electrical signaling, but a combination of chemical as well as electrical processes.
'Indifference' is what distinguishes AI from NI. The former's programming is indifferent to value or meaning, devoid of significance; the latter's existence is critically dependent on the sensibilities of emotive states that make a difference to living creatures. Cognitive information has emotive qualities transformed into NI, which render stimuli meaningful in the ever-present drive to survive.
Q: Are 'emotional intelligence' or 'rational emotions' contradictory terms?
A: The former is not a contradiction, but a redundancy. There cannot be intelligence without emotions and visa versa. The latter is an 'antinomy', a logical contradiction [100,101].
'Reason' or 'rationale' are artifacts of language. In that only homo sapien excercises this talent, it does not address the universal issues of neuro-physiology or neuro-chemistry.
Kant faulted "pure reason". Presumably, reason could be "pure" if it did not have emotive content, like geometry or calculus. But this would be self-defeating for describing 'reason'. 'Value, 'worth', 'desirability', 'need', etc. all have emotive qualities that underlie any 'reasonable' judgement. Emotive factors are what render "meaning" in everyday life. Only in arithmetic, mathematics and logic is reasoning or intelligence pure, but incomplete [102], as well as,
'demotive'. There are limitations to what can be proved for 'reason', though this is irrelevant to our interest here.
The natural signaling of neurons is enunciated in emotions, for which human language is barely adequate to describe, though attempted by songwriters and poets. Animals don't speak, but nevertheless experience emotions and an understanding of their circumstances, hallmarks of intelligence. They also exhibit aspects of logical thought (cited above).
Turing's opinion that digital computers can in fact mimic the actions of a human" is not credible [13,14]. Hebb's model of 'synaptic plasticity' and electric signaling as the basis for memory is deeply flawed [40,41]. As pointed out by von Neumann, at the molecular level of the nerve membrane, electrical and chemical processes tend to merge; molecular changes alter the neuron's electrical properties accompanied by changes in the relative electrical potential [16a].
In short, the computer is an inadequate paradigm for the brain. Its "information" is embodied in a silicon chip, physically encoded as bits (0 1). The lengths to which computer programmers and theoreticians go to suggest that they mimic emotive states experienced by a neural net are remarkable. They use words like "neuromorphic" on the basis of binary algorithms or silicon constructs that are not at all biologic (as per a recent supplement to Science). On the basis of "verbal prestidigitations", neurobiologic terms are appropriated, to construct 'affective architecture' with 'neural nets' that are actually coupled microprocessors, supposing that semantic representations or verbal constructs simulate the emotive states experienced by neural creatures.
The fantasy of science fiction writers is a "transference process", whereby neural memory could be encoded in memory chips or transferred from the chip to the brain. But the real business of neuroscientists is to decipher the biological neural code whereby emotive memories are inscribed in the 'wetware' of the living neural net.
8. Evolution
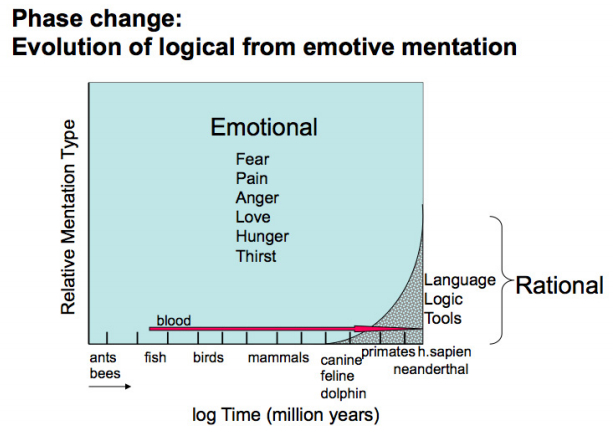
As psyche evolved from physiology, so did logic emerge, like a phase transition, from emotive mentation (Figure 6).
Homo sapiens with mental talents cannot be considered as apart from the Natural Order of living creatures. Vestiges of bacterial signaling with biomodulating molecules recur in the signaling modality of more complex neural creatures (Table 1). Emotive mentation is undoubtedly the basic mode of the psychic experience of all creatures (Figure 6), but blurred in humans by the supremacy of verbal thinking, where language dominates conscious thought and logic emerges.
9. Conclusion
Though the physical cosmos in which we exist is mapped out in great detail by physicists who describe Relativistic interactions of planets, stars and galaxies with black holes, grave uncertainties remain, incompleteness abounds even in the core of our mathematical thinking. The quantum realities of condensed matter, dark matter and dark energy still escape the physicists' grasp with its uncertainties and 'entangled' sub-atomic materiality. In quantum reality, 'observation' cannot be separated from 'observer'. So too in the study of cognition, 'mentation' cannot be considered separately from the 'mentator'.
In spite of electromagnetic explorations of the 'cosmos' of our brains, with electrodes, fMRI, PET, and CAT scans, we cognitive scientists too are in the dark. The map of our psyche remains unchartered, terra incognita, intimate, yet unfathomable; a 'blank box' whose emotive dimensions we have yet to plumb.
We suggest that the mental talents of 'biologic condensed matter' must be described in chemical terms, just like other physiologic processes. In that mentation and memory are inextricably entangled, a clue to the mechanism of the latter may reveal that of the former.
Our tripartite mechanism [88,89,90,91,92,93] provides a psycho-chemical description of a memory code and emotive memory. Here, the nECM is the 'medium of representation'; the dopant (metals and NTs) are the 'symbols of representation'. Effectively, we propose a correspondence between psychic (emotive) states and physiologic states, both expressed in chemical terms (Table 1). The cuinfo (Figures 3 and 4) are the chemographic representations of past stimuli (cog-info) by which neural nets mentates and remembers.
NI is a talent ascribed to living organisms which experience feelings and emotions to adapt to an everchanging environment, to obtain food, to survive and to reproduce. By contrast, AI is manifest by a computer programmed to produce a logical output based on binary input. But is this "intelligence"? There cannot be intelligence without emotions and vice versa. We experience conscious life but don't understand the darkened processes occurring in our heads when we emote, remember or forget. Thus, we tend to agree with Kant's position that a 'psychological science' is impossible [100,101]. But we can identify the major components involved in generating mental processes.
A propos Descartes' mind-body conundrum or Ryle's "ghost in the machine"
[103], one cannot fully describe mental processes by purely logical expressions. Thus, we suggest that the mind and memory are not dissociated from the body, but inextricably linked properties of its complex biochemical workings [95]. Mind and body are a complex unity, psyche emerges from physiology and chemistry, emerging and surviving as an ensemble of qualities.
As quipped by Terry Winograd (cited in [96]): "AI is no closer to intelligence than alchemists to gold". Perhaps it is time for "the term 'artificial intelligence' to be replaced by something more modest and less provisional" [19].
We suggest the terms of either 'artifact intelligence' (ARTI) or 'machine intelligence' (MI), neither of which imply emulation of neural qualities, but simply refer to the computational capability of an electronic artifact with a recall function.
The development of computerized artifacts interfacing with the brain not only to move muscles but to also perform mental chores, continues. Such artifacts would contribute superior logical qualities (speed, connection to the internet, high storage capacity for facts, mathematical skills). But lets not forget that neural brains contribute emotional qualities, creativity and rendering judgements of value, worth and priority, the hallmarks of true intelligence.
Acknowledgements
A memorium to my late wife and fan, the artist Georgette Batlle (1940-2009), for kindly receiving my discourses on the chemical basis of thought. Thanks to friends, Lilly Rivlin (New York, NY) and the late Bill Needle (Eastchester, NY) for their early encouragement and financial support in the period 1980-1984. I appreciate ongoing discussions with Karine Ahouva Leopold (Paris), about feelings and emotions. — By GM
The references presented in previous Parts of this series, are also appropriate here. In the interest of space, many works have not been cited again, though they all contribute to the knowledge base of neurobiology and cognitive sciences. Those cited below were chosen to establish particular points of fact.
We stand on their shoulders, to glimpse vistas of neural memory and intelligence.
Conflict of Interest
GM is a founder of MX Biotech Ltd., with the commercial goal to develop new classes of "memory materials" and devices.
CG is emeritus professor of Chemistry at Hebrew University (Jerusalem), active in developing and patenting peptide-based tools for surgery and pharmacology.
Notwithstanding, the ideas forwarded here by us both are scientifically genuine and presented in good faith, without commercial clouding of the concepts expressed herein.









 DownLoad:
DownLoad: