1. Introduction
Phytoplankton constitutes the bottom level of the aquatic food web and plays a fundamental role in the aquatic ecosystem. Phytoplankton bloom (PB) can assert severe negative consequences on ecosystems and social economics. In the past decades, there have been numerous field or experimental and also some mathematical modeling studies on the impact of some specific factors contributing to the growth of phytoplankton. Many researchers focused on the role of nutrients played on PB. Many studies show that eutrophication is the main reason leading to PB [9,18]. Johnson et al. [24] and Phillips et al. [30] stressed the importance of sediment phosphorus release in the restoration of very shallow lakes. Shukla et al. [32] modeled and analyzed PB in a lake caused by discharge of nutrients. Those studies can help to understand the contribution to PB from the different specific points. Nevertheless, most of the studies ignored the impact of temperature, which is thought to be a possible key triggering factor of PB.
There have been some studies emphasizing on the effect of constant temperature on the growth of phytoplankton [8,40]. Especially, Chen et al [5] presented a sound frame work on the effect of constant temperature on the growth of phytoplankton. They defined a helpful index called basic reproductive index to fully characterize the relationship between the dynamic evolution of phytoplankton and temperature.
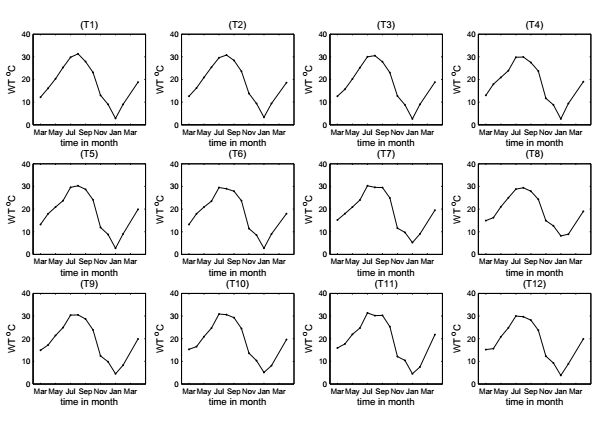
The model considering the effect of constant temperature on the growth of phytoplankton is unsuitable for modeling PB that recurs seasonally. Then some aquatic ecologists have been shifting their attentions to seasonal variations of phytoplankton composition and has been attracted by concepts of periodicity, succession and response to environmental changes [33,38]. Some field or experimental studies (such as our field study in Fig. 2 and 3) suggested that the dominant variations in both phytoplankton composition and environmental variables are seasonal over a consistent annal cycle in lake and strongly related to the annual cycles of temperature [7,21,39]. Our goal of this paper is to develop modeling approaches for understanding the effect of seasonal changing temperature on the growth of phytoplankton and model the complex dynamics of seasonally recurring phytoplankton blooms.
The temperature plays important roles in many aspects during the process of phytoplankton metabolism. The impacts of temperature on the metabolism of phytoplankton are traditionally described by the Q10 rule [11,14,42], which asserts that a change of the temperature by 10oC will multiply the rate at mean temperature by a factor Q10, that is to say, the Q10 temperature coefficient is a measure of the rate of change of a biological or chemical system as a consequence of increasing the temperature by 10oC. The nonlinear nature of biological responses to temperature are indeed topics of high priority [18]. Aquatic ecologists focused on the relationship between temperature and the growth rate of phytoplankton [2,31,40], and the nutrients releasing rate from sediments [26], and the death rate of phytoplankton [8,25].
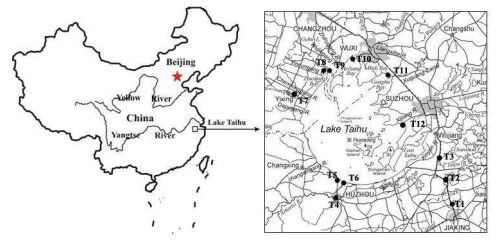
Located in the southern part of the Yangtze River delta, Lake Tai is the third largest freshwater lake in China with a surface area of about 2,338 square kilometers (about 902 square miles), an average depth of 2 meters, and maximum depth 3 meters. Lake Tai has been used as the important freshwater sources in the yangtze river delta on edge of Chinese eastern coast. Its water quality and environmental conditions have an important impact on the development of this area. In recent years, with the fast development of industry and agriculture process, waste water and domestic sewage without thorough treatment were discharged into Lake Tai Basin, then those pollutions gradually worsen the water quality and assert considerably negative impact on the ecological environment system of Lake Tai Basin. The water pollution of cyanobacteria blooms has become a severe problem in this area. At present, most of the studies were focused on Wuxi Meiliang bay of Lake Tai and the pollution in other typical areas around Lake Tai were less explored.
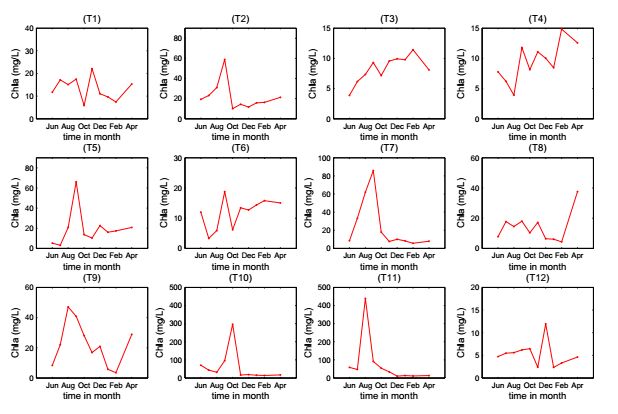
From March 2008 to April 2009, we have made an detailed field investigation of the water qualities and temperature variations around Lake Tai. The study was conducted in 12 selected monitor stations (i.e., MS) set in the typical areas around Lake Tai (Fig 1). We sampled the water, collected data, monitored and assessed the water quality once a month. The specimen water was sampled from 0.5m deep below the surface of water. The water temperature (WT) was field determined simultaneously on the sampling spot by water thermometer (instrument: Water-checker 2010, HACH). Then the water samples were taken back to the laboratory immediately in seal evades the light preservation and the other index of performance were mensurated and analyzed. Particularly, Chlorophyll-a is determined by the ultraviolet spectrophotometry (instrument: UV2450 Spectrophotometer, Shimadzu) and the total soluble reactive phosphorus (PO4-P) is monitored by Ion Chromatography method (instrument: DIONEX ICS-90). The annual mean values of PO4-P (Pin1) are listed in Table 3.
Table 1. Location of monitor stations (MS).
| MS | Name | Longitude | Latitude |
| T1 | Jia Xing Canal | E120°43′3″ | N30°48′5″ |
| T2 | Wang Jiang Jing | E120°42′31″ | N30°53′6″ |
| T3 | Ping Wang Bridge | E120°38′14″ | N30°59′49″ |
| T4 | Hu Zhou Source | E120°4′23″ | N30°51′51″ |
| T5 | Xiao Mei Kou | E120°6′1″ | N30°55′43″ |
| T6 | New Port | E120°7′32″ | N30°56′18″ |
| T7 | Yi Xing Industry | E119°47′48″ | N31°21′31″ |
| T8 | Zhou Tie Sewage | E119°59′54″ | N31°27′20″ |
| T9 | Yi Xing Rv/Lake | E120°0′30″ | N31°27′10″ |
| T10 | Wu Xi Mei Liang | E120°7′25″ | N31°30′13″ |
| T11 | Wu Xi Lake | E120°21′4″ | N31°27′57″ |
| T12 | Su Zhou Lake Tai | E120°46′55″ | N31°13′17″ |
Table 3. Values used for field application.
| MS | Tmean | α | φ | Pin1 (mg⋅L−1) |
| T7 | 19.18 | -11.37 | 7.1527 | 0.364 |
| Mean | 18.90 | -11.68 | 0.8611 | 0.242 |
The density of phytoplankton is expressed by the density of Chlorophyll-a. The time series and observed patterns of water temperature and Chlorophyll-a in the targeted monitor stations Ti(i=1,2,..,12) are illustrated in Fig. 2 and 3, respectively. Our experiments, long-term observations, and our compilation of collected data suggest obviously seasonal patterns of the water temperature and Chlorophyll-a. The water temperature and the Chlorophyll-a increase first, then decrease, and their maxima and minima occur around August and January, respectively. It is well known that, since 1990s, the PB or algae bloom occurs annually in Lake Tai [9]. The annual cyclic dynamics of phytoplankton in shallow lake is far from being well understood.
The remainder of this paper is organized as follows. In section 2, we propose a time-varying nutrient-phytoplankton dynamic model including the time-varying effect of temperature on metabolism of phytoplankton. In section 3, an ecological reproductive index is proposed and the existence and stability of periodic solutions are proved by coincidence degree theory and Lyapunov direct method. Section 4 carries out numerical simulations to expound both the long term cyclic dynamics and the short term effect of daily temperature on the growth of phytoplankton. The filed application is then carried out for Lake Tai to validate our model. The paper ends with conclusion and some interesting discussion.
2. Model formulation
In this section, following the clues and framework in [5], we formulate a dynamical model governed by non-autonomous ordinary differential equations for a lake with inflow and outflow of nutrient and study the impact of time-varying temperature on the dynamic evolution of both the phytoplankton and the nutrient. We assume that the lake is a physically homogeneous shallow lake or the well-mixed surface layer of a stratified water column, which thoroughly mixed at all times, so that there are no spatial gradient of concentrations.
The forced phytoplankton-nutrient compartment model consists of two state variables. Let A(t) and P(t) be the densities of phytoplankton and soluble mineral nutrient (say phosphorus) at time t in units of milligram of Chlorophyll-a per stere and in units of milligram of nutrient per stere, respectively. The system is assumed to be governed by three basic processes: the phytoplankton nutrient uptake and growth, the death of phytoplankton, and the dilution of the nutrient.
The loss of phytoplankton due to natural mortality is assumed to be proportional to its density A and is determined by m, a parameter taking into account relatively constant grazing or predation by higher tropic levels. The loss due to the intraspecific competition is modeled by the quadratic mortality term bA2. The exchange of the nutrient in lake with the external water is denoted by a(Ps−P), where Ps is the density of total soluble nutrient input. The uptake of phytoplankton for nutrient is assumed to be Upf(P)A with Up being the maximum nutrient uptake rate of phytoplankton and f(P) being the nutrient-limited functional response. The growth of phytoplankton is assumed to be maximum growth rate μopt limited by the nutrient uptake. Then the frame model is regulated by the following equations
|
{dAdt=μoptf(P)A⏟growth−mA⏟natural mortality−bA2⏟crowding loss,dPdt=aPs⏟input−Upf(P)A⏟uptake−aP⏟dilution loss.
|
(1)
|
Next, we discuss the mathematical formulation of the components of (1), in particular, we will expound their dependence on the temperature.
Nutrient-limited functional response. The nutrient-limited functional response f(P) usually satisfies the following properties [13,27]
|
f(P)∈C2, f(0)=0, f′(P)>0, lim
|
(2)
|
The most typical and common used is the so-called Hill function
|
f_n(P)=\frac{P^n}{H_P^n+P^n},
|
(3)
|
which incorporates the Holling family of functional responses [22] as special cases, where H_P is the half-saturation constant for nutrient uptake. For example, if n=1, then (3) reduces to the classical Holling type Ⅱ functional response and depicts a decreasing rate of change of ingestion as food becomes more abundant such that the relationship is a concave downward curve. If n=2, then (3) is the classic sigmoidal Holling type Ⅲ functional response, which can be expressed in terms of Michaelis-Menten parameters and is concave downward only once the food surpasses a certain level (the inflection point). Motivated by the Holling family, a more general one can be extended by the following formulation to model the nutrient uptake of phytoplankton
|
f_3(P)=\frac{P^{r_1}}{P^{r_1}+H_2P^{r_2}+H_1},
|
where r_1>r_2\geq0 and H_i>0 for i=1,2. The four parameters govern the shape of the response curve, no matter it is a concave downward curve or a sigmoidal curve.
Temperature is a key environmental factor for the lake system and asserts essential impacts on the nutrient uptake, growth and death of phytoplankton, the nutrient releasing from particulate nutrients, and so on. Next, we shall deliberately discuss these metabolism progresses respectively.
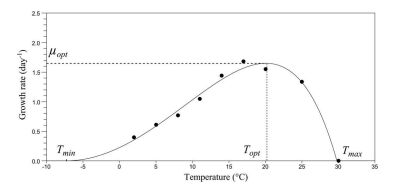
Temperature-dependent uptake and growth. The nutrient uptake and growth of phytoplankton are heavily affected by the variation of temperature. There are several model candidates depicting the effect of temperature such as linear model [1,34], Michaelis-Menten-Monod saturating model [34], optimal exponential model [3,40] and Arrhenius model [17,19]. In this study, we adopt the so-called cardinal temperature model with inflexion (CTMI) proposed by Rosso et al [31], which is validated for a large range of species. As we all known, phytoplankton grows much better under more suitable temperature condition and halts growth under extremely low or high temperature. Bernard [2] shows that the CTMI can accurately represent the growth of microalgae. The CTMI includes four key parameters and three of them are cardinal temperatures with a biological significance, which makes the model rather straightforward to calibrate and facilitates the estimation with experimental data. It predicts the growth rate for temperatures between T_{min} and T_{max}, that is, \mu_{opt}\cdot g(T), where
|
g(T)=
\begin{cases}
0,~~T<T_{min},\\
\phi(T),~~T_{min}<T<T_{max}, \\
0,~~T>T_{max},
\end{cases}
|
(4)
|
with
|
\phi(T)=\frac{(T-T_{max})(T-T_{min})^2}{(T_{opt}-T_{min})[(T_{opt}-T_{min})(T-T_{opt}) - (T_{opt}-T_{max})(T_{opt}+T_{min}-2T)]}.
|
Here, g(T) is the impact factor of water temperature modeling the direct effect of temperature on phytoplankton growth. The maximum growth rate \mu_{opt} occurs when T = T_ {opt}, where T_{opt} is the optimal (most appropriate) temperature for the phytoplankton's production (growth). Fig. 4 illustrates the shape of CTMI. The CTMI depicts the relationship between growth rate and temperature and is more credible and acceptable [2,4,20].
Temperature-dependent mortality. Water temperature essentially affects the natural mortality of phytoplankton. Higher temperature may lead to higher death rate [25]. Ding [8] adopted an exponential model to address the death rate with respect to water temperature, which reads
|
m(T)=m_0+K_1\theta_1^{T-T_{ref}},
|
where m_0 is the minimum death rate of phytoplankton, K_1 is the respiration rate of phytoplankton, \theta_1 is the temperature coefficient, and T_{ref} is the reference water temperature.
Temperature-dependent nutrient release. We assume that there is an external source of nutrients (say phosphorus) flowing into the lake and the densities write as P_{in1} and P_{in2}, where P_{in1} denotes the soluble nutrient and P_{in2} represents the particulate nutrient. Denote by P_b the particulate nutrient in bottom sediments. Moreover, the particulate nutrient in the water column and the nutrient in the sediments release soluble nutrient at rate \gamma. The releasing rate \gamma is affected by temperature and then it can be written as [26] \gamma(T)=K_2\theta_2^{T-T_{ref}}, where K_2 and \theta_2 are positive coefficients. Therefore, the total input soluble nutrient in the water column reads \hat{P}_s=aP_{in1}+\gamma(T)(P_{in2}+P_b):=aP_s.
Time-varying temperature. In real world application, the environmental factors and resources vary or fluctuate in time. The environmental fluctuations are likely to have a significant effect on the dynamic evolution of aquatic ecosystems. In order to study the effect of time-varying temperature forcing phytoplankton, T must be time-dependent (say T(t)). T(t) can be fitted by some simple functions or their combination to illustrate the varying temperature such as the constant function, step function, quadratic function, and so on.
Consider the specific case that the temperature is assumed to be varying periodically, i.e., T(t) represents a periodic function. A convenient and commonly applied scheme is that of sinusoidal forcing [14,23,29]
|
T(t)=T_{mean}+\alpha \sin(\Omega t+\varphi),
|
(5)
|
where T_{mean} represents the mean temperature and \Omega governs the period. When the forcing is annual, and t is in units of months, then \Omega=\pi/6. The parameter \alpha controls the amplitude of forcing. It is obvious that, if \alpha=0, the model collapses to an unforced system. This case has been well explored by Chen et al [5], where the temperature is simplified to be constant or on an average, i.e., T=T_{mean}. Chen et al [5] have proved that such a model can not admit any periodically oscillating dynamics. That is to say, the time-independent phytoplankton-nutrient model proposed in [5] can not catch or characterize the seasonal pattern of phytoplankton bloom. Although (5) is also a crude simplification, it serves as a first approximation for investigating how seasonal factors influences the model's dynamics.
To sum up, the objective phytoplankton-nutrient system takes the following form
|
\left\{
\begin{split}
&\frac{dA}{dt}=\mu_{opt} g(T(t))f(P)A-m(T(t))A-bA^2,\\
&\frac{dP}{dt}=aP_s(T(t))-U_pg(T(t))f(P)A-aP.
\end{split}\right.
|
(6)
|
The description, unit, default value (when available), and reference resource for each parameter are summarized in Table 2.
Table 2. Parameters of model (6) with default values used for numerical studies.
| Par. | Description | Value | Unit | Ref. |
| U_p | maximum nutrient uptake coefficient | 0.05 | \mathrm{day}^{-1} | [40] |
| \mu_{opt} | maximum growth rate of phytoplankton | 0.3-1.6 | \mathrm{day}^{-1} | [2] |
| T_{opt} | optimal water temperature | 20-30 | ^{\circ}\mathrm{C} | [2] |
| T_{min} | minimum water temperature | -10-0 | ^{\circ}\mathrm{C} | [2] |
| T_{max} | maximum water temperature | 30-40 | ^{\circ}\mathrm{C} | [2] |
| T_{ref} | reference water temperature | 20 | ^{\circ}\mathrm{C} | [8] |
| m_0 | natural mortality rate of phytoplankton | 0.13 | \mathrm{day}^{-1} | [8] |
| K_1 | Respiration rate of phytoplankton | 0.1-0.5 | \mathrm{day}^{-1} | [8] |
| \theta_1 | temperature dependence coefficient | 1.11 | - | [8] |
| K_2 | temperature dependence coefficient | 0.0004-0.1 | \mathrm{day}^{-1} | [26] |
| \theta_2 | temperature dependence coefficient | 1.02-1.14 | - | [26] |
| H_1 | coefficient for nutrient uptake | 0.6227 | \mathrm{mg}^{2}\cdot \mathrm{L}^{-2} | Defaulted |
| H_2 | coefficient for nutrient uptake | 0.0320 | \mathrm{mg}^{}\cdot \mathrm{L}^{-1} | Defaulted |
| r_1 | coefficient for nutrient uptake | 2 | - | Defaulted |
| r_2 | coefficient for nutrient uptake | 1 | - | Defaulted |
| P_{in1} | density of total input soluble phosphorus | 0.364 | \mathrm{mg}\cdot\mathrm{L}^{-1} | Defaulted |
| P_{in2} | density of total input solid phosphorus | 0.5 | \mathrm{mg}\cdot\mathrm{L}^{-1} | Defaulted |
| P_{b} | density of solid phosphorus in bottom sediments | 0.5 | \mathrm{mg}\cdot\mathrm{L}^{-1} | Defaulted |
| a | dilution rate | 0.62 | \mathrm{day}^{-1} | Defaulted |
| b | density limiting coefficient | 0.023 | \mathrm{L}\cdot(\mathrm{day}\cdot\mathrm{mg})^{-1} | Defaulted |
3. Oscillatory dynamics of model (6)
In this section, we explore the dynamics of (6) and present some results on the positive invariance, the existence and globally asymptotic stability of boundary and internal cyclic dynamics. In order to facilitate the following discussion, write
|
g(t):=g(T(t)),~~m(t):=m(T(t)),~~P_s(t):=P_s(T(t)),
|
which are assumed to be continuous and nonnegative.
3.1. Positive invariance and dissipativity
For a bounded continuous function h(t) defined on R, define
|
h^u:=\mathop {\sup }\limits_{t\in R}h(t),~~h^l:=\mathop {\inf }\limits_{t\in R}h(t).
|
Theorem 3.1. If \mu_{opt}g^lf(m_2)-m^u>0 and aP_s^l-U_pg^uM_1>0, then the set \Gamma defined by
|
\Gamma:=\{(A,P)\in R^2\mid~m_1\leq A\leq M_1,~m_2\leq P\leq M_2 \}
|
(7)
|
is positively invariant with respect to (6), where
|
\begin{align*}
M_1:=\frac{\mu_{opt}g^u-m^l}{b},~~~~~~~~ M_2:=P_s^u,
\end{align*}
|
|
\begin{split}
m_1:=\frac{\mu_{opt}g^lf(m_2)-m^u}{b},~ m_2:=\frac{aP_s^l-U_pg^uM_1}{a}.\\
\end{split}
|
(8)
|
Proof. Let (A(t),P(t)) be the solution of (6) through (A(t_0),P(t_0))\in\Gamma. From the phytoplankton equation in (6), it follows that
|
A'(t)\leq bA(t)[\frac{\mu_{opt}g^u-m^l}{b}-A(t)]=bA(t)[M_1-A(t)], ~t\geq t_0.
|
(9)
|
A standard comparison argument shows that
|
0<A(t_0)\leq M_1~\Rightarrow~ A(t)\leq M_1, t\geq t_0,
|
which, together with the nutrient equation in (6), produces
|
P'(t)\leq a(P_s^u-P(t))=a(M_2-P(t)), ~t\geq t_0,
|
(10)
|
and hence
|
0<P(t_0)\leq M_2~\Rightarrow~ P(t)\leq M_2, ~t\geq t_0.
|
Similarly, the nutrient equation in (6) yields
|
P'(t)\geq a[\frac{aP_s^l-U_pg^uM_1}{a}-P(t)]=a[m_2-P(t)],~ t\geq t_0,
|
(11)
|
whence
|
P(t_0)\geq m_2 ~\Rightarrow~P(t)\geq m_2,~t\geq t_0.
|
Moreover, by the phytoplankton equation of system (6), we have
|
A'(t)\geq bA(t)[\frac{\mu_{opt}g^lf(m_2)-m^u}{b}-A(t)]=bA(t)[m_1-A(t)],~t\geq t_0,
|
(12)
|
which implies
|
A(t_0)\geq m_1~\Rightarrow~A(t)\geq m_1,~t\geq t_0.
|
Therefore, \Gamma is positively invariant with respect to (6). The proof is complete.
Corollary 1. Let A(t),P(t) be a solution of (6) with A(t_0)>0 and P(t_0)>0. Then \limsup\limits_{t\rightarrow+\infty}P(t) leq M_2. Moreover, if \mu_{opt}g^lf(m_2)-m^u>0, then \liminf\limits_{t\rightarrow+\infty}A(t)\geq m_1 and \limsup\limits_{t\rightarrow+\infty}A(t)\leq M_1; if aP_s^l-U_pg^uM_1>0, then \liminf\limits_{t\rightarrow+\infty}P(t)\geq m_2.
Theorem 3.2. If \mu_{opt}g^lf(m_2)-m^u>0 and aP_s^l-U_pg^uM_1>0, then (6) is ultimately bounded with respect to \Gamma, i.e., (6) is dissipative.
3.2. Ecological reproductive index
In the rest of Section 3, T(t) is assumed to be \omega-periodic, i.e., there exists an \omega>0 such that T(t)=T(t+\omega), and hence
|
g(t)=g(t+\omega),~~m(t)=m(t+\omega),~~P_s(t)=P_s(t+\omega).
|
In order to characterize the population dynamics of phytoplankton, motivated by the computational formula of a threshold parameter for periodic compartmental epidemic models given by [37], here we introduce the ecological reproductive index R_0 for the periodic nutrient-phytoplankton model (6). It is not difficult to show that (6) always admit a phytoplankton-free state E_0=(0,P_*(t)), where
|
P_*(t)=(e^{a\omega}-1)^{-1}\int_t^{t+\omega}aP_s(s)e^{-a(t-s)}ds
|
(13)
|
is the unique positive periodic solution of the following system
|
\frac{dP}{dt}=aP_s(t)-aP.
|
(14)
|
Let E=(A,P)^T, then we rewrite the model (6) as
|
\frac{dE}{dt}=\mathcal{F}(t,E)-\mathcal{V}(t,E),
|
(15)
|
where \mathcal{V}(t,E)=\mathcal{V^-}-\mathcal{V^+},
|
\mathcal{F}(t,E)=\begin{pmatrix}\mu_{opt} g(t)f(P))A\\0\end{pmatrix},~
\mathcal{V^-}=\begin{pmatrix}m(t)A+bA^2\\aP+U_Pg(t)f(P)A\end{pmatrix},~
\mathcal{V^+}=\begin{pmatrix}0\\aP_s(t)\end{pmatrix}.
|
(16)
|
By carrying out arguments similar to those in [10,Lemma 1], one has
|
D_E\mathcal{F}(t,E_0)=\begin{pmatrix}F(t) & 0 \\0 & 0\end{pmatrix},~
D_E\mathcal{V}(t,E_0)=\begin{pmatrix}V(t) & 0 \\J(t) & a\end{pmatrix},
|
(17)
|
where F(t)=\mu_{opt} g(t)f(P_*(t)) and V(t)=m(t). The reproduction rate of phytoplankton at E_0 is F(t) and the removal rate of phytoplankton at E_0 is V(t). Then we get the following cooperative system
|
\frac{dA}{dt}=\mu_{opt} g(t)f(P_*(t))A-m(t)A=(F(t)-V(t))A.
|
(18)
|
Denote by \Phi_{F(\cdot)-V(\cdot)}(t) the monodromy matrix of (18), by \rho(\Phi_{F(\cdot)-V(\cdot)}(\omega)) the spectral radius of \Phi_{F(\cdot)-V(\cdot)}(\omega), and by \Phi_{V(\cdot)}(t) the monodromy matrix of the linear \omega-periodic differential system \frac{dz(t)}{dt}=V(t)z. Assume that Y(t,s), t\geq s is the evolution operator of the linear \omega-periodic system
|
\frac{dy(t)}{dt}=-V(t)y,
|
(19)
|
that is, for each s\in R, Y(t,s) satisfies
|
\frac{d}{dt}Y(t,s)=-V(t)Y(t,s),~\forall t\geq s,~ Y(s,s)=1.
|
(20)
|
Hence, the monodromy matrix \Phi_{-V(\cdot)}(t) of (19) is equal to Y(t,0), t\geq 0.
Assume that \phi(s) is \omega-periodic in s and denotes the initial distribution of phytoplankton individuals. Then F(s)\phi(s) is the rate of the new population generated by initial fertile phytoplankton individuals being introduced at time s. Given t>s, then Y(t,s)F(s)\phi(s) gives the distribution of those fertile individuals that were newly produced at time s and remain in the fertile compartments at time t [36]. It follows that
|
\psi(t):=\int_{-\infty}^t Y(t,s)F(s)\phi(s)ds=\int_0^\infty Y(t,t-a)F(t-a)\phi(t-a)da
|
is the distribution of the accumulative new individuals at time t produced by all those fertile individuals \phi(s) introduced at time previous to t.
Let C_\omega denote the ordered Banach space of all \omega-periodic functions from R to R and is equipped with the maximum norm \|\cdot\|. Define a linear operator L on C_\omega by
|
(L\phi)(t)=\int_0^\infty Y(t,t-a)F(t-a)\phi(t-a)da,~\forall t\in R, ~\phi\in C_{\omega},
|
(21)
|
that is
|
(L\phi)(t)=\int_0^\infty\mu_{opt} g(t-a)f(P_*(t-a))e^{-\int_{t-a}^t m(s)ds}\phi(t-a)da, ~\forall t\in R, ~\phi\in C_{\omega}.
|
From [36] and [37], it follows that the ecological reproductive index R_0 is given by \rho(L), where \rho denotes the spectral radius of L.
In order to formulate the explicit expression of R_0, we need to introduce the linear \omega-periodic system
|
\frac{dw}{dt}=[-V(t)+\frac{F(t)}{\sigma}]w,~~t\in R_+
|
(22)
|
with \sigma\in(0,\infty). Since F(t) is nonnegative and -V(t) is cooperative, it follows that \rho(\Phi(\omega,\sigma)) is continuous and nonincreasing in \sigma\in(0,\infty) and \lim_{\lambda\rightarrow\infty}\rho(\Phi(\omega,\sigma))<1. It is not difficult to verify that (6) satisfies the assumptions (A_1) - (A_7) in [37]. Now, we list below two main conclusions from [37], which will be essential for the formulation of R_0 and our main findings in this study.
Lemma 3.3. ([37] \mathrm{Theorem 2.1}) The following statements are valid:
(ⅰ) If \rho(W(\omega,\sigma))=1 has a positive solution \sigma_0, then \sigma_0 is an eigenvalue of operator L, and hence R_0>1.
(ⅱ) If R_0>1, then \lambda=R_0 is the unique solution of \rho(W(\omega,\sigma))=1.
(ⅲ) R_0=0 if and only if \rho(W(\omega,\sigma))<1 for all \sigma>0.
Lemma 3.4. ([37] \mathrm{Theorem 2.2}) The following statements hold.
(ⅰ) R_0=1 if and only if \rho(\Phi_{F(\cdot)-V(\cdot)}(\omega))=1;
(ⅱ) R_0>1 if and only if \rho(\Phi_{F(\cdot)-V(\cdot)}(\omega))>1;
(ⅲ) R_0<1 if and only if \rho(\Phi_{F(\cdot)-V(\cdot)}(\omega))<1.
Let W(t,s,\lambda), t\geq s be the evolution operator of (22) on R. Note that
|
W(t,s,\sigma)=\Phi_{(F/\sigma)-V}(t),~~\Phi_{F-V}(t)=W(t,0,1),~~t\geq 0.
|
By Theorem 2.1 and 2.2 in [37], the ecological reproductive index can be also defined as \sigma_0 such that \rho(\Phi_{(F/\sigma_0)-V}(\omega))=1, which can be straightforward to calculate as follows
|
R_0=\left(\displaystyle\int_0^\omega \mu_{opt} g(t)f(P_*(t))dt\right)\left(\displaystyle\int_0^\omega m(t)dt\right)^{-1}.
|
The ecological reproductive index R_0 is a function of varying temperature and nutrient input. R_0 is a key indicator of phytoplankton fecundity measuring the average new born phytoplankton produced by one unit of phytoplankton during the average phytoplankton life span in one temperature period.
3.3. Boundary cyclic dynamics
In this subsection, we explore the boundary cyclic dynamics of (6) by establishing the existence and globally asymptotic stability of the boundary \omega-periodic solution of (6).
Definition 3.5. A bounded non-negative solution (\hat{x}(t),\hat{y}(t)) of (6) is said to be globally asymptotically stable (i.e., GAS) if, for any other solution (x(t),y(t))^T of (6) with positive initial values, one has
|
\mathop {\lim }\limits_{t\rightarrow+\infty}(|x(t)-\hat{x}(t)|+|y(t)-\hat{y}(t)|)=0.
|
Lemma 3.6. ([41] \mathrm{Lemma 2.1}) Let \kappa=(\ln\rho(\Phi_{F(\cdot)-V(\cdot)}(\omega)))/\omega. Then there exists a positive \omega-periodic function v(t) such that e^{\kappa t}v(t) is a solution of (18).
Theorem 3.7. (6) always has a boundary \omega-periodic solution E_0(t)=(0, P_*(t)). If R_0<1, then E_0(t) is GAS.
Proof. By (6), one has \frac{dP}{dt}\leq aP_s(t)-aP. Consider the system
|
\frac{d\bar{P}}{dt}=aP_s(t)-a\bar{P}.
|
(23)
|
It is trivial to show that P_*(t) is an \omega-periodic solution of (23). Take V(t)=|\bar{P}(t)-P_*(t)|, then the Lyapunov direct method implies that, for (23), P_*(t) defined by (13) is GAS. Hence, \lim_{t\rightarrow\infty} |\bar{P}(t)-P_*(t)|=0. Then, for any \varepsilon >0, there exists a \hat{t}>0 such that \bar{P}(t)\leq P_*(t)+\epsilon, t>\hat{t}. By comparison principle, for (6), one has P(t)\leq P_*(t)+\epsilon. Then
|
\frac{dA}{dt}\leq[\mu_{opt} g(t)f(P_*(t)+\epsilon)-m(t)]A:=(F(t,\epsilon)-V(t))A,
|
(24)
|
where F(t,\epsilon)=\mu_{opt}g(t)f(P_*(t)+\epsilon). By Lemma 3.4, R_0<1 if and only if \rho(\Phi_{F(\cdot)-V(\cdot)}(\omega))<1. Due to the continuousness and boundedness of f(P), we can take \epsilon>0 being small enough such that \rho(\Phi_{F(\cdot,\epsilon)-V(\cdot)}(\omega))<1. By Lemma 3.6 and the standard comparison principle, there exists a positive \omega-periodic function v(t) such that A(t)\leq cv(t)e^{\kappa t}, where \kappa<0, c>0, and A(0)\le cv(0). Hence, \lim_{t\rightarrow\infty}A(t)=0. By the theory of asymptotically periodic system [43,Section 3.2], one has \lim_{t\rightarrow\infty}P(t)=P_*(t). Therefore, E_0(t) is GAS when R_0<1.
3.4. Internal cyclic dynamics
In the following, we investigate the internal cyclic dynamics of (6) by establishing some sufficient criteria for the existence and GAS of positive periodic solution of (6). For the reader's convenience, we shall summarize below a few concepts and results from [16] that will be essential for the following discussion.
Let X, Z be normed vector spaces, L:{\rm{Dom}}\; L\subset
X\rightarrow Z be a linear mapping, and N:X\rightarrow Z be a continuous mapping. The mapping L will be called a Fredholm mapping of index zero if \dim {\rm{Ker}}\; L={\rm{codim\;Imm}}\; L<+\infty and {\rm{Imm}}\; L is closed in Z. If L is a Fredholm mapping of index zero, then there exist continuous projectors P:X\rightarrow X and Q:Z\rightarrow Z such that {\rm{Imm}}\; P={\rm{Ker}}\; L, {\rm{Imm}}\; L={\rm{Ker}}\;
Q={\rm{Imm}}\; (I-Q). It follows that L|{\rm{Dom}}\; L\cap {\rm{Ker}}\; P:(I-P)X\rightarrow
{\rm{Imm}}\; L is invertible. We denote the inverse of that map by K_P. If \Omega is an open bounded subset of X, the mapping N will be called L-compact on \overline{\Omega} if QN(\overline{\Omega}) is bounded and K_P(I-Q)N:\overline{\Omega}\rightarrow X is compact. Since {\rm{Imm}}\;
{Q} is isomorphic to {\rm{Ker}}\; L, there exist isomorphisms J:{\rm{Imm}}\;
Q\rightarrow {\rm{Ker}}\; L.
Lemma 3.8 (Continuation theorem[16]). Let L be a Fredholm mapping of index zero and let N be L-compact on \overline{\Omega}. Suppose
(a) for each \lambda\in(0,1), every solution x of Lx=\lambda
Nx is such that x\notin \partial\Omega;
(b) QNx\neq 0 for each x\in\partial\Omega\cap Ker L and deg
\{JQN,\Omega\cap Ker L,0 \} \neq 0. Then the equation Lx=Nx has at least one solution lying in {\rm{Dom}}\; L\cap\overline{\Omega}.
Theorem 3.9. Assume that f(P) is strictly increasing with 0\leq f(P)<1 for P\geq 0 and f(0)=0. If
|
\hat{R_0}=\frac{\mu_{opt}\bar{g}f(K_2)}{\bar{m}}>1,
|
(25)
|
then (6) has at least one strictly positive \omega-periodic solution, where
|
F(x)=ax+U_p\bar{g}f(x)e^{K_1},~~K_1=\ln\frac{\mu_{opt}\bar{g}}{b}+2\omega
\mu_{opt}\bar{g},~~K_2=F^{-1}(a\bar{P_s})-2\omega a\bar{P_s}>0.
|
Proof. Considering the biological significance of (6), we specify A(0)>0 and P(0)>0. To facilitate the discussion below, we introduce the following notations
|
\overline{g}=\frac{1}{\omega}\int_0^{\omega}g(t)dt,~~\bar{m}=\frac{1}{\omega}\int_0^{\omega}m(t)dt,~~\bar{P_s}=\frac{1}{\omega}\int_0^{\omega}P_s(t)dt.
|
Let A(t)=\exp\{x_1(t)\} and P(t)=x_2(t), then (6) rewrites
|
\begin{split}
&\frac{dx_1(t)}{dt}=\mu_{opt} g(t)f(x_2(t))-m(t)-b\exp(x_1(t)),\\
&\frac{dx_2(t)}{dt}=a(P_s(t)
-x_2(t))-U_pg(t)f(x_2(t))\exp(x_1(t)). \end{split}
|
(26)
|
Define
|
X=Z=\{x(t)=(x_1(t),x_2(t))^T\in C(R,R^2),x(t+\omega)=x(t)\},
|
and \|x\|=\|(x_1,x_2)^T\|=\max_{t\in[0,\omega]}|x_1(t)|+\max_{t\in[0,\omega]}|x_2(t)| for any x\in X(or Z). Then X and Z are Banach spaces endowed with the norm \|\cdot\|. Let
|
Nx=
\left(\begin{array}{ccc}
\mu_{opt} g(t)f(x_2(t))-m(t)-b\exp(x_1(t)) \\
a(P_s(t) -x_2(t))-U_pg(t)f(x_2(t))\exp(x_1(t))
\end{array}\right),~~x\in X,
|
|
Lx=\frac{dx(t)}{dt},~Px=\frac{1}{\omega}\int_0^{\omega}x(t)dt,~x\in X;~~
Qz=\frac{1}{\omega}\int_0^{\omega}z(t)dt, z\in Z.
|
Then, it is not difficult to show that {\rm{Ker}}\; L=R^2, {\rm{Imm}}\; L=\{z\in
Z:\int_0^{\omega}z(t)dt=0\} is closed in Z, \dim {\rm{Ker}}\; L=2={\rm{codim}}\;
{\rm{Imm}}\; L, and P, Q are continuous projectors such that {\rm{Imm}}\;
P={\rm{Ker}}\; L, {\rm{Ker}}\; Q={\rm{Imm}}\; L={\rm{Imm}}\; (I-Q). Therefore, L is a Fredholm mapping of index zero. Furthermore, the generalized inverse (to L)K_P:{\rm{Imm}}\; L\rightarrow {\rm{Ker}}\; P\cap {\rm{Dom}}\; L is given by K_P(z)=\int_0^t{z(s)}ds-1/\omega\int_0^\omega\int_0^tz(s)dsdt. By the Arzela-Ascoli theorem, it is not difficult to show that N is L-compact on \overline{\Omega} with any open bounded set \Omega\in X.
Now we are at the right position to search for an appropriate open bounded subset \Omega for the application of the continuation theorem. Corresponding to the operator equation Lx=\lambda Nx, \lambda\in(0,1), one has
|
\begin{split}
&\frac{dx_1(t)}{dt}=\lambda\{\mu_{opt} g(t)f(x_2(t))-m(t)-b\exp(x_1(t))\},\\
&\frac{dx_2(t)}{dt}=\lambda\{a(P_s(t)
-x_2(t))-U_pg(t)f(x_2(t))\exp(x_1(t))\}. \end{split}
|
(27)
|
Let x=x(t)\in X be a solution of (27) for some certain \lambda\in(0,1). Integrating (27) from 0 to \omega produces
|
\int_0^\omega{\{\mu_{opt}
g(t)f(x_2(t))-m(t)-b\exp(x_1(t))}\}dt=0,
|
(28)
|
|
\int_0^\omega\{a(P_s(t)
-x_2(t))-U_pg(t)f(x_2(t))\exp(x_1(t))\}dt=0,
|
(29)
|
then
|
\int_0^\omega\{m(t)+b\exp(x_1(t))\}dt=\int_0^\omega \mu_{opt}
g(t)f(x_2(t))dt\leq \int_0^\omega \mu_{opt}
g(t)dt=\omega \mu_{opt}\bar{g},
|
(30)
|
|
\int_0^\omega{aP_s(t)dt=\int_0^\omega
\{ax_2(t)+U_pg(t)f(x_2(t))\exp(x_1(t))}\}dt.
|
(31)
|
From (27) - (31), it follows that
|
\begin{split}
\displaystyle\int_0^\omega|\dot{x}_1(t)|dt & = \lambda\displaystyle\int_0^\omega{|\mu_{opt} g(t)f(x_2(t))-m(t)-b \exp(x_1(t))}|dt\\
& < \displaystyle\int_0^\omega|\mu_{opt} g(t)f(x_2(t))|dt+\displaystyle\int_0^\omega |m(t)+b \exp(x_1(t))|dt=2\omega\mu_{opt}\overline{g},
\end{split}
|
and
|
\begin{split}
\displaystyle\int_0^\omega|\dot{x}_2(t)|dt &= \lambda\displaystyle\int_0^\omega{|a(P_s(t) -x_2(t))-U_pg(t)f(x_2(t))\exp(x_1(t))}|dt\\
&< \displaystyle\int_0^\omega|aP_s(t)|dt+\displaystyle\int_0^\omega |ax_2(t)+U_pg(t)f(x_2(t))\exp(x_1(t))|dt<2\omega a\overline{P_s}.
\end{split}
|
Since x(t)=(x_1(t),x_2(t))^T\in X, there exist \xi_i,
\eta_i\in[0,\omega] such that
|
x_i(\xi_i)=\mathop {\min }\limits_{t\in[0,\omega]}x_i(t),~~
x_i(\eta_i)=\mathop {\max }\limits_{t\in[0,\omega]}x_i(t), i=1,2.
|
By (28), one has
|
b\omega \exp(x_1(\xi_1))\leq\int_0^\omega\{m(t)+b\exp(x_1(t))\}dt\leq \int_0^\omega \mu_{opt} g(t)dt=\omega \mu_{opt}\bar{g},
|
that is x_1(\xi_1)\leq\ln[\mu_{opt}\bar{g}/b], then
|
x_1(t)\leq
x_1(\xi_1)+\int_0^\omega|\dot{x}_1(t)|dt\leq\ln\frac{\mu_{opt}\bar{g}}{b}+2\omega
\mu_{opt}\bar{g}:=K_1.
|
By (29), one has x_2(\xi_2)\leq P_s,
then
|
x_2(t)\leq x_2(\xi_2)+\int_0^\omega|\dot{x}_2(t)|dt\leq \bar{P_s}+2\omega
a\bar{P_s}.
|
Moreover, (31) implies
|
\int_0^\omega{aP_s(t)dt\leq \int_0^\omega
\{ax_2(\eta_2)+U_pg(t)f(x_2(\eta_2))\exp(K_1)}\}dt,
|
then
|
a\bar{P_s}\leq ax_2(\eta_2)+U_p\bar{g}f(x_2(\eta_2))\exp(K_1):=F(x_2(\eta_2)).
|
Since f(P) is strictly increasing with 0\leq f(P)<1 for P\geq 0, then F(P) is strictly increasing too. Moreover, F(0)=0<a\bar{P_s} and F(\bar{P_s})=a\bar{P_s}+U_p\bar{g}f(\bar{P_s})\exp(K_1)>a\bar{P_s}, therefore F^{-1}(a\bar{P_s}) exists within the interval (0,\bar{P_s}). Then one can verify that
|
x_2(\eta_2)\geq F^{-1}(a\bar{P_s})>0,
|
whence
|
x_2(t)\geq x_2(\eta_2)-\int_0^\omega|\dot{x}_2(t)|dt\geq
F^{-1}(a\bar{P_s})-2\omega a\bar{P_s}=K_2>0.
|
Therefore, \max_{t\in[0,\omega]}|x_2(t)|\leq\max \{| \bar{P_s}+2\omega
a\bar{P_s}|, K_2 \}:=K_3. On the other hand, by (28),
|
\int_0^\omega \mu_{opt} g(t)f(K_2)dt\leq (\bar{m}+b\exp(x_1(\eta_1)))\omega,
|
then
|
x_1(\eta_1)>\ln\frac{\mu_{opt}\bar{g}f(K_2)-\bar{m}}{b},
|
thus
|
x_1(t)\geq
x_1(\eta_1)-\int_0^\omega|\dot{x}_1(t)|dt\geq\ln\frac{\mu_{opt}\bar{g}f(K_2)-\bar{m}}{b}-2\omega
\mu_{opt}\bar{g}.
|
Therefore,
|
\mathop {\max }\limits_{t\in[0,\omega]}|x_1(t)|\leq\max\{|\ln
\frac{\mu_{opt}\bar{g}}{b}+2\omega \mu_{opt}\bar{g}|,
|\ln\frac{\mu_{opt}\bar{g}f(K_2)-\bar{m}}{b}-2\omega
\mu_{opt}\bar{g}|\}:=K_4.
|
Clearly, K_i(i=1\cdots4) are independent of \lambda. Under the assumption in Theorem 3.9, the system of algebraic equations
|
\begin{align*}
\mu_{opt} \bar{g}f(v_2)-\bar{m}-bv_1&=0,~~~
a(\bar{P_s}-v_2)-U_p\bar{g}f(v_2)v_1=0.
\end{align*}
|
has a unique solution (v_1^*,v_2^*)^T\in R^2 with v_1^*>0 and v_2^*>0. Denote K=K_3+K_4+K_5, where K_5>0 is sufficiently large such that \|(\ln(v_1^*),v_2^*)^T\|=|\ln(v_1^*)|+|v_2^*|\leq K_5. Take \Omega=\{ x(t)=(x_1(t),x_2(t))^T\in X:\|x\|<K \}, then \Omega verifies the requirement (a) in Lemma 3.8. When x\in\partial\Omega\cap {\rm{Ker}}\; L=\partial\Omega\cap R^2, x is a constant vector in R^2 with \|x\|=K. Then
|
QNx=
\left(\begin{array}{ccc}
\mu_{opt} \bar{g}f(x_2)-\bar{m}-b\exp(x_1) \\
a(\bar{P_s} -x_2)-U_p\bar{g}f(x_2)\exp(x_1)
\end{array}\right)\neq0.
|
Furthermore, in view of the assumptions in Theorem 3.9, direct calculations show that \deg\{JQNx,\Omega\cap KerL,0\}\neq0. Here J can be the identity mapping since {\rm{Imm}}\; P={\rm{Ker}}\; L. By now we have proved that \Omega verifies all the requirements in Lemma 3.8. Hence, (26) has at least one solution x^*(t)=(x_1^*(t),x_2^*(t))^T in {\rm{Dom}}\; L\cap\overline{\Omega}. Set A^*(t)=e^{x_1^*(t)}, P^*(t)=x_2^*(t), then (A^*(t),P^*(t))^T is an \omega-periodic solution of system(6) with strictly positive components. The proof of Theorem 3.9 is complete.
Next, we go ahead with investigating the globally asymptotic stability of the positive \omega-periodic solution of (6).
Lemma 3.10. Let h be a real number and f be a non-negative function defined on [h,+\infty) such that f is integrable on [h,+\infty) and is uniformly continuous on [h,+\infty). Then \lim_{t\rightarrow+\infty}f(t)=0.
Theorem 3.11. Let (A^*(t),P^*(t)) be the positive periodic solution of (6). If
|
R_1:=\frac{\mu_{opt}g^lf(m_2)}{m^u}>1,~~aP_s^l>U_pg^uM_1,
|
|
\mathop {\inf }\limits_{t\in R}\{b-U_pg(t)f(M_2)\}>0,~~\inf\limits_{t\in R}\{U_pg(t)m_1-\mu_{opt}g(t)\}>0,
|
(32)
|
where m_i, M_i, i=1,2, are defined in (8). Then (A^*(t),P^*(t)) is GAS.
Proof. Let (A(t),P(t))^T be any solution of (6) with positive initial value. Since \Gamma is an ultimately bounded region of (6), there exists T_1>0 such that (A(t),P(t))\in\Gamma and (A^*(t),P^*(t))\in\Gamma for t\geq t_0+T_1.
Consider the Lyapunov function defined by
|
V(t)=|\ln\{A(t)\}-\ln\{A^*(t)\}|+|P(t)-P^*(t)|.
|
A direct calculation of the right derivative of V(t) along the solutions of (6) leads to
|
\begin{split}
V'(t)=& -a|P(t)-P^*(t)|-b|A(t)-A^*(t)|\\
&+sgn\{P(t)-P^*(t)\}U_pg(t)(-f(P(t))A(t)+f(P^*(t))A^*(t))\\
&+sgn\{A(t)-A^*(t)\}\mu_{opt}g(t)(f(P(t))-f(P^*(t)))\\
\leq & -a|P(t)-P^*(t)|-b|A(t)-A^*(t)|+U_pg(t)f(P(t))|A(t)-A^*(t)|\\
&-U_pg(t)A^*(t)|f(P(t))-f(P^*(t))|+\mu_{opt}g(t)|f(P(t))-f(P^*(t))|\\
\leq & -a|P(t)-P^*(t)|-(b-U_pg(t)f(M_2))|A(t)-A^*(t)|\\
&-(U_pg(t)m_1-\mu_{opt}g(t))|f(P(t))-f(P^*(t))|.
\end{split}
|
Note that there are some terms containing f(P(t))A(t)-f(P^*(t))A^*(t)) in the right-hand side of the above inequality and
|
f(P^*(t))A^*(t)-f(P(t))A(t)=A^*(t)(f(P^*(t))-f(P(t))+f(P(t))(A^*(t)-A(t)),
|
from (32), it follows that there exists a positive constant \phi>0 such that
|
D^+V(t)\leq -\phi[|A(t)-A^*(t)|+|P(t)-P^*(t)|+|f(P(t))-f(P^*(t))|],~t\geq t_0+T_1.
|
(33)
|
Integrating both sides of (33) from t_0+T_1 to t (\geq t_0+T_1) produces
|
\begin{split}
V(t)+\phi\int_{t_0+T_1}^t[|A(s)-A^*(s)|&+|P(s)-P^*(s)|+|f(P(s))-f(P^*(s))|]ds\\
&\leq V(t_0+T_1)<+\infty.
\end{split}
|
Then
|
\begin{split}
\int_{t_0+T_1}^t[|A(s)&-A^*(s)|+|P(s)-P^*(s)|+|f(P(s))-f(P^*(s))|]ds\\
&\leq V(t_0+T_1)/\phi<+\infty,~t\geq t_0+T_1,
\end{split}
|
Therefore, |A(s)-A^*(s)|+|P(s)-P^*(s)|\in L^{1}([t_0+T_1,+\infty)).
The boundedness of A^*(t) and P^*(t) and the ultimate boundedness of A(t) and P(t) imply that A(t), P(t), A^*(t) and P^*(t) all have bounded derivatives for t>t_0+T_1 (from the equations satisfied by them). Then it follows that |A(t)-A^*(t)|+|P(t)-P^*(t)| is uniformly continuous on [t_0+T_1,+\infty). By lemma 3.10, one has
|
\mathop {\lim }\limits_{t\rightarrow+\infty}(|A(t)-A^*(t)|+|P(t)-P^*(t)|)=0.
|
The proof is complete.
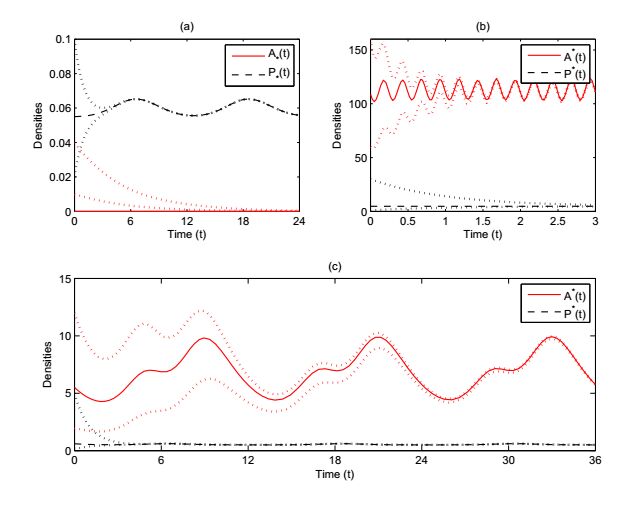
In summary, we have established some sufficient criteria for the boundary and internal cyclic dynamics of (6). Fig. 5(a) and (b) illustrate such scenarios, where the parameter values are deliberately specified such that the criteria in Theorem 3.7 and Theorem 3.11 are satisfied, respectively. In addition, it is not difficult to show that
|
R_0\geq\frac{\displaystyle\int_0^\omega \mu_{opt} g^lf(m_2)dt}{\displaystyle\int_0^\omega m^udt}=R_1, ~~ i.e., ~~ R_1>1 ~\mathrm{implies} ~R_0>1.
|
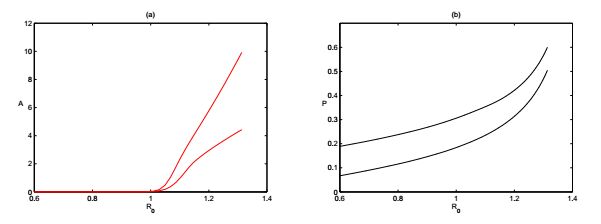
The criteria established above are of sufficient type and have some room for further improvement. Fig. 5(c) illustrates such an example, where the conditions in Theorems 3.11 are not satisfied (i.e., R_1<1<R_0) but the numerical simulation shows that (6) still admits a positive periodic solution being GAS. Moreover, in Fig. 6, the bifurcation diagrams of (6) with R_0 being the bifurcation parameter suggests that (6) admits a dichotomous cyclic dynamics, that is, the global attractor of (6) is the boundary \omega-periodic solution if R_0<1, and is the internal positive \omega-periodic solution if R_0>1. Now we shall propose a challenging conjecture that the ecological reproductive index R_0=1 is the threshold that completely characterize the global dynamics of (6). From Fig. 6, it is also observed that the amplitude of cyclic oscillation of phytoplankton increases with the increasing of R_0 and it is quite the opposite for nutrient,
4. Numerical analysis and applications
In this section, based on the above theoretical analysis, by using the numerical simulations and field applications, we further investigate the ecological impact and consequence of temperature variation and the system's corresponding response.
4.1. Effect of seasonal temperature
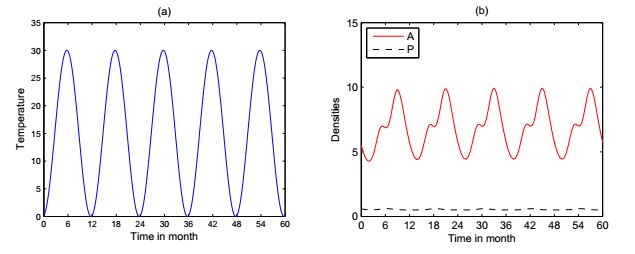
The general form of (6) and the definition of R_0 imply that the periodic dynamics produced by (6) are very robust to a wide array of periodic functions in that the qualitative dynamics can be reproduced independent of the qualitative form of the forcing. The seasonal patterns of phytoplankton follow characteristic climatology. This temporal structure of seasonal variability arises because the annual climate cycle is the primary driver of biomass variability. This finding biologically implies that both phytoplankton and nutrient variables displayed strong temporal variations strongly related to cycles of water temperature (Fig. 7) and their annual cycles can be tuned to match the climate cycle. In Fig. 7, some numerical experiments are performed to (6) in order to observe the seasonal periodic patterns of phytoplankton growth and the robustness to the temperature variation.
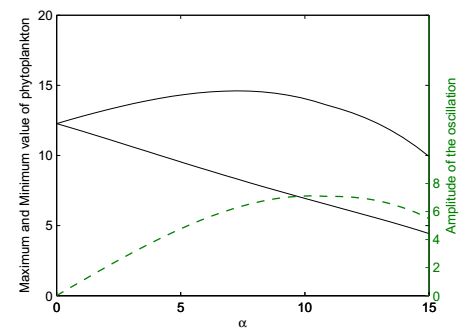
Fig. 8 elaborates the relationship between the amplitude of phytoplankton cyclic oscillation and the cyclic forcing of water temperature. The figure shows the amplitude of the cyclic oscillation of phytoplankton increases first and then decreases with the increasing of the strength of cyclic forcing of water temperature. The relationship between the amplitude of temperature and the phytoplankton amplitude is not simply monotonously consistent. The amplitude of phytoplankton oscillation achieves a maximum value at some intensity of forcing temperature.
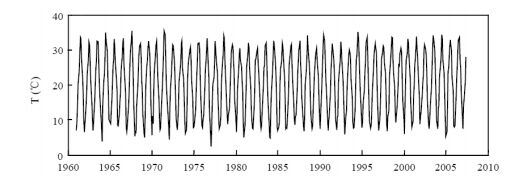
4.2. Filed application in Lake Tai
Based on the analysis of 47 years observation data of 4 weather stations (i.e., Dongshan, Wuzhong, Wuxi, and Yixing) around Lake Tai [35], Fig. 9 illustrates the trends of the monthly mean temperature of Lake Tai from 1961-2007, which develops a typical cyclic fluctuation pattern. Then, the modulation of water temperature T can be represented as a periodic solution T(t+\omega )=T(t) with maxima at the optimal season, where \omega is the period of forcing, which is taken to be monthly. A convenient and commonly applied scheme is that of sinusoidal forcing
|
T(t)=T_{mean}+\alpha\sin(\Omega t+\varphi).
|
(34)
|
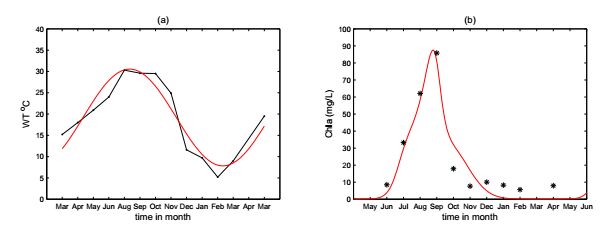
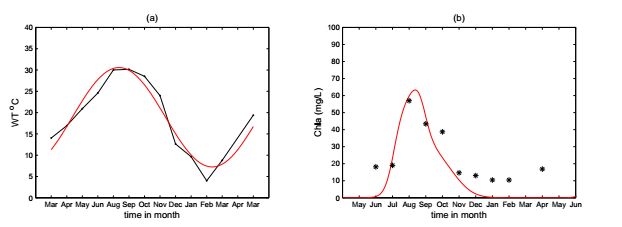
Since the forcing is assumed to be monthly and t is in units of months, then \Omega=\pi/6. We choose T_7 as a case study and we also simulate the whole lake by averaging the collected data. We fitted model parameters in (34) to the data sets of water temperature collected from the monitor stations T_i (i=1,2,...,12) using the least square method. The fitted values of parameters in (34) are listed in Table 3 and the fitted curves are presented by solid lines in Fig. 10(a) and Fig. 11(a). Except the water temperature T(t), the nutrient P_{in1} takes the values in Table 3 and all the other parameters in (6) are held fixed at the values from published sources in the available experimental evidence of Lake Tai (see Table 2 for details) and are assumed to be constant across monitor stations and constant over time. The approach in this way has the advantage of providing additional check on the performance and adaptability of the model: does it produce patterns similar to the data, even though it was not fitted to those data?
According to studies on zooplankton composition and feeding rates of crustacean in Lake Tai [6,7], the zooplankton there could never reach values high enough to control Microcystis production. Moreover, the dominant fish population in Lake Tai was zooplankton-feeding fish and phytophagous fish abundance was insignificant to control the Microcystis bloom. That is to say, phytoplankton in Lake Tai should therefore not be controlled by the grazing of either zooplankton or fish. Therefore, the top-down control can be reasonably ignored and the bottom-up formulation is adequate as a general description in mathematical modeling. Therefore, the nutrient-phytoplankton model established in this study can be applied to model and to predict phytoplankton dynamics in Lake Tai.
In Lake Tai, temperature plays an important role in the phytoplankton composition and the dominant variations in phytoplankton composition are seasonal and are strongly related to the annual cycles of temperature [6,7]. It is reasonable to assume that the annual cycles of growth, reproduction, and senescence of phytoplankton are finely tuned to the annual climate cycle having a period of one year. Cyclic behavior of phytoplankton has been shown to occur in both the field and the laboratory cultures and reconciling the predictions of mathematical models with the nonequilibrium dynamics of experimental communities has proved to be challenging [15].
As example, we only fit our model to monitor set T_7 and the average Chlorophyll-a of 12 monitor stations. From Fig. 10(b), it is observed that the predictions of long-term dynamics of the parameterized model are in good agreement with the observed dynamics in both the oscillatory population behavior and cycle phases. Both the observed dynamics and the prediction of our model reveals a strong correlation between the water temperature and the cyclic dynamics of phytoplankton. With the rising of water temperature, the phytoplankton growth rare speeds up and the phytoplankton (represented by the density of Chlorophyll-a) increases accordingly. The water temperature not only affects the physicochemical process but also induces the variations of other environmental factors such as the PH value et al. The seasonal patterns of phytoplankton in Lake Tai follow characteristic climatology. This temporal structure of seasonal variability arises because the annual climate cycle is the primary driver of biomass variability. Our model reproduces this structure with input from the temperature and provides further insight into the mechanisms that led to the annually cyclic oscillation of phytoplankton population.
We treat Lake Tai as a whole and consider the average of the collected data in each monitoring station. Fig. 11 shows the average temperature and chlorophyll-a. The numerical simulation shows that the prediction curve well matches the changes of chlorophyll-a biomass. It is not difficult to observe that the fitness in Fig. 10 is better than that in Fig. 11, which is due to the fact that the whole lake contains more uncertain impact factors. It can be more accurate to predict a portion than a whole. Despite this, our model can simulate the trend of changes of phytoplankton biomass in the whole lake.
4.3. Short term response to the changing temperature
In order to better assess the model performance, adaptability, and to analyze the impact and consequences of temperature on model dynamics, below we present numerical simulations to show short time responses to the changing temperature.
We consider the water temperature being constant with an outbreak. In general, the temperature can be simulated by the following convenient and common formulation
|
T(t)=\max(T_{mean},T_{high}-\delta(t-5)^2),~~t\in[0,15],
|
where T_{mean} is the mean temperature in the corresponding season, T_{high} denotes the highest temperature which occurs in the 5th day, and \delta is the parameter governing the width of 'open mouth' of the temperature variation. The dashed lines in green in Fig. 12 figure out the trend of temperature.
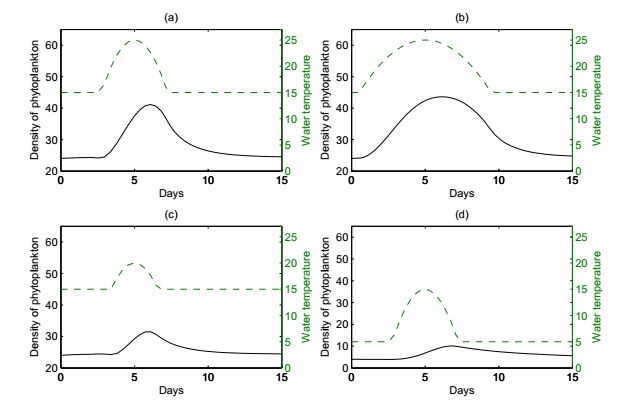
In all the four cases in Fig. 12, the density of phytoplankton also shows an outbreak under the corresponding temperature forcing. One can study Fig. 12 by comparing (a) with (b), (c), and (d). The wider 'open mouth' of temperature variation leads to the wider 'open mouth' of the phytoplankton outbreak (Fig. 12(a) and (b)). In addition to this finding, we also find that the peak value of phytoplankton in (b) is higher than that in (a). That is to say, longer period high temperature causes the phytoplankton stay in higher value for long time. The magnitude of the temperature variation is also important. The bigger the temperature changes, the stronger the phytoplankton fluctuates (Fig. 12(a) and (c)). Even though with the same magnitude of the temperature variation, the mean temperature also plays an important role. One can consider the case (a) as summer and case (d) as winter. The temperature with the same magnitude causes the different results (Fig. 12(a) and (d)). That is to say, phytoplankton bloom is more likely to happen during the summer. The four cases in Fig. 12 also illustrate that the peak of the density of phytoplankton occurs later than the time maximum temperature occurs (Fig. 12(a)). That is to say, temperature may have a lag effect on growth of phytoplankton. The time of maximum of phytoplankton falls in the range where T(t) decreases with time. It provides us warning the phytoplankton bloom after the high temperature.
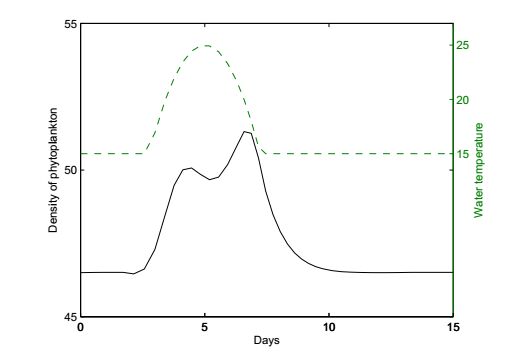
We would like to point out that the phytoplankton with different optimal temperatures can have different responses to even the same temperature forcing. The time series of phytoplankton with optimal temperature T_{opt}=23 ^oC is illustrated by the solid line in black in Fig. 13. For the phytoplankton with lower optimal temperature, something shows different. There will present a valley between two peaks when encountering the same temperature condition (Fig. 12(a) and Fig. 13). It is not difficult to explain this phenomenon. Around the 5th day, the temperature is higher than the optimal temperature for growth of phytoplankton. The excessive temperature may have a negative effect on growth of phytoplankton. This result warns us that, even though the density of phytoplankton decreases, we should also be on alert of the outbreak of phytoplankton when the temperature is high.
5. Conclusion and discussion
Because of ignoring the time-varying nature of growth rate and environmental biomass of phytoplankton, the traditional\break autonomous model could not well explain why phytoplankton usually occur in high temperature seasons [28]. In this study, in order to investigate the effect of seasonal temperature on the growth of phytoplankton, by incorporating the time-varying feature of temperature, we propose a new time-dependent bottom-up nutrient-phytoplankton interacting model. Our model provides a reasonable explanation to understand the mechanism of phytoplankton bloom.
Our model has made some improvements of the traditional models. Effect of temperature on metabolism of phytoplankton like growth, nutrient uptake, natural mortality, and nutrient releasing from sediments are analyzed systematically and comprehensively. Especially, a more realistic model named CTMI is incorporated into our model. CTMI is determined by three parameters (T_{opt}, T_{min} and T_{max}) with biological significance depicting temperature effect on growth rate. An ecological reproductive index is formulated to establish the threshold result of (6). Through the analysis of the non-autonomous periodic model, the existence of positive periodic solution is proved by using coincidence degree theory and its global stability is achieved by constructing suitable Lyapunov function. Our theoretical findings work for very general functional response. Through the results of our simulation, the phytoplankton biomass oscillates periodically with the seasonal temperature and the amplitude of phytoplankton biomass is very robust to the variation of water temperature. But the oscillation amplitude of phytoplankton seems not positively correlated to the amplitude of temperature. The amplitude of phytoplankton cyclic oscillation increases first and then decreases with the increasing of the cyclic forcing of water temperature. In addition, the effect of daily temperature on the growth of phytoplankton is also discussed by some short-term numerical simulations. The results can explain some mechanisms of the phytoplankton bloom. The outbreak of phytoplankton biomass is related to the daily average temperature, the variation of temperature and how long it remains in high temperature. Our model without delay term can even simulate that the peak of phytoplankton biomass occurs a few days later than the peak of temperature. This gives a better understanding of the phytoplankton bloom often happens following the high temperature period. The numerical simulation and filed application are carried out for Lake Tai to assess the performance and the adaptability of our model. The dynamics of the model predictions agree well with our experimental data.
Certainly, in order to obtain a desired model to well expound the mechanism of temperature working on the growth of phytoplankton or even the triggering mechanism of PB, we still has a very long way to go. Freund [14] found that an average blooms are correlated with rapid upward temperature fluctuations and speculate on their possible role as trigger mechanisms. Daily average temperature may have more immediate effect on the phytoplankton growth and bloom. The effect of daily temperature on phytoplankton bloom should be studied intensively. To some extend, our model is still an idealized one, for example, here we view temperature as a periodic function of time, yet in the real world, the water temperature changes in some random way [28]. Hence, it is more realistic to take into account the stochastic noise in the equation predicting water temperature in our model and to implement further theoretical or numerical analysis.
Our study provides a preliminary explanation of how temperature contributes to the recurrent outbreaks of PB. To further understand the mechanism of PB, one should consider other abiotic and biotic factors that are responsible for PB. The light intensity, precipitation, ecological stoichiometry of growth-limiting nutrient (e.g., the ratio of nitrogen to phosphorus, expressed as N:P) etc., may also have significant effect on the metabolism of phytoplankton. Although our climate-driven bottom-up nutrient-phytoplankton model sheds some new light on the mechanism of phytoplankton dynamics, the alternative regulation of phytoplankton abundance can come from other biotic processes such as the important top-down control. The food web interactions also have a profound effect on the population dynamics of phytoplankton bloom species and it is left for our future effort.









 DownLoad:
DownLoad: