1. Introduction
This paper is inspired by the nano-ecology experiments on the bacterium Escherichia coli by Keymer et al. reported upon in [6] and the subsequent chemotactic reaction-diffusion model developed and analyzed in [3] prompted by the experiments. In the experiment, Keymer et al. fabricated a one-dimensional array of 85 "microhabitat patches (MHP's)" for the E.coli which are linked by corridors. The corridors allow the bacteria to move from one MHP to the next, and are sufficiently more narrow than the MHP's that the MHP's may be viewed as the "nodes" in the overall environment. Each MHP is connected to feeding channels through which a controllable amount of nutrient passes. Specifically, an individual MHP has dimensions 100μm (length) ×100μm (width) ×30μm (depth). By comparison, a corridor connecting two adjacent MHP's is 50μm (length) ×5μm (width) ×30μm (depth). Each MHP is separately attached via two feeding channels to the nutrient source. Each channel has 5 "nanoslits" of dimensions 20μm (length) ×15μm (width) ×200nm (depth) through which nutrient and waste but not bacteria may pass, and the device is such that each "nanoslit" may kept open or closed. In [6], the three primary parameters describing the overall bacterial habitat are the "coupling strength" or flow rate through the corridors, the degree of openness of the feeding channels, and the carrying capacity of the individual MHP's.
In [3], the authors develop a reaction-diffusion-advection model based on the experiments reported in [6], while also taking into account that bacteria often aggregate on the basis of "self-attraction mediated by the excretion of chemoattractants". Their derivation leads to a quasilinear parabolic system for the densities of bacteria and nutrient substrate in a one dimensional habitat, in which bacteria self-aggregate and aggregate in response to nutrient substrate abundance.
In this paper, our aim is to model the situation described in [6] by means of a discrete-diffusion (or patch-island) model for the densities of bacteria and nutrient that also can incorporate bacterial self-aggregation and/or bacterial cueing upon nutrient substrate abundance. We believe that this approach allows us to capture the discrete manner in which micro-habitat patches are embedded in the overall "landscape" that is true to the spirit of [6], while also capturing aggregative behavior as highlighted in [3]. Taking account of the linear structure of the fabricated habitat in [6] leads to "nearest neighbor" dispersal between patches, i.e., bacteria from the ith micro-habitat patch are constrained so as to move directly only to patches i−1 and i+1. Consequently, our patch model takes on a generalized tridiagonal structure. Indeed, the purely diffusive aspect of dispersal in our model by itself would lead to a cooperative tridiagonal model. The asymptotic predictions ([4] and [8]) of such models are particularly clean, predicting that all orbits tend to equilibria, and these facts inform our analysis to a degree. On the other hand, our modeling and analysis are also informed by several other factors. The most interesting scenarios in the model come when some MHP's are net favorable locales while others are not. In such cases, it is reasonable to think in terms of source-sink population dynamics and of keen interest to determine if the rescue effect arising from dispersal from favorable patches to unfavorable ones promotes persistence throughout the landscape. Consequently, movement rates through corridors are key to a mathematical analysis of the model in much the way that diffusion rates would be in a reaction-diffusion setting. Indeed, discrete diffusion models are often viewed as spatially implicit surrogates for reaction-diffusion models and there is a general expectation that results in the reaction-diffusion setting have parallels in the discrete diffusion framework. Here, in particular, we find strong parallels to reaction-diffusion models with indefinite weight functions in reflecting or closed habitats ([1]; [7]). Moreover, our model is also complicated by the aggregative aspects of dispersal that we include. Specifically, when we incorporate aggregative dispersal into the discrete diffusion framework, we obtain a vector field that is Lipschitz continuous but not continuously differentiable. So we can invoke the existence and uniqueness of solutions to initial value problems for first order systems of ordinary differential equations to guarantee that we have a well-defined dynamical system. However, we cannot directly apply the Hartman-Grobman Theorem to analyze stability of equilibria. We circumvent this obstacle in our asymptotic analysis by drawing upon results from persistence theory ([2]), specifically the Acyclity Theorem and practical persistence estimates.
Two further aspects of our model merit comment at this point. First of all, our patch model has the feature that at equilibrium, if the bacteria density is zero in some patch, it is zero in all patches. That such is the case is an inherent property of the modeling framework. Indeed, the discrete diffusion component of dispersal leads to an "irreducible" coupling of the patches unless some corridor is completely closed, in which case we have two entirely separated landscapes. This feature is analogous to the maximum principle in a reaction-diffusion context. However, one should note that bacteria density in unfavorable patches "far away" from a source patch would be expected to be arbitrarily low and we will illustrate this point via numerical calculations.
The second feature of our model that we should note concerns the dynamics within a single patch in the absence of dispersal between patches. Like [6] and [3], we posit logistic dynamics for the bacteria. The traditional "r-K" form of the logistic model, used in both [6] and [3] has
where x is population density, r is the intrinsic growth rate and K is the carrying capacity of the habitat. In [6] and [3] and in our model, the bacterial density is linked to the nutrient density through the dependence of r on nutrient density. In unfavorable patches r will be negative or zero. In such case, there is no mechanism for growth and one should expect that the bacterial density tends toward zero. However, if r<0 and x>K, dx/dt>0. For this reason, we will write the logistic equation in the form
where α>0. When r>0, (2) is equivalent to (1) with K=r/α. When r≤0, x(t) tends to zero as t→∞ for all nonnegative x(0). This alteration has a significant ramification for the coupled bacteria-nutrient interaction within a single patch. Namely, there are only two equilibrium configurations possible for the bacteria-nutrient system as opposed to the three in [6]. The first possibility is that the nutrient influx rate is too low relative to the component d of r that represents the natural mortality of the bacteria and the bacteria population vanishes and the nutrient is at its input value. The other is that nutrient influx is high enough relative to d for the bacteria to survive and the bacteria density is at the r/α value determined by the balance of resource availability and natural mortality. The third equilibrium in [6] results from having a nutrient level in which r=0. In this event, damped oscillatory behavior leading to this equilibrium is observed in [6]. By employing (2) in place of (1) we do not see such behavior in the predictions of our model.
The remainder of the paper is structured as follows. We discuss within patch dynamics in section 2, leading to the development of the multi-patch model in section 3. We present our mathematical analysis of the model in sections 4 and 5. In section 4, we consider general discrete diffusion rates, whereas in section 5, we assume diffusion rates are equal. We discuss the results of our numerical investigations in section 6. We end by drawing some biological conclusions in section 7.
2. The single patch model
As noted in the introduction, the single patch dynamics of the system in [6] and [3] are described by
|
dpdt=(μs−d)p(1−pK)dsdt=λ(1−s)−εμsp
|
(3)
|
where p is the density of the bacteria, s is the density of the substrate that the bacteria feed upon, μ is the bacterial growth rate under the maximal sustainable substrate level and d is bacterial mortality. K represents the carrying capacity of the habitat, λ is the flow rate through the feeding corridor, and ε is a conversion factor from the consumption of substrate to the birth of bacteria. In this formulation, ε>1. As discussed in the introduction, we modify (3) to (4) below to allow for the possibility that μs−d can be negative. In so doing, K will no longer represent carrying capacity. The other parameters retain the same meanings as in (3). We make one further adjustment that will be significant once we are in the multi-patch setting. Namely, as scaled by 1−s, the maximum sustainable density for the substrate is one. As described in [6], the degree of openness of the feeding channels is adjustable. As a result, we want to allow a maximal sustainable density below one in that case. We use the parameter β∈(0,1] for this purpose. Consequently, our single patch model is expressed as
|
dpdt=(μs−d)p−p2Kdsdt=λ(β−s)−εμsp.
|
(4)
|
To analyze (4), observe first that (4) has either one or two equilibria. To this end, note that the substrate density s is a lower solution to
which converges over time to β. If μβ−d<0, then the bacterial density is a lower solution to
for t≫0 and consequently (p,s)→(0,β) as t→∞. A modified argument holds when μβ−d=0.
So now suppose μβ−d>0. An equilibrium (p∗,s∗) with p∗≠0 satisfies
and
so that s∗ must satisfy
|
εμ2K(s∗)2+(λ−εμKd)s∗−λβ=0
|
(5)
|
so that
|
s∗=(εμKd−λ)+√(εμKd−λ)2+4λβεμ2K2εμ2K
|
is the only positive root of (5). Setting f(s)=εμ2Ks2+(λ−εμKd)s−λβ, we have f(0)=−λβ while f(β)=εμKβ(μβ−d)>0 so that s∗<β. Additionally, f(d/μ)=λ(d/μ−β)<0 so that d/μ<s∗<β and 0<p∗<K(μβ−d). In particular, there is a unique componentwise positive equilibrium to (4).
It is easy to check that the Jacobian matrix for an equilibrium to (4) is
which is
when (p,s)=(0,β). Consequently (0,β) is a saddle point unstable in the p direction. Since
|
dsdt≤λ(β−s)dpdt≤(μβ−d)p−p2K
|
for t sufficiently large, orbits to (4) with p(0)>0 and s(0)>0 are drawn into the positively invariant rectangle
|
D={(p,s)|0≤p≤K(μβ−d),0≤s≤β}.
|
In particular, (p∗,s∗) lies within the rectangle. At (p∗,s∗) the Jacobian matrix simplifies to
Thus the determinant of the Jacobian matrix at (p∗,s∗) is positive and the trace is negative, so that (p∗,s∗) is locally asymptotically stable. Setting
|
B=1ps,F=(μs−d)p−p2K,andG=λ(β−s)−εμps
|
one may calculate that
in the interior of D. Consequently, we have by Dulac's Criterion and Poincarˊe-Bendixson theorem that (p∗,s∗) is in fact globally asymptotically stable relative to orbits with p(0)>0,s(0)>0.
3. The multi-patch model
Here we take a discrete-diffusion (patch island) approach to model dispersal between adjacent patches, which is linear, augmented by a discrete version of nonlinear chemotactic aggregation, where the advection is biased toward higher conspecific density or higher substrate concentration. Both effects are included in the reaction-advection-diffusion model in [3] which mirrors discussion in [6]. The linear level dispersal is standard in models of this type. To model chemotactic self-aggregation, we will posit a tendency for the bacteria to go from, say, patch i to patch (i+1) whenever the bacterial density is higher in patch (i+1) than in patch i. Moreover, as the simplest quantitative representation, we will assume this tendency is proportional to the difference between the densities in the two patches. As such, a term of the form
is subtracted from dpi/dt and added to dpi+1/dt, where pi is the bacterial density in patch i. The corresponding term in modeling chemotactic advection toward higher substrate concentration is
where si is substrate concentration in patch i. Once bacteria move from one patch to another, they are identified as residents of the new patch, so that local population dynamics in patch i only involve pi and si. Our analysis will consider the case of an arbitrary number of patches (MHP's). The full model takes the form
|
dp1dt=−D21p1+D12p2−γp1max{p2−p1,0}+γp2max{p1−p2,0}−νp1max{s2−s1,0}+νp2max{s1−s2,0}+(μs1−d)p1−αp21ds1dt=λ(β1−s1)−εμs1p1⋮dpidt=Di,i−1pi−1+Di,i+1pi+1−Di−1,ipi−Di+1,ipi+γpi−1max{pi−pi−1,0}−γpimax{pi−1−pi,0}+γpi+1max{pi−pi+1,0}−γpimax{pi+1−pi,0}+νpi−1max{si−si−1,0}−νpimax{si−1−si,0}+νpi+1max{si−si+1,0}−νpimax{si+1−si,0}+(μsi−d)pi−αp2idsidt=λ(βi−si)−εμsipi⋮dpndt=−Dn−1,npn+Dn,n−1pn−1−γpnmax{pn−1−pn,0}+γpn−1max{pn−pn−1,0}−νpnmax{sn−1−sn,0}+νpn−1max{sn−sn−1,0}+(μsn−d)pn−αp2ndsndt=λ(βn−sn)−εμsnpn
|
(6)
|
where i=2,…,n−1. Here Dij denotes the rate of diffusion from patch j into patch i (note that j=i−1 or j=i+1), γ denotes the strength of chemotactic bacterial self-aggregation, and ν the strength of bacterial cueing upon relative substrate concentrations. The single patch parameters μ, d, λ and ε have the same meanings as in the preceding section, as does also βi, except βi is allowed to vary from patch to patch. As noted in the introduction, this feature reflects the design of the experimental device in [6]; namely, it is possible to control the maximal available substrate concentration in each patch. Finally, we find it convenient to replace 1/K by α in the bacterial logistic dynamics. The parameters γ, ν, μ, d, ε and α reflect bacterial traits which can be reasonably considered as independent of patch. Similar reasoning applies to λ relative to the substrate.
In the analysis that follows, we will set ν=0 so as to focus primarily on bacterial self-aggregation. Our motivation here is several-fold. First of all, when bacteria cue upon conspecific density, it is not unreasonable to think of them indirectly cueing upon relative substrate concentration. Second, a term such as
is bounded by νβi+1pi. Hence it is relatively insignificant as a dispersal term compared to the linear movement terms if ν is small relative to the Dij independent of bacteria density. Such is not the case with the bacterial self-aggregation. Thirdly, our analysis turns to a large extent on the observation that the system with either form of chemotactic aggregation or both is irreducible in the bacterial density. By this statement, we mean that if pi≡0 for some i, it is identically zero for all i. Such follows from the tridiagonal structure and the positivity of diffusion coefficients. This feature can be regarded as akin to a maximum principle in a reaction-diffusion setting. Consequently, we will focus only on the case with bacterial self-aggregation which we believe to be interesting in and of itself.
4. Analysis Ⅰ: General diffusion rates
We will give persistence results for the n-patch analogue of (6) with ν=0 under the assumption that the diffusion rates Dij (j=i−1 or i+1) are positive. Here, it is useful first to present the special case when n=2 separately. To this end, we consider the model
|
dp1dt=(−D21p1+D12p2)−γp1max{p2−p1,0}+γp2max{p1−p2,0}+(μs1−d)p1−αp21ds1dt=λ(β1−s1)−εμs1p1dp2dt=(D21p1−D12p2)−γp2max{p1−p2,0}+γp1max{p2−p1,0}+(μs2−d)p2−αp22ds2dt=λ(β2−s2)−εμs2p2
|
(7)
|
Here we are interested in the solution flow for (7) on the set X={(p1,s1,p2,s2):pi≥0,0≤si≤βi,i=1,2}. Ultimately, our analysis of (7) on X relies on Theorem 4.5 of [9]. Thieme's result is an extension of the celebrated Acyclicity Theorem of persistence theory due to [5]. A key hypothesis in Theorem 4.5 of [9] is that the solution flow for (7) is forward invariant on the set
|
X1={(p1,s1,p2,s2):pi>0,0<si<βi,i=1,2},
|
so we start our discussion with a verification of this fact.
Proposition 1. The solution flow for (7) is forward invariant on X1.
Proof. Suppose that (p1(t),s1(t),p2(t),s2(t)) is a solution of (7) with pi(0)>0 and 0<si(0)<βi for i=1,2. Suppose that this solution does not remain in X1 for all t>0. By continuity, there is a smallest t1>0 so that (p1(t),s1(t),p2(t),s2(t))∈X1 for 0≤t<t1 with (p1(t1),s1(t1),p2(t1),s2(t1))∈∂X1. In such case, either si(t1)=βi or 0 for at least one i or pi(t1)=0 for at least one i.
So consider
Since si≥0 and pi≥0 on [0,t1], si is a subsolution of the problem
on [0,t1]. Hence si(t1)<βi. On the other hand, if we let Mi=max{pi(t):t∈[0,t1]}, si is a supersolution of
|
dwdt=λ(βi−(1+εμMiλ)w)w(0)=si(0)
|
which guarantees that si(t1)>0. So now consider the equation for p1. It is easy to see that p1 is a supersolution of
|
dydt=(μs1−d−D21−γmax{p2−p1,0})y−αy2y(0)=p1(0)
|
Thus p1(t1)>0. An analogous argument showing that p2(t1)>0 leads us to conclude that (p1(t1),s1(t1),p2(t1),s2(t1)) is not in ∂X1, a contradiction. So the solution flow is forward invariant on X1.
Observe, for example, that if si(0)=βi and pi(0)>0, then si(t)<βi for all t>0. Consequently, the solution flow of (7) is not forward invariant on ∂X1. The Acyclicity Theorem of [5] would require such. It is one of the key insights of [9] to remove this requirement.
Next we show that the solution flow of (7) is asymptotically bounded or point dissipative. To this end, observe that
|
ddt(p1+p2)=(μs1−d)p1−αp21+(μs2−d)p2−αp22≤ρ(p1+p2)−α(p21+p22)
|
where ρ=max{μβ1−d,μβ2−d,1}. Now (p1+p2)2≤2(p21+p22), which implies that
|
ρ(p1+p2)−α(p21+p22)≤ρ(p1+p2)−α2(p1+p2)2.
|
Consequently, given any σ>0, there is a T=T(p1(0),p2(0)) such that
for t≥T. In light of Proposition 1, this establishes
Proposition 2. Solutions of (7) are asymptotically bounded in X.
We observe that Propositions 1 and 2 extend in an analogous manner to the n-patch analogue of (6) with ν=0. We shall use this fact in the sequel as needed without further argument.
Verifying permanence or uniform persistence in (7) via Theorem 4.5 of [9] requires an understanding of the flow of (7) restricted to the boundary of X1. Here effectively the boundary of X1 is having si≡βi or pi≡0 for i=1 or i=2. It is immediate that si≡βi for i=1 or 2 implies that pi≡0. The tridiagonal structure of the model at the linear level forces pj≡0 where j≠i. Having pj≡0 in turn implies that sj→βj as t→∞. Consequently, the only element of w(∂X1) is {(0,β1,0,β2)} and the acyclicity requirement in Theorem 4.5 of [9] is automatic (again due to the tridiagonal structure, which is analogous to having a maximum principle in a reaction-diffusion model). So it becomes the case that (7) is permanent or uniformly persistent if and only if the stable manifold of {(0,β1,0,β2)}, denoted Ws({(0,β1,0,β2)})∩X1=∅. So we have:
Theorem 4.1. The system (7) is permanent (uniformly persistent) if and only if
We now examine when Theorem 4.1 holds. We begin with some simple observations. Note from (7) that
|
d(p1+p2)dt=(μs1−d)p1+(μs2−d)p2−α(p21+p22)
|
(8)
|
If μβ1−d<0 and μβ2−d<0, we have by (8) that p1+p2 is a subsolution of the initial value problem
where c_=max{μβ1−d,μβ2−d}<0. Consequently, for any initial data with pi(0)≥0, we get that p1→0 and p2→0 as t→∞, which in turn implies that Ws({(0,β1,0,β2)})∩X1≠∅. On the other hand, suppose that μβ1−d>0 and μβ2−d>0 and that (p1(t),s1(t),p2(t),s2(t))→(0,β1,0,β2) for some initial data (p1(0),s1(0),p2(0),s2(0)) with pi(0)≥0 and p1(0)+p2(0)>0. Then pi(t)>0 and 0<si(t)<βi for all t>0 and for t sufficiently large, say t≥T1, p1+p2 is a supersolution of the initial value problem
|
dzdt=cz−αz2z(T1)=p1(T1)+p2(T1),
|
where c is positive and less than min{μβ1−d,μβ2−d}.
Consequently, given any σ∈(0,c/α), there is a T2>T1 so that p1(t)+p2(t)>c/α−σ for all t≥T2. In particular, it is not possible for a solution of (7) starting in X1 to converge to {(0,β1,0,β2)}. So if μβ1−d>0 and μβ2−d>0, Ws({(0,β1,0,β2)})∩X1=∅. The upshot is as follows. If both microhabitat patches are unfavorable, the bacteria goes extinct in both patches over time, regardless of its dispersal pattern. On the other hand, if both patches are favorable, the bacterial species persists in both, again regardless of its dispersal pattern. Consequently, the only case in which dispersal behavior can have an impact on the asymptotic predictions of the model is when we have so-called source sink dynamics, where in the growth rate μβi−d is positive in one patch (meaning a favorable or source habitat) but negative in the other (meaning an unfavorable or sink habitat).
So for the remainder of this section, we assume that μβ1−d>0 while μβ2−d<0. Assume initially that there is no bacterial self-aggregation; i.e., γ=0 in (7). In this case, the Hartman-Grobman Theorem is applicable to enable us to decide whether or not Ws({(0,β1,0,β2)})∩X1=∅.
The Jacobi matrix at (0,β1,0,β2), J(0,β1,0,β2) is given by
|
J(0,β1,0,β2)=[−D21+μβ1−d0D120−εμβ1−λ00D210−D12+μβ2−d000−εμβ2−λ]
|
(9)
|
We will use σ to denote the eigenvalues of J(0,β1,0,β2) in (9). It is not difficult to see that σ=−λ is a double eigenvalue (reflecting the restorative tendency of the substrate when bacterial abundance is low) and the other eigenvalues of J(0,β1,0,β2) are the eigenvalues of the matrix A given by
|
A=[−D21+(μβ1−d)D12D21−D12+(μβ2−d)].
|
(10)
|
So the other two eigenvalues are given by
where Tr=μ(β1+β2)−2d−(D12+D21) and Δ=(μβ1−d)(μβ2−d)−D12(μβ1−d)−D21(μβ2−d) are the trace and determinant of A. When D12=D21=0, there is no dispersal between microhabitat patches and we have persistence of the bacteria in patch 1 and extinction in patch 2. Notice that when D12=0=D21, Δ<0 while Tr could be of either sign. When D12 and D21 are positive and small, Δ remains negative. Consequently, J(0,β1,0,β2) admits one positive eigenvalue and we have that Ws({(0,β1,0,β2)})∩X1=∅, and the model predicts persistence of the bacteria in both microhabitat patches. Here the subsidy from patch one rescues the bacterial population in patch two, an example of source-sink dynamics at work. If Tr<0 when D12=0=D21, it remains negative for all positive values of D12 and D21. If Tr>0 when D12=0=D21, it will eventually become negative as D21 increases. By re-writing Δ and Tr as
|
Δ=(μβ1−d−D21)(μβ2−d)−D12(μβ1−d)Tr=(μβ1−d−D21)+(μβ2−d−D12)
|
it is easy to see that Δ remains negative as D21 increases until after the point at which Tr becomes negative as D21 increases. It is also easy to see from the above that Δ will become positive once D21 is large enough. When this happens both eigenvalues of A have negative real parts and we conclude that Ws({(0,β1,0,β2)})∩X1≠∅. Consequently, the bacteria from the first patch over disperse to the second patch, effectively turning the first patch into a sink. The bacteria go extinct in both patches if the density in patch 1 becomes too diminished.
So suppose now that D12>0, D21>0 and γ>0, so that we take bacterial self-aggregation into account. Theorem 4.1 remains valid. Suppose that D21 is small enough so that μβ1−d−D21>0. Let r1 and r2 be positive numbers so that
and suppose there is a solution of (7) with pi(0)>0, si(0)∈(0,βi),i=1,2 so that (p1(t),s1(t),p2(t), s2(t))→(0,β1,0,β2) as t→∞. Choose T>0 so that for t≥T,
|
p1(t)<w<μ(β1−r1)−d−D21−r2αs1(t)>β1−r1
|
and
Then
|
dp1dt=(−D21p1+D12p2)−γp1max{p2−p1,0}+γp2max{p1−p2,0}+(μs1−d)p1−αp21≥−D21p1−γp1max{p2−p1,0}+(μs1−d)p1−αp21.
|
Now max{p2−p1,0}≤p2. So −γp1max{p2−p1,0}≥−γp1p2. Since p2<r2/γ, we get that
Hence we obtain that for t≥T,
|
dp1dt≥(μ(β1−r1)−d−D21−r2)p1−αp21.
|
Consequently, p1(t)≥ρ(t), where ρ(t) is the solution of
|
dρdt=(μ(β1−r1)−d−D21−r2)ρ−αρ2
|
on (T,∞) with ρ(T)=p1(T). Since ρ→μ(β1−r1)−d−D21−r2α as t→∞, we get that p1(t)>w for t≫T, a contradiction. So there can be no such orbit and thus
So (7) remains permanent when γ>0, D12>0 and D21 is positive and small.
When γ=0 and D12>0 is fixed, (7) loses permanence when D21 becomes large enough so that the determinant Δ of A in (10) becomes positive. For γ>0 and D12>0 and fixed, we establish that (7) is not permanent for D21 sufficiently large via the following result.
Proposition 3. For γ>0 and D12>0 fixed, (7) does not admit a componentwise positive equilibrium for D21 sufficiently large.
Proof. Suppose (7) admits an equilibrium with pi>0 and si∈(0,βi) for i=1,2. Then we have that
|
D21p1+γp1max{p2−p1,0}−(μs1−d)p1+αp21=(D12+γmax{p1−p2,0})p2
|
which is equivalent to
|
D21+γmax{p2−p1,0}−(μs1−d)+αp1=(D12+γmax{p1−p2,0})(p2p1)
|
(11)
|
For the time dependent problem, we have
|
ddt(p1+p2)≤(μβ1−d)(p1+p2)−α2(p1+p2)2
|
so that p1 and p2 are ultimately bounded above by any number greater than [2(μβ1−d)/α], independent of the value of D21. Therefore, componentwise positive equilibria are bounded independent of D21.
One easily observes that the left hand side of (11) tends to +∞ as D21→+∞. So if we have componentwise positive equilibria to (7) for arbitrarily large values of D21, the ratio p2/p1 must tend to +∞ as D21→+∞, since D12+γmax{p1−p2,0} is bounded independent of D21 (Dividing the equilibria equation for p1 by D21 shows that p1→0 as D21→+∞ were there any such solutions).
However, if we add the equations for p1 and p2 we get
|
0=(μs1−d)p1−αp21+(μs2−d)p2−αp22.
|
Thus
|
0=(μs1−d)−αp1+(μs2−d)p2p1−αp22p1
|
which implies
|
[d−μs2+αp2](p2p1)=μs1−d−αp1.
|
Recall that μβ1−d>0 and μs2−d≤μβ2−d<0. Consequently d−μs2+αβ2>0 and we get
|
p2p1=μs1−d−αp1d−μs2+αp2≤μβ1−dd−μβ2
|
independent of D21. Consequently, (7) can have no equilibrium with p1 and p2 positive for sufficiently large D21.
Propositions 1 and 2 and Theorem 4.1 extend to the analogues of (7) for an arbitrary number of micro habitat patches, so that permanence or uniform persistence is determined by the stable manifold of {(0,β1,0,β2,...,0,βn)}. Indeed, we can readily obtain that the system is permanent so long as μβi−d>0, μβi−d−Di−1,i−Di+1,i>0 for some i (with appropriate analogues if i=1 or n).
So the situation of primary interest is when μβi−d>0 for one value of i and negative for all others. For the sake of specificity, assume μβ2−d>0 and μβi−d<0 for i≠2. Assuming a componentwise positive equilibrium, we may argue as in Proposition 3 that
|
(D21+γmax{p2−p1,0})(p1p2)+(D23+γmax{p2−p3,0})(p3p2)=D12+D32−(μs2−d)+αp2.
|
Consequently, if D12+D32 becomes large we get that p1/p2 or p3/p2 must become large. On the other hand, adding all the p equations yields
|
0=n∑i=1(μsi−d)pi−α(n∑i=1p2i)
|
which we can re-write as
|
∑i≠2(d−μsi+αpi)(pip2)=(μs2−d−αp2)
|
Since d−μsi+αpi>0 then for each i≠2, we get
|
pip2≤μs2−d−αp2d−μsi+αpi≤μβ2−dd−μβi.
|
So there can not be permanence of the system if diffusion from patch 2 is too large. Again, the interpretation is that patch 2 effectively becomes a sink instead of a source if D12+D32 is too large.
5. Analysis Ⅱ: Equal diffusion rates
In this section we focus on the case where the diffusion rates of the bacteria are everywhere equal. Our purpose is to highlight further the parallel between the role of diffusion in our model as compared to its role in a reaction-diffusion analogue, such as [7]. Again, we consider the case where exactly one patch is a source; i.e., where μβi−d>0 for exactly one i. In parallel to [7], we will also assume that ∑ni=1(μβi−d)<0. The results from the previous section when γ>0 carry over when D (the common diffusion rate) is small and may be framed as asserting the persistence of the bacteria in all MHP's in that case. Here we will take γ=0 and consider the predictions of the model as D varies from 0 to ∞. What we observe is that there is a critical value ˆD of D so that we get a prediction of persistence of bacteria in all MHP's when 0<D<ˆD and extinction when D>ˆD.
To this end, for the sake of specificity, we take μβ1−d>0 and μβi−d<0 for i=2,...,n. Let ai=|μβi−d| and assume that a1−a2−a3−...−an<0. The predictions of the analogue to Theorem 4.1 can be discerned via the eigenvalues of the matrix
|
A1(D)=(a1−DD0…000D−a2−2DD…000⋮⋱⋮000…D−an−1−2DD000…0D−an−D)
|
Since A1(D) is a real symmetric matrix, all of its eigenvalues are real. The main result of this section is the following
Theorem 5.1. There is a unique positive number ˆD such that for 0≤D<ˆD the matrix A1(D) has only one positive eigenvalue. The multiplicity of this eigenvalue is one and the other eigenvalues are all negative. For D>ˆD the eigenvalues of A1(D) are all negative.
Remark 1. Since γ=0, the Hartman-Grobman Theorem implies that Ws({(0,β1,⋯,0,βn)})∩X1≠∅ when D>ˆD.
Before proving this result, we introduce some notation and make some preliminary observations. We transform A1(D) by performing the following sequence of row operations: starting with row i=1 and ending with row n−1, add row i to row i+1 which yields the matrix
|
B1(D)=(a1−DD0…000a1−a2−DD…000a1−a2−a3−D…000⋮⋱⋮a1−a2−a3…−an−2−an−1−DDa1−a2−a3…−an−2−an−1−an)
|
Next we perform the following sequence of column operations: starting with column j=n and ending with column 2, add column j to column j−1. This yields the matrix
|
C1(D)=(a1D0…00a1−a2−a2D…00a1−a2−a3−a2−a3−a3…00⋮⋱⋮cn−1,1cn−1,2cn−1,3…−an−1Dcn,1cn,2cn,3…−an−1−an−an)
|
where cn,1=a1−a2−a3−⋯−an. Notice that the determinant is invariant under all these row and column operations. Thus we have the following
Lemma 5.2. The polynomial p1(D)=detA1(D)=detC1(D) is of degree n−1 in D and
|
p1(D)=(−1)n−1(a1−a2−a3−⋯−an)Dn−1+⋯+(−1)n−1a1a2⋯an.
|
Proof. The constant term of p1 can easily be extracted by taking the determinant of the diagonal matrix A1(0). To extract the highest degree term, consider the determinant as the sum over all permutations of {1,…,n}.
|
detC1(D)=∑σ∈Snsgn(σ)n∏i=1ci,σ(i)
|
and notice that since D does not appear in the last row, no term in this sum can be of degree higher than n−1. Further, the only term in this sum of degree n−1 is
|
c1,2c2,3c3,4⋯cn−1,ncn,1=(a1−a2−a3−⋯−an)Dn−1
|
and the corresponding permutation σ is the n-cycle (1,2,3,…,n) which is even if n is odd and odd if n is even.
Notice that the lowest and highest degree terms of p1 have opposite signs. Hence p1 must have at least one root in (0,∞). Another thing to observe: by the Gershgorin Circle Theorem, the eigenvalues of A1(D) all lie in the union of intervals
|
[a1−2D,a1]∪n−1⋃j=2[−aj−4D,−aj]∪[−an−2D,−an].
|
Notice that this implies that all positive eigenvalues must lie in the interval (0,a1]. That leads to the following
Lemma 5.3. Let D1≤D2 be the smallest and largest positive roots of p1(D). Then for all D in the interval [0,D1) the matrix A1(D) has exactly one positive eigenvalue. This eigenvalue is of multiplicity one and all other eigenvalues are negative. Further, for all D in the interval (D2,∞) all eigenvalues of A1(D) are all negative.
Remark 2. Theorem 5.1 follows once we show D1=D2.
Proof. The diagonal matrix A1(0) has exactly one positive eigenvalue with the rest negative. Since the eigenvalues of A1(D) are all real and depend continuously on D, as one increases D from zero the positivity of one and the negativity of the rest of the eigenvalues can only change at a point where their product, p1(D), passes through zero. Thus A1(D) must have the desired properties for 0≤D<D1.
Similarly, for D>D2 no eigenvalue of A1(D) can change sign. Since limD→∞p1(D)=∞ if n is even and limD→∞p1(D)=−∞ if n is odd, positive eigenvalues of A1(D) in (D2,∞) must occur in pairs. Let j be the number of pairs of these positive eigenvalues and let λ1(D),…λ2j(D) be the positive eigenvalues. Then by the Gershgorin Circle Theorem
|
|p1(D)|=|λ1(D)⋯λ2j(D)λ2j+1(D)⋯λn(D)|≤a2j1(max2≤k≤n(ak)+4D)n−2j.
|
(12)
|
By Lemma 5.2, p1(D) is of degree n−1 in D while the right-hand side of (12) is of degree n−2j in D. But this can only be true for all D sufficiently large if j=0.
As mentioned in the remark above, to complete the proof of Theorem 5.1, we must show that p1 has no more than one positive root. This would follow if p1 was monotone in D on (0,∞), but there are counterexamples to this even when n=2. To this point in this section, a subscript on A1 and p1 may seem like an unnecessary bit of notation, but we now consider some other matrices.
For 1<k<n we define the principal minors of A1(D)
|
Ak(D)=(−ak−2DD0…000D−ak+1−2DD…000⋮⋱⋮000…D−an−1−2DD000…0D−an−D)
|
and take An(D)=(−an−D). Further, we define the polynomials pk by
As with A1(D), by the Gershgorin Circle Theorem, for k>1, the eigenvalues of the symmetric matrices Ak(D) all lie in the union of intervals
|
n−1⋃j=k[−aj−4D,−aj]∪[−an−2D,−an]
|
and thus the eigenvalues of Ak(D) are all negative. Hence Ak(D) is negative definite (i.e. −Ak(D) is positive definite). Finally it is convenient to introduce symmetric positive definite matrices ˆAk(D), the negative of Ak(D) with the diagonal reversed. That is, for 1<k<n
|
ˆAk(D)=(an+D−D0…000−Dan−1+2D−D…000⋮⋱⋮000…−Dak+1+2D−D000…0−Dak+2D)
|
and ˆAn(D)=−An(D)=(an+D). Since flipping the diagonal of Ak can be accomplished with an even total number of column and row swaps, we have
|
det(Ak(D))=(−1)n−k+1det(ˆAk(D))
|
Since the matrices ˆAk are positive definite, they each have a Cholesky factorization Rk. That is, there exist upper triangular matrices Rk with positive diagonal entries such that
Starting in the upper left corner, we let rn be the (only) entry of Rn and hence
Then for 2<k≤n, by partitioning
we see that
|
ˆAk−1=RTk−1Rk−1=(ˉRTkˉRkˉRTkvk−1vTk−1ˉRkvTk−1vk−1+r2k−1)=(ˆAkbbTak−1+2D)
|
where
Thus we see that in fact ˉRk=Rk, that
and hence also that
As mentioned above, p1 may not be strictly monotone for D>0, but by expanding p1 along the first column of A1 we see
|
p1(D)=(a1−D)p2(D)−D2p3(D).
|
Since ˆA2(D) is positive definite for D≥0, p2(D) is never zero there. We next consider the quotient
|
Q(D)=p1(D)p2(D)=a1−D−D2p3(D)p2(D)
|
(14)
|
in our final
Lemma 5.4. The function Q is strictly decreasing on [0,∞) with Q(0)=a1and
|
limD→∞Q(D)=a1−a2−a3−⋯−an.
|
In particular, Q has a unique root ˆD in [0,∞).
Remark 3. Since the roots of p1 and Q coincide for D>0, this ˆD is the same as in Theorem 5.1 and is also D1 and D2 in Lemma 5.3. Thus Theorem 5.1 follows immediately from Lemma 5.4.
Proof. From (14) we consider
|
f2(D)=−D2p3(D)p2(D)−D=−D2det(A3(D))det(A2(D))−D=D2det(ˆA3(D))det(ˆA2(D))−D=D2det(R3)2det(R2)2−D=D2det(R3)2det(R3)2r22−D=D2r22−D.
|
Recall from (13) that r2n=an+D. We use induction starting with
|
fn(D)=D2r2n−D=D2D+an−D=−DanD+an.
|
Notice that
|
fn′(D)=−a2n(D+an)2<0,forD≥0
|
Further, fn(0)=0 and fn(D)→−an as D→∞.
Assume that for 2<k≤n
satisfies
|
fk(D)→−ak−ak+1−⋯−anasD→∞.
|
(17)
|
Notice
|
fk−1(D)=D2r2k−1−D=D2ak−1+2D−D2/r2k−D=D2ak−1+D−(D2/r2k−D)−D=D2ak−1+D−fk(D)−D=D2−D(ak−1+D−fk(D))ak−1+D−fk(D)=−D(ak−1−fk(D))D+(ak−1−fk(D)).
|
Hence
|
fk−1′(D)={[−(ak−1−fk(D))+Dfk′(D)][D+(ak−1−fk(D))]=+D(ak−1−fk(D))(1−fk′(D))}/(D+(ak−1−fk(D)))2={−D(ak−1−fk(D))−(ak−1−fk(D))2+D2fk′(D)+Dfk′(D)(ak−1−fk(D))+D(ak−1−fk(D))−Dfk′(D)(ak−1−fk(D))}/(D+(ak−1−fk(D)))2={−(ak−1−fk(D))2+D2fk′(D)}/(D+(ak−1−fk(D)))2
|
which is negative for D≥0. Since fk−1(0)=0, fk−1(D) must be negative for D>0. Thus (15) and (16) of the induction hypothesis hold for fk−1. Finally
|
limD→∞fk−1(D)=limD→∞−ak−1+fk(D)1+(ak−1−fk(D))/D.=−ak−1−ak−⋯−an,
|
which completes the induction step. Notice that
and Lemma 5.4 follows. As mentioned above, this proves Theorem 5.1.
6. Numerical investigations
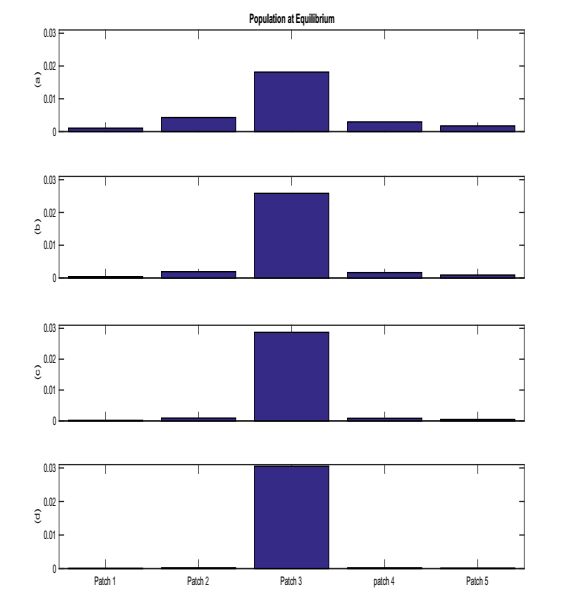
We have shown in the preceding sections that if there is a single source patch, the model predicts persistence of the bacteria in the micro-habitat patch array so long as the diffusion rates are not too large. The model is spatially implicit, but the underlying assumption that the array is linear (i.e. one must pass through patch i to get to patch (i+1) or patch (i−1)) enables us to think of the number of patch spaces between two patches as a surrogate for distance. In this section, we want to explore the asymptotic spatial arrangement of the population equilibrium distribution. It is certainly reasonable to expect that the population value in an MHP decreases as the bacteria is further away from a source patch, since it passes through MHP's that are net unfavorable. But it is interesting to consider how fast it decreases, and how is this impacted by the variation in net unfavorability among the sink patches and by the strength of the bacterial tendency to self-aggregate. In this section we explore numerically the input that various features of the model (6) and its analogues have upon the predictions of the models. We used the ode45 function in MATLAB to integrate numerically in the model. We begin in Experiment 1 with the role of self-aggregation of bacteria, measured through the parameter γ. We illustrate the role of bacterial self-aggregation in (6) with 5 microhabitat patches (MHP's). In (a)−(d) of Figure 1, all parameters except γ are fixed. Here Dij=D=0.01, β1=0.2, β2=0.2, β3=0.8, β4=0.02, β5=0.38, μ=0.15, ε=1.2, λ=0.004, d=0.06 and α=0.002. Only μβ3−d>0. γ varies across (a)−(d) with γ=0 (a), γ=4 (b), γ=10 (c), γ=50 (d). We see that increasing γ leads to an equilibrium distribution where the abundance of the bacteria is increasingly concentrated in the source patch, patch 3. Consequently we can see that self-aggregation works to concentrate bacteria in the favorable habitat. See Figure 1.
Experiment 2 considers a case where there are 7 microhabitat patches. The middle patch, patch 4, is favorable, meaning that μβ4−d>0, while μβi−d is negative for all other patches. Here Dij=D=0.01, μ=0.15, ε=1.2, λ=0.004, d=0.06, γ=4 and α is now 0.00002. We explore the interplay between implicit distance from the unique source patch and relative disparity among maximal substrate input values. Here the βi's are ordered with β1<β2<β3<β4>β5>β6>β7. We hold β1, β2, β4, β6 and β7 fixed with β1=0.1, β2=0.12, β4=0.6, β6=0.04, β7=0.02 so that β1=5β7 and β2=3β6. We initially have β3=0.3 and β5=0.14. In this instance we get p1>p7, p2>p6 and p3>p5, much as we would expect. We gradually reduce β3 and increase β5 till β3=0.14 and β5=0.3. When we have \beta_{3}=0.2 and \beta_{5}=0.24 so that \beta_{3} is now less than \beta_{5}, we get p_{3}<p_{5}. However, at this point p_{2} remains larger than p_{6}. By reducing \beta_{3} to 0.15 and increasing \beta_{5} to 0.29, we get that p_{3}<p_{5} and also p_{2}<p_{6}, reflecting having sufficient disparity between p_{3} and p_{5}. At this point, p_{1} remains larger than p_{7}, reflecting that \beta_{1}=5\beta_{7}. Such remains the case when \beta_{3}=0.14 and \beta_{5}=0.3. If we now keep \beta_{3} at 0.14, but increase \beta_{5} to 0.39 (just below the breakeven point 0.4 for \mu\beta-d), we get p_{1}<p_{7}. See Table 1.
Table 1. (Experiment 2) We display equilibrium values for the model (6) with 7 MHP's. Values of all parameters except \beta_{3} and \beta_{5} are fixed as in the text. Values for (\beta_{3},\beta_{5}) for each experiment are: (a) (0.3, 0.14), (b) (0.26, 0.18), (c) (0.24, 0.2), (d) (0.2, 0.24), (e) (0.16, 0.28), (f) (0.15, 0.29), (g) (0.14, 0.3), (h) (0.14, 0.39).
| Patch Number |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| a | 0.0000589 | 0.000331 | 0.00187 | 0.0134 | 0.00139 | 0.000208 | 0.0000305 |
| b | 0.0000584 | 0.000307 | 0.00172 | 0.0133 | 0.00148 | 0.000219 | 0.0000324 |
| c | 0.0000530 | 0.000297 | 0.00165 | 0.0133 | 0.00153 | 0.000226 | 0.0000333 |
| d | 0.0000497 | 0.000278 | 0.00154 | 0.0133 | 0.00164 | 0.000242 | 0.0000356 |
| e | 0.0000470 | 0.000263 | 0.00144 | 0.0133 | 0.00178 | 0.000259 | 0.0000382 |
| f | 0.0000463 | 0.000259 | 0.00142 | 0.0134 | 0.00181 | 0.000264 | 0.0000389 |
| g | 0.0000457 | 0.000256 | 0.00140 | 0.0134 | 0.00185 | 0.000269 | 0.0000397 |
| h | 0.0000472 | 0.000264 | 0.00145 | 0.0145 | 0.00229 | 0.000326 | 0.0000478 |
7. Conclusions
This paper has been inspired by the nano-ecology experiments on the bacterium Escherichia coli by Keymer et al. described in [6] and the subsequent chemotactic reaction-diffusion model developed and analyzed in [3] which was prompted by the experiments. Our main aim was to model the system via an island-patch or discrete-diffusion system so as to capture the discrete nature of the micro-habitat patches (MHP's) within the overall array of patches and corridors. We also modified the formulation of logistic growth in the within-patch model so as to allow for net negative growth rates in individual patches.
The linear nature of the array of MHP's results in a tri-diagonal system in which the bacteria must pass through patch i in order to transit from patch i-1 to patch i+1 or vice versa. Such a highly connected system leads to a discrete diffusion model which is irreducible (with or without the extenuating effect of chemotactic aggregation). The impact of irreducibility here is precisely analogous to that of the maximum principle in a diffusive model in a continuous space setting.
The prediction of the model is either that the bacteria persist in all MHP's or that they tend toward extinction in all patches. Moreover, one may use acyclicity results from persistence theory to see that which alternative obtains is determined by whether the stable set of the equilibrium with the bacteria absent contains any fully nontrivial initial configuration of the system (as in Theorem 4.1). Such is a consequence of the Acyclicity Theorem of persistence theory via the results of [9].
The model exhibits strong source-sink dynamics when resource flow into some MHP's is set low enough so that a bacteria population is not sustainable in such patches in isolation. In such instances, diffusive dispersal may serve as a rescuing mechanism. Indeed, if there is a single patch in which the bacteria can survive in isolation (what we term a favorable patch), a slow rate of diffusion from the favorable patch leads to coexistence in all patches. However, if the rate of diffusion from the favorable patch is too high relative to diffusion into it from adjacent patches, the rescue effect is insufficient and the bacteria tend to extinction in the system. Such is the case whether or not there is bacterial self-aggregation in the system.
Of course, such a disparity in dispersal is not possible in the special but natural case when the diffusion rates are the same in all patches. Here we consider the case when patch 1 is the sole favorable patch and the overall habitat is unfavorable in the sense that the sum over all patches of net growth rates is negative. This assumption is analogous to the assumption that the integral of the growth rate is negative in [7]. In this case, when there is no bacterial self-aggregation, persistence is equivalent to the instability of the bacteria absent equilibrium. We show in Theorem 2 that there is a unique positive threshold value of the diffusion rate D so that the bacteria absent equilibrium is unstable for diffusion rates below the threshold and stable for values above the threshold. Such is the case even though the determinant of the relevant Jacobi matrix is not monotonic as a function of the diffusion rate.
Based on our numerical experiments, the effect of bacterial self-aggregation appears to be to concentrate the population in favorable MHP's. In our two experiments, we consider the situation where we have 5 and 7 patches wherein the middle patch is favorable while the overall environment is net unfavorable in the sense we have described. The long term population density is positive in all patches but trails off when one moves away from the favorable patch. As the self-aggregation parameter is increased in Experiment 1 the disparity between the density in the favorable patch and the density elsewhere becomes more and more pronounced. Experiment 2 suggests that the interplay of patch "distance" and maximal substrate rates is nuanced. In the experiment, we kept maximal substrate rates constant in patches 1, 2, 4, 6 and 7 and varied them in patches 3 and 5, with \beta_{1}<\beta_{2}<\beta_{3}<\beta_{4}>\beta_{5}>\beta_{6}>\beta_{7}, with \beta_{1}=5\beta_{7} and \beta_{2}=3\beta_{6}, and with only \mu\beta_{4}-d>0. When \beta_{3} is considerably larger than \beta_{5}, we found the equilibrium populations (the p_{i}'s) match the relations among the maximal substrate rates (the \beta_{i}'s). As \beta_{3} decreases and \beta_{5} increases, we first reverse the equilibrium sizes of p_{3} and p_{5}. If the disparity between \beta_{3} and \beta_{5} is not too large, it remains the case that p_{2}>p_{6} and p_{1}>p_{7}, suggesting that the disparity in maximal substrate rates (\beta_{1}=5\beta_{7} and \beta_{2}=3\beta_{6}) is outweighing the feed from the inner most unfavorable patches (p_{3} and p_{5}). Once \beta_{3} is small enough relative to \beta_{5}, we find that p_{2}<p_{6} even though \beta_{2}=3\beta_{6}. If \beta_{3} is still further smaller than \beta_{5}, p_{1}<p_{7}, even though \beta_{1}=5\beta_{7}.









 DownLoad:
DownLoad: 


