Foraging movements of predator play an important role in population dynamics of prey-predator systems, which have been considered as mechanisms that contribute to spatial self-organization of prey and predator. In nature, there are many examples of prey-predator interactions where prey is immobile while predator disperses between patches non-randomly through different factors such as stimuli following the encounter of a prey. In this work, we formulate a Rosenzweig-MacArthur prey-predator two patch model with mobility only in predator and the assumption that predators move towards patches with more concentrated prey-predator interactions. We provide completed local and global analysis of our model. Our analytical results combined with bifurcation diagrams suggest that: (1) dispersal may stabilize or destabilize the coupled system; (2) dispersal may generate multiple interior equilibria that lead to rich bistable dynamics or may destroy interior equilibria that lead to the extinction of predator in one patch or both patches; (3) Under certain conditions, the large dispersal can promote the permanence of the system. In addition, we compare the dynamics of our model to the classic two patch model to obtain a better understanding how different dispersal strategies may have different impacts on the dynamics and spatial patterns.
1.
Introduction
One of powerful tools to study the evolution of Riemannian metrics on a given Riemannian manifold Md is the normalized Ricci flow equation
introduced by Hamilton [1] for a family of a Riemannian metrics g(t) on M, where Ricg and Sg are the Ricci tensor and the scalar curvature of a metric g, respectively. Many papers are devoted to a class of Riemannian manifolds M called homogeneous, on which the isometry group Isom(M) acts transitively, see [2,3,4,5]. Any Riemannian homogeneous manifold M can be identified (is diffeomorphic) to some homogeneous space G/H with G=Isom(M) being a Lie group according to the Myers and Steenrod theorem and H=Gm the isotropy subgroup at a given point m∈M. A large class consists of reductive homogeneous spaces G/H, where G is a compact and semisimple Lie group and H is a connected closed subgroup of G. Let g and h be the corresponding Lie algebras of G and H, and g=h⊕p be a reductive decomposition of g orthogonal with respect to the Killing form B defined on g so that Ad(H)p⊂p. Since B is negative definite, −B defines an Ad(G)-invariant inner product ⟨⋅,⋅⟩=−B(⋅,⋅) on g. Assume that p admits a decomposition p1⊕⋯⊕pk into pairwise inequivalent irreducible Ad(H)-modules of dimensions di=dimpi such that d1+⋯+dk=d=dim(G/H). Then, any G-invariant symmetric covariant 2-tensor on G/H can be written as c1⟨⋅,⋅⟩|p1+⋯+ck⟨⋅,⋅⟩|pk, where c1,…,ck are some real numbers. In particular, so is any G-invariant metric g(⋅,⋅)=x1⟨⋅,⋅⟩|p1+⋯+xk⟨⋅,⋅⟩|pk on G/H, where xi∈R+, i=1,…,k. The Ricci tensor of this metric has the form Ricg(⋅,⋅)=x1r1⟨⋅,⋅⟩|p1+⋯+xkrk⟨⋅,⋅⟩|pk, where ri=ri(x1,…,xk) are components of the Ricci tensor [6]. The decomposition p=p1⊕⋯⊕pk allows (1.1) to split into a system of k nonlinear autonomous differential equations
In particular, an interesting question is finding if the normalized Ricci flow preserves the positivity of the curvature of Riemannian metrics on a given manifold. In [7,8] some results were obtained concerning this question on the Wallach spaces SU(3)/T2, Sp(3)/Sp(1)×Sp(1)×Sp(1), F4/Spin(8). The case of generalized Wallach spaces with coinciding parameters a1=a2=a3∈(0,1/2) was considered in [9]. Some extensions of the results of [9] can be found in [10,11]. Recently, in [12] the results of [9] were generalized to the general case a1,a2,a3∈(0,1/2) according to the classification of [13]:
Theorem 1 (Theorem 5 in [12]). The normalized Ricci flow (1.1) evolves certain invariant Riemannian metrics with positive Ricci curvature to metrics with mixed Ricci curvature on every generalized Wallach space with a1+a2+a3≤1/2.
Theorem 2 (Theorem 6 in [12]). The following assertions hold for generalized Wallach spaces with a1+a2+a3>1/2:
1) The normalized Ricci flow (1.1) evolves all invariant Riemannian metrics with positive Ricci curvature to metrics with positive Ricci curvature if θ≥max{θ1,θ2,θ3};
2) The normalized Ricci flow (1.1) evolves certain metrics with positive Ricci curvature to metrics with positive Ricci curvature if θ≥max{θ1,θ2,θ3} fails,
where θ:=a1+a2+a3−1/2 and θi:=ai−12+12√1−2ai1+2ai, i=1,2,3.
Theorem 3 (Theorem 7 in [12]). The following assertions hold for SO(k+l+m)/SO(k)×SO(l)×SO(m), k≥l≥m>1 (denoted by GWS 1 according to [13]). Under the normalized Ricci flow (1.1)
1) All invariant Riemannian metrics with positive Ricci curvature can be evolved into metrics with positive Ricci curvature if either k≤11 or one of the conditions 2<l+m≤X(k) or l+m≥Y(k) is satisfied at each fixed k∈{12,13,14,15,16};
2) At least some invariant Riemannian metrics with positive Ricci curvature can be evolved into metrics with positive Ricci curvature if k≥17 or if X(k)<l+m<Y(k) for k∈{12,13,14,15,16};
3) The number of GWS 1 spaces on which any original metric with Ric>0 maintains Ric>0 is finite, whereas there are infinitely (countably) many GWS 1 on which Ric>0 can be preserved at least for some original metrics with Ric>0,
where X(k):=2k(k−2)k+2+√k2−12k+4−k+2 and Y(k):=2k(k−2)k+2−√k2−12k+4−k+2.
Since (l,m)≠(1,1), the case of the space SO(n)/SO(n−2)×SO(1)×SO(1) cannot be covered by Theorem 3. In the present paper we study the above question on the preservation of positivity of the Ricci curvature for the homogeneous space SO(n)/SO(n−2) diffeomorphic to the Stiefel manifold V2Rn. In general VkRn, k≤n, can be defined as the set of n×k matrices A with real entries such that AtA=Ik, where At means the transpose of A and Ik is the k×k identity matrix. VkRn becomes a compact smooth manifold in the subspace topology inherited from the topology of Rn×k. It is known that for k<n, the group SO(n) acts on VkRn transitively and VkRn is diffeomorphic to the reductive homogeneous space SO(n)/SO(n−k). In the case of these spaces there are equivalent submodules which may cause a complicated decomposition of the Ricci tensor. Although the decomposition of p admits two equivalent submodules p1 and p2 causing the dependence of an SO(n)-invariant metric of SO(n)/SO(n−2) on four parameters, it was proved in [14] that SO(n)-invariant metrics on SO(n)/SO(n−2) can be reduced to a diagonal form and described by an Ad(SO(n−2))-invariant inner product
on p=p1⊕p2⊕p3 (see also [15]). The corresponding Ricci tensor is Ricg(⋅,⋅)=x1r1⟨⋅,⋅⟩|p1+x2r2⟨⋅,⋅⟩|p2+x3r3⟨⋅,⋅⟩|p3. Clearly, d1=dimp1=n−2=dimp2=d2 and d3=dimp3=1 with d=2n−3.
The main result of this paper is contained in the following theorem.
Theorem 4. On every Stiefel manifold SO(n)/SO(n−2) with n≥3, the normalized Ricci flow (1.1) evolves any metric (1.3) to a metric with positive Ricci curvature.
2.
Results
The following expressions were found in [16] for the components of the Ricci tensor of the metric (1.3):
Then, the scalar curvature Sg=d1r1+d2r2+d3r3 takes the form
Substituting (2.1) and (2.2) into (1.2) the following system of ordinary differential equations can be obtained on SO(n)/SO(n−2), n≥3:
where
2.1. The set R+ and its structural properties
Denote by R+ the set of metrics (1.3) which admit positive Ricci curvature
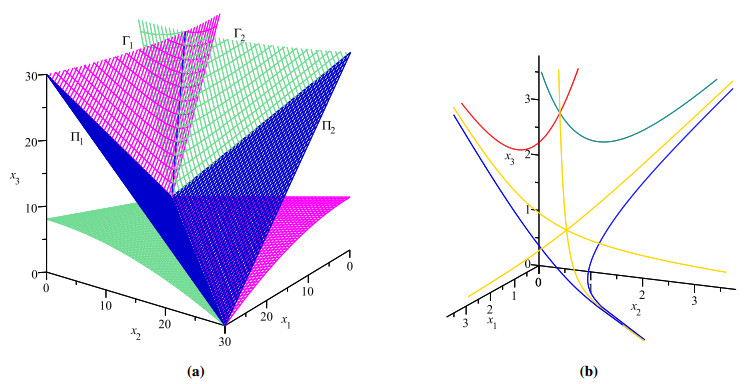
Observe that r3=0 is equivalent to (x1−x2+x3)(x2−x1+x3)=0 for every n≥3. Therefore, R+ is bounded by two planes −x1+x2+x3=0 and x1−x2+x3=0 in any case, where x1,x2,x3>0. Denote them by Π1 and Π2, respectively. Let Γ1 and Γ2 be those components of the cones r1=0 and r2=0 defined by the equations (see Figure 1)
respectively. We denote the other components
by Γ−1 and Γ−2, respectively (the lower surfaces in Figure 1 in magenta and aquamarine). Let Π3 be the plane x1+x2−x3=0 and L be the ray (p,p,(2n−4)p), p>0 (depicted in blue color in Figure 1).
Lemma 1. For all n≥3, the set R+ has the boundary
with ˜Γ1={(μt,νt,t)|t>0,0<ν≤˜ν}⊂Γ1 and ˜Γ2={(νt,μt,t)|t>0,0<ν≤˜ν}⊂Γ2, where μ=√ν2−2(n−2)ν+1 and ˜ν=(2n−4)−1. Moreover, Π1∩Π2=Π1∩˜Γ1=Π2∩˜Γ2=∅ and ˜Γ1∩˜Γ2=L for all n≥3.
Proof. Let us consider Γ1∩Γ2. The system of equations
is equivalent to the system of r1=0 and r2=0. It is easy to see that x3=(n−2)(x1+x2) is a consequence of the system corresponding to Γ1∩Γ2. Substituting this expression for x3 into the second equation in the system, we obtain
If n≥4, then x1=x2. Hence, the straight line x1=x2=p>0, x3=2(n−2)p denoted by L is a common part of the cones Γ1 and Γ2. If n=3, then (2.4) implies that Γ1=Γ2=Π3.
The system above also admits the extra solution x1=x2, x3=0. Obviously, it corresponds to Γ−1∩Γ−2.
The component Γ1 of the cone r1=0 can be parameterized as
where μ=√ν2−2(n−2)ν+1 and
is the smallest root of the quadratic equation ν2−2(n−2)ν+1=0 (by symmetry, for the component Γ2 of r2=0, we have x2=μt, x1=νt, x3=t).
For all n≥4 the conic components Γ1 and Γ2 have extra pieces not relating to the set R+. Since Γ1∩Γ2=L then necessarily μ=ν, implying the critical value ˜ν=(2n−4)−1. It is easy to see that the useful part ˜Γ1 of Γ1 can be parameterized by values t>0 and 0<ν≤˜ν. The extra part of Γ1 corresponds to the values t>0 and ˜ν<ν<l. The description of ˜Γ2 is obvious from symmetry. The equality ˜Γ1∩˜Γ2=L is obvious too. The system of the equations −x1+x2+x3=0 and x1−x2+x3=0 implies that x3=0. Analogously, it follows from Π1∩Γ1 and Π2∩Γ2 that x2=0 and x1=0. Therefore, Π1∩Π2=Π1∩Γ1=Π2∩Γ2=∅ for xi>0 implying Π1∩Π2=Π1∩˜Γ1=Π2∩˜Γ2=∅. □
2.2. The vector field V on the boundary ∂(R+)
Introduce the vector field
associated with the differential system (2.3).
Lemma 2. For every n≥3, the vector field V associated to the system (2.3), when restricted to its boundary ∂(R+) takes values in the domain R+.
Proof. By Lemma 1 the planes Π1 and Π2 bound the domain R+ for every n≥3. Denote by n1 and n2 their normals (−1,1,1) and (1,−1,1). We claim that the inner product (V,n1) is positive at every point of Π1 for all n≥3. Indeed, Π1 can be parameterized as x2=u, x3=v, x1=u+v with u,v>0. Then,
on Π1 for n≥3, where
The same inequality (V,n2)=2n−2>0 holds on the plane Π2 for all n≥3. Indeed, Π2 can be parameterized as x1=u, x3=v, x2=u+v and f1|Π2=f2|Π1, f2|Π2=f1|Π1, f3|Π2=f3|Π1.
The case n=3. According to Lemma 1, we have one more plane Π3 that bounds the domain R+. Note that f1,f2, and f3 take the following forms on Π3:
Then, we obtain (V,n3)=f1|Π3+f2|Π3−f3|Π3=2>0 on Π3, where n3=(1,1,−1) is the normal of Π3.
Since the normals n1, n2 and n3 are directed inside the domain R+ the inequalities (V,ni)>0 imply that the vector field V is directed towards R+ on every point of the boundary ∂(R+)=Π1∪Π2∪Π3.
The case n≥4. Then, ∂(R+)=Π1∪Π2∪˜Γ1∪˜Γ2 by Lemma 1. It suffices to consider the surface ˜Γ1={(μt,νt,t)|t>0,ν∈(0,˜ν]}, where ˜ν=(2n−4)−1.
The components of the normal m=∇r1=(∂r1∂x1,∂r1∂x2,∂r1∂x3) to the conic component Γ1 have the forms
It is easy to check that 12(n−2)<n−2−√(n−1)(n−3)≤1n−2 for n≥3. Then, the inequalities 0<ν≤˜ν<l<1n−2<n−2 yield that
on Γ1 and, in particular, on ˜Γ1 implying that m is directed inside the domain R+ for all n≥4.
We claim that the inner product (V,m) is positive on every point of ˜Γ1. Indeed, by calculations in Maple, we obtain that sign(V,m)=sign(F−G), where
Since F>0 and G>0 for all n≥4 and all ν∈(0,˜ν] the sign of F−G coincides with the sign of the polynomial
We claim that p(ν)>0 for all ν∈(0,˜ν] and all n≥4. It is more convenient to consider the interval [0,1]⊃(0,˜ν] instead of (0,˜ν]. Since the discriminant
of the polynomial p(ν) is positive for every n≥4 then p(ν) has no multiple roots in [0,1]. Therefore, we can use Sturm's method for our goal. Construct the sequence of Sturm polynomials p0=p, p1=p′0, pi+1=−rem(pi−1,pi), where rem(pi−1,pi) is the remainder of the division of pi−1 by pi, i=1,2,3. Then, for ν=0 we obtain using Maple that
where
for n≥4, where α4≠0 for n≥4 since the unique acceptable divisor n=467 of 1401 does not satisfy α4=0.
Evaluate now pi at ν=1:
where α6=24+60(n−3)+63(n−3)2+35(n−3)3+10(n−3)4+(n−3)5>0.
It follows that the Sturm sequence has the same number of sign changes, namely 1, for both ν=0 and ν=1 under the condition n≥4. Therefore, p(ν) has no real roots in the interval [0,1] for all n≥4. Since p(0)>0 we have p(ν)>0 for all ν∈[0,1], in particular, this is true for all ν∈(0,˜ν]. Therefore, (V,m)>0 on ˜Γ1. Since the normal m is directed into the domain R+, as shown above the vector field V is directed towards R+ on the surface ˜Γ1. By symmetry, the analogous assertion holds for V on the surface ˜Γ2⊂Γ2. □
2.3. Invariant sets and singular points of the system (2.2)
Let Σ be the surface defined by the equation Vol(x1,x2,x3)=c, c>0, where
is the volume function for the metric (1.3). Introduce the following subsets of Σ (curves on Σ) as well
In Figure 1 the curves I1,I2,I3 are depicted in gold for c=1 and n=4.
Lemma 3. The following assertions hold for the system (2.3):
1) The algebraic surface Σ is invariant for every n≥3 and every c>0;
2) The curve I3 is invariant for every n≥3 and every c>0;
3) The curves I1 and I2 are also invariant for every c>0 if n=3.
4) For all n≥3 the following inclusions are true:
Proof. 1) Actually the first assertion can easily be proved for system (1.2). Put Vol=xd11⋯xdkk and U:=Vol−c. Then, the invariance of Σ is equivalent to the inner product (∇U,V) vanishing on it. Indeed
due to Sg=∑ki=1diri and d=∑ki=1di (see also Lemma 2 in [17]).
2) The invariance of I3 is equivalent to the vector field V being parallel to the tangent of I3 at its every point. Direct calculations confirm this property:
3) It suffices to observe that I1,I2, and I3 can be obtained by cyclic permutations in (τ,τ,cτ−2) in the case n=3. Moreover, x0=(3√c,3√c,3√c) by Lemma 4. However, for n≥4, the curves I1 and I2 cannot pass through the point x0 and hence cannot be invariant.
4) Choose I1. Substituting x1=c1n−2τ1−nn−2, x2=τ and x3=τ into Π1 and Π2 we obtain
Analogously r1 and r2 take the following forms on I1:
Then, Π2|I1>0 and r1|I1>0 for τ>0 and n≥3. But Π1|I1>0 only for τ>τ1, where τ1:=22−nc is the single root of the equation 2−c1n−2τ−1n−2=0.
Note that r2|I1>0 for all n≥3 if τ>τ1:
By symmetry, for I2 we have
Now consider I3. Then,
Therefore, r1|I3=r2|I3>0 for n≥3 and τ>τ2:=(2n−4c)13−2n. □
Remark 1. As follows from (2.7), I1 intersects the cone r2=0 at the point (c1n−2τ1−nn−20,τ0,τ0), where τ0 is defined from the equation c1n−2τ−1n−20=2(n−2) for all n≥3. However, this point does not belong to the set R+ since Π1|I1=τ(2−c1n−2τ−1n−2)≤0 at τ=τ0. Indeed, 2−2(n−2)=6−3n≤0 for n≥3. Actually, here we deal with the intersection of I1 with another component Γ−2 of the cone r2=0, establishing that Γ−2 is the extra component which has no relation to the set R+ (the lower surface in aquamarine in Figure 1). Thus, I1 does not intersect the useful component Γ2 of r2=0 (see (2.4)). A similar conclusion can be obtained for I2, by interchanging the indices by symmetry.
Lemma 4. The following assertions hold for the system (2.3) at a fixed c>0:
1) For every n≥3 the system (2.3) has the unique family of one-parameter singular (equilibrium) points given by the formula
The actual value q=q0 of the parameter q at which x0 belongs to Σ is
2) If n=3, then Σ is the stable manifold of x0 with the tangent space Es=Span{(−1,1,0),(−1,0,1)} and, hence, x0∈Σ is a stable node. Moreover, I1,I2 and I3 are one-dimensional stable submanifolds for x0.
3) If n≥4, then x0 is a saddle with the tangent spaces Es=Span{(1,1,−4(n−2)2(n−1)−1)} and Eu=Span{(−1,1,0)} of corresponding manifolds (separatrices) on Σ. Moreover, the stable separatrix is exactly I3 for all n≥4.
4) For all n≥3, the singular point x0 also admits the center manifold with the tangent Ec=Span{(1,1,κ)}.
Proof. Fix c>0 and use ideas of [17].
1) Every singular (equilibrium) point of the system (1.2) is also an invariant Einstein metric of a considered space G/H. Conversely, every Einstein metric of G/H is a singular point of (1.2). Such a conclusion easily follows from the observation that the equalities f1=⋯=fk=0 and r1=⋯=rk=d−1Sg are equivalent. In particular, according to [14,18], the Stiefel manifold SO(n)/SO(n−2) admits the unique SO(n)-invariant Einstein metric (1,1,κ) up to scale for every n≥3 which is also the unique singular point of the system (2.3). The actual value q0 providing x0∈Σ can easily be found from the condition
To establish that x0∈R+ for all n≥3, it suffices to check the definition of the set R+:
Denote by χ(λ,x) the characteristic polynomial of the Jacobian matrix J(x) of the vector field V(x) associated with the differential system (2.3), x=(x1,x2,x3). Then, the cubic equation
admits three real roots
for x=x0=(q,q,κq).
2) If n=3, then λ1=λ2=−q−1<0. Therefore x0 is a stable (attracting) node on every Σ with the stable manifold Ws=Σ admitting the tangent space spanned by the eigenvectors (−1,1,0) and (−1,0,1) corresponding to the eigenvalue λ1 of multiplicity 2.
In addition, I1,I2 and I3 are invariant for n=3 by Lemma 3. Moreover, I1,I2 and I3 are also subsets of the stable manifold Σ and hence each of them is stable.
3) For n≥4, we have λ1λ2<0. Therefore, x0 is a saddle on Σ with one dimensional stable and unstable manifolds (separatrices) both contained in Σ. The tangent space Es of the stable separatrix is spanned by the eigenvector (1,1,−4(n−2)2(n−1)−1) corresponding to λ2=−q−1<0. The eigenvector (−1,1,0) corresponds to λ1>0.
In addition, I3 maintains the property of invariance for all n≥4 by Lemma 3 and in fact it is the stable manifold of the saddle x0. Indeed, since ˙x1(τ)≡1, ˙x2(τ)≡1, ˙x3(τ)=(4−2n)cτ3−2n we have
for τ=q0 corresponding to the saddle point x0=(q0,q0,κq0)∈I3⊂Σ. Therefore, the vector (1,1,−4(n−2)2(n−1)−1) is tangent to I3 at x0. On the other hand, this vector spans the stable eigenspace Es of x0 as shown above. Therefore, the stable manifold (separatrix) Ws of x0 coincides with I3 for every n≥4.
4) Finally, λ3=0 is responsible for the center (slow) manifold with the tangent space spanned by the eigenvector (1,1,κ) for all n≥3. □
Remark 2. Actually, we are interested in the special case c=1 which corresponds to the metrics (1.3) of unit volume and, therefore, has a purely geometric meaning. Studies of (2.3) on Σ with an arbitrary c>0 can easily be reduced to the "geometric" case, c=1, by the change of variables xi=Xi3√c and t=τ3√c in (2.3) based on homogeneity of the functions fi and autonomy of the system (2.3) (see also [17]). Thus, in the sequel we assume that c=1 without loss of generality.
2.4. Structural properties of the set Σ∩R+
We need the sets γ1=Σ∩˜Γ1, γ2=Σ∩˜Γ2 (the curves in red and teal respectively in Figure 1) and π1=Σ∩Π1, π2=Σ∩Π2 (the curves in blue color there).
Lemma 5. For all n≥3, the set Σ∩R+ is bounded by the smooth and connected curves π1,π2,γ1 and γ2 such that:
1) π1∩π2=π1∩γ1=π2∩γ2=∅ and the components in the pairs (π1,π2), (π1,γ1) and (π2,γ2) approach each other arbitrarily closely at infinity (which we denote by π1→π2, π1→γ1 and π2→γ2);
2) The curves γ1 and γ2 have a single common point P12(¯p,¯p,(2n−4)¯p), where ¯p=(c2n−4)12n−3.
Proof. Intersections and long time behaviors of the curves πi,γi, i=1,2. Since γ1∩γ2=(˜Γ1∩˜Γ2)∩Σ and ˜Γ1∩˜Γ2=L by Lemma 1, the set γ1∩γ2 consists of the single point P12, where ¯p is defined as the unique root of the equation pn−2pn−2(2n−4)p=c, for a given n≥3.
By analogy, π1∩π2=π1∩γ1=π2∩γ2=∅ easily follows from Π1∩Π2=Π1∩˜Γ1=Π2∩˜Γ2=∅, also known from Lemma 1, for all n≥3. To prove that π1 and γ1 approximate each other at infinity we use the approach developed in [12]: we will show π1→I2 and γ1→I2 instead of directly showing that π1→γ1 (note that it is quite difficult to derive it directly from the corresponding systems which define π1 and γ1). According to Lemma 3, we know that I1,I2,I3⊂R+ for sufficiently large τ (more precisely, for all τ>max{τ1,τ2}).
Moreover, Lemma 3 also implies the following limits for every fixed n≥3 (see formulas (2.6)–(2.8)):
Therefore, π1→γ1 at infinity as close as we want. Then, π2→γ2 is clear from symmetry. Finally, Π1|I3=Π2|I3=τ−2(n−2)→0 as τ→+∞, implying that π1→π2.
Smoothness and connectedness of the curves πi,γi, i=1,2. Substituting x2=tx1, where t>0, into r3=0, we easily get that (t−1)2x21−x23=0. Taking into account the condition xn−21xn−22x3=c (the equation of the surface Σ), we obtain the parametric equations
for π1 and π2 with t∈(0,+∞)∖{1} so that the interval (0,1) corresponds to π1 and (1,+∞) corresponds to π2. By analogy, putting x2=tx3 in r1=0, the equations
can be obtained for the curve Σ∩Γ1 with Ψ(t)=√t2−2(n−2)t+1 and l is given in (2.5). The representation x1=ψ2(t), x2=ψ1(t), x3=ψ3(t) is clear for the curve Σ∩Γ2 due to symmetry, t∈(0,l). It is clear that γ1⊂Σ∩Γ1 and γ2⊂Σ∩Γ2, and hence γ1 and γ2 can be parameterized by the same functions ψ1,ψ2,ψ3, but with t∈Δ, where Δ is some interval such that Δ⊂(0,l). To clarify Δ, recall Lemma 1, according to which the curves Σ∩Γ1 and Σ∩Γ2 leave tails (extra pieces) not related to the set Σ∩R+ after their intersection in the case n≥4, and coincide if n=3. So to eliminate those extra pieces, take into account x1=x2 at the unique point P12∈γ1∩γ2, which implies the equation Ψ(t)=t with the unique root ˜t=(2n−4)−1. Thus, in what follows we assume that Δ=(0,˜t].
Now it is easy to see that the functions ϕ1,ϕ2, and ϕ3 are differentiable on the sets (0,1) and (1,+∞). Therefore, the curves π1 and π2 are smooth. The curve π1 must be connected, as it is the image of the connected set (0,1) under the continuous function t↦(ϕ1(t),ϕ2(t),ϕ3(t)), t∈(0,1). So is π2, being the continuous image of the connected set (1,+∞). Smoothness and connectedness of γ1 and γ2 follow analogously from the differentiability of the functions t↦(ψ1(t),ψ2(t),ψ3(t)) and t↦(ψ2(t),ψ1(t),ψ3(t)), where t∈Δ. □
Proof of Theorem 4. Step 1. Any trajectory of (2.3) originating in R+ remains there forever. Indeed, by Lemma 2, the vector field V associated with the system (2.3) is directed into R+ on every point of ∂(R+), for all n≥3. Therefore, no trajectory of (2.3) can leave R+: if x(0)∈R+ then x(t)∈R+ for all t>0. According to the definition of the set R+, this means that (1.1) preserves the positivity of the Ricci curvature of metrics (1.3) on SO(n)/SO(n−2): metrics with positive Ricci curvature can be evolved only into metrics with positive Ricci curvature.
Step 2. Any trajectory originating in the exterior of R+ enters R+ in finite time. To prove this assertion we use Lemma 4. It suffices to study (2.3) on Σ∩R+, where Σ are the invariant surfaces of (2.3) responsible for dominant motions of its trajectories corresponding to nonzero eigenvalues λ1 and λ2, according to Lemmas 3 and 4. Any movement caused by λ3=0, for all n≥3, can be neglected because it can only occur within the domain R+ itself, along the eigenvector (1,1,κ) (as slow transitions between different invariant surfaces):
By Lemma 4, for every n≥3, there exists q=q0 such that x0∈Σ∩R+. Therefore, every trajectory of (2.3) originated in Σ∩extR+ must intersect the boundary Σ∩∂(R+) in finite time and enter the set Σ∩R+ governed by the stable manifold Ws=Σ (and by the stable submanifolds I1,I2, and I3 as well) of the unique stable node x0 in the case n=3, and by the separatrices Ws=I3⊂Σ and Wu⊂Σ of x0 being the unique saddle for every n≥4 (see Figure 2). The domain Σ∩R+ is able to receive all trajectories due to the fact that it is unbounded, with the boundary Σ∩∂(R+) consisting of the curves π1,π2,γ1, and γ2 in R3 such that π1∩π2=π1∩γ1=π2∩γ2=∅, according to Lemma 5. This is also quite consistent with the facts established above. Indeed, if Σ∩∂(R+) was a bounded set, then in order to satisfy Lemma 2, the dynamics of the system (2.3) would be different from those described in Lemma 4 contradicting it. Another significant circumstance that causes all trajectories to enter R+ and remain there forever for all n≥4 is that the separatrices Ws and Wu are subsets of R+ at infinity since none of them can reach (intersect or touch) the boundary Σ∩∂(R+), according to Lemma 2.
Thus, we proved that on the Stiefel manifold SO(n)/SO(n−2), n≥3, the normalized Ricci flow (1.1) evolves all metrics (1.3) (of mixed or positive Ricci curvature) into metrics with positive Ricci curvature. Theorem 4 is proved. □
3.
Planar illustrations
Clearly, the volume function Vol=xn−21xn−22x3 is a first integral of (2.3). Based on this fact, the system (2.3) could equivalently be reduced to the following planar system:
where ˜fi(x1,x2):=fi(x1,x2,φ(x1,x2)) and φ(x1,x2):=(x1x2)2−n. The corresponding singular point of (3.1) is ˜x0=(q0,q0), where q0=2n−3√(n−1)(2n−4)−1.
On the other hand, it is well known that χ(λ,x0)=λ3−ρλ2+δλ, where ρ=trace˜J(˜x0) and δ=det˜J(˜x0) are the trace and the determinant, respectively, of the Jacobian matrix ˜J(˜x) of the system (3.1), evaluated at its singular point ˜x=˜x0. Consequently,
According to the theory of planar dynamical systems, ˜x0 is a hyperbolic stable node of (3.1) for n=3 since δ>0, ρ<0, and σ=0. Clearly, ˜x0 is a hyperbolic saddle of (3.1) for all n≥4 since δ<0. These results are illustrated in Figure 3.
Using the idea in [9], the dynamics of (2.3) can be illustrated on the plane x1+x2+x3=1 (denoted by Π0) preserving the dihedral symmetry of the problem. In Figure 4, the relevant results are depicted, where the edges of the big triangle correspond to xi=0 on Π0; the curves Π0∩˜Γ1, Π0∩˜Γ2 and Π0∩Π1, Π0∩Π2 are depicted in red, teal, and blue, respectively; the yellow circle (or ellipse) represents the curve defined by the systems of the equations x20−(2n−4)(x1+x2)x0+(x1−x2)2=0 and x1+x2+x3=1, where the first one is equivalent to Sg=0. These illustrations confirm the well known general fact that the normalized Ricci flow preserves the positivity of the scalar curvature of invariant metrics on every compact homogeneous space (see [19,20]).
4.
Conclusions
The geometric problem considered in the article can be of some interest from the point of view of the dynamical systems. It is not easy to find the smallest invariant set (or minimal invariant sets) of the flow. In Theorem 4 we proved that, for every invariant set Σ of the system (2.3) defined as xn−21xn−22x3=c, there exists its invariant subset Σ∩R+. Similar results were obtained in [9,12,17] for (1.1) reduced to a dynamical system on generalized Wallach spaces; see for instance the case that a∈(1/6,1/4)∪(1/4,1/2) in [9, Theorem 3], the case that a=1/6 in [9, Theorem 4] and the case that a∈[1/4,1/2) in [17, Theorem 2] (see cases 4 and 5), which concern invariance of certain sets related to generalized Wallach spaces with a1=a2=a3=a. The case that a1+a2+a3>1/2 was studied in [12, Theorem 6], where some additional conditions were found on the parameters a1,a2,a3, which provide the invariance of a set analogous to R+.
Use of AI tools declaration
The author declares he has not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The author declares there is no conflicts of interest.









 DownLoad:
DownLoad: