Optimal control analysis of malaria-schistosomiasis co-infection dynamics

Kazeem Oare Okosun; Robert Smith?

doi:10.3934/mbe.2017024

Mathematical Biosciences and Engineering, 2017, 14(2): 377-405. doi: 10.3934/mbe.2017024.

Export file:

Format

RIS(for EndNote,Reference Manager,ProCite)
BibTex
Text

Content

Citation Only
Citation and Abstract

Optimal control analysis of malaria-schistosomiasis co-infection dynamics

Kazeem Oare Okosun, Robert Smith?

1. Department of Mathematics, Vaal University of Technology, Andries Potgieter Boulevard, Vanderbijlpark, 1911, South Africa
2. Department of Mathematics, The University of Ottawa, 585 King Edward Ave, Ottawa ON K1N6N5, Canada

Received: , Published:

Abstract Full Text(HTML) Figure/Table Related pages

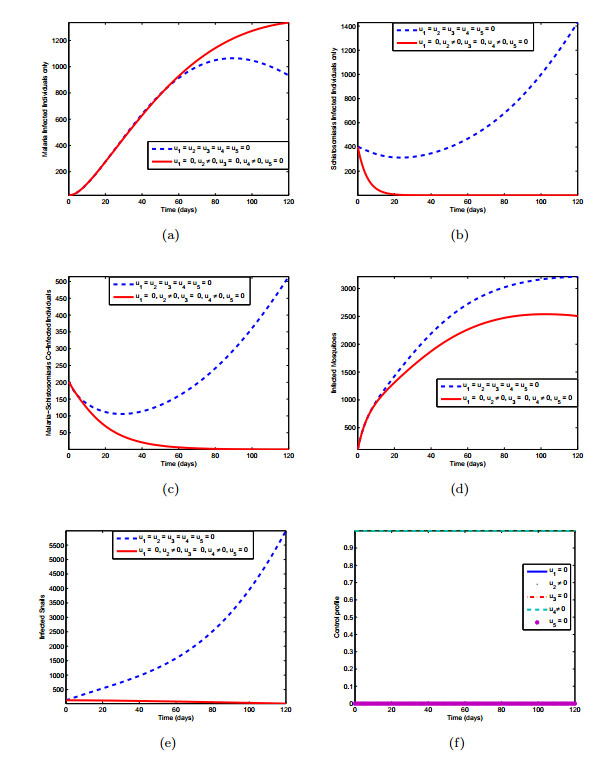
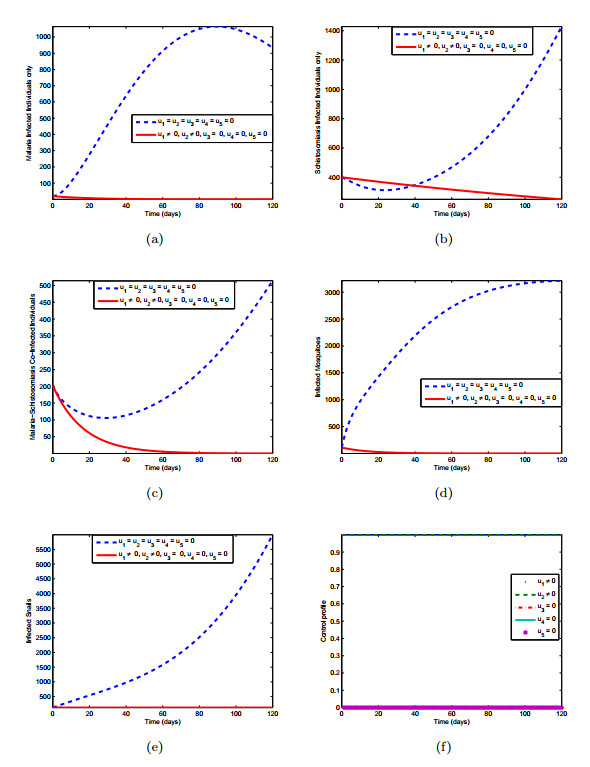
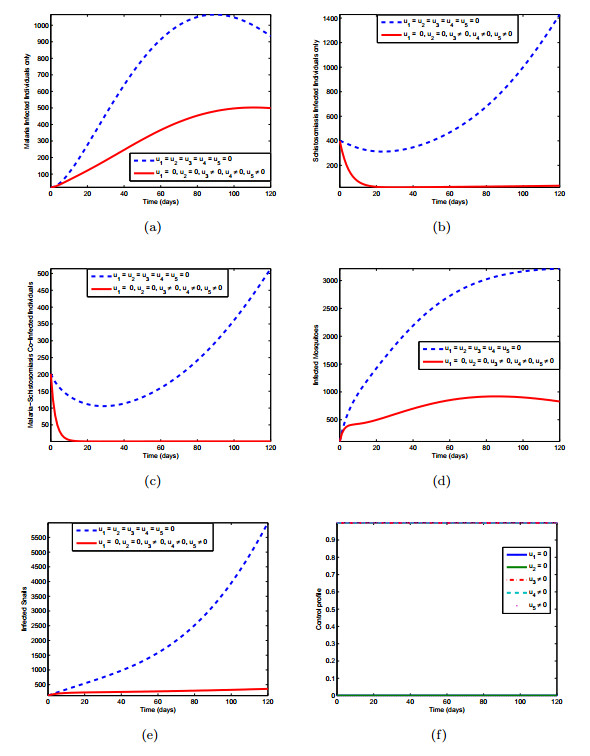
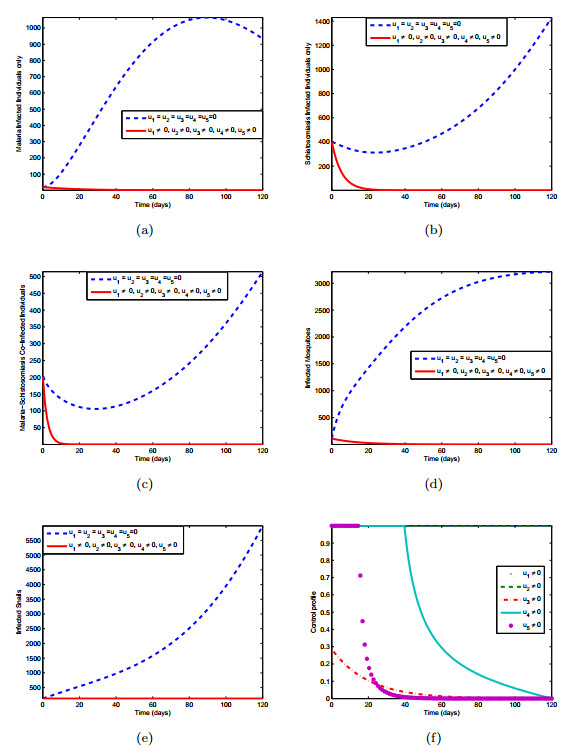
This paper presents a mathematical model for malaria-schistosom-iasis co-infection in order to investigate their synergistic relationship in the presence of treatment. We first analyse the single infection steady states, then investigate the existence and stability of equilibria and then calculate the basic reproduction numbers. Both the single-infection models and the co-infection model exhibit backward bifurcations. We carrying out a sensitivity analysis of the co-infection model and show that schistosomiasis infection may not be associated with an increased risk of malaria. Conversely, malaria infection may be associated with an increased risk of schistosomiasis. Furthermore, we found that effective treatment and prevention of schistosomiasis infection would also assist in the effective control and eradication of malaria. Finally, we apply Pontryagin's Maximum Principle to the model in order to determine optimal strategies for control of both diseases.

Figure/Table

Supplementary

Article Metrics

Keywords: Malaria; schistosomiasis; optimal control

Citation: Kazeem Oare Okosun, Robert Smith?. Optimal control analysis of malaria-schistosomiasis co-infection dynamics. Mathematical Biosciences and Engineering, 2017, 14(2): 377-405. doi: 10.3934/mbe.2017024

References:

[1] B. M. Adams,H. T. Banks,H. Kwon,H. T. Tran, Dynamic multidrug therapies for HIV: Optimal and STI control approaches, Mathematical Biosciences and Engineering, 1 (2004): 223-241.
[2] F. B. Agusto, Optimal chemoprophylaxis and treatment control strategies of a tuberculosis transmission model, World Journal of Modelling and Simulation, 5 (2009): 163-173.
[3] F. B. Agusto,K. O. Okosun, Optimal seasonal biocontrol for Eichhornia crassipes, International Journal of Biomathematics, 3 (2010): 383-397.
[4] R. M. Anderson and R. M. May, Infectious Diseases of Humans: Dynamics and Control, Oxford University Press, 1991, Oxford.
[5] K. W. Blayneh,Y. Cao,H. D. Kwon, Optimal control of vector-borne diseases: Treatment and Prevention, Discrete and Continuous Dynamical Systems Series B, 11 (2009): 587-611.
[6] J. G. Breman,M. S. Alilio,A. Mills, Conquering the intolerable burden of malaria: What's new, what's needed: A summary, Am. J. Trop. Med. Hyg., 71 (2004): 1-15.
[7] C. Castillo-Chavez,B. Song, Dynamical model of tuberculosis and their applications, Math. Biosci. Eng., 1 (2004): 361-404.
[8] Z. Chen,L. Zou,D. Shen,W. Zhang,S. Ruan, Mathematical modelling and control of Schistosomiasis in Hubei Province, China, Acta Tropica, 115 (2010): 119-125.
[9] E. T. Chiyaka,G. Magombedze,L. Mutimbu, Modelling within host parasite dynamics of schistosomiasis, Comp. Math. Meth. Med., 11 (2010): 255-280.
[10] J. A. Clennon,C. G. King,E. M. Muchiri,U. Kitron, Hydrological modelling of snail dispersal patterns in Msambweni, Kenya and potential resurgence of Schistosoma haematobium transmission, Parasitology, 134 (2007): 683-693.
[11] S. Doumbo,T. M. Tran,J. Sangala,S. Li,D. Doumtabe, Co-infection of long-term carriers of Plasmodium falciparum with Schistosoma haematobium enhances protection from febrile malaria: A prospective cohort study in Mali, PLoS Negl. Trop. Dis., 8 (2014): e3154.
[12] M. Finkel, Malaria: Stopping a Global Killer, National Geographic, July 2007.
[13] Z. Feng,A. Eppert,F. A. Milner,D. J. Minchella, Estimation of parameters governing the transmission dynamics of schistosomes, Appl. Math. Lett., 17 (2004): 1105-1112.
[14] W. H. Fleming,R. W. Rishel, null, Deterministic and Stochastic Optimal Control, Springer Verlag, New York, 1975.
[15] J. H. Ge,S. Q. Zhang,T. P. Wang,G. Zhang,C. Tao,D. Lu,Q. Wang,W. Wu, Effects of flood on the prevalence of schistosomiasis in Anhui province in 1998, Journal of Tropical Diseases and Parasitology, 2 (2004): 131-134.
[16] P. J. Hotez,D. H. Molyneux,A. Fenwick,E. Ottesen, Ehrlich and S. Sachs et al., Incorporating a rapid-impact package for neglected tropical diseases with programs for HIV/AIDS, tuberculosis, and malaria, PLoS Med., 3 (2006): e102.
[17] M. Y. Hyun, Comparison between schistosomiasis transmission modelings considering acquired immunity and age-structured contact pattern with infested water, Mathematical Biosciences, 184 (2003): 1-26.
[18] H. R. Joshi, Optimal control of an HIV immunology model, Optimal Control Applications in Mathematics, 23 (2002): 199-213.
[19] A. Kealey,R. J. Smith?, Neglected Tropical Diseases: Infection, modelling and control, J. Health Care for the Poor and Underserved, 21 (2010): 53-69.
[20] J. Keiser,J. Utzinger,M. Caldas de Castro,T. A. Smith,M. Tanner,B. Singer, Urbanization in sub-Saharan Africa and implication for malaria control, Am. J. Trop. Med. Hyg., 71 (2004): 118-127.
[21] D. Kirschner,S. Lenhart,S. Serbin, Optimal Control of the Chemotherapy of HIV, J. Math. Biol., 35 (1997): 775-792.
[22] J. C. Koella,R. Anita, Epidemiological models for the spread of anti-malaria resistance, Malaria Journal, 2 (2003): p3.
[23] C. M. Kribs-Zaleta,J. X. Velasco-Hernandez, A simple vaccination model with multiple endemic states, Math. Biosci., 164 (2000): 183-201.
[24] V. Lakshmikantham, S. Leela and A. A. Martynyuk, Stability Analysis of Nonlinear Systems, Marcel Dekker, New York and Basel, 1989.
[25] S. Lenhart and J. T. Workman, Control Applied to Biological Models, Chapman and Hall, London, 2007.
[26] J. Li, D. Blakeley and R. J. Smith?, The failure of $ R_0 $, Comp. Math. Meth. Med. , 2011 (2011), Article ID 527610, 17pp.
[27] G. Li,Z. Jin, Global stability of a SEIR epidemic model with infectious force in latent, infected and immune period, Chaos, Solutions and Fractals, 25 (2005): 1177-1184.
[28] Q. Longxing, J. Cui, T. Huang, F. Ye and L. Jiang, Mathematical model of schistosomiasis under flood in Anhui province Abstract and Applied Analysis, 2014(2014), Article ID 972189, 7pp.
[29] A. D. Lopez,C. D. Mathers,M. Ezzati,D. T. Jamison,C. J. Murray, Global and regional burden of disease and risk factors, 2001: Systematic analysis of population health data, Lancet, 367 (2006): 1747-1757.
[30] E. Mtisi,H. Rwezaura,J. M. Tchuenche, A mathematical analysis of malaria and Tuberculosis co-dynamics, Discrete and Continuous Dynamical Systems Series B, 12 (2009): 827-864.
[31] Z. Mukandavire,A. B. Gumel,W. Garira,J. M. Tchuenche, Mathematical analysis of a model for HIV-Malaria co-infection, Mathematical Biosciences and Engineering, 6 (2009): 333-362.
[32] S. Mushayabasa and C. P. Bhunu, Modeling Schistosomiasis and HIV/AIDS co-dynamics, Computational and Mathematical Methods in Medicine, 2011(2011), Article ID 846174, 15pp.
[33] S. Mushayabasa,C. P. Bhunu, Is HIV infection associated with an increased risk for cholera? Insights from mathematical model, Biosystems, 109 (2012): 203-213.
[34] I. S. Nikolaos,K. Dietz,D. Schenzle, Analysis of a model for the Pathogenesis of AIDS, Mathematical Biosciences, 145 (1997): 27-46.
[35] K. O. Okosun,R. Ouifki,N. Marcus, Optimal control analysis of a malaria disease transmission model that includes treatment and vaccination with waning immunity, BioSystems, 106 (2011): 136-145.
[36] K. O. Okosun,O. D. Makinde, Optimal control analysis of malaria in the presence of non-linear incidence rate, Appl. Comput. Math., 12 (2013): 20-32.
[37] K. O. Okosun,O. D. Makinde, A co-infection model of malaria and cholera diseases with optimal control, Mathematical Biosciences, 258 (2014): 19-32.
[38] L. S. Pontryagin, V. G. Boltyanskii, R. V. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Wiley, New York, 1962.
[39] R. Ross, The Prevention of Malaria, Murray, London, 1911.
[40] P. Salgame,G. S. Yap,W. C. Gause, Effect of helminth-induced immunity on infections with microbial pathogens, Nature Immunology, 14 (2013): 1118-1126.
[41] A. A. Semenya,J. S. Sullivan,J. W. Barnwell,W. E. Secor, Schistosoma mansoni Infection Impairs Antimalaria Treatment and Immune Responses of Rhesus Macaques Infected with Mosquito-Borne Plasmodium coatneyi, Infection and Immunity, 80 (2012): 3821-3827.
[42] K. D. Silué,G. Raso,A. Yapi,P. Vounatsou,M. Tanner,E. Ńgoran,J. Utzinger, Spatially-explicit risk profiling of Plasmodium falciparum infections at a small scale: A geostatistical modelling approach, Malaria J., 7 (2008): p111.
[43] R. J. Smith? and S. D. Hove-Musekwa, Determining effective spraying periods to control malaria via indoor residual spraying in sub-saharan Africa Journal of Applied Mathematics and Decision Sciences, 2008(2008), Article ID 745463, 19pp.
[44] R. W. Snow,C. A. Guerra,A. M. Noor,H. Y. Myint,S. I. Hay, The global distribution of clinical episodes of Plasmodium falciparum malaria, Nature, 434 (2005): 214-217.
[45] R. C. Spear,A. Hubbard,S. Liang,E. Seto, Disease transmission models for public health decision making: Toward an approach for designing intervention strategies for Schistosomiasis japonica, Environ. Health Perspect., 10 (2002): 907-915.
[46] P. van den Driessche,J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 180 (2002): 29-48.
[47] R. B. Yapi,E. Hürlimann,C. A. Houngbedji,P. B. Ndri,K. D. Silué, Infection and Co-infection with Helminths and Plasmodium among School Children in Côte d'Ivoire: Results from a National Cross-Sectional Survey, PLoS Negl. Trop. Dis., 8 (2014): e2913.
[48] X. N. Zhou,J. G. Guo,X. H. Wu, Epidemiology of schistosomiasis in the people's republic of China, 2004, Emerging Infectious Diseases, 13 (2007): 1470-1476.

show all references

Reader Comments

your name: * your email: *

Copyright Info: 2017, Kazeem Oare Okosun, et al., licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution Licese (http://creativecommons.org/licenses/by/4.0)

Download full text in PDF

Associated material

Metrics