1. Introduction
Since the beginning of the HIV epidemic, it is estimated that 75 million people have been infected with HIV and 36 million have died [40]. HIV spans the globe, affecting every country, although some have fared worse than others. This is especially apparent in sub-Saharan Africa, with an estimated 5% of all adults infected [40]. HIV is not restricted to certain age groups, and, despite prevention programs and awareness campaigns, HIV incidence continues to increase, particularly amongst men who have sex with other men (MSM).
Fortunately, there have been numerous medical advancements since AIDS and HIV were defined in 1982-85. In 1986, the first antiretroviral therapy (ART) was introduced to prolong the life of individuals affected with HIV and reduce its spread. This changed the perspective of HIV to that of a chronic disease. Questions are now raised as to why the incidence rate continues to increase amongst certain population groups. Numerous surveys attempt to explain an individuals' reasoning, but the results have been varied, showing evidence of increased risky behaviour as well as decreased or no change in behaviour. [12,22,28,32]. The imminence of prophylactic HIV vaccines (such as one being developed at The University of Western Ontario [39]) would have an enormous impact worldwide, but also raises some new interesting questions, chief among them being how to asses its impact on individuals contemplating whether to engage in casual sex, specifically in unprotected casual sex.
Population models have been useful in understanding and predicting the spread of HIV [20,36,18,31,19]. To better understand how one individual can affects change at population level game-theoretical models have been used [30,33] These models illuminate a feedback mechanism where individual's choices may affect the population, which in turn affect the choices an individual is likely to make.
Game theory dates back to late 1940s with the works of von Neumann and Morgenstern [37] and later those of Nash [26] in the early 1950s. A game is a mathematical framework to describe decision-making by individuals engaged in competitive situations, where they can behave noncooperatively or cooperatively. Noncooperative game theory is nowadays widely used in applied areas such as economics, engineering, operations research, evolutionary biology and social sciences (psychology and cognitive sciences) see [4,15,16] and many references therein. The question of existence and computation of Nash strategies for a given game can be tackled with various methods, such as the reaction-curves method, optimization techniques, variational inequalities, computational methods (such as genetic algorithms, evolutionary computation), or a replicator-dynamics equilibrium, etc. [4,10,21,0,11].
Generalized Nash games (GN) with finite dimensional strategy sets were first studied by Arrow and Debreu in [1], followed by [29,23,34,27], with a recent review in [14]. The formulation of the generalized Nash game as a variational inequality problems dates back to Bensoussan [5], while [34] gives first equivalence results for finite-dimensional GN games and quasivariational inequalities.
In this paper, we model casual (sexual) encounters as a noncooperative generalized Nash game between 2, 3, or 4 players, where each player's HIV status is known to both one's self, and to the player they choose to interact with. We do not model in this paper a population-level transmission process. All players have personal preferences ranked in utility of unprotected and protected sex outcomes, and they are given expected utilities of the casual encounter, depending on possible outcomes: unprotected sex outcome (USE), or protected/no-sex outcome (PSE). We model a player's strategy vector as their probabilities of being engaged in USE with other players. We further introduce multiplayer GN games to analyze casual encounters between players belonging to different age groups, where partner choice is closely tied to a player's age. This age-stratified game model is introduced here to investigate the possibility of offering a prophylactic HIV vaccine to the youngest age group, perhaps before they become sexually active (similar to the HPV vaccine). Then we study the effects of individual choices on HIV transmission where different age groups interact and have differing levels of access to treatment options.
In our previous work on the topic, we modelled a similar setup of casual encounters with an agent-based model of the population [33,35], and we analyzed how groups can emerge from coevolution of HIV spread with partner choices and risk perception, where we also assumed that a player's true HIV status is only known to themselves. In this model, unlike our previous simulation-based work, we construct a theoretical model to identify and analyze Nash equilibria with respect to the decisions players make. This allows us to better understand: a) the impact of personal preferences for unprotected sex; and b) the impact of heterogeneity of players (division in age groups) and initial HIV age composition both in presence and absence of a prophylactic vaccine.
To the best of our knowledge, modelling HIV transmission with age-stratified multiplayer GN games models is absolutely novel in the literature. There are a handful of examples of multiplayer GN games in applied problems (the River Basin problem, electricity markets [25], cap-and-trade agreements [14], voluntary vaccination models [11]), so our work here is unique in pushing the boundaries of modelling using GN games.
The structure of the paper is as follows: In Section 2, we present a 2-player game while in Section 3 we formulate the multiplayer games of casual encounters between players in age groups. Throughout, we investigate the sensitivity of players' Nash strategies and of HIV transmission when changes in utility rankings, efficacy of prophylactic treatment and group-specific initial HIV age composition are taken into account. We close with a few conclusions and future work.
2. Casual encounter games as generalized Nash games
In general, a multiplayer game involves a finite number of players, denoted here by N>0. A generic player i∈{1,...,N} is thought to have a strategy set Si⊂Rni, whose strategies are vectors xi∈Si, and a payoff function fi:Si→R. A Nash equilibrium of a multiplayer game is defined as follows:
Definition 2.1. Assume each player is rational and wants to maximize their payoff. Then a Nash equilibrium is a vector x∗∈K:=S1×...×SN which satisfies the inequalities:
|
∀i,fi(x∗i,x∗−i)≥fi(xi,x∗−i),∀xi∈Si
|
where x−i:=(x1,...,xi−1,xi+1,...,xN).
For several decades, there exists, in the game theoretic literature, the concept of a generalized Nash (GN) game [1,29], which in brief is a game such as above, where however each player's strategy set Si is in fact dependent on the vector of strategies of other players [14]. It is known that in general a GN game has entire sets of Nash equilibria (as defined above), and it is also known that very few solution methods exist to date to compute all these for a given game. In particular, the subclass of GN games with shared constraints (SC) [27,13] has developed more than its generic GN games counterparts. These are GN games where each player has an individual constraint set (applied only to their vector of strategies, such as Si:=Si(xi) here), however all players in a game have to also obey a shared constraint, i.e., a set of inequalities involving other players' strategies. This class of games is detailed in [27,13,14] and most recent work by the first author developed a theory and a computational method for finding the entire solutions set of a GNSC [9].
In this paper, we need to use the framework of GN theory, as our player interactions lead to casual sexual encounters in a closed population, thus the encounters have to obey a counting rule from both an HIV+ and and HIV− player viewpoint. This constraint is in fact a shared constraint by all players, which naturally leads us to consider multiplayer GN games.
There are results asserting existence of generalized Nash equilibria for the type of games we model (see for instance [13,34,29] and references therein). One such approach is that of finding a small subset of solutions of a GN game by reformulating the GN game into a variational problem as below in Definition 2.2. Once the Ⅵ is proven to have solutions, computational methods are employed to find its solution set.
Definition 2.2. Given a set K ⊂ Rn, closed and convex, and given F : K → Rn a continuous function, the variational inequality (Ⅵ) problem is to find a vector x∗ ∈ K such that
The existence of a solution to the Ⅵ problem in Definition 2.2 can be shown in many mathematical contexts (see [24]) but, specifically for our cases here, we use the results in [13]. Specifically, we solve for generalized Nash strategies of players where F(x):=(−∂f1(x)∂x1,....,−∂fN(x)∂xN) and where K={S1×...×SN∣g(x)≤0}, where g(x) is the shared constraint.
To solve the Ⅵ problem we compute its solution set as the set of critical points of a projected dynamical system (see [2,8]) given by
|
dxdτ=PTK(x(τ))(F(x(τ))),x(0)∈K,
|
(1)
|
where F(x):=(∇x1f1,...,∇xNfN). The advantages are three-fold: we can assert existence of solutions to the game (given known results of existence of solutions to (1); we can use computational methods developed for projected systems to analyze and compute Nash equilibria for the game; and we can check if/when uniqueness of Nash strategies can be asserted.
It is known that the system (1) is well-defined if F is Lipschitz continuous on K, where K is a closed and convex set. Under these assumptions, solutions to this system exist and are unique through each initial point x(0)∈K. A projection-type algorithm can be used to compute its trajectories and its stationary points such as the ones in [2,8]. To answer the uniqueness question, we numerically explore the set of initial conditions of system (1) and study how many (and what values of) Nash strategies we uncover.
2.1. Two-player casual encounter game.
Let us consider now a casual encounter between two individuals from a general population of individuals aged 15 and over. A player can have one of two statuses: HIV negative (HIV−) or HIV positive (HIV+). Let us then denote by ϵ−, respectively ϵ+, the proportion of HIV negative, respectively HIV positive individuals so that ϵ− + ϵ+=1. Now, let us define by P1 and P2 respectively two players such that their statuses are s1:=HIV+ and s2:=HIV−. Define by xi∈[0,1]2,xi=(xi−,xi+),i∈{1,2} a player's probability vector of having unprotected sex, where xi− is probability of unprotected sex (USE) with an HIV− player and xi+ is the probability of USE with an HIV+ player. We try to find out, via our game model, what are the probabilities of having unprotected sex as a result of a casual encounter, based on their preference of sex outcomes.
Utility ranking of preferences of each player is given based on the HIV status of the individual they might engage with, which is considered known to them, as well as based on the type of sexual outcome they may find themselves in, namely USE, or PSE (where by PSE we amalgamate preferences of either protected sex or no sex outcomes).
Specifically, we assign as a numerical value for the utility of a sexual encounter the range of [0,1]. We consider throughout the paper that USE(+,+)=1, USE(−,−)=1 and that, as in [33], USE(+,−)<1 and USE(−,+)<1. This is to say that players are rational, and prefer unprotected sexual encounters with players of same status over all other outcomes.
Let us define the expected utilities for Pi,i∈{1,2} out of a casual encounter as: Ei−: = expected utility from interacting with an HIV− player and Ei+: = expected utility from interacting with an HIV+ player. For P1, who is HIV+, these are:
|
E1−=ρ[x1−USE(+,−)+(1−x1−)PSE(+,−)] and
|
|
E1+=ρ[x1+USE(+,+)+(1−x1+)PSE(+,+)]
|
where ρ is the activity parameter of P1. This represents a multiplicative factor controlling overall sexual activity level. It is outlined further in Section 3.
Then the overall expected utility of the encounter for P1 is:
|
E1(x1−,x1+)=ϵ+E1−+(1−ϵ+)E1+.
|
Similarly, for P2, whose status is HIV−, we have:
|
E2−=ρ[x2−USE(−,−)+(1−x2−)PSE(−,−)],
|
|
E2+=ρ[x2+USE(−,+)+(1−x2+)PSE(−,+)].
|
|
Thus E2(x2−,x2+)=ϵ+E2−+(1−ϵ+)E2+.
|
Now let us recall that ϵ+ depends on the probabilities of players P1 and P2 to have unprotected sex. Consequently, we express ϵ+ as:
|
ϵ+=ϵ+(0)+[x1−ϵ+(0)+x2+ϵ−(0)]τ
|
(2)
|
where ϵ+(0) is the initial (before the game) fraction of HIV+ people in the population, and τ=0.02 is the known transmission probability of HIV [17].
Last but not least, we need to make sure that the number of possible sexual encounters that lead to transmission is the same whether counted from the P1 or P2 perspective. This leads us to the constraint:
|
ϵ−∑i∈HIV−xi+=ϵ+∑i∈HIV+xi−⇔(1−ϵ+)x2+=ϵ+x1−,
|
with ϵ+ as in (2).
Players P1 and P2 want to maximize their expected utilities E1(x1,x2) and E2(x1,x2) subject to (x1,x2) in the set
|
K:={S1×S2∣(1−ϵ+)x2+=ϵ+x1−}
|
where
|
Si={xi=(xi−,xi+)∈[0,1]2,0≤xi−+xi+≤1,i=1,2}.
|
Due to expression (2) we see that these utilities have actual dependencies on the other player's choices, so our model is a 2-player game with nonlinear payoffs.
2.2. Base case scenarios, parameter values and uniqueness of Nash strategies
At this stage, a discussion of parameter values we define as our ''base case scenario'' throughout the rest of the manuscript is needed. We outlined above our starting assumptions on the utility ranking values for USE(+,+) and USE(−,−). Furthermore, we also assume USE(+,−)=0 and USE(−,+)=0 and PSE(s1,s2)=0, for any status values s1≠s2∈{+,−} and PSE(−,−)=USE(+,+)=0.25>0. The latter values mean that a protected sex outcomes or no sex outcome is less preferred than USE by all players, but a PSE outcome with a partner of same status has a positive utility for all players.
The base values used in our simulations, unless otherwise noted, are listed in Table 1.
Table 1. This table outlines the base case preferences for different sexual acts given a players' status.
| P1 | P2 | Utility for USE | Utility for PSE | Range |
| HIV+ | HIV+ | USE(+,+)=1 | PSE(+,+)=0.25 | [0,1] |
| HIV+ | HIV- | USE(+,−)=0 | PSE(+,−)=0 | [0,1] |
| HIV- | HIV+ | USE(−,+)=0 | PSE(−,+)=0 | [0,1] |
| HIV- | HIV- | USE(−,−)=1 | PSE(−,−)=0.25 | [0,1] |
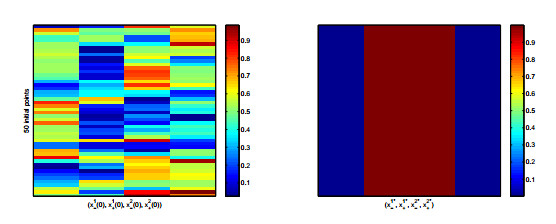
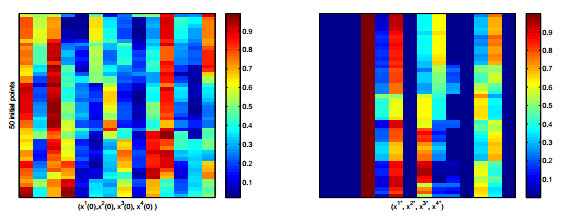
In general, it is expected that a Nash game will have multiple equilibria. We took a numerical approach to investigate the type of Nash equilibria we get in the game above. We first set the rest of our game parameters as described in Table 2 below. We then vary the initial conditions of the game reformulated as in equation (1), using experiments with uniformly distributed points from K. We ran 100 simulations, each starting with 50 uniformly distributed initial values (x1−,x1+,x2−,x2+)∈K, and the only resulting Nash equilibrium strategies are the ones pictured in Figure 1. This specifically shows a (unique) Nash point (0,1,1,0) regardless of the initial conditions, i.e., players have USE with others from same status groups only. However, this base case, though ideal in the sense of the type of behaviour suggested, is not realistic, since under Nash strategies (0,1,1,0) no one would have unprotected sex with a positive partner, thus HIV would die out in the population.
Table 2. Parameter definitions and parameter values for baseline scenario. Here τ is a fixed probability of transmission per contact.
| Term | Definition | Baseline value | Range |
| τ | Probability of HIV spread from an HIV+ player to an HIV− player through USE | 0.02 | - |
| ϵ+(0) | Initial proportion of HIV+ individuals in the population. | 0.05 | 5% of population |
| ϵ−(0) | Initial proportion of HIV− individuals in the population. | 0.95 | 95% of population |
In the next section, we investigate the sensitivity of these results with respect to changes in utilities for casual sex with players of opposite status.
2.2. Analysis of the 2-player encounter game
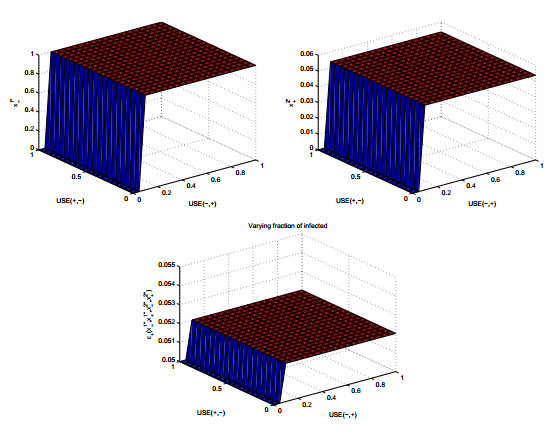
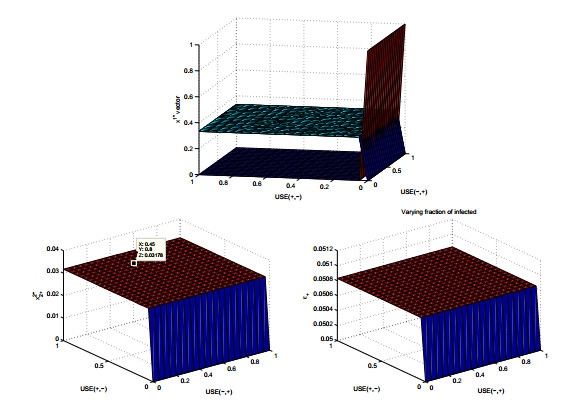
In this section we are interested in investigating the effects of varying base utilities on the equilibrium strategies of both players to have unprotected sex in a casual encounter, namely on x1∗− and x2∗+. This question was not investigated in our previous works [33,35]. We then track the effect of these changes on the overall fraction of infected individuals, ϵ+. We use Table 2 to describe the values of our parameters. We compute the general Nash equilibrium points as described in the previous Section 2.1. Figure 2 shows the impact that changing utilities has on x1∗−,x2+, as these strategies relate to HIV spread. We plotted 3-dimensional surfaces that observes these changes while varying both USE(−,+) and USE(+,−) over the range [0,1]. We also plotted the change in ϵ+ according to the same changes in utilities.
We see a change in the equilibrium solution for both x1∗− and x2∗+ as we vary USE(+,−) values, and a similar impact on values of ϵ+. In contrast, varying USE(−,+) values has no effect on the equilibrium values of players' strategies. A new set of Nash strategies, obtained for instance for a value of USE(+,−)=0.5 is (x1−,x1+,x2−,x2+)=(1,0,0.9463,0.0537) as seen in Figure 2, whereas the equilibrium strategies for instance for USE(+,−)=0.08 are (x1∗−,x1∗+,x2∗−,x2∗+)=(0.4282, 0.5718, 0.9773, 0.0227).
3. Multiplayer game
We extend next the 2-player game presented in Section 2.2 to a multiplayer game, to capture interactions between players belonging to different age groups, as a possibly important factor in HIV transmission [7]. We consider here a population with 5 age cohorts, 15-20, 20-30, 30-40, 40-50 and 50+. Age group 1 (G1), representing 15-20 year-old individuals, interacts with individuals from their age group plus with individuals of the 20-30 age cohort (G2). Age group 2 (G2), representing 20-30 year-old individuals, interacts with individuals from their own age cohort, plus with individuals in their adjacent age groups, i.e. G1 and 30-40 year-olds (G3). This continues for the 3rd and 4th age groups, with the 5th age group (G5) interacting with themselves and the 40-50 (G4) age cohort. Surveys have shown that HIV prevalence varies greatly by age group, with youth accounting for a substantial amount of infections [6]. In general, interactions can be modeled in a variety of ways, subject to differing assumptions. We guided our groups interactions here following our previous model [35].
A game is defined by choosing one HIV+ player (always taken to be Player 1) in one of the groups at a time; the other players in a game will have an HIV− status and will belong to the age cohorts allowed to interact with the age cohort P1 belongs to. Following the age-group interactions allowed above, if P1 belongs to G1 or G5, then the HIV− players will be from the same or adjacent groups; thus we model these interactions as a 3-player game. Whenever P1 is chosen in one of the G2, G3, or G4, then we model their interactions as a 4-player game.
Let us denote by gamei,i∈{1,...,5} one of the games describes above, such that
We assume first that HIV+ individuals are spread among the five groups; thus each age group has a subgroup of HIV+ individuals of size ϵGi+(0),i∈{1,...,5} so that 5∑i=1ϵGi+(0)=ϵ+(0)=5% as in Section 2. We start first by assuming an even spread of HIV+ individuals among age groups: ϵGi+(0)=0.01.
Finally, each age group has a differing activity parameter ρi,i∈{1,...,5} given by: ρ1=0.5,ρ2=1,ρ3=0.8,ρ4=0.6,ρ5=0.3, representing a multiplicative factor controlling overall sexual activity level relative to the second age group, by age. Each Pi has an expected utility Ei of unprotected sex in a casual encounter, assuming they are aware of their partner status:
|
Ei:=ϵ+Ei+(x)+(1−ϵ+)Ei−(x),∀i∈{1,2,3}.
|
3.1. 3-player game.
We start by setting up the game concerning age cohort 15-20, where we choose P1 to be HIV+ in G1. Then P2 and P3 are HIV− players from age groups G1,G2 respectively. The vector of strategies of player Pi is xi=(xi1−,xi1+,xi2−), where by xij− we denote the probability of Pi to have unprotected sex with an HIV− individual in Gj, and by xij+ the probability of unprotected sex with an HIV+ individual in Gj.
We define their expected utilities as:
|
E1−=ρ1[(x11−+x12−)USE(+,−)+(1−(x11−+x12−))PSE(+,−)]
|
|
E1+=ρ1[(x11+)USE(+,+)+(1−x11+)PSE(+,+)]
|
Then P1's strategies have to satisfy: 0≤x11−,x11+,x12−≤1 and that x11−+x11++x12−=1.
Similarly for P2 an HIV− individual ∈ G1, and P3 an HIV− individual ∈ G2, we get (for j={2,3}):
|
Ej−=ρj−1[(xj1−+xj2−)USE(−,−)+(1−(xj1−+xj2−))PSE(−,−)]
|
|
Ej+=ρj−1[(xj1+)USE(−,+)+(1−xj1+)PSE(−,+)]
|
Each player strategies have to satisfy (j∈{2,3}): 0≤xj1−,xj1+,xj2−≤1 and xj1−+xj1++xj2−=1.
As a consequence of the interaction between players, the fractions of HIV+ individuals in G1 and G2 change now as follows (note that ϵGj+(game1)=ϵGj+(0),j∈{3,4,5}):
|
ϵG1+(game1)=ϵG1+(0)+τ[x11−ϵG1+(0)+x21+ϵG1−(0)], and
|
|
ϵG2+(game1)=ϵG2+(0)+[x12−ϵG1+(0)+x31+ϵG2−(0)]τ
|
Then we compute
|
ϵ+(game1):=5∑i=1ϵGi+(game1).
|
(3)
|
Last but not least, we need to impose the shared constraint that the number of possible sexual encounters that lead to transmission is the same when counted from each of the + and − players' perspective. This leads us to the constraint:
|
(1−ϵ+(game1))(x21++x31+)=ϵ+(game1)(x11−+x12−),
|
with ϵ+(game1) as in (3).
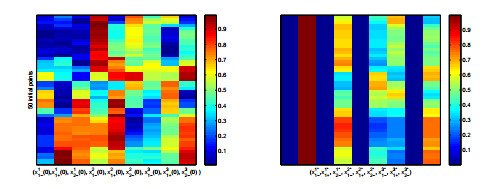
We investigate uniqueness of solutions for the generalized Nash equilibrium strategies computed as in Section 2.2. Figure 3 shows a non-unique Nash point while varying initial conditions of system (1). We ran 100 simulations each starting with 50 uniformly distributed initial values and the compiled results are always as in Figure 3. As expected, the equilibrium strategies are not unique, however, the equilibrium strategies for players engaging in USE with players of opposite status (namely x1∗1−,x1∗2− for P1 and respectively x2∗1+ for P2 and x3∗1+ for P3) are always unique, and all equal to 0.
3.2. Results & discussion: 3-player game
Similar to studying the 2-player game, we study the effects of varying USE(−,+) and USE(+,−) on the choices of players and on the fraction ϵ+ of the population, with baseline values of Table 2.
We know from our previous section that equilibrium strategies found for this game are not unique, thus initial conditions for the computation of equilibrium strategies under varying parameters are important. In order to derive our analysis, we use as initial conditions one of the equilibrium points computed in the subsection above:
|
x_∗=((0,1,0),(0.6369,0,0.3631),(0.62,0,0.38)),
|
(4)
|
relying on the fact that all equilibrium strategies for players engaging in USE with players of opposite status in the baseline scenario are 0. The new equilibrium strategies pictured above are:
|
x_∗=((0.5,0,0.5),(0.62,0.02,0.36),(0.62,0,0.38)).
|
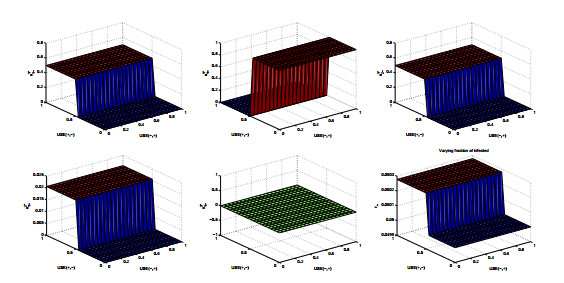
Figure 4 shows more refined results than those in the 2-player scenario. Choices for P3 interacting with the HIV+ player are not shown, as they are not changed from the initial values. Varying USE(+,−) affects the strategies of P1 interacting with both P2 and P3 (upper left and upper right panels of Figure 4), while varying USE(−,+) affects the strategies of P2 interacting with P1 (upper middle panel of Figure 4). We see a switch in strategy of P2 as USE(−,+) increases from 0 to 1. With increase in both utilities of USE with players of opposite status, P1's choices move to unprotected sex with both P2, while P2, engages with P1, though not exclusively (they maintain nonzero strategies of unprotected sex with players of HIV− status as well). The impact on the infection levels from such a game alone is shown to have an increasing direction. The infected fraction in the population (lower left panel of Figure 4) increases from the baseline value of 0.05% to ϵ+(game1)=0.05028%, most affected by values of USE(−,+) beyond a threshold of ≈0.5.
3.2. 4-player game
We describe next the 4-player game arising from choosing for instance P1 as an HIV+ player in G2 (the game will be identical for a choice of P1 in either G3 or G4).
We denote P1 as HIV+ from G2 and P2, P3 and P4 as HIV− players from G1, G2 and G3 respectively. The vectors of strategies are as follows:
|
P1:0_≤(x11−,x12−,x13−,x12+)≤1_ s.tx11−+x12−+x13−+x12+=1
|
|
P2:0_≤(x21−,x22−,x22+)≤1_ s.t. x21−+x22−+x22+=1
|
|
P3:0_≤(x31−,x32−,x33−,x32+)≤1_ s.t. x31−+x32−+x33−+x32+=1
|
|
P4:0_≤(x42−,x43−,x42+)≤1_ s.t. x42−+x43−+x42+=1
|
The expected utilities for these individuals are listed below, starting with P1 representing HIV+ individuals from G2:
|
E1−=ρ2[(x11−+x12−+x13−)USE(+,−)+(1−(x11−+x12−+x13−))PSE(+,−)]
|
|
E1+=ρ2[x12+USE(+,+)+(1−x12+)PSE(+,+)]
|
Similarly for P2 who is an HIV− individual ∈ G1 we have:
|
E2−=ρ1[(x21−+x22−)USE(−,−)+(1−(x21−+x22−))PSE(−,−)]
|
|
E2+=ρ1[x22+USE(−,+)+(1−x22+)PSE(−,+)]
|
For P3 an HIV− individual ∈ G2:
|
E3−=ρ2[(x31−+x32−+x33−)USE(−,−)+(1−(x31−+x32−+x33−))PSE(−,−)]
|
|
E3+=ρ2[x32+USE(−,+)+(1−x32+)PSE(−,+)]
|
Finally, for P4, an HIV− individual ∈ G3 we have:
|
E4−=ρ3[(x42−+x43−)USE(−,−)+(1−(x42−+x43−))PSE(−,−)]
|
|
E4+=ρ3[x42+USE(−,+)+(1−x42+)PSE(−,+)]
|
As a result of interactions allowed in this game, the fraction of the infected individuals changes in groups 1, 2, 3 (note that ϵGj+(game2)=ϵGj+(0),j∈{4,5}):
|
ϵGj+(game2)=ϵGj+(0)+τ[xj1−ϵG2+(0)+xj+12+ϵGj−(0)],j∈{1,2,3}
|
hen we compute
|
ϵ+(game2):=5∑i=1ϵGi+.
|
(5)
|
Last but not least, we need to impose the shared constraint that the number of possible sexual encounters that lead to transmission is the same when counted from each of the + and − players' perspective. This leads us to the constraint:
|
(1−ϵ+(game2))(x22++x32++x42+)=ϵ+(game2)(x11−+x12−+x13−),
|
with ϵ+(game2) as in (5).
We again investigate uniqueness of solutions as we did in Section 2.2. Figure 5 shows non-unique Nash points while varying initial conditions of (1). We ran 100 simulations each starting with 50 uniformly distributed initial values and the compiled results are always as in Figure 5. As expected, the equilibrium strategies are not unique, however, the equilibrium strategies for players engaging in US with players of opposite status (namely x1∗1−,x1∗2−,x1∗3− for P1 and respectively x2∗2+ for P2, x3∗2+ for P3 and x4∗2+ for P4) are always unique, and all equal to 0.
3.4. Results & discussion: 4-player game
Similar to studying the 2-player and 3-player games, we vary USE(+,−) and USE(−,+) and study the Nash choices of players, as well as the evolution of the ϵ+(game2) fraction. From our previous section, equilibrium strategies found for this game are not unique, thus initial conditions for the computation of equilibrium strategies under varying parameters are important. In order to derive our analysis, we use as initial conditions one of the equilibrium points computed in the subsection above
|
x∗_=((0,0,0,1),(0.2799,0.7201,0),(0.3174,0.3651,0.3175,0),(0.5339,0.4661,0)),
|
(6)
|
relying on the fact that all equilibrium strategies for players engaging in USE with players of opposite status in the baseline scenario are 0.
Figure 6 shows results similar to the 3-player scenario, where HIV− individuals engage with HIV+ individuals as USE(−,+) increases. Choices for P1 become x1∗2+=0, x1∗1−=x1∗2−=x1∗3−≈0.334, thus P1 engages in USE with opposite status HIV players only, beyond a threshold of USE(−,+)≈0.1 (note that P1 here is in G2, which is the most active group). Choices of P2 vary slightly into USE with P1, with x2∗2+≈.0.032, while maintaining positive strategies with P3,P4. Choices of P3 and P4 for USE with P1 do not change from 0 (not shown).
The impact on the infection levels from such a game alone is shown to have an increasing direction. The infected fraction in the population (lower left panel of Figure 6) increases from the baseline value of 0.05% to ϵ+(game2)=0.5082%, most affected by positive values of USE(−,+).
3.3. Compounded effect of multiplayer games on HIV transmission
Recall that by gamei,i∈{1,...,5} we denoted the game where P1 who is HIV+ belongs to Gi. We let pi,i∈{1,...,5} be the size of the age group Gi in the population (which was taken to be 20% for all groups in previous sections) so that ϵgi+(0):=piϵ+(0)=pi⋅0.01, i∈{1,...,5}. We denote by γi the probability of gamei taking place. Given that each game leads to possible unprotected sex among HIV+ and HIV− players, we estimate the infected fraction of individuals in each group, after interactions occur, to be described as follows:
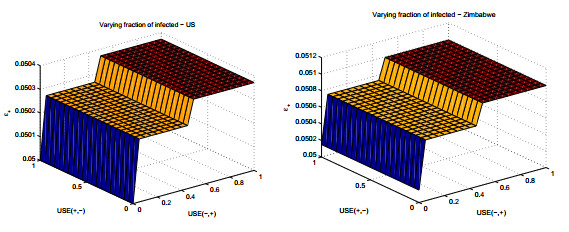
ϵGi+=5∑k=1γkϵGi+(gamek) where for each i,k∈{1,...,5} we have that ϵGi+(gamek) are defined as in Section 3. The overall fraction of infected individuals in the population is obtained by adding the fractions above, after compiling the results for each game: ϵ+=(5∑i=1ϵGi+). For two quick examples, we plot ϵ+ in Figure 7 using p=(0.086,0.173,0.159,0.170,0.412) the estimated size of the age groups according to U.S. census [40,38], and p=(0.21,0.313,0.18,0.12,0.18) using Zimbabwe census data [41], both assuming γk=1,∀k.
As we have stated in previous sections, in both analyses of game1 and game2, we are dependent on initial meaningful states in order to evolve them while varying USE(+,−) and USE(−,+). For consistency of all simulations presented here, we use as initial data for the compounded games the points x_∗ in (4) for the 3player games, and the point x∗_ in (6) for the 4player games. Figure 7 presents our results, where clearly we see that the level of infection will be higher in the Zimbabwe population, as it contains more numerous younger age groups.
4. Prophylactic vaccine in youngest group
In this section we investigate implementing a theoretical prophylactic vaccine within the population, with efficacy μ. Consequently, we adjust some of the baseline utilities as follows: a) the utility for an unvaccinated HIV− individual interacting with an HIV+ individual, i.e., USE(−,+) is increased from 0 to 0.25 due to the assumption that unvaccinated individuals aware of a vaccination program would place higher utility for USE given an increased level of protection through treatment optimism [12]1; b) we define USE(−,+,vacc)=0.5 as the utility for HIV− vaccinated individuals engaging in USE with HIV+; c) we define (1−μ)τ to be the relative reduction in transmission. This will affect the variation of ϵ+(game1) and ϵ+(game2), as we assume P2 in game1 and P2 in game2 are now HIV− and vaccinated.
1This is an assumption only; treatment optimism can in fact increase HIV transmission, as we show in [35].
The population sizes are adjusted to fit p=(0.086,0.173,0.159,0.170,0.412) with pi,i∈{1,...,5} the estimated size of the age group according to U.S. census [40,38] and p=(0.21,0.313,0.18,0.12,0.18) using Zimbabwe census data [41].
We investigate what impact these changes have on HIV transmission if HIV− players in youngest age class are vaccinated. We run the compounded games of Section 3 for both U.S. and Zimbabwe populations assuming that γk=1 for all k∈{1,...,5}. We now have:
|
game 1: P2∈G1isHIV−vaccinated,P3∈G2 isHIV−unvaccinated
|
|
game 2: P2∈G1 isHIV−vaccinated,P3,P4 areHIV−unvaccinated.
|
Games 3, 4, 5 do not involve players in G1, by the rules of our interactions, hence there is no vaccinated HIV− player in these games.
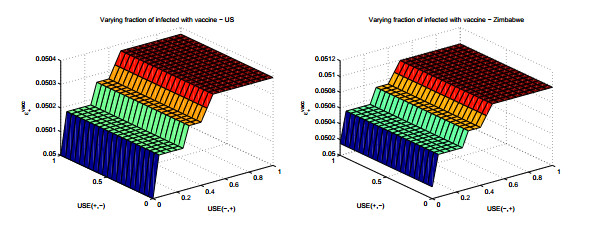
Results presented are dependent on varying the vaccine efficacy USE(+,−)∈[0,1] and USE(−,+)∈[0.25,1]. Figure 8 illustrates the compounded results for the U.S. and Zimbabwe data. We see that the fraction ϵ+ show similar behaviour for both populations, with Zimbabwe at higher overall prevalence. It is also notable that if values of USE(−,+)>0.4, the infection level reaches the same value as in the unvaccinated population. Thus, too much confidence in the efficay of a vaccine leads HIV− unvaccinated players to raise their preference for USE with HIV+ players, thus leading in fact to a nondecrease in HIV infection.
The increase in ϵ+ remains less than 1% as a result of initial HIV prevalence, transmission probability, as well as implementing a one-off game. In cases where the games are repeated, then every repetition brings a small possible increase in the value of ϵ+, which over time leads to potentially more significant increases.
5. Conclusions
The previous sections outlined a one-off casual sexual encounters game for 2, 3 and 4 player variations dependent on status and age. Our most interesting conclusions are that preferences of HIV− players towards unprotected sex have the largest impact on HIV transmission in the population. In games with age group interactions, and assumed treatment introduced for the youngest group, populations with higher proportion of youth see a decrease in HIV prevalence through a possible implementation of a theoretical prophylactic vaccine in these age groups similar to the HPV case.
We showed that generalized Nash equilibria exist and can be computed for these types of games. Moreover, we demonstrated the sensitivity of GN equilibria with respect to varying players' utilities of unprotected sex with partners of opposite HIV status, giving an appreciation for how changes in individual decisions may contribute to an increase in HIV transmission.
As we expanded from 2-player to 3-and 4-player games, we in fact refined the interactions among the individuals in a population, previously regarded as one-on-one positive-negative outcomes. Given that the sizes of groups and activity parameter values matter, we saw that the increase in transmission due to a single instance of a 3-player or a 4-player game is smaller than in a 2-player game. However, the biggest contributing factor in changing HIV transmission is found to be due to the HIV− players' ranking of USE with an HIV+ player. Compounding over the age groups and adjusting for HIV prevalence in the population, we showed that a higher increase in transmission arises in populations with a larger youth composition.
We need to stress again here that the value of this modelling framework depends on the initial conditions of a population under observation, especially in the case of multiplayer groups. Moreover, knowing specific equilibrium strategies within the population of players can lead to sensitivity analyses having these specific equilibrium strategies as initial values. Last but not least, the fact that mathematically a generalized Nash game has in fact sets of equilibria gives strength to this modelling paradigm, in the sense that differing initial conditions in a players' population can give rise to different outcomes, which seems more appropriate to model real life encounter outcomes.
As future work, it would be interesting to include incorporation of ART for HIV+ individuals, which could show how adjusting their utilities may affect transmission. It would also be interesting to conduct a repeated game in order to better see how transmission evolves and how this evolution affects the overall risk assessment and spread of HIV.
Acknowledgments
This work has been funded by the National Science and Engineering Research Council of Canada. The authors gratefully acknowledge this support.
The authors would like to thank the anonymous referees for their excellent suggestions that led to a clearer presentation of our work. It is through their suggestions that we have come to realize the naturally arising shared constraint which pushed our models into the generalized Nash game applications presented here.









 DownLoad:
DownLoad: