1. Introduction
In the United States of America, human papillomavirus (HPV) is the most common sexually transmitted infection (STI) in males and females [8]. Most sexually active males and females will get at least one type of HPV infection at some point in their lives [5]. In the United States, about 79 million are currently infected with HPV and about 14 million people become newly infected each year [8]. There are more than 150 different types of HPV [7]. Health problems related to HPV include genital warts and cancer. Most people infected with genital HPV do not know they are infected and never develop symptoms or health problems from it. Some people find out they have HPV when they get genital warts. Females may find out they have HPV when they get an abnormal Pap test result during cervical cancer screening. Others may only find out once they have developed more serious problems from HPV, such as cancer [5]. Most HPV infections cause no symptoms and are not clinically significant, but persistent infection can lead to disease or cancer.
Mathematical epidemic models have been used to study HPV infections in various populations. For example, Alsaleh and Gummel [1] in a recent paper, used a deterministic model to assess the impact of vaccination on both high-risk and low-risk HPV infection types. Ribassin-Majed and Clemencon [14] used a deterministic mathematical model to assess the impact of vaccination on non-cancer causing HPV (6/11) in French males and females. Lee and Tameru [13] used a deterministic model to assess the impact of HPV on cervical cancer in African American females (AAF). In all these studies, the HPV models have a constant recruitment function for the demographic equations.
In this paper, we use a two-sex HPV model with "fitted" logistic demographics to study the HPV disease dynamics in AAF and African American males (AAM) of 16 years and older. Using US Census Bureau data for AAF and AAM populations, we illustrate that the "fitted" logistic demographic equation captures the African American (AA) population better than the constant recruitment demographic equation. We compute the basic reproduction number, R0 , and perform sensitivity analysis on R0. We obtain that in the AA population R0<1. In addition, we use an extension of the model with vaccination classes to assess the impact of vaccination on the AAF and AAM populations.
The paper is organized as follows: In Section 2, we introduce a demographic equation for AAF (respectively, AAM) and we "fit" it to the US Census Bureau data of AAF (respectively, AAM) of 16 years and older. We introduce, in Section 3, a two-sex African American HPV model. In Section 4, we study disease-free equilibria and compute the basic reproduction number R0. In Section 5, we introduce the model with vaccination. In Section 6, we study disease-free equilibria and compute the basic reproduction number Rv0 for HPV model with vaccination. We summarize our results in Section 7.
2. Demographic equations
In [14], Ribassin-Majed et al. used a HPV model with constant recruitment rate in the demographic equation to study HPV disease dynamics in male and female populations of France. In the absence of the HPV disease, the demographic equation of their model is the following ordinary differential equation:
where N is total population of males or females and for both males and females μ is the constant per capita mortality rate and Λ is the constant recruitment rate. In [13], Lee and Tameru used Model (1) as the demographic equation for their single sex HPV model in African Americans.
In this paper, we use logistic models that are "fitted" to the 2000−2014 US Census Bureau population data of AAF and AAM of 16 years and older (see Tables 1-2) as the demographic equations for AAF and AAM in a HPV model.
Table 1. 2000 to 2014 US Census Bureau AAF population data.
|
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
| AAF population 16 years and older [12,16] |
13,825,055 |
14,041,520 |
14,259,413 |
14,473,927 |
14,707,490 |
14,952,963 |
15,224,330 |
15,486,244 |
15,743,096 |
15,992,822 |
16,176,048 |
16,471,449 |
16,696,303 |
16,918,225 |
17,139,986 |
| AAF total population [12,16] |
18,787,192 |
19,013,351 |
19,229,855 |
19,434,349 |
19,653,829 |
19,882,081 |
20,123,789 |
20,374,894 |
20,626,043 |
20,868,282 |
21,045,595 |
21,320,013 |
21,543,051 |
21,767,521 |
21,988,307 |
Table 2. 2000 to 2014 US Census Bureau AAM population data.
|
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
| AAM population 16 years and older [12,16] |
11,909,507 |
12,124,810 |
12,332,791 |
12,518,252 |
12,756,370 |
12,996,123 |
13,266,163 |
13,517,841 |
13,765,707 |
14,006,594 |
14,181,655 |
14,490,027 |
14,724,637 |
14,950,933 |
15,176,189 |
| AAM total population [12,16] |
17,027,514 |
17,249,678 |
17,454,795 |
17,631,747 |
17,856,753 |
18,079,607 |
18,319,259 |
18,560,639 |
18,803,371 |
19,033,988 |
19,260,298 |
19,487,042 |
19,719,238 |
19,945,997 |
20,169,931 |
From Tables 1 and 2, we note that both male and female populations of African Americans of 16 years and older as well as the total populations exhibit increasing trends from 2000 to 2014. In the next section, we use a logistic differential equation model to "capture" the AA population data of Tables 1 and 2.
2.1. Demographic equation for AAF and AAM
In [3], Brauer and Castillo-Chavez used the logistic equation "fitted" to United States Census Bureau data to model the total United States population. We use the same approach to "fit" the solution of the following logistic equation to the AAF population of 16 years and older (see Table 1) and the AAM population of 16 years and older (see Table 2).
|
dNidt=(ri−μi)Ni(1−NiKi(ri−μi)/ri),t≥0,
|
(2)
|
where index i=f refers to the female and index i=m refers to the male. Ni(t) is the total population of AAF of 16 years and older at time t if i=f, respectively, the total population of AAM of 16 years and older at time t if i=m. The constant μi is the death rate of population, ri is the intrinsic growth rate of population and Ki is the carrying capacity.
N0i is the size of the population at time t=0, where year 2001 in Tables 1 and 2 is t=0. The solutions of (2) are
|
Ni(t)=0andNi(t)=Ki(ri−μi)/ri1+(Ki(ri−μi)/riN0i−1)e−(ri−μi)t.
|
(3)
|
Let
Rdi is the demographic threshold of the population. When the constant intrinsic growth rate, ri, is bigger than the per capita mortality rate of population, μi, then Rdi>1. However, Rdi<1 when ri is less than μi. Consequently, for every N0i>0, when Rdi>1 then the nontrivial solution Ni(t) approaches the "death" adjusted carrying capacity,
and the population persists. However, when Rdi<1 then Ni(t)→0 as t→∞ and the population goes extinct.
2.2. AAF and AAM "fitted" logistic demographic equations
Equation (2) gives the per capita growth rate, dNi/dtNi, for the total AAF population of 16 years and older when i=f and the total AAM population of 16 years and older when i=m. That is, if Ni(t)≠0, then
|
dNi/dtNi=(ri−μi)(1−NiKi(ri−μi)/ri).
|
(4)
|
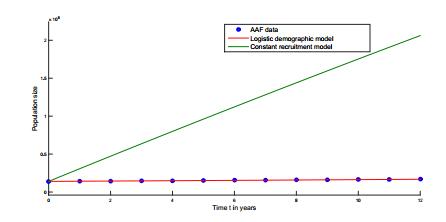
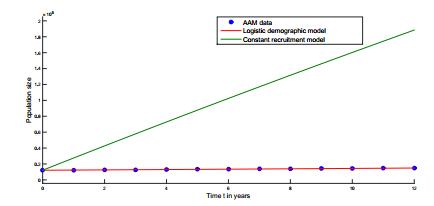
Using the 2002−2014 US Census Bureau data of Table 1 (respectively, Table 2), we estimate the values of dNf/dt (respectively, dNm/dt) by symmetric differences. We then graph the per capita growth rate, Y=dNf/dtNf (respectively, Y=dNm/dtNm) versus the AAF (respectively, AAM) population. Then the line with equation Y=0.021298978−4.02117×10−10Nf (respectively, Y=0.019877926−1.9980893×10−10Nm) "fits" the resulting curve. Therefore, the AAF (respectively, AAM) population of 16 years and older exhibits a logistic behavior (see Figures 1 and 2, respectively).
Fitting the line to the curve gives rf−μf=0.021298978>0 and rf/Kf=4.02117×10−10 (respectively, rm−μm=0.019877926>0 and rm/Km=1.9980893×10−10). So, we estimate the intrinsic growth rate of AAF (respectively, AAM) to be rf=0.028564978 (respectively, rm=0.028104926) and the carrying capacity of AAF (respectively, AAM) is Kf=71,036,484 (respectively, Km=140,659,009). From our estimates of rf and μf we note that Rdf>1 and K∗f=52,967,117 (rounded). Similarly, from our estimates of rm and μm we note that Rdm>1 and K∗m=99,484,673 (rounded).
Using our estimates, we express the nontrivial solution (3) of the logistic growth model for AAF of 16 years and older as
|
Nf(t)=52,967,1171+2.772176873e−0.021298978t,
|
(5)
|
and for AAM of 16 years and older as
|
Nm(t)=99,484,6731+7.205050059e−0.019877926t,
|
(6)
|
where year 2001 is taken as t=0.
The plot of the data of AAF of 16 years or older and solution (5) in Figure 1 show that our "fitted" model captures the AAF data of Table 1. Similarly, the plot of the data of AAM of 16 years or older and solution (6) in Figure 2 show that our "fitted" model captures the AAM data of Table 2.
2.3. AAF and AAM "fitted" logistic equation versus constant recruitment model
When the population in equation (1) consists only of AAF (i=f) or of AAM (i=f) of 16 years and older, then the solution is
|
Ni(t)=Λiμi+(N0i−Λiμi)e−μit.
|
(7)
|
Using the initial condition N0f=14,041,520 [12] (respectively, N0m=12,124,810 [12]), the parameters Λf=16,821,072 (52% of AA population are female [2,13]) and μf=0.007266 [6] (respectively, Λm=15,527,714 (48% of AA population are male [2,13]) and μm=0.008227 [6]), solution (7) becomes
|
Nf(t)=2,315,038,811−2,300,997,291e−0.007266t,
|
(8)
|
and
|
Nm(t)=1,887,409,019−1,875,284,209e−0.008227t.
|
(9)
|
In Figure 1, we compare the "fitted" solution (8) of Model (1), and our "fitted" solution (5) of Model (2), to the US Census Bureau data in Table 1. Figure 1 shows that Model (2), the "fitted" logistic model, captures better the 2000−2014 US Census Bureau data of the AAF population of 16 years and older than Model (1), the constant recruitment demographic equation used in the France study [14] and in the study of Lee and Tameru [13].
Similarly, Figure 2 shows that, as in the female population, the "fitted" solution (9) of Model (1) over estimates the AAM US Census Bureau data while our "fitted" solution (5) of Model (2) captures it.
3. A two-sex African American HPV model
To study the HPV dynamics in male and female African American populations of 16 years and older, we assume that the total AAF population (respectively, total AAM population) of 16 years and older is governed by Model (2) with i=f (respectively, Model (2) with i=m). As in [14], we divide the population into four compartments: Sf= susceptible AAF population, Sm= susceptible AAM population, If= HPV infected AAF population, Im= HPV infected AAM population. It is known that females and males recover from HPV at about the same rate [11]. We now introduce the following mathematical model that uses our "fitted" logistic demographics for the total population.
|
{dSfdt=rfNf(1−NfKf)−σfSfImNf+Nm+δIf−μfSf,dSmdt=rmNm(1−NmKm)−σmSmIfNf+Nm+δIm−μmSm,dIfdt=σfSfImNf+Nm−(δ+μf)If,dImdt=σmSmIfNf+Nm−(δ+μm)Im,
|
(10)
|
where Nf=Sf+If>0, Nm=Sm+Im>0 and the model parameters with their values are listed in Table 3.
Table 3. Table of model parameters.
| Parameter (per day) | Description | Reference |
| μf=0.007266 | Death rate for AAF population | [6] |
| μm=0.008227 | Death rate for AAM population | [6] |
| δ=0.9 | Clearance rate | [11] |
| rf=0.028564978 | Intrinsic growth rate for AAF population | Estimated |
| rm=0.028104926 | Intrinsic growth rate for AAM population | Estimated |
| Kf=71,036,484 | Carrying capacity for AAF population | Estimated |
| Km=140,659,009 | Carrying capacity for AAF population | Estimated |
| σf=0.5 | Infection rate for AAF population | [1] |
| σm=0.4 | Infection rate for AAM population | [1] |
Notice that since
|
Nf(t)=Sf(t)+If(t)andNm(t)=Sm(t)+Im(t),
|
adding the Sf−equation to the If−equation (respectively, adding the Sm−equation to the Im−equation) gives the AAF demographic equation (2) with i=f (respectively, AAM demographic equation (2) with i=m).
Consequently, in Model (10), the total AAF and AAM populations, governed by our "fitted" logistic equations (5) and (6) are bounded. We will study Model (10) with the parameter values listed in Table 3 and with the initial conditions listed in Table 4.
Table 4. Initial conditions for HPV Model (10).
| Sf(0) | = | 8,618,960 |
| Sm(0) | = | 7,119,370 |
| If(0) | = | 5,422,560 |
| Im(0) | = | 5,005,440 |
Notice that in Table 4, Sf(0)+If(0)=Nf(0) of Table 1 (respectively, Sm(0)+Im(0)=Nm(0) of Table 2), where t=0 is year 2001.
3.1. Boundedness of Orbits
In this section, we show that Model (10) is well-posed. In particular, we obtain that all orbits are nonnegative and there is no population explosion in Model (10).
Theorem 3.1. All solutions of Model (10) are nonnegative and bounded.
Proof. Consider the following nonnegative initial conditions Sf(0)=S0f≥0, Sm(0)=S0m≥0, If(0)=I0f≥0 and Im(0)=I0m≥0.
If I0f=0, then from the If−equation of Model (10), we obtain that dIfdt|t=0=σfS0fI0mN0f+N0m≥0. Hence, If(t)≥0 for all t≥0 [15].
Similarly, if I0m=0, then from the Im−equation of Model (10), we obtain that dImdt|t=0=σmS0mI0fN0f+N0m≥0. Hence, Im(t)≥0 for all t≥0 [15].
If S0f=0, then from the Sf−equation of Model (10), we obtain that dSfdt|t=0=rfI0f(1−I0fKf)+δI0f. I0f≤Kf. Hence, Sf(t)≥0 for all t≥0.
Similarly, if S0m=0, then from the Sm−equationn of Model (10), we obtain that dSmdt|t=0=rmI0m(1−I0mKm)+δI0m. I0m≤Km. Hence, Sm(t)≥0 for all t≥0.
Recall that Nf(t) is bounded, Sf(t)+If(t)=Nf(t), Sf(t)≥0 and If(t)≥0. Hence, Sf and If are bounded. Similarly, Sm and Im are bounded.
Let X=[SfSmIfIm] and F(X)=[rfNf(1−NfKf)−σfSfImNf+Nm+δIf−μfSfrmNm(1−NmKm)−σmSmIfNf+Nm+δIm−μmSmσfSfImNf+Nm−(δ+μf)IfσmSmIfNf+Nm−(δ+μm)Im].
Then Model (10) is equivalent to
In AAF population, Rdf>1 implies that for t>0, Nf(t)>0 and limt→∞Nf(t)=K∗f when Nf(0)>0. Similarly, in AAM population, Rdm>1 implies that for t>0, Nm(t)>0 and limt→∞Nm(t)=K∗m when Nm(0)>0. Hence, Nf(t)+Nm(t)>0 in Model (10) and F is C1. Consequently, with our parameters from Table 3 and initial conditions from Table 4, Model (10) has a unique nonnegative solution for t≥0.
4. Disease-free equilibria, stability and basic reproduction number (R0)
Unlike in [14], it is possible for Model (10) to exhibit up to four disease-free equilibrium points (DFEs), where Rdf>1 and Rdm>1.
Since Rdf>1 and Rdm>1, then Model (10) has four DFEs, P00=(0,0,0,0), Pf0=(K∗f,0,0,0), Pm0=(0,K∗m,0,0), and a DFE with both susceptible AAF and AAM with no HPV infected individuals, Pfm=(K∗f,K∗m,0,0).
Since Rdf>1 and Rdm>1, P00 is unstable.
To determine the stability of Pf0, we compute the Jacobian matrix at Pf0.
|
J|Pf0=[μf−rf02μf−rf+δ−σf0rm−μm02μm−rm+δ00−(δ+μf)σf000−(δ+μm)].
|
J|Pf0 has the following four eigenvalues: λ1=μf−rf, λ2=rm−μm, λ3=−(σ+μf) and λ4=−(σ+μm). All model parameters are positive so λ3<0 and λ4<0. Hence, the stability of Pf0 is determined by the sign of μf−rf and rm−μm. Rdm>1 implies rm>μm>0 and λ2>0. Hence, Pf0 is unstable.
Similarly, to determine the stability of Pm0, we compute the Jacobian matrix at Pm0.
|
J|Pm0=[rf−μf0rf+δ00μm−rm−σm2μm−rm+δ00−(δ+μf)000σm−(δ+μm)].
|
J|Pm0 has the following five eigenvalues: λ1=rf−μf, λ2=rm−μm, λ3=−(σ+μf) and λ4=−(σ+μm). Hence, the stability of Pm0 is determined by the sign of rf−μf and rm−μm. Rdf>1 implies rf>μf>0 and λ1>0. Hence, Pm0 is unstable.
To determine the stability of Pfm, we recall that in this case, for N0f>0 and N0m>0, limt→∞Nf(t)=K∗f and limt→∞Nm(t)=K∗m. Consequently, Model (10) reduces to the following "limiting" system:
|
{dIfdt=σf(K∗f−If)ImK∗f+K∗m−(δ+μf)If,dImdt=σm(K∗m−Im)IfK∗f+K∗m−(δ+μm)Im,dSfdt=rfK∗f(1−K∗fKf)−σfSfImK∗f+K∗m+δIf−μfSf,dSmdt=rmK∗m(1−K∗mKm)−σmSmIfK∗f+K∗m+δIm−μmSm.
|
(11)
|
Using the next generation matrix method [17] we obtain the following two matrices
|
F=[σf(K∗f−If)ImK∗f+K∗mσm(K∗m−Im)IfK∗f+K∗m00]
|
|
andV=[(δ+μf)If(δ+μm)Im−rfK∗f(1−K∗fKf)+σfSfImK∗f+K∗m−δIf+μfSf−rmK∗m(1−K∗mKm)+σmSmIfK∗f+K∗m−δIm+μmSm].
|
Then, using the Jacobian matrices of F and V evaluated at the DFE of (11), Qfm=(0,0,K∗f,K∗m), we obtain the following matrices,
|
DF(Qfm)=[F000]andDV(Qfm)=[V0WU],
|
where F=[0σfK∗fK∗f+K∗mσmK∗mK∗f+K∗m0],V=[δ+μf00δ+μm],W=[−δσfK∗fK∗f+K∗mσmK∗mK∗f+K∗m−δ] andU=[μf00μm].
Hence,
|
FV−1=1K∗f+K∗m[0σfK∗fδ+μmσmK∗mδ+μf0].
|
By the next generation matrix method [17], the reproduction number for Model (10), R0, is the spectral radius of the next generation matrix, ρ(FV−1), and
|
R0f=σfK∗f(δ+μf)(K∗f+K∗m)andR0m=σmK∗m(δ+μm)(K∗f+K∗m).
|
R0f (respectively, R0m) is directly proportional to the product of the infection rate of AAF population and the proportion of AAF population at the death-adjusted equilibrium point (respectively, the infection rate of AAM population and the proportion of AAM population at the death-adjusted equilibrium point) and inversely proportional to the sum of clearance rate and death rate for AAF population (respectively, the sum of clearance rate and death rate for AAM population).
When rf>μf and rm>μm, then R0<1 implies the DFE, Pfm, is locally asymptotically stable, whereas R0>1 implies Pfm is unstable [17]. Using the parameter values in Table 3, it is easy to see that R0f=0.1915<1 and R0m=0.2874<1. Hence, R0=0.2346<1. That is, in our Model (10) the DFE Pfm, is locally asymptotically stable.
It is interesting to note that in [13], Lee and Tameru, obtained R0=0.519798<1 with a one sex HPV model under a constant recruitment. Since their model over estimates the AA population, their R0 is bigger than 0.2346. However, both models predict that R0<1 and HPV infection cannot get started in a fully susceptible AA population [13].
To find an effective mitigation strategy that seeks to reduce HPV infection in AA population within the shortest time possible, in the next section, we use sensitivity analysis to study the impact of each model parameter on R0.
4.1. Sensitivity analysis of R0
Sensitivity indices are used to measure the relative change in a state variable when a parameter changes. Typically, the normalized forward sensitivity index of a variable to a parameter is defined as the ratio of the relative change in the variable to the relative change in the parameter. When the variable is a differential function of the parameter, the sensitive index may be alternatively defined using partial derivatives [4,10,18,19].
Definition 4.1([4,10,18,19]). The normalized forward sensitivity index of a variable, u, that depends differentiably on a parameter, q, is defined as:
We use Definition 4.1 to derive the sensitivity indices of the basic reproduction number R0 and we evaluate them using parameter values of Table 3.
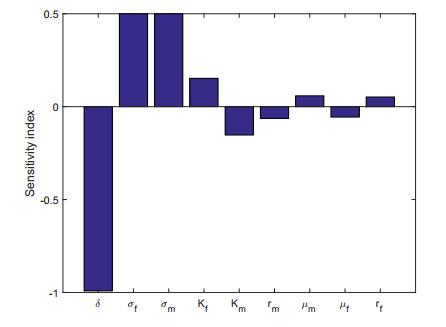
Increasing (respectively, decreasing) the clearance rate, δ, by 1% will decrease (respectively, increase) the value of R0 by about 0.99%. Increasing (respectively, decreasing) the infection rate of the AAF population, σf, by 1% will increase (respectively, decrease) the value of R0 by about 0.5%. Increasing (respectively, decreasing) the infection rate of the AAM population, σm, by 1% will increase (respectively, decrease) the value of R0 by about 0.5%.
4.2. African American male and female HPV model simulations
To illustrate the impact of HPV on AAF and AAM populations of 16 years and older, we simulate Model (10) with the parameter values listed in Table 3 and the initial conditions listed in Table 4.
Table 5. Normalized sensitivity indices and order of importance of R0 to the nine parameters in Table (3).
| Parameter | Sensitivity index of R0 | Order of Importance |
| δ | -0.9915 | 1 |
| σf | 0.5000 | 2 |
| σm | 0.5000 | 3 |
| Kf | 0.1526 | 4 |
| Km | -0.1526 | 5 |
| rm | -0.0631 | 6 |
| μm | 0.0586 | 7 |
| μf | -0.0561 | 8 |
| rf | 0.0520 | 9 |
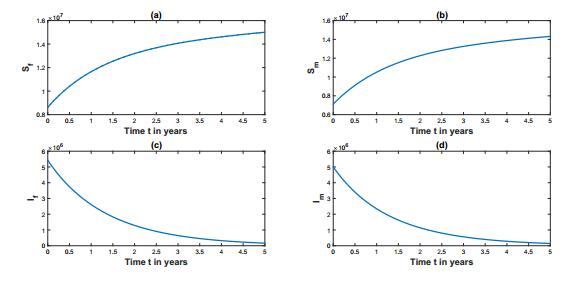
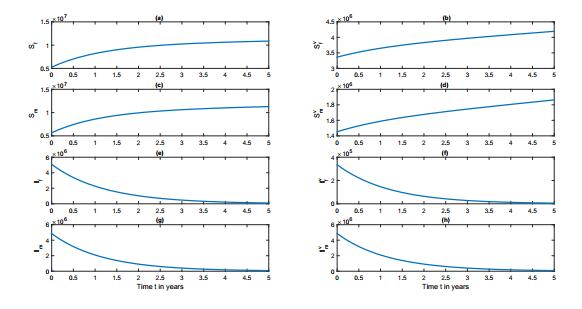
Simulations of our HPV Model (10) are performed using Matlab software, and are illustrated in Figure 4. Figure 4 (a) shows that susceptible population of AAF of 16 years and older, Sf, increases over time. Similarly, Figure 4 (b) shows that susceptible population of AAM of 16 years and older, Sm, increases over time. In the total AA population, R0<1 and as expected, Figure 4 (c) shows that the AAF HPV infected population of 16 years and older, If, decreases monotonically with time and Figure 4 (d) shows that the AAM HPV infected population of 16 years and older, Im, decreases monotonically with time.
To protect against HPV infections, HPV vaccines are available for males and females. Gardasil and Cervarix are two HPV vaccines that have market approval in many countries. Next, we introduce an extension of Model (10) with vaccinated male and female classes. We will use the extended model to study the impact of vaccination on Figure 4.
5. A two-sex African American HPV model with vaccination
To introduce HPV vaccination in AAF and AAM populations of Model (10), we let pf (respectively, pm) denote the proportion of HPV vaccinated females (respectively, males). For both males and females, we let τ denote the success rate of the vaccine. In AA population, τ=90% [14].
As in [14], we divide the AA population into eight compartments. Sf= non vaccinated susceptible AAF population, Svf= vaccinated susceptible AAF population, Sm= non vaccinated susceptible AAM population, Svm= vaccinated susceptible AAM population, If= non vaccinated HPV infected AAF population, Ivf= vaccinated HPV infected AAF population, Im= non vaccinated HPV infected AAM population, Ivm= vaccinated HPV infected AAM population. Then Model (10) with vaccination in both AAF and AAM of 16 years and older becomes the following model.
|
{dSfdt=rf(1−pf)Nf(1−NfKf)−σfSfIm+IvmNf+Nm+δIf−μfSf,dSvfdt=pfrfNf(1−NfKf)−(1−τ)σfSvfIm+IvmNf+Nm+δIvf−μfSvf,dSmdt=rm(1−pm)Nm(1−NmKm)−σmSmIf+IvfNf+Nm+δIm−μmSm,dSvmdt=pmrmNm(1−NmKm)−(1−τ)σmSvmIf+IvfNf+Nm+δIvm−μmSvm,dIfdt=σfSfIm+IvmNf+Nm−(δ+μf)If,dIvfdt=(1−τ)σfSvfIm+IvmNf+Nm−(δ+μf)Ivf,dImdt=σmSmIf+IvfNf+Nm−(δ+μm)Im,dIvmdt=(1−τ)σmSvmIf+IvfNf+Nm−(δ+μm)Ivm,
|
(12)
|
where Nf=Sf+Svf+If+Ivf>0 and Nm=Sm+Svm+Im+Ivm>0 and the model parameters and their values are listed in Table 3. We will study Model (12) with parameter values listed in Table 3 and with the initial conditions listed in Table 6, where pf=39%, pm=20.4% and τ=90%.
Table 6. Initial conditions for HPV Model (12).
| Sf(0) | = | 5,257,566 |
| Svf(0) | = | 3,361,394 |
| Sm(0) | = | 5,667,019 |
| Svm(0) | = | 1,452,351 |
| If(0) | = | 5,086,421 |
| Ivf(0) | = | 336,139 |
| Im(0) | = | 4,860,205 |
| Ivm(0) | = | 145,235 |
Note that in Table 6, Sf(0)+Svf(0)+If(0)+Ivf(0)=Nf(0) of Table 1 (respectively, Sm(0)+Svm(0)+Im(0)+Ivm(0)=Nm(0) of Table 2) where t=0 is year 2001.
Proceeding exactly as in Theorem 3.1, we obtain the following result.
Theorem 5.1. All solutions of Model (12) are nonnegative and bounded.
6. Disease-free equilibrium, stability and basic reproduction number Rv0
Notice that when all vaccinated classes are missing (Svf=Svm=Ivf=Ivm=0) and pf=pm=τ=0, then Model (12) reduces to Model (10).
From Model (12), the demographic equations for the female and male total populations are respectively the following:
|
{dNfdt=rfNf(1−NfKf)−μfNf,dNmdt=rmNm1−NmKm)−μmNm.
|
(13)
|
The equilibrium points of Model (13) are (Nf,Nm)=(0,0), (0,K∗m), (K∗f,0) and (K∗f,K∗m). Since Rdf>1 and Rdm>1, (Nf,Nm)=(0,0), (0,K∗m) and (K∗f,0) are unstable and (K∗f,K∗m) is asymptotically stable.
As in Model (10), to state the "limiting" system of Model (12), we replace Nf by K∗f and Nm by K∗m. Since Nf=Sf+Svf+If+Ivf=K∗f and Nm=Sm+Svm+Im+Ivm=K∗m, the "limiting" system for Model (12) is the following system of equations.
|
{dSfdt=rf(1−pf)K∗f(1−K∗fKf)−σfSfIm+IvmK∗f+K∗m+δIf−μfSf,dSmdt=rm(1−pm)K∗m(1−K∗mKm)−σmSmIf+IvfK∗f+K∗m+δIm−μmSm,dIfdt=σfSfIm+IvmK∗f+K∗m−(δ+μf)If,dIvfdt=(1−τ)σf(K∗f−Sf−If−Ivf)Im+IvmK∗f+K∗m−(δ+μf)Ivf,dImdt=σmSmIf+IvfK∗f+K∗m−(δ+μm)Im,dIvmdt=(1−τ)σm(K∗m−Sm−Im−Ivm)If+IvfK∗f+K∗m−(δ+μm)Ivm,
|
(14)
|
DFE of System (14) is (Sf,Sm,If,Ivf,Im,Ivm)=((1−pf)K∗f,(1−pm)K∗m,0,0,0,0). Using the next generation matrix method [17] we obtain the following two matrices
|
F=[σfSfIm+IvmK∗f+K∗m(1−τ)σf(K∗f−Sf−If−Ivf)Im+IvmK∗f+K∗mσmSmIf+IvfK∗f+K∗m(1−τ)σm(K∗m−Sm−Im−Ivm)If+IvfK∗f+K∗m00]
|
|
andV=[(δ+μf)If(δ+μf)Ivf(δ+μm)Im(δ+μm)Ivm−rf(1−pf)K∗f(1−K∗fKf)+σfSfIm+IvmK∗f+K∗m−δIf+μfSf−rm(1−pm)K∗m(1−K∗mKm)+σmSmIf+IvfK∗f+K∗m−δIm+μmSm].
|
Let Q=(If,Ivf,Im,Ivm,Sf,Sm)=(0,0,0,0,(1−pf)K∗f,(1−pm)K∗m). Evaluating the Jacobian matrices of F and V at Q, we obtain the following matrices
|
DF(Q)=[F000]andDV(Q)=[V0WU],
|
where
|
F=[00σf(1−pf)K∗fK∗f+K∗mσf(1−pf)K∗fK∗f+K∗m00(1−τ)σfpfK∗fK∗f+K∗m(1−τ)σfpfK∗fK∗f+K∗mσm(1−pm)K∗mK∗f+K∗mσm(1−pm)K∗mK∗f+K∗m00(1−τ)σmpmK∗mK∗f+K∗m(1−τ)σmpmK∗mK∗f+K∗m00],
|
|
V=[δ+μf0000δ+μf0000δ+μm0000δ+μm],U=[μf00μm]
|
|
andW=[−δ0σf(1−pf)K∗fK∗f+K∗mσf(1−pf)K∗fK∗f+K∗mσm(1−pm)K∗mK∗f+K∗mσm(1−pm)K∗mK∗f+K∗m−δ0].
|
Hence,
|
FV−1=[00σf(1−pf)K∗f(δ+μm)(K∗f+K∗m)σf(1−pf)K∗f(δ+μm)(K∗f+K∗m)00(1−τ)σfpfK∗f(δ+μm)(K∗f+K∗m)(1−τ)σfpfK∗f(δ+μm)(K∗f+K∗m)σm(1−pm)K∗m(δ+μf)(K∗f+K∗m)σm(1−pm)K∗m(δ+μf)(K∗f+K∗m)00(1−τ)σmpmK∗m(δ+μf)(K∗f+K∗m)(1−τ)σmpmK∗m(δ+μf)(K∗f+K∗m)00].
|
By the next generation matrix method [17], the reproduction number for Model (12), Rv0, is the spectral radius of the next generation matrix, ρ(FV−1), and
|
Rv0=ρ(FV−1)=√Rv0fRv0m,where
|
|
Rv0f=(1−τpf)σfK∗f(δ+μf)(K∗f+K∗m)andRv0m=(1−τpm)σmK∗m(δ+μm)(K∗f+K∗m).
|
Rv0<1 implies DFE ((1−pf)K∗f,pfK∗f,(1−pm)K∗m,pmK∗m,0,0,0,0), is locally asymptotically stable, whereas Rv0>1 implies DFE is unstable [17].
|
Rv0f=(1−τpf)R0fandRv0m=(1−τpm)R0m.
|
Since 0<1−τpf<1 and 0<1−τpm<1, Rv0<R0<1.
Thus, adopting a HPV vaccination program decreases the basic reproduction number, R0, in AA population.
Using the parameter values of Table 3, τ=90% [14], pf=39% [9] and pm=20.4% [9], we obtain that Rv0f=0.1243 and Rv0m=0.2346. Hence, Rv0=0.1708.
In the next section, we use sensitivity analysis to illustrate the impact of model parameters on Rv0.
6.1. Sensitivity analysis of Rv0
We use Definition 4.1 to derive the sensitivity indices of the basic reproduction number Rv0 and we evaluate them using, τ=90%, pf=39%, pm=20.4% and parameter values of Table (3).
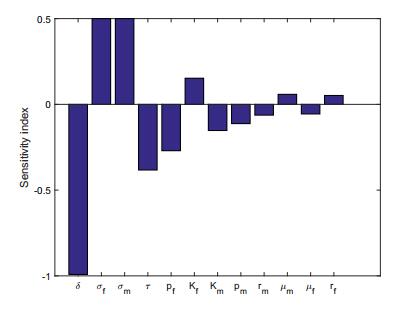
From Table 7 and Figure 5, increasing (respectively, decreasing) the clearance rate, δ, by 1% will decrease (respectively, increase) the value of Rv0 by about 0.99%. Increasing (respectively, decreasing) the infection rate of the AAF population, σf, by 1% will increase (respectively, decrease) the value of Rv0 by about 0.5%. Increasing (respectively, decreasing) the infection rate of the AAM population, σm, by 1% will increase (respectively, decrease) the value of Rv0 by about 0.5%. Increasing (respectively, decreasing) the success rate of vaccination, τ, by 1% will decrease (respectively, increase) the value of Rv0 by about 0.38%. Increasing (respectively, decreasing) the proportion of HPV vaccinated females, pf, by 1% will decrease (respectively, increase) the value of Rv0 by about 0.27%.
Table 7. Normalized sensitivity indices and order of importance of Rv0 to model parameters.
| Parameter | Sensitivity index of Rv0 | Order of Importance |
| δ | -0.9915 | 1 |
| σf | 0.5000 | 2 |
| σm | 0.5000 | 3 |
| τ | -0.3829 | 4 |
| pf | -0.2704 | 5 |
| Kf | 0.1526 | 6 |
| Km | -0.1526 | 7 |
| pm | -0.1124 | 8 |
| rm | -0.0631 | 9 |
| μm | 0.0586 | 10 |
| μf | -0.0561 | 11 |
| rf | 0.0520 | 12 |
6.2. African American male and female HPV model with vaccination simulations
To illustrate the impact of HPV on AAF and AAM populations of 16 years and older when a vaccination program is applied with τ=90%, pf=39% and pm=20.4%, we simulate Model (12) with the parameter values listed in Table 3 and the initial conditions given in Table 6.
Simulations of our HPV Model (12) are performed using Matlab software, and are illustrated in Figure 6. Figures 6 (a-b) show that susceptible population of AAF of 16 years and older, Sf (respectively, vaccinated AAF of 16 years and older Svf), increases over time. Similarly, Figures 6 (c-d) show that susceptible population of AAM of 16 years and older, Sm (respectively, vaccinated AAM of 16 years and older Svm), increases over time. In the total population of African American population, Rv0<1 and as expected, Figures 6 (e-f) show that the AAF HPV infected population of 16 years and older, If (respectively, vaccinated AAF of 16 years and older Ivf), decreases monotonically with time and Figures 6 (g-h) show that the AAM HPV infected population of 16 years and older, Im (respectively, vaccinated AAM of 16 years and older Ivm), decreases monotonically with time.
To study the impact of the presence of the vaccinated class on the results of Figure 4, we simulate Model (12) using initial conditions in Table 8. For these simulations of Model (12), we keep all the parameter values at their current values in Figure 4, where τ=90%, while we vary pf and pm.
Table 8. Initial conditions for HPV model.
 | pf=39%
pm=20.4% | pf=50%
pm=50% | pf=70%
pm=70% |
| Sf(0) | 5,257,566 | 4,309,480 | 2,585,688 |
| Svf(0) | 3,361,394 | 4,309,480 | 6,033,272 |
| Sm(0) | 5,667,019 | 3,559,685 | 2,135,811 |
| Svm(0) | 1,452,351 | 3,559,685 | 4,983,559 |
| If(0) | 5,086,421 | 4,991,612 | 4,819,233 |
| Ivf(0) | 336,139 | 430,948 | 603,327 |
| Im(0) | 4,860,205 | 4,649,472 | 4,507,084 |
| Ivm(0) | 145,235 | 355,969 | 498,356 |
Note that in Figure 6 and Table 6, Sf(0)+Svf(0) (respectively, If(0)+Ivf(0)) is the same as Sf(0) (respectivrly, If(0)) of Table 4 and Figure 4. Similarly, in Figure 6 and Table 6, Sm(0)+Svm(0) (respectively, Im(0)+Ivm(0)) is the same as Sm(0) (respectivrly, Im(0)) of Table 4 and Figure 4.
6.3. Impact of HPV vaccination
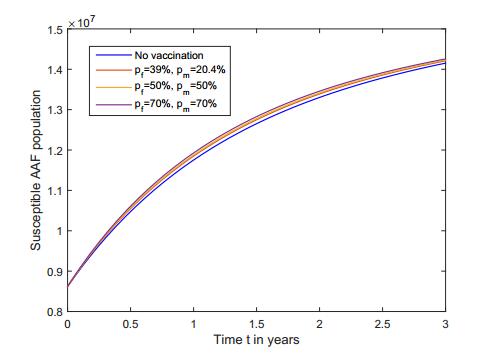
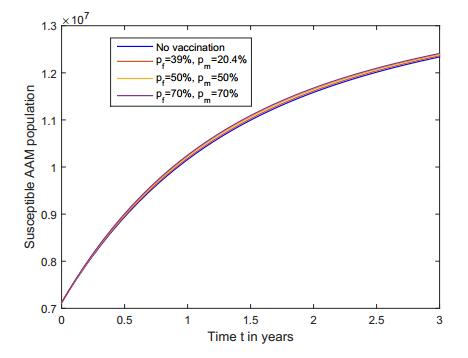
In AA population, Rv0<R0<1. Consequently, with and without vaccination, the susceptible population increases while the infective population decreases over time. In Figures 7 and 8, we illustrate that in both AAF and AAM populations, the increase in the susceptible populations is higher when a vaccination policy is adopted than when the population is not being vaccinated.
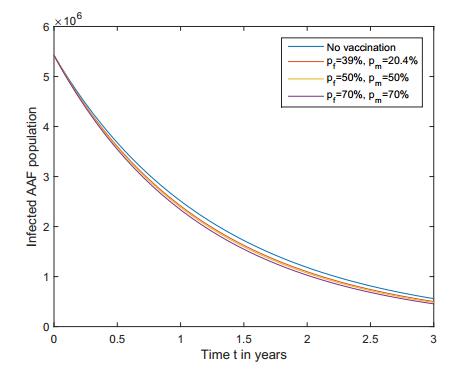
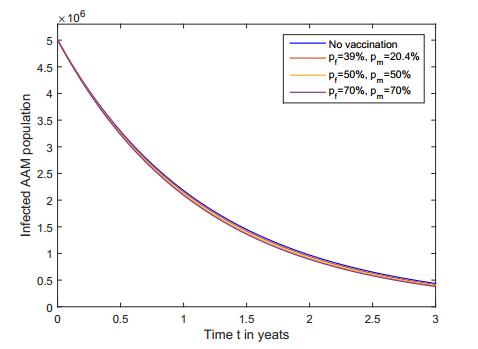
Furthermore, in both AAF and AAM populations, Figures 9 and 10 show that the number of infected populations is lower when the population is under a vaccination policy than when the population is not being vaccinated. Thus, HPV vaccines that provide partial immunity to both AAF and AAM populations of 16 years and older not only lower the number of HPV infectives but increase the number of susceptibles in both female and male populations.
Furthermore, we obtained in Figures 7-10 that the increase (respectively, decrease) in the susceptible (respectively, HPV infective) populations is larger when a bigger proportion of the population is vaccinated.
7. Conclusion
We use a two-sex HPV model with "fitted" logistic demographics to study HPV disease dynamics in AAF and AAM populations of 16 years and older. In agreement with Lee and Tameru [13], we obtained that in AA population, R0<1 and HPV cannot get started in a fully susceptible AA population.
Using sensitivity analysis on R0, we obtained the following results:
● Increasing (respectively, decreasing) the clearance rate, δ, by 1% will decrease (respectively, increase) the value of R0 by about 0.99%.
● Increasing (respectively, decreasing) the infection rate of the AAF population, σf, by 1% will increase (respectively, decrease) the value of R0 by about 0.5%.
● Increasing (respectively, decreasing) the infection rate of the AAM population, σm, by 1% will increase (respectively, decrease) the value of R0 by about 0.5%.
In the second part of the paper, we extended our model to include vaccination classes in both male and female AA populations of 16 years and older. We obtained that in AA population when the vaccination program is implemented, Rv0<1. Using sensitivity analysis on Rv0, we obtained the following results:
● Increasing (respectively, decreasing) the clearance rate, δ, by 1% will decrease (respectively, increase) the value of R0 by about 0.99%.
● Increasing (respectively, decreasing) the infection rate of the AAF population, σf, by 1% will increase (respectively, decrease) the value of R0 by about 0.5%.
● Increasing (respectively, decreasing) the infection rate of the AAM population, σm, by 1% will increase (respectively, decrease) the value of R0 by about 0.5%.
● Increasing (respectively, decreasing) the success rate of vaccination, τ, by 1% will decrease (respectively, increase) the value of R0 by about 0.38%.
● Increasing (respectively, decreasing) the proportion of HPV vaccinated females, pf, by 1% will decrease (respectively, increase) the value of R0 by about 0.27%.
Furthermore, using the extended model with vaccination we obtained the following results:
● Adopting a vaccination policy lowers HPV infections in both AAF and AAM populations.
● Vaccinating a larger proportion of AAF and AAM populations leads to fewer cases of HPV infections in the vaccinated population.
Acknowledgments
This research was partially supported by National Science Foundation under grant DUE-1439758.









 DownLoad:
DownLoad: