1. Introduction
The epidemic problem man-environment in [3] is stated as optimal control problem. The functional consists of three members and the state equations are governed by two PDE: parabolic linear equation and nonlinear first order equation with feedback operator on the boundary.
Thus optimal control problem (P) is to minimize
|
J(u1,u2,w)=∫T0∫ΩF(u2(t,x)dxdt+∫T0∫∂Ωh(w(t,x))dxdt+∫Ωl(u2(T,x))dx
|
(1)
|
over all (u1,u2,w) subject to state system
|
∂u1∂t−Δu1+a11u1=0,in Q=(0,T)×Ω,
|
(2)
|
|
∂u2∂t+a22u2−g(u1)=0,in Q,
|
(3)
|
|
u1(0,x)=u01(x), u2 (0,x)=u02(x) for x∈Ω,
|
(4)
|
|
∂u1∂ν+αu1=K∗u2=∫ΩK(t,x,σ)u2(t,x)dx, (t,σ)∈∑1=(0,T)×Γ1,
|
(5)
|
|
∂u1∂ν=0 in ∑2=(0,T)×Γ2.
|
(6)
|
where Ω is a bounded and open subset of R2 with a sufficiently smooth boundary Γ=Γ1∪Γ2, a11,a22 and α are positive constants, and
|
K(t,x,σ,w)=N∑i=1wi(t,σ)Ki(x,σ) for t∈[0,T], x∈Ω, σ∈Γ1,
|
(7)
|
Ki∈L∞(Ω×Γ1), wi∈L∞((0,T)×Γ1) for i=1,...,N. We set w(t,σ)=(w1(t,σ),...,wN(t,σ)), it is a control function, control on the boundary. We assume F,g,l to be continuous in R, F,g≥0 and h:RN→ˉR=[−∞,+∞] is convex, lower semicontinuous. Moreover we assume that there exists a bounded closed subset M⊂RN such that h(w)=+∞ for w∉M, i.e. we assume that control w∈M. The following particular case is considered as important in the model problem:
where
|
hi(r)={λ/r2if 0<r≤a,+∞otherwise.
|
(9)
|
The following K
|
K(t,x,σ,w)=w(t)K(σ), t∈[0,T], σ∈Γ1,
|
(10)
|
with wi=w, i=1,2,...,N and
where χi is the characteristic function of the interval [xi−ηi,xi+η], xi∈Γ1, i=1,2,...,m, η>0 is also investigated in [3]. The points xi are related to the treatment of the sewage output. In [1] for that problem existence and necessary optimality conditions, as well two gradient type algorithms are derived. In [4] analytical results are given in support of the well posedness of the problem.The essential point in the convergence of gradient algorithm (using the necessary optimality conditions -Pontryagin maximum principle) is that it starts from arbitrary control function and stop when the difference between two computed controls in next two steps is smaller than given ε. However, we do not know whether the calculated sequence of controls converges to optimal control or the values of the cost functional for those controls converge to optimal value. Moreover, we do not know when to stop the proces in order to get near optimal value i.e. whether for calculated controls the cost of the functional is near optimal value (we do not know it a priori). We need sufficient optimal conditions to grasp such an information. In the literature there is not any optimal control theory of sufficient optimality conditions which can be applied to the above control problem. The main reason is that we deal with the state equations having controls on the boundary. In the next section we develop new dual dynamic programming theory to derive verification theorem -sufficient optimality conditions for problem (1)-(5). However the main advantage of this paper is that we also develop sufficient conditions for ε-optimality i.e. we formulate conditions which allow us to assert that for calculated control (e.g. numerically) we know how far we are from optimal value. Just this approximate theory is fundamental for our numerical algorithm. The control w=(w1,...,wN) on the boundary we call admissible boundary control and a solution (u1,u2) corresponding to it we call admissible state. The set of admissible controls and states we denote by Ad.
2. Dual dynamic programming approach for (1)-(6)
The dual approach to dynamic programming was first introduced in [8] and then developed in several papers to different optimal control problems governed by: elliptic, parabolic and wave equations (see e.g. [5], [11], [10], [9]). The essential point in this dual approach is that we do not deal directly with a value function but with some auxiliary function, defined in a dual set, satisfying dual dynamic equation. The auxiliary function allow us to derive sufficient optimality condition for primal value function. The dual approach has some advantages: we do not need any properties of the value function such as smoothness or convexity. However it has also some disadvantages: the auxiliary function must satisfy a kind of generalised transversality conditions which is a little restrictive. The approach we present here was inspired by PhD thesis [7] of the first author where the model of distortion compensation (elliptic system of equations) was investigated. A new challenge in the control problem (1)-(6) is that the problem under consideration has the control on the boundary and with fixed initial conditions. Therefore we need really to construct a new dual dynamic programming type approach for problem (1)-(6). Thus let us start first with the definition of a dual set. Let P⊂R3+3 be an open set of the variables (t,x,p)=(t,x,y0,y), y∈R2, y0≤0, (t,x)∈Q={(s,z); z∈Ω,0<s<T}. Denote by
|
Y={(y0,y)=p;(t,x,p)∈P}.
|
(12)
|
Denote by clP the closure of P and by P1, P2, clY its subsets:
|
P2={(t,x,p);(t,x)∈(0,T)×Γ2},
|
|
clY={(y0,y)=p;(t,x,p)∈clP}.
|
Let u be a vector of pairs coordinates (u1,u2), Δxu=(Δxu1,0), f(t,x,u)= (f1(t,x,u), f2(t,x,u)) where
g(t,x,u,w)=(g1(t,x,u,w),g2(t,x,u,w)) where
|
g1=−αu1+∫ΩK(t,x,σ,w)u2(t,x)dx,
|
(15)
|
Let us introduce an auxiliary function V:clP→R belonging to H2(P) (Sobolev space of functions having second weak derivatives) and satisfying "transversality condition":
|
V(t,x,p)=y0Vy0(t,x,p)+yVy(t,x,p)for(t,x,p)∈clP,
|
(17)
|
where Vy0, Vy are partial derivative of V. Denote by u:clP→R2 a function of six variables (t,x,y0,y). In the sequel we shall assume that
|
u(t,x,p)=−Vy(t,x,p),(t,x,p)∈clP.
|
(18)
|
We shall consider not all admissible controls and corresponding to them admissible states but only those which relate to u. To this effect we introduce for given fixed ξ(⋅)∈(H2(Ω))2 the following set
|
Adu={(u(⋅),w(⋅))∈Ad;existp(t,x)=(y0,y(t,x)),(t,x)∈Q,y(⋅)∈(H2(Q))2,y0≤0,(t,x,p(t,x))∈clP,y(0,x)=ξ(x),u(t,x)=u(t,x,p(t,x)),(t,x)∈clQ}.
|
(19)
|
In fact our optimal control problem we shall study just on the set Adu. We consider condition (17) and function (18) just on the set clP. The function p:Q→R3 we call dual trajectory while u:Q→R2 we call primal trajectory. The function u from (18) builds a relation between dual and primal trajectory. Next define a dual optimal value SD
|
SD=inf(u,w)∈Adu−y0J(u,w).
|
(20)
|
Notice that in spite of that our problem depends on time we cannot perturb it with respect to initial data and time (they are fixed) as it is usually done in classical optimal control theory. This is why a dual dynamic approach to the above problem seems to be the only one possible. Thus let us introduce a dual Hamilton-Jacobi equation in P for our problem:
|
Vt(t,x,p)−ΔxV(t,x,p)+yf(t,x,−Vy(t,x,p))+y0F(−Vy2(t,x,p))=0
|
(21)
|
and dual Hamilton-Jacobi type equation on P1
|
infw∈M{∂V(t,x,p)∂ν+yg(t,x,−Vy(t,r,p),w)−y0h(w)}=0,
|
(22)
|
|
∂V(t,x,p)∂ν=0,for(t,x,p)∈P2,
|
(23)
|
|
−y0Vy0(T,x,p)=−y0l(−Vy2(T,x,p)).
|
(24)
|
We should stress that the notion of dual Hamilton-Jacobi equation appears also in convex optimization (see [2]). However the above dual Hamilton-Jacobi equation is completely different than that in [2]. Our problem is nonconvex and we do not use any tools from convex analysis.
3. Sufficient optimality conditions
The dual approach to dynamic programming described in the former section allow us to formulate and to prove a kind of verification theorem ensuring sufficient optimality conditions for our problem (20). We would like to stress that we are working now in dual space clP and with auxiliary function V defining, by (18) the set Adu. Define the set
|
P={p(t,x)=(y0,y(t,x)),(t,x)∈Q;(t,x,p(t,x))∈clP,y(⋅)∈(H2(Q))2,y(0,x)=ξ(x),exist(u(⋅),w(⋅))∈Adu,u(t,x)=−Vy(t,x,p(t,x)),(t,x)∈Q∪Γ}.
|
Theorem 3.1. Assume that there exists V∈H2(P) satisfying (21)-(24), (17). Let ˉu(t,x,p)=−Vy(t,x,p), (ˉu(⋅),ˉw(⋅))∈Adˉu, (ˉy0,ˉy(t,x))=ˉp(t,x)∈P, ˉu(t,x) =−Vy(t,x,ˉp(t,x)), (t,x)∈Q∪Γ, Γ=Γ1∪Γ2, and
|
Vt(t,x,ˉp(t,x))−ΔxV(t,x,ˉp(t,x))+ˉy(t,x)f(t,x,−Vy(t,x,ˉp(t,x)))+ˉy0F(−Vy2(t,x,p¯(t,x))),
|
(25)
|
|
∂V(t,x,ˉp(t,x))∂ν+ˉy(t,x)g(t,x,−Vy(t,x,ˉp(t,x)),ˉw(t,x))−ˉy0h(ˉw(t,x))=0,
|
(26)
|
|
−y0Vy0(T,x,ˉp(T,x))=−y0l(−Vy2(T,x,ˉp(T,x))),
|
(27)
|
|
∂V(t,x,ˉp(t,x))∂n=0,for(t,x,ˉp(t,x))∈P2.
|
(28)
|
Then
is an optimal pair with respect to all (u(⋅),w(⋅))∈Adˉu i.e.
Proof. We follow the standard way in proofs of verification theorems. Thus take any (u(⋅),w(⋅))∈Adˉu and corresponding to it p(⋅)∈P such that u(t,x)=−Vy(t,x,p(t,x)), (t,x)∈Q∪Γ, t∈[0,T]. From transversality condition (17) we infer that, for (t,x,p)∈P, (remember ΔxVy=(ΔxVy1,0)
|
Vt(t,x,p(t,x))−ΔxV(t,x,p(t,x))=ˉy0(ddtVy0(t,x,p(t,x))−ΔxVy0(t,x,p(t,x)))+y(t,x)(ddtVy(t,x,p(t,x))−ΔxVy(t,x,p(t,x))).
|
(29)
|
From (2)-(5) (see also (13)-(14)) we have
|
ddtVy(t,x,p(t,x))−ΔxVy(t,x,p(t,x))=−f(t,x,−Vy(t,x,p(t,x))).
|
(30)
|
Putting (30) into (29) and applying (21) we get equality
|
y0(ddtVy0(t,x,p(t,x))−ΔxVy0(t,x,p(t,x)))+y0F(−Vy(t,x,,p(t,x))).
|
(31)
|
Following the same way as above but now using equality (25) we come to the equality
|
ˉy0(ddtVy0(t,x,ˉp(t,x))−ΔxVy0(t,x,ˉp(t,x)))+ˉy0F(−Vy(t,x,ˉp(t,x)))=0.
|
(32)
|
Now we consider dual Hamilton-Jacobi type equation on Γ1 i.e. relations (22)-(24). Considering transversality condition at the points belonging to P1 we have
|
∂V(t,x,p(t,x))∂ν=y0∂Vy0(t,x,p(t,x))∂ν+y(t,x)∂Vy(t,x,p(t,x))∂ν.
|
(33)
|
From (2)-(5) (see also (15)-(16)) we have, for the same (u(⋅),w(⋅)) and p(⋅) at P1
|
∂Vy(t,x,p(t,x))∂ν=−g(t,x,−Vy(t,x,p(t,x)),w(t,x)).
|
(34)
|
Putting (34) into (33) and applying (22) we get inequality at P1
|
ˉy0∂Vy0(t,x,p(t,x))∂ν≥y0h(w(t,x))
|
(35)
|
Similarly we get equality at P1
|
ˉy0∂Vy0(t,x,ˉp(t,x))∂ν=−ˉy0h(ˉw(t,x)).
|
(36)
|
Let us integrate over Q equality (31) and equality (32). Next we apply boundary conditions (28), (36) and (35), (36), then we get
|
y0∫ΩVy0(T,x,p(T,x))dx−y0∫ΩVy0(0,x,p(0,x))dx+y0∫T0∫ΩF(−Vy2(t,x,p(t,x)))dxdt+y0∫T0∫∂Ωh(w(t,x))dxdt≤0,ˉy0∫ΩVy0(T,x,ˉp(T,x))dx−ˉy0∫ΩVy0(0,x,ˉp(0,x))dx+ˉy0∫T0∫ΩF(−Vy2(t,x,ˉp(t,x)))dxdt+ˉy0∫T0∫∂Ωh(ˉw(t,x))dxdt≤0.
|
(37)
|
From the above relations, (24), (27) and taking into account that ˉy(0,x)=y(0,x)=ξ(x) we infer that
|
−ˉy0∫T0∫ΩF(−Vy2(t,x,ˉp(t,x)))dxdt−ˉy0∫T0∫0∂Ωh(ˉw(t,x))dxdt−ˉy0∫Ωl(−Vy2(T,x,p(T,x)))dx≤y0∫T0∫ΩF(−Vy2(t,x,p(t,x)))dxdt−y0∫T0∫∂Ωh(w(t,x))dxdt−y0∫Ωl(−Vy2(T,x,p(T,x)))dx.
|
Directly from (37) and (27) we infer
Corollary 1. The dual optimal value can also be defined with the help of Vy0 i.e. we have
|
ˉy0∫ΩVy0(0,x,ˉp(0,x))dx=−ˉy0∫T0∫ΩF(−Vy2(t,x,ˉp(t,x)))dxdt−ˉy0∫T0∫0∂Ωh(ˉw(t,x))dxdt−ˉy0∫Ωl(−Vy2(T,x,ˉp(T,x)))dx.
|
4. Dual feedback control
In optimal control theory all what we want to find is to calculate optimal control and optimal value. However, in practice, a feedback control is more important than a value function. It turns out that the dual dynamic programming approach allows to define a kind of a feedback control. In fact with the help of the dual feedback control we can formulate and prove the verification theorem. Surprisingly, the dual feedback control have better properties than the classical one in spite of that it appears on the boundary. First we define general feedback control on the boundary and then optimal feedback control.
Definition 4.1. A function w=w(t,x,p)=(w1(t,x,p),...,wN(t,x,p)) defined in P1 with values in M, we call dual feedback controls, if, for each p∈clY, there exists any solution u(t,x,p)=(u1(t,x,p),u2(t,x,p)) of the equation
|
∂u∂t−Δu,=f(t,x,u), (t,x)∈Q
|
with the boundary condition
|
∂u1∂ν+αu1=∫ΩN∑i=1wi(t,σ,p)Ki(x,σ)u2(t,x)dx,(t,σ)∈∑1.
|
Next step is to define optimal dual feedback control.
Definition 4.2. Dual feedback controls ˉw(t,x,p) defined in P1 we call optimal dual feedback controls if there exist functions ˉu(t,x,p) corresponding to ˉw(t,x,p) as in the former definition and there exists a function ˉp(⋅)∈P defined in ˉQ such that there exists a pair (ˉu(⋅),ˉw(⋅))∈Adˉu defined by
|
ˉu(t,x)=ˉu(t,x,ˉp(t,x)),(t,x)∈ˉQ,
|
|
ˉw(t,x)=ˉw(t,x,ˉp(t,x)),(t,x)∈∑1
|
with optimal value Sˉu,ˉy0D
Following the same way as in the proof of Theorem 3.1 one can prove the theorem on sufficient optimality conditions for our problem (1)-(5) in terms of optimal dual feedback controls.
Theorem 4.3. Let ˉw(t,x,p), defined in P1, be dual feedback control and let ˉu(t,x,p) be the function corresponding to ˉw as in the Definition 4.1. Assume that there exists in P a H2(P) solution V(t,x,p) to (21)-(24) such that
and that condition (17) in P is satisfied. Let ˉp(⋅)∈P, defined in ˉQ, be such that there exists a pair (ˉu(⋅),ˉw(⋅))∈Adˉu
|
Sˉu,ˉy0D=−ˉy0∫ΩVy0(0,x,ˉp(0,x))dx
|
and that ˉu(t,x)=ˉu(t,x,ˉp(t,x)), (t,x)∈ˉQ, ˉw(t,x)=ˉw(t,x,ˉp(t,x)),(t,x)∈∑1. Then ˉw(t,x,p) defined in P1 is optimal dual feedback control.
5. Sufficient conditions for ε-optimality
The theory presented in the last two subsections being in terms of dual dynamic programming gives us a possibility to find at least formally the optimal value. However in practice it is difficult (or even impossible) to solve equations stated there in exact form. In fact we solve such a system using different approximate (numerical) methods. Therefore what we can get then is eventually approximate optimality. This is why in this section we present dual dynamic approach to sufficient conditions for approximate (ε-optimality) optimality. Just dual ε-optimality conditions are base to construct computational method for approximate optimality. Let us recall that for fixed ˉy0 and ˉu the dual optimal value is defined as
|
Sˉu,ˉy0D=inf(w,u)∈Adˉu−y0∫T0F(−Vy2(t,x,p(t,x)))dx
|
|
−y0∫T0∫∂Ωh(w(t,x)dxdt−y0∫Ωl(−Vy2(T,x,p(T,x)))dx.
|
Dual ε-optimal value for problem (1)-(5) we call each value Su,ˉy0εεD satisfying inequality
|
Sˉu,ˉy0D≤Su,ˉy0εεD≤Sˉu,ˉy0D−4εˉy0ε.
|
(38)
|
Let us fix m>0. As for ε-optimal value we use in general inequality instead of equality, it suggests that expressions allowing to derive Theorem 3.1 should satisfy also suitable inequalities. Thus we shall use the following system of inequalities for auxiliary function ˜V: dual Hamilton-Jacobi inequality
|
εˉy0ε≤˜Vt(t,x,p)−Δx˜V(t,x,p)+yf(t,x,−˜Vy(t,x,p))+y0F(−˜Vy2(t,x,p))≤0
|
(39)
|
and dual Hamilton-Jacobi type inequality on P1:
|
εˉy0ε≤infw∈M{∂˜V(t,x,p)∂ν+yg(t,x,−˜Vy(t,x,p),w)−y0h(w)}≤0,
|
(40)
|
|
∂˜V(t,x,p)∂ν=0,for(t,r,p)∈P2,
|
(41)
|
|
−y0˜Vy0(T,x,p)=−y0l(−˜Vy2(T,x,p)).
|
(42)
|
˜Vy satisfies instead of boundary conditions of type (5)-(6) the following inequality in P1(each coordinate):
|
0≥∂˜Vy(t,x,p)∂ν+g(t,x,−˜Vy(t,x,p),w)≥εmˉy0ε.
|
(43)
|
We want to apply our theory to numerical solutions of (2)-(6), therefore instead of system of equations we shall deal with systems of inequalities:
|
0≤∂u∂t−(Δu1,0)−f(t,x,u)≤−εmˉy0ε
|
(44)
|
satisfying the boundary condition
|
0≥−∂u∂ν+g(t,x,u,w(t,x))≥εmˉy0ε,
|
(45)
|
Thus in this section by the set of admissible controls and states i.e. satisfying (44)-(45) we denote Adε.
6. ε-optimality
Now we are ready to describe the concept of ε-optimal pair, to formulate and to prove sufficient ε-optimality for problem (1)-(6) i.e. ε-version of verification theorem. Assume that there exists ˜V satisfying (17) and (39)-(43). Then we define similarly as in section 2
|
uε(t,x,p)=−˜Vy(t,x,p),(t,x,p)∈clP.
|
(46)
|
For ˉy0ε and uε we define similarly as in section 2 Adu
|
Aduε={(u(⋅),w(⋅))∈Adε;existp(t,x)=(y0,y(t,x)),(t,x)∈Q,y(⋅)∈(H2(Q))2,y0≤0,(t,x,p(t,x))∈clP,y(0,x)=ξ(x),u(t,x)=uε(t,x,p(t,x)),(t,x)∈clQ}
|
and Pε
|
Pε={p(t,x)=(ˉy0ε,y(t,x)),(t,x)∈Q;(t,x,p(t,x))∈clP,y(⋅)∈(H2(Q))2,sup(t,x)∈Q|y(t,x)|R2≤m, y>0, exist(u(⋅),w(⋅))∈Aduε,u(t,x)=−˜Vy(t,x,p(t,x)),(t,x)∈Q∪Γ}.
|
Now we are ready to define notions of ε-optimal dual feedback control ˉwε(t,x,p) and of ε-optimal pair (ˉuε(⋅),ˉwε(⋅)).
Definition 6.1. Dual feedback control ˉwε(t,x,p) we call ε-optimal dual feedback control if there exist a function ˉuε(t,x,p) in P, accordingly to Definition 4.1 and a function ˉpε(⋅)∈Pε defined in ˉQ, such that the pair defined by
|
ˉuε(t,x)=ˉuε(t,x,ˉpε(t,x)),(t,x)∈ˉQ,ˉwε(t,x)=ˉwε(t,x,ˉpε(t,x)),(t,x)∈ˉQ
|
(47)
|
belongs to Adˉuε and that this pair defines ε-optimal value
|
Sˉuεˉy0εεD=−ˉy0ε∫Ω˜Vy0(0,x,ˉpε(0,x))dx.
|
(48)
|
Definition 6.2. For given ˜V∈H2(P) satisfying (17) and (39)-(43) let ˉuε(t,x,p) in P be defined by (46). Let ˉpε(⋅)∈Pε be defined in ˉQ and let ˉuε be defined by (47). Let ˉwε(⋅) be any admissible control such that (ˉuε(⋅),ˉwε(⋅))∈Adˉuε. The pair (ˉuε(⋅),ˉwε(⋅)) we call ε-optimal pair with respect to all pairs (u(⋅),w(⋅))∈Adˉuε if
|
−ˉy0ε∫T0∫ΩF(−Vy2(t,x,ˉpε(t,x)))dx−ˉy0ε∫T0∫∂Ωh(ˉwε(t,x))dxdt−ˉy0ε∫Ωl(−Vy2(T,x,ˉpε(T,x)))dx≤−ˉy0ε∫T0∫ΩF(−,Vy2(t,x,p(t,x)))dx−ˉy0ε∫T0∫∂Ωh(w(t,x))dtdx−ˉy0ε∫Ωl(−Vy2(T,x,p(t,x)))dx−4εˉy0ε.
|
Having all the above notions we can formulate the verification theorem for ε-optimality.
Theorem 6.3. Assume that there exists ˜V∈H2(P) satisfying (17) and (39)-(43). Take ˉpε(⋅)∈Pε and (ˉuε(⋅),ˉwε(⋅))∈Adˉuε such that ˉuε(t,x)=−˜Vy(t,x,ˉpε(t,x)), (t,x)∈ˉQ. Moreover, assume that the trio (ˉuε(⋅),ˉwε(⋅),ˉpε(⋅)) satisfies
|
ddt˜Vy(t,x,ˉpε(t,x))−Δx˜Vy(t,x,ˉpε(t,x))+f(t,x,−˜Vy(t,x,ˉpε(t,x)))≥ˉy0εεm, (t,x)∈Q,
|
(49)
|
|
−εmˉy0ε≥˜Vt(t,x,ˉpε(t,x))−Δx˜V(t,x,ˉpε(t,x))+ˉyε(t,x)(f(t,x,−˜Vy(t,x,ˉpε(t,x))+ˉy0εF(−˜Vy2(t,x,ˉpε(t,x,))),,
|
|
∂˜V(t,x,ˉpε(t,x))∂ν+ˉyε(t,x)g(t,x,−˜Vy(t,x,ˉpε(t,x)),ˉwε(t,x))−ˉy0εh(ˉwε(t,x))≤−εmˉy0ε,
|
(50)
|
|
−ˉy0ε˜Vy0(T,x,ˉpε(t,x))=−ˉy0εl(−˜Vy2(T,x,ˉpε(T,x))),∂˜V(t,x,ˉpε(t,x))∂ν=0,for(t,x,p¯ε(t,x))∈P2.
|
(51)
|
Then the pair (ˉuε(⋅),ˉwε(⋅)) is an ε-optimal with respect to all pairs (u(⋅),w(⋅))∈Adˉuε
Proof. Take any (u(⋅),w(⋅))∈Adˉuε and p(⋅)∈Pε such that u(t,x)=−˜Vy(t,x,p(t,x)), (t,x)∈Q. We follow the same way as in the proof of Theorem 3.1, i.e. from (17) we have, for (t,x,p)∈P,
|
˜Vt(t,x,p(t,x))−Δx˜V(t,x,p(t,x))=ˉy0ε(ddt˜Vy0(t,x,p(t,x))−Δx˜Vy0(t,x,p(t,x)))+y(t,x)(ddt˜Vy(t,x,p(t,x))−Δx˜Vy(t,x,p(t,x))).
|
Similarly, we have by (44)
|
−ddt˜Vy(t,x,p(t,x))+Δx˜Vy(t,x,p(t,x))−f(t,x,−˜Vy(t,x,p(t,x)))≥0
|
and then applying (39) (having in mind that y>0) we get inequality
|
ˉy0ε(ddt˜Vy0(t,x,p(t,x))−Δx˜Vy0(t,x,p(t,x)))+ˉy0εF(−˜V(t,x,,p(t,x)))≥εˉy0ε
|
(52)
|
and using inequality (25) we come to the inequality
|
−εˉy0ε≥¯yε0(ddt˜Vy0(t,x,ˉpε(t,x))−Δx˜Vy0(t,x,ˉpε(t,x)))+ˉy0εF(−˜V(t,x,ˉpε(t,x))).
|
(53)
|
Considering transversality condition at the points belonging to Γ we have
|
∂˜V(t,x,p(t,x))∂ν=ˉy0∂˜Vy0(t,x,p(t,x))∂ν+y(t,r)∂˜Vy(t,x,p(t,x))∂ν.
|
(54)
|
From (43) we have, for the same (u(⋅),w(⋅)) and p(⋅), at P1
|
~∂Vy0(t,x,p(t,x))∂ν+g(t,x,−~Vy(t,x,p(t,x),w(t,x)))≤0.
|
Hence we get inequality at P1
|
εˉy0ε≤ˉy0ε∂,˜Vy0(t,x,,p(t,x))∂ν+ˉy0εh(w(t,x)).
|
(55)
|
Similarly, using (50) we get inequality at P1
|
ˉy0ε∂,˜Vy0(t,x,,ˉpε(t,x))∂ν+ˉy0εh(ˉwε(t,x))≤−εˉy0ε.
|
(56)
|
Let us integrate over Q, inequality (52) and (53). Next we apply boundary conditions (55), (56), respectively, and then we get
|
ˉy0ε∫Ω˜Vy0(T,x,p(T,x))dx−ˉy0ε∫Ω˜Vy0(0,x,p(0,x))dxˉy0ε∫T0∫ΩF(−~Vy2(t,x,,p(t,x)))dx+ˉy0ε∫T0∫∂Ωh(,w(t,x))dtdx≥2εˉy0ε,
|
|
¯yε0∫Ω˜Vy0(T,x,ˉpε(T,x))dx−ˉy0ε∫Ω˜Vy0(0,x,ˉpε(0,x))dx+ˉy0ε∫T0∫ΩF(−~Vy2(t,x,ˉpε(t,x)))dx+ˉy0ε∫T0∫∂Ωh(ˉwε(t,x))dtdx≤−2εˉy0ε.
|
From the above relations we infer that
|
−ˉy0ε∫T0∫ΩF(ˉu2ε(t,x))dx−ˉy0ε∫T0∫∂Ωh(ˉwε(t,x))dtdx−ˉy0ε∫Ωl(ˉu2ε(T,x))≤−ˉy0ε∫T0∫ΩF(−~Vy2(t,x,p(t,x)))dx−ˉy0ε∫T0∫∂Ωh(w(t,x))dtdx−ˉy0ε∫Ωl(u2(T,x)dx−4εˉy0ε.
|
This is just the assertion of the theorem.
6.1. Computational algorithm
The sufficient conditions formulated for ε-value function allows us to build numerical approach to calculate suboptimal pair (ˉuε(⋅),ˉwε(⋅)). The algorithm, we present below, ensures that we find in finite number of steps suboptimal pair.
Algorithm:
1. Fix m>0, ε>0 and calculate auxiliary function ˜V from (39)-(43).
2. Form Aduε as a finite family of N pairs (u(⋅),w(⋅)):
a) Define controls wn in Γ1, n=1,…,N.
b) To calculate un,n=1,…,N, solve inequalities (44)-(45).
3. Find minimal value of J(un,wn), n=1,…,N and corresponding to it pair denote by (ˆu(⋅),ˆw(⋅)).
4. Assume ˉy0ε=−1 and determine ˆy(⋅) from the relation
|
ˆu(t,x)=−˜Vy(t,x,−1,ˆy(t,x)).
|
(57)
|
5. For ˜V and (ˆu(⋅),ˆw(⋅),ˆy(⋅)) check the inequalities (53)-(56)
a) If ˜V and (ˆu(⋅),ˆw(⋅),ˆy(⋅)) satisfy (53)-(56)
then (ˆu(⋅),ˆw(⋅)) is an ε-optimal pair and J(ˆu,ˆw) is an ε-optimal value.
b) If ˜V and (ˆu(⋅),ˆw(⋅),ˆy(⋅)) do not satisfy (53)-(56)
then go to 2.
6.2. Numerical calculations
Numerical experiments we do for the same data as in [1] i.e. Ω=(0,1)×(0,1), T=1, β=50, γ=2, Γ1 is one of the side of Ω corresponding to the seashore. It is assumed that control w is only time dependent, one dimensional and then K(x,σ)=w(t)K0(x,σ), where K0(x,σ)=∑mi=1aiχi(σ)˜χi(x), with χi the characteristic function of the interval [xi,xi+1]. We denote by ˜χi the characteristic function of the rectangular subdomain Ωi=[xi,xi+1]×[0,1]⊂Ω where the knots xi belong to Γ1. The constants ai are weights assigned to the subdomains Ωi. For g it is chosen expression βu11+γu1. The number m=4, the knots are equidistant and ai=0.1. The initial conditions u1≠0 on Ωs=[0.3,0.7], u1=0 on Ω∖Ωs, u2=0 on Ω. For the cost functional it is considered F=0, l(u)=u and h(w)=w−2. Control w has values in [1,2]. In order to make calculations we apply FreeFem++-cs 14.3 package from the site http://freefem-cs.software.informer.com/14.3/ and we implement in this application the steps from the above algorithm. We divided time interval [0,1] on 10 equal intervals and consider differences instead of derivative in time. We choose N=500. Next we choose randomly in each step of time controls w from [1,2]. We included to the set of admissible controls as one of the control that which is considered in [1] as optimal control. Next we calculated corresponding u1,u2 and the values of J(u,w). Then we found the minimal value among those of J. We repeated these procedure 5 times and chosen minimal value from those five former minimal values and wrote down corresponding ˆu,ˆw. These are at t=0.0,0.1,0.2,...,0.9,1,
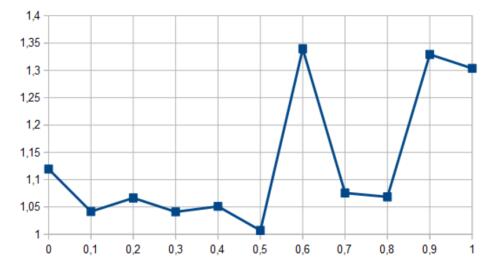
ˆw=1.11941,1.04171,1.06656,1.04117,1.05112,1.00715,1.33937,1.07568,1.06864,1.32913,1.30369 and the graph of it is:
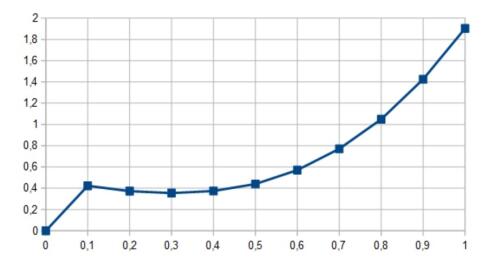
ˆu1(t)=∫Ωˆu1(t,x)dx=0,0.422815,0.372519,0.354227,0.374098,0.439481,0.57045,0.770489,1.04842,1.42482,1.90287
the graph of it is:
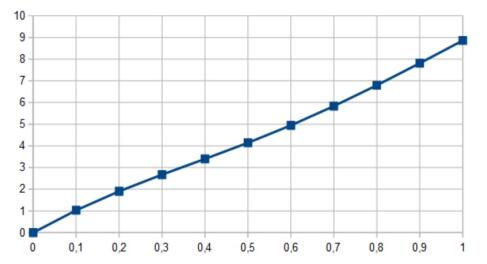
ˆu2(t)=∫Ω2(t,x)dx=0,1.02899,1.90447,2.6737,3.40012,4.1412,4.94705,5.83374,6.79449,7.81148,8.8582
the graph of it is:
The ε-value of the functional J(ˆu,ˆw)=8.92283. Next we follow the steps 4. and 5. from the former subsection. It turn out that for ε=0.003 the pair (ˆu,ˆw) is ε-optimal. It differs from [1], the value of our functional is smaller (in [1] it equals 12.38386) and we found different control ^w.
Acknowledgments
The paper was inspired by the lecture given by V. Capasso during the conference Micro and Macro Systems in Life Sciences in Bedlewo 2015.









 DownLoad:
DownLoad: