1. Introduction
The potential negative impacts associated with the use of fossil fuel plants include, but are not limited to, their adverse environmental effects, impacts on human health and well-being, and economic factors that add to end user costs. To further the US EPA’s effort to reduce CO2 emissions from existing power plants by 30% by 2030 [1], distributed generation (DG) through solar photovoltaic systems is a viable option to mitigate the negative impacts of centralized fossil fuel consuming power plants. Distributed generation (DG)refers to a variety of small, modular power-generating technologies that can be combined with load management and energy storage systems to improve the quality and reliability of our electricity supply [2].
A number of research studies have been conducted by scholars in both Europe and North America to examine different aspects of the problem of integrating increasing PV capacity into existing electricity markets. For example, Walla et al. [3] discussed how to determine thehosting capacity for a large PV system and suggested ways to improve this capacity. Their study considered three different demographic areas, rural, city and suburban, in Sweden and their paperprovides a clear explanation of how to increase the hosting capacity when power is low by looking at the factors that can influence hosting capacity within the design of the PVsystem, namely increasing the tap changer settings, inverter curtailment, and reactive power control. Understanding exactly how the hosting capacity functions are a crucial step when planning the design and implementation of a large number of solar separate installations, especially in the context of the large capacity project that is the subject of our study.
Jo and Otanicar[4] developed a method for estimating the geographic distribution of the available roof surface area for a county wide application of photovoltaics that integrated building and population density information into a geographic information system (GIS). They took into account the effect of shade by visually inspecting satellite digital imagery for average building typologies to quantify the rooftop area available for PV installationsin the city of Chandler, Arizona.
Leitelt [5] took an alternative approach for a study set in Chapel Hill, North Carolina, using Light Detention and Ranging (LiDAR) to locate possible locations for solar panels throughout the town. A solar map was createdto help educate the public on the possible implementation and the benefits installing solar panels could bring for their town. Solar mapping has become a critical tool for those seeking to encourage the expansion of renewable energysources and is also a major asset for communities considering the creation of a solar PV program. Leiteltprovidesexamples of how solar mapping has already inspired cities to implement solar systems and evaluated the solar suitability for Chapel Hill by assessingPV system costs, installation costs and thepayback period. He noted that this type of solarmap can serve as a useful informational tool to help homeowners and businesses gain an understanding of the suitability of their specific property before they install a solar array.
Sauter and Watson [6] pointed out the importance of social acceptance regarding renewable energy projects. Compared to large-scale infrastructure facilities, modular renewable energy technologies are more personal, requiring “active” social acceptance. In comparison to coal and wind power production, individual homeowners perceive solar photovoltaic technology as being more intrusive. This may be because individual homeowners are directly impacted throughout the process of the agreement, construction, and lifetime of the system, depending on the type of contract agreed upon. Social acceptance is not an initial step of the implementation process but rather a critical element that should be considered throughout every phase of the project. As funding is often the largest barrier for solar PV, it becomes pertinent to offer incentives that prompt consumers to consider incorporating the proposed technology. Further research is required to investigate new approaches to incentivizing the economic benefits to increase “active” social acceptance.
Although many researchers have assessed the feasibility and impact of increasing solar PV system capacity, none have suggested a comprehensive method that can be used to examine the suitability of rooftop solar PV installs based upon the actual solar resource potential of specific rooftops, and hence their energy generation potential. There is therefore a need for a way to evaluate the suitability of implementing a large scale DG system based on rooftop solar PV systems. Here we describe a study that conducted a detailed analysis of rooftops in Normal, a town with a population of just over 52, 000 people located in Central Illinois, to determine those that are best suited for DG solar PV applicationsand. quantify their energy generation potential. This paper focusesspecifically on discovering the solar irradiance potential by utilizing the dynamic capabilities of Geographic Information Systems (GIS) which can help effectively and efficiently design a distributed generation plan. In addition, we integrate the GIS analysis outputs into a photovoltaic performance model to precisely estimate the energy generation potential of the rooftop solar PV systems in the case study area.
2. Methodology
2.1. LiDAR Data Processing
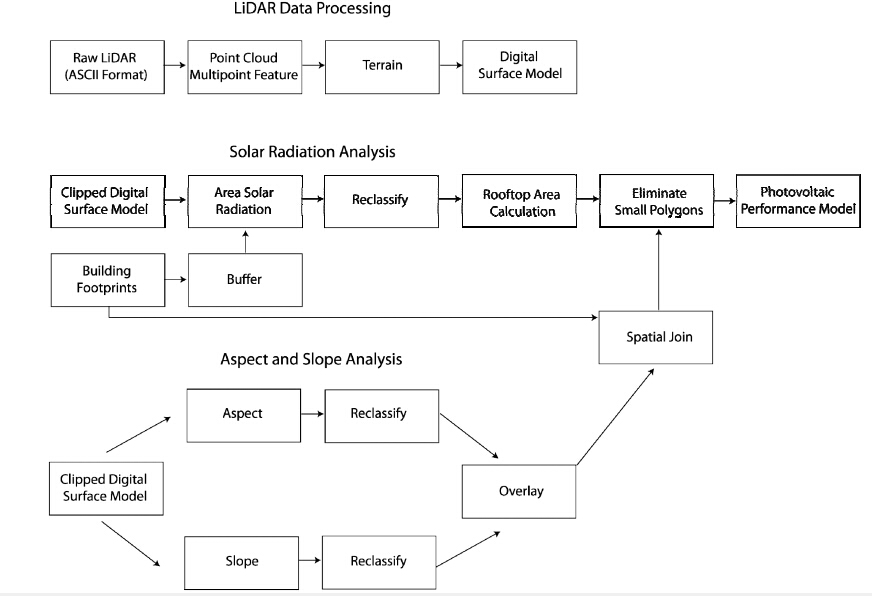
Raw LiDAR (Light Detection and Ranging) data files in ASCII (.xyzi) format covering the Town of Normal in Central Illinois were acquired from the McLean County Regional Planning Commission. The LiDAR datasets were acquired by the county from an outside contractor to meet the requirements of several local government projects. Since rooftop characteristics as well as potential shading by other features such as trees were of most importance for the current study, all LiDAR data included 1st return signals. 81 total data tiles were required to cover the extent of the entire town. First, each LiDAR data tile was converted from the native ACSII format into a point cloud (ESRI geodatabase multipoint feature) for visual inspection, with an average point spacing of .277 meters. Next, LiDAR processing tools in the GIS software were used to calculate the average point spacing between points to determine an ideal spatial resolution for interpolation and conversion to raster format. The multipoint features for each grid were then converted to an ESRI Terrain dataset (e.g., TIN) and then interpolated, one at a time, to create raster grids of continuous elevation surfaces (e.g., digital surface model) at a spatial resolution of 0.277 meters, equivalent to high resolution aerial imagery. Hillshade (shaded relief) maps were then created for each digital surface model as a visual inspection to ensure that each grid tile was pre-processed correctly prior to further processing and analysis (Figure 1). Following conversion of each LiDAR tile to a digital surface model, all 81 grids were merged to create one seamless raster grid of the entire study area. Finally, the seamless digital surface model was then clipped to building footprints in the town, also acquired from the McLean County Regional Planning Commission, in order to restrict all further analysis to building rooftops and to minimize processing time.
2.2. Solar Radiation Analysis
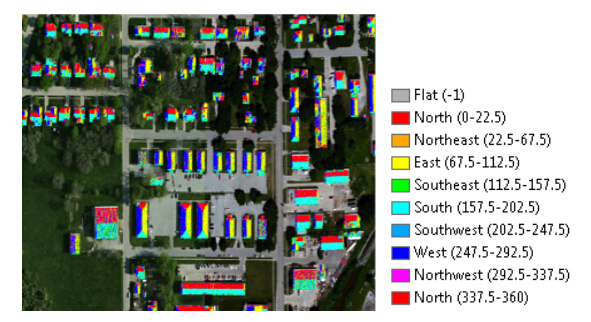
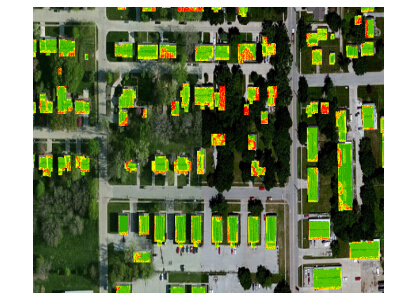
Next, solar radiation was calculated to estimate the overall potential for rooftop illumination based on proximity to features such as trees or other buildings. First, to identify all possible sources of rooftop shading, a 150-foot buffer was created around the building footprint layer and was used to clip the original digital surface model created from the LiDAR point cloud. The clipping operation reduced the size of the raster for the Area Solar Radiation tool in ArcGIS (version 10.2), which is computationally intensive. Next, the Area Solar Radiation tool was run on the clipped raster, which estimates overall solar radiation for each pixel in a raster grid based on geographic location as well as topographic and landscape features in the raster surface. A benefit of using the 1st return LiDAR dataset in the analysis was that not only could topography be accounted in the solar estimation, but also the influence of shading from neighboring buildings and tree cover for each rooftop. The resulting solar radiation layer was then clipped to the exact building footprint (e.g., to eliminate the 150-foot buffer used to account for shading from neighboring buildings and tree cover) and reclassified into one of three values: high potential, primarily consisting of south facing sloping roofs ranging from 45,001-56, 529 Wh/m2/year, medium potential, which mainlycomprised flat roofs that ranged from 29,501-45, 000 Wh/m2 and low potential, which contained all of the shaded roofs as well as the north facing roofs ranging from 0-29,500 Wh/m2 (Figure 2). Each rooftop was then converted to a polygon so the total area for moderate and good rooftops could be calculated. The eliminate tool was run to remove any area less than 8.76 square meters, which was assumed to be the minimum area threshold to be suitable for a PV system installation.
2.3. Aspect and Slope Analysis
As a way to contextualize results from the solar radiation analysis, slope and aspect were also calculated for each building rooftop. The purpose of the aspect and slope analysis was to provide additional characteristics of each building rooftop that could be merged with the solar radiation analysis. To identify the south-facing rooftops that would provide the best exposure to solar radiation, the Aspect tool in GIS was applied to the clipped digital surface model. The resulting map layer was then reclassified into a binary classification: 1) values of the output consisting of sloping roofs that face south and 2) sloping roofs that face another direction (east, west or north) (Figure 3). In essence, this step identified rooftops that would receive maximum solar radiation over the course of the year based on geographic orientation only. Next, a slope layer was calculated to identify flat roofs, with the resulting slope raster also classified into a binary classification: 1) flat (0% slope) and 2) sloping (greater than 0%) (Figure 4). All rooftops that were 1) flat or 2) south facing were then combined via an overlay operation into a new raster grid for visualization on a resulting map for visual comparison to the solar radiation analysis results.
2.4. Merging Solar Radiation Analysis with Aspect and Slope
The resulting combined aspect and slope layer were spatially joined to the building footprint results from the solar radiation analysis and summarized to create an attribute table join. This join makes it possible to search and categorize the different percentage system offset sizes, and to determine how much area on each building has solar potential and the overall slope and orientation of that area. Figure 5 shows anexample of the process of transforming the solar radiation results raster to identify the optimal solar radiation area. A summary of the all steps in the GIS analysis is provided in Figure 6.
2.5. Photovoltaic Performance Model
Following the GIS analysis, we utilized a photovoltaic performance model to estimate the electrical production based upon the geographical potential of rooftop PV systems, taking into account the available area, pitch, slope, and orientation.
The GIS results from the first section were incorporated into the energy modeling tool, System Advisor Model (SAM), to assess the annual electrical energy production potential. SAM is based on an hourly simulation engine that interacts with performance and finance models to calculate the projected energy output, energy costs, and cash flows [7]. Climate data from ground monitoring stations and NASA’s global satellite/analysis data, including temperature, humidity, wind, and solar radiation, are utilized in this simulation to estimate the output that would be expected of PV systems in Normal. Typically, PV systems can range from 8 to 18% efficiency depending on the module type, which could be mono-crystalline silicon, poly-crystalline silicon, or thin film (amorphous) silicon PV systems [8].
After evaluating a number of different PV modules available commercially, the Kyocera Solar KD 315GX-LPB with a maximum power of 315 watts per module, was selected for this study based upon its availability and ability to withstand the extreme weather conditions typically experienced in the case study area. This reference system, with an appropriate tilt angle based on the current building rooftop conditions in Normal, was utilized to estimate the potential energy production of DG solar PV systems.
Four different systems were modeled based on the electrical usage each system’s total production could offset of the average amount electricity residential and small businesses in the town consume annually (8811 kWh per building in 2013). These four different systems represent energy offsets of 20%, 40%, 60%, and 80% of the average electricity consumption for the buildings in Normal, respectively. The different system sizes were chosen to provide a good basis for developing a better understanding of how these systems would influence the town and to promote a simple assessment and thus enhance replicability. Once the number of modules and inverters required for each had been confirmed, we were able to estimate how large an area each system would need. These outputs contributed to the findings for the solar radiation analysis within GIS.
3. Results and Discussion
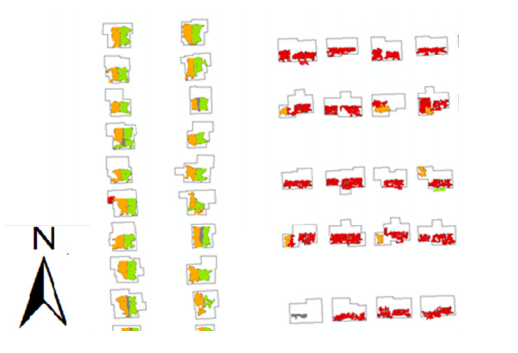
The GIS analyses determined the solar radiation potential of each building’s rooftop space. Figure 7 represents a grouping of buildings and their potential solar areas along with the direction that each roof faces. Figure 8 shows an example of a building that is predominantly flat with smaller areas within it that are sloped and facing east, west or south.
These analyses provide useful insights regarding multiple different aspects of how an individual rooftop’s solar potential is affected by its roof tilt and roof direction, and the quantitative statistical analysis also identifies geographical phenomena and correlations with the solar potential of each roof and where it is located in the town. Subsequently, SAM was utilized to design the four different systems modeled and the area needed to offset the specific energy offset percentage assigned to each.
The area required for a PV system installation is an important factor for identifying the exact number of buildings that would be available to host each of the four different sized systems modeled for Normal. Table 1 shows the SAM PV system simulation results and the area required for each system; the system sizes range from 1.5 kW to 5.3 kW. For the PV systems to achieve their maximum output each year, we focused on those south facing roofs with a solar potential of moderate (yellow) to good (red) that were identified in the first GIS analysis of the solar potential of the town, shown in Figure 2. Once the exact number of buildings in each category had been identified and the total electricity output of each system quantified, the results were matched with the available rooftops in the town to achieve the assigned system offsets.
Table 1. System specifications.
|
Offset
|
Module
|
Inverter
|
System Size
(kW)
|
Annual Energy (kWh)
|
Area Required(m2)
|
Number of Buildings Identified
|
|
20%
|
KD 315GX-LPB
|
YC-5001 240V
|
1.3
|
1762
|
8.78
|
9, 718
|
|
40%
|
KD 315GX-LPB
|
YC-5001 240V
|
3.0
|
3869
|
19.75
|
7, 760
|
|
60%
|
KD 315GX-LPB
|
YC-5001 240V
|
4.1
|
5588
|
30.72
|
6, 377
|
|
80%
|
KD 315GX-LPB
|
YC-5001 240V
|
5.2
|
7048
|
35.10
|
5, 908
|
Combining the GIS analysis with the PV performance model for Normal identified 17,999 buildings with some solar potential out of the 19,430 buildings in the town. Different PV system sizes to offset the buildings’ average annual electrical usage of 8811 kWh by 20%, 40%, 60%, and 80%, are identified and the number of available buildings is listed in Table 1. These specific numbers can be utilized to categorize the buildings into four different groups and thus permit the PV systems on the buildings to be modeled in a structured way rather than having to model all the buildings individually.
The outcomes of the integrated GIS and PV performance modeling analyses reveal a significant opportunity for the town of Normal, Illinois that should encourage the community to take the next step in implementing modular solar PV devices as part of a town-wide DG system. Using a methodology unique to this particular research problem can assist other communities todevelop a replicable model to assist in the optimization of community modular solar PV system implementations. A number of uncertainties associated with the GIS analysis need to be addressed including the slope of the roofs and the further inclusion of the non-south facing roofs.
4. Conclusion
The GIS and PV performance model assessment of the town of Normal, Illinois, developed for this study revealed the great potential benefit to the town of implementing modular solar devices due to the abundant suitable rooftop space for PV installations. These results and recommendations are unique to this municipality, providing the town with a significant opportunity to invest in their energy future based solely on the town’s rooftop solar potential. The benefits of DG are beginning to gain more widespread acceptance, as seen by the recent DG carve out for the state of Illinois. However, before any of the associated impacts of the implementation of solar modular devices as part of a DG plan can become reality, a realistic method for determining the solar potential of a specific area must be developed. The original methodologies presented in this study combine to create a replicable model for calculating the solar irradiance potential and will serve as a basis for further research, building on the results reported here. Utilizing GIS in conjunction with this PV performance model is a unique aspect of this study, which utilized well-established and accessible tools and should thus enable others to perform similar research that applies the same approach to their own location.
Quantifying the potential solar irradiance on the 17,999 building rooftops in the town was achievable utilizing the dynamic capabilities of LiDAR data coupled with GIS analyses. The results produced by GIS enabled an accurate depiction of the number of suitable buildings available to offset four different levels, 20%, 40%, 60%, and 80%, of the town’s average annual energy consumption for residential and small commercial buildings. To achieve each of these offset percentage options, the modular systems needed were designed and simulated in the PV performance model to determine the area required to accommodate each system, as well as its subsequent potential energy production. By utilizing the available roof space of the 9,718 buildings in the case study area, a total of 39.27 MW solar photovoltaic systems can provide electrical generation of 53,061 MWh annually.
This research project provides a replicable model for determining the solar potential of rooftops in a specific area as a basis for future studies. The results of this paper can be applied to develop the optimal design of a distributed generation plan for the town of Normal, in Central Illinois, USA. In addition to the potential energy benefits for this municipality, this research study sought to present a new approach that could be applied by others to generate a reliable model to establish a distributed generation plan for their own locality. Beyond the technical evaluation provided in this study, the development and implementation of distributed generation necessitates further research that encompasses economic, social, and environmental factors and impacts. An in-depth consideration of these variables through appropriate analysis will collectively ensure the optimization of DG in Normal, Illinois, and in any other location in which the new method is replicated.
Conflict of Interest
All authors declare no conflictsof interest in this paper.










 DownLoad:
DownLoad: