An ODE system modeling the competition between two species in a two-patch environment is studied.Both species move between the patches with the same dispersal rate. It is shown that the species with largerbirth rates in both patches drives the other species to extinction, regardless of the dispersal rate. The more interesting case is when both species have the same average birth rate but each species has larger birth rate in one patch. It has previously been conjectured by Gourley and Kuang that the species that can concentrate its birth in a single patch wins if the diffusion rate is large enough, and two species will coexist if the diffusion rate is small. We solve these two conjectures by applying the monotone dynamics theory, incorporated with a complete characterization of the positive equilibrium and a thorough analysis on the stability of the semi-trivial equilibria with respect to the dispersal rate. Our result on the winning strategy for sufficiently large dispersal rate might explain the group breeding behavior that is observed in some animals under certain ecological conditions.
1.
Introduction
In the real world many systems can be described by complex networks, ranging from nature to society. Recently the study of epidemic systems on complex networks has attracted a lot of attention and interest [1,2,3]. Within these studies, individuals are modeled as nodes, and possible contacts between individuals are linked by edges. The susceptible-infected-susceptible (SIS)[4], the susceptible-infected (SI) [5], the susceptible-infected-recovered (SIRS) [6], and the susceptible-exposed-infected-recovered (SEIRS) models on complex networks [7] have been extensively studied recently. According to reference[8], successful immunization strategies can be developed only by taking into account the inhomogeneous connectivity properties of scale-free networks. Alberto d'Onofrio description of the global behavior of the web-based SIS epidemic model is given in reference [9]. Jie Lou et al. studied the transmission dynamics and immunization strategies of sexually transmitted diseases on scale-free networks [10]. One of reasons for studying networks is to understand the mechanisms by which diseases and other things, such as disease information spread over. For instance, the study of networks of sexual contact [11,12] is helpful for us to understand and perhaps control the spread of sexually transmitted diseases. It also has been shown that there is an epidemic threshold on the homogeneous Watts Strogatz small-world network model, while the epidemic model on SF networks has no epidemic threshold; infections can be proliferated, whatever small infection rate they have. This result disproves the threshold theory in traditional epidemiology.
As we all know, human behavior in an epidemic include the contacts between human, media coverage, vaccination, migration of population etc. In fact, these factors are important for infectious disease spread. Particularly, it is media coverage which make people knowledgeable about the diseases to take precautions such as social distancing, wearing protective masks, vaccination etc. At present, some researchers take the media converge into considering on mathematical models and there is a lot of evidence that media coverage can play an appreciable role in the spread and control of infectious diseases [13,14,15,16]. Zuo et al. proposed a compartment epidemic model with delay, and discussed the influence of consciousness planning on the spread and control of infectious diseases in a specific area [17]. In reference [18,19], the influence of media during influenza epidemics is simulated. In recent paper [20], the authors review the literature on the effect of media on infectious disease outbreaks, and they considered a deterministic differential equation mean field SIS epidemic model for the spread of an infection in the presence of awareness programs, and analyzed two types of time delays and then perform simulations based on real parameter values to verify their theoretical results. However, the spread of an infectious disease depends not only on the characters of the disease, but also on the structure of the population. Thus many epidemic models with media coverage on network are proposed [21,22]. Wang et al. [21] studied SIS models with media coverage in complex networks. They discussed the relationship between the parameters of the model and the basic reproduction number, and analyzed the stability of equilibria. Yuan et al. [22] proposed an epidemic disease model about the effect of awareness programs on complex networks, where the contacts between nodes were treated as a social network, and two forms on increasing rate of awareness programs were analyzed. These results can suggest effective control strategies, such as proportional immunization, targeted immunization etc., to prevent disease through media coverage and education activities on networks.
Based on predecessors' work, we propose a complex network model with media converge for predicting the future course of any epidemic such as smallpox, measles and flu, and so on. We consider that due to media converge, some susceptible will avoid their contacts with the infective. In the dynamic analysis, we use the method of next generation matrix to obtain the expression of the reproduction number and the condition for existence of the endemic equilibria. Furthermore, we analyze the eigenvalues of Jacobian matrix to prove the stability of the disease-free equilibrium and the permanence of infection. Two immunization strategies were considered: proportional and target immunization, and by comparing the two immunization strategies, it was found that the target immunization was better than proportional immunization in controlling the spread of the disease. Finally, we take some numerical simulations to illustrate the effect of media coverage on the disease.
This paper is organized as follows. We first propose the model in Section 2. Section 3 is devoted to the existence of equilibria and basic reproduction number, followed by the stability of the disease-free equilibrium and the permanence of infection, and then two immunization strategies are given. Numerical simulations and analysis are given in Section 4. Section 5 concludes the paper.
2.
A model with media coverage
In this paper we consider the whole population and their contacts in networks. When disease transmission is modeled on networks, individuals are treated as nodes, and potential contacts among individuals as edges. To address the heterogeneity in the contacts among individuals, the population is divided into $ n $ distinct groups of size $ N_{k} (k = 1, 2, \ldots, n) $ such that each individual in group $ k $ has exactly $ k $ contacts; Here $ n $ denotes the maximum degree of all nodes. If the whole population size is $ N $, then $ N = N_{1} + N_{2} + \cdots + N_{n} $ and the degree distribution is $ p(k) = N_{k}/N $. The value $ \langle k\rangle = \sum\limits_{k = 1}^{n}kp(k) $ is the average number of contacts each node.
We consider the fundamental epidemic model: SIS model. In this model each individual can be in two states: $ S $, susceptible to the disease, and $ I $, infectious individuals. Denote by $ S_{1k}(t) $, $ S_{2k}(t) $ and $ I_{k}(t) $ the number of unaware susceptible, the aware susceptible and infected individuals within the group $ k $ at time $ t $, respectively; then $ N_{k}(t) = S_{1k}(t) + S_{2k}(t)+I_{k}(t) $. It is assumed that the disease spreads due to direct contacts between susceptible and infected individuals only. In order to incorporate the dimensions of massive news coverage, we introduce the information variable $ M(t) $ to describe the cumulative density of media coverage in that region at time $ t $.
Based on the above assumptions, we have the following dynamic model of $ 3n+1 $ ordinary differential equations:
In this model, $ k = 1, 2, \cdots, n $. The parameter $ \beta $ is transmission rate per contact between one susceptible and one infectious individual; parameter $ \gamma $ is recovery rate of infected individuals; since the information reported by the media is always available, parameter $ \xi $ represents the conversion rate of transformation from high susceptible to low susceptible; parameter $ q $ denotes the probability that the person transformed into a highly susceptible person after recovery; parameter $ \mu_{0} $ is depletion rate of media coverage due to ineffective implementation; parameter $ m_{0} $ is density level of media coverage on the disease from another region with the disease; parameter $ \omega $ is the media reporting rate being implemented.
Here in uncorrelated networks, $ \Theta(t) $ represents the expectation that any given edge points to an infected individual, defined as:
And we consider the media coverage function $ B(M, k) = \frac{kM(t)}{a+kM(t)} $ as being similar to the Michaelis-Menten function $ p_{1}(M) = \frac{cM}{c+dM} (c, d\geq0) $ (see[15,21] and the references cited therein). $ B(M, k) $ measures the impact of media coverage on a individual in group $ k $, which is related to the number of people he/she meets and the current density level of media coverage. The term $ βB(M, k) $ measures the effect of the reduction of transmission rate between susceptible and infectious individuals due to the reporting of infectious cases in the media. The half-saturation constant $ a > 0 $ reflects the impact of media coverage on contact transmission. All parameters in the model are assumed to be positive except that $ m_{0} $ is nonnegative.
Note that $ \frac{dS_{1k}(t)}{dt}+\frac{dS_{2k}(t)}{dt}+\frac{dI_{k}(t)}{dt} = 0 $, which means that $ S_{1k}(t) + S_{2k}(t)+I_{k}(t) = N_{k} $ is constant. Denote the relative densities of the unaware susceptible nodes, the aware susceptible nodes and infected nodes of degree $ k $ at time $ t $ by $ s_{1k}(t) = \frac{S_{1k}(t)}{N_{k}} $, $ s_{2k}(t) = \frac{S_{2k}(t)}{N_{k}} $, $ i_{k}(t) = \frac{I_{k}(t)}{N_{k}} $, respectively and $ \Theta(t) = \frac{1}{\langle k\rangle}\sum\limits_{k = 1}\limits^{n}kp(k)i_{k}(t) $. Then system (2.1) can be rewritten as:
with the normalization condition $ s_{1k}(t)+s_{2k}(t)+i_{k}(t) = 1 $, and $ \Omega\doteq\prod_{k = 1}^{n}[0, 1]\times[m_{0}/\mu_{0}, (m_{0}+\omega N)/\mu_{0}] $ is the region of attraction, which attracts all solutions initiating in the interior of the positive orthant.
3.
Analysis of the model
3.1. The stability of the disease-free equilibrium
It can be easily see system (2.2) always exists a unique disease-free equilibrium $ E_{0}(\underbrace{0, 1, 0\ldots, 0, 1, 0}_{3n}, M_{0}) $, where $ M_{0} = m_{0}/\mu_{0} $. We notice that only compartments $ i_{k} $ are involved in the calculation of the basic reproduction number $ R_{0} $, which is defined as the expected number of secondary infections produced by an index case[23]. For this disease-free equilibrium $ E_{0} $, the production of new infections $ \mathcal{F} $ and the rate of transfer of individuals $ \mathcal{V} $ are given respectively by
Then we have the derivatives at the disease-free equilibrium $ E_{0} $:
where $ a_{1} = \frac{a}{a+M_{0}} $, $ a_{2} = \frac{2 a}{a+2M_{0}} $, $ \cdots $, $ a_{n} = \frac{n a}{a+nM_{0}} $. Thus, the reproduction number is given by $ R_{0} = \rho(\bar{F}\bar{V}^{-1}) $, the spectral radius of the matrix $ \bar{F}\bar{V}^{-1} $. Then we obtain the basic reproduction number as follows:
Remark 1. When $ m_{0}\rightarrow 0^{+} $, we obtain $ R_{0} = \frac{\beta\langle k^{2}\rangle}{\gamma\langle k\rangle} $, which is consistent with the classical result obtained by Pastor et al.[4]. If $ m_{0} = 0 $, the existence of media coverage will not change the epidemic threshold, but it may affect the prevalence of the disease.
For the stability of the disease-free equilibrium we have the following result.
Theorem 1 If $ R_{0} < 1 $, the disease-free equilibrium $ E_{0} $ of system (2.2) is locally asymptotically stable, whereas if $ R_{0} > 1 $ the disease-free equilibrium $ E_{0} $ is unstable.
Proof The Jacobian matrix of system (2.2) at the disease-free equilibrium $ E_{0} $ is
where
The matrix $ J|_{E_{0}} $ has one eigenvalues which is equal to $ -\mu_{0} $. Next we need to find the eigenvalues of the matrix $ F $, where
By analysis, the eigenvalues of $ F $ are only related to $ F_{1} $ and $ F_{4} $, the matrix $ F_{1} $ has $ n $ eigenvalues which are equal to $ -\xi $, and has $ n $ eigenvalues which are equal to $ 0 $. Through the determinant changes, the matrix $ F_{4} $ has $ (n-1) $ eigenvalues which are equal to $ -\gamma $ and one eigenvalue which is equal to $ \frac{\beta a\mu_{0}}{\langle k\rangle}\sum\limits_{k = 1}\limits^{n}\frac{k^{2}p(k)}{a\mu_{0}+km_{0}}-\gamma $. Obviously, if $ R_{0} < 1 $, we can get $ \frac{\beta a\mu_{0}}{\langle k\rangle}\sum\limits_{k = 1}\limits^{n}\frac{k^{2}p(k)}{a\mu_{0}+km_{0}}-\gamma $ is negative. Thus the proof is completed.
For the globally stability of the disease-free equilibrium, we have
Theorem 2 If $ R_{0} < 1 $, the disease-free equilibrium $ E_{0} $ of system (2.2) is globally asymptotically stable.
Proof From system (2.2), we have
Let us consider the following auxiliary system:
The basic reproduction number for system (3.2) is $ R_{0}^{'} = \frac{\beta\langle k^{2}\rangle}{\gamma\langle k\rangle} $. When $ R_{0} < 1 $, since $ R_{0} $ is decreasing function of $ m_{0} $, we can get $ R_{0}^{'} = \lim\limits_{m_{0}\rightarrow 0^{+}}R_{0}\leq1 $. Since the first equation of system (3.2) is independent of the second, according to the results obtained by d'Onofrio et al.[9], we can obtains that the disease-free equilibrium is globally asymptotically stable if $ R^{'}_{0} < 1 $, i.e.$ \lim\limits_{t\rightarrow+\infty}i_{k}(t) = 0 $, $ k = 1, 2, \cdots, n. $ The limit system of the information variable $ M(t) $ satisfies $ \frac{dM(t)}{dt} = m_{0}-\mu_{0}M(t) $, $ M(t) = \frac{m_{0}-ce^{-\mu_{0}t}}{\mu_{0}} $, and it comes to $ \lim\limits_{t\rightarrow +\infty} M(t) = M_{0} $. By comparison arguments, we know that the disease-free equilibrium $ E_{0} $ is globally attractive for system (2.2). Thus if $ R_{0} < 1 $, the disease-free equilibrium $ E_{0} $ of system (2.2) is globally asymptotically stable.
3.2. The existence of the endemic and permanent
As for the existence of the endemic equilibrium of system (2.2), we have the following theorem.
Theorem 3 If $ \gamma\xi\omega N\langle k\rangle+a\mu_{0}\xi\beta\geq\gamma nm_{0}q\beta $, and $ R_{0} > 1 $, system (2.2) exists one and only one positive equilibrium $ E^{\ast}(s^{\ast}_{11}, s^{\ast}_{21}, i^{\ast}_{1}, ..., s^{\ast}_{1n}, s^{\ast}_{2n}, i^{\ast}_{n}, M^{\ast}) $.
Proof To discuss the endemic equilibrium, by imposing the stationary condition we consider the following equations:
The fourth equation of (3.3) yield $ M^{\ast} = \frac{m_{0}+\omega Ni^{\ast}}{\mu_{0}} $, where $ i^{\ast} = \sum\limits_{k = 1}\limits^{n}p(k)i^{\ast}_{k} $. The first equation of (3.3) yield
The second equation of (3.3) yield
Then we obtain
Thus
Substituting $ M^{\ast} $ into the expression of $ i_{k}^{\ast} $, then we get
Substituting $ i_{k}^{\ast} $ into the expression of $ \Theta(t) $, then we obtain a self-consistency equation as follows:
Here
So, we obtain
where
Obviously, $ N\langle k\rangle\omega q\xi-\beta k^{2}m_{0}q+a\beta k\mu_{0}+\beta k^{2}m_{0} = N\langle k\rangle\omega q\xi+a\beta k\mu_{0}+\beta k^{2}m_{0}(1-q) > 0 $, and $ N\langle k\rangle\gamma\omega q-N\langle k\rangle\gamma\omega-a\beta k\mu_{0} = N\langle k\rangle\gamma\omega (q-1)-a\beta k\mu_{0} < 0 $, we have $ \gamma\xi\omega N\langle k\rangle+a\mu_{0}\xi\beta\geq\gamma nm_{0}q\beta $, so $ \gamma\xi\omega N\langle k\rangle+a\mu_{0}\xi\beta\geq\gamma km_{0}q\beta $, for $ k = 1, 2, \cdots n $, so $ C > 0 $. And we know, $ \beta kq\Theta-\beta k\Theta-\xi = \beta k\Theta(q-1)-\xi < 0 $, $ a\beta^2k^2\mu_{0}\Theta^2-\beta\gamma k^2m_{0}q\Theta+a\beta\gamma k\mu_{0}\Theta+a\beta k\mu_{0}\Theta\xi+\beta\gamma k^2m_{0}\Theta+a\gamma\mu_{0}\xi+\gamma km_{0}\xi = a\beta^2k^2\mu_{0}\Theta^2+k\Theta(a\mu_{0}\gamma+a\mu_{0}\xi+\gamma km_{0}(1-q))\beta+\gamma\xi(a\mu_{0}+km_{0}) > 0 $, so $ D < 0 $. Thus
That it is to say, if $ R_{0} > 1 $, there exists a unique positive the endemic equilibrium $ E^{\ast}(s^{\ast}_{11}, s^{\ast}_{21}, i^{\ast}_{1}, ..., s^{\ast}_{1n}, s^{\ast}_{2n}, i^{\ast}_{n}, M^{\ast}) $ of system (2.2).
Theorem 4 Suppose $ R_{0} > 1 $, then system (2.2) is permanent of infection, that is, there exists a $ \epsilon > 0 $, such that $ \liminf\limits_{t\rightarrow\infty}i_{k}(t) > \epsilon, k = 1, 2, ..., n $, for any solution of (2.2) with $ s_{1k}(0) > 0 $, $ s_{2k}(0) > 0 $, $ i_{k}(0) > 0 $, and $ M(0) > 0 $.
Proof The argument is similar to that of Lemma $ 3.5 $ of De Leenheer and Smith[24], which is based on Theorem $ 4.6 $ of Thieme[25]. For simplicity, we denote
to be the state variable of (2.2) and $ x(t) $ represents a solution of (2.2). Define
and
In the following, we show that system (2.2) is uniformly persistent with respect to $ (\mathcal{X}_{0}, \partial \mathcal{X}_{0}). $
Obviously, $ \mathcal{X} $ is positively invariant with respect to (2.2). We can also see that $ \mathcal{X}_{0} $ is positively invariant with respect to (2.2) since
Furthermore, there exists a compact set $ \mathcal{B} $ in which all solutions of (2.2) initiating in $ X $ will enter and remain there.
Denote
and
Restricting (2.2) on $ \mathcal{M}_{0} $ gives
Clearly, the system (3.4) has a unique equilibrium $ E_{0} $. It is easy to see from the first and third equations of (3.4) that all $ s_{1k}(t) $ and $ i_{k}(t) $ tend to zero as $ t\rightarrow \infty. $ Then, $ s_{2k}(t)\rightarrow 1 $ as $ t\rightarrow \infty $ since $ s_{1k}(t)+s_{2k}(t)+i_{k}(t) = 1. $ So, $ \Omega = E_{0}. $
Note that $ E_{0} $ is a covering of $ \Omega $, which is isolated and is acyclic. To finish the proof, it suffices to show that $ E_{0} $ is a weak repeller for $ \mathcal{X}_{0} $, that is
where $ x(t) $ is any arbitrary solution of (2.2) with $ x(0)\in X_{0} $. We only need to prove $ W^{s}(E_{0})\bigcap X_{0} = \emptyset $, where $ W^{s}(E_{0}) $ is the stable manifold of $ E_{0} $. We take the contradiction and assume that it's not true. Then there exists a solution $ x(t)\in X_{0} $ such that $ s_{1k}(t)\rightarrow0 $, $ s_{2k}(t)\rightarrow1 $ and $ i_{k}(t)\rightarrow0 $ as $ t\rightarrow\infty $. Since $ R_{0} = \frac{\beta a\mu_{0}}{\gamma\langle k\rangle}\sum\limits_{k = 1}\limits^{n}\frac{k^{2}p(k)}{a\mu_{0}+km_{0}} > 1 $, we can choose $ \nu > 0 $ such that $ (1-\nu)R_{0} > 1 $. For such $ \nu > 0 $, there exists a $ T > 0 $ such that, for $ t\geq T $, $ 0\leq s_{1k}(t) < \nu $, $ 1-\nu < s_{2k}(t)\leq1 $, and $ 0\leq i_{k}(t) < \nu $. Let
In fact $ V(t) = \langle k\rangle\Theta(t) $. Then, for $ t\geq T $, we have
Since $ (1-\nu)R_{0} > 1 $, it follows immediately that $ V(t)\rightarrow\infty $ as $ t\rightarrow\infty $, which contradicts with the fact that $ V(t) $ is bounded. This completes the proof.
3.3. Immunization strategies
Vaccination is very helpful in controlling vaccine preventable diseases[8,12]. In this section we discuss system (2.2) with two immunization schemes: the proportional immunization and the targeted immunization.
3.3.1. Proportional immunization
Let $ f $ be the immunization rate, $ 0 < f < 1 $. Then system (2.2) becomes
Similar arguments as those in Section $ 3 $ give us the basic reproduction number
Compare the expressions of $ \hat{R}_{0} $ and $ R_{0} $, when $ f = 0 $, there is no immunity, $ \hat{R}_{0} = R_{0} $, otherwise $ \hat{R}_{0} < R_{0} $, indicating that the immune strategy is effective. When $ f\rightarrow0 $, i.e.$ \hat{R}_{0}\rightarrow0 $, it means that under the strategy of total immunity, the disease cannot be transmitted on complex networks.
3.3.2. Targeted immunization
In addition to proportional immunization, target immunization is also an effective immunization strategy. Define the threshold of two network nodes are $ k_{1} $ and $ k_{2} $ respectively, $ k_{1} < k_{2} $ and the immunization rate $ f_{k} $ depends on the degree $ k $. Then $ f_{k} $ is as follows:
Here $ \overline{f_{k}} = \sum\limits_{k}f_{k}p(k) $ is the average immunological rate, then we can re-write system (2.2) as
By recalculating the basic number of regeneration, we get
Since $ \langle k^{2}f_{k}\rangle = \overline{f}\langle k^{2}\rangle+\sigma $, where $ \sigma $ is the covariance of $ f_{k} $ and $ k^{2} $, and
When appropriately small $ k $ is taken, $ \sigma $ can be guaranteed to be greater than 0, therefore:
Obviously, we can get $ \widetilde{R_{0}}\leq R_{0} $, which implies that targeted immunization can be effective in controlling the spread of disease. If note $ f = \overline{f_{k}} $, we can get $ \widetilde{R_{0}}\leq \hat{R}_{0} $, it means that for the same average immune rate, target immunity is more effective than proportional immunity.
4.
Numerical simulations
In this section, the stability of the disease-free equilibrium and endemic equilibrium are simulated respectively. We consider the dynamical process on BA random scale-free networks with $ p(k) = 2m^{2}k^{-3} $ and $ m = 3 $.
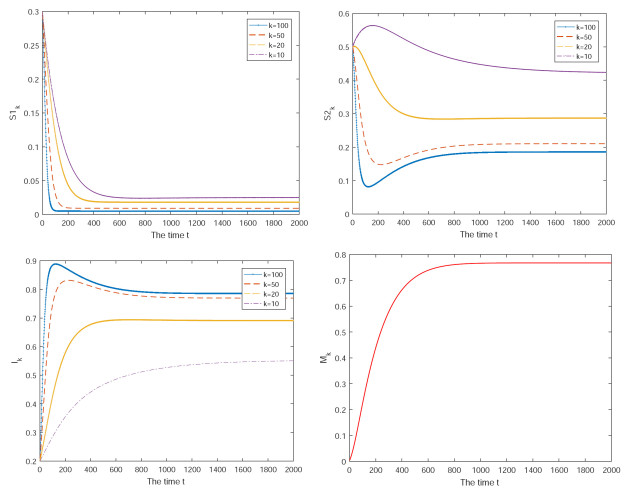
Firstly, numerical simulations are presented to illustrate the results of system (2.2). In the simulations the parameters are given by the reference [6,21], which are as follows: $ N = 1000 $, $ \beta = 0.02 $, $ \gamma = 0.11 $, $ \xi = 0.05 $, $ q = 0.2 $, $ \omega = 0.0005 $, $ m_{0} = 0.12 $, $ \mu_{0} = 0.11 $, $ a = 10 $, then $ M = m_{0}/\mu_{0} = 1.09 $ and $ R_{0} < 1 $, thus the disease-free equilibrium is globally asymptotically stable. As shown in Fig. 1, when $ R_{0} < 1 $, even for a large fraction of the infected at the initial time, the disease will disappear and all the individuals will become the aware susceptible. Moreover, the larger the cumulative density of media coverage is, the faster the disease dies out.
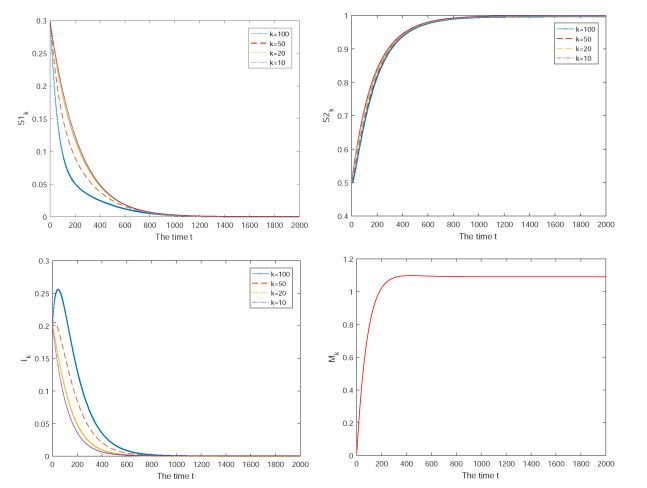
Secondly, the parameters are given by $ N = 1000 $, $ \beta = 0.02 $, $ \gamma = 0.021 $, $ \xi = 0.05 $, $ q = 0.2 $, $ \omega = 0.0005 $, $ m_{0} = 0.003 $, $ \mu_{0} = 0.05 $, $ a = 10 $, $ M = m_{0}/\mu_{0} = 0.06 $[6,21], then $ R_{0} > 1 $. One can see that, the disease will converge to a positive stationary level, even for a small fraction of the infected at the initial time, which means that the positive equilibrium is stable.
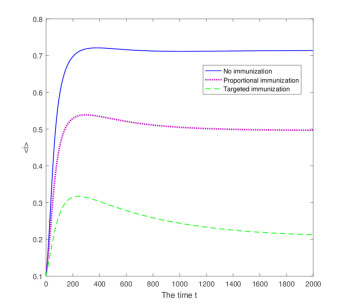
Finally, we consider the effects of immunization with the same values of parameters in the first case. In Fig. 3, we take $ f = 0.2 $ in the proportional immunization, and $ f_{k} = 0.5 $ for $ 5 < k < 10 $ in the targeted immunization
Numerical simulation verified the two immune strategy for disease control are effective, and the target immune strategy is more effective than proportion immunization strategy.
5.
Conclusion
In this paper, we divided the susceptible into two parts (susceptible without aware, the aware susceptible) and added media information reports to study the impact of media reports on disease transmission. We obtained that when $ R_{0} < 1 $, the disease-free equilibrium is globally asymptotically stable, while when $ R_{0} > 1 $, the disease-free equilibrium instability, and the disease is permanent. In order to further control the spread of the disease, we studied two immunization strategies: proportional immunization and target immunization, both of which can control the spread of the disease well, but the target immunization is more effective. There will be more better strategies in the control the spread of the disease, and in the future we will continue to study them and get more better results.
Acknowledgments
The authors would like to thank the reviewers for their helpful comments and valuable suggestions, and the support of the National Sciences Foundation of China(11571324, 61403393), the Fund for Shanxi "1331KIRT", Shanxi Scholarship Council of China and the Scientific Activities of Selected Returned Overseas Professionals in Shanxi Province.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: