The Michaelis-Menten (MM) function is a fractional linear function depending on two positive parameters.These can be estimated by nonlinear or linear least squares methods.The non-linear methods, based directly on the defect of the MM function, can fail and not produce any minimizer.The linear methods always produce a unique minimizer which, however, may not be positive. Here we give sufficient conditions on thedata such that the nonlinear problem has at least one positive minimizer and also conditions for the minimizer of the linearproblem to be positive.
We discuss in detail the models and equilibrium relations of a classical operator-repressor system,and we extend our approach to the MM problem with leakage and to reversible MM kinetics.Thearrangement of the sufficient conditions exhibits the important role of data that have aconcavity property (chemically feasible data).
1.
Introduction
Phosphorus is an essential/key nutrient required by planted crops for growth and other vital metabolic processes. It is next to nitrogen in terms of significance for plant sustenance [1]. However, despite the phosphorus second position status with being a growth-limiting nutrient, it is not atmospherically present and cannot be fixed biologically, unlike nitrogen [2]. The soluble phosphate fertilizer application in soil encourages maximum/optimum growth of plants and importantly improves soil health. Supplying the required number of phosphorus to crops enhances the growth/development of roots and can lead to early plant maturity. Also, it is significant in the formation of seeds, vital in all plant metabolic processes, plant growth enhancement, and the ability of plants to resist phytopathogens [3]. Microbial phosphate-solubilizers can biotransform phosphatic compounds insoluble to soluble forms for plant assimilation in soil [4,5]. The mineralization of organic phosphate contributes immensely to the phosphorus-cycling function in agriculture. Organic phosphate has contributed a greater percentage of total soil phosphate; however, many microorganisms that are found in the rhizosphere and the surrounding soil have phosphate-solubilizing ability influence by microbial phosphatases [6].
Maize (Zea mays L) is globally important and it is an intensely grown cereal plant all over the globe. It is a commercially cultivated crop worldwide. Maize (Zea mays L.) is a highly prized food crop worldwide [7,8]. It is consumed throughout the globe as a staple food. It is economically important in industrial sectors; pharmaceutical, food, livestock feed, paper, and even in the energy industry [9]. Thus, based on its economic value, the demand for maize is always high. It is used as a nutritious food source and important in industry for producing various values-added products [10].
The search for sustainable options for reducing agrochemical intensification of crop productivity is an important research theme in today’s global crop production processes. Justifiable drawbacks of agrochemical applications in the crop production value chain are they are nonrenewable resources and not eco-friendly, groundwater is polluted, cost of energy is high, biodiversity is impacted negatively, as well as the issue of eutrophication [11]. Thus, the use of green technology like the deployment of microbial resources as bioinoculating agents that are safer and ecologically sustainable are viable alternatives to synthetic chemical applications in agricultural productivity [12].
This research represents an attempt to isolate atoxigenic Aspergillus flavus strains and assess their plant growth enhancement capability when used as biofertilizer for the growth of maize. UV- irradiation mutation of the atoxigenic Aspergillus flavus strains was performed for the enhancement of their phosphate-solubilizing ability. Biofertilizers increase the availability of nutrients required to plants by fixing nitrogen through solubilization of phosphates by producing metabolites that enhances the growth of plants. Biofertilizers are viable alternatives in decreasing the usage of synthetic fertilizers and other agrochemicals. Biofertilizers play an important role in soil health and improve plant fitness through microbial mediated metabolite production. Biofertilizers are harmless, natural biological resources that function efficiently. Therefore, phosphate solubilizing microorganisms as biofertilizers provide ecologically friendly agricultural input that is cheaper and economical than the commonly used synthetic fertilizers [13]. The usage of phosphate biofertilizers is an encouraging approach to enhance world food security through the improvement of agricultural yield in developing countries in Africa and Asia [14].
This investigation determined the beneficial effects of non-toxigenic A. flavus strains that are phosphate solubilizers as biofertilizer to enhance growth parameters and mineral elements content of maize plants.
2.
Materials and method
2.1. Experimental location
This investigation was done in Nigeria, at the Research Institute for Stored Product (NSPRI), Ilorin. Ilorin is a town in Kwara state of Nigeria located in the North central geopolitical zone with characteristics of the guinea savanna zone vegetation (Longitude N 8.3° and Latitude E 4.33°). This research experiment was conducted in the year 2017–2019.
Sample collection and experimental conditions
Samples were collected from the rhizosphere soil of planted maize crop. Soil was scrapped carefully to about 6–7 cm depth; soil sample was collected into an aluminum foil paper, using an auger and was transported to laboratory for further analysis. The soil sample was processed immediately for the isolation of phosphate solubilizing fungi [15]. The phosphate solubilizing fungi strains were the wild-type originally isolated from the rhizospheric soil of maize plant, while the maize was obtained from Germplasm collection of NSPRI. The potting experimental study was conducted in a greenhouse.
The cycle of light/dark received by the plant during pot experimental growth stage was 12 hours light and 12 hours dark cycle.
2.2. Isolating fungi phosphate solubilizers
Phosphate solubilizing fungi (PSF) were isolated from the above-named soil sample by serial dilution using Pikovskaya medium agar containing tri-calcium phosphate (TCP) [16]. Appropriate soil dilutions were plated on Pikovskaya agar medium by spread plate method before incubation at 28 ± 2 ℃ for 7 days. The fungal isolates that formed halo zone clearance of insoluble calcium phosphate, while growing on (Pikovskaya agar) plate were selected as potential phosphate solubilizers [17].
2.3. Determination of Aflatoxin-production potential of Aspergillus flavus using cultural screening method
Coconut agar i.e desiccated neutral red incorporated coconut agar (NRDCA) was used to screen for the ability of Aspergillus flavus to produce aflatoxins in order to determine and certify its safety as biofertilizer. In brief, neutral red desiccated coconut agar (NRDCA) is a formulated medium that is used for the detection of aflatoxigenic fungi and direct visual determination of aflatoxins.
200 grams of desiccated coconut is soaked in 1litre of hot distilled water and blended to obtain the filtrate. To the filtrate, 2% agar powder is added and homogenized by gentle heating. To the homogenized medium is added 0.3% neutral red stain before sterilization by autoclaving. The fungal isolate was inoculated on petri-plate using coconut agar to detect aflatoxin production following [18]. protocol. Aflatoxigenic positive isolate was expected to indicate yellow color following incubation on agar plate and fluorescence at (365 nm) UV irradiation.
2.4. Strain improvement
The mutants of the selected non-aflatoxigenic Aspergillus flavus isolates were developed with the use of UV irradiation at 254 nm wavelength. The isolates were grown in Pikovskaya broth for 7 days and the mycelium was macerated with the help of a tissue homogenizer. 5ml of the mycelia suspension (35–40 CFU/ml) was transferred to Pikovskaya agar plates and exposed to UV “irradiation for 90, 60, 30, and 15 minutes respectively”. Aspergillus flavus isolates that were irradiated with UV light for 15, 30, 60 and 90 minutes were designated as AF15, AF30, AF60, AF90 mutants.
100 µl of irradiated mycelia suspension was inoculated on PDA plate and incubation of plates done at 28 ± 2 ℃ for 72 h along with the control (non-mutated A. flavus isolate). The survived colonies were obtained after 72 h of incubation [19].
Thereafter, fungi isolate phosphate solubilization capability was determined both quantitatively and qualitatively [20].
2.5. Phosphate solubilization assay
Qualitative assay for phosphate solubilizing activity
Pure culture of wild AF (original isolates) and its mutants were spot inoculated (1.0 × 106 spores/ml of isolates) at the center of already prepared agar plates of Pikovskaya agar medium. The incubation of plates was done at room temperature for 7 days. Fungi isolates that solubilizes insoluble phosphates contained in (PKA agar medium plate), forming greater than 5.0 cm zone of solubilization were preferentially selected as phosphate solubilizers, and maintained as stock isolates on PDA for subsequent studies. The zone of phosphate solubilization (cm) formed around colonies was recorded after every 24 hours for 7 days. The solubilizing efficiency of the fungi was calculated using the formula.
Pikovskaya medium with known amount of phosphorus containing 0.005 g/L bromophenol blue (BPB) was prepared [21]. The isolates that were positive on tri-calcium phosphate solubilization (Pikovskaya agar) medium were tested further for phosphate solubilization in broth culture medium.
The incubation of isolates in Pikovskaya broth medium was at 28 ± 2 ℃ for 3–4 days followed by centrifugation at 5000 rpm for 15 mins. The fungal cultures were filtered after centrifugation using Whatman filter paper. 1 ml from the filtrate was mixed with 10 ml of ammonium molybdate and the content was diluted to 45 ml. Chlorostanus acid (0.25 ml) was added to each treatments and final volume were made up to 50 ml using distilled water. Appearance of blue color intensity of the solutions was measured using a colorimeter at 600 nm. The amount of phosphorus solubilized was calculated and obtained with the help of a standard curve [22].
2.6. Pot trial experiment
A greenhouse pot trial experiment was carried out with 6 treatments and 3 replications. All the experimental pots were treated with their respective isolates. The maize seeds were collected from the Horticultural Research Institutes (NIHORT), Ibadan. The seeds were sown in the plastic pots (4 seeds/pot) filled with 10 kg of sterilized loamy soil. All the fungal isolates were grown in Pikovskaya broth in 20 ml each at the corresponding temperature. Seeds of maize were surface sterilized and spore suspensions (4 ml) of 1 × 106 spores/ml of all isolates were inoculated into soils 48 h prior to sowing. Un-inoculated pot was the control [23]. The observed data on seedling height (cm), percentage seed germination (%), height of plant (cm), leaves number, dry matter (g), cob length (cm), cob weight (g), 100 grain weight (g), grain yield (g/pot). The experimental set-up was replicated thrice and is as described below:
(Influence of Aspergillus flavus (AF) strains as bioinoculants on growth parameters and mineral nutritional content of maize plant.)
Treatment 1 – Maize seeds + AF90;
Treatment 2 – Maize seeds + AF60;
Treatment 3 – Maize seeds + AF30;
Treatment 4 – Maize seeds + AF15;
Treatment 5 – Maize seeds + wild AF;
Treatment 6 – Maize seeds only (control).
2.7. Statistical data analysis
Data on all parameters studied was statistically inferred using one-way (ANOVA). Data was analyzed using PROC GLM SAS software. Data were recorded in triplicates and analyzed, while means were separated using Duncan multiple range test (DMRT) and probability significance level was 95%.
3.
Results
3.1. Phosphate solubilizing activity of Aspergillus flavus
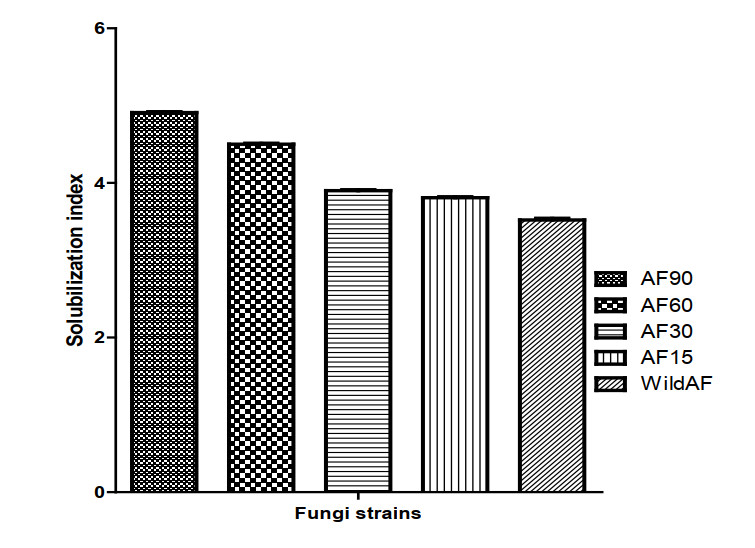
The phosphate solubilization results obtained in this investigation indicated differences (p < 0.05) for all the A. flavus strains used. Among all the fungi strains that was assessed for phosphate solubilization potential on Pikovskaya agar medium qualitatively, the mutant Aspergillus flavus (AF90) strain showed maximum level of phosphate solubilization activity (This is reflected in Figure 1).
Also, the quantitative phosphate solubilizing analysis indicated that Aspergillus flavus mutant (AF90) showed maximum level of phosphate solubilization (7.3 ppm) efficiency/activity and the wild type of the Aspergillus flavus (Wild AF) recorded the least/lowest solubilization efficiency of (3.2 ppm) after 7 days of incubation (Table 1).
3.2. Pot trial experiment
Also, results obtained in the pot trial experiment to investigate the effectiveness of Aspergillus flavus and its mutants to enhance the growth parameters and elemental nutritional composition of the maize plant, indicated that there was significant increases in agronomic parameters for shoot length (cm), percentage seed germination (%), plant height (cm), plant leaves number, cob length (cm), cob weight (g), 100 grain weight (g), grain yield (g/pot) when treatments with the fungi strain inoculants were compared to the control. These results are shown in Tables 2–6.
4.
Discussion
In this study, Aspergillus flavus efficient strains in solubilizing phosphate were isolated and characterized. Also, the toxigenic screening assay for aflatoxin production was conducted on these strains and they were confirmed to be non-toxigenic. In both qualitative and quantitative phosphate solubilization assay analysis, these Aspergillus flavus strains were also confirmed as phosphate solubilizers. Thereafter, the influence of these fungi strains was tested on the agronomic growth parameters and mineral nutrient content of maize plants.
The highlights of this study are that efficient strains of non-toxigenic Aspergillus flavus with the capability to solubilize phosphate can be beneficial in promoting both the agronomic growth parameters and increasing mineral nutrient content of maize plants.
The results obtained indicated that the A. flavus strains are efficient phosphate solubilizers and solubilize phosphate in broth culture to varying quantities. These results are similar to studies done by [24,25]. They all reported fungi that belong to the genus Aspergillus as phosphate solubilizers. Also, in a study by [26], it was reported that Aspergillus spp showed diverse levels of phosphate solubilization activity in broth culture using different mineral sources. Thus, it was explained that this solubilizing ability is due to their production of phosphate-degrading enzymes.
Besides, the results obtained for maize plant growth improvement showed that plant heights of the A. flavus strain treated pots were found to be more than the untreated control plant. Also, the germination percentage, shoot length, the number of leaves produced, as well as the maize grain yield at harvest were enhanced by the A. flavus strains inoculation treatment compared to the un-inoculated control. The results from our findings on the improvement of agronomic growth parameters correlate with reported outcomes of investigations of [27,28]. They reported that phosphate solubilizing fungi can increase plant heights in pot experiments and under field conditions. The results correlate with findings obtained by [29,30], whose work focused on the influence of fungi phosphate solubilizers on yield and nutritional content of maize (Zea mays L) and wheat (Triticum aestivum L). Their findings also recorded enhanced dry matter production of maize when inoculated with Penicillium spp and Aspergillus awamori.
Wang X [31], also noted that the application of phosphate-solubilizing fungi increases the growth of planted crops. Fungi that solubilize phosphates enhance agronomic growth parameters of planted crops and are key components of global sustainable agroecological productivity [32]. Their deployment as biofertilizers improve phosphate availability to crops and reduces the number of synthetic phosphate fertilizers required for planted crops [33,34]. Phosphate solubilizing fungi improve the growth of plants by the production of vital biomolecules like lytic enzymes, ACC deaminase, antimicrobial substances, siderophores, hormonal production, hydrogen cyanide, among others [35,36,37,38,39].
The main mechanism of action of phosphate solubilizing fungi is by secretion of organic acids that chelates with phosphate ions, thereby releasing soluble phosphate [40]. Organic acids, thus, secreted, acidify the soil environment and thus solubilizing insoluble orthophosphate ions to soluble phosphate ions that plants can easily assimilate [41,42]. Our findings in this investigation of improvement in agronomic growth parameters and nutritional elemental contents of maize attributable to phosphate solubilizing Aspergillus flavus strains with biofertilizer capabilities further corroborates earlier research reports of phosphate solubilizers beneficial impacts on different crops [43,44,45].
Despite the impressive results obtained in this pot experimental trial of using phosphate solubilizing Aspergillus flavus strains to improve agronomic yield and nutritional content of maize plants, there is still ground to cover and questions needing answers. Further research studies on the improvement of phosphate solubilizing fungi at the genomic level to determine the genes that regulate phosphate solubilization need to be investigated. Also, experimental field studies on fungus' phosphate solubilizing ability to enhance the maize growth considering abiotic and biotic stressors should be looked into.
5.
Conclusion
Results from these investigations indicated that mutated strains of Aspergillus flavus are efficient phosphate solubilizers and that when used as bioinoculants on maize plants, can lead to higher beneficial influence on agronomic yield and mineral nutrients composition in maize compared with the un-inoculated control. An addition to existing knowledge of using microbial inoculants as an alternative to synthetic phosphate fertilizer is highlighted in this study. Therefore, more research into diverse ecological habitats for beneficial microorganisms that can serve as biofertilizing agents/alternatives to synthetic agrochemicals for maize yield enhancement should be explored.
Acknowledgments
The authorities in LAUTECH and (NSPRI), Nigeria, are well appreciated.
Conflict of interest
The authors had no potential contrary interest.









 DownLoad:
DownLoad:


