Tuberculosis (TB) is a global emergency. The World Health Organization reports about 9.2 million new infections each year, with an average of 1.7 million people killed by the disease. The causative agent is Mycobacterium tuberculosis (Mtb), whose main target are the macrophages, important immune system cells. Macrophages and T cell populations are the main responsible for fighting the pathogen. A better understanding of the interaction between Mtb, macrophages and T cells will contribute to the design of strategies to control TB. The purpose of this study is to evaluate the impact of the response of T cells and macrophages in the control of Mtb. To this end, we propose a system of ordinary differential equations to model the interaction among non-infected macrophages, infected macrophages, T cells and Mtb bacilli. Model analysis reveals the existence of two equilibrium states, infection-free equilibrium and the endemically infected equilibrium which can represent a state of latent or active infection, depending on the amount of bacteria.
1.
Introduction
Organic acids are a vital part of the chemical composition of wine because of their strong influence on the wine flavor, aroma and stability. Titratable acidity, volatile acidity and pH are important wine properties of total acidity, however understanding the chemistry of individual primary acids is critical to creating a sensory wine profile [1]. High-performance liquid chromatography (HPLC) is a common analytical method used to separate and quantify these organic acids. Many analytical methods have been developed and optimized to separate these organic acids through HPLC in matrices other than wine, such as olive oil [2], soil [3] and citrus juice [4]. The HPLC methods are similar to methods used for wine analysis. Several works were reported on quantifying acids in wines based on color [5], grape variety [6] or wine brand [7]. There have also been studies that focused on quantifying acids in wines from specific locations, such as Hungary [8] and Portugal [9]. Other studies have looked at how environmental factors, such as climate change [10], climate influences [11], geographical origin [12], temperature [13], and season [14] affect the wine production, composition and quality.
One wine-producing region in particular that has yet to be studied in terms of organic acid content is the Annapolis Valley in Nova Scotia, Canada. Climate is one of the most important factors that determines what type of grapes can grow in a specific region, which is why cooler-climate wines may differ so vastly from warmer-climate wines [15]. While the ideal wine-making climate is usually characterized by places such as the Bordeaux region of France, Spain, Italy, Napa Valley in California and regions of southern Australia, cooler-climate areas are still able to produce wines with very distinct characteristics [16]. One way that cooler-climate regions can be categorized is by a mean temperature below 20 ℃ during the warmest month of the year [16]. In wine-making regions of Nova Scotia, the Labrador Current ensures cool temperatures in the summer and very cold temperatures in the winter (Table 1), which poses certain limitations on the grape variety that can be successful grown and wine type that can be produced [16]. For example, certain Vitis vinifera vines are susceptible to freezing injuries when subjected to temperatures below 0 ℃ in Nova Scotia's winter; however, this climate limitation may be beneficial to developing a large icewine industry in the area [16]. Since cooler climates cause the growing season to begin late, grape varieties in Nova Scotia may not reach maturity during harvest, thus producing lighter wines that are higher in acidity [16]. Further, temperatures in other provinces of Atlantic Canada (New Brunswick, Prince Edward Island and Newfoundland) are even lower than that in Nova Scotia, resulting in an inability to grow grapes. However, the wine industry in these provinces flourishes by using a variety of local ingredients such as blueberry, strawberry, apple, rhubarb and maple syrup.
The objective of this study was to characterize organic acid profiles of cold-climate wines in comparison to traditional warmer-climate wines. In this study, the organic acid composition of wines from Nova Scotia were compared to wines from warmer-climate regions to determine whether there were any significant differences, and wines of different grape type and fruit type were compared to determine acidic variation between wine types. This study quantified 10 organic acids: tartaric, pyruvic, malic, lactic, acetic, citric, succinic, fumaric, ascorbic and oxalic acids. In addition, acidity parameters such as pH, volatile acidity and titratable acidity were also included to characterize wine samples.
2.
Materials and methods
2.1. Chemicals
All chemicals were of reagent grade. Sodium hydroxide (≥98%), absolute ethanol (≥99.8%), phosphoric acid (≥99%), succinic acid (≥99%), L-(+)-lactic acid (≥98%) and pyruvic acid (≥98%) were purchased from Sigma-Aldrich Canada (Oakville, Canada). Sodium phosphate monobasic (≥99%), fumaric acid (≥99%), DL-malic acid (≥99%) and L-ascorbic acid (≥99%) were purchased from VWR (Mississauga, Canada). Acetic acid (≥99.7%) and oxalic acid (≥99%) were purchased from Fisher Scientific (Ottawa, Canada). Citric acid (≥99.5%) was purchased from ACP Chemicals (Montreal, Canada). Ultrapure water was used in preparing solutions and made in-house.
2.2. Samples and preparation
Wine samples were purchased from Nova Scotia Liquor Cooperation or supplied by the respective wineries. The types of wine included red, white, rose, icewine, rhubarb, apple, maple, blueberry, cloudberry, cranberry, strawberry, raspberry, black currant and berry blend. The wines were produced from a variety of locations including Canada (Nova Scotia, New Brunswick, Newfoundland), USA (California, Michigan), France, Spain and Australia. The vintage year of the samples ranged from 2007 to 2015. The wines that were studied are listed in Table 1 where the climate information were taken from climate-data.org [17]. A code was assigned to each wine in Table 1.
The wine samples were filtered through 0.45 μm PTFE membrane filter and diluted 1:10 in 10% ethanol before injection. Wine samples were stored in darkness at 4 ℃ before equipment analysis.
2.3. HPLC analysis
The organic acids were separated using reversed-phase high-performance liquid chromatography (RP-HPLC) [18]. An HP/Agilent 1050 HPLC with a multi-wavelength UV detector was used in the experiment. Chromatographic separation was performed using a 300 mm Restek Allure organic acid column with a particle size of 5 μm and an internal diameter of 4.6 mm. The flow rate was 0.5 mL/min and the sample injection size was 10 μL. The column was operated at 35 ℃, and the samples were eluted isocratically with a 100 mM phosphate buffer solution at pH 2.5. To optimize the sensitivity of measurement, a detection wavelength of 230 nm was used to determine the absorbance peaks of ascorbic acid and fumaric acid, while a detection wavelength of 215 nm was used to determine the absorbance peaks of the other eight organic acids.
Five-level calibration curves up to 1000 mg/L were prepared daily to ensure the quality of the HPLC-UV calibration. A linear regression was used for most acids, except for citric acid and acetic acid, which used a quadratic regression. Quality control samples including blank samples and spiked control samples that were measured after the calibration and between every seven samples to verify the accuracy of the calibration curve. Recoveries for all the compounds in the control samples were in the range of 89% to 114%.
2.4. Titratable acidity (TA), pH and volatile acidity (VA)
The pH of the wine was measured using a HACH HQ30-D Portable Meter with a PHC101 pH Electrode. The titratable acidity was measured for each wine sample by titrating the sample against 0.1 M NaOH. During titrations, the pH was recorded using the pH meter and the equivalence point was determined from the pH titration curve. The total titratable acidity was reported as lactic acid in g/L.
The volatile acidity was measured using a cash still method [19], and the distillate collected was titrated against 0.1 M NaOH. The equivalence point was determined by phenolphthalein indicator, and the volatile acidity was reported as acetic acid in g/L.
Quality control samples of lactic acid and acetic acid were used in the determination of the titratable acidity and volatile acidity, respectively. The recoveries for these compounds ranged from 94% to 112%.
2.5. Statistics and principal component analysis
All statistical tests were performed using OriginPro 2015. Ascorbic acid and oxalic acid were not included in any statistical test, except for principal component analysis (PCA) with berry and other wines, because they were not detected. Analysis of variance (ANOVA) was applied to the parameters studied, and the mean values were compared by one-way ANOVA with a 95% confidence level to determine whether mean differences were statistically significant. A p-value less than 0.05 signified a statistically significant difference in the mean. A Spearman's correlation rank was used to determine the strength of correlation between parameters with a 95% confidence level. Spearman's coefficients (ρ) were interpreted as very weakly (0–0.3), weakly (0.3–0.5), moderately (0.5–0.7), strongly (0.7–0.9), and very strongly (0.9–1.0) correlated. PCA was performed on the data to highlight dominant patterns in the data matrix in terms of complementary set of scores and loading plots [5].
3.
Results and discussion
3.1. Categorization of wines
For the purpose of this study, the wines were separated in two different ways. The first division was by wine types in five categories: Red, berry, white, rose and other. Other wines included rhubarb, maple, apple and icewine, which were only analyzed in PCA. Separation by wine type was necessary, because different grapes or fruits used to produce wine have diverse naturally occurring acids and unique fermentation processes, which yield distinctive experimental and statistical results.
The second type of categorization was based on average annual temperature, which was influenced by location. The grape wines from Nova Scotia wine-making region, Annapolis Valley, were placed in a category called NS, due to a much cooler climate with an average yearly temperature of 6.4 ℃ and a mean temperature below 20 ℃ during the warmest month of the year (Table 1). The grape wines from California, Australia, Spain and France were placed in the other category called other locations, because these locations have warmer climates, with average yearly temperatures ranging from 12.7 ℃ to 17.0 ℃ and a mean temperature above 20 ℃ during the warmest month of the year (Table 1). Climate, particularly temperature, was chosen as the criteria of the second type of categorization, because of its significant and well-understood effects on wine acid composition [16]. Warmer yearly temperatures allow for longer growing times and more grape maturation, while cooler yearly temperatures reduce growing times leading to less mature grapes [16]. As a grape enters veraison, the overall acidity decreases, while its sugar content increases [16]. Therefore, it is expected that cooler climate wines are produced from less ripe grapes and have a greater acidity level than warmer climate wines. For the purposes of this study, conclusions were drawn based on measured acid concentrations, which might include some supplementary acids added by vintners during wine-making.
Although representative wine samples were selected, however, not all regions or types of wines could be covered in this study. Further, some wines might be made of or mixed with grapes grown in other provinces, states or countries. This information of grape sources for wine samples used in this study was not available. The complexity of grape sources could add uncertainty in discussion on the impact of climate. However, regulations of most jurisdictions and winery associations do not allow their wines to be made of foreign grapes or limit foreign grapes to a small fraction only.
In many cold-climate regions in Canada, fruit wines made of various berries become an important agricultural product with local characteristics. Fruit wines have different chemical composition in comparison to grape wines. For example, tartaric acid is a primary organic acid in grape and citrus fruits, but it is not common in other fruits [20]. Fruit wines were included in this study because they are important for cold climate oenology, but one should keep in mind that they are different to grape wines.
3.2. Statistical analysis
Table 2 shows the average concentration and standard deviation for each parameter studied based on type of wine and location. In a comparison of wine types, red wines were on average relatively high in lactic acid (4.65 ± 2.45 g/L), volatile acidity (0.74 ± 0.19 g/L) and acetic acid (125 ± 32 mg/L), while they were relatively low in malic acid (0.584 ± 0.311 g/L) and pyruvic acid (11.2 ± 6.5 mg/L). Berry wines showed the greatest variation among the four types of wine, with very high relative mean concentrations of citric acid (1.48 ± 1.08 g/L) and pyruvic acid (44.9 ± 18.9 mg/L), and very low mean concentration of tartaric acid (0.0313 ± 0.0827 g/L) and malic acid (0.462 ± 0.101 g/L). White and rosé wines were similar with relatively high average titratable acidity (8.23 ± 1.35 g/L and 10.24 ± 2.27 g/L, respectively) and malic acid (1.98 ± 0.93 g/L and 3.71 ± 2.12 g/L, respectively), and relatively low mean concentrations of volatile acidity (0.47 ± 0.18 g/L and 0.40 ± 0.08 g/L, respectively). For wine locations, NS wines had relatively high mean concentrations of lactic acid, titratable acidity and malic acid (4.55 ± 2.50 g/L, 9.63 ± 1.51 g/L and 2.01 ± 2.12 g/L, respectively) compared to other locations. In cold climate, malic acid and lactic acid have a low rate of degradation, while the rate is considerably faster in hot weather [20]. On average, wines produced in other locations were moderately higher in succinic acid and pyruvic acid (0.955 ± 0.388 g/L and 17.0 ± 8.9 mg/L, respectively) compared to NS wines.
For type of wine, one-way ANOVA tests showed that the mean differences among the parameters were statistically different (2.5 × 10−10 < p < 0.033), except for fumaric acid (p = 0.59). For the categorization based on climate, one-way ANOVA tests showed that titratable acidity (p = 3.9 × 10−5) and lactic acid (p = 0.0037) were the only parameters that had statistically significant mean differences. The mean values of both of these parameters were significantly higher in NS wines than that in other locations, which suggests that shorter ripening times for cooler-climate wines might result in higher acidity.
Spearman's rank correlation determined the strength of correlation between the different parameters for all the wines in one data set. Pyruvic acid had a moderate negative correlation with lactic acid (ρ = −0.544), and volatile acidity had a moderate positive correlation with acetic acid (ρ = 0.682). Volatile acidity is primarily composed of acetic acid, so the positive correlation between the two parameters was expected. Strong and very strong correlations (ρ > 0.7) were not found between any of the parameters, suggesting that most organic acids exist independently in wines.
3.3. Multivariate analysis
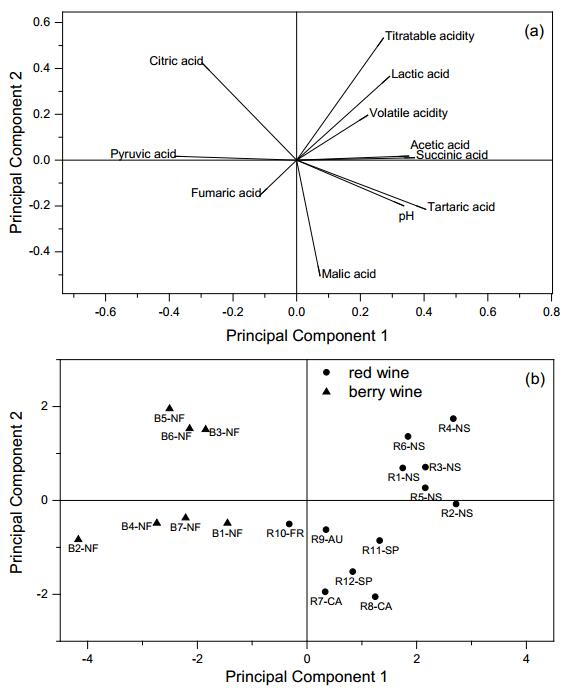
Principal component analysis (PCA) was performed on three sets of data separated by wine type: Red vs. berry, white vs. rose, and berry vs. other. For the first PCA test on red vs. berry wines (Figure 1), eigenvalues for the first four principal components (PC) accounted for 64.4% of the total variance, while PC1 and PC2 accounted for 34.5% and 11.7% of the total variance, respectively. Ascorbic acid and oxalic acid were not included because they were not detected in these wine samples. From the loadings of the variables (Figure 1a), tartaric acid (0.405) and succinic acid (0.370) were the dominant features in PC1. Titratable acidity (0.532) and citric acid (0.424) were the dominant features of PC2. In examining PCA scores of red and berry wine samples in a two-dimensional plot of the first two PCs (Figure 1b), the largest separation was found between wine types (red vs. berry) and then between locations. All of the red wines except R10-FR are located in the positive part of PC1, while all the berry wines are located in the negative part of PC1. According to the loading plot in Figure 1a, the red wines located in the positive part of PC1 were relatively higher in TA, tartaric acid, succinic acid and lactic acid compared to berry wines. According to Figure 1a, the berry wines located in the negative part of PC1 were relatively higher in citric acid and pyruvic acid concentration compared to red wines. The wines were separated even further in Figure 1b by location and type of berry. The Nova Scotia wines were grouped in the positive part of PC2, with the exception of R2-NS; however, this wine was still in close proximity to the other Nova Scotia wines. The wines from other locations were all grouped in the negative part of PC2. According to the loading plot in Figure 1a, the Nova Scotia red wines were relatively higher in TA and lactic acid, while the red wines from other locations were relatively higher in malic acid. The data suggests that the separation of red wines in Figure 1b could be due to climate factors, because cooler climate grapes have less time to mature, leading to higher total acidity levels. The berry wines were also separated based on type of berry, with the cranberry, raspberry and black currant wines in the positive part of PC2 and the blueberry, cloudberry, strawberry and berry blend wines in the negative part of PC2.
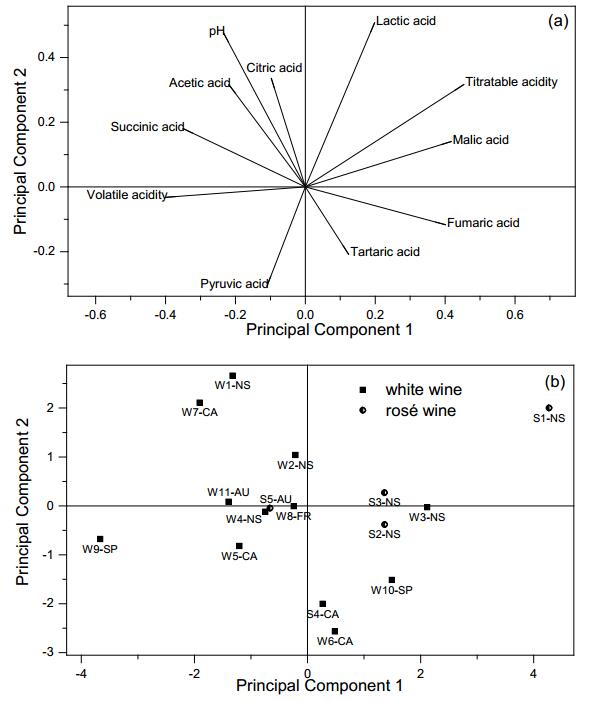
The white and rose wines were analyzed together using PCA and examined in two-dimensional plots in Figure 2. Ascorbic acid and oxalic acid were not including because they were not found in white and rose wines. Eigenvalues of the four major PCs accounted for 65.5% of the total variance. From the loadings of the variable, titratable acidity (0.453) and malic acid (0.417) were the dominant features in PC1, accounting for 26.8% of the total variance. Lactic acid (0.507) was the dominant feature of PC2, accounting for 15.8% of the total variance. In Figure 2b, the separation between white and rose wines was not clear, with 80% of the rose wines in the positive part of PC1 and 73% of white wines in the negative part of PC1. The loading plot in Figure 2a suggests that rose wines had relatively higher concentrations of lactic acid, malic acid and TA, compared to the white wines. There was no significant separation based on location, suggesting that grapes used for rose and white wines might be less differentiated due to climate variation.
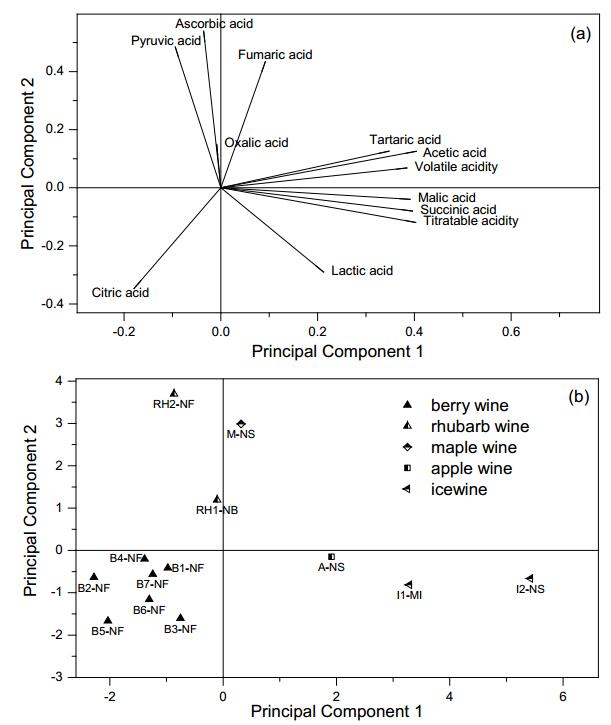
The berry and other wines were analyzed together using PCA of all the parameters except pH. Results are examined in two-dimensional plots in Figure 3. Four major PCs with eigenvalues higher than 84.9% of the total variance were obtained. From the loadings of variables (Figure 3a), acetic acid (0.403), titratable acidity (0.403), succinic acid (0.396) and malic acid (0.391) are the dominant features in PC1, accounting for 42.2% of total variance. Pyruvic acid (0.484) was the dominant feature of PC2, accounting for 22.7% of total variance. In Figure 3b, it is evident that berry wines were well separated from the other wines and grouped together in the negative part of PC1 and PC2, which was indicative of relatively high citric acid concentration, according to the loading plot in Figure 3a. The rhubarb wines were both found in the positive part of PC2 and the negative part of PC1, which suggested relatively high oxalic acid and ascorbic acid concentrations. Oxalic acid is commonly found in rhubarb wines, because oxalic acid is present in high concentrations in rhubarb fruit [21]. The maple wine was closest to the rhubarb wine; however, it was in the positive part of PC1 and PC2. The icewines were in close proximity to the apple wine, which were all located in the positive part of PC1 and the negative part of PC2. This indicated relatively high malic acid, TA and lactic acid, as shown in the loading plot in Figure 3a. High malic acid concentrations were expected in apple wine, due to the high concentration of the acid in apple fruit [22]. High TA is common in icewine due to the specialized wine-making process of the wine [23]; however, the Nova Scotia icewine appeared to be more acidic than the Michigan icewine, which might be related to Nova Scotia's lower average yearly temperature of 6.4 ℃ compared to 9.8 ℃ in that region of Michigan.
Winemaking technologies can introduce considerable difference in chemical composition of wines. Organic acids in grape may not be transferred directly to finished wine. Yeast and bacteria can break down or create organic acids in the fermentation process. For example, malic acid and lactic acids in red and white wines are related to malolactic fermentation [20]. The impact of fermentation will be further investigated in future research.
4.
Conclusion
The analysis of ten organic acids was performed using HPLC-UV on 41 wines grouped in categories based on either wine type or winery location. Red wines were on average relatively high in lactic acid (4.65 ± 2.45 g/L) and relatively low in malic acid (0.584 ± 0.311 g/L), while berry wines had very high mean concentrations of citric acid (1.48 ± 1.08 g/L) and very low mean concentrations of tartaric acid (0.0313 ± 0.0827 g/L). On average, white wines were relatively high in titratable acidity (8.23 ± 1.35 g/L) and relatively low in volatile acidity (0.47 ± 0.18 g/L). Rose wines had very high mean concentrations of malic acid (3.71 ± 2.12 g/L) and low volatile acidity mean concentrations (0.40 ± 0.08 g/L), compared to other wine types. For wine locations, NS wines were on average relatively high in lactic acid (4.55 ± 2.50 g/L), titratable acidity (9.63 ± 1.51 g/L) and malic acid (2.01 ± 2.12 g/L), compared to other locations.
One-way ANOVA tests showed that among the different types of wine, the mean differences of the parameters were all statistically significant (2.5 × 10−10 < p < 0.033), with the exception of fumaric acid (p = 0.59) and ascorbic and oxalic acid. When analyzing only NS wines and other location wines, titratable acidity (p = 3.9 × 10−5) and lactic acid (p = 0.0037) were the only parameters with mean differences that were statistically significant. Both these parameters had higher mean concentrations for NS wines compared to other location wines. PCA was able to produce a very strong separation between red and berry wines, as well as a strong separation between red wines from NS and other locations. This significant difference between the red wines from NS compared to other locations could be due to cooler climate grapes having less time to mature, leading to higher acidity levels.
Acknowledgements
The authors would like to acknowledge support provided by Acadia University and the Natural Sciences and Engineering Research Council of Canada (NSERC).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: