Feedback loops are found to be important network structures in
regulatory networks of biological signaling systems because they are
responsible for maintaining normal cellular activity. Recently,
the functions of feedback loops have received extensive attention.
The existing results in the literature mainly focus on verifying
that negative feedback loops are responsible for oscillations,
positive feedback loops for multistability, and coupled feedback
loops for the combined dynamics observed in their individual loops.
In this work, we develop a general framework for studying systematically
functions of feedback loops networks. We investigate the general
dynamics of all networks with one to three nodes and one to two feedback loops. Interestingly, our results are consistent with Thomas' conjectures although we assume each node in the network undergoes a decay, which corresponds to a negative loop in Thomas' setting. Besides studying how network structures influence dynamics at the linear level, we explore the
possibility of network structures having impact on the nonlinear
dynamical behavior by using Lyapunov-Schmidt reduction and singularity theory.
1.
Introduction
Phosphorus (P) is an important element in crop production underpinning global food security. Its deficiency is widely considered a major biophysical constraint to food production on large areas of farmland in sub-humid and semi-arid Africa [1,2]. Phosphorus dynamics in soil is complex, involving both chemical and biological processes and the long-term effects of sorption and desorption processes. Therefore, the characterization of soil capacity to sorb phosphate is a prerequisite for phosphorus fertilizer recommendation particularly in the Sahelian acid soils of Africa with high risk of soil phosphorus sorption.
Availability of phosphorus is primarily dependent on soil pH. At low pH (<5.5), soils have greater amounts of iron and aluminum oxides which can complex phosphate ions. Under such low conditions, variscite and strengite are likely regulating factors of inorganic P solubility [3]. In neutral-to-calcareous soils, P retention is dominated by precipitation reactions [4] with P adsorbed on the surface of calcium carbonate and clay minerals [5]. Phosphorus-sorption processes in soils contribute to important problems in agriculture, which may be a deficiency of the nutrient or its eutrophication in aquatic systems [6]. Low P use efficiency is a common problem in crop production, due to strong P fixation mechanisms through sorption or precipitation reactions in soils [7].
The use of Tilemsi phosphate rock has been suggested as P fertilizer for smallholder farmers by many researchers for crop production. However, there is a dearth of published information on phosphorus sorption characteristics under this important soil amendment in the Sahelian zone of sub-Saharan Africa (SSA). The few studies on Tilemsi phosphate rock reported in literature were limited to its uptake under solubilizing microorganisms [8] and economic and agronomic evaluation of its use [9]. This is despite the rising interest in its use by crop farmers in SSA due to increasing mineral fertilizer prices globally. In this study, we evaluated the P-sorption capacity of TPR on major soils in Sahelian zone of Mali. The study also evaluated grain yield under different forms of the TPR (powder and pellet) in comparison with water-soluble phosphorus (diammonium phosphate) at different rates of application. We hypothesized that the different P forms applied to the Sahelian soils at varied rates will result in differing P availabilities and grain yields.
2.
Materials and methods
2.1. Soil sampling
Samples from four soil series, i.e., Longorola (Gleysol), Danga (Fluvisol), Niessoumama (Arenosol) and Konobougou (Acrisol) [10], were collected from farmers' fields at 0–20 cm depth. These are representative soils for crop production across the Sahelian zone of Mali [11] and are mainly used in the cultivation of arable crops. Sorghum (Sorghum bicolor) is mainly grown in rotation with pearl millet (Pennisetum glaucum) on the Acrisol and the Arenosol and rice (Oryza sativa) on the Gleysol and Fluvisol. Soil samples were analyzed for particle size distribution using the pipette method described by [12]. Soil pH was measured in 1:1 soil:water ratio using a pH meter (Mahita Model 907). Organic carbon was determined by wet dichromate oxidation with sulphuric acid [13]. Exchangeable bases (Ca2+, Mg2+, K+ and Na+) were determined in 1.0 M ammonium acetate extract. Exchangeable acidity (H+ and Al3+) was determined in 1.0 M KCl extract [14].
2.2. Phosphorus sorption isotherm
Five grams of each soil was equilibrated for seven days at 25 ± 2 ℃ in 50 mL of 0.01 M calcium chloride (CaCl2) solution containing six rates of P from finely ground Tilemsi phosphate rock (0, 10, 20, 40, 80,160 mg/L) and 2 drops of formol. The mixture was stirred well to allow for complete dissolution of the finely grounded phosphate rock. The mixtures were placed in 50 ml centrifuge tubes and shaken for 30 minutes twice daily [15]. The soil samples were replicated four times. A control (equilibrium with soil sample and calcium chloride solution with 0 mg/L of Tilemsi phosphate rock) was incubated for each soil and similarly treated. After the seven days of equilibration, the supernatants were filtered through micropore filter paper (Whatman No. 42) and analyzed for P using Technicon Auto Analyzer Ⅱ.
The quantity of P sorbed in soil was assumed as the difference between P initially added and P in the supernatant solution. Phosphorus sorption curves were fitted from P sorbed in the soil and P in the filtrate using the Langmuir sorption isotherm.
2.3. Evaluation of sorption data
The linear form of the Langmuir surface equation was used to calculate parameters that are indices of the capacity for, and the intensity of, P sorption by the soil. The Langmuir model isotherm Equation (1) is widely used for modeling adsorption equilibrium data. The linearization method is mostly applied for estimation of the Langmuir parameters [16].
where C is the concentration of P in equilibrium solution (mg P/mL), X is the amount of P remaining in soil (mg P/kg soil), Xm is the sorption maximum (mg P/kg soil) and KL is the coefficient related to bonding energy. The sorption maximum (Xm) was calculated from the reciprocal of the slope (Xm = 1/slope) of the adsorption isotherms. This parameter reflects the magnitude of sorption sites available for P adsorption. Degree of phosphorus saturation (DPS) was computed as per [17] below.
2.4. Filed experiment
A field experiment was conducted in two consecutive cropping seasons (i.e., 2 years, one season per year) on the same plots to investigate the effects of P application on crop yield. This was considered to show how the physical forms of the P fertilizer (i.e., powder TPR vs. granulated TPR vs. water-soluble P fertilizer) affect P dissolution/availability and grain yield in the Sahel.
The experiment was carried out on the Acrisol also used for maize production in the Sahel. The field experimental site (Konobougou, 12°55′N, 6°46′W) is characterized by lateritic uplands alternating with gentle slopes and lowlands, in which rainfall ranges from 600 to 800 mm [18] whilst the length of growing season ranges from 90 to 100 days. The area is characterized by a high amplitude maximum temperature of 42 ℃ and a minimum of 24 ℃ in December to January and an average of 32 ℃ in May. The area experiences alternating two main seasons: the dry season and the rainy season [19]. The topography of the region is dominated by flat surfaces with an average altitude of about 300 m and hills that seldom exceed 400 m in altitude.
The field experiment was a factorial combination of three rates of phosphorus: (ⅰ) 0 kg/ha (control), (ⅱ) 11 kg/ha and (ⅲ) 16 kg/ha and three types/forms of phosphorus: (ⅰ) TPR powder, (ⅱ) TPR pellet (ⅲ) and water-soluble diammonium phosphate (Table 1) in a randomized complete block design (RCBD) with three replications.
2.5. Fertilizer application
Tilemsi phosphate rock pellet, powder and DAP were applied at 11 kg of P/ha and 16 kg of P/ha and KCl at 30 kg K/ha incorporated into the surface soil prior to planting. Both the powdered and pellet forms of the TPR used had P2O5 composition of 28% (Table 2). The TPR pellets had an average diameter of 2 mm. Urea was applied at 150 kg N/ha in splits. To balance the rate of nitrogen from the DAP (18 kg N/100 kg), the same amount was calculated from urea and applied to other plots except the control plots.
2.6. Planting and harvest
Seeds of Sotubaka maize variety were obtained from the "Programme Maïs" of Sotuba Research Center (IER). The growth period is 90–100 days. The maize seeds were sown using hoes at spacing of 50 × 70 cm within the incorporation zone of fertilizer (2–7 cm beneath the soil surface). Four seeds were sown per hill and seedlings were thinned to two per hill two weeks after sowing. Three middle rows from each plot were harvested at physiological maturity to evaluate grain yield. The harvested (net plot) area was 4.2 m2. Grain yield per plot was converted to kg/ha.
2.7. Data analysis
Relationships between P sorption parameters and selected soil chemical properties were correlated. Data on maize grain yield was subjected to Analysis of Variance (ANOVA) using GenStat statistical software (9th edition). Significant differences between treatment means were established at p = 0.05 using the Duncan's multiple range test (DMRT).
3.
Results
3.1. Soil characterization
The organic matter content of the soils ranged from 1.0% in Konobougou to 2.7% in Langora series (Table 3). Soil available P content of Longorola (Gleysol) and Konobougou (Acrisol) were below 5.0 mg/kg soil whilst that of Danga (Fluvisol) and Niessoumana (Arenosol) were ≥10 mg/kg soil. All soils had a clay content < 25 % except the Gleysol (45%). Soil pH ranged from 4.3 to 9.0 and exchangeable acidity from 0.03 to 0.43 cmolc/kg soil, with the highest value recorded in the Longorola soil (the Gleysol).
3.2. Phosphorus sorption isotherm and degree of phosphorus saturation
The phosphorus sorption varied among the four soils (Table 4). The Longorola soil (Gleysol) with the highest clay and organic matter contents exhibited the highest P sorption. The linearized Langmuir sorption model described adequately the sorption behaviour (R2 ≥ 0.78) of the soils (Table 4). Sorption maxima ranged from 59 to 200 mg P/kg while sorption affinity constant ranged from 0.30 to 1.66 mg/L (Table 4). The degrees of phosphorus saturation were generally low and ranged from 2.39% in the Gleysol to 6.47% in the Arenosol with high sand content (Table 4).
3.3. Relationship between P sorption parameters with soil properties
Soil clay, organic matter content, exchangeable acidity, potassium and aluminium saturation were positively correlated with P sorption parameters (Xmax and KL) (Table 5). Exchangeable acidity was positively correlated (r = 0.95) to the sorption affinity constant. Similarly, a positive and strong relationship (r = 0.91) was observed between SOM and the sorption affinity constant. A weak positive relationship was observed between soil pH and sorption maxima (r = 0.19).
In this experiment, the principal component (PC) analysis partitioned the total variance into four components contributing maximum to the total variability of the phosphorus absorption maximum (X max) among the soil chemical traits. The analysis showed first 2 PCs having Eigen values > 1, explaining 96.65% of the total variation (Table 6). The first principal component (PC1), which explained 72.05% variation, was associated mainly with soil acidity (Al + H), aluminium saturation, clay content, soil organic matter and silt content. The second principal component (PC2) was responsible for about 24.60% of the variation and was mainly related to Ca, K, Na and soil pH.
3.4. Effect of soil amendments on soil available phosphorus content
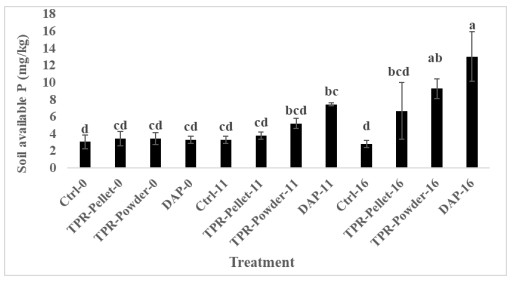
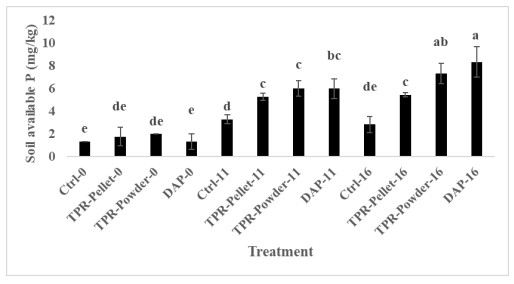
Soil available P (Bray-1 P) was measured from the field plots at the end of each cropping season (Figures 1 and 2). The interaction between phosphorus fertilizer type/form and rate of application significantly (p < 0.001) influenced soil available P content (Figure 1). In the first year of experimentation and for the phosphorus types used (DAP and TPR), there was an increase in available P content with increased P application (Figure 1). At both 11 and 16 kg/ha rates of phosphorus application, DAP treated plots produced similar soil available P contents as TPR powder treatment which were significantly higher than levels observed in TPR pellet treated plots.
3.5. Effect of P forms and rate of application on maize grain yield
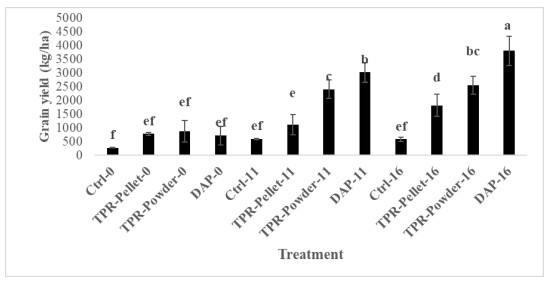
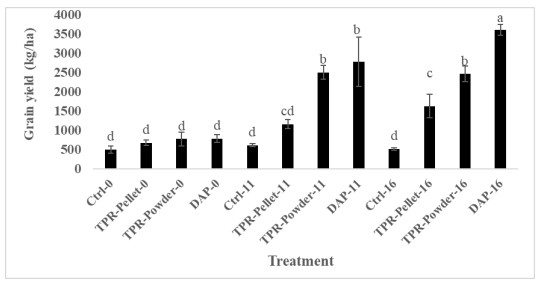
A general increase in maize grain yield was observed in phosphorus-treated plots in both seasons of experimentation (Figures 3 and 4). Significant difference was observed in maize grain yield between DAP and the TPR forms in both seasons at 11 and 16 kg P/ha (Figures 3 and 4). Tilemsi phosphate rock in powder form produced significantly greater grain yield than TPR in pellet form and the control at both 11 and 16 kg P/ha during the two growing seasons (Figures 3 and 4). The DAP increased grain yield by about 40% over Tilemsi phosphate rock in the pellet form at 16 kg P/ha in both seasons (Figures 3 and 4).
4.
Discussion
Soil clay and soil organic matter contents influenced P adsorption (Table 5). The influence of clay content on P sorption has been previously reported in both tropical and temperate soils [20,21]. It is well established that P in soil solution reacts with soil minerals and its sorption and desorption processes are influenced by soil aggregate size [21]. Due to its colloidal nature and greater surface area, the presence of clay favours soil reactions. According to [22], the sorption of phosphate onto the clay or soil systems occurs mainly through chemical precipitation. In this regard, the phosphate ion reacts with iron and aluminum at low pH, forming insoluble compounds belonging to the variscite-strengite isomorphous series [3]. This Al3+ may occupy exchange sites of the clay and, in part, enter solution to react with the phosphate ion. This seems to explain the positive relationship observed between Al saturation and P adsorption maximum (Tables 5 and 6). In an earlier study, Borggard et al. [23] reported close relationship between soil capacity to adsorb phosphate and the soil aluminium oxides content. At higher pH, phosphate ions may be precipitated by calcium and magnesium present in the soil or clay solution [5]. The sorption of phosphate to clay has also been attributed to negative anion adsorption mechanism [22].
The strong relationship observed (r = 0.67; Table 5) between organic matter and P sorption maxima is indicative of its role as constituent of the soil sorption complex responsible for binding of anions [6]. Yang et al. [24] reported direct influence of organic matter on adsorption of phosphorus in a black soil in northern China. Also, [25] observed that the amount of P adsorbed increased when SOM was removed from an Andisol, indicating that SOM occupied sites that could adsorb P through competitive adsorption. From our study, the Gleysol with the highest amount of SOM had the highest P sorption capacity whilst the Acrisol with the least SOM content exhibited the lowest P sorption. Our results (Table 5) also showed a positive relationship (r = 0.53) between P adsorption maximum and the bonding energy KL. The P bonding energy (KL) is a key parameter describing the affinity of soil for P [26] with a higher KL value indicating stronger P adsorption [27]. These observations seem to suggest that the presence of SOM provided additional sorption sites in the soil. According to [28], the influence of SOM on P sorption may comprise four key processes involving (1) competition between SOM and P for mineral adsorption sites, (2) complexation of surface metals and release into solution thereby decreasing adsorption sites, (3) increased repulsion of phosphate anions by sorbing SOM to positive sorption sites and (4) formation of cation bridges leading to increases in P sorption sites. We observed strong correlation between organic matter and clay (r = 0.97, Table 5), indicating strong organo-mineral interaction.
Our results seem to show initial P levels of the four soils exerting a controlling influence on P sorption capacities (r = 0.59, Table 5). Although soil available P contents were generally low, the relatively higher contents in Danga and Niessoumana (≥10.0 mg/kg) than in Longorola (4.79 mg/kg) may have accounted for their relatively lower P sorption capacities than Longorola soil. The differences in the initial soil P levels may have arisen principally from differential P inputs as part of cropping histories of the soils. It has been shown that previous application of P reduces a soil's capacity to adsorb further P due to its slow movement through the soil [29]. In this respect, [15] reported that a portion of the previously added P had been converted into a form which occupied P adsorption sites, blocking them from further reaction. Results reported by [15] revealed that with past P fertilizer application, uncultivated soil could sorb 1.5 times more P than cultivated soil.
The sorption behaviour of the soils studied was adequately described by the Langmuir model with R2 values ≥ 0.78. The appropriateness of the Langmuir equation to describe the sorption of the soils suggest that adsorption is the dominant mechanism of P retention in these soils [30]. Phosphorus adsorption maxima were influenced by some soil properties (Table 6), showing positive correlations with clay content, SOM and aluminium saturation. The strong and positive correlation between P adsorption maxima and clay content (r = 0.78) was because as the level of clay in the soil increases, the number of fixation sites increases [31].
Soil pH negatively correlated with Langmuir constant of adsorption (KL), while a weak correlation was found between pH and P sorption maxima (Table 6). These results seem to be in close agreement with those reported by [32] on the relationship between P sorption and soil pH. Lalljee [33] and [34] reported negative correlation between P sorbed and pH and concluded that the availability of P is mostly dependent on soil pH. However, [35] argues that soil pH does not affect phosphorus retention directly and that it is a proxy that shows how minerals such as iron, aluminium and calcium interact with phosphorus and affect its availability and/ or retention.
In this paper, we also computed the degree of phosphorus saturation (DPS) which is a useful index for identifying soils at risk for P loading [36]. The DPS values observed were low for all the soils studied in the Sahel, being below the critical limit of 25%. The critical limit of 25% has been used to determine the surplus of P that can be applied to the soil before it gets saturated with phosphorus [36].
Grain yields under water-soluble DAP treatment were greater (p < 0.05) in both years of cropping than under pellet and powder TPR forms although P availability was similar in both DAP and TPR (powder) plots (Figures 1 and 2). This is despite attempt to balance the N difference between the two fertilizer types through addition of equivalent quantity of N from urea to the TPR treatments. Grain yield from grounded TPR (powder) increased over yield obtained under pelleted TPR suggesting the role of greater surface area in P availability and subsequent yield increase. Results (Figure 1) showed increased P availability in TPR powder plots over pelleted TPR. In tropical and subtropical acidic soils, low P availability is a factor limiting plant growth [37,38].
5.
Conclusions
Soil clay and organic matter contents played key roles in P sorption from TPR in the Sahelian soils. The sorption maxima under the amendment ranged from 59 to 200 mg/kg. The degree of phosphorus saturation was generally below the critical limit and was greater in the Arenosol than all soils. The TPR (powder) produced similar soil available phosphorus levels as the water-soluble DAP but with the DAP producing greater grain yields. The study provides useful information on P sorption characteristics of soils under TPR amendment which is limitedly studied and is useful for stakeholders towards crop yield improvement.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
We thank Alliance for Green Revolution in Africa (AGRA) for funding this work through the PhD research of the first author and the Laboratory of Soils and Plant Analysis of IER/ Sotuba, Mali for providing facilities for the analysis.
Conflict of interest
All authors declare no conflict of interest.









 DownLoad:
DownLoad: