Mean value of the Hardy sums over short intervals

1.   Introduction

The Sobolev equation plays an important role in partial differential equations (PDEs) because of its significant physical background, such as consolidation of clay ^[1], thermodynamics ^[2] and flow of fluids through fissured rock ^[3].

In this article, a Legendre-tau-Galerkin method in time and its multi-interval form will be considered for the following 2D Sobolev equations:

where coefficients $\mu$, $\varepsilon$, $\gamma$ are known positive parameters. Though the the time interval is normally (0, T] and $T > 0$, we set the interval as $I = (-1, 1]$ and the spatial domain is $\Omega = (-1, 1)\times(-1, 1)$. We consider the time interval $I = (-1, 1]$ just to simplify the presentation of the theoretical analysis and the algorithm implementation process.

Because of the great difficulty in obtaining analytical solutions of PDEs, various numerical methods ^[4,5,6,7] have been proposed to approximate the exact solutions. For the Sobolev equations, there have been many studies investigating the numerical solutions. In ^[8,9,10], some finite volume element methods were presented in space to solve the two-dimensional Sobolev equations combined with the finite difference schemes in time. The continuous interior penalty finite element method, space-time continuous Galerkin method and finite difference streamline diffusion method were applied in ^[11,12,13] for solving Sobolev equations with convection-dominated term, respectively. In ^[14], discontinuous Galerkin scheme in space and Crank-Nicolson scheme in time were considered for approaching the exact solutions of generalized Sobolev equations. In ^[15], Shi and Sun studied an $H^1$-Galerkin mixed finite element method for solving Sobolev equations and presented the existence, uniqueness and superconvergence results of the discrete scheme. In ^[16,17], a block-centered finite difference scheme and a time discontinuous Galerkin space-time finite element scheme for nonlinear Sobolev equations were established respectively, and stability and global convergence of the schemes were strictly proved. In ^[18], the Legendre spectral element method in space combined with the Crank-Nicolson finite difference technique in time were considered. In ^[19], the nonlinear periodic Sobolev equations were investigated by the Fourier spectral method.

As is well known, the spectral method is distinguished from other numerical methods by its exponential convergence, and when the spectral method is applied to time-dependent partial differential equations in both space and time (namely, space-time spectral method ^{[20,21,22,23,24,25]}), the mismatched accuracy caused by the spectral discretization in space and the finite difference method in time can be solved successfully. In ^[26], we constructed a space-time Legendre spectral scheme for the linear multi-dimensional Sobolev equations for the first time and the exponential convergence was obtained in both space and time. The main purpose of this paper is to study the multi-interval form of the Legendre space-time fully discrete scheme of two-dimensional Sobolev equations by dividing the time interval. It is worth noting that compared with the single interval method, the multi-interval spectral method ^[27,28,29] can adopt parallel computation, reduce the scale of the problem effectively and improve the flexibility of the algorithm. Considering the asymmetry of the first order differential operator, the fully discrete scheme is constructed by applying a Legendre-tau-Galerkin method in time based on the Legendre Galerkin method in space. In addition, we still apply the Fourier-like basis functions ^[30] in space to diagonalize the stiff matrix and the mass matrix simultaneously, which greatly saves the computing time and memory.

The organization of this article is as follows. In Section 2, we first provide some related notations, then establish the single interval Legendre space-time spectral fully discrete scheme of Eq (1.1) and give the stability analysis and $L^2(\Sigma)$-error estimates. In Section 3, we divide the time interval and develop the multi-interval Legendre space-time spectral fully discrete scheme of the equations, and then strictly prove the $L^2(\Sigma)$-error estimates. In Section 4, by using Fourier-like basis functions in space and selecting appropriate basis functions in time, we present the implementation of the multi-interval fully discrete scheme. In Section 5, numerical tests are included to access the efficiency and accuracy of the method. Finally, some conclusions are made in Section 6.

2.   Theoretical analysis of single interval Legendre spectral method in time

Throughout the paper, the Sobolev spaces in spatial directions are the standard notations used, namely,

where $\epsilon = (\epsilon_1, \epsilon_2)\; (\epsilon_i\geq 0$ are integers and $|\epsilon| = \epsilon_1+\epsilon_2)$, $D^\epsilon v(x, y) = \frac{\partial^{|\epsilon|}v}{\partial x^{\epsilon_1}\partial y^{\epsilon_2}}$ and $\|\cdot\|_{r, \Omega}$ is denoted by $\|\cdot\|_\Omega$ when $r = 0$.

The temporal direction involves a weighted Sobolev space $L^2_{\omega_{\alpha, \beta}}(I)$ endowed with the norm and product

where the weight function is $\omega_{\alpha, \beta}(t) = (1-t)^\alpha(1+t)^\beta$. If $\alpha = \beta = 0$, the norm $\|\cdot\|_I$ and inner product $(\cdot, \cdot)_I$ are denoted in the space $L^2(I)$.

Furthermore, the weighted space-time Sobolev space $L^2_{\omega_{\alpha, \beta}}(I; H^r(\Omega))$ is endowed with the norm

if $r = 0$, the norm $\|\cdot\|_{L^2_{\omega_{\alpha, \beta}}(I; H^r(\Omega))}$ is denoted by $\|\cdot\|_{L^2_{\omega_{\alpha, \beta}}(I; L^2(\Omega))}$; if $\alpha = \beta = 0$, the norm $\|\cdot\|_{L^2_{\omega_{\alpha, \beta}}(I; H^r(\Omega))}$ is denoted by $\|\cdot\|_{L^2(I; H^r(\Omega))}$; if $r = 0$ and $\alpha = \beta = 0$, the norm $\|\cdot\|_{L^2_{\omega_{\alpha, \beta}}(I; H^r(\Omega))}$ is denoted by $\|\cdot\|_{L^2(I; L^2(\Omega))} = \|\cdot\|_\Sigma$.

Let $P_\iota$ be a space of polynomials of degree $\leq$ $\iota$ on $[-1, 1]$ and $L = (M, N)$, where $M$ and $N$ are a pair of given positive integers. In order to develop the single interval Legendre spectral method in time, we define

Then applying the Green's formula, we obtain the following single interval Legendre space-time fully discrete scheme of (1.1): Find $u_L\in \mathbf{V}_N^0 \otimes P_M(I)$ satisfying

where $\mathbb{P}_N^1$ denote the spatial projection operator and its definition will be given below.

2.1.   Stability analysis

Firstly, we introduce the definition of spatial projection operator and the corresponding lemma. Next, we present the existence, uniqueness and stability conclusion for the solution of (2.5).

Definition 2.1. ^[31] Denote $H^1_0(\Omega) = \{v\in H^1(\Omega):v|_{\partial\Omega} = 0\}$, then the orthogonal projection in space $\mathbb{P}_N^1:H^1_0(\Omega)\rightarrow \mathbf{V}_N^0$ is given by

Lemma 2.1. ^[31] If $v\in H^1_0(\Omega)\cap H^r(\Omega)$ and $r\geq1$, we have

Theorem 2.1. Assume that $u_0(x, y)\in H^1_0(\Omega)\cap H^r(\Omega)\; \; (r\geq1)$ and $f \in L^2(\Sigma)$, then the scheme (2.5) has a unique solution $u_L$ satisfying

Proof. Taking $v = (1-t)\partial_tu_L(\in \mathbf{V}_N^0\otimes V_M)$ and using the integration by parts, we can get for the left-hand side of (2.5)

namely,

similarly,

Additionally, by the Cauchy-Schwarz inequality and Young's inequality, the right-hand side of (2.5) can be estimated as

Collecting (2.9)–(2.14) leads to

namely,

For initial conditions $u_L(-1)$ and $\nabla u_L(-1)$ in (2.16), according to Lemma 2.1, we can easily get the following estimate:

Thus, combining estimations (2.16) and (2.17), we immediately attain the stability conclusion.

Remark 2.1. From stability conclusion, there exists a zero solution if $f = 0$ and $u_0 = 0$. In other words, we can easily obtain the existence and uniqueness of $u_L$.

2.2.   Error analysis

The purpose of this section is to show an $L^2(\Sigma)$-error estimate of the single interval Legendre space-time spectral method by applying the dual technique. Now, we first introduce following definition and lemma of the time projection operator which will be covered later..

Definition 2.2. ^[28] The orthogonal projection in time $\boldsymbol{\Pi}_M:H^1(I)\rightarrow P_M(I)$ is given by

and $\boldsymbol{\Pi}_M u(-1) = u(-1)$.

Lemma 2.2. ^[28] (a) If $u\in H^\sigma(I)$ and $\sigma\geq1$, then

(b) If $u\in H^\sigma(I)$ and $\sigma\geq2$, then

Let $U = \mathbb{P}^{1}_N\boldsymbol{\Pi}_M u$. Now we decompose the error into: $u_L-u = (u_L-U)+(U-u)$ and denote $\tilde{u} = u_L-U$. So according to (2.5) we have

According to the Definitions 2.1 and 2.2, for the right-hand side terms of (2.21) we get

Then (2.21) can be simplified as follows:

According to the definition of $\tilde{u}$ and $\boldsymbol{\Pi}_M$, we note

Now, we give the $L^2(\Sigma)$-error estimates of the single interval Legendre space-time spectral scheme.

Theorem 2.2. Suppose $u_L$ and $u$ are the solutions of the scheme (2.5) and problem (1.1), respectively. If $u_0\in H^r(\Omega)\cap H_0^1(\Omega)$ and $u\in H^\sigma(I; H^r(\Omega)\cap H_0^1(\Omega))$ for integers $r\geq1$, then:

(a) For $\sigma\geq1$,

(b) For $\sigma\geq2$,

Proof. In order to use the dual technique to attain the $L^2(\Sigma)$-error estimates, denote $H'(I) = \{v\in H^1(I):v(-1) = 0\}$. Then for Eq (2.25) we can write its dual equation: For a given $g\in\mathbf{V}_N^0 \otimes P_M(I)$, obtain $u_g\in\mathbf{V}_N^0\otimes V_M$ such that

Firstly, we present the existence and uniqueness of $u_g$. Assuming $g = 0$ and taking $e = \partial_t^{-1}[\omega_{-1, 0}u_g]\doteq\int_{-1}^t\frac{1}{1-s}u_g\mathrm{d}s$ in (2.29), then we have

namely,

where $\varphi = \partial_t^{-1}[\omega_{0, -1}\nabla u_g]$ and similarly

Collecting (2.30)–(2.34), we have

Then $u_g = 0$.

Now, in order to derive the estimate of $\tilde{u}$, we first consider the estimates of $u_g$, $\partial_tu_g$, $\partial_t\nabla u_g$.

Taking $e = -(1+t)\partial_tu_g$ in (2.29), we can get

Collecting (2.36)–(2.39), we can obtain

Then we get

Next, based on the above estimates we deduce the estimate of $\tilde{u}$. When $g = \tilde{u}, \; e = \tilde{u}$ in (2.29) and utilizing integration by parts, we can see

Then we get

Finally, according to the triangle inequality, we deduce

Then, by Lemmas 2.1 and 2.2, we directly derive the final $L^2(\Sigma)$-error estimates.

3.   Theoretical analysis of multi-interval Legendre spectral method in time

In order to construct the multi-interval form of the Legendre space-time spectral fully discrete scheme, we take $a_1 = -1$, $a_{K+1} = 1$, $a_k < a_{k+1}$ and denote $I_{k} = (a_k, a_{k+1}]$, $c_k = a_{k+1}-a_k$, $d_k = c_k/2$, namely, $I = \bigcup\limits^K_{k = 1}I_k,$ where $K$ is a known positive integer.

Denote

where $v^k(t) = v(t)|_{I_k}, \; \tilde{\omega}_{\alpha, \beta} = \frac{(1-t)^\alpha}{d_k^\alpha}(2-\frac{1-t}{d_k})^\beta\; (t\in I_k)$ and the definition of $\|v^k(t)\|^2_{I_k, \tilde{\omega}_{\alpha, \beta}}$ is presented in Section 2.

Moreover, let $\Sigma_k = \Omega\times I_k$ and denote

where $v^k(t) = v(t)|_{\Sigma_k}$ and the definition of $\|v^k(x, y, t)\|_{L^2_{\tilde{\omega}_{\alpha, \beta}}(I_k; H^r(\Omega))}$ is presented in Section 2.

Let $M = (M_1, \cdots, M_K)$ and $L = (N, M)$. Define the space of trial and test functions in time

where $P_{M_k}(I_k)$ is a space of polynomials of degree $\leq M_k$ on time span $I_k$ and $M-1 = (M_1-1, \cdots, M_K-1)$.

Then applying the Green's formula, we can write the multi-interval Legendre space-time spectral fully discrete scheme of (1.1) as: Find $u_{L}^K\in \mathbf{V}_N^0 \otimes X_K^{M}$ satisfying

The stability analysis of (3.4) is similar to the single interval method, so we only provide the error analysis of the scheme. Firstly, we introduce the following definition and lemma of the multi-interval projection operator in time.

Definition 3.1. ^[28] The orthogonal projection in time $\boldsymbol{\Pi}_{M}:H^1(I)\rightarrow X_K^{M}$ is given by

with $\boldsymbol{\Pi}_{M} u(-1) = u(-1)$.

Lemma 3.1. ^[28] If $u\in H^\sigma(I)$ and $\sigma\geq1, \; \bar{M} = \min\limits_{1\leq k\leq K}M_k$, we have

where $u^k = u|_{I_k}$.

Denote $U_K = \mathbb{P}^{1}_N\boldsymbol{\Pi}_{M} u$. Now, we decompose the error into: $u-u_{L}^K = (u-U_K)+(U_K-u_{L}^K)$ and denote $\tilde{u}_K = U_K-u_{L}^K$. We note $\tilde{u}_K(x, y, -1) = 0$. Then according to the scheme (3.4), $\forall v\in \mathbf{V}_N^0\otimes \widetilde{X}_K^{M}$, we have

By using the Definitions 2.1 and 3.1, we can see for some terms of the formula (3.7)

Then (3.7) can be simplified as follows:

Now, we give the $L^2(\Sigma)$-error estimate of the multi-interval Legendre space-time spectral scheme.

Theorem 3.1. Suppose $u$ and $u_{L}^K$ are the solutions of the problem (1.1) and scheme (3.4), respectively. If $u\in H^\sigma(I; H^r(\Omega)\cap H_0^1(\Omega))$ for integers $r, \sigma\geq1$, then

where $u^k = u|_{\Sigma_k}$.

If $d_k = d, M_k = M$, we have

Proof. Similar to the analysis of the $L^2(\Sigma)$-error estimate of the single interval scheme, we also take the dual technique to give the proof. Considering the dual equation of (3.11), for a given $g\in\mathbf{V}_N^0 \otimes X_K^{M}$, we obtain $u_g\in\mathbf{V}_N^0\otimes \widetilde{X}_K^{M}$ such that

The existence and uniqueness of $u_g$ can be easily attained, so we focus on using the dual equation ($3.14$) to present the $L^2(\Sigma)$-error estimate.

In order to derive the estimate of $\tilde{u}$, we take $g = \tilde{u}_K$ and $w = \tilde{u}_K$ in Eq ($3.14$),

Now, to deduce the estimates of of $u_g$ and $\nabla u_g$, taking $w = \int_{-1}^t\frac{1}{1-s}u_g\mathrm{d}s\doteq\partial_t^{-1}[\omega_{-1, 0}u_g]$ in Eq ($3.14$),

then we get

Taking estimates (3.17) into inequality (3.15) have

namely, error estimate of $\tilde{u}_K$ is that

Finally, according to the triangle inequality, we deduce

4.   Implementation

In this section, we present the detailed implementation of the multi-interval case by taking Fourier-like basis functions in space and the appropriate basis functions in time. Regarding the single interval case, please see ^[26] for more information.

Let

Then, according to the scheme (3.4), we can see for each $k\; (1\leq k\leq K)$, we find $u^{(k)}\in \mathbf{V}_N^0\otimes P_{M_k}(I_k)$ such that

where $u^{(0)}(x, y, a_1) = \mathbb{P}_N^1u_0(x, y).$

Furthermore, let

then the scheme (4.2) can be converted into: Find $w^{(k)}\in \mathbf{V}_N^0\otimes P_{M_k}(I_k)$ such that

In order to the operability of the scheme (4.3), we try to separate it into two parts: Find $w_q^{(k)}\in \mathbf{V}_N^0\otimes P_{M_k}(I_k)\; (q = 1, 2)$ such that

The solution of the scheme (4.3) is obtained by

The choice of basis functions $\phi_n(x)$ and $\phi_s(y)\; (0\leq n, s\leq N-2)$ can refer ^[26]. Regarding the temporal local trail functions $\psi^k_m(t)$ and test functions $\tilde{\psi}^k_m(t)\; (0\leq m\leq M_k-1)$, please see ^[28]. Let

and $v^{(k)}(x, y, t) = \phi_{n'}(x)\phi_{s'}(y)\tilde{\psi}^{(k)}_{m'}(t)$, where $n', s' = 0, 1, \cdots, N-2$ and $m' = 0, 1, \cdots, M_k-1$, we can see that $W^{(k)} = W_1^{(k)}-W_2^{(k)}$.

Denote the sets of LGL points and weights in spatial directions by $\{x_{\tilde{n}}, \varpi_{\tilde{n}}\}_{{\tilde{n}} = 0}^{N+1}$ and $\{y_{\tilde{s}}, \varpi_{\tilde{s}}\}_{{\tilde{s}} = 0}^{N+1}$, and denote the set of LGL points in time span $I_k$ by $\{t_{\tilde{m}}, \dot{\varpi}_{\tilde{m}}\}_{\tilde{m} = 0}^{M_k+1}$. Define

Then, we can get the matrix form of the scheme (4.4) as follows:

where matrices ${\rm Diag}(\lambda_{n})$, ${\rm Diag}(\lambda_{s})$, $I_{N-1}$, $\Phi_x$ and $\Phi_y$ in spatial directions are given in ^[26], and matrices $C^{(k)}$ and $D^{(k)}\; (1\leq k\leq K)$ in temporal direction are given in ^[28]. Then, by the properties of matrix multiplication in ^[32], Eq (4.9) can be formulated as

where

Now, we try to get the matrix form of scheme (4.5). According to the processing means in ^[28], similarly, we have

Then

where $\{\lambda_{n}\}_{n = 0}^{N-2}$ are corresponding eigenvalues of mass matrices and $\{\sigma_{m}^{(k)}\}_{m = 0}^{M_k-1}$ can refer to (4.33) in ^[28]. Denote $\lambda_{n, s} = \mu(\lambda_{n}+\lambda_{s})+\gamma\lambda_{n}\lambda_{s}$, then according to the values of $\{\sigma_{m}^{(k)}\}_{m = 0}^{M_k-1}$ we can get the matrix form of scheme (4.5) as follows:

where

The Eq (4.14) above can also be converted to a form similar to Eq (4.10).

In summary, the algorithm can be implemented as follows:

(1) For each $k\geq 1,$ compute $W^{(k)}_1$ by (4.9).

(2) Obviously, $W^{(1)} = W_1^{(1)}.$ For each $k\geq 2,$ assume that $W^{(k-1)}$ have been obtained, then $W_2^{(k)}$ is obtained by (4.14) easily.

(3) $W^{(k)} = W_1^{(k)}-W_2^{(k)}$ for each $k\geq 2.$

5.   Numerical experiments

We mainly devote this section to demonstrate the accuracy and efficiency of the multi-interval Legendre space-time spectral method by utilizing numerical examples for the 2D Sobolev equations. Regarding the numerical results of the single interval Legendre space-time spectral methods for the multi-dimensional Sobolev equations, one can refer ^[26].

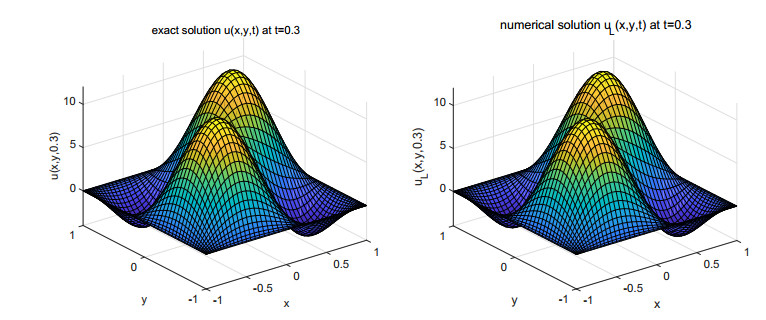
Example 5.1. We consider the 2D Sobolev equations (1.1) on the time interval $I = (0, 2]$ with the following exact solution:

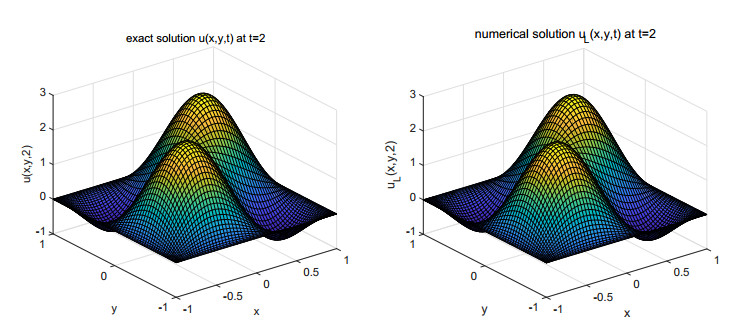
In this example, the two-interval Legendre space-time spectral method is applied to attain the numerical solution $u_L$. We divide the time interval $I = (0, 2]$ into $I_1 = (0, 0.3]$ and $I_2 = (0.3, 2]$, namely, $a_1 = 0, a_2 = 0.3$ and $a_3 = 2$. Under the premise of setting constants $\varepsilon = \mu = \gamma = 1$, we compare the images of numerical solutions $u_L$ and exact solutions $u$ at different times in Figures 1 and 2. From these figures we can deduce that the image of the numerical solutions very well simulate the image of the exact solutions.

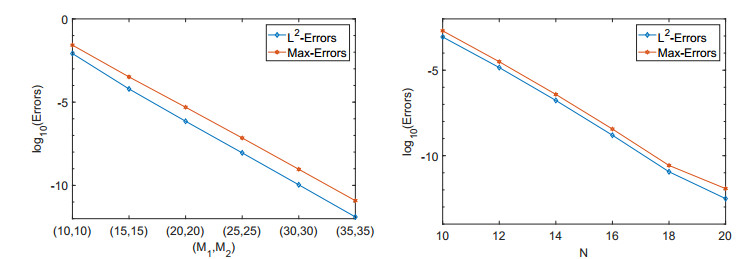
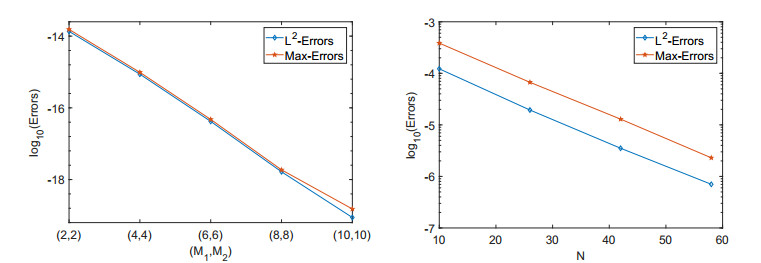
To show the spectral accuracy of the proposed method, we plot the maximum point-wise errors and $L^2(\Sigma)$-errors using semi-log coordinates in Figure 3. The numerical results indicate that the proposed method obtained the exponential convergence in both time and space.

In Tables 1 and 2, we show $L^2(\Sigma)$-errors in space and time, respectively, mainly to compare the numerical effects of the proposed method applying the Fourier-like basis functions and the traditional basis functions. We can then observe that multi-interval method taking Fourier-like basis functions attain better efficiency.

In Table 3, we compare the temporal $L^2(\Sigma)$-errors obtained by using the single-interval Legendre spectral method and the two-interval Legendre spectral method for the same $N$ and $\varepsilon = \mu = \gamma = 1$. One can find that the two-interval method show a great improvement in accuracy compared with the single-interval method.

Example 5.2. In this example we consider the 2D Sobolev equations (1.1) on time interval $I = (0, 2]$ with the unknown exact solution. The source term is $f = 0$ and the initial condition is taken as

We also consider the two-interval Legendre space-time spectral method in time. We divide the time interval $I = (0, 2]$ into $I_1 = (0, 1.3]$ and $I_2 = (1.3, 2]$, namely, $a_1 = 0, a_2 = 1.3$ and $a_3 = 2$. In Figure 4, we depict the numerical solutions $u_L(x, y, t)$ at $t = 1.3$ and $t = 2$ with $(M_1, M_2) = (30, 30), \; N = 60$ and $\varepsilon = \mu = \gamma = 1$.

For the unknown of the exact solution, there is no uniform standard to compare the efficiency of the single interval Legendre space-time spectral method with the two-interval method. Thus in Figure 5 by taking the numerical solutions obtained under $(M_1, M_2) = (30, 30)$ and $N = 60$ as a reference, we plot the temporal and spatial errors of the proposed method with $\varepsilon = \mu = \gamma = 1$. One can clearly observe that two-interval Legendre space-time spectral method possess the spectral accuracy both in time and space.

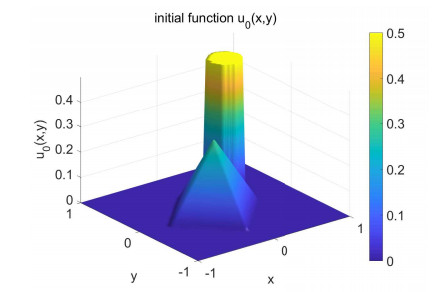
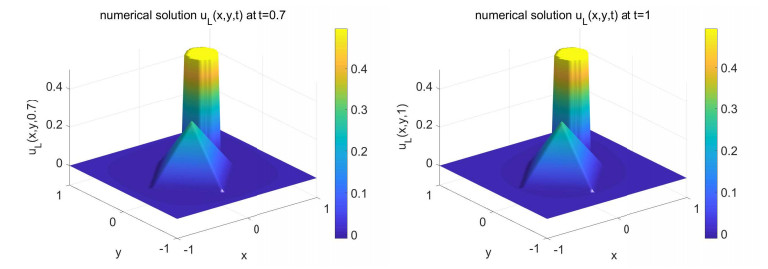
Example 5.3. This example is devoted to exploring the 2D Sobolev equations (1.1) on time interval $I = (0, 1]$ with the exact solution, which is not regular enough and unknown in advance. The source term is $f = 0$ and the initial condition is taken as, see Figure 6,

We divide the time interval $I = (0, 1]$ into $I_1 = (0, 0.7]$ and $I_2 = (0.7, 1]$ to consider the two-interval Legendre space-time spectral method. In Figure 7, we depict the numerical solutions $u_L(x, y, t)$ derived by the proposed method at $t = 0.7$ and $t = 1$ with $(M_1, M_2) = (30, 30), \; N = 60$ and $\varepsilon = \mu = \gamma = 1$.

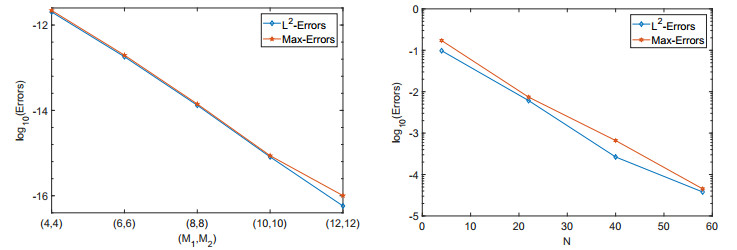
In Figure 8, by taking the numerical solutions obtained under $(M_1, M_2) = (30, 30)$ and $N = 60$ as a reference, we present the temporal and spatial errors with $\varepsilon = \mu = \gamma = 1$. One can clearly observe that our method possess spectral accuracy both in time and space.

6.   Discussion and conclusions

As previously seen, the spectral method is commonly used to formulate the numerical scheme in space combined with the finite difference method in time, but in most cases, the infinite accuracy in space and finite accuracy in time leads to a unbalanced scheme. In order to avoid this problem, in this paper we use the Legendre-Galerkin method in space and the Legendre-tau-Galerkin method in time to study two-dimensional Sobolev equations. We have succeeded in obtaining spectral convergence in both time and space. In particular, the multi-interval form of the proposed method is also considered. In the theoretical analysis, we not only prove the stability of the single and multi-interval numerical scheme, but also give strict proof of the $L^2(\Sigma)$-error estimates by using the dual technique, where a better error estimate is obtained for the single interval form and the optimal error estimate is obtained for multi-interval form. Compared with the single interval method, the multi-interval spectral method succeeds in reducing the scale of problems, adopting the parallel computers and improving the flexibility of algorithm. Another highlight of this paper is that the Fourier-like basis functions, different from the traditional basis functions, are adopted for the Legendre spectral method in space. Since the mass matrix obtained by Fourier-like basis functions is a diagonal matrix, the computing time and memory can be effectively reduced in the implementation of the algorithm. Numerical experiments show that our method can attain the spectral accuracy both in time and space, and the multi-interval method in time is more efficient than the single one.

In a future study, we will extend our method to the numerical solutions of the nonlinear Sobolev equation by using appropriate technique to deal with the nonlinear terms effectively.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (12161063), Natural Science Foundation of Inner Mongolia Autonomous Regions (2021MS01018), Program for Innovative Research Team in Universities of Inner Mongolia Autonomous Region (NMGIRT2207).

Conflict of interest

We declare no conflicts of interest in this paper.