This paper proposes novel single and double integral inequalities with arbitrary approximation order by employing shifted Legendre polynomials and Cholesky decomposition, and these inequalities could significantly reduce the conservativeness in stability analysis of linear systems with interval time-varying delays. The coefficients of the proposed single and double integral inequalities are determined by using the weighted least-squares method. Also former well-known integral inequities, such as Jensen inequality, Wirtinger-based inequality, auxiliary function-based integral inequalities, are all included in the proposed integral inequalities as special cases with lower-order approximation. Stability criterions with less conservatism are then developed for both constant and time-varying delay systems. Several numerical examples are given to demonstrate the effectiveness and benefit of the proposed method.
1.
Introduction
Time-delay systems exist in many practical situations as industry process, biological, ecological groups, telecommunication, economy, mechanical engineering, and so on. A time-delay in a system often induces oscillation and instability, which motivated a huge number of researchers to study the stability analysis with various criteria [1,2,3]. Evaluation of system stability with a constant delay has been studied extensively and lots of theoretical tools have been presented like characteristic equation and eigenvalues analysis [4,5]. Those methods have been well established currently which can derive effective criteria smoothly with numerical efficiency. However, this type of criteria cannot be applied to a time-varying delay system and some other methodologies have been employed.
Generally, two different methodologies have been employed: the first one is so called input-output method that treats a delay as an uncertain operator, and transforms the original time-varying delay system into a closed loop between a nominal LTI system and a perturbation depending on the delay. The stability criteria of which have been well developed by using conventional robustness tools like Small Gain Theorem [6,7], Integral Quadratic Constraint or Quadratic Separation [8,9]. The conservativeness is small for a slowly varying delay, but large for a quickly one because it depending on the upper bound on the derivative of the delay. Another technique is based on the proper construction of Lyapunov-Krasovskii functions. The conservativeness of this method comes from two aspects: the choice of functional and the bound on its derivative. It is not easy to find an appropriate Lyapunov-Krasovskii functional (LFK) to obtain less conservative criteria since it contains both the delay and its bounds.
In earlier research, only a single integral term was employed as a part of LFK to analysis and handle the time delay in systems [10,11,12]. Up to now, double, triple, even quadruple integral terms has been developed which usually bring more effective stability criteria [13,14,15]. And also an augmented and a delay-partitioning LKF method were proposed to reduce the conservativeness, and the difficulty now lies in the bounds of the integrals that appear in the derivative of the functional for a stability condition [16,17].
Previously, The Jensen inequality and Wirtinger-based integral inequality were reported as the integral inequality method that yields less conservative stability criteria [2,18]. Delay-dependent strategy and delay-independent approach under time-varying delays, uncertainties and disturbance are employed to stability analysis. Delay-dependent strategy has been received many attentions as a result of its less conservatism than delay-independent [19,20,21,22,23,24,25,26,27]. Later, the first- and second-order reciprocally convex approach were proposed based on a new kind of linear combination of positive functions weighted by the inverses of squared convex parameters emerges when the Jensen inequality was applied to partitioned double integral terms in the derivation of LMI conditions [28,29]. And the optimal divided method and the secondary partitioning method were provided for stability criteria in double integral terms in LPF [30,31].
Recently, the integral term with higher order approximation has been proposed, such as Wirtinger-based double integral inequality [32], free-matrix-based integral inequality [33], auxiliary function-based integral inequality [34]. These inequalities provided less conservation of stability criteria that those of the Jensen or Wirtinger-based single integral inequities. Especially, a novel integral inequality which called Bessel-Legendre (B-L) inequality has only been applied to the system with constant delays [35,36,37,38]. And also multiple-integral inequalities were newly developed to give high-order approximation to the original integral, the associated integral terms in LPF are also increased [39,40].
In this study, a new single integral inequality is proposed through using shifted Legendre polynomials, and then the double integral inequality is developed with the utilization of Cholesky decomposition. Both single and double integral inequalities are with arbitrary approximation order, which encompasses the well-known Jensen and Wirtinger-based inequalities, auxiliary function-based integral inequalities, and even the B-L inequality. The proposed two inequalities yield improved stability criteria with less conservativeness.
This paper is organized as follows. Section 2 introduces the relevant theories of shifted Legendre polynomials-based single and double integral inequalities, and section 3 and 4 provide application of proposed methods to systems with constant and time-varying delays, including numerical examples.
2.
Shifted Legendre polynomials-based single and double integral inequalities
2.1. Shifted Legendre polynomials for single integral
The classical shifted Legendre polynomials are a set of functions analogous to the Legendre polynomials, but defined on the interval [0,1] as follows
where pi(s) denotes the i-order shifted Legendre polynomial, wi,j denotes the jth coefficient of pi(s).
We here call classical shifted Legendre polynomials as the shifted Legendre polynomials for single integral with the following coefficient
where Cji denotes the combination which can be written using factorials as
Shifted Legendre polynomials obey the orthogonality relationship, i. e.
where δnm denotes the Kronecker delta.
Also we can represent shifted Legendre polynomials for single integral in the matrix form as follows
The relationship between Lm(s) and Um(s) is obtained
where Wm is the coefficient matrix with the following form
It's obvious that Wn is a lower triangular matrix.
With similar formulation, (2.4) can be rewritten as
2.2. Shifted Legendre polynomials for double integral
The interest of shifted Legendre polynomials for double integral is that the orthogonality relationship exists if we use double integral instead of single integral.
The double integral of the product of two classical shifted Legendre polynomials can be obtained as follows
which can also be extended using the form of matrix
Considering that Hm is a real-valued symmetric positive semi-definite matrix, we can gain the associated lower triangular matrix using Cholesky decomposition
where
Since Bm>0, Hm has the unique Cholesky decomposition. Unfortunately, (2.10) shows that Lm(u) is not a proper set of basic functions when the double integral is employed instead of single integral. Thus, we need to find new ones. We introduce the linear combination of {pj(s)} as follows
i.e.
where Dm denotes the transition matrix from Lm(u) to ˉLm(u) with the form
In order to obtain the proper shifted Legendre polynomials for double integral, the following equation should be solved.
where {dij} and {hij} are coefficients to be determined.
Substituting (2.11) into (2.16) yields
By solving a serial of linear equations of (2.17), the matrices Dm and ˉHm are achieved as following
Thus the vector of shifted Legendre polynomials are achieved
where, by (2.6),
2.3. Shifted Legendre polynomials-based single integral inequality
For continuously vector function ˙x(τ):[a,b]→Rn, the associated function ˙˜x(s):[0,1]→Rn is defined as follows
where τ=(b−a)s+a.
We can develop the relationships between the single integrals of ˙x(τ) and ˙˜x(s)
The best weighted square approximation can be obtained with minimizing the following cost function
where R>0 denotes a symmetric positive-defined matrix with proper dimensions, ˜f(s) denotes the approximation function defined as follows
where βi∈Rn denotes the weight corresponding to the shifted Legendre polynomial pi(s) for single integral.
Substituting (2.25) into (2.24) yields
where ωi denotes the integral of the product of ˙˜x(s) and the i-th shifted Legendre polynomial pi(s) for single integral. sym() is defined as the sum of vector/matrix with its own transpose sym(x)=x+xT.
i.e.
where ˆWm denotes the extension matrix associated to Wm
where I denotes the identity matrix with proper dimensions.
Substituting (2.23) into (2.28) yields
According to the static condition of (2.26), we obtain
The second condition of (2.26)
It means that the optimal β∗i=(2i+1)ωi/(b−a) leads to the only minimum cost value
Lemma 1 (shifted Legendre polynomials-based single integral inequality): For any symmetric positive-defined constant matrix R∈Rn×n, R>0, and vector function ˙x(t):[a,b]→Rn such that the integrations concerned are well defined, then the following inequality exists
Proof: It can be obtained from (2.33) observably.
Remark 1: The right term of the proposed single integral inequality (2.34) is approximation with arbitrary order to the left term, i.e., when ˙x(t)=c0+c1t+⋯+cmtm, ci∈Rn, i=0,1,⋯,m, the left term is exactly equal to the right term.
Proof: The function ˙x(t)=c0+c1t+⋯+cmtm can be rewritten as
where
˙˜x(s) can also be expressed by serial of shifted Legendre polynomials {pk(s)} as follows
where
Thus the left term of (2.34) becomes
This complete the proof.
Remark 2: The integral inequality (2.34) degenerates to Jensen inequality when m=0[2].
Proof: Substituting m=0 into (2.34) yields
This complete the proof.
Remark 3: The integral inequality (2.34) degenerates to Wirtinger-based inequality when m=1[18].
Proof: According to (2.30) we have
Substituting (2.41) and (2.42) into (2.34) yields
This complete the proof.
2.4. Shifted Legendre polynomials-based double integral inequality
For continuously vector function ˙x(τ):[a,b]→Rn, and it's associated function ˙˜x(s):[0,1]→Rn defined in (2.22), we can develop the relationships between the double integrals of ˙x(τ) and ˙˜x(s) as follows
where
The best weighted square approximation with double integral can be obtained with minimizing the following cost function
where R>0 denotes a positive-defined matrix with proper dimensions, ˜g(u) denotes the approximation function defined as follows
where βi∈Rn denotes the weight corresponding to the shifted Legendre polynomial ˉpi(s) for double integral.
Substituting (2.46) into (2.45) yields
where νi denotes the integral of the product of ˙˜x(s) and the i-th shifted Legendre polynomial pi(s) for single integral
i.e.
where ˆˉWm denotes the extension matrix associated to ˉWm
Substituting (2.44) into (2.49) yields
According to the static condition of (2.47), we obtain
The second condition of (2.47)
It means that the optimal β∗i=2i+2b−aνi leads to the only minimum cost value
Lemma 2 (shifted Legendre polynomials-based double integral inequality): For any positive-defined constant matrix R∈Rn×n, R>0, and vector function ˙x(t):[a,b]→Rn such that the integrations concerned are well defined, then the following inequality exists
Proof: It can be obtained from (2.54) observably.
Remark 1: The right term of the proposed single integral inequality (2.34) is approximation with arbitrary order to the left term, i.e., when ˙x(t)=c0+c1t+⋯+cmtm, ci∈Rn, i=0,1,⋯,m, the left term is exactly equal to the right term.
Proof: The function ˙x(t)=c0+c1t+⋯+cmtm can be rewritten as
where
˙˜x(s) can also be expressed by serial of shifted Legendre polynomials {ˉpk(s)} as follows
where
Thus the left term of (2.34) becomes
This complete the proof.
Remark 2: The integral inequality (2.34) degenerates to auxiliary function-based integral inequality when m=1[34].
Proof: According to (2.51) we have
Note that ν0 and ν1 are just the coefficients of auxiliary function-based integral inequality. This complete the proof.
3.
Applications to systems with constant delays
3.1. Systems with constant delays
Let us consider the following linear system with constant delay interval
where x(t)∈Rn denotes the state vector of the system with n dimensions, A and Ah are real known constant matrices with appropriate dimensions, the continuously differentiable functions φ(t) denote the initial condition, h≥0 denotes the system's constant delay.
Theorem 1: The system (3.1) is asymptotically stable if there exist matrices P>0, Q>0, R>0 and S>0 such that the following conditions hold [41]:
where the notations in (3.2) are intermediate variables that defined properly in previous and in the process of proof, which can be found as B in (3.10), C in (3.12), e1,e2 in (3.10), h in (3.1), Ae in (3.11), Ψ in (3.13), ˆWm in (2.29), Ωm in (2.34), ˉΨ in (3.14), ˆˉWm in (3.7), ˉΩm in (3.18).
Proof: We define a set of functions {yk(t)} as follows
The time derivatives of yk(t) can be obtained as follows
And the initial we have
Let a=t−h, b=t, we can obtain {ωk} and {νk} for shifted Legendre polynomials-based single and double integral inequalities, respectively
We define extra-states χ(t) and ξ(t) as follows
The extra-states χ(t) can be expressed by ξ(t)
where
where ek=[000⏟k−1I000⏟m+2−k] denotes the k-th row coefficient of ξ(t), In and 0n denote the identity and zeros matrix with dimensions n×n, respectively.
And the system (3.1) can be rewritten as
where Ae=Ae1+Ahe2.
The time derivative of χ(t) can be obtained as follows
where
According to (3.6) and (3.8), we have
where
With similar method, we have following according to (3.7) and (3.8)
where ˉΨ=[0nm×n0nm×nInm]
In order to analysis the stability of the system (3.1), we consider the following Lyapunov-Krasovskii functional (LKF) candidates
Taking the time derivative of V(t) yields
Recalling that (2.34) and (2.55), following inequalities are employed to yield the upper bound of ˙V(t)
This complete the proof.
3.2. Examples
Example 1: We consider the well-known delay dependent stable system (3.1) with following coefficient matrices as given in [29]:
Using delay sweeping techniques the maximum allowable delay hmax=6.1725 can be obtained. Also many recent papers provide different results using Jensen inequality, Wirtinger-based inequality, and so on. The allowable maximum delays are shown in Table 1. We observe that the upper bounds obtained by our proposed inequalities are significantly better than those in other literatures.
Example 2: We consider the dynamics of machining chatter with following coefficient matrices as firstly studied in [36]:
where K denotes a parameter.
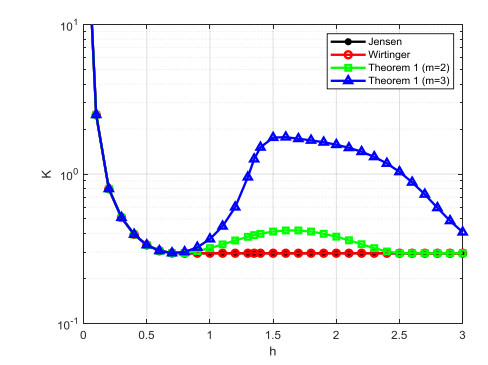
It's obviously that the system is stable with K less than some upper bound. Here we try to the upper bound in various delays. It's shown that Lemma 1 and Lamme 2 yield more stability region than those derived from Jensen and Wirtinger-based Lemma, as illustrated in Figure 1. When the parameter K≤0.295, the system is still stable even the delay is very large, such as h=500.
4.
Applications to systems with time-varying delays
4.1. Systems with time-varying delays
Let us consider the following system with interval time-varying delay:
where x(t)∈Rn denotes the state vector of the system with n dimensions, A and Ah are real known constant matrices with appropriate dimensions, the continuously differentiable functions h(t) and φ(t) denote the system's time-varying delay and the initial condition, respectively.
Assumption 1: The delay function h(t) and its differential ˙h(t) both have finite bounds, i.e., there exist scales h2≥h1>0 and μ1≤μ2≤1 such that
Theorem 2: The system (4.1) is asymptotically stable if there exist matrices P>0, Q1>0, Q2>0, Q3>0, R1>0, R2>0, R3>0, and S1>0, S2>0, S3>0 such that the following conditions hold[41]:
where the notations in (4.2) are intermediate variables that defined properly in previous and in the process of proof, which can be found as B2 in (4.8), C2 in (4.11), e1,e2,e3,e4 in (3.10), h1,h2 in (4.6), μ2 in (4.16), Ae in (3.11), Ψ1,Ψ2,Ψ3 in (4.14), ˉΨ1,ˉΨ2,ˉΨ3 in (4.14), Wm in (2.7), ˆWm in (2.29), ˆˉWm in (3.7), Ω1,Ω2,Ω3 in (4.13), ˉΩm in (3.18), ˉΩ1,ˉΩ2,ˉΩ3 in (4.13).
Proof: If the delay h is varying with time t, then we can develop from (3.3)
If h=h1 or h=h2 is a constant variable, (3.3) yields
We introduce the following extra-states ˆχm(t) and ˆξm(t) as follows
The extra-states can be expressed by ˆξm(t)
where
And the system (3.1) can be rewritten as
where Ae=[AAh0n×(nm+2n)]
The time derivative of ˆχm(t) can be obtained as follows
where
where
In order to analysis the stability of the system (4.1), we consider the following Lyapunov-Krasovskii functional (LKF) candidates
where
Taking the time derivative of Vk(t) yields
where
Thus the sum of ˙Vk(t), k=1,2,⋯,10 yields
Notice that Ξ(h,˙h)≤Ξ(h2,μ2) for all h∈[h1,h2] and ˙h∈[μ1,μ2], we can develop that ˙V(t)≤ξT(t)Φξ(t)<0, where
This complete the proof.
4.2. Examples
Example 1: We also consider the well-known delay dependent stable system (4.1) with following coefficient matrices as given in [29]:
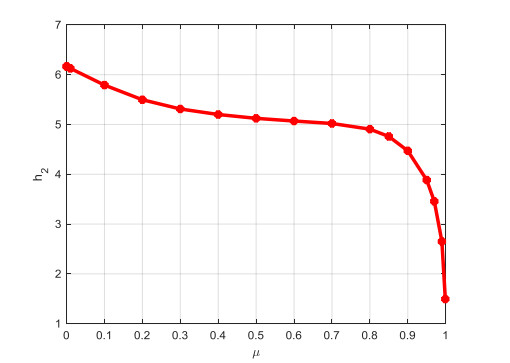
The delay rate bounds μ1=−μ, μ2=μ. We herein calculate the allowable upper bound h2 for various delay rate μ via Theorem 2, as illustrate in Figure 2. It's shown that h2 deceases continuously with delay rate μ growing.
The allowable upper bounds h2 varying with given μ are shown in Table 2. We observe that the upper bounds obtained by Theorem 2 are significantly better than others. Theorem 1 provides the least conservative results.
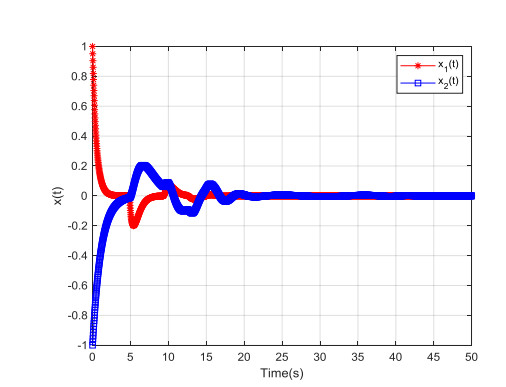
For simulation, let the time-varying delay h(t)=3+2cos(0.25t), which means that h1=1, h2=5, μ1=−0.5, and μ2=0.5. The initial condition of the system is chosen as x(0)=[1,−1]T. The time history of system states is illustrated in Figure 3. As our expectation, both states asymptotically converge to zero despite the previous vibration.
Example 2: Consider the time-varying delay system (4.1) with the following parameters [33]:
When the delay is constant (μ=0), the analytical upper bound can be obtain hmax=π. The improvement of our approach is shown in Table 3. It's verified that the advantage of Theorem 2 is over the results in other literatures.
5.
Conclusions
New single and double integral inequalities with arbitrary approximation order are developed through the use of shifted Legendre polynomials and Cholesky decomposition. These two inequalities encompass several former well-known integral inequities, such as Jensen inequality, Wirtinger-based inequality, auxiliary function-based integral inequalities, and bring new less-conservative stability criteria by employing proper Lyapunov-Krasovskii functionals. Several numerical examples have been provided which show large improvements compared to existing results in both constant and time-varying delay systems.
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive comments that have greatly improved the quality of this paper.
This work is supported by Shanghai Nature Science Fund under contract No. 19ZR1426800, Shanghai Jiao Tong University Global Strategic Partnership Fund (2019 SJTU-UoT), WF610561702, and Shanghai Jiao Tong University Young Teachers Initiation Programme, AF4130045.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: