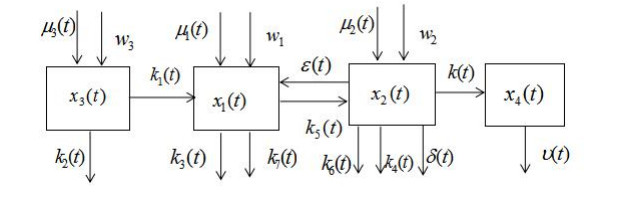
In this paper, the metabolic regulation model of the body during weight loss is established according to the numerical variation law of the three major nutrients and the biological principles. The changing trend of the solution of the model is qualitatively analyzed by using the theory of time-varying differential equation. According to the normal values of the three major nutrients and the ketone body, the sufficient conditions for safe weight loss under the three ways of weight loss during dieting, exercise and drug are provided respectively. Combining with the actual data, the model parameters are identified by the numerical analysis method. The feasible range and simulation curve of the three major nutrients and the ketone body under three weight loss modes are given as well. Finally, the unsafe factors in the process of weight loss are analyzed, and the weight loss suggestions beneficial to health are given.
1.
Introduction
The human T-lymphoblastic leukemia virus (HTLV), the first human retrovirus to have been discovered in the late 1970s, belongs to the subfamily of retroviral RNA oncoviruses. These viruses can lead to chronic, lifelong infections, with the main subtypes being type Ⅰ and type Ⅱ. Despite being one of the few examples of human oncogenic viruses, it has received relatively little public attention [1,2]. This may be attributable to its relatively low prevalence in high-income countries and the current high level of societal concern about the HIV epidemic. The most recent estimates of the total number of individuals infected with HTLV-1 are at least 30 million. Infection with HTLV-1 can result in serious and potentially fatal complications. The virus has been associated with a wide variety of clinical conditions, most notably adult T-cell leukemia/lymphoma (ATL) and a chronic and progressive neurological condition known as HTLV-1-associated myelopathy (HAM) [3,4]. It is estimated that less than 5% of individuals infected with HTLV-1 will develop these diseases. At the same time, the remainder are classified as "healthy carriers" who may also develop symptoms such as lung and bladder infections. Furthermore, an analysis revealed that HTLV-1 infection was associated with a 57% increase in all-cause mortality, including several inflammatory conditions such as uveitis, infectious dermatitis, and polyarthritis. There is currently no treatment for HTLV-1, and there is a lack of global screening for this infection. Risk assessment is further complicated by the development of adult T-cell lymphoma or HTLV-associated myelopathy [5,6,7].
The viral protein Tax is a key antigen expressed by cells effectively infected by HTLV-1. It is involved in the activation of the transcription of HTLV-1 genes and the proliferation of infected T cells [8]. Mathematical models can provide insight into the study of the disease, extending earlier relevant models in conjunction with the role of the viral protein Tax in the process of infection. This allows for the accounting of the highly dynamic interplay between viral expression and transcriptional latency. Li M Y and Lim A G [8] have differentiated the class of infected cells into two pools, latent and active, giving the following model based on HTLV-1 infection:
combining x(t)+u(t)≪K and dy(t)=[σu(t)−ay(t)]dt calculates that y(t)<σKa. All parameters are assumed to be positive constants, and their biological significances are given in Table 1. A transfer diagram for the described interactions is shown in Figure 1.
Mathematical models provide valuable insights into the complex dynamics of disease transmission, forming a critical foundation for public health policy. Many scholars have developed theoretical studies on various deterministic infectious disease models [9,10,11]. Research on HTLV-1 dynamics has also yielded significant results. Wang and Ma [12]investigated the global kinetics of the HTLV-1 infection response-diffusion model considering factors such as mitotic division of infected cells and CTL immune response; Khajanchi et al. [13] investigated a mathematical model of CD8+ T cell response to HTLV-1 and performed a sensitivity analysis to explore the dynamic response to HTLV-1 infection and its role in the pathogenesis of HTLV-1-associated myelopathy/tropical spastic paralysis (HAM/TSP); Wang et al. [14] developed a model incorporating two time delays, showing through numerical simulations that intracellular delays stabilize the infection's steady state, while immune response delays can destabilize it. They also noted that intracellular delay affects both the magnitude and the time required for convergence to the steady state. These studies have significantly advanced the understanding of HTLV-1 dynamics.
As the complexity of epidemiological modeling increases, researchers are increasingly inclined to introduce stochastic factors to improve the predictive power and accuracy of models. In recent years, Bayesian filtering (especially Kalman filtering and particle filtering) has become an important tool for quantifying and estimating stochasticity in dynamical systems, and has been widely used especially in epidemiological modelling. Vasileios E Papageorgiou et al. [15] proposed a novel particle filtering method for assessing the dynamics of monkeypox outbreaks; Calvetti D et al. [16] focused on Bayesian particle filtering-based dynamic epidemic transmission models, especially for COVID-19, and the study showed that the algorithm has significant accuracy in estimating the proportion of latently infected individuals through computer simulations and experiments with real data; Jos Elfring et al. [17] discussed the popularization and application of the standard algorithm for particle filtering. On the other hand, Markov methods also have important applications in describing stochasticity in the spread of infectious diseases, and Artalejo JR et al. [18] provide insights into the computational methods of stochastic SEIR models and provide powerful tools for analyzing stochastic behavior during disease transmission. These methods can not only enhance the predictive performance of existing epidemiological models, but can also be applied to other public health problems with uncertainty and dynamic evolution.
In real life, various organisms and populations are inevitably affected by the external environment. The presence of environmental noise means that parameters such as birth and death rates are subject to some kind of random perturbation. Several different types of stochastic epidemiological kinetic models have been developed and extensively studied. There are broadly two approaches in the existing literature to describe random effects in reality: Either linear perturbations or Ornstein-Uhlenbeck processes [19,20,21]. The Ornstein-Uhlenbeck process is a mathematical model that describes the evolution of random variables with mean-reverting properties. It can be used to simulate dynamical systems that exhibit short-term fluctuations and long-run convergence to the mean. Edward Allen [22] reviews two commonly used methods for incorporating environmental change factors into models of biological systems and concludes that the mean reversion process has some advantages over linear functions of white noise in modifying environmental change parameters. Zhou Baoquan et al. [23] formulated and studied a stochastic epidemic model with media coverage and two mean-reverting Ornstein-Uhlenbeck processes, and investigated the effects of random noise and media coverage on the spread of epidemics. Cai Yongli et al. [24] showed through their study that the Ornstein-Uhlenbeck process is a well-established method for introducing stochastic environmental noise into biologically realistic population dynamics models. Su Tan et al. [25] considered a stochastic SEIV epidemic model incorporating vaccination and general morbidity and derived a density function around the equilibrium point. Shi Z, Jiang D [26] studied a stochastic HIV model in which the parameters were perturbed by the Ornstein-Uhlenbeck process. The process is also described in the literature [27,28,29].
In this article the infection rate β in the system (1.1) is subject to fluctuations due to environmental noise, oscillating around the mean value ˉβ. To model natural fluctuations in the infection rate β over time or changes in environmental factors, we treat it as a random variable. Define β(t) as a stochastic process that varies over time [30]:
where ˉβ is a positive constant representing β(t) averaged over the long term, α denotes the rate of mean reversion, B(t) stands for Standard Brownian Motion, and θ denotes the intensity of white noise. In this paper, B(t) is defined on {Ω,{Ft}t≥0,P}, which is a complete probability space with filtration {Ft}t≥0 satisfying the incremental and right-continuous. F0 contains all P–empty sets. Solving the above equation gives β(t)=ˉβ+(β(0)−ˉβ)e−αt+θ∫t0e−α(t−s)dB(s), calculating the expectation and variance of β(t) separately, we have
when t→0+, we have E(β(t))→β(0) and Var(β(t))→0, and it can be seen that it is reasonable to use the Ornstein-Uhlenbeck process to describe the evolution of the infection rate β over time under the influence of noise.
Thus, we can obtain a stochastic kinetic model for HTLV-1 infection:
where β+=max{β(t),0}, combined with the above analyses, the feasible domain of system (1.2) is
In this paper, we develop techniques and theory for threshold dynamics of stochastic model (1.2) incorporating the Ornstein-Uhlenbeck process, including the theory of uniqueness of the existence of global solutions in Section 2 and sufficient conditions for the existence of a stationary distribution of the system (1.2) in Section 3. Meanwhile, we further give the solution theory of special algebraic equations and the exact expression of the local probability density function of the system (1.2), and finally verify the correctness of our theory using numerical simulations.
2.
Existence uniqueness of the global solution
Theorem 2.1 For any initial values (x(0),u(0),y(0),β(0))∈Γ, the system (1.2) has a unique global solution (x(t),u(t),y(t),β(t)), and is maintained with probability one in Γ.
Proof. It is evident that the coefficients of the system (1.2) satisfy the local Lipschitz condition. Consequently, there exists a unique solution for t∈[0,τe), where τe represents the moment of explosion [30]. Let Rn=(−n,−n)×(−n,−n)×(−n,−n)×(−n,−n), for any initial value (x(0),u(0),y(0),β(0))∈Γ, there exists a sufficiently large integer m0 satisfying (lnx(0),lnu(0),lny(0),β(0))∈Rm0, for any m≥m0, define τm=inf{t∈(0,τe)|(lnx(t),lnu(t),lny(t),β(t))∉Rm}, it is clear that τm is an increasing function concerning m. In the subsequent proof, we define inf{∅}=+∞,τ∞=limm→+∞τm; hence τ∞≤τe. The following proves that τ∞=+∞ and thus can show that τe=+∞.
Adoption of the counterfactual: Assumptions τ∞≠+∞, there exists 0<ε0<1 and a positive constant m∗,T0>0 satisfying
whereGm={τm≤T0|(lnx(t),lnu(t),lny(t),β(t))∉Rm,t∈(0,τm)}, defining non-negative functions
combined with the Itˆo formula [30]:
where
Integrating and taking the expectation gives
combined with Eq (2.1), for any ξ∈Gm, we get V(x(τm,ξ),u(τm,ξ),y(τm,ξ),β(τm,ξ)) outweigh (em−1−m)∧(e−m−1+m)∧m22, so
let m→∞, which gives
this is a contradictory assertion, which invalidates our original assumption, i.e., τ∞=+∞. Therefore, there exists a unique global solution (x(t),u(t),y(u),β(t)) for the system (1.2).
3.
Existence of a stationary distribution
In contrast to deterministic models, stochastic models lack positive equilibria. Consequently, this section will investigate whether the stochastic model (1.2) exhibits a stationary distribution indicative of the persistence of the epidemic.
Theorem 3.1. If
then there exists a stationary distribution for system (1.2). Where
Proof. Taking the function V1=−lnu−c1lnx−c2lny, applying the Itˆo formula yields
where P(t)=β(t)−ˉβ, seek to solve
we can have
consequently
where
The function V2=V1+c1ˉβay is taken, and the Itˆo formula is applied, which yields
Taking the function V3=−lnx−lny−ln(K−x−u)+β22, applying the Itˆo formula yields
where
Taking the function ˉV=MV2+V3, the function has a minimum point in the feasible domain ˉV(x0,u0,y0,β0), so we make V=ˉV−ˉV(x0,u0,y0,β0), applying the Itˆo formula to it gives
where
Next, we first verify that related properties of F(x,u,y,β), defining bounded closed sets
divide the set Γ∖Dε into the following five regions:
meet the conditions:
where
Case 1. Consider the region Dcε,1,
Case 2. Consider the region Dcε,2,
Case 3. Consider the region Dcε,3,
Case 4. Consider the region Dcε,4,
Case 5. Consider the region Dcε,5,
Thus, there exists a sufficiently small ε satisfying that for any (x,u,y,β)∈Γ∖Dε there is F(x,u,y,β)≤−1, and it can be demonstrated that there exists a positive constant number H satisfying the following condition: for any (x,u,y,β)∈Dε has
integrate both sides of (3.1) and take the expectation to obtain
combining β(t) and the ergodic property of P(t), it follows that
it can be obtained by taking the lower limit:
consequently
therefore, there is a stationary distribution for the system (1.2).
4.
Probability density function
The study of stationary distributions has significant implications for disease. The calculation of the density function in the vicinity of the quasi-equilibrium point in the presence of such distributions can assist in the study of the distribution of disease at a given moment in time.
First we set the quasi-equilibrium point to (x∗,u∗,y∗,ˉβ), let X1=x−x∗,X2=u−u∗,X3=y−y∗,X4=β−ˉβ, solving for the Jacobi matrix yields
then the linearized system can be written as:
where
rewriting the above system of equations into the form of a matrix equation
where
There exists a unique probability density function Φ(X1,X2,X3,X4) for the system in the vicinity of the quasi-equilibrium point, the form of which can be obtained by the following Fokker-Planck equation [31]:
Φ(X1,X2,X3,X4) can be described by a quasi-Gaussian distribution
where, c is a constant satisfying the normalization condition ∫R4Φ(X1,X2,X3,X4)dX1dX2dX3dX4=1, and the real symmetric matrix P satisfies PG2P+ATP+PA=0, defining that P−1=Σ, the above equation can be rewritten as
Theorem 4.1 If Rs0>1, and satisfies
the normal probability density function Φ(x,u,y,β) of the solution of system (1.2) in the vicinity of the quasi-equilibrium point can be expressed as
where Σ is a positive definite matrix, and
the exact form of Σ2,Σ4 will be given in the proof.
Proof. First, we determine that the matrix A is a Hurwitz matrix, computing the characteristic polynomials of A as follows:
combining the conditions gives
Take the primitive matrix J1=(0001100001000010), calculate and obtain
continuing with the elementary transformations, take the matrix J2=(100001000a24a14100001), calculate and obtain
where
since a3 must not be zero, we discuss whether a1 is zero in the following:
(Ⅰ) a1≠0
Take the primitive transformation matrixJ3=(10000100001000−a3a11), calculate and obtain
where
Noting that J=J3J2J1, then Eq (4.4) can be rewritten as
rewriting Eq (4.5) yields
let Y4=X4,Y3=a6X3+a7X4,Y2=dY3,Y1=dY2, so the calculation yields the standard R1 matrix for A3 as
where
therefore, the calculation can be obtained
according to the invariance of the matrix elementary transformation, the characteristic polynomial is also invariant. Hence, we obtain
we can know that
let
rewrite the equation Q1G21QT1+(Q1A3Q−11)(Q1ΣQT1)+(Q1ΣQT1)(Q1A3Q−11)T=0 to read
calculation can be obtained
computing
thus, Σ2 is a positive definite matrix, since
therefore
is also positive definite.
(Ⅱ) a1=0
Take the primitive transformation matrixJ4=(1000010000010010), calculate and obtain
noting that L=J4J2J1, Eq (4.4) can be rewritten as
rewriting Eq (4.7) yields
let Y4=X4,Y3=a2X3−a22X4,Y2=dY3,Y1=dY2, so the calculation yields the standard R1 matrix for A4 as
where
Since, in this case, a1=0, i.e., a21=a22a24a14−a11a24a14, the calculation therefore reduces to
n1–n4 is defined as above; calculate and obtain
let
rewrite the equation Q2G22QT2+(Q2A4Q−12)(Q2ΣQT2)+(Q2ΣQT2)(Q2A4Q−12)T=0 as
the calculation gives Σ4=Σ2; similarly, in this case
thus
is also positive definite.
Combining the above two cases, the expression for the probability density function near the quasi-equilibrium point is
5.
Disease extinction
In addition to the aforementioned considerations, the study of the conditions that lead to the extinction of infectious diseases will also play a significant role in the subsequent treatment and control of these diseases. This section will present the conditions that result in the extinction of diseases.
Theorem 5.1 Let (x(t),u(t),y(t),β(t)) be a solution of model (1.2) with any initial value (x(0),u(0),y(0),β(0)), if
then we have limt→∞u(t)=limt→∞y(t)=0, i.e., the infection of system (1.2) will become exponentially extinct in the long run.
Proof. Constructor W(t)=u(t)+μ+σσy(t), next we apply the Itˆo formula to lnW,
integrating Eq (5.1) from 0 to t and dividing both sides by t yields
combining this with the powerful number theorem for martingale yields
taking the upper limit of Eq (5.2) and combining it with Eq (5.3) yields
where
Therefore, we have limt→∞W(t)=0, i.e., limt→∞u(t)=limt→∞y(t)=0, implying that both latently infected as well as actively infected cells of the system (1.2) will be exponentially extinct in the long term. The theorem is proved.
6.
Numerical simulation
In the numerical simulation, discretization of stochastic models is a very important and significant step, and the choice of discretization method has a great impact on the accuracy, stability, and computational efficiency of the numerical solution. The common numerical discretization methods are the Euler-Markov method and the Milstein method.
The Euler-Markov method is the simplest and most widely used method for discretizing the SDE. It is a first-order approximation that uses the discretized form of the SDE to update the solution at each step, and includes both deterministic drift and random noise terms, but its accuracy is limited to first-order convergence of the step sizes. Milstein's method is a higher-order method (second-order convergence) with a higher accuracy compared to Euler-Markov's method, and in addition to the drift and diffusion terms, Milstein's method also includes an additional term. In addition to the drift and diffusion terms, the Milstein method includes an additional term to account for the interaction between the random noise and the diffusion coefficients. This additional term improves the approximation of the solution, especially for complex SDEs where the influence of the noise term is large. In this section, we use the Milstein method [32,33], and the discretized equations are as follows:
where, (xj,uj,yj,βj)Tis the corresponding value for the jth iteration of Eq (6.1), Δt denotes the time increment, and ξj represents an independent Gaussian random variable.
Example 6.1 Select the parameter values in Table 2; in the absence of infection, the normal CD4+ helper T-cell count averages 1000 cells/mm3 [8], and we consider a target cell carrying capacity of 800 cells/mm3. Calculate the conditions for the existence of a stationary distribution.
calculations show that, under this set of parameters, there is a stationary distribution for system (1.2), implying that uninfected cells, latently infected cells, and actively infected cells will persist near the quasi-equilibrium point. It is clear from Figure 2 that there is a stationary distribution of the system around the quasi-equilibrium point x∗=63.586,u∗=98.179,y∗=14.727.
Example 6.2 In this section, we use numerical simulation to study the effect of other parameters on the system (1.2). First, we set K=500, and the rest of the parameters are the same as in Table 2. Based on this, we study the effect of three different δ on the latent infected and active infected cells, δ=0.04,δ=0.25 and δ=0.35. Respectively, bringing them into Re0, we can obtain the following results:
when δ=0.04, Re0=0.030.04(0.04×0.01×500+0.135+0.04×500×0.001√0.2×π)=0.27<1,
when δ=0.25, Re0=0.030.04(0.25×0.01×500+0.135+0.25×500×0.001√0.2×π)=1.157>1,
when δ=0.35, Re0=0.030.04(0.35×0.01×500+0.135+0.35×500×0.001√0.2×π)=1.579>1.
By calculating that under the first set of parameter values, the disease will go to extinction, and under the next two sets of parameter values, the disease will persist. Figure 3 illustrates this point; at the same time, looking at Figure 3, it is not difficult to see that, under the premise of the disease's persistence, with the δ getting bigger, u(t) and y(t) will be maintained around a larger value. Biologically speaking, the more susceptible cells become latent through infection, the more cells will be transformed into active infection, so our simulation results are reasonable.
Example 6.3 It is of paramount importance to study the transition time of an infected cell from its initial state x(0),u(0),y(0) to a sustained state x(s),u(s),y(s) and finally to an extinct state (x(e),u(e),y(e)), which can be referred to as the first passage time (FPT) [34]. The first passage time represents the time required for a random trajectory to reach another state for the first time; the average value of the FPT becomes the MFPT [35,36].
In this section, we choose N = 500 and perform 500 cycles to obtain the average time required for the system (1.2) to reach a stationary distribution for the first time under different α and θ, respectively, with the rest of the parameters remaining the same as those in Table 2, and the plotted images are shown in Figure 4. The average time required to reach extinction for the first time in the system (1.2) with different α and θ is shown in Figure 5 for the first set of parameters chosen from Example 6.2.
Example 6.4 In this section, we investigate the impact of random factors on disease extinction, maintaining all other parameters constant, and observing the change in Re0 for different values of [α,θ]. As illustrated in Figure 6, Re0 decreases as α increases or θ decreases. This implies that as the rate of regression to the mean increases or as the noise intensity decreases, the disease is effectively controlled and tends to become extinct. This is a realistic and biologically significant outcome.
7.
Conclusions
The objective of this paper is to investigate the dynamical impact of the Ornstein-Uhlenbeck process on the HTLV-1 model. A number of different and suitable Lyapunov functions were constructed to prove the conclusions drawn. The following paragraphs present the main results of this study:
(ⅰ) For the stochastic model, after considering the perturbations, we show that for any initial value, there exists a unique solution to the system (1.2);
(ⅱ) By establishing a series of suitable Lyapunov functions, we prove the existence of a unique stationary distribution for the system at Rs0>1 and perform numerical simulations to verify the results, see Figure 2;
(ⅲ) After proving the existence of a stationary distribution, we give a concrete expression for the local normal density function corresponding to the stochastic system (1.2) in the neighborhood of the quasi-equilibrium state, provided that the conditions are satisfied;
(ⅳ) The threshold condition Re0 for disease extinction is given, see Figure 3, and the effects of mean reversion rate α and noise intensity θ on this condition are also investigated, see Figure 6;
(ⅴ) 500 simulations were performed to obtain the average elapsed time for the stochastic system to reach the stationary distribution state for the first time as well as the extinction state for different initial values as well as parameters, see Figures 4 and 5.
It is important to note that this study has certain limitations. First, we have focused on modeling the parameter infectivity β to follow the Ornstein-Uhlenbeck process. However, the model could be made more realistic by assuming that other parameters in the system (1.1) also satisfy the Ornstein-Uhlenbeck process. Moreover, we have derived local probability density expressions for the stochastic system near the quasi-equilibrium point, but a global probability density expression remains an open question. Additionally, further investigation is needed to determine whether other types of stochastic disturbances might be more appropriate for this problem.
In the paper, we use β+=max{β(t),0} to ensure non-negativity of the infection rate in the system. However, the non-negativity of the infection rate can also be ensured by considering the Ornstein-Uhlenbeck process that includes a logarithmic transformation, i.e., dlnβ(t)=α(lnˉβ−lnβ(t))dt+θdB(t), for which we will carry out related work to investigate this. In addition, discussion work considering the effect of adding multiple Ornstein-Uhlenbeck processes on the model results is also underway.
Author contributions
Yan Ren: Conceptualized the study, carried out the theoretical analysis, and wrote the first draft; Yan Cheng and Yuzhen Chai: Contributed to the design of the mathematical framework and assisted with interpretation and revision; Ping Guo: Contributed to the software implementation and analysis. All authors have read and approved the final version of the manuscript for publication.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work is supported by the Shanxi Provincial Natural Science Foundation, China (No.202303021211026); the Shanxi Province Returned Overseas Students Support Program, China (No.2023-038); the National Natural Science Foundation of China (No.12301521); Shanxi Provincial Natural Science Foundation (No.20210302124081).
Conflict of interest
The authors declare that they have no competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.









 DownLoad:
DownLoad: