Adaptive fuzzy control for nonlinear systems with sampled data and time-varying input delay

1.   Introduction

This paper considers the following heteroscedastic model:

In this equation, $g(x)$ is a known mean function, and the variance function $r(x)(r(x): = f^2 (x))$ is unknown. Both the mean function $g(x)$ and variance function $r(x)$ are defined on $[0, 1]$. The random variables $U_{1}, \ldots, U_{n}$ are independent and identically distributed $(i.i.d.)$ with ${\rm{E}}[U_{i}] = 0$ and $V[U_{i}] = 1$. Furthermore, the random variable $X_{i}$ is independent of $U_{i}$ for any $i \in\{{1, \cdots, n}\}$. The purpose of this paper is to estimate the $m$th derivative functions $r^{(m)}(x) (m\in N)$ from the observed data $({{X_1}, {Y_1}}), \cdots, ({{X_n}, {Y_n}})$ by a wavelet method.

Heteroscedastic models are widely used in economics, engineering, biology, physical sciences and so on; see Box ^[1], Carroll and Ruppert ^[2], Härdle and Tsybakov ^[3], Fan and Yao ^[4], Quevedo and Vining ^[5] and Amerise ^[6]. For the above estimation model (1.1), the most popular method is the kernel method. Many important and interesting results of kernel estimators have been obtained by Wang et al. ^[7], Kulik and Wichelhaus ^[8] and Shen et al. ^[9]. However, the optimal bandwidth parameter of the kernel estimator is not easily obtained in some cases, especially when the function has some sharp spikes. Because of the good local properties in both time and frequency domains, the wavelet method has been widely used in nonparametric estimation problems; see Donoho and Johnstone ^[10], Cai ^[11], Nason et al. ^[12], Cai and Zhou ^[13], Abry and Didier ^[14] and Li and Zhang ^[15]. For the estimation problem (1.1), Kulik and Raimondo ^[16] studied the adaptive properties of warped wavelet nonlinear approximations over a wide range of Besov scales. Zhou et al. ^[17] developed wavelet estimators for detecting and estimating jumps and cusps in the mean function. Palanisamy and Ravichandran ^[18] proposed a data-driven estimator by applying wavelet thresholding along with the technique of sparse representation. The asymptotic normality for wavelet estimators of variance function under $\alpha-$mixing condition was obtained by Ding and Chen ^[19].

In this paper, we focus on nonparametric estimation of the derivative function $r^{(m)}(x)$ of the variance function $r(x)$. It is well known that derivative estimation plays an important and useful role in many practical applications (Woltring ^[20], Zhou and Wolfe, ^[21], Chacón and Duong ^[22], Wei et al.^[23]). For the estimation model (1.1), a linear wavelet estimator and an adaptive nonlinear wavelet estimator for the derivative function $r^{(m)}(x)$ are constructed. Moreover, the convergence rates over $L^{\tilde{p}} (1 \le \tilde{p} < \infty)$ risk of two wavelet estimators are proved in Besov space $B_{p, q}^{s}(\mathbb{R})$ with some mild conditions. Finally, numerical experiments are carried out, where an automatic selection method is used to obtain the best parameters of two wavelet estimators. According to the simulation study, both wavelet estimators can efficiently estimate the derivative function. Furthermore, the nonlinear wavelet estimator shows better performance than the linear estimator.

This paper considers wavelet estimations of a derivative function in Besov space. Now, we first introduce some basic concepts of wavelets. Let $\phi$ be an orthonormal scaling function, and the corresponding wavelet function is denoted by $\psi$. It is well known that $\{{\phi _{\tau, k}}: = 2^{\tau/2}\phi(2^{\tau}x-k), {\psi _{j, k}}: = 2^{j/2}\psi(2^{j}x-k), j\geq\tau, k\in \mathbb{Z}\}$ forms an orthonormal basis of $L^{2}(\mathbb{R})$. This paper uses the Daubechies wavelet, which has a compactly support. Then, for any integer $j_*$, a function $h(x) \in {L^2}({[{0, 1}]})$ can be expanded into a wavelet series as

In this equation, $\Lambda_{j} = \{0, 1, \ldots, 2^{j}-1\}$, ${\alpha _{j_{*}, k}} = {\langle {h, {\phi _{j_{*}, k}}}\rangle _{{[{0, 1}]}}}$ and ${\beta _{j, k}} = {\langle {h, {\psi _{j, k}}}\rangle _{{[{0, 1}]}}}$.

Lemma 1.1. Let a scaling function $\phi$ be t-regular (i.e., $\phi\in{\mathscr{C}^{t}}$ and $| {{D^\alpha}\phi(x)}|\le c{({1 + {{|x|}^2}})^{-l}}$ for each $l\in{\mathbb{Z}}$ and $\alpha = 0, 1, \ldots, t)$. If $\left\lbrace \alpha_{k}\right\rbrace \in{l_p}$ and $1\le p \le \infty$, there exist $c_{2} \ge c_{1} > 0$ such that

Besov spaces contain many classical function spaces, such as the well known Sobolev and Hölder spaces. The following lemma gives an important equivalent definition of a Besov space. More details about wavelets and Besov spaces can be found in Meyer ^[24] and Härdle et al. ^[25].

Lemma 1.2. Let $\phi$ be t-regular and $h \in {L^p}({{[0, 1]}})$. Then, for $p, q\in[{1, \infty})$ and $0 < s < t$, the following assertions are equivalent:

(i) $h \in B_{p, q}^s({{[0, 1]}})$;

(ii) $\{{{2^{js}}{{\|{h-{P_j}h}\|}_p}}\}\in{l_q}$;

(iii) $\{{{2^{j({s-\frac{1}{p} + \frac{1}{2}})}}{{\|{{\beta _{j, k}}}\|}_p}}\}\in{l_q}$.

The Besov norm of $h$ can be defined by

where $\left\| {{\beta _{j, k}}} \right\|_p^p = \sum\limits_{k \in {\mit\Lambda _j}} {{{\left|{{\beta _{j, k}}}\right|}^p}}$.

2.   Wavelet estimators and main theorem

In this section, we will construct our wavelet estimators, and give the main theorem of this paper. The main theorem shows the convergence rates of wavelet estimators under some mild assumptions. Now, we first give the technical assumptions of the estimation model (1.1) in the following.

A1: The variance function $r:[0, 1]\rightarrow \mathbb{R}$ is bounded.

A2: For any $i\in\{0, \ldots, m-1\}$, variance function $r$ satisfies $r^{(i)}(0) = r^{(i)}(1) = 0$.

A3: The mean function $g:[0, 1]\rightarrow \mathbb{R}$ is bounded and known.

A4: The random variable $X$ satisfies ${X}\sim U({{[0, 1]}})$.

A5: The random variable $U$ has a moment of order $2\tilde{p}\left(\tilde{p} \ge1\right)$.

In the above assumptions, A1 and A3 are conventional conditions for nonparametric estimations. The condition A2 is used to prove the unbiasedness of the following wavelet estimators. In addition, A4 and A5 are technique assumptions, which will be used in Lemmas 4.3 and 4.5.

According to the model (1.1), our linear wavelet estimator is constructed by

In this definition, the scale parameter $j_{*}$ will be given in the following main theorem, and

More importantly, it should be pointed out that this linear wavelet estimator is an unbiased estimator of the derivative function $r^{(m)}(x)$ by Lemma 4.1 and the properties of wavelets.

On the other hand, a nonlinear wavelet estimator is defined by

In this equation, $\mathbb{I}_{A}$ denotes the indicator function over an event $A$, ${t_n} = 2^{mj}\sqrt{{\ln n}/n}$,

$\rho_{n} = 2^{mj}\sqrt{n/{\ln n}}$, and $w_{j, k} = \int_{0}^{1} {{g^2}(x){(-1)^{m}{\psi^{(m)} _{j, k}}(x)}dx}$. The positive integer ${j_*}$ and ${j_1}$ will also be given in our main theorem, and the constant $\kappa$ will be chosen in Lemma 4.5. In addition, we adopt the following symbol: ${x_+}: = \max\{{x, 0}\}$. $A\lesssim B$ denotes $A\leq cB$ for some constant $c > 0$; $A\gtrsim B$ means $B\lesssim A$; $A\thicksim B$ stands for both $A\lesssim B$ and $B\lesssim A$.

In this position, the convergence rates of two wavelet estimators are given in the following main theorem.

Main theorem For the estimation model (1.1) with the assumptions A1-A5, $r^{(m)}(x)\in B_{p, q}^s({{[0, 1]}})$$(p, q \in \left[1, \infty\right)$, $s > 0)$ and $1 \le \tilde{p} < \infty$, if $\{p > \tilde{p} \ge 1, s > 0\}$ or $\{1 \leq p \leq \tilde{p}, s > 1/p\}$.

(a) the linear wavelet estimator $\hat r_n^{lin}(x)$ with $s' = s-({\frac{1}{p}-\frac{1}{\tilde{p}}})_+$ and ${2^{{j_*}}}\sim{n^{\frac{1}{{2s' + 2m+1}}}}$ satisfies

(b) the nonlinear wavelet estimator $\hat r_n^{non}(x)$ with ${2^{{j_*}}}\sim{n^{\frac{1}{{2t+2m+1}}}}$ $\left(t > s\right)$ and ${2^{{j_1}}}\sim \left(\frac{n}{{\ln n}}\right)^{\frac{1}{2m+1}}$ satisfies

where

Remark 1. Note that $n^{-\frac{s\tilde{p}}{2s+1}} \; (n^{-\frac{(s-1/p+1 /\tilde{p})\tilde{p}}{2(s-1 /p)+1}})$ is the optimal convergence rate over $L^{\tilde{p}} (1\leq \tilde{p} < +\infty)$ risk for nonparametric wavelet estimations (Donoho et al. ^[26]). The linear wavelet estimator can obtain the optimal convergence rate when $p > \tilde{p}\ge1$ and $m = 0$.

Remark 2. When $m = 0$, this derivative estimation problem reduces to the classical variance function estimation. Then, the convergence rates of the nonlinear wavelet estimator are same as the optimal convergence rates of nonparametric wavelet estimation up to a $\ln n$ factor in all cases.

Remark 3. According to main theorem (a) and the definition of the linear wavelet estimator, it is easy to see that the construction of the linear wavelet estimator depends on the smooth parameter $s$ of the unknown derivative function $r^{(m)}(x)$, which means that the linear estimator is not adaptive. Compared with the linear estimator, the nonlinear wavelet estimator only depends on the observed data and the sample size. Hence, the nonlinear estimator is adaptive. More importantly, the nonlinear wavelet estimator has a better convergence rate than the linear estimator in the case of $p\leq\tilde{p}$.

3.   Simulation study

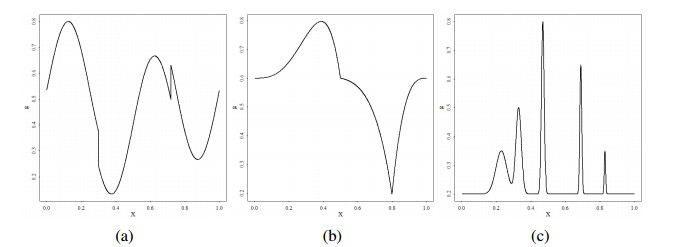
In order to illustrate the empirical performance of the proposed estimators, we produce a numerical illustration using an adaptive selection method, which is used to obtain the best parameters of the wavelet estimators. For the problem (1.1), we choose three common functions, $HeaviSine$, $Corner$ and $Spikes$, as the mean function $g(x)$; see Figure 1. Those functions are usually used in wavelet literature. On the other hand, we choose the function $f(x)$ by $f_{1}(x) = 3(4x-2)^{2} e^{-(4x-2)^{2}}$, $f_{2}(x) = sin(2\pi sin\pi x)$ and $f_{3}(x) = -(2x-1)^{2}+1$, respectively. In addition, we assume that the random variable $U$ satisfies $U\sim N[0, 1]$. The aim of this paper is to estimate the derivative function $r^{(m)}(x)$ of the variance function $r(x) (r = f^{2})$ by the observed data $(X_{1}, Y_{1}), \ldots, (X _{n}, Y_{n})$. In this section, we adopt $r_{1}(x) = [f_{1}(x)]^{2}$, $r_{2}(x) = [f_{2}(x)]^{2}$ and $r_{3}(x) = [f_{3}(x)]^{2}$. For the sake of simplicity, our simulation study focuses on the derivative function $r'(x)(m = 1)$ and $r(x)(m = 0)$ by the observed data $(X_{1}, Y_{1}), \ldots, (X _{n}, Y_{n}) \; (n = 4096)$. Furthermore, we use the mean square error ($MSE\; (\hat r(x), r(x)) = \frac{1}{n}\sum\limits_{i = 1}^{n}(\hat r(X_{i})-r(X_{i}))^{2}$) and the average magnitude of error ($AME\; (\hat r(x), r(x)) = \frac{1}{n}\sum\limits_{i = 1}^{n}|\hat r(X_{i})-r(X_{i})|$) to evaluate the performances of the wavelet estimators separately.

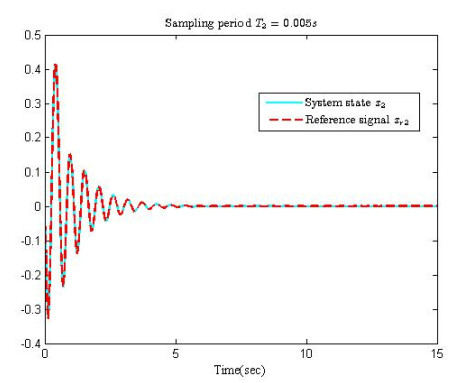
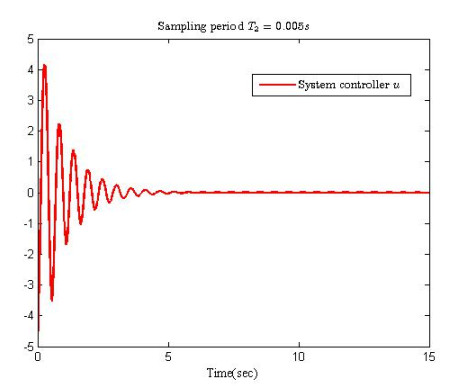
For the linear and nonlinear wavelet estimators, the scale parameter $j_{*}$ and threshold value $\lambda\; (\lambda = \kappa t_{n})$ play important roles in the function estimation problem. In order to obtain the optimal scale parameter and threshold value of wavelet estimators, this section uses the two-fold cross validation (2FCV) approach (Nason ^[27], Navarro and Saumard ^[28]). During the first example of simulation study, we choose $HeaviSine$ as the mean function $g(x)$, and $f_{1}(x) = 3(4x-2)^{2} e^{-(4x-2)^{2}}$. The estimation results of two wavelet estimators are presented by Figure 2. For the optimal scale parameter $j_{*}$ of the linear wavelet estimator, we built a collection of $j_{*}$ and $j_{*} = 1, \ldots, log2(n)-1$. The best parameter $j_{*}$ is selected by minimizing a 2FCV criterion denoted by 2FCV$(j_{*})$; see Figure 2(a). According to Figure 2(a), it is easy to see that the 2FCV$(j_{*})$ and MSE both can get the minimum value when $j_{*} = 4$. For the nonlinear wavelet estimator, the best threshold value $\lambda$ is also obtained by the 2FCV$(\lambda)$ criterion in Figure 2(b). Meanwhile, the parameter $j_{*}$ is same as the linear estimator, and the parameter $j_{1}$ is chosen as the maximum scale parameter $log2(n)-1$. From Figure 2(c) and 2(d), the linear and nonlinear wavelet estimators both can get a good performance with the best scale parameter and threshold value. More importantly, the nonlinear wavelet estimator shows better performance than the linear estimator.

In the following simulation study, more numerical experiments are presented to sufficiently verify the performance of the wavelet method. According to Figures 3–10, the wavelet estimators both can obtain good performances in different cases. Especially, the nonlinear wavelet estimator gets better estimation results than the linear estimator. Also, the MSE and AME of the wavelet estimators in all examples are provided by Table 1. Meanwhile, it is easy to see from Table 1 that the nonlinear wavelet estimators can have better performance than the linear estimators.

4.   Proof of main theorem

4.1.   Auxiliary results

Now, we provide some lemmas for the proof of the main Theorem.

Lemma 4.1. For the model (1.1) with A2 and A4,

Proof. According to the definition of ${\hat \alpha _{j, k}}$,

Then, it follows from A4 that

Using the assumption of independence between ${U_i}$ and ${X_i}$,

Meanwhile, the conditions ${\rm{V}}[{U_1}] = 1$ and ${\rm{E}}[{U_1}] = 0$ imply ${\rm{E}}[{U_1^{2}}] = 1$. Hence, one gets

by the assumption A2.

On the other hand, one takes $\psi$ instead of $\phi$, and $w_{j, k}$ instead of $\int_{0}^{1} {{g^2}(x){(-1)^{m}{\phi^{(m)} _{j, k}}(x)}dx}$. The second equation will be proved by the similar mathematical arguments. □

Lemma 4.2. (Rosenthal's inequality) Let $X_{1}, \ldots, X_{n}$ be independent random variables such that ${\rm{E}}[X_{i}] = 0$ and ${\rm{E}}[|X_{i}|^{p}] < \infty$. Then,

Lemma 4.3. For the model (1.1) with A1–A5, $2^{j}\le n$ and $1\le\tilde{p} < \infty$,

Proof. By (4.1) and the independence of random variables ${X_i}$ and ${U_i}$, one has

In this above equation, $A_{i}: = {Y_i^{2}{(-1)^{m}{\phi^{(m)}_{j, k}}(X_i)}}-{\rm{E}}\left[{Y_i^{2}{(-1)^{m}{\phi^{(m)}_{j, k}}(X_i)}} \right]$.

According to the definition of $A_{i}$, one knows that ${\rm{E}}\left[A_{i}\right] = 0$ and

The assumption A5 shows ${\rm{E}}[{U_1^{2\tilde{p}}}]\lesssim 1$. Furthermore, it follows from A1 and A3 that

In addition, and the properties of wavelet functions imply that

Hence,

Especially in $\tilde{p} = 2$, ${\rm{E}}\left[\left|A_{i}\right|^{2}\right] \lesssim 2^{2mj}$.

Using Rosenthal's inequality and $2^{j}\le n$,

Then, the first inequality is proved.

For the second inequality, note that

with (4.2) and $K_{i}: = {Y_i^{2}{(-1)^{m}{\psi^{(m)}_{j, k}}(X_i)}}-\int_{0}^{1} {{g^2}(x){(-1)^{m}{\psi^{(m)} _{j, k}}(x)}dx}.$

Let $B_{i}: = K_{i}\mathbb{I}_{\left\{|K_{i}| \leq \rho_{n}\right\}}-{\rm{E}}\left[K_{i}\mathbb{I}_{\left\{|K_{i}| \leq \rho_{n}\right\}}\right]$. Then, by the definition of ${\hat \beta }_{j, k}$ in (2.4),

Similar to the arguments of $A_{i}$, it is easy to see that ${\rm{E}}\left[B_{i}\right] = 0$ and

Especially in the case of $\tilde{p} = 2$, one can obtain ${\rm{E}}\left[\left|B_{i}\right|^{2}\right] \lesssim 2^{2mj}.$ On the other hand,

According to Rosenthal's inequality and $2^{j}\le n$,

Then, the second inequality is proved. □

Lemma 4.4. (Bernstein's inequality) Let $X_{1}, \ldots, X_{n}$ be independent random variables such that ${\rm{E}}[X_{i}] = 0$, $|{{X_i}}| < M$ and ${\rm{E}}[|X_{i}|^{2}] : = \sigma^{2}$. Then, for each $\nu > 0$

Lemma 4.5. For the model (1.1) with A1–A5 and $1\leq\tilde{p} < +\infty$, there exists a constant $\kappa > 1$ such that

Proof. According to (4.5), one gets $K_{i} = {Y_i^{2}{(-1)^{m}{\psi^{(m)}_{j, k}}(X_i)}}-\int_{0}^{1} {{g^2}(x){(-1)^{m}{\psi^{(m)} _{j, k}}(x)}dx}$, $B_{i} = K_{i}\mathbb{I}_{\left\{|K_{i}| \leq \rho_{n}\right\}}-{\rm{E}}\left[K_{i}\mathbb{I}_{\left\{|K_{i}| \leq \rho_{n}\right\}}\right]$ and

Meanwhile, (4.6) shows that there exists $c > 0$ such that ${\rm{E}}\left[|K_{i}|\mathbb{I}_{\left\{\left|K_{i}\right| > \rho_{n}\right\}}\right] \leq c{t_n}$. Furthermore, the following conclusion is true.

Note that the definition of $B_{i}$ implies that $|{{B_i}}|\lesssim \rho_{n}$ and ${\rm{E}}\left[B_{i} \right] = 0$. Using the arguments of Lemma 4.3, ${\rm{E}}[{B_{_i}^2}] : = \sigma^{2} \lesssim 2^{2mj}$. Furthermore, by Bernstein's inequality,

Then, one can choose large enough $\kappa$ such that

□

4.2.   Proof of main theorem

Proof of (a): Note that

Hence,

$\blacksquare$ The stochastic term ${\rm{E}}\left[\left \| \hat r_n^{lin}(x)-{P_{j_{*}}}r^{(m)}(x) \right \|^{\tilde{p}}_{\tilde{p}}\right]$.

It follows from Lemma 1.1 that

Then, according to (4.3), $|{{\mit\Lambda _{{j_*}}}}|\sim{2^{j_*}}$ and ${2^{{j_*}}} \sim{n^{\frac{1}{{2s' + 2m+1}}}}$, one gets

$\blacksquare$ The bias term $\left \| {P_{j_{*}}}r^{(m)}(x)-r^{(m)}(x) \right \|^{\tilde{p}}_{\tilde{p}}$.

When $p > \tilde{p} \ge 1$, $s' = s-({\frac{1}{p}-\frac{1}{\tilde{p}}})_+ = s$. Using Hölder inequality, Lemma 1.2 and $r^{(m)} \in B_{p, q}^s({{[0, 1]}})$,

When $1 \leq p\leq\tilde{p}$ and $s > \dfrac{1}{p}$, one knows that $B_{p, q}^s({{[0, 1]}}) \subseteq B_{\tilde{p}, \infty}^{s'} ({{[0, 1]}})$ and

Hence, the following inequality holds in both cases.

Finally, the results (4.8)–(4.10) show

Proof of (b): By the definitions of $\hat r_n^{lin}(x)$ and $\hat r_n^{non}(x)$, one has

Furthermore,

In this above inequality,

$\blacksquare$ For $T_{1}$. According to (4.9) and ${2^{{j_*}}}\sim{n^{\frac{1}{{2t + 2m+1}}}}$ $\left(t > s\right)$,

$\blacksquare$ For $T_{2}$. Using similar mathematical arguments as (4.10), when $p > \tilde{p} \ge 1$, one can obtain $T_{2}: = \left\| r^{(m)}(x)-{P_{{j_1} + 1}}r^{(m)}(x)\right\| ^{\tilde{p}}_{\tilde{p}} \lesssim 2^{-j_{1}\tilde{p}s}$. This with ${2^{{j_1}}}\sim \left(\frac{n}{{\ln n}}\right)^{\frac{1}{2m+1}}$ leads to

On the other hand, when $1 \leq p\leq\tilde{p}$ and $s > \dfrac{1}{p}$, one has $B_{p, q}^s({{[0, 1]}}) \subseteq B_{\tilde{p}, \infty}^{s-{\frac{1}{p}+\frac{1}{\tilde{p}}}} ({{[0, 1]}})$ and

Therefore, for each $1 \le \tilde{p} < \infty$,

$\blacksquare$ For $Q$. According to Hölder inequality and Lemma 1.1,

Note that

Meanwhile,

Then, $Q$ can be decomposed as

where

$\blacksquare$ For ${Q_1}$. It follows from the Hölder inequality that

By Lemma 4.3, one gets

This with Lemma 4.5, $|{{\mit\Lambda _{j}}}|\sim{2^{j}}$ and ${2^{{j_1}}}\sim \left(\frac{n}{{\ln n}}\right)^{\frac{1}{2m+1}}$ shows that

$\blacksquare$ For ${Q_2}$. One defines

Clearly, ${2^{{j_*}}}\sim{n^{\frac{1}{{2t+2m + 1}}}} \left(t > s\right) \le {2^{j'}}\sim \left(\frac{n}{\ln n} \right)^{\frac{1}{{2s + 2m+1}}} < {2^{{j_1}}}\sim \left(\frac{n}{\ln n} \right) ^{\frac{1}{2m+1}}$. Furthermore, one rewrites

$\blacksquare$ For ${Q_{21}}$. By Lemma 4.3 and ${2^{j'}} \sim \left(\frac{n}{\ln n} \right)^{\frac{1}{{2s + 2m+1}}},$

$\blacksquare$ For ${Q_{22}}$. Using Lemma 4.3, one has

When $p > \tilde{p} \ge 1$, by the Hölder inequality, ${t_n} = 2^{mj}\sqrt{{\ln n}/n}$, ${2^{j'}}\sim\left(\frac{n}{\ln n} \right)^{\frac{1}{{2s + 2m+1}}}$ and Lemma 1.2, one can obtain that

When $1\leq p\leq\tilde{p}$, it follows from Lemma 1.2 that

Take

Then, (4.19) can be rewritten as

When $\epsilon > 0$ holds if and only if $p > \frac{\tilde{p}(2m+1)}{2s+2m+1}$, $\delta = \frac{s}{2s+2m+1}$ and

When $\epsilon\le0$ holds if and only if $p \leq \frac{\tilde{p}(2m+1)}{2s+2m+1}$, $\delta = \frac{s-1/p+1 / \tilde{p}}{2(s-1 /p)+2m+1}$. Define

and obviously, ${2^{j'}} \sim \left(\frac{n}{\ln n} \right)^{\frac{1}{{2s + 2m+1}}} < 2^{j''} \sim \left(\frac{n}{\ln n}\right) ^{\frac{\delta}{s-1/p+1/\tilde{p}}} < {2^{{j_1}}}\sim \left(\frac{n}{\ln n} \right) ^{\frac{1}{2m+1}}$. Furthermore, one rewrites

For ${Q_{221}}$. Note that $\frac{\tilde{p}-p}{2}+\frac{\delta \epsilon }{s-1/p+1 /\tilde{p}} = \tilde{p} \delta$ in the case of $\epsilon\le0$. Then, by the same arguments of (4.20), one gets

For ${Q_{222}}$. The conditions $1\leq p\leq\tilde{p}$ and $s > 1/p$ imply $B_{p, q}^s({{[0, 1]}}) \subset B_{\tilde{p}, q}^{s-\frac{1}{p}+\frac{1}{\tilde{p}}}({{[0, 1]}})$. Similar to (4.18), one obtains

Combining (4.18), (4.21), (4.23) and (4.24),

This with (4.16) and (4.17) shows that

$\blacksquare$ For ${Q_3}$. According to the definition of ${2^{j'}}$, one can write

$\blacksquare$ For ${Q_{31}}$. It is easy to see that

$\blacksquare$ For ${Q_{32}}$. One rewrites ${Q_{32}} = \sum\limits_{j = j' + 1}^{{j_1}} 2^{j(\frac{1}{2}-\frac{1}{\tilde{p}}){\tilde{p}}} \sum\limits_{k \in {\mit\Lambda _j}} |{\beta _{j, k}}|^{\tilde{p}} {\mathbb{I}_{\{|{{\beta _{j, k}}}|\le 2\kappa {t_n}\}}}$. When $p > \tilde{p}\ge1$, using the Hölder inequality and Lemma 1.2,

When $1\leq p\leq\tilde{p}$, one has

For the case of $\epsilon > 0$, one can easily obtain that $\delta = \frac{s}{2s+2m+1}$ and

When $\epsilon \le 0$, $\delta = \frac{s-1/p+1 /\tilde{p}}{2(s-1 /p)+2m+1}$. Moreover, by the definition of $2^{j''}$, one rewrites

Note that

On the other hand, similar to the arguments of (4.24), one has

Therefore, in all of the above cases,

Finally, combining the above results (4.14), (4.15), (4.25) and (4.26), one gets

This with (4.11)–(4.13) shows

5.   Conclusions

This paper considers wavelet estimations of the derivatives $r^{(m)}(x)$ of the variance function $r(x)$ in a heteroscedastic model. The upper bounds over $L^{\tilde{p}} (1\leq \tilde{p} < \infty)$ risk of the wavelet estimators are discussed under some mild assumptions. The results show that the linear wavelet estimator can obtain the optimal convergence rate in the case of $p > \tilde{p}\ge1$. When $p\leq\tilde{p}$, the nonlinear wavelet estimator has a better convergence rate than the linear estimator. Moreover, the nonlinear wavelet estimator is adaptive. Finally, some numerical experiments are presented to verify the good performances of the wavelet estimators.

Acknowledgments

We would like to thank the reviewers for their valuable comments and suggestions, which helped us to improve the quality of the manuscript. This paper is supported by the Guangxi Natural Science Foundation (No. 2022JJA110008), National Natural Science Foundation of China (No. 12001133), Center for Applied Mathematics of Guangxi (GUET), and Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation.

Conflict of interest

All authors declare that they have no conflicts of interest.