In this study, we propose a novel second-order numerical formula that approximates the Caputo-Fabrizio (CF) fractional derivative at node tk+12. The nonlocal property of the CF fractional operator requires O(M2) operations and O(M) memory storage, where M denotes the numbers of divided intervals. To improve the efficiency, we further develop a fast algorithm based on the novel approximation technique that reduces the computing complexity from O(M2) to O(M), and the memory storage from O(M) to O(1). Rigorous arguments for convergence analyses of the direct method and fast method are provided, and two numerical examples are implemented to further confirm the theoretical results and efficiency of the fast algorithm.
1.
Introduction
Fractional derivatives, which have attracted considerable attention during the last few decades, can be defined according to their type. These include the Caputo [1,2,3,4,5,6,8,7,9,10,11,12,13], Riemann-Liouville [14,15,16,17,18,19,20,21], Riesz [22,23,24,25,26], and Caputo-Fabrizio (CF) [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46] types. Especially for the CF derivative, there were many related reports based on some discussions of different aspects, see the above references, and the Refs. [43,44,45]. In order to better grasp the fractional order problem, one can refer to the related works [47,48] and other fractional books.
Based on these fractional derivatives, numerous models have been developed. However, these models are difficult to solve directly by applying the general analytical methods because of the existence of fractional derivatives. This problem has inspired scholars to develop numerical algorithms to derive numerical solutions efficiently. In [5,49,50,51], a few high-order approximation formulas for the Riemann-Liouville, Caputo, and Riesz fractional derivatives were proposed and developed using different techniques or ideas. Recently, high-order discrete formulas for the CF fractional derivatives were designed and discussed in Refs. [32,33,34,35,36,37,38].
Another difficulty for simulating the models with fractional derivatives is the non-locality which greatly reduces the efficiency of the algorithm and requires much more memory storage compared with the traditional local models. Specifically, to obtain the approximation solutions {Uk}Mk=1 with M a positive integer, for the fractional models its computing complexity is O(M2), and the memory storage is O(M), in contrast to the local models with O(M) and O(1), respectively. For fast algorithms aimed at the Riemann-Liouville, Caputo, and Riesz fractional derivatives, see Refs. [14,52,53,54,55]. However, few scholars studied the fast algorithm for the CF fractional derivative. To the best of our knowledge, authors in [39] proposed numerically a fast method for the CF fractional derivative without further analysing the error accuracy.
In this study, our aim is to construct a novel efficient approximation formula for the following CF fractional derivative [31]
where t∈[0,T], 0<T<∞. Our contributions in this study mainly focus on
∙ Propose a novel second-order approximation formula for the CF fractional derivative with detailed theoretical analysis for the truncation error.
∙ Develop a fast algorithm based on the novel discretization technique which reduces the computing complexity from O(M2) to O(M) and the memory storage from O(M) to O(1). Moreover, we theoretically show that the fast algorithm maintains the optimal convergence rate.
The remainder of this paper is structured as follows. In Section 2, we derive a novel approximation formula with second-order convergence rate for the CF fractional derivative. In Section 3, we develop a fast algorithm by splitting the CF fractional derivative into two parts, the history part and local part, and then rewrite the history part by a recursive formula. Further we prove the truncation error for the fast algorithm. In Section 4, two numerical examples are provided to verify the approximation results and the efficiency of our fast algorithm. In Section 5, we provide a conclusion and offer suggestions for future studies.
Throughout this article, we denote C as a positive constant, which is free of the step size Δt.
2.
Novel approximation formula for the Caputo-Fabrizio fractional derivative
To derive a novel approximation formula, we choose a uniform time step size Δt=TM=tk−tk−1 with nodes tk=kΔt,k=0,1,⋯,M, where M is a positive constant. We denote uk=u(tk) on [0,T].
We next give a discrete approximation of CF fractional derivative CF0∂αtu(t) at tk+12(k≥1)
where ξj generally depending on s satisfies ξj∈(tj−12,tj+12) for j≥1 and ξ0∈(t0,t12). The coefficients Mkj and error Rk+12 are defined as follows
From (2.1), we obtain the following approximation formula for CF0∂αtu(tk+12) with k≥1.
Based on this discussion, we obtain the novel approximation formula (2.4). We next discuss the truncation error of the novel approximation formula.
Theorem 1. For u(t)∈C3[0,T], the truncation error Rk+12(k≥0) satisfies the following estimate
where the constant C is independent of k and Δt.
Proof. According to formula (2.3), we can obtain:
For the term I1, using integration by parts, we can arrive at:
Next, for the term I_{2} , by using the mean value theorem of integrals, we obtain:
where t_{0}\leq t_{\varepsilon}\leq t_{\frac{1}{2}} .
For the term I_{3} , we can easily obtain:
Similarly, we can estimate the term I_{4} as follows:
Finally, for the term I_{5} , we can derive:
Based on the aforementioned estimates for the terms I_1 , \cdots, I_5 , we can complete the proof of the Theorem.
3.
Fast algorithm
It is obvious that the approximation formula (2.4) is nonlocal since the value at node t_{k+\frac{1}{2}} for the CF fractional derivative is concerned with all the values of u^j , j = 0, 1, \cdots, k, k+1 , which means the computing complexity when apply the formula (2.4) to ODEs is of O(M^2) and the memory requirement is O(M) . In the following analysis, inspired by the work [14], we develop a fast algorithm based on the new discretization technique used in this paper, with which the computing complexity is reduced from O(M^2) to O(M) and the memory requirement is O(1) instead of O(M) .
We split the derivative _0^{CF}D_t^\alpha u(t_{k+\frac{1}{2}}) for k\geq 1 into two parts: the history part denoted by C_h(t_{k+\frac{1}{2}}) and the local part denoted by C_l(t_{k+\frac{1}{2}}) , respectively, as follows
For the local part C_l(t_{k+\frac{1}{2}}) , we have
where M^k_j is defined by (2.2), and the truncation error R^{k+\frac{1}{2}}_l is
For the history part C_h(t_{k+\frac{1}{2}}) , we rewrite it into a recursive formula when k\geq 2 in the following way
and when k = 1 ,
Careful calculations show that
For the term C_h^{(2)}(t_{k+\frac{1}{2}}) , by similar analysis for the Theorem 1, we have
where, for k\geq 2 ,
and, for k = 1 ,
For the truncation error R_l^{k+\frac{1}{2}} and R_h^{k+\frac{1}{2}} defined respectively by (3.3) and (3.8)-(3.9), we have the estimates that
Lemma 1. Suppose that u(t)\in C^3[0, T] , then for any k\geq 1 , R_l^{k+\frac{1}{2}} and R_h^{k+\frac{1}{2}} satisfy
where the constant C is free of k and \Delta_t .
Proof. To avoid repetition we just prove the estimate for R^{k+\frac{1}{2}}_l , since the estimate for R^{k+\frac{1}{2}}_h can be derived similarly. By the definition (3.3), we have
Then, for the term L_1 , using integration by parts and the Taylor expansion for \exp(t) at zero, we have
For the terms L_2 and L_3 , by the mean value theorem of integrals we can easily get L_2 \leq C\Delta_t^3 and L_3 \leq C\Delta_t^3 . Hence, we have proved the estimate for R^{k+\frac{1}{2}}_l .
Now, based on the above analysis, and for a better presentation, we can introduce an operator {}^{CF}_0 \mathcal{F}_t^{\alpha} for the fast algorithm defined by
where the history part \mathcal{F}_h(t_{k+\frac{1}{2}}) satisfies
We note that with (3.13) and (3.14), u^{k+1} only depends on u^k , u^{k-1} and u^{k-2} , which reduces the algorithm complexity from O(M^2) to O(M) and the memory requirement from O(M) to O(1) .
The following theorem confirms the efficiency of the operator {}^{CF}_0 \mathcal{F}_t^{\alpha} , with which we can still obtain the second-order convergence rate.
Theorem 2. Assume u(t) \in C^3[0, T] and the operator {}^{CF}_0 \mathcal{F}_t^{\alpha} is defined by (3.13). Then
where the constant C is independent of k and \Delta_t .
Proof. Combining (3.1), (3.2), (3.4)-(3.5) with (3.13), (3.14), we can get
Then, next we mainly analyse the estimate for \big|C_h(t_{k+\frac{1}{2}})-\mathcal{F}_h(t_{k+\frac{1}{2}})\big| . Actually, by definitions we obtain
We introduce some notations to simplify the presentation. Let
Then, the recursive formula (3.17) reads that
where the term \mathcal{R}_h^{k+1} is defined by
Now, by (3.7) and (3.14) as well as the Lemma 1, we can get
and
Noting here that L\in (0, 1) we have
Combining (3.19), (3.21)-(3.23), we obtain that
Now, with (3.16), (3.17), (3.24) and the Lemma 1, we complete the proof for the theorem.
4.
Numerical tests
To check the second-order convergence rate and the efficiency of the fast algorithm for the novel approximation formula, we choose two fractional ordinary differential equation models with the domain I = (0, T] . Let U^k be the numerical solution for the chosen models at t_k , and define U^0 = u(0) . Define the error as Err(\Delta_t) = \max_{1\leq k \leq M}|U^k-u^k| . For the sufficiently smooth function u(t) , we have the approximation formulas for u(t_{k+\frac{1}{2}}) and its first derivative \frac{\mathrm{d}u}{\mathrm{d}t}\big|_{t = t_{k+\frac{1}{2}}} :
Then, combined with results (2.5) and (3.15), the second-order convergence rate in the following tests is expected.
4.1. Example 1
First, we consider the following fractional ordinary differential equation with an initial value:
Next, by taking the exact solution u(t) = t^2 and the initial value \varphi_0 = 0 , we derive the source function as follows:
Direct scheme: Based on the novel approximation formula (2.4), we derive the following discrete system at t_{k+\frac{1}{2}} :
Case k = 0
Case k\geq 1
Fast scheme: Applying the fast algorithm to the equation (4.2), we can get, for k\geq 1 :
where \mathcal{F}_h(t_{k+\frac{1}{2}}) is defined by (3.14). For the case k = 0 , the formula (4.4) is used to derive U^1 .
Let T = 1 . By calculating based on the direct scheme (4.4)–(4.5) and the fast scheme (4.6), we obtain the error results by choosing changed mesh sizes time step \Delta_{t} = 2^{-10}, 2^{-11}, 2^{-12}, 2^{-13}, 2^{-14} for different fractional parameters \alpha = 0.1, 0.5, 0.9 , respectively, in Table 1. From the computed results, we can see that the convergence rate for both of the schemes is close to 2, which is in agreement with our theoretical result.
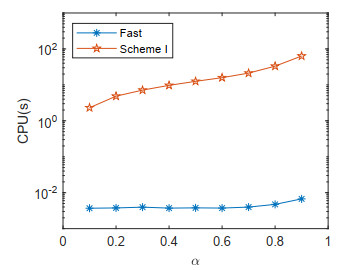
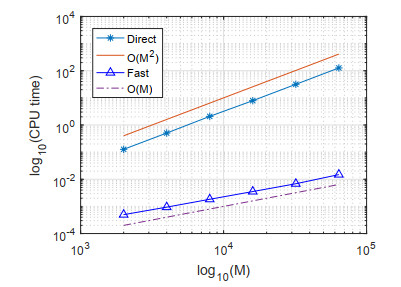
Moreover, we manifest the efficiency of our fast scheme in two aspects: (i) by comparing with a published second-order scheme [35] which is denoted as Scheme I and (ii) with the direct scheme (4.5). In Figure 1, we take T = 10 and plot the CPU time consumed for Scheme I and our fast scheme under the condition |Err(\Delta_t)|\leq 10^{-7} for each \alpha = 0.1, 0.2, \cdots, 0.9 . It is evident that our fast scheme is much more efficient. Further, to check the computing complexity of our direct and fast schemes, we depict in Figure 2 the CPU time in seconds needed with \alpha = 0.1 in the \log - \log coordinate system, by taking T = 1 , M = 10^3\times 2^m , m = 1, 2, \cdots, 6 . One can see that the fast scheme has reduced the computing complexity from O(M^2) to O(M) .
4.2. Example 2
We next consider another initial value problem of the fractional ordinary differential equation:
where the exact solution is u(t) = \exp(2t) , the initial value is \psi_0 = 1 , and the source function is:
Direct scheme: For the model (4.7), we formulate the Crank-Nicolson scheme based on the new approximation formula (2.4) at t_{k+\frac{1}{2}} as follows:
Case k = 0
Case k\geq 1
Fast scheme: Applying the fast algorithm to the model (4.7), we have, for k\geq 1 :
Similarly, we also compute and list the convergence data in Table 2 to show further the effectiveness of the novel approximation and the fast algorithm.
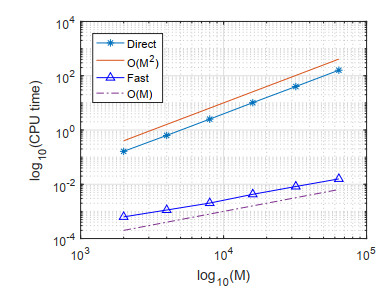
From the computed data summarized in Table 2, both of the schemes have a second-order convergence rate, and the fast scheme indeed improves the efficiency of the novel approximation formula without losing too much precision. Similarly as the Example 1 , we compare in Figure 3 the times for both of the methods under different M = 10^2 \times 2^m , for \alpha = 0.9 and m = 1, 2, \cdots, 6 in the \log - \log coordinate system. One can see clearly that the computing complexity for the direct scheme is O(M^2) , and for the fast scheme it is O(M) .
5.
Conclusion and suggestions for future study
In this study, we constructed a novel discrete formula for approximating the CF fractional derivative and proved the second-order convergence rate for the novel approximation formula. To overcome the nonlocal property of the derivative, we proposed a fast algorithm that tremendously improves the efficiency of the approximation formula. Moreover, we demonstrated the fast algorithm maintains the second-order convergence rate. In future works, this novel approximation formula and fast algorithm can be applied with the finite element, finite difference, or other numerical methods to specific fractional differential equation models with Caputo-Fabrizio derivatives.
Acknowledgments
The authors are grateful to the three anonymous referees and editors for their valuable comments and good suggestions which greatly improved the presentation of the paper. This work is supported by the National Natural Science Fund (11661058, 11761053), the Natural Science Fund of Inner Mongolia Autonomous Region (2017MS0107), the program for Young Talents of Science, and Technology in Universities of the Inner Mongolia Autonomous Region (NJYT-17-A07).
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: