Fekete-Szegö inequality for a subclass of analytic functions defined by Komatu integral operator

1.   Introduction

Nowadays most business providers use inventory theory in order to provide their clients with the goods they require while increasing their percentage of profit and increasing their customer base. Inventory theory focuses on controlling inventory levels of commodities in order to satisfy consumer demand. The majority of models have systems in place to look for answers to two key questions. The first is the appropriate time to place an order that increases the inventory level, and the second is the appropriate order quantity. The assumptions they make about cost structure, demand, and the physical properties of the policy are what give them their complexity. Since each company's circumstances are different and have specific characteristics and restrictions, there is no universal answer for all inventory models, and there are a lot of different models that might be used. This is dependent on several assumptions made about important factors including demand, costs, and the actual structure of the policy.

In this paper, we consider the stochastic inventory model where demand is seen as stochastic. Our aim is to select a set of $m$ best policies with the minimum cost. The holding, ordering, and shortage costs make up the total cost of the model. The complexity of this problem comes from the stochastic nature of the problem which requires a huge amount of computer simulation to get estimates of the average total cost. However, when the computational budget is limited, the available computation needs to be distributed in a clever way in order to get the correct selection. Moreover, we are also interested in measuring the final solution, thus the expected opportunity cost is used to assess the quality of the solution obtained.

In order to solve this problem and find the optimal policy or a set of optimal policies in cases where there is a limited computation budget is available to be distributed on different policies, then rather than distributing the computations evenly, the optimal computing budget allocation procedure is used to select a subset of optimal policies, Chen et al. ^[1,2]. Therefore, the policies that have more impact on the solution will be given more computation, but at the same time, we do not neglect the other policies. Kim and Nelson ^[3], claim that stochastic simulation can be used for establishing the measure of performance for every policy in simulation. The statistical selection methods are utilized to choose the best possible policy or a set of the best policies out of a limited number of options. In order to assess the selection quality, one needs to use some metrics because the simulation techniques being employed have a chance to make an unsuitable selection. There are two measures:

(1) The probability of Correct selection, $(P(CS))$ in which correct selection signifies the best possible simulated policy, selected out of a large but finite set of alternatives Chen et al. ^[1,2]. However, this measure is not always appropriate because it computes the percentage of selecting correct policies rather than their cost, so it deals with near-optimal solutions same as the worst policy.

(2) The second measure is the expected opportunity cost, $(E(OC))$ for a potentially incorrect selection, opportunity cost here is the difference between the total cost of the actual best policy and the total cost of the selected policy, Chick and Inoue ^[4,5], Chick and Wu ^[6]. Therefore, near-optimal solutions have a small impact on wrong selection and the measure is more realistic.

The aim of this study is to utilize the second measure which is the estimated opportunity cost as a criterion for the quality of choosing the best $m$ stochastic inventory policies. This aim is challenging to achieve since only a small class of performance indicators can be numerically evaluated, and using simulation to determine this value is expensive and consumes more time, particularly when considering large number of policies. Gao and Chen ^[7] have put a framework for selection procedures based on the expected opportunity cost, Gao et al. ^[8] have developed an approach to select the best out of a finite set of alternatives based on the expected opportunity cost and compare the $E(OC)$ with the $P(SC)$ and show that they are asymptotically equivalent. We will adapt the procedure of Gao et al. ^[8] and modify it to solve the stochastic inventory problem and use it to select a subset of the best stochastic inventory models on a finite horizon. Most of the previous procedures for selecting the best inventory model(s) use the $P(CS)$ rather than $E(OC)$. Gao et al. ^[9] have developed a subset selection using regression metamodel. Almomani et al. ^[10,11] proposed a combined statistical procedure measured by $E(OC).$ Almomani and Alrefaei ^[12] provide a sequential approach for choosing a subset which is comprised of efficient designs. The OCBA has gained attention recently, see Al-Salem et al. ^[13]. Almomani et al. ^[14] studied stopping rules for selecting the optimal solution, Alrefaei et al. ^[15] provided an approximation of the probability of correct selection. For a recent review of methods used for selecting Xu et al. ^[16].

While more modern procedures help to minimize the $E(OC)$ and have gained importance in many applications, conventional selection approaches detect the best possible policy with higher probability by maximizing $P(CS)$. The likelihood of making a bad choice will be reduced by these new selection techniques. Our goal in this paper is to use statistical selection techniques to resolve the inventory management issue. We provide a method for allocating the computing budget for choosing an adequate $m$ inventory policy and evaluating the effectiveness of the choice using the estimated opportunity cost $E(OC)$.

The rest of the paper is organized as follows: In Section 2, we formulate the stochastic inventory problem, and details the background on the stochastic inventory models. In Section 3 we present the method for selecting the best $m$ policies using the optimal computing budget allocation approach in terms of the expected opportunity cost. Section 4 contains a numerical example of a stochastic inventory model. Finally, Section 5 concludes the study.

2.   Problem formulation

In this section, we present the formulation of the problem that we consider in this paper which is the stochastic inventory model $(s, S)$ with periodic review. We first introduce some used notations:

$(s, S):$ is the stochastic inventory model;

$I:$ the inventory level;

$s:$ the inventory level at which and order is placed;

$S:$ the largest inventory level;

$OCBA:$ the optimal computing budget allocation;

$OCBA_m:$ the optimal computing budget allocation for selecting the best $m$ policies;

$EOC:$ the expected opportunity cost;

$TC(i)$: the total cost for policy $i$;

$\Theta$: the set of all policies;

$k$: the total number of policies;

$T$: the total number of simulation replications;

$Y_{it}$: the output of the $t^{th}$ simulation replication for policy $i$;

${Y_i}$: the actual mean of policy $i$;

$\bar{Y_i}$: the sample mean of policy $i$;

$\sigma_i^2$: the variance of policy $i$;

$N_i$: the number of simulation replications for policy $i$;

$i^{*}$: the true best policy;

$b$: the policy with smallest sample mean;

$\delta_{i} = \bar{Y}_{i}-c$, where $c$ is a constant between the best and the next best policy;

$\alpha_i = \delta_i / \sigma_i.$

In the stochastic inventory model $(s, S)$, it is assumed that the demand is stochastic. When the inventory level $I$ is reduced below or equal to a reordering point $s$, an order of $S-I$ is made, and the cost of doing so is known as the ordering cost. When a demand occurs and the level $I$ reduces to zero, a shortage occurs, and a cost is therefore imposed called the shortage cost. To reduce overall costs, there must be a balance between the holding cost, the price of keeping a stocked inventory and other costs. The resultant problem is a stochastic optimization problem and simulation is used to determine the estimated total cost. The goals of the inventory management problem are to make it more productive by making a balance between accomplishing things quickly but more expensively, and slowly but cheaply. Such a plan would include the best inventory management practices, which would lower the total cost of ordering, holding, and inventory shortage. The stochastic inventory problem $(s, S)$ is written as:

where $TC(i)$ is the total cost of policy $i$, and $\Theta$ is the set of all policies in $(s, S)$.

One of the most important elements in managing uncertainty in inventory is the demand. In case the demand is random, but probability distribution is known for the demand, we may use basic mathematical reasoning to derive the best distributional strategies. Finding the right probability distribution of demand to suit the model is the most crucial phase in the process. There is a widespread belief that distinct demand events take place separately. A Poisson distribution is the most typical distribution for the magnitude of the demand over a certain length of time. The interval between two successive requests may be distributed normally. For the time period of demand, other distributions such as the uniform distribution and the exponential distribution may also be employed. It is crucial to concentrate on how the starting inventory level and the amount of demand throughout a given time relate to one another.

An excess occurs when there is still some inventory following a request because the demand is lower than the quantity of supply. But if demand exceeds supply, there will be a stock shortfall, leading to incomplete demand; this is referred to as a shortage. Uncertainty about demand will be taken into account in stochastic inventory models. Continual or periodic review is used to divide stochastic inventory models into two categories to restock the inventory the next time frame. It is decided how much to order in the next period after determining its current inventory level after the conclusion of the previous session.

Our focus will be on a single item that is subject to periodic review, complete backlog, and random lead times, with $K$ as the ordering cost for set-up and $u$ for cost per item. Backlog is considered to have a shortage cost of $\pi$ per item per unit of time and a holding cost of one item per period of time is $h$. The product has multi-modal distribution per demand, while the time in demand is independent, and $\lambda$ rate denotes the identically distributed exponential random variables. Initial inventory level $I$ is where the inventory level begins. According to the demand in the final period, inventories will gradually decrease over time.

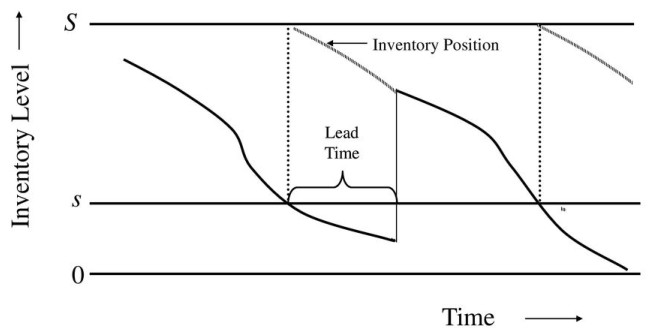
The inventory level is recalculated at the conclusion of each period to decide whether or not a fresh order is required at the start of the subsequent period. When a certain demand arises, we compare the demand values to the stock available during the time. If the demand value is greater than the stock quantity, a defect or inventory shortage occurs. Otherwise, there is a surplus rather than a shortage. We place an order at the conclusion of this period if $I$ is below the necessary level; otherwise, there is no need to do so. The inventory model $(s, S)$ is depicted in Figure 1, see Debadyuti ^[17].

The order quantity in mathematical terms is written as,

the inventory level during the start of the period is given by $I$.

The ordering, holding, and shortage costs are added together to get the total cost. The order cost is $K+uZ$ if $Z$ items are ordered, here $K$ defines the setup (fixed) cost that is constant and $u$ is the incremental cost per item. With $\pi$ as shortage cost per period per item, the shortage cost is equal to $\pi \bar{I}^{-}$, where the area under the curve of demand is given by $\bar{I}^{-}$ when a shortage occurs divided by the total period. $h \bar{I}^{+}$, is holding cost with $h$ is the cost of holding one item in one period of time, $\bar{I}^{+}$ is the area under the demand curve in normal mode (with items in inventory level) divided by the total period. Thus, the total cost is estimated using the following expression:

3.   Selecting the best m stochastic inventory policies

In this section, we discuss how to select a subset of best $m$ policies of the stochastic $(s, S)$ inventory model. We first introduce the optimal Computing Budget Allocation ($OCBA_m$) approach that will be used to select the optimal subset. Then, we discuss the expected opportunity cost $EOC_m$ that will be used as a quality measure of the selection. Then we present the algorithm that will be used for the subset selection.

3.1.   Optimal computing budget allocation

Consider a situation where a finite amount of computing resources must be divided across many alternative strategies in order to assess each one's performance and identify the one that performs the best. It is not a good idea to spend a lot of simulation time on particular policies since they often have little effect on the final outcome. The optimum computing budget allocation method, put out by Chen et al. ^[18], divides the available budget among the policies in accordance with how they would affect the outcome. More examples of the proposed policies than the other policies will be provided. See Chen ^[19], Banks ^[20], Pedrielli et al. ^[21] and Goodwin et al. ^[22].

Consider $k$ stochastic policies with means $Y_i$, $i = 1, \dots, k$, Chen et al.^[1,2] provided the $OCBA_m$ approach for selecting the suitable $m$ policy. It is assumed that $T$ (the total computation) is known in advance, they frame the problem to maximize $P(CS_m)$ subject to the total number of samples, where $CS_m$ stands for the best $m$ policies are selected. This problem is defined as follows Chen et al.^[1,2]:

where the total computational budget available is given by $T$, the number of competent policies is $k$, and the number of simulation samples to policy $i$ is given by $N_i.$ For each policy $i,$ $Y_{it}$ is the $t^{th}$ simulation sample where $t = 1, \dots, N_i.$ To estimate the mean value $Y_i,$ let $\bar{Y}_i = \frac{1}{N_i} \sum_{j = 1}^{N_i} Y_{it}$ be the mean estimate for policy $i$. Assume that the mean of $\{\bar{Y}_{1}, \bar{Y}_{2}, \ldots, \bar{Y}_{k}\}$ be ordered as $\bar{Y}_{i_1} \leq \bar{Y}_{i_2} \leq \ldots \leq \bar{Y}_{i_k}$. Then, the subset $S_m = \{i_1, i_2, \ldots, i_m\}$ will be selected. $P(CS_m)$ is the probability that $S_m$ is comprised of best actual $m$ policies, that is $\max_{i \in S_m} Y_{i} \leq \min_{i \notin S_m} Y_{i}$, with $Y_{i}$ defines the mean (unknown) of policy $i$.

Alrefaei et al. ^[23] in their research have approximated ''The Asymptotic Probability of Correct Selection", $APCS_m$ and have shown that it is maximized if for every $i, j$ policies with $i \neq j$,

where $\delta_{i} = \bar{Y}_{i}-c$ and $c$ is a constant between $Y_{i_m}$ and $Y_{i_{m+1}},$ we should mention also that the relation between $N_i$ and $N_j$ has been shown by Chen et al. ^[2]. Further it can be noted that, for a fixed $s$ index, we have $\frac{ N_s}{\sigma_s^2 / \delta_s^2} = \frac{N_j}{ \sigma_j^2/\delta_j^2}, \; \; \forall \; j = 1, \ldots, k.$ Hence we get, $N_j = \frac{\sigma_j^2}{\delta_j^2} \frac{\delta_s^2}{ \sigma_s^2 }N_s = \frac{\alpha_s^2}{\alpha_j^2} N_s,$ recall that $\alpha_j = \delta_j / \sigma_j.$ Therefore,

As $\sum_{j \in \Theta} N_j = T$, we get $\sum_{j \in \Theta} \frac{\alpha_s^2}{\alpha_j^2} N_s = T.$

For facilitating the computation, assume $D_s = \sum_{j \in \Theta} \frac{\alpha_s^2}{\alpha_j^2}$ and $D_j = {\alpha_s^2}/{\alpha_j^2}.$ Therefore, the number of samples for each policy are given by

More details on the $OCBA_m$ approach can be found in Chen and Lee ^[24], Gao and Chen ^[7], Gao et al. ^[8], Gao et al. ^[9], Lin et al. ^[25], Fu et al. ^[26] and Zhou et al. ^[27].

3.2.   The expected opportunity cost $E(OC)$

The $E(OC)$ has grown in importance in several commercial and engineering applications, which has resulted in a newly developed selection methodology in an effort to lower the opportunity cost ($OC$) of a potentially inaccurate selection. In the presence of simulation, the $OC$ represents the difference between the mean of the actual best policy and the mean of the selected unknown policy. $OC = Y_{b}-Y_{i^{*}}$, with $b$ representing the policy with the smallest sample mean and $i^{*}$ is the actual best policy. In case the best policy is selected correctly, the opportunity cost becomes zero. Therefore,

The expected opportunity cost, $E(OC)$ is the expected value $E(OC) = E(Y_{b}-Y_{i^{*}})$. In general, $N_1, N_2, \ldots, N_n$ is chosen for minimizing the $E(OC)$, given that the total budget of computing is limited. It was also argued by He et al. ^[28] that computing $E(OC)$ is expensive, but there is a need to reduce the $E(OC)$. This was also discussed in other studies by Gupta and Miescke ^[29], Chick and Inoue ^[4], Chick and Inoue ^[5], Chick and Wu ^[6] and Xiao et al. ^[30] all covered a review on $OC$. We may get the $OC$ by utilizing the estimated values of the unknown means as it is the variance between the unknown means. In our study, the $OC$ was determined by taking the sample mean of the final inventory policy costs once the simulation is completed.

3.3.   The $OCBA_m$ algorithm for selecting the best $m$ inventory policies

Algorithm (1) below uses the $OCBA_m$ based on $E(OC)$ for selecting a set of $m$ best stochastic inventory policies.

4.   Numerical example

To estimate $E(OC_m)$, we conducted an experiment on a generic example of the stochastic inventory model with artificial data. In this experiment, an inventory model with various parameter values is solved using the $OCBA_m$ technique. The stochastic inventory model with periodic review $(s, S)$ inventory model was employed in this experiment. When a single item is under a periodic review, random lead and full backlog times (distributed uniformly between periods- 0.5 and 1.0), with on-hand inventory (＄1 per item per period), ordering cost (which includes ＄32 per order set-up cost fixed and a ＄3 per item incremental cost), along with the backlog cost (＄5 per item per period). Demand items quantity in every demand is categorized as $1, 2, 3,$ and $4,$ with $1/6, 1/3, 1/3,$ and $1/6,$ probabilities respectively, and the duration between demands is considered to be an identically distributed, independent, exponential random variable.

Using Algorithm (1), the goal is to find the $m$ inventory policies with the lowest overall cost in order to choose the optimal inventory policies. The $E(OC_m)$ is what we use to gauge how well the algorithm is working. Additionally, reducing $E(OC_m)$ is desirable. The algorithm is implemented under a specific parameter setting. It is assumed that number of best selected inventory policies $m = 3$ and the number of inventory policies $n = 10$ with policies: $(s_{i}, S_{i}) =$ $\{(20, 60),$ $(40, 60),$ $(30, 70),$ $(40, 70),$ $(20, 80),$ $(60, 80),$ $(20, 90),$ $(30, 90),$ $(50, 90),$ $(40,100)\}.$ First, a simulation is run for every policy. The actual best policies are $(20, 60), (30, 70),$ and $(20, 80)$ for this experiment.

For this experiment, we utilized a total budget of $T = 500$, a simulated sample increment of $\Delta = 10$, and the size of the initial sample $t_{0} = 5$. This experiment concluded with 10 replications for choosing the top 3 inventory policies. The results are shown in Table 1. The "Best Policies" from the table refer to three policies of the inventory which are chosen by the algorithm as the optimal option. With "$TC_m$" to be the mean total cost of the actual best policies which are $(20, 60), (30, 70),$ and $(20, 80)$. The value "$TC_{OCBA_m}$" is the estimated mean average of the total cost of the three selected policies by the proposed algorithm. Hence, $E(OC_m) = |TC_m - TC_{OCBA_m}|.$ Here, we use the absolute value to calculate the $E(OC_m)$ since our target is the difference between $TC_m$ and $TC_{OCBA_m}$ not which one is the largest; note that in some replications it can be that the $TC_{OCBA_m}$ is larger than $TC_m$ and vice versa.

From Table 1, in the first replication, the algorithm selects inventory policies (30, 70), (60, 80) and (20, 80), with the calculated average of the total cost for selected policies is 224.6602761118. It means that we get the minimum total cost in this replication when the inventory policies are $(s_{i}, S_{i}) =$ $\{$(30, 70), (60, 80), (20, 80)$\},$ note that the policies (30, 70) and (60, 80) do not belong to the actual 3 best inventory policies where the policy (20, 80) belongs to the actual best subset of policies, therefore using the probability of correct selection measure implies that $P(CS_m) = 0.33$ which is too small. However, the expected $E(OC_m)$ here is $9.4\times10^{-9}$, obviously the average total cost for the three policies chosen by Algorithm 1 is close to the average total cost for the best three policies. which means that using the $E(OC_m)$ measure gives a better indication of the selected subset. The average values of the estimated $P(CS_m)$ and $E(OC_m)$ over 10 replications are given in the last row. As seen in this row the $E(OC_m)$ gives better indication about the elected subset than the $P(CS_m)$ measure. The experiment given above is extended for hundred replications. The outcomes depict that on average the opportunity cost expected for choosing three policies is $E(OC_m) = 3.5\times10^{-9}$, which is close to 0. Figure 2 demonstrates the $E(OC_m)$ values when the experiment is conducted with 100 replications.

As we examine the impact of the initial sample size $t_0$ on Algorithm (1), it is important to keep in mind that if $t_0$ is too small, there is a risk of receiving inaccurate early estimates of the overall cost. If the size is large, we can devote more computational time to unrelated policies, hence a balance value of $t_0$ should be considered for getting a better outcome. Algorithm 1 is implemented with $\Delta = 10$ on different values of $t_0 = 5, 10$ and $20$. The total budget, for $t_0$ values over 100 replications for the average $E(OC_m)$ over the $100$ replications is shown in Figure 3. From the graph, it is clear that for any value of $t_0$ the algorithm performs well and gives a very small value of $E(OC_m)$ and for $t_0 = 20$, the $E(OC_m)$ is very close to zero.

If $\Delta$ is large, then most of the computation time is lost on the sampling solution which does not affect the best selection. To see the effect the value of $\Delta$ on the performance of the algorithm we implement it on several values including $\Delta =$ $10, 20$ and $40$. The results are shown in Figure 4. It is obvious that the algorithm performs well for all values of $\Delta$ but gives some preferences to $\Delta = 40$ at which the $E(OC_m)$ approaches zero.

Now we increase the number of inventory policies to $n = 40$, these are: $(s_{i}, S_{i}) =$ $\{(20, 40),$ $(20, 50),$ $(30, 50),$ $(30, 60),$ $(20, 70),$ $(50, 70),$ $(30, 80),$ $(40, 80),$ $(50, 80),$ $(40, 90),$ $(60, 90),$ $(70, 90),$ $(20,100),$ $(30,100),$ $(50,100),$ $(60,100),$ $(70,100),$ $(80,100),$ $(20,110),$ $(30,110),$ $(40,110),$ $(50,110),$ $(60,110),$ $(70,110),$ $(80,110),$ $(90,110),$ $(20,120),$ $(30,120),$ $(40,120),$ $(50,120),$ $(60,120),$ $(70,120),$ $(80,120),$ $(90,120),$ $(100,120),$ $(20,130),$ $(30,130),$ $(40,130),$ $(50,130),$ $(60,130)\}.$ We seek to select the subset of 5 best policies, $m = 5$. The actual best 5 policies for this experiment are: $(20, 40), (20, 50), (20, 70), (30, 50)$ and $(30, 60)$. Apply Algorithm 1 to select the top 5 inventory policies. We investigate how the algorithm's performance is impacted by the simulation parameters, including initial sample size $t_0$ and the increase in simulation samples $\Delta$. We assume the given budget is $T = 2500$ that need to distributed among all the policies to select the best 5. We first run the algorithm when $\Delta = 20$, and $t_{0} = 10$, Table 2 lists the experimental results, with 10 replicates for selecting the top 5 inventory policies.

As we have seen in the first example, the expected opportunity cost gives a better measure for the selected subset than the probability of correct selection. The average over 10 replications is given the in last row, $E(OC_m) = 0.795663$ and $P(CS_m) = 0.82$. We run the experiment for one hundred replicates. The experimental outcomes reveal that the average value of the expected opportunity cost for selecting 5 inventory policies is $E(OC_m) = 0.9420510355$. Figure 5 shows $E(OC_m)$ values for the 100 replications.

To see the impact of the parameters $t_0$ and $\Delta$ on the algorithm, it is first conducted for several values of $t_0$ including $t_0 = 10, 20$ and $40$. Figure 6 displays the average value $E(OC_m)$ against the total budget spent over the 100 replications. It is clear that the average value of $E(OC_m)$ approaches zero as the number of computational budgets increases for all values of $t_0$.

Now the algorithm is conducted using several values of $\Delta$ including $\Delta =$ $10, 20$ and $40$ for selecting the best 5 inventory policies, and the results are shown in Figure 7. Again we see that the average value $E(OC_m)$ approaches zero as the computational budget increases for all values of $\Delta$. Therefore, we conclude that the algorithm is robust.

It is further noted that in the second experiment there were 40 policies, it was observed that the performance of this method is comparatively worse as compared to the first experiment, 10-policies from $E(OC_m)$ contexts of incorrect selection. It is because in the 40-policies experiment we use the Algorithm (1) to select 5 inventory policies and if anyone from these 5 policies does not belong to the actual best set of policies; $(20, 40), (20, 50), (20, 70), (30, 50)$ and $(30, 60),$ this means the selection will be considered as an incorrect selection. However, from the two experiments, 10-policies and 40-policies, it was observed that Algorithm (1) performed better in selecting the best $m$ inventory policies with minimum $E(OC_m)$, with the different parametric settings.

5.   Conclusions

In this study, we discussed how to select a subset of the best policies with the minimum total cost of a stochastic inventory management problem. The total costs includes the ordering, handling and shortage cost. The optimal computing budget allocation $OCBA_m$ approach is used for selecting the best $m$ inventory policies in the context of the expected opportunity cost $E(OC_m)$ as a measure of quality. The $OCBA_m$ is implemented on an inventory model using different parameter settings and compared with the probability of correct selection $P(CS_m)$ measure. It is clear that the algorithm is robust as it gives good solutions over a wide range of the initial sample size $t_0$ and the increment in each step, $\Delta$, but of course, the selection of the initial sample size $t_0$ is crucial because using a small value will not give detailed information about the model, however, large values will consume more effort on irrelevant solutions. Moreover, it also assumes that all details about the model are in hand. However, using the $E(OC_m)$ gives better measurement than $P(CS_m)$ because even if the selected subset is not the actual subset, the total costs of the selected policies are very close to that of the actual ones. Therefore, the $E(OC_m)$ is very close to zero. However, using the $P(CS_m)$ gives that the probability of correct selection is small. So we recommend using the expected opportunity cost as a measure of selection quality. In the future, we are interested to extend the work for solving supply chain management problems.

We suggest for decision-makers and managers to use the expected opportunity cost as a measure of performance for selecting the best policies rather than the probability of correct selection, the reason for that they may need extensive simulation runs in order to increase the correct selection.

Conflict of interest

The authors declare that they have no conflicts of interest.