A total variable-order variation model for image denoising

Abdelilah Hakim; Anouar Ben-Loghfyry

doi:10.3934/math.2019.5.1320

AIMS Mathematics, 2019, 4(5): 1320-1335. doi: 10.3934/math.2019.5.1320. Research article

Export file:

Format

RIS(for EndNote,Reference Manager,ProCite)
BibTex
Text

Content

Citation Only
Citation and Abstract

A total variable-order variation model for image denoising

Abdelilah Hakim, Anouar Ben-Loghfyry

LAMAI laboratory, university of Cadi Ayyad, Faculty of sciences and technology, Marrakesh, Morocco

Received: , Accepted: , Published:

Abstract Full Text(HTML) Figure/Table Related pages

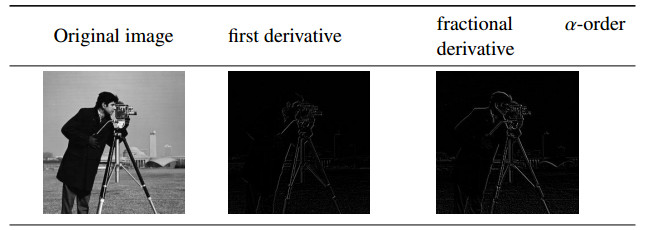
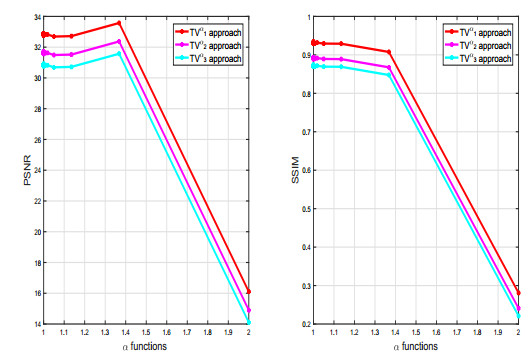
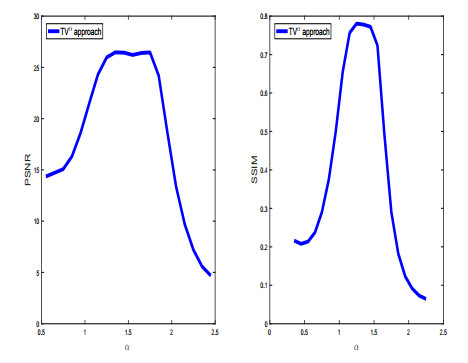
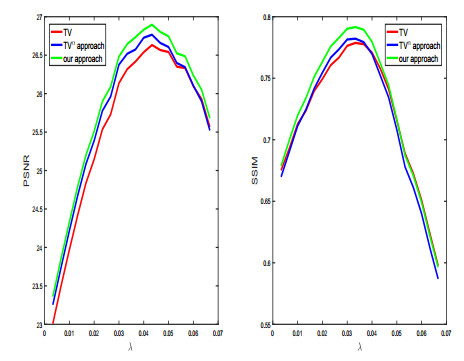
In this paper,we explore a new variational model based on the fractional derivative and total variation.Due to some metrics,our approach shows great results compared to other competitive models.In particular,deleting the noise and preserving edges,features and corners are headlights to our approach.For the fractional variable-order derivatives,different discretizations were presented to comparison.The theoretical results are validated by the Primal Dual Projected Gradient (PDPG) Algorithm which is well adapted to the fractional calculus.

Figure/Table

Supplementary

Article Metrics

Keywords: fractional derivative; total variation; image denoising; primal dual; finite difference

Citation: Abdelilah Hakim, Anouar Ben-Loghfyry. A total variable-order variation model for image denoising. AIMS Mathematics, 2019, 4(5): 1320-1335. doi: 10.3934/math.2019.5.1320

References:

1. R. Acar and C. R. Vogel, Analysis of bounded variation penalty methods for ill-posed problems, Inverse problems, 10 (1994), 1217-1229.
2. B. Ahmad, M. Alghanmi, S. K. Ntouyas, et al. A study of fractional differential equations and inclusions involving generalized caputo-type derivative equipped with generalized fractional integral boundary conditions, Aims Press, 2018.
3. J. Bai and X.-C. Feng, Fractional-order anisotropic diffusion for image denoising, IEEE T. Image Process., 16 (2007), 2492-2502.
4. A. Laghrib, A. Ben-loghfyry, A. Hadri, et al. A nonconvex fractional order variational model for multi-frame image super-resolution, Signal Process-Image, 67 (2018), 1-11.
5. A. Chambolle and P.-L. Lions, Image recovery via total variation minimization and related problems, Numerische Mathematik, 76 (1997), 167-188.
6. T. F. Chan, S. Esedoglu and F. Park, A fourth order dual method for staircase reduction in texture extraction and image restoration problems. In:2010 IEEE International Conference on Image Processing, (2010), 4137-4140.
7. T. F. Chan, A. M. Yip and F. E. Park, Simultaneous total variation image inpainting and blind deconvolution, Int. J. Imag. Syst. Tech., 15 (2005), 92-102.
8. F. Dong and Y. Chen, A fractional-order derivative based variational framework for image denoising, Inverse Probl. Imag., 10 (2016), 27-50.
9. C. Frohn-Schauf, S. Henn and K. Witsch, Multigrid based total variation image registration, Computing and Visualization in Science, 11 (2008), 101-113.
10. P. Getreuer, Total variation inpainting using split bregman, Image Processing On Line, 2 (2012), 147-157.
11. S. N. Ghate, S. Achaliya and S. Raveendran, An algorithm of total variation for image inpainting, IJCER, 1 (2012), 124-130.
12. M. Macias and D. Sierociuk, An alternative recursive fractional variable-order derivative definition and its analog validation. In:ICFDA'14 International Conference on Fractional Differentiation and Its Applications, IEEE, 2014.
13. W. Malesza, M. Macias and D. Sierociuk, Matrix approach and analog modeling for solving fractional variable order differential equations. In:Advances in Modelling and Control of Noninteger-Order Systems, Springer, 2015.
14. P. Ostalczyk, Stability analysis of a discrete-time system with a variable-, fractional-order controller, B. Pol. Acad. Sci.-Tech., 58 (2010), 613-619.
15. D. C. Paquin, D. Levy and L. Xing, Multiscale image registration, Int. J. Radiat. Oncol., 66 (2006), S647.
16. I. Podlubny, Fractional differential equations:an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Elsevier, 1998.
17. C. Poschl and O. Scherzer, Characterization of minimizers of convex regularization functionals, Contemporary mathematics, 451 (2008), 219-248.
18. L. I. Rudin, S. Osher and E. Fatemi, Nonlinear total variation based noise removal algorithms, Physica D:nonlinear phenomena, 60 (1992), 259-268.
19. D. Sierociuk, W. Malesza and M. Macias, On the recursive fractional variable-order derivative:equivalent switching strategy, duality, and analog modeling, Circ. Syst. Signal Pr., 34 (2015), 1077-1113.
20. D. Sierociuk and M. Twardy, Duality of variable fractional order difference operators and its application in identification, B. Pol. Acad. Sci.-Tech., 62 (2014), 809-815.
21. J. Zhang and K. Chen, A total fractional-order variation model for image restoration with nonhomogeneous boundary conditions and its numerical solution, SIAM J. Imaging Sci., 8 (2015), 2487-2518.
22. Z. Zhang, An undetermined time-dependent coefficient in a fractional diffusion equation, Inverse Probl. Imag., 11 (2017), 875-900.
23. D. Zosso and A. Bustin, A primal-dual projected gradient algorithm for efficient beltrami regularization, Comput. Vis. Image Und., (2014), 14-52.

show all references

Reader Comments

your name: * your email: *

Download full text in PDF

Associated material

Metrics