AIMS Mathematics, 2019, 4(3): 648-662. doi: 10.3934/math.2019.3.648

Research article Topical Section

Export file:

Format

  • RIS(for EndNote,Reference Manager,ProCite)
  • BibTex
  • Text

Content

  • Citation Only
  • Citation and Abstract

Modeling of the continuous casting process of steel via phase-field transition system. Fractional steps method

Costică Moroşanu

“Al. I. Cuza” University, Department of Mathematics, 700506, Iaşi, Romania

Received: , Accepted: , Published:

Topical Section: Mathematical modeling

Abstract    Full Text(HTML)    Figure/Table    Related pages

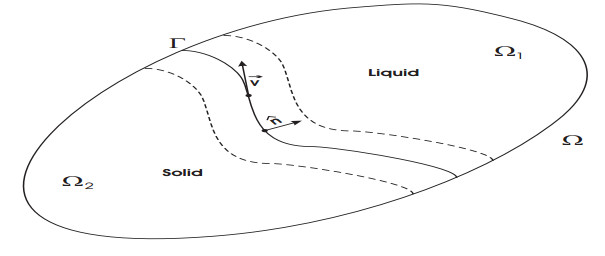
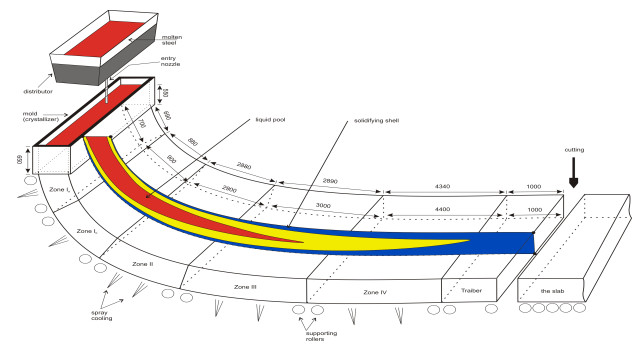
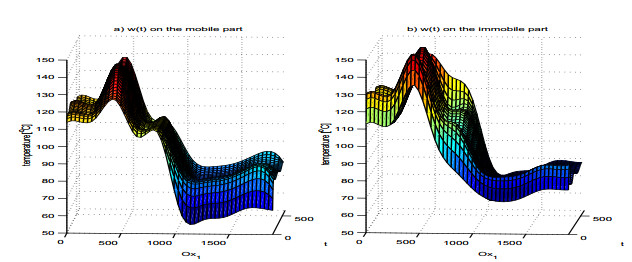
Here we consider the phase field transition system (a nonlinear system of parabolic type), introduced by G. Caginalp to distinguish between the phases of the material that is involved in the solidification process. On the basis of the convergence of an iterative scheme of fractional steps type, a conceptual numerical algorithm is elaborated in order to approximate the solution of the nonlinear parabolic problem. The advantage of such approach is that the new method simplifies the numerical computations due to its decoupling feature. The finite element method (fem) in 2D is used to deduce the discrete equations and numerical results regarding the physical aspects of solidification process are reported. In order to refer the continuous casting process, the adequate boundary conditions was considered.
  Figure/Table
  Supplementary
  Article Metrics
Download full text in PDF

Export Citation

Article outline

Copyright © AIMS Press All Rights Reserved