1. Introduction
Since the discovery of the piezoelectric effect in 1880, the demand for advanced functional materials in transducer technology has been increasing. Several applications have emerged because of the growing need for sensors and actuators (biomedical, transport, communication, robotic, electro-acoustic, etc.) [1].
Three main classes of piezoelectric materials are known: crystals, ceramics and polymers. Inorganic materials (crystals or ceramics) were the first to be discovered and are still commercialized due to their good piezoelectric coefficient. Compared to their inorganic counterparts, piezoelectric polymers have several advantages, namely being lightweight, low cost, highly flexible and thin, making them suitable for large-area applications [2]. However, most of the piezoelectric polymers, mainly poly(vinylidene fluoride) (PVDF) and its copolymers, have shown a relatively weak quasi-static piezoelectric coefficient (d33) of around 20 to 28 pC/N [3]. Therefore, the need for polymer-based materials with good piezoelectric properties led to the development of piezoelectric cellular polymers, called ferroelectrets. These voided polymers, with artificial piezoelectric behavior, have shown interesting piezoelectric properties (see Table 1) with a wide range of possibilities for their optimization.
Table 1. List of different methods to improve the piezoelectric properties of ferroelectrets.
| Step |
Method/ Treatment |
Effect |
Refs. |
| During film preparation |
Blending with a high melt strength polymer (such as adding low density PE (LDPE) to linear low density PE (LLDPE)) |
Morphological effect by stronger cell walls able to bear the extensional forces, thus preventing structure collapse. |
[4,5,6,7,8,9,10,11] |
| Nucleating agents addition (such as talc, calcium carbonate, short carbon fibers, etc.) |
Morphological effect by increasing cell nucleation density and producing more uniform and stable structure. |
[5,11,12,13,14,15,16] |
| Biaxial stretching (such as film extrusion-blowing) |
Morphological and mechanical effects by controlling cell shape and size in both longitudinal and transversal directions. |
[5] |
| After film preparation (post-processing) |
Temperature/pressure treatment |
Morphological and mechanical effects by controlling cell shape and size. |
[17,18] |
| Multilayer films superposition (three or more layers) |
Electrical effect: increased dipoles number leading to higher voltage under stress. |
[19] |
| Charge storage stability (such as treatment with hydrofluoric acid or orthophosphoric acid) |
Electrets properties improvement (thermal and time stability) by applying chemical treatments. |
[20,21] |
The paper is organized as follows. Firstly, definitions are given and the piezoelectric effect is discussed with a short historical perspective. Then, ferroelectrets and their differences with classical piezoelectric materials (ferroelectric materials) are presented. Finally, the preparation of these materials with their charging process, optimization, and recent applications is described.
2. Piezoelectricity
2.1. Fundamentals
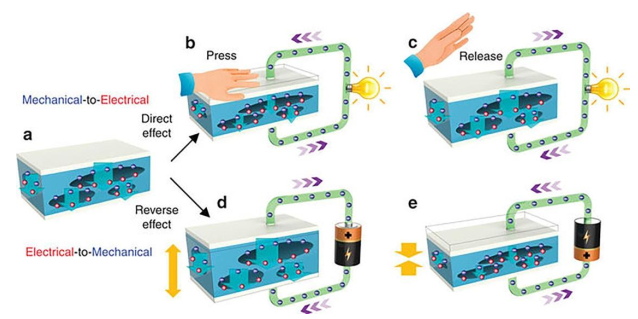
The term piezoelectricity is a combination of two words: "piezo" which is a Greek word meaning pressure, and "electricity", obviously referring to electrical charges. In fact, piezoelectric materials can convert mechanical energy into electrical energy [22,23]. As shown in Figure 1, the piezoelectric effect can occur in all directions and can be divided in two main effects: the direct piezoelectric effect, corresponding to the production of electrical charges under mechanical stress, and the inverse piezoelectric effect associated to the deformation of a material when subjected to an electric field.
Crystals, such as quartz (SiO2), were the first piezoelectric materials discovered around 1880 [25]. Their piezoelectricity comes from the displacement of atoms in their unit cells. When no stress is applied on the material, the positive and negative charges are equally distributed so that there is no potential difference. However, when a deformation is applied, the barycenters of the positive and negative charges are separated, hence, a change in the electric dipole moments occurs. The charges no longer cancel each other out and a potential difference exists.
Ferroelectrics constitute another piezoelectric family and represent the largest number of piezoelectric materials [26]. Their piezoelectric activity manifests itself as a result of external polarization [26,27,28]. In fact, ferroelectrics are materials having a spontaneous electric polarization below their ferroelectric Curie temperature (TC). At temperatures above TC, the crystals are nonpolar and no longer ferroelectric, thus behaving like normal dielectrics. On the other hand, the polarization of ferroelectrics can be reoriented by the application of an external electrical field. Ferroelectrics are made of several very small randomly oriented ferroelectric domains (formed by self-assembly) so that the electric fields created cancel each other and there is no net polarization on the material. Each domain contains some polarized crystals in the same direction and every domain is separated from others by domain walls. The internal dipoles are reoriented by the application of an external electric field, leaving a remnant polarization after field removal [26,27,28]. This remnant polarization (electric dipoles) also changes when a stress is applied, leading to piezoelectricity. The most well-known ferroelectric materials are ceramics, such as PZT. Some polymers have also shown ferroelectric properties due to their polar structure containing molecular dipoles. Similar to ceramic materials, these dipoles can be reoriented and kept in a preferred orientation state by an external electric field. PVDF is one of the most commonly used piezoelectric polymers exhibiting considerable flexibility in comparison with PZT, but has a poor d33 coefficient [26,27,28].
To improve the polymers' piezoelectric sensitivity, cellular structures were explored. Their development in the late 1980 was a response to the growing need to have piezoelectric materials combining the interesting properties of polymers and high piezoelectric coefficients [29,30]. The internal structure of polymer films is a two-phase morphology made from a solid polymer (continuous phase or matrix) and gaseous cells (dispersed phase or bubbles). When the polymer surfaces surrounding the voids are charged with an external electric field, the charged polymer foam behaves like a ferroelectric material. In fact, applying a large electric field across the film ionizes the gas molecules in the voids, thus opposite charges are accelerated and accumulated on each side of these voids. Such "artificially" embedded dipoles respond to mechanical stress (direct piezoelectric effect) or an externally applied electrical field (inverse piezoelectric effect) similar to piezoelectric materials [31]. More details of the poling procedure will be discussed in Section 3.3.
2.2. Modeling
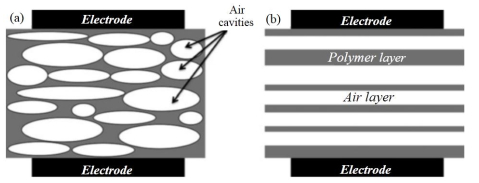
As discussed above, ferroelectrets are cellular charged polymer films with closed cavities exhibiting strong d33 coefficients. As a first approximation, the foam can be represented by a stack of alternating solid and gas layers characterized by the same macroscopic piezoelectric coefficient as the initial material (Figure 2).
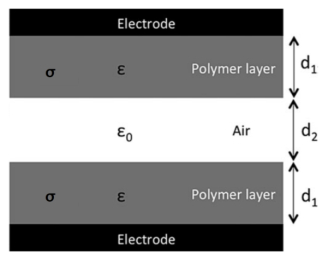
The system is then simplified to a three-layer structure: an air layer enclosed by two polymer layers (Figure 3). The piezoelectric coefficient (d33) can be defined as the ratio of the induced charge (Q) to the applied force (F) perpendicular to the film surface [2]. The main parameters controlling the piezoelectric behavior of a specific structure are the charge density on the cavities inner surface (σ), the polymer and the air permittivity (ε), the elastic stiffness c33 (elastic modulus), as well as the polymer (d1) and gas (d2) thickness layer leading to [32,33,34]:
|
d33=QF=εσc331+d2/d1(1+ε∗d2/d1)2
|
(1)
|
This simple model highlights the influence of the ferroelectrets mechanical and electrical properties on the macroscopic response of the cellular films.
3. Fabrication of ferroelectret films
The processing of piezoelectric cellular polymer films involves several stages, each one requiring the control and optimization of the different parameters involved, as well as the use of specific equipment. In this section, the conditions and techniques used for each step are presented and discussed based on existing work taken from the literature.
3.1. Development of the cellular structure
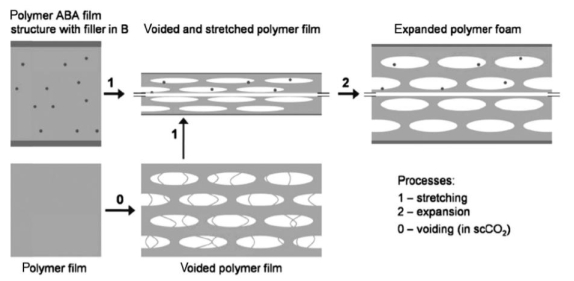
The first step is obtaining the cellular structure. In the literature, a wide variety of techniques for making cellular films has been proposed. These techniques can be classified in two categories: stretching and foaming methods (Figure 4). The stretching method consists of producing a polymer composite film filled with small solid particles and then stretching it to create voids around the solid particles by delamination at the particle-matrix interface [4,35]. In fact, the objective is to create micro-cracks generating a high level of interfacial stresses on the particles. Under mechanical loading (stretching), these particles are zones of crack initiation and propagation leading to the production of a cellular structure. On the other hand, foaming consists in generating a cellular structure via a blowing agent. Several blowing agents have been developed, depending on the desired foam morphologies. They can be divided in two classes: physical blowing agents (PBA) where a gas (or a volatile liquid) is directly injected into the polymer, and chemical blowing agents (CBA), which are molecules generating the blowing gas after some heat-induced chemical decomposition [4,35]. The obtained gas is dissolved in a polymer, and then nuclei are created by imposing a thermodynamic instability (pressure drop or temperature jump).
3.2. Foaming steps
The foaming process consists mainly of four main stages: saturation (blowing agent addition), nucleation (bubble formation), expansion (bubble growth) and stabilization (final morphology). The principles of each step are detailed next.
3.2.1. Saturation
This step involves the dissolution of a fluid (often supercritical) at high pressure. Again, the gas could be directly injected or generated via a chemical agent, and then dissolved in the polymer matrix. The objective is to obtain a homogeneous and uniform polymer–gas mixture, which is critical for high quality (homogeneous) foam production. For instance, the system pressure during extrusion or molding must be higher than the solubility pressure (also known as the saturation pressure) corresponding to the amount of injected blowing agent. Otherwise, undissolved gas pockets (large voids) can form and this is detrimental to the foaming process and the cellular structure homogeneity. Therefore, it is important to determine the solubility data for various blowing agents in different polymers to determine the amount of gas to inject (PBA) or powder to add (CBA) depending on the targeted density reduction (amount of void to generate). This information is important for the production of homogeneous and stable cellular structures [35].
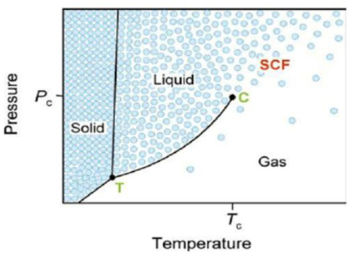
It should be noted that the use of supercritical fluids as PBA is known to result in the creation of a large number of small cells which can grow to produce microcellular foams due to high mass transfer rates into polymers [2]. This state is reached when the fluid pressure and temperature are above the critical point (see Figure 5). Under these conditions, the fluid can behave simultaneously like a gas (easier diffusion) and a liquid (easier dissolution). The most commonly used supercritical fluids are nitrogen (N2) and carbon dioxide (CO2). In comparison with CO2, N2 has the advantage of being above its supercritical temperature at room temperature. Thus, increasing the pressure above its supercritical pressure (3.4 MPa) is the only condition needed to create N2 supercritical conditions [4].
CBA can be classified in two categories: exothermic and endothermic. The majority of exothermic CBA generates N2 upon decomposition (such as azodicarbonamide), while the primary gas generated from endothermic CBA (such as sodium bicarbonate and citric acid) is CO2 [38].
3.2.2. Nucleation
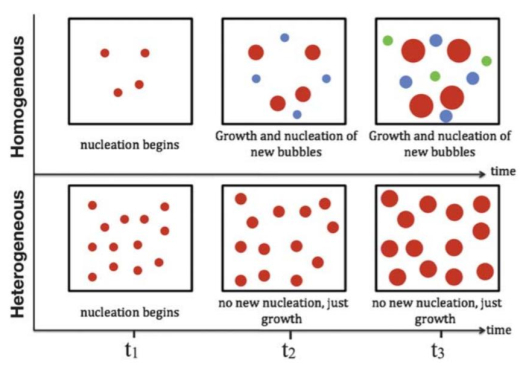
Nucleation is the transformation of a large number of gas molecules into small cells (micron-size). In fact, the already saturated system becomes supersaturated when the gas solubility is reduced through a thermodynamic instability. This instability can be achieved by either a temperature increase [39,40,41] or a pressure drop [42,43]. Consequently, the polymer–gas solution tends to form small bubbles (nuclei) so that a low-energy stable state can be restored. There are two nucleation types according to the classical theory, which is widely accepted to explain the nucleation process: homogeneous and heterogeneous nucleation (see Figure 6) [44,45,46,47].
Homogenous nucleation is a phase separation process in which bubble nucleation randomly occurs throughout the neat polymer-gas solution. In fact, the dissolved gas (blowing agent) forms a second phase (bubbles) in the primary phase (polymer matrix). On the other hand, heterogeneous nucleation requires preferred bubble nucleation sites such as impurities in the polymer matrix or sites provided by additives like nucleating agents (see Table 1 for typical nucleating agents). Generally, heterogeneous nucleation requires less energy (activation energy barrier) than homogeneous nucleation.
3.2.3. Expansion (cell growth) and stabilization
Resulting from gas diffusion (from the matrix to the cells), the bubbles continue to grow after nucleation. This is due to the decreased gas solubility in the polymer associated to decreasing pressure, as well as the cells tendency to grow to minimize the pressure difference, as the pressure inside the cells is higher than the surrounding matrix due to surface tension effects [35,48,49]. Several system parameters affect the cell growth mechanism such as gas concentration, viscosity, diffusion coefficient, and the number of nucleated bubbles. Cell expansion is mainly limited by the amount of gas available or the cooling level as the matrix becomes too stiff to allow further cell growth. To prevent cellular structure degradation during cell growth, three critical issues should be taken into consideration: cell coarsening, cell coalescence, and cell collapse. Proper strategies should be implemented to prevent these phenomena, which are detrimental to the cell-population density (number of cell per unit volume) and may degrade the foams mechanical properties [35,48,49].
3.2.4. Optimizing the temperature profile
To optimize the quality (homogeneity) of cellular films, the processing conditions must be carefully controlled. The temperature profile is one of the most important parameters influencing the foaming step. Generally, the temperature should be kept relatively low in the feeding zone to avoid premature decomposition of the blowing agent which would cause gas losses. Then, the temperature must be increased in the melting zone to ensure complete CBA decomposition and achieve homogeneous dissolution/dispersion of the generated gases before the pumping zone. The most sensitive temperature is at the die: a temperature too high leads to low melt strength of the matrix producing excessive foaming as well as bubble wall rupture, cell collapse, surface defects and bubble instability; but if the temperature is too low, limited bubble nucleation and growth occurs. So the temperature profile should be high enough in the intermediate section of the extruder (melting zone) to fully melt the polymer and fairly low near the die to increase the melt strength and avoid processing instability. More details about temperature profile and other parameters influencing foaming step can be found elsewhere [5].
3.3. Polymer ferroelectret films processing
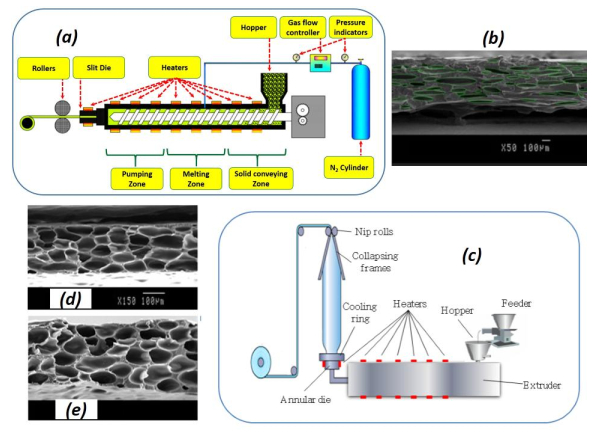
Polymer ferroelectret cellular films are generally produced using standard polymer processes such as extrusion and injection. Since the cellular structure is very important for piezoelectric properties optimization, these methods must allow a good foam morphology control. Here, some of the recent foaming processes based on extrusion (which is the most used process in the plastic industries) are presented to obtain a suitable structure for electrical charging (Figure 7).
3.3.1. Extrusion-calendaring foaming process (uniaxial stretching)
A continuous extrusion-calendaring foaming method was developed in 2017. Low cost thin cellular polypropylene (PP) foams were produced using nitrogen as a physical blowing agent and calcium carbonate (CaCO3) as a nucleating agent [15]. The developed films had a uniform eye-like structure with a cell aspect ratio of 5.4 in the longitudinal direction, which is needed for good cellular piezoelectric films (see Figure 7a, b) [15]. This led to a good quasi-static piezoelectric coefficient (d33) of around 800 pC/N.
3.3.2. Blown-film extrusion (biaxial stretching)
A method to produce polyethylene microcellular films using extrusion-blowing was developed in 2018 (Figure 7c). The 3D cellular structure was controlled for thin (less than 300 μm) polyethylene (PE) films using a chemical blowing agent (azodicarbonamide) and nucleating agent (talc) [5]. The main advantage of this process is that biaxial stretching is applied on the foaming samples providing a complete control of cell deformation in all directions. The different processing parameters, such as the take-up ratio (TUR), blown-up ratio (BUR), flow rate, screw speed, etc., were optimized resulting in a fine and uniform cell morphology (relative foam density of 0.62 and high cell density of 5.9 × 106 cells/cm3) of the foamed film with a well-developed ellipsoidal cellular structure (cell aspect ratio of around 4 in both longitudinal and transversal directions) which is required for high piezoelectric sensitivity (Figure 7d, e), since a high amount of surface area is generated per unit volume.
3.3.3. Other methods
Several other methods have also been proposed to produce ferroelectrets such as [50]:
● The template-based fabrication: consisting on utilizing a thermo-formed material to form a cellular structure in a sandwiched polymer films. Generally, the obtained cells are uniform and relatively large.
● Microfabrication: In this method, a structure with well-defined uniform micron-sized voids is formed by means of a microelectromechanical system (MEMS) fabrication process.
● Screen printing: It is a printing technique allowing to produce a uniform cell structure but with large cell sizes.
3.4. Electrical charging
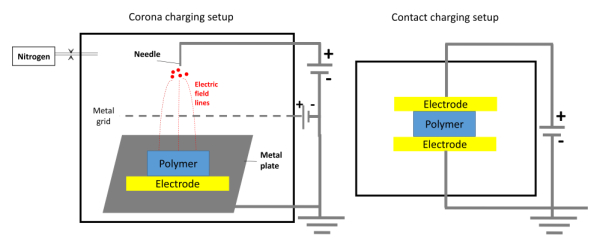
Electrical charging is a crucial step in ferroelectrets manufacturing. It involves applying a strong electric field leading to the accumulation of internal charges on the cell surfaces as shown in Figure 8. These charges of opposite polarity on opposite sides create the macroscopic dipoles. Mechanical stimulations causing a variation in the thickness direction of the electrically charged voids result in an electrical signal between the electrodes connected to the films' surface. Thus ferroelectrets are obtained with ferroelectric properties [51,52,53].
Several charging methods can be used to generate the dipoles in the polymer foam. The most common methods are direct contact charging and corona discharge. The direct contact charging method consists of directly applying a high electric voltage on the electrodes placed on either side of the film. The applied electric fields for different piezoelectric polymers are in the 5–100 MV/m range [53]. The electrodes can be deposited under vacuum or glued by an adhesive tape. This method is simple but only allows charging the film section located between both electrodes and is relatively expensive compared to corona discharge. In fact, the latter is cheaper and more feasible on an industrial scale as the method consists in imposing a potential difference between a needle and a conductive plate, thus creating an electric field over the entire plate width. As shown in Figure 8, this assembly consists of three main parts: the tip of the positively charged electrode, the negatively charged metal plate, and the metal grid. The strong ionization resulting from the corona effect bombards with electrons the film surface, thus creating positive and negative charges on both sides of the film surface. A more intense field allows a better ionizing gas molecules' polarization as described by Paschen's law (Eq 2). To get good contact with the ground, it is preferable that the sample bottom be coated with an electrode [41,42,43,44,45,46,47,48,49,50,51,52,53].
In general, the idea is to impose a potential difference on the cells allowing ionization of the gases they contain. The minimum voltage for a cell to be charged is related to the permittivity of the layers on the electric field created through the sample during electrical charging as [54]:
|
Vmin=Emin(εgazεpd1+d2)
|
(2)
|
where Vmin and Emin are respectively the minimum voltage to activate the micro-discharges and the electrical field obtained from the Paschen's law.
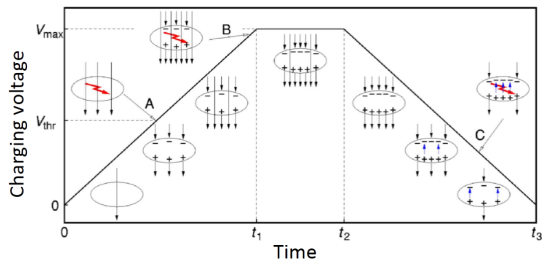
It is important to mention that there is no charge created below the minimum voltage (Vmin), also called the threshold voltage (Vthr) or simply the Paschen minimum, which is associated with the Paschen micro-discharges (dielectric barrier discharges or DBD). In addition, increasing the charging voltage beyond Vmin provides a field greater than the fields of the dipoles created, generating new micro-discharges and thus maximizing ion production. This directly results in d33 improvement [55]. Figure 9 is a model describing the charging process. The point A indicates the start of internal breakdown upon reaching the Paschen minimum. During DBD, charges are separated and trapped on the top and bottom cells surfaces. An electric field opposite to the externally imposed field is induced by the trapped charges. Point B is reached by further increasing the applied voltage. Thus, a second series of breakdown events may occur, increasing the charges density captured in the voids. The applied voltage is then reduced down to point C where a phenomenon of reverse discharge under the influence of trapped charges occurs tending to overcompensate the applied field [55].
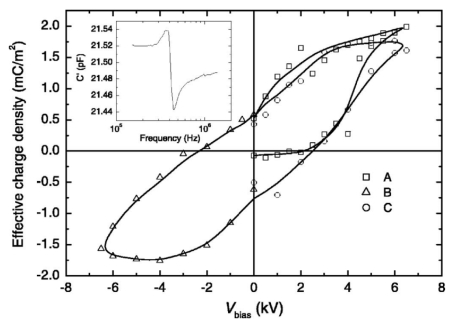
The hysteresis curves of the surface charge density (ξ) allow the understanding of the discharge magnitude when the imposed voltage is removed (Vc = 0). Figure 10 illustrates that the effective charge density after the electric field removal is about 0.5 mC/m2 for a PQ50 film from Nan Ya Plastic Corporation [56].
The electrical field intensity inside the cells is of the order of 80–100 MV/m and the loading time of about 60 s for films between 37 and 100 μm placed 3–4 cm from the corona tip [56,57,58]. The mechanism of charge separation is explained by Paschen's law relating the arc formation to the product of gas pressure (p) and the distance (d) between the electrodes.
3.5. Paschen's law
The electric charging is based on Paschen's law, which represents the phenomenon of electrical discharges in an "initially" non-conductive gas between two electrodes. For cellular films, the internal cell walls play the role of the electrodes. Since gases are electrical insulators, electrical breakdowns can only occur under specific conditions for which local and temporary gas ionization takes place. At this point, the gas state is called a plasma and this state is electrically conductive. The charges then pass through the plasma under the influence of the electric field and each electron will collide with the gas atoms thus producing new electrons (avalanche phenomenon). When the field is removed, the positive and negative charges remain separated sticking to the internal cell walls. Paschen's law (Eq 3) enables to calculate the minimum potential difference required (Vmin) between the electrodes as a function of their distance to produce an electric discharge for a given gas:
The term (p d) represents the pressure-distance product, while the parameters A and B are intrinsic to the gas used, and γ is the second ionization constant. So the product (p d) is proportional to the number of atoms or molecules located between the electrodes. This explains the existence of a minimum on the curves of Figure 10:
● When (p d) > (p d)opt: The electrons undergo a large number of collisions passing from the anode to the cathode slowing down their speed, hence higher voltage is required.
● When (p d) < (p d)opt: The avalanche phenomenon becomes less probable since the electrons are covering more space to meet atoms and ionize them, hence lower voltage must be applied [59].
Therefore, the charging process is strongly influenced by the dimensions (height, b) of the cavities, the gas composition inside the cavities, and the pressure.
4. Optimization of the piezoelectric properties of charged cellular polymers
4.1. Morphological and mechanical effects
The piezoelectric response of ferroelectrets originates from optimized cell morphology, elastic-foam properties and optimized charge trapping within the foam structure. The morphological properties (cells size, shape and density) of cellular polymers are related to the processing conditions and directly affect their mechanical and piezoelectric properties. On this basis, the optimization of ferroelectrets must pass through a careful morphological properties control and a good understanding of the relationship between the mechanical and piezoelectric properties.
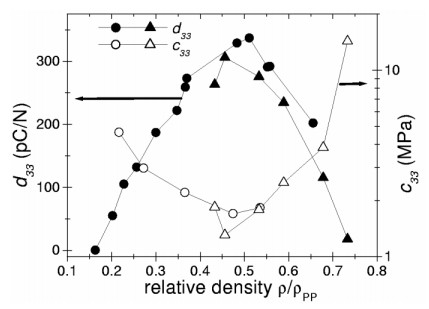
To obtain a good piezoelectric activity, the cellular structure must be developed through the whole area of the samples. It is also advantageous to create a high cell density allowing to maximize the available charging area. However, the film mechanical integrity should not be lost by reducing too much the matrix density. So cell height (b) should be carefully considered. As detailed in Section 3.4, charging is not possible if b is too small, but the piezoelectric coefficient d33 is inversely proportional to the elastic modulus (Eq 1). So the elastic modulus control is of great importance. The literature reports that foam density is the main parameter affecting the elastic modulus. Figure 11 experimentally confirmed the inverse relationship between the elastic stiffness c33 (elastic modulus) and the piezoelectric coefficient d33, as well as the important effect of the relative density for anisotropic PP cellular films. For these samples, the lowest elastic stiffness is obtained for films having a relative density of about 0.45 [60,61]. In fact, a high relative density corresponds to a large elastic modulus (more material to resist the pressure) and less voids to charge, thus a smaller piezoelectric coefficient is consequently obtained. Similar observations about the effect of anisotropic foams density on the mechanical properties were reported via numerical simulations [61].
However, the relative density is not the only parameter affecting the mechanical properties of a foam which can also be represented by cell size, cell shape (or aspect ratio) and density. Several studies have investigated this effect [61], while different models were developed to link the morphology to the mechanical properties. The most widespread model is the power-law model [62]:
where E* and Es are respectively the Young's modulus of the foam and the solid (unfoamed matrix), while C and n are model parameters function of the micro-structure. Gibson and Ashby [59] presented experimental results on various cellular materials and their observations suggested that n = 2 is a good approximation. Since the dependence of effective properties on the micro-structure are not well understood in mixtures, the exact values for C and n are not known, which is a limitation to optimize and predict the composite/foam properties. However, several studies have reported that an eye-shaped cell structure with an aspect ratio a/b > 4 is optimum for good piezoelectric activity [2,54,63,64].
Computer simulations have also been performed to predict the relations between the mechanical and morphological properties of cellular materials [65,66]. Tuncer simulated the elastic properties of ferroelectric cell structures using two different geometrical models: truss-like (straight boundary structure) and eye-shaped (curved boundary structure) [66]. The following quadratic power-law expression (modified Eq 5) was used:
where q is the relative density and C is a model parameter. The results showed that the eye-shaped structure has lower Young's modulus than the truss-like at low solid concentrations (q < 0.15). However, negligible differences were obtained at intermediate (0.15 < q < 0.85) and high (q > 0.85) solid contents. Simulation results for three different unit-cell ratios (a/b = 2, 4, and 8) were also presented for both structures. It was found that increasing the a/b ratio led to lower elastic moduli for the range of solid concentrations and type of structure studied [66].
Although numerical simulations are very interesting to allow a better trend understanding for the foam structural effects, they generally use perfect structures not achievable at laboratory and industrial scales. Experimental work is still needed for validation and more precise models must be further developed.
4.2. Different methods used to enhance piezoelectricity of ferroelectrets
Several methods and treatments are available to optimize the ferroelectrets' piezoelectric activity by controlling the mechanical and morphological properties, and also by improving the electrical charge conditions and electrets properties such as charge trapping capacity, charging time and thermal stability. These treatments can be performed before or after the cellular film preparation and Table 1 reports on the most important works on ferroelectrets properties.
4.3. Enhanced thermal and temporal stability of the piezoelectric coefficient
In addition to its sensitivity, the stability of the piezoelectric coefficient of electromechanical transducer materials is a critical factor. Obviously, piezoelectric stability of ferroelectrets is highly dependent on the charge trapping properties of the polymer; i.e., on how effectively charges deposited on the voids inner surfaces can be retained over a wide range of times and temperatures [67]. The interfaces between amorphous and crystalline zones of the polymer are believed to limit electric charges drift [67]. Therefore, a film with more interface area should better retain its charges and piezoelectric effect. In the same context, it was shown that a higher degree of crystallinity gives a better charge stability towards temperature and time [68].
Surface modification can also be a solution to improve the charge stability of ferroelectrets [67,68,69,70]. Different treatments such as corona charging at elevated temperatures, quenching or pre-aging before charging, controlled aging or annealing after charging, have a significant effect. Some chemical treatments have also proved their efficiency. For example, the modifications of PE ferroelectrets with phosphorus trichloride (PCl3) and titanium tetrachloride (TiCl4) vapor, as well as orthophosphoric acid (H3PO4) all resulted in significantly enhanced charge stability. For PP ferroelectrets, treatment with fluorine gas was very efficient in terms of thermal stability. However, the effect of these different treatments on the degree of crystallinity and the piezoelectric stability is not yet well quantified and more efforts should be done to model the relation between these parameters [67,68,69,70].
5. Polymers used as ferroelectrets and their properties
The ferroelectret potential of different polymers was investigated using a variety of preparation methods. Cellular PP is the most investigated polymer in this context. It has become the workhorse of ferroelectret technology mainly due its high piezoelectric coefficient. Depending on the processing method and the characteristics of the applied electric field, a wide range of piezoelectric coefficient (130–2100 pC/N) has been reported [2]. Cellular PE has recently been investigated as a ferroelectret material [71,72]. Cellular PE films were fabricated with a thickness of 30 μm, a porosity ranging from 58 to 85% and pores diameter of about 0.3 μm distributed throughout the sample. The films were charged via corona poling with a distance (d) between the discharge tip and the cellular PE films of 8 mm and a needle voltage of 7 kV. A piezoelectric coefficient between 200 and 400 pC/N was recorded [72]. Commercial closed cell PE foams of 480 µm were used in another study [73]. The films underwent "thermal stretching" consisting of simultaneous sample heating to 100 ℃ and mechanical stretching, thus decreasing film thickness and increasing cell deformation. Finally, a corona discharge voltage of 12 kV was applied for 5 min leading to a piezoelectric coefficient up to 170 pC/N [73].
Fluorocarbon polymers, such as several kinds of Teflon [polytetrafluoroethylene (PTFE), fluoroethylenepropylene (FEP), tetrafluoroethylene-per-fluoromethoxyethylene copolymer (PFA), and amorphous Teflon (AF)] have shown good electrets (charge storage) properties allowing them to be used as ferroelectrets [67]. Porous AF films were prepared by casting a solution of Teflon (Dupont) resin in Fluorinert (FC-77). Cellular films were obtained, and 3 to 8 layers were cast on top of each other. The final thicknesses achieved were between 9 and 60 μm and typical densities were around 500 kg/m3 [74]. The sandwich films were charged in a point-to-plane corona discharge at –15 kV for 15–30 s at room temperature. The surface potential applied was between 21.0 and 21.5 kV. As a result, a strong piezoelectric effect was generated with a coefficient up to 600 pC/N and a stable piezoelectric sensitivity up to 120 ℃ [74]. Tubular-channel FEP-film ferroelectret has also been produced by laminating two FEP films around a PTFE template at 300 ℃. Then, the PTFE template was removed from the laminated stacks. A piezoelectric coefficient up to 160 pC/N was recorded with a thermally stable charge up to 130 ℃ [75].
Polyester ferroelectrets have also been investigated such as polyethylene terephthalate (PET) foams [76,77] and polyethylene naphthalate (PEN) [78,79,80] produced through physical foaming with supercritical CO2. The optimized PET and PEN ferroelectrets exhibited high piezoelectric coefficient of 500 and 140 pC/N respectively, with a stable sensitivity up to 80 ℃, slightly higher than cellular polyolefin ferroelectrets. For example, PEN ferroelectrets are still piezoelectrically active even after storage at 100 ℃ for 5 days. Finally, cyclo-olefin polymer (COP) and copolymer (COC) ferroelectrets with a maximum d33 of about 1000 pC/N and a continuous service temperature (CST) of 100 ℃ were also developed [81].
The piezoelectric properties of typical ferroelectrets are summarized in Table 2.
Table 2. Comparison of the piezoelectric properties of typical ferroelectrets.
| Ferroelectrets |
d33 range (pC/N) |
CST (℃) |
Refs. |
| Cellular PP |
140–2100 |
50 |
[2,67] |
| Cellular PE |
200–400 |
- |
[67,72,73] |
| Cellular AF |
600 |
120 |
[74] |
| Cellular FEP |
50–160 |
- |
[75] |
| Cellular PET |
23–500 |
- |
[76,77] |
| Cellular PEN |
60–140 |
80 |
[78,79,80] |
| COP and COP |
15–1000 |
100 |
[81] |
6. Applications
Several ferroelectret applications have been proposed, demonstrated and commercially realized. An overview of the recent applications of cellular polymer films is presented to highlight their potential for innovative new products.
6.1. Impact sensors
Impact sensors are one of the main ferroelectrets common use. In fact, the stresses created by the foam deformation during impact depend on the speed and the force of the striking object which are controlling impact energy. When the shock exceeds a predetermined threshold, an alert can be sent to a connected electronic device (computer, tablet or phone), thus making more informed decisions. For example, head trauma is common in sport, such as American football. Unfortunately, the signs are not always visible and several players say they feel good, even if they are not. Produced by XOnano smart foam company [82], piezoelectric polymer foams inside the helmet emits an electric charge at the moment of impact. This charge is picked up by a microprocessor placed on the helmet top. The impact is evaluated and the results are transmitted to the trainer or team doctor. A coach will know in just a few seconds how hard his player has been hit and have a better idea if the player can continue playing or must leave immediately and be examined for concussion.
Also, with this technology, a car can give a virtual image of an accident helping first responders to know the severity of a collision even before they arrive on the scene. Insurance companies can also use this technique to assess the details of a car accident. Due to the subjectivity of most evaluation methods, insurance companies pay billions of dollars every year on fake or inflated insurance claims. Once an automobile contains this piezoelectric cellular polymer film, claims evaluation can become very accurate [82].
6.2. Human body
Several ferroelectret sensors are developed to detect human body activities. For example, the registration of body motion is an interesting technique allowing the control of human–computer interfaces or real devices. Information related to muscle activity is important for the study of body motion (biomechanics). Such information must be registered for different purposes such as diagnostics, rehabilitation and entertainment [83,84]. For example, muscle activities are recorded in rehabilitation training for patients with motor-function impairments to evaluate treatment performance [85]. Likewise, in biomedical devices such as prosthetic arms, the body-motion information is detected, then the motor commands are extracted and used for device control [86]. Force myography (FMG) is an important approach to detect body motion. In this case, the mechanical force signal associated with muscle activity is exploited. In fact, muscle contractions are accompanied by a change of muscle volume generating pressure in radial directions. The purpose of FMG is to record a force-distribution map [87]. Ferroelectrets have recently been developed for FMG due to their large piezoelectric coefficients, small elastic moduli, high flexibility, good stretchability and adaptability to various shapes. In fact, porous PP films (50 µm in thickness) with gas-filled cavities of the central section of around 100 μm in the lateral directions and 5 μm in thickness have been used as sensors recording the radially directed force-distribution signals generated by muscle contractions. By extracting the signal characteristics, the FMG models could be recognized with algorithms. Upper-limb motions of hand closing/opening and wrist pronation/supination/flexion/extension were registered with good accuracies [87].
The respiration of humans can also be recorded with cellular polymers due to their good sensitivity, even if the transducers are not directly fixed to the skin [85]. Developed by Emfit (Finland), cellular PP films have been placed directly on beds for long-term respiration monitoring. The sensor signals measured during human motion are proportional to the respiration signal. The recorded information can give information on sleep quality [88].
6.3. Transport applications
Ferroelectret sensors have also been developed to optimize the comfort of different transport means. For example, the noise in the cabins of cars, trains and aircrafts is a great source of nuisance for travelers, and a significant amount of research and development is devoted to active noise control. The noise-generating vibration may be detected by means of ferroelectret polymer layers to determine the vibration frequency and amplitude. After recording, a sound wave with optimum frequency and amplitude (anti-sound) is generated and focused to locally (at the human ears) cancel the noise [89].
Orthopedic diagnostics is also an interesting issue in automotive applications. Ferroelectrets were developed to monitor seats and backrests pressure distribution to optimize/design office chairs or seats in cars/trains/aircrafts for improved back comfort [89].
6.4. Acoustic applications
Including audio, ultrasonic and infrasonic frequency ranges, acoustic transducers are vibration-based electromechanical transducers operating in the acoustic spectrum range (20–20,000 Hz). These transducers include microphones, loudspeakers, and hydrophones [88,90,91]. Microphone ferroelectret sensors are already on the market and produced by Emfit and B-Band (Finland) [85,89].
Another type of electromechanical sensors is acoustic emission sensors (AES). These sensors passively detect the acoustic signals due to a system mechanical or shape change. Their main difference with ultrasonic transducers is that they detect the acoustic signal passively, while an ultrasonic transducer transmits a signal and receives the reflected signal to detect any change. AES are generally exploited where continuous monitoring is needed, such as material fracture or device failure, while ultrasonic transducers are used in automated machinery and medical imaging [50]. More examples of recent ferroelectric acoustic applications can be found in the literature [92,93].
6.5. Tactile sensing applications
A tactile sensor is a device measuring a physical phenomenon such as shape, force, temperature or softness. This type of sensor has potential uses in medicine as well as in robotics [94]. Ferroelectrets are starting to be suitable for such applications, mainly in measuring force or pressure. For example, PP ferroelectret has been used in a large area touchpad sensor. To identify the touch location, this sensor analyzes four different voltage signals at the corners of a cellular PP. A flexible and self-powered keyboard converts the mechanical stimuli applied on the keyboard to an electrical signal used to show the pressed letter on a computer monitor also made from ferroelectret transducers [95].
6.6. Other applications
Several other ferroelectret applications have been studied and developed for different general applications. The most important ones are accelerometers [96,97], games [98] and robotics [99]. Moreover, several applications are expected in the near future depending on the sensitivity level and the general performance/cost ratio of the materials developed.
More information on the subject can be obtained in reviews about electroactive polymers [100], as well as about predicting the properties of ferroelectrets by numerical simulations [58,101].
7. Conclusions and future directions in the field
Despite their non-polar nature, internally charged cellular polymers provide a novel class of materials called ferroelectrets with close analogies to ferroelectrics. This allows the development of a wide range of applications, but also induces several challenges for materials and processing optimization, such as increasing the piezoelectric coefficient (d33) as well as improving the long term and thermal stability of the piezoelectric activity.
Ferroelectrets are clearly distinguished from traditional piezoelectric materials, such as PZT, due to their softness, great ability to be developed and optimized, and their outstanding properties such as low cost, light weight, and good piezoelectric properties. Optimum development of these materials needs a multidisciplinary undertaking of polymer chemistry (materials synthesis), physics (materials characterization), mechanics (elastic properties), polymer processing and chemical engineering (development of industrial foaming processes), materials science (ferroelectric and ferroelectret materials), as well as the ability to develop engineering applications such as sensors, transducers, acoustics, and others. So a great potential is expected for future applications. In fact, this paper may only be "surface" evaluation of their enormous potential. There is no doubt that other attractive topics or interesting applications are waiting to be discovered. It is expected that these materials will be integral components of numerous devices improving the quality of life by delivering high-quality audio and practically noise-free environments, vital medical information, enhanced security, etc.
It is also expected that improvement in material preparation techniques will allow obtaining more homogenous cellular structure and also the development of models quantifying the relationships between the mechanical, morphological and piezoelectric properties will be a key to optimize ferroelectrets capacities.
Acknowledgments
Financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC) and Fonds Québécois de la Recherche sur la Nature et les Technologies (FRQNT) was received for this work.
Conflict of interest
None.









 DownLoad:
DownLoad: