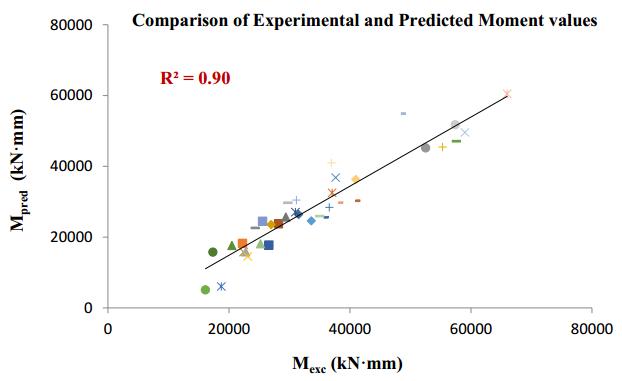
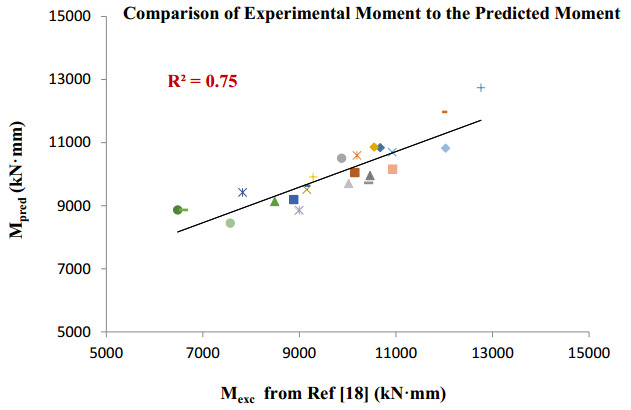
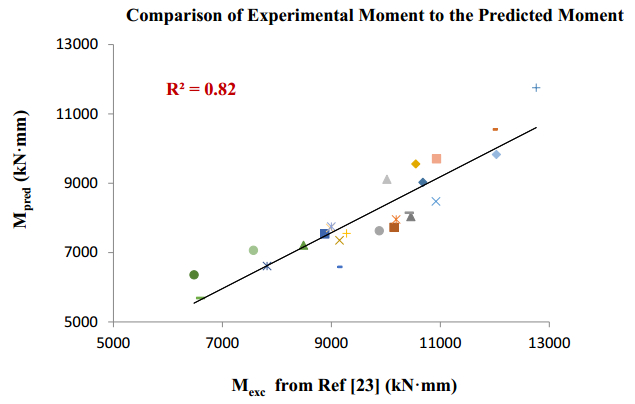
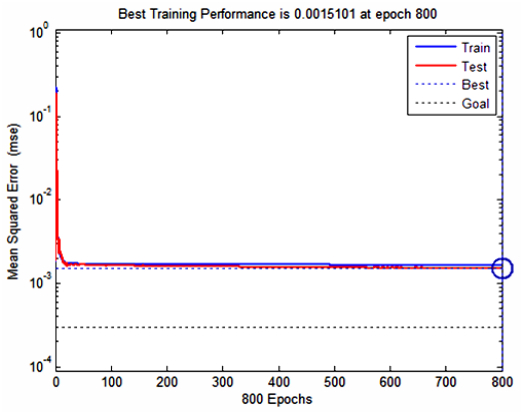
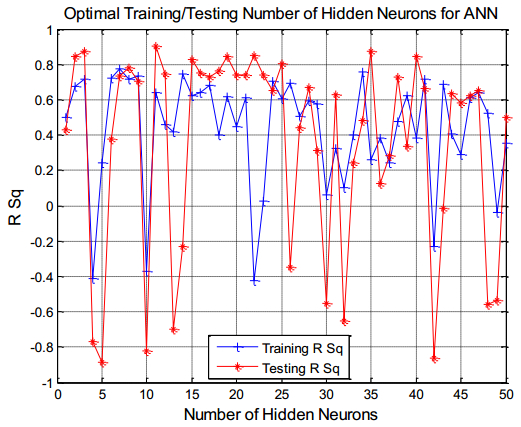
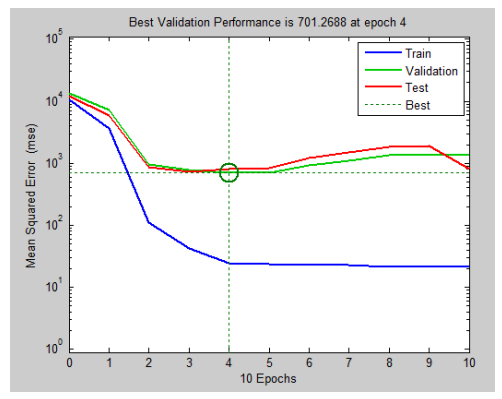
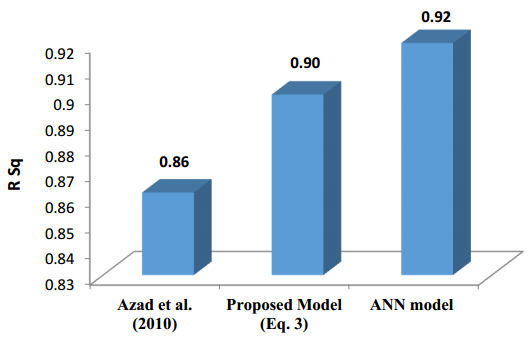
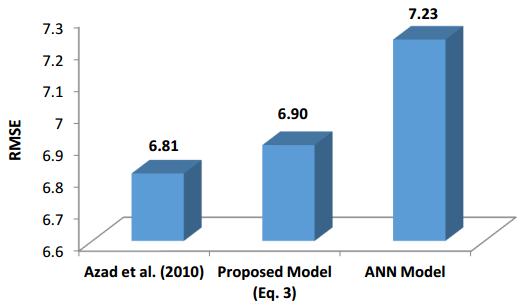
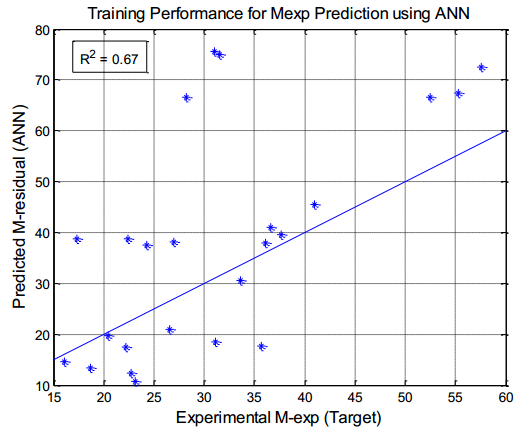
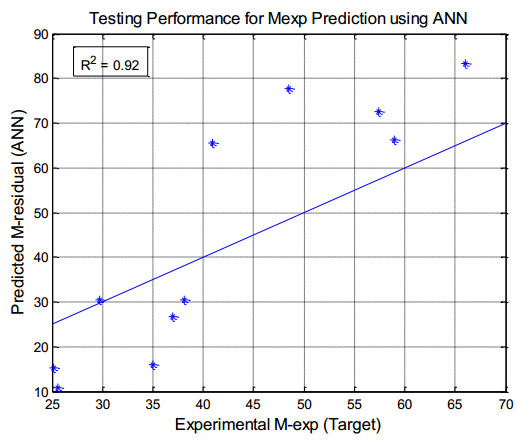
There have been many extensive studies on the prediction of the residual strength of corroded reinforced concrete beams from experimental and theoretical perspectives in the past. This article corroborated the findings of Azad et al. (2010) pertaining to the residual strength and safety of the corroded beams and an insight to develop an improved regression model to obtain more practical outcomes. The proposed model has further been verified with the past research data to obtain a validation error to its minimum count. The study is also followed by the use of soft computing technique like Artificial Neural Networks (ANN) to establish a method with substantial improvement in the prediction results of residual strength. One ANN model is proposed to predict the residual capacity of corroded reinforced concrete beams using the same data from Azad et al. (2010). The effects of fixed data stratification on the performance of the models have been studied. The results of the ANN model were found to be in good agreement with experimental values. When compared with the results of Azad et al. (2010), the ANN model with fixed data stratification gave a better prediction for residual strength with reference to correlation coefficient and error reduction. Hence, the reliability of ANN model is assured with the prediction work followed in this study.
1.
Introduction
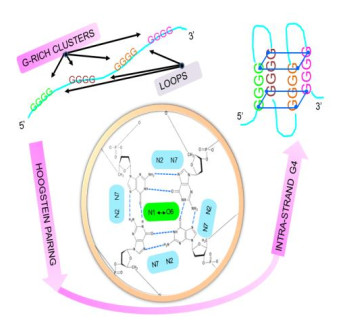
G-quadruplex or G-tetrad (G4), is a thermodynamically stable structural element that is formed between clusters/stretches/tracts of Guanine (G) residues (|x|≥3) and is intra- or inter-molecular [1,2,3]. The intervening loops whence applicable are composed of one or more nucleotide(s) (N∈{A, U, T, G, C}) (Figure 1). G4 is found in DNA (telomeres, double-strand break sites, transcription start sites) and in the untranslated region(s) (5'-, 3'-UTR, introns) of mRNA [4,5]. In vivo, G4 may function to preserve the telomeric ends of chromosomes, repress or promote transcription and regulate translation [4,5]. The generic representation of an intra-strand G4 may be described as follows:
𝑡 ≔ 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝐺𝑢𝑎𝑛𝑖𝑛𝑒𝑠 𝑝𝑒𝑟 𝐺 − 𝑟𝑖𝑐ℎ 𝑐𝑙𝑢𝑠𝑡𝑒𝑟
ℎ ≔ 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑙𝑜𝑜𝑝 − 𝑓𝑜𝑟𝑚𝑖𝑛𝑔 𝑔𝑒𝑛𝑒𝑟𝑖𝑐 𝑖𝑛𝑡𝑒𝑟𝑣𝑒𝑛𝑖𝑛𝑔 𝑛𝑢𝑐𝑙𝑒𝑜𝑡𝑖𝑑𝑒𝑠
𝑘 ≔ 𝐶𝑙𝑢𝑠𝑡𝑒𝑟 𝑖𝑛𝑑𝑒𝑥
𝑚 ≔ 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑠𝑡𝑟𝑎𝑛𝑑𝑠
𝐺 ≔ 𝐺𝑢𝑎𝑛𝑖𝑛𝑒
𝐴 ≔ 𝐴𝑑𝑒𝑛𝑖𝑛𝑒
𝑇 ≔ 𝑇ℎ𝑦𝑚𝑖𝑛𝑒
𝐶 ≔ 𝐶𝑦𝑡𝑜𝑠𝑖𝑛𝑒
𝑁 ≔ 𝐴𝑛𝑦 𝑛𝑢𝑐𝑙𝑒𝑜𝑡𝑖𝑑𝑒
The high melting temperature (Tm~600C) of G4 implies that the mature quadruplex is stable and refractory to unfolding. This is partly due to stabilizing Hoogsteen (N7gu1-N2gu2; O6gu1-N1gu2) and reverse Hoogsteen (N7gu1-N1gu2; O6gu1-N2gu2) hydrogen bonding as well as π-orbital stacking between the purine rings of non-contiguous guanine pairs (gu1, gu2) (Figure 1) [6,7]. Additionally, the presence of Adenine residues in the intervening loops, variable loop length (h~1-30 Mer) and permutation have all been shown to contribute to the stability and thence persistence of the mature quadruplex [8,9,10,11].
Despite the wide range of methods available that can predict G4 formation in DNA/RNA, there is poor agreement between sequence-based motif locators and empirically derived biophysical data [12,13,14,15]. Motif-independent methods such as those that directly measure the GC-content or the GC-/AT-skew of a query sequence and utilize this data to train machine learning algorithms may address some of these discrepancies [16,17,18].
Investigations into transcribed RNA suggests that secondary and tertiary forms (5'- and 3'-UTRs) may not only coexist with stretches of unfolded ribonucleotides, but can also be read by the ribosomal machinery. Non-canonical translation is described as: a) translation from atypical start sites AUG→{CUG, GUG} or b) peptides (≤100 aa) of short open reading frames (sORF)-encoded polypeptides (SEPs) and upstream open reading frames (uORFs) [19,20,21,22]. The latter are rarely silent and can function as modulators of metabolism (S-Adenosylmethionine decarboxylase, AMD1) or transcription (activating transcription factor, ATF4, H19; yeast AP-1 like, YAP1) and as generic transcription factors (general control protein, GCN4) [19]. G4 has also been observed in one or more exons of the prion protein (PRNP, exon 2), zinc finger protein (ZNF669, exon 1), β-amyloid secretase (BACE1, exon 3) and the estrogen receptor 1 (ESR1, exon 4) among several others [16,23,24,25,26,27,28,29].
Whilst the presence of segments of folded mRNA may have a significant influence on the yield of the protein product(s), the effect on sequence whence part of the protein coding segment (PCS) is largely unknown [4,5,30,31,32,33]. Proteopathies are diseases that result directly from agammaegates of truncated and misfolded proteins. These may occur secondary to a faulty translation machinery such as a ribosome that has stalled on encountering a secondary or tertiay folded mRNA sub segment. Recent data suggests ~45% of the human genome may code for proteins that are either intrinsically disordered (IDPs) or comprise one or more sub-segments that are disordered (IDRs) [34]. The absence of delineable structural features notwithstanding, disordered regions are characterized by short linear motifs (SLiMS) and/or molecular recognition features (MoRFs) [34,35]. The improper folding and heightened degradation rates could lead to perturbed proteostasis and thence contribute to the pathogenesis of proteopathies [34,35]. Primary proteopathies are likely to result directly from mutations (point, chromosomal translocations) in the PCS of a gene. These include sickle cell disease (βE6→V6-mediated defective polymerization), amylin-based type Ⅱ Diabetes Mellitus, Cystic Fibrosis (cystic fibrosis transmembrane conductance regulator), Alzheimer's disease (Amyloid β-peptide) and Parkinson's disease (α-synuclein) [36,37]. Secondary proteopathies, in contrast, result from motif or molecular mimicry of a host protein(s) by a pathogen. These are further classified into acute and chronic variants depending on the onset, genesis and/or resolution of the resultant infection or infestation [34,35].
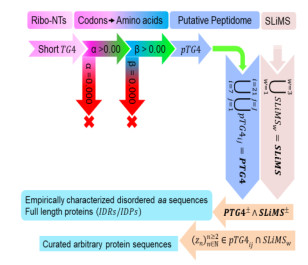
G4 is known to stall the ribosome during translation and the resultant protein is truncated and/or degraded at an accelerated rate. The manuscript subsumes ribosomal read-through of mRNA with a G-quadruplex and assesses influence of the translated product to proteostasis. Here, I present a mathematical model of a short G4 (20–60 Mer) in the PCS, i.e., translatable G-quadruplex (TG4), in the mRNA of a hypothetical gene. The mapping uses several novel indices to annotate, classify and select suitable Guanine-containing codons (α) and amino acids (β). A generic algorithm then computes and validates, as proof-of-principle, possible peptides (pTG4ij) that correspond to the modeled TG4 (pTG4ij∈PTG4~TG4). Co-occurrence, homology and the distribution of overlapping/shared amino acids between PTG4 and the disorder promoting SLiMS are used to infer probable mechanisms of TG4~PTG4 facilitated misfolding. Standard bioinformatics indices (accuracy, precision, recall, p-value) are used to arrive at these conclusions.
2.
Materials and methods
2.1. Mathematical expression for the canonical peptidome of a short translatable G-quadruplex (PTG4)
The objective of this investigation is to model a short G4 in an arbitrary PCS (TG4) which when translated will result in a set of peptides (PTG4) with an average length that is less than 100 amino acids. The hypothesis explored in this manuscript is that in the event of a ribosomal read-through, the translated mRNA, with its G4 will result in a modified protein product. This protein will then exhibit considerable propensity to misfold on account of the presence of one or more members of the PTG4.
2.1.1 Model of a translatable G-quadruplex (TG4)
SEPs-derived peptides with the lowest molecular weight (~2.5 KDa) and with lengths varying from ~7–20 aa were identified and used to define the boundaries of the peptides that comprise PTG4 [20,21]. The TG4 (m = 1) is therefore, modeled as an intra-strand sub sequence of the mRNA of a hypothetical gene and has a length of ~20–60 Mer. This is represented (with symbols and variable names as explained in Def. 1) as follows:
2.1.2. Codon association as a suitable representation of the TG4
Since the Guanine-rich clusters and loops are contiguous, the aforementioned model (Def.2) of the TG4 may be approximated with a sequence of codons and is as under:
The algorithm to compute L, which is the number of codons needed to model TG4 is presented and is as follows:
𝑁 ≔ 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑟𝑖𝑏𝑜𝑛𝑢𝑐𝑙𝑒𝑜𝑡𝑖𝑑𝑒𝑠 𝑟𝑒𝑞𝑢𝑖𝑟𝑒𝑑 𝑡𝑜 𝑚𝑜𝑑𝑒𝑙 𝑇𝐺4
𝐿 : = 𝑇𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑜𝑑𝑜𝑛𝑠 𝑛𝑒𝑒𝑑𝑒𝑑 𝑡𝑜 𝑚𝑜𝑑𝑒𝑙 𝑇𝐺4 (7 ≤ 𝐿 < 21)
𝑞 ≔ 𝑞𝑡ℎ 𝑐𝑜𝑑𝑜𝑛
𝑟 ≔ 𝑅𝑒𝑚𝑎𝑖𝑛𝑑𝑒𝑟 = {0, 1, 2}
𝑒, 𝑢 : = 𝐺𝑒𝑛𝑒𝑟𝑖𝑐 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠
𝑪𝑶𝑫 ≔ 𝑆𝑒𝑡 𝑜𝑓 𝑣𝑒𝑟𝑡𝑒𝑏𝑟𝑎𝑡𝑒 𝑐𝑜𝑑𝑜𝑛𝑠
2.1.3. Codon classification and amino acid composition of PTG4
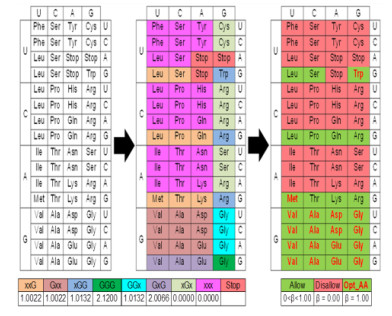
The codons selected for modelling TG4 (Def. 3) comprised suitably scored Guanine-containing vertebrate codons (gCOD+n⊂COD) for the Guanine-rich clusters/stretches/tracks (3≤t≤9;Defs. 1 and 2) and generic/no-stop codons for the intervening loops (Figures 2 and 3). Briefly, a Guanine-containing codon (gCODn) is scored by considering its association with two similar flanking codons, i.e., gCODn-1, gCODn, gCODn+1 such that there is at least one occurrence of 'GGGG' (δ≥1.0) (Figures 2 and 3). This non-trivial case (4≤t≤9) is chosen since its trivial equivalent t = 3, is already subsumed (Defs. 1 and 2). Numerically,
𝛾 : = 𝑃𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑜𝑓 𝑐𝑜𝑑𝑜𝑛 𝑜𝑐𝑐𝑢𝑟𝑟𝑒𝑛𝑐𝑒 (𝛾 = 1/64 ≈ 0.02)
𝜃 ≔ 𝑃𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑜𝑓 𝑐𝑜𝑑𝑜𝑛 𝑜𝑐𝑐𝑢𝑟𝑟𝑒𝑛𝑐𝑒 𝑤𝑖𝑡ℎ𝑖𝑛 𝑎 𝑔𝑟𝑜𝑢𝑝 (𝜃 = {0.04, 0.11, 0.33, 1})
𝛿 ≔ 𝐷𝑖𝑠𝑡𝑖𝑛𝑐𝑡 𝑜𝑐𝑐𝑢𝑟𝑟𝑒𝑛𝑐𝑒𝑠 𝑜𝑓 ′𝐺𝐺𝐺𝐺′(𝛿 = {0, 1, 2, 6})
Ω ≔ 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑐𝑜𝑑𝑜𝑛𝑠 𝑤𝑖𝑡ℎ 𝛿 (Ω = {0, 1, 2})
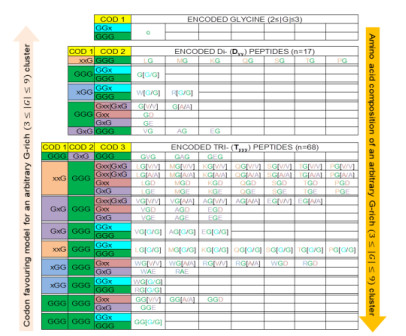
Since the genetic code is degenerate, amino acids mapped from the selected codons are further scored and grouped (g1, g2, g3) (Figures 3 and 4).
gCOD+amino:= set of optimal codons for each amino acid (αaminocodon>0.0000)
CODamino:= Set of codons for each amino acid
2.1.4. Characterize the peptidome corresponding to TG4 (PTG4)
Whilst amino acids from groups 1 and 2 (β > 0.00) (3) can represent the modeled G-rich clusters (y∈g1∪g2 = Y), no constraint was imposed on the amino acids (z) used to model the loops (z∈g1∪g2∪g3 = Z) (Figures 3 and 4). The peptidome (PTG4) evaluated by this study is a combinatorial association of peptides such that the molecular weight is ~0.8–2.3 KDa and length of any arbitrary member is ~7–20 aa (Figure 4). This may be represented as follows:
𝑷𝑻𝑮𝟒 : = 𝑃𝑒𝑝𝑡𝑖𝑑𝑜𝑚𝑒 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑡𝑜 𝑇𝐺4
𝑝𝑇𝐺4𝑖𝑗 : = 𝑗𝑡ℎ 𝑐𝑎𝑛𝑜𝑛𝑖𝑐𝑎𝑙 𝑎𝑚𝑖𝑛𝑜 𝑎𝑐𝑖𝑑 𝑓𝑜𝑟𝑚 𝑜𝑓 𝑃𝑇𝐺4 𝑤𝑖𝑡ℎ "i" 𝑎𝑚𝑖𝑛𝑜 𝑎𝑐𝑖𝑑𝑠
𝑖 : = 𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑎𝑚𝑖𝑛𝑜 𝑎𝑐𝑖𝑑𝑠 𝑡ℎ𝑎𝑡 𝑐𝑜𝑚𝑝𝑟𝑖𝑠𝑒 𝑡ℎ𝑒 𝑚𝑜𝑑𝑒𝑙𝑙𝑒𝑑 𝑷𝑻𝑮𝟒
𝐽 : = 𝑀𝑎𝑥𝑖𝑚𝑢𝑚 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑎𝑛𝑜𝑛𝑖𝑐𝑎𝑙 𝑝𝑇𝐺4 𝑓𝑜𝑟 "𝑖" 𝑎𝑚𝑖𝑛𝑜 𝑎𝑐𝑖𝑑𝑠
2.1.5. Establish proof-of-principle of biological relevance of PTG4
A dataset that comprises experimentally validated G4-forming mRNA segments of several genes (n = 99) was downloaded (http://scottgroup.med.usherbrooke.ca/G4RNA/) and used to investigate the distribution of G4 [16]. Genes which possess non-redundant RNA (R) sub sequences in the PCS are translated in 6 reading frames using an online tool (http://web.expasy.org/translate). The peptides generated are classified as those: ⅰ) with one or more uninterrupted stretch of N-terminal amino acids of length ≥7 aa (~A), ⅱ) with an in-frame termination signal designated as 'STOP' (~B) and ⅲ) without any termination signal, i.e., absence of a 'STOP' in their sequence (~C). The translated peptides are classified as "VALID" ((B∩A)∪(C∩A)) and then queried for matches with pTG4ij(7≤i≤20,j∈N). The PERL scripts that are required to parse and process the resulting data files have been developed in house and the pseudocode for the same is presented as additional information (Pseudocode, PS1: Supplementary Text 1).
2.1.6. In silico assessment of PTG4 to misfolding induced proteostasis
This is done by examining the occurrence of PTG4 in amino acid/protein sequences of disordered regions (IDRs) and full-length proteins with disordered regions (IDPs). DisProt 7.0 (http://disprot.org), is a database of experimentally validated and non-redundant sequences of IDRs and IDPs [38]. The sequences (|IDR| = 1445;|IDP| = 800) that comprise these are queried for occurrences of pTG4ij(7≤i≤20,j∈N) (Supplementary Texts 2 and 3). A preliminary partitioning schema divides these datasets into two distinct subsets, i.e., #pTG4ij≥1 (PT+≡PPOS⊂{IDR, IDP}; (Def.6)) and #pTG4ij = 0 (PT-≡PNEG⊂{IDR, IDP}; (Def. 7)). The extent of co-occurrence of one or more SLiMSw≡SL (w = {1, 2, 3}) with pTG4ij (SL±∈{PPOS, PNEG}) (Defs.8 and 9) is then evaluated to infer relevance of PTG4 to misfolding induced proteostasis. The distribution of overlapping/shared sequences of amino acids ((zn)n≥2∈(pTG4ij∩SLiMSw); zn∈Z; ) (Def.10), is examined in protein sequences from taxonomically diverse organisms with ScanProsite (https://prosite.expasy.org/scanprosite). The proof behind this rationale is presented:
𝒁 : = 𝑆𝑒𝑡 𝑜𝑓 𝑎𝑚𝑖𝑛𝑜 𝑎𝑐𝑖𝑑𝑠 (𝑧𝑛 ∈ 𝒁)
𝑝𝑇𝐺4𝑖𝑗 : = 𝐶𝑎𝑛𝑜𝑛𝑖𝑐𝑎𝑙 𝑎𝑚𝑖𝑛𝑜 𝑎𝑐𝑖𝑑 𝑓𝑜𝑟𝑚 𝑜𝑓 𝑷𝑻𝑮𝟒
𝑺𝑳𝒊𝑴𝑺 : = 𝑆𝑒𝑡 𝑜𝑓 𝑠ℎ𝑜𝑟𝑡 𝑙𝑖𝑛𝑒𝑎𝑟 𝑚𝑜𝑡𝑖𝑓𝑠 (𝑆𝐿𝑖𝑀𝑆𝑤 ∈ 𝑺𝑳𝒊𝑴𝑺)
𝑖, 𝑗, 𝑛, 𝑤 : = 𝐼𝑛𝑑𝑖𝑐𝑒𝑠 𝑜𝑓 𝑚𝑒𝑚𝑏𝑒𝑟𝑠 𝑜𝑓 𝒁, 𝑷𝑻𝑮𝟒, 𝑺𝑳𝒊𝑴𝑺
2.2. Statistical measures to compute and assess biological relevance of TG4
The indices utilized by this study to establish relevance of matched instances of various motifs/co-motifs in the peptide/protein sequences of interest include the accuracy (A), precision (P), recall (R) and the p-value. A 2X2 table which represents the categorized data (2.1.4) is constructed and used to compute various bioinformatics indices. This is outlined as under:
𝑇𝑁 ≔ 𝑇𝑟𝑢𝑒 𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑒 (|𝒔𝑵𝑬𝑮 ∩ 𝑷𝑵𝑬𝑮| = |𝒔𝑵𝑬𝑮|) ≡ 𝑆𝐿−𝑃𝑇− (𝐷𝑒𝑓. 11)
𝐹𝑃 ≔ 𝐹𝑎𝑙𝑠𝑒 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑒 (|𝑺𝑵𝑬𝑮 ∩ 𝑷𝑷𝑶𝑺| = |𝑺𝑵𝑬𝑮|) ≡ 𝑆𝐿−𝑃𝑇+ (𝐷𝑒𝑓. 12)
𝐹𝑁 ≔ 𝐹𝑎𝑙𝑠𝑒 𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑒 (|𝒔𝑷𝑶𝑺 ∩ 𝑷𝑵𝑬𝑮| = |𝒔𝑷𝑶𝑺|) ≡ 𝑆𝐿+𝑃𝑇− (𝐷𝑒𝑓. 13)
𝑇𝑃 ≔ 𝑇𝑟𝑢𝑒 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑒 (|𝑺𝑷𝑶𝑺 ∩ 𝑷𝑷𝑶𝑺| = |𝑺𝑷𝑶𝑺|) ≡ 𝑆𝐿+𝑃𝑇+ (𝐷𝑒𝑓. 14)
The equations may then be written as:
The p-values for these analyses are computed by comparing the frequency of occurrence of all pTG4ij in a test sequence (ϕpTG4ij) with the same in randomly-generated (v∈V) sequences of similar lengths (ϕpTG4vij), i.e., 7-50 aa (1≤v≤10000) and > 50 aa (1≤v≤100000) (Pseudocode, PS2: Supplementary Text 1):
The frequency of occurrence of overlapping sequences of amino acids ((zn)n≥2∈(pTG4ij∩SLiMSw); zn∈Z) in pre-compiled and curated protein sequences (ϕ(zn)) across taxa is compared with randomly chosen sequences of comparable lengths (ϕ(vzn); n = 5000). These are used to estimate statistical significance, i.e., p-value = ϕ(vzn)/ϕ(zn) (8).
3.
Results
The data presented discusses implementation of a model of short intra-strand TG4 for various values of α and β, populates PTG4 and establishes the equivalence TG4~PTG4. Co-occurrence and homology studies between PTG4 and the SLiMS in IDRs/IDPs and generic protein sequences across taxa are used to infer probable mechanisms of TG4~PTG4 facilitated misfolding-induced proteostasis.
3.1. Suitability of Guanine-containing codons as a model for an arbitrary G-rich cluster of TG4
An association-competent codon not only takes into account the presence of a Guanine residue, but also gives weightage to its position (Figures 1–3, Table 1). This schema partitions standard vertebrate codons into those with a high- (Ranks 1-4;α > 0.0000) or low- (Rank 5;α = 0.0000) propensity to form a contiguous cluster of Guanine residues (Figures 3 and 4, Table 1). Whilst, 'GGG' (Rank 1;α = 2.12) can associate with ({GGG, GxG, xGG, GGx, Gxx, xxG}) bilaterally (δ = 6;Ω = 2), 'GxG' (Rank 2; α = 2.0066) can do so only with 'GGG' (δ = 1;Ω = 2). On the other hand, the codon subsets 'GGx' and 'xGG' (Rank 3;α = 1.0132) can form two clusters of contiguous Guanine residues with 'GGG' and 'xGG'/ 'GGx' unilaterally (δ = 2;Ω = 1). Similarly, the subsets 'xxG' or 'Gxx' (Rank 4;α = 1.0022), can form contiguous Guanines with a single occurrence of 'GGG' (δ = 1;Ω = 1) (Figures 3 and 4, Table 1). Conversely, codons with either a single occurrence of a central Guanine residue 'xGx' or no Guanine residues 'xxx' (Rank 5;α = 0.0000) are unable to form the 'GGGG' and are excluded from this study (Figures 3 and 4, Table 1).
Abbreviations
𝛾: General probability of a codon (𝛾 = 1/64 ≅ 0.02)
𝜃: Probability of codon within a group (𝜃 = {0.04, 0.33, 0.11, 1.00})
𝛿: Number of distinct codon sets that could complete 'GGGG' (𝛿 = {0, 1, 2, 6})
Ω: Number of adjacent positions that contain 𝛿 (Ω = {0, 1, 2})
𝛼: Threshold for selecting codons that may favour G-quadruplex formation
x: Codon specific generic ribonucleotide {𝐴, 𝐺, 𝑈, 𝐶}
aa: Amino acid
Ter: Stop codons {𝑈𝐴𝐺, 𝑈𝐺𝐴, 𝑈𝐴𝐴}
3.2. Validation studies of PTG4 in known G4-forming exons to establish equivalence (TG4~PTG4)
An estimate of the possible combinations of the simplest peptide (∑i=7∑j=Jj=1pTG4ij = 8.00E+03;GlyzGlyzGlyzGly; J = (20)3; i = lengthp(TG4ij) = 7 aa; z∈Z) (Figures 3 and 4, Table 2). This justifies usage of PTG4 (pTG4ij∈PTG4) as a generic representation of the putative peptidome encoded by the TG4 (PTG4). Approximately ~12% (n = 11) of in silico translated amino acid sequences from exon-derived TG4 possesses one of more "STOP" signals and include ESR1, longer RNA variants of PRNP (85 nt) and BCL2 (29 n t, 33 nt, 34 nt) (Table 3; Table 1, Supplementary Text 2). With the exceptions of KCNH2/ZNF669 and the shorter variants of PRNP (14 nt, 15 nt, 20 nt, 24 nt), "VALID" sub sequences are found for BACE1, BCL2, ESR1, PRNP (long) and TERF2 (Table 3; Tables 1A and 1C). Interestingly, all the genes considered possessed at least one occurrence of PTG4 (P = 100%, n = 6) (Table 3; Table 1B). This finding, despite the small sample size is proof-of-principal that the TG4 can be mapped to definite peptide sequences, i.e., TG4~PTG4. Since this can occur only after a ribosomal read through of the G4 containing mRNA, it raises the intriguing possibility that PTG4 whence part of a larger protein may increase its propensity to undergo misfolding. This notion is investigated in non-redundant sequences of IDRs (PTG4~10%, n = 145;0.00≤p-value≤0.20) and IDPs (PTG4~34%, n = 269;0.00≤p-value < 0.5) (Table 4; Tables 2 and 3).
Abbreviations
gCOD+amino : Guanine-containing optimal codons excluding STOP (UAG) (𝛼 > 0.000)
COD−amino : Non-optimal codon excluding STOP (UGA, UAA) (𝛼 = 0.000)
𝑪𝑶𝑫𝒂𝒎𝒊𝒏𝒐 = gCOD+amino + COD−amino : All codons for an amino acid
Abbreviations
𝐼𝐷𝑅𝑠: Intrinsically disordered regions
𝐼𝐷𝑃s: Intrinsically disordered proteins
𝑧: Any amino acid
𝑆𝐿𝑖𝑀𝑆1: [𝑆𝑇]𝑃𝑧𝑅
𝑆𝐿𝑖𝑀𝑆2: [𝐸𝐷]𝑧𝑧[𝐷𝐸][𝐴𝐺𝑆]
𝑆𝐿𝑖𝑀𝑆3: [𝐾𝑅]𝑧𝑃𝑧𝑧𝑃
𝑆𝐿−𝑃𝑇−: |𝑺𝑵𝑬𝑮 ∩ 𝑷𝑵𝑬𝑮|
𝑆𝐿−𝑃𝑇+: |𝑺𝑵𝑬𝑮 ∩ 𝑷𝑷𝑶𝑺|
𝑆𝐿+𝑃𝑇−: |𝑺𝑷𝑶𝑺 ∩ 𝑷𝑵𝑬𝑮|
𝑆𝐿+𝑃𝑇+: |𝑺𝑷𝑶𝑺 ∩ 𝑷𝑷𝑶𝑺|
𝑅1𝑇: 𝑆𝐿−𝑃𝑇− + 𝑆𝐿−𝑃𝑇+
𝑅2𝑇: 𝑆𝐿+𝑃𝑇− + 𝑆𝐿+𝑃𝑇+
𝐶1𝑇: 𝑆𝐿−𝑃𝑇−+ 𝑆𝐿+𝑃𝑇−
𝐶2𝑇: 𝑆𝐿−𝑃𝑇+ + 𝑆𝐿+𝑃𝑇+
𝐴: Accuracy
𝑃: Precision
𝑅: Recall
3.3. The peptidome of the translatable G-quadruplex may trigger misfolding of the encompassing protein
The amino acids that comprise the peptide members of PTG4 and the short linear motifs (g1, g2 vs SLiMS) are well conserved. The co-occurrence of PTG4 with SLiMS in the IDRs (A~85-89%;0.00 < p-value≤0.05) suggests that this association is non-trivial and may favor all purported mechanisms of misfolding (hyperphosphorylation, proteolytic cleavage, complex formation) (Table 4; Tables 2 and 3). However, the higher precision of PTG4 with the proteolytic-SLiMS suggests that this may predominate (Table 4; Tables 2 and 3). The data with the IDPs suggests a similar predilection for proteolytic cleavage (A~40-77%;P~99%;0.00 < p-value < 0.05, although hyperphosphorylation (P~60%;0.00 < p-value < 0.05) and complex-promotion (P~30%;0.00 < p-value < 0.05) may constitute viable alternatives to the genesis of misfolding (Table 4; Tables 2 and 3). The presence of overlapping sequences of amino acids between PTG4 and the SLiMS when examined in protein sequences from taxonomically diverse organisms is degenerate for SLiMS1 (number of matches = 6251) and SLiMS3 (number of matches = 1480) (Table 5; Table 4). In contrast, the corresponding data for SLiMS2 (number ofmatches = 3759;0.00 < p-value < 0.05) is statistically significant (Table 5). The taxonomic spread includes archaea (n = 150), bacteria (n = 1735), viruses (n = 84), green land plants (n = 199), fungi (n = 182), eukaryotic invertebrates (n = 43) and vertebrates (n = 700) (Table 4).
Abbreviations
𝑝𝑇𝐺4𝑖𝑗: Members of putative peptidome (𝑝𝑇𝐺4𝑖𝑗 ∈ 𝑷𝑻𝑮𝟒)
𝑆𝐿𝑖𝑀𝑆𝑤: Short linear motifs (𝑆𝐿𝑖𝑀𝑆𝑤 ∈ 𝑺𝑳𝒊𝑴𝑺)
𝑧𝑛: Shared sequence(s) of amino acids between 𝑷𝑻𝑮𝟒 and 𝑺𝑳𝒊𝑴𝑺
𝑖, 𝑗, 𝑤, 𝑛: Indices to characterize members of 𝑷𝑻𝑮𝟒, 𝑺𝑳𝒊𝑴𝑺, 𝒁
4.
Discussion
The significant association and homology between PTG4 and the SLiMS along with the equivalence data (PTG4~TG4) suggest that TG4 may influence proteostasis in a multitude of ways (Tables 1–5; Tables 1–4, Supplementary Text 2–4).
4.1. TG4 may effect stability of mRNA and indirectly influence proteostasis
The short TG4 modeled in this study has an average loop length (h~2 Mer) which may contribute to thermodynamic stability by restricting the mobility of the participating strands (1) [8,9,10,11]. The physical presence of TG4 will result in a stalled ribosome and translation which is prolonged, inefficient and incomplete [31,32,33]. Interestingly, this analysis also includes UAG (Amber; α > 0.0000), which when present in-frame will prematurely terminate translation and result in a truncated protein (Table 1) [39]. Whilst nonsense-mediated mRNA decay may be triggered if the stop codon is within ±50 Mer of the exon-junction complex (EJC), a read-through may occur nonetheless. The resulting protein sequences may be modified which in tandem with one or more occurrences of PTG4 and/or SLiMS would predispose the same to agammaegate and result in a proteopathy [39,40].
4.2. Mechanism(s) of PTG4-mediated misfolding
Whilst the preponderance of Glycine (Gly) might impart heightened flexibility and limit the formation of stabilizing secondary structural elements in the hypothetical protein, Proline (Pro) confers rigidity and may retard proper folding. There is also remarkable conservation between the amino acids that comprise PTG4 and the SLiMS. These include the complex-promoting hydrophobic (Ala, Val, Met, Trp) and ionic (Asp, Glu, Lys, Arg) residues, along with nucleophile-favoring Serine and Threonine (Figures 3 and 4, Tables 2–5). Whilst, the former may favor agammaegation by non-covalent interactions, the latter may promote phosphorylation-mediated charge imbalance and thence misfolding. Interestingly, the loops of G4 whence modeled by Adenine-containing codons (Axx) are translated to Lysine (K), Arginine (R), Serine (S), Threonine (T) and Isoleucine (I); all of which may also promote misfolding (Figures 3 and 4, Tables 2-5) [8,9,10,11,34,35]. The distribution of PTG4 amongst physiologically relevant proteins further suggests that the peptide-mediated misfolding may influence/regulate signal transduction, cytoskeleton organization, metabolism, synaptic transmission and transcription/translation (Table 6; Table 5).
Note: DP≔DisProt ID
4.3. Degeneracy of PTG4 with SLiMS in non-vertebrate taxa may favor development of secondary proteopathies
The distribution of overlapping/shared amino acids in protein sequences of non-vertebrates suggests that PTG4 is either completely degenerate with the SLiMS or present in proportions that is statistically significant (Tables 5 and 6; Tables 4 and 5). These data imply that motif-mimicry too, might constitute a probable cause (tropism, oncogenic potential, virulence) of infection/infestation-mediated acute/chronic proteopathies [34,35,41,42]. The contribution(s) of misfolding to the pathogenesis of secondary proteopathies is however, debatable. Whilst, there is evidence that mislocalization of proteins can precipitate misfolding, mimicry itself may result in exonuclease-mediated proteolytic cleavage and thence trigger an infective proteopathy [43,44]. Additionally, the presence of sequences of amino acids such as Proline and Threonine in viral or fungal proteins may be responsible for creating and/or maintaining a milieu conducive to the genesis of infective/transmissible proteopathies, viz., a high charge density and imbalance of electrostatic interactions [43,44].
5.
Conclusions
The coexistence of potentially translatable G-quadruplexes (TG4) with unfolded ribonucleotides in the PCS of an mRNA transcript may have important consequences for protein homeostasis. Here, I have investigated the contribution of a short intra-strand translatable G-quadruplex and its associated peptidome (TG4~PTG4) to the genesis of misfolding-induced proteostasis. The co-occurrence, homology and distribution of overlapping/shared amino acids of PTG4 with the SLiMS suggests that this may occur by truncation, complex formation, increased charge density and/or accelerated degradation. An additional mechanism that is also supported is motif-mimicry by pathogens which may trigger the development of infective proteopathies. The putative peptidome (~7–20 aa) that corresponds to the short translatable G-quadruplex delineated by this investigation may be utilized as novel markers of both the primary and secondary proteopathies.
Author's contribution
SK outlined and designed the study, designed and conceptualized the algorithm(s) and formulae for prediction, wrote mathematical proofs to establish rigor, collated the data, constructed the models, formulated the filters, carried out the computational analysis, wrote all necessary code and the manuscript.
Conflict of interest
The author declares no conflict of interest.









 DownLoad:
DownLoad: