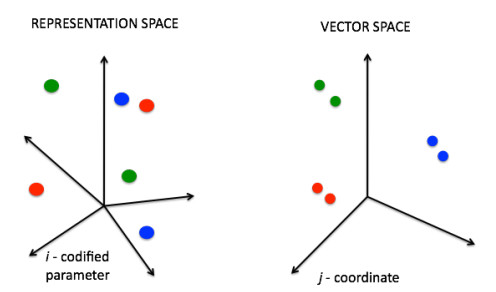
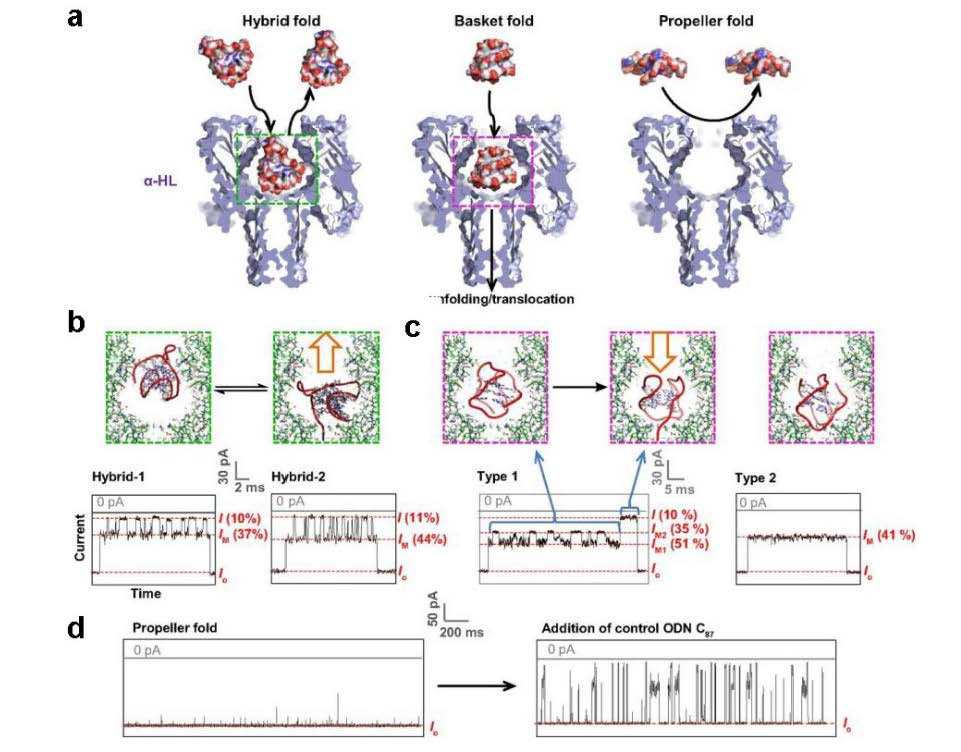
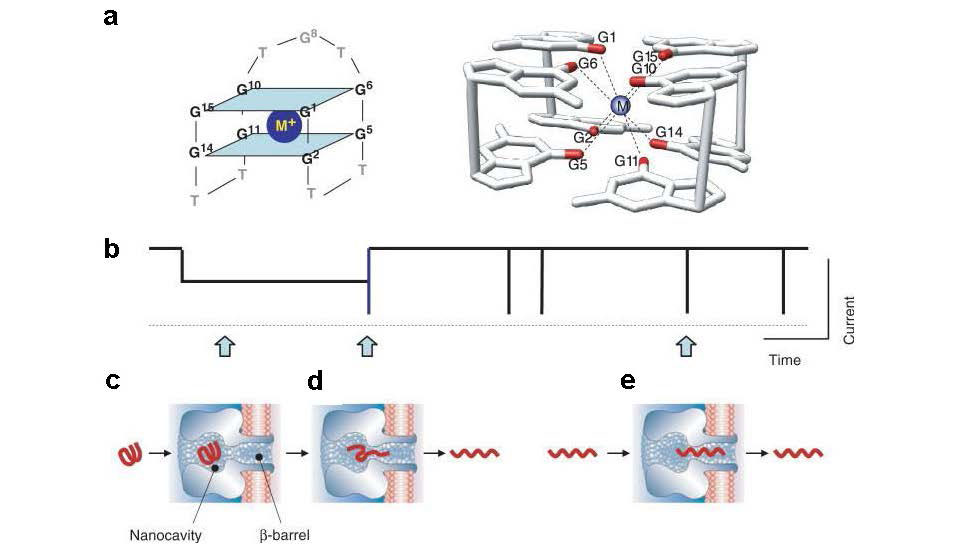
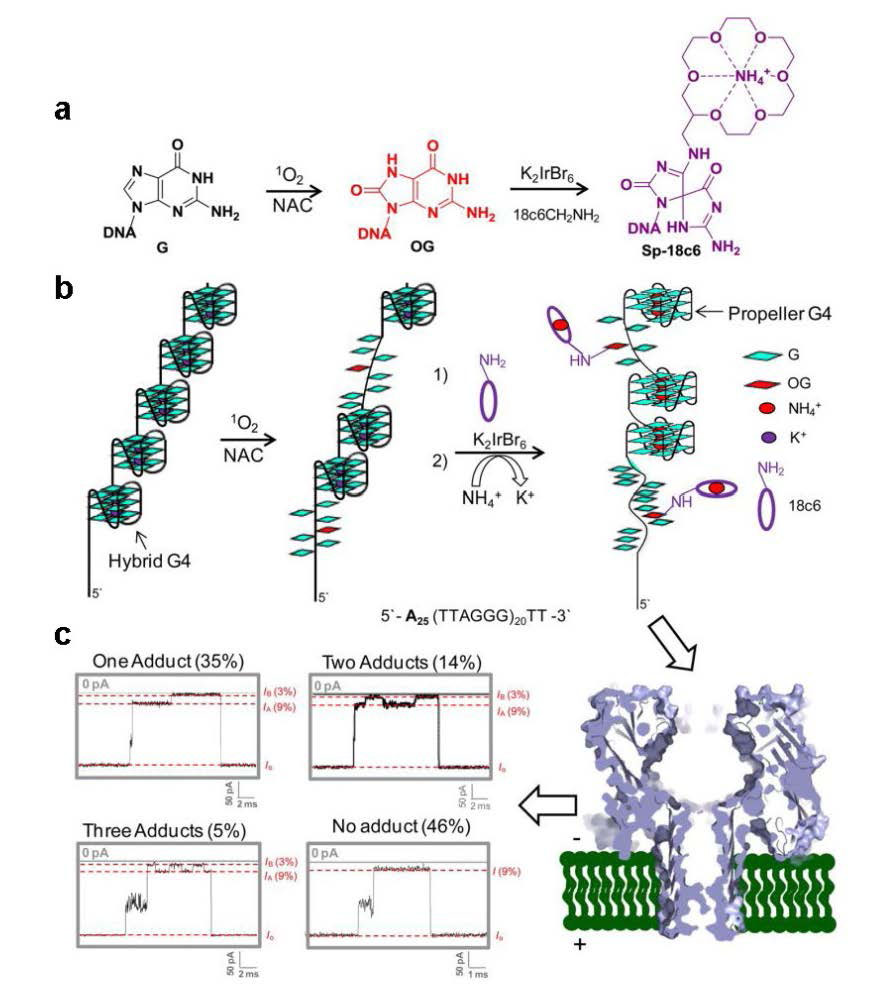
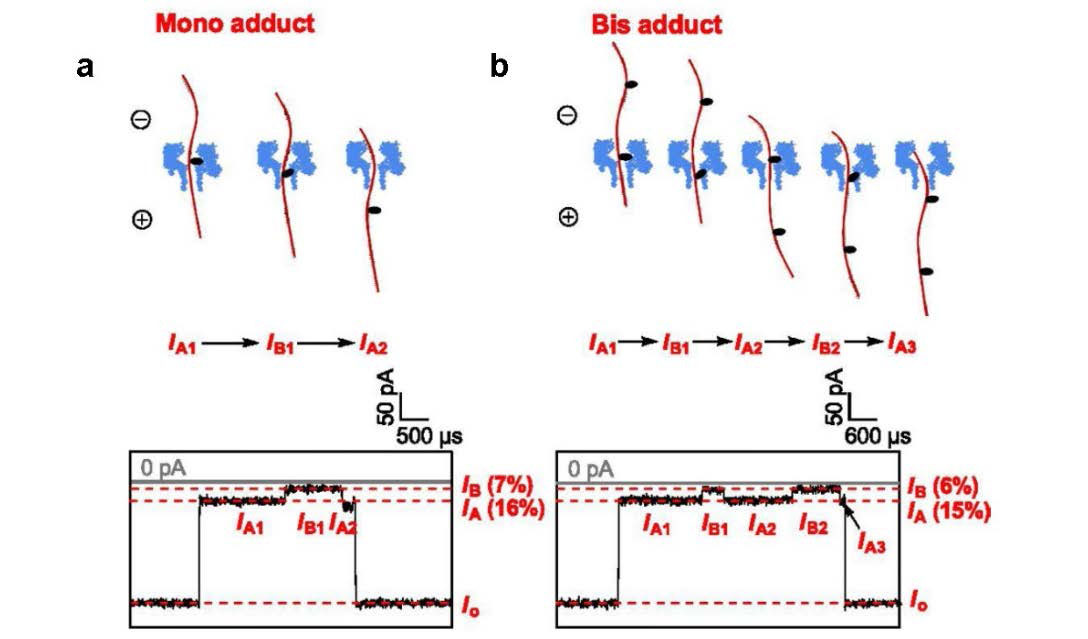
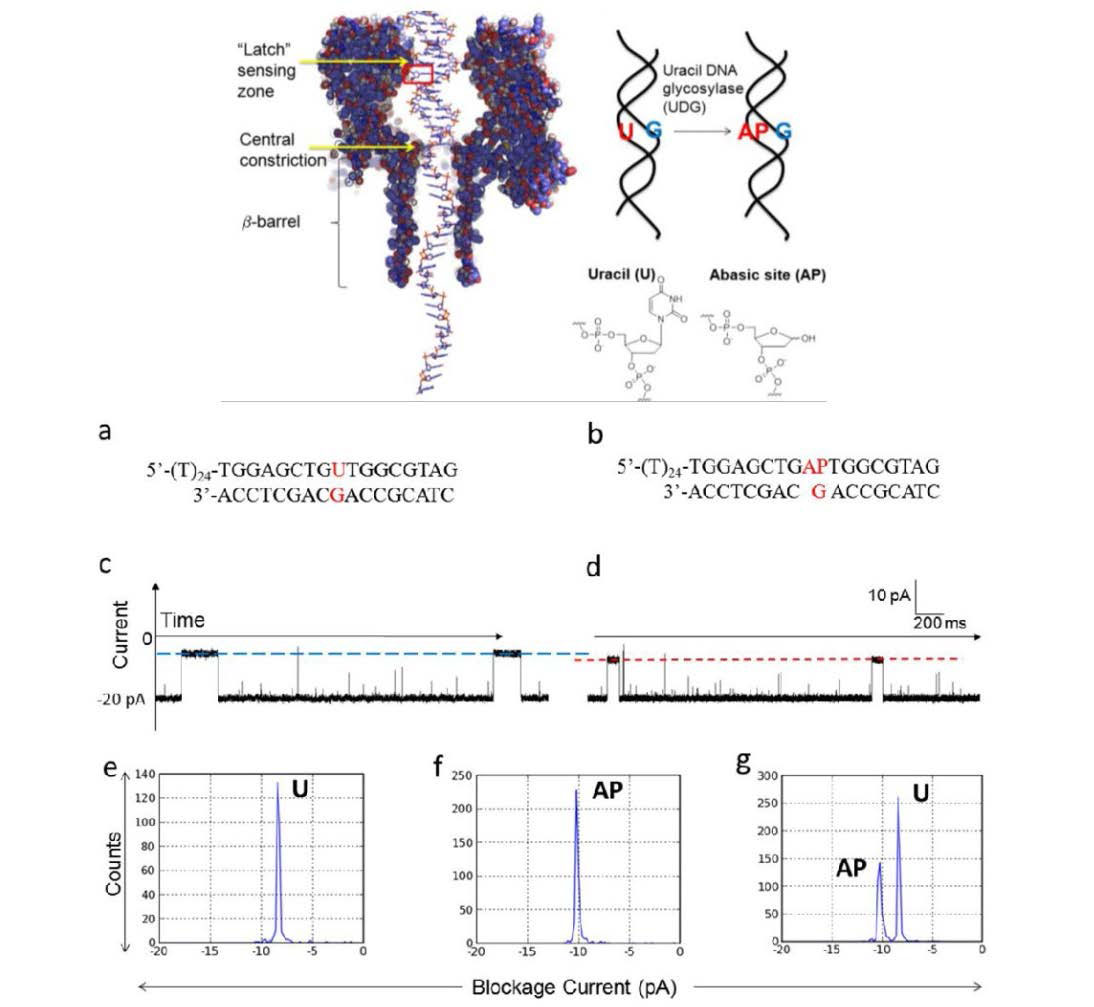
The α-hemolysin nanopore has been studied for applications in DNA sequencing, various single-molecule detections, biomolecular interactions, and biochips. The detection of single molecules in a clinical setting could dramatically improve cancer detection and diagnosis as well as develop personalized medicine practices for patients. This brief review shortly presents the current solid state and protein nanopore platforms and their applications like biosensing and sequencing. We then elaborate on various epigenetic detections (like microRNA, G-quadruplex, DNA damages, DNA modifications) with the most widely used alpha-hemolysin pore from a biomedical diagnosis perspective. In these detections, a nanopore electrical current signature was generated by the interaction of a target with the pore. The signature often was evidenced by the difference in the event duration, current level, or both of them. An ideal signature would provide obvious differences in the nanopore signals between the target and the background molecules. The development of cancer biomarker detection techniques and nanopore devices have the potential to advance clinical research and resolve health problems. However, several challenges arise in applying nanopore devices to clinical studies, including super low physiological concentrations of biomarkers resulting in low sensitivity, complex biological sample contents resulting in false signals, and fast translocating speed through the pore resulting in poor detections. These issues and possible solutions are discussed.
1.
Introduction
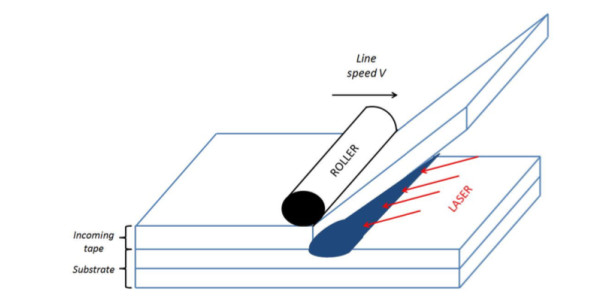
Among composite forming processes for manufacturing structural parts based on the consolidation of pre-impregnated preforms, e.g., sheets, tapes, etc., the automated tape placement (ATP) appears as one of the most interesting techniques due to its versatility and its in-situ consolidation, thus avoiding the use of autoclave. In particular, to obtain the cohesion of two thermoplastic layers two specific physical conditions are needed (a) an almost perfect contact (intimate contact) and (b) a temperature enabling molecular diffusion within the process time window, while avoiding thermal degradation. To reach this goal, a tape is placed and progressively bonded to the substrate consisting of the tapes previously laid-up. Due to the low thermal conductivity of usual resins, an intense local heating is usually considered (laser, gas torches, etc.) in conjunction with a local pressure applied by the consolidation roller moving with the heating head, as sketched in Figure 1. Thus, the two main factors to ensure the intimate contact at the plies surfaces are pressure and heat. Intimate contact is required to promote the molecular diffusion. In this process heat plays a double role, on one hand it enhances molecular mobility and on the other hand, the decrease of the material viscosity with the temperature increase, facilitates the squeeze flow of the heated asperities located on the ply surfaces under the compression applied by the consolidation roller.
The numerical model of ATP was introduced in [1] by using the so-called Proper Generalized Decomposition (PGD) [2,3,4,5,6]. The separated representation involved in the PGD enables the 3D high-resolution solution of models defined in degenerated domains where at least one of their characteristic dimensions remains much smaller than the others and also constructing solutions of parametric models where the model parameters are considered as extra-coordinates [7,8].
Physical modelling and simulation for Automated Tape Placement (ATP) have been proposed in [9] to study the influence of material and process parameters, while consolidation modelling and sPGD-based non-linear regression have been used in [10] to identify the main surface descriptors for a comprehensive characterization of the tape surfaces.
The present paper revisits first the consolidation modeling and its high resolution simulation, enabling the evaluation of the time evolution of the degree of intimate contact –DIC– when two rough surfaces are put in contact, heated and compressed.
In the present work, as we are addressing tapes involved in the ATP process sketched in Figure 1, the roughness squeezing mainly occurs along the transverse direction (the one related to the tape width) induced by the roller compression. Thus, the flow occurs in the transverse section in which the surface reduces to a one-dimensional curve (the so-called surface profile).
In order to extract a concise and complete description of rough surfaces, topological data analysis –TDA– [11,12,13,14] is then introduced, with all the main techniques that it involves, in particular the so-called persistence diagrams and images.
Then, the persistence images are considered for classifying surfaces or for acting as surface descriptors that will be involved in a regression relating them to a quantity of interest –QoI–, in the present study the final DIC reached in the consolidation process, enabling real-time decision making.
2.
Consolidation modelling
In our recent works [9,15,16] we proposed simulating the consolidation on the real surfaces instead of the, sometimes too crude, approximations of them based on the use of fractal representations or the ones based on the description of asperities from the use of rectangular elements [17,18].
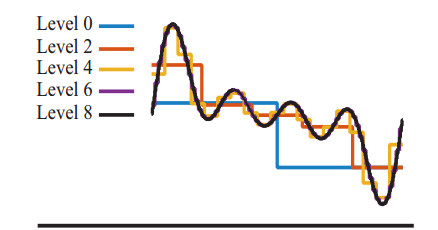
As sketched in Figure 2, a Haar-based wavelet representation [9] of a rough surface results in a multi-scale sequence of rectangular patterns, from the coarse scale (level 0) to the finest one (level 8) that constitutes a quite precise representation of the considered surface (the one illustrated in Figure 2). The smoother is the surface, the less levels in the description are required.
The advantage of such a representation consisting of hierarchical rectangles is double: (ⅰ) from one side it facilitates the high-resolution of the thermal problem while accounting for all the interface details and their time evolution; and on the other (ⅱ) it allows squeezing the rectangles of a certain level (from the finest level to the coarser one) while retaining the lubrication hypotheses, fact that simplifies significantly the flow modeling and the calculation of the interface evolution when squeezing the asperities. Both aspects are revisited below.
1. As soon as the rough surface profile is represented in a step-wise way consisting of $ \mathtt R $ rectangular elements, with each rectangle $ r $ having a length $ l_r $ and a height $ h_r $, assumed centered at $ x_r $, each rectangle can be expressed by its characteristic function in a separated form $ \chi_r(x, z) = \mathcal L_r(x) \mathcal H_r(z) $, with $ \mathcal L_r(x) $ and $ \mathcal H_r(z) $ given respectively by Eqs 1 and 2,
and
that allows expressing the conductivity at the interface level according to Eq 3,
where $ {\bf K}_a $ and $ {\bf K}_c $ represent the air and composites conductivities, with the former assumed isotropic and the last concerning the composite conductivity transverse components.
This separated representation of the thermal conductivity allows looking for a separated representation of the temperature field within the proper generalized decomposition –PGD– framework, according to Eq 4.
that by decoupling the 2D heat equation solution into a sequence of 1D problems for computing the functions $ X_i(x) $ and $ Z_i(z) $ allows an extremely fine resolution as discussed in [9].
As the asperities squeezing progresses, the surface evolves and with it the height of the different rectangular elements. The conductivity separated representation must be updated and the thermal problem solved again to compute the updated temperature field (4).
2. As soon as the temperature field is available, the polymer viscosity can be evaluated and the asperities will flow under the applied pressure. As commented, the description of the surface by using rectangular elements, with their characteristic length $ \overline{l} $ much larger that its characteristic height $ \overline{h} $, i.e. $ \overline{l} \gg \overline{h} $, makes possible the use of the lubrication hypotheses, widely addressed in our former works [16].
The surface updating procedure is quite simple. We consider all the compressed rectangles, and solve in them the squeeze flow model, while assuming that the pressure in all the other elements vanishes. As soon as the pressures are available in all the rectangles that are being compressed, the velocity field and more precisely the flow rates can be obtained at the lateral boundaries. The fluid leaving each rectangular element that is being compressed is transferred to the neighbor rectangular element that increases its height accordingly in order to ensure the mass conservation.
As it can be noticed, this procedure allows unimaginable level of accuracy, however, despite of the speed-up that separated representation offers, its use online for predicting the thermal and flow coupled problem for any incoming rough tape is not an option.
3.
Surface descriptors based on homology persistence
In this section we introduce the data and methods used, in particular the TDA and its related procedures (persistent diagrams and images), even if other approaches exist, e.g. [10,19].
The proposed methodology proceeds in three main stages:
1. Processing the surface profiles data;
2. Compute persistent diagrams and images;
3. Construct the regressions relating the surface topological descriptors and the quantities of interest –QoI–, concretely the DIC.
3.1. Processing the surface profiles data
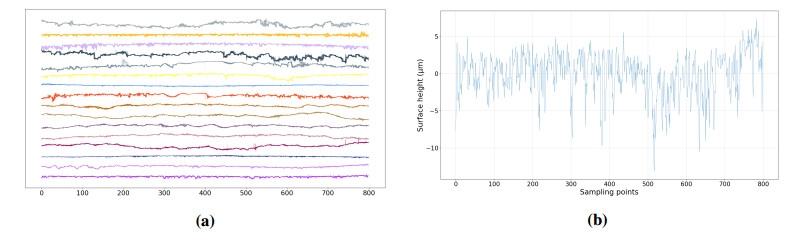
In order to classify the main surface descriptors of a tape surface, we will consider samples scanned with a 3D non contact profilometer, with a 3.5 um resolution and where each sample has a length of approximately 3 mm (along the tape width). A set of 1359 surface profiles were extracted from $ 16 $ different pre-impregnated composite tapes provided by different customers using different impregnation process, each one represented by $ 800 $ measured data points $ \left\{S_{\ell}^{(k)}: 1 \le \ell \le 800, \, 1 \le k \le 1359 \right\} $.
The main goal is to give a procedure to construct a classification $ \mathcal C(S) $, that is, a map ensuring $ \mathcal{C}(S^{(k)}) = i \ \text{ if and only if } \ S^{(k)} \ \text{was extracted from the tape} \ i $, with $ i = \{ 1, 2, \dots, 16 \} $.
In particular, to facilitate data comparison the profiles are corrected by subtracting the average height. Figure 3 depicts the different surfaces in each of the 16 classes, as well as normalized profile.
3.2. Persistence diagrams and images
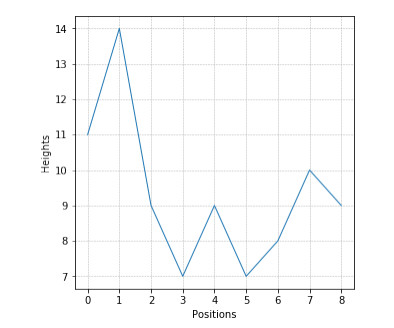
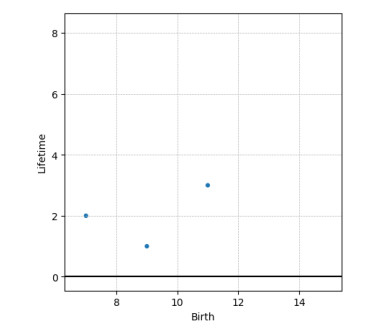
The persistence diagram consists of a one-to-one local-minimum-local-maxixum pairing. To illustrate the procedure we consider a simple case of a profile described by 9 heights, $ S = \{ 11, 14, 9, 7, 9, 7, 8, 10, 9\} $, that corresponds to the 9 data points depicted in Figure 4: $ \{ (0, 11), (1, 14), (2, 9), (3, 7), (4, 9), (5, 7), (6, 8), (7, 10), (8, 9) \}. $
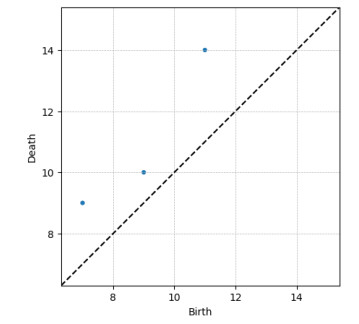
Now, we consider the 4 local minimum: $ \{ (0, 11), (3, 7), (5, 7), (8, 9) \} $ and the only 3 local maximum: $ (1, 14), (4, 9), (7, 10) $. We associate $ (0, 11) $ to $ (1, 14) $, then $ (8, 9) $ to $ (7, 10) $ and finally $ (5, 7) $ to $ (4, 9) $. The remaining local minimum $ (3, 7) $ can not be paired to any other local maximum because all of them have already been paired. The local-minimum-local-maximum paired heights constitutes the so-called persistence diagram $ \mathcal{PD}(S) $, in our example $ \mathcal{PD}(S) = \{(7, 9), (9, 10), (11, 14) \} $, with the minimum of the pair representing the topological occurrence birth, whereas the associated maximum its death.
In our example, consisting of the 9 data and the three topological occurrences composing, the associated persistence diagram is shown in Figure 5.
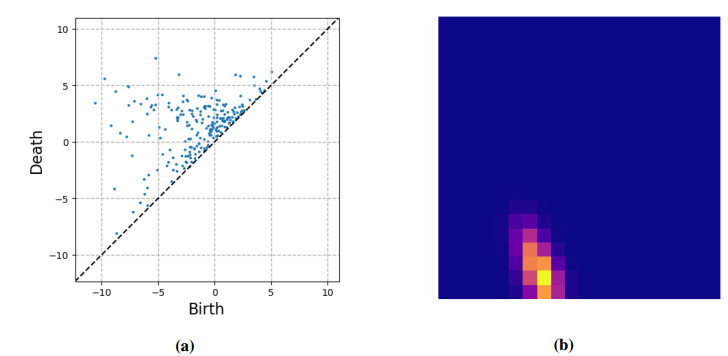
In the two dimensional representation associated to the persistence diagram, each data point $ (x, y) $ verifies the relationship $ y \geq x $ (the topological occurrence birth precedes its death) and then points locate above the bisector $ x = y $. The topological representation provided by the persistence diagram offers a very concise description of any curve (e.g. surface profiles, time-series, etc.) and the change in their topological features as considered in [13,14,20,21].
In order to use the persistence diagram and perform vectorial operations such as the ones required in classification, we must transform the persistence diagram into a vectorial representation of it, the so-called persistence image [22,21].
For that purpose, we first introduce the so-called lifetime diagram $ \mathcal{T}(S) $ associated to the function $ \mathcal{PD}(S) $, defined in Eq 5.
where $ y-x $ represent the lifetime of the topological occurrence. In our example we have $ \mathcal{T}(S) = \{(7, 2), (9, 1), (11, 3)\} $, that is illustrated in Figure 6.
Next, we will construct a persistent image as follows. We consider a continuous piecewise derivable non-negative weighting function (with $ (x, y) \in \mathcal T(S) $, $ w(x, 0) = 0 $ and $ w(x, y_{max}) = 1 $, with $ y_{max} = \max(y) $, that can be approximated by a linear function of the lifetime $ y $, e.g. $ w(x, y) = y/y_{max} $) and a bivariate normal distribution $ g_{x, y}(u, v) $ centered at each point $ (x, y) \in \mathcal T(S) $ and with its variance $ \sigma $, $ \sigma > 0 $, scaling with the maximum of the lifetime diagram [21,22], then we define the variable $ \rho_S(u, v) $ expressed in Eq 6:
with $ (u, v) \in \mathcal D $, with $ \mathcal D $ a compact domain (for example the domain in which $ \mathcal T(S) $ is defined).
Now, the domain $ \mathcal D $ is partitioned in a series of non-overlapping subdomains covering it, the so-called pixels $ P_i $, with $ \mathcal D = \cup_{i = 1}^\mathtt P P_i $, and function $ \rho_S(u, v) $ averaged in each of those pixels, that will define the persistence image $ \mathcal PI(S) $. Thus each of the $ \mathtt P $ pixels of the persistence image $ \mathcal{PI}(S) $ takes the value given by Eq 7:
As the profile that served to illustrate the different concepts contains too few topological occurrences, to illustrate what a persistence image resembles to, we consider a profile related to one of the measured rough surfaces $ S $, compute the persistence diagram $ \mathcal{PD}(S) $, then its associated lifetime diagram $ \mathcal T(S) $, and finally its persistence image $ \mathcal{PI}(S) $. Figure 7 shows $ \mathcal{PD}(S) $ and $ \mathcal{PI}(S) $, the last employing $ 20 \times 20 $ pixels, i.e. $ \mathtt P = 400 $ with a variance $ \sigma $ in the normal distribution $ g_{x, y}(u, v) $ given by Eq 8:
3.3. Images classification versus clustering
When applying the rationale just described to the 1359 rough surfaces $ S^{(k)} $, $ k = 1, \dots, 1359 $, we will obtain the associated 1359 persistence diagrams $ \mathcal{PD}(S^{(k)}) $, lifetime diagrams $ \mathcal{T}(S^{(k)}) $ and persistence images $ \mathcal{PI}(S^{(k)}) $, $ k = 1, \dots, 1359 $.
Thus each surface produced a persistence image composed of $ \mathtt P = 400 $ pixels. These images are expected belonging to 16 different classes, the 16 families of composite tapes. Obviously, trying to proceed to that classification directly from the surface raw data $ S^{(k)} $ seems a tricky issue because the proximity is not well defined when using a standard Euclidean metric. The same surface taken with a small shift will induce a significant difference. Metrics based on the topology seem more robust because the appealing associated invariance properties. Thus, more than trying to classify from the raw data, persistence images seem to be the right starting point.
3.3.1. Images classification
Image classification is a procedure to automatically categorize images into classes, by assigning to each image a label representative of its class. A supervised classification algorithm requires a training sample for each class, that is, a collection of data points whose class of interest is known. Labels are assigned to each class of interest. The classification is thus based on how close a new point is to each training sample. The Euclidean distance is the most common distance metric used in low dimensional data sets. The training samples are representative of the known classes of interest to the analyst.
In order to classify the persistence images we can use any state of the art technique. In our case we considered the Random Forest classification [23]. We train the random forest (consisting of 400 trees) by using $ 65 \% $ of the the persistence images (the remaining $ 35\% $ serving to evaluate the classification performances), where a label was attached to each one, a label precisely specifying the family, among the 16 composites considered, to which it belongs.
With the trained random forest one expects, from a given persistence image, obtaining in almost real-time the family to which it belongs, of major interest in process control.
3.3.2. Images clustering
Unsupervised learning algorithms aim at finding unknown patterns in data sets without pre-existing labels. Clustering is used in unsupervised learning to group, or segment, data that has not been labelled, classified or categorized. It is based on the presence or absence of commonalities in each new piece of data. This approach also helps detect anomalous data points that do not fit into either group.
One of the most popular clustering techniques, the $ k $-means, aims at partitioning the observations into $ k $ clusters in which each observation belongs to the cluster with the nearest mean or center [23]. The cluster center serves as a prototype of the cluster population. The observations are then allocated according to the criterion of minimizing the within-cluster variances, which is a squared Euclidean distance. The data can be then labelled according to their respective clusters (arbitrarily numbered).
To determine the optimal number of clusters we proceed as follows. For different values of $ k $, $ k $-means is trained with the whole data-set, and the data-labelled depending on the cluster to which each data belongs. Then, $ k $-means is applied again but now with only $ 65\% $ of the data. Then, for each data the cluster to which it belongs is compared to the label (cluster to which it belonged when all the data was employed in the $ k $-means). A parametric variance analysis allows determining the optimal value of $ k $, that in our case resulted as expected $ k = 16 $.
As soon as the best number of cluster is determined, $ k = 16 $ in our case, $ k $-means proceeds with the whole data to generate the reference labels (cluster to which each data belongs). Then, the process repeats but now employing only $ 65\% $ of the data. Finally we estimate for the remaining $ 35\% $ of the data to which cluster it is associated and compare with its label to have an estimation of the clustering performances.
3.4. Predicting the degree of intimate contact
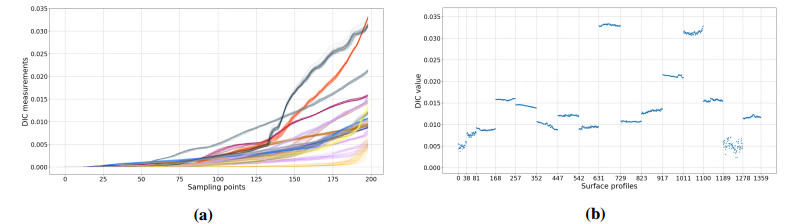
The consolidation process of all the available surfaces (1359) was simulated by using the PGD-based high-resolution solver described in Section 2. The evolution of the DIC, that is, the fraction of the surface in perfect contact, was evaluated at the different time steps. Figure 8a depicts the DIC evolution for the 1359 surfaces during the first 200 time steps of the consolidation process. As it can be noticed the dispersion of the DIC is quite small within each one of the 16 composite tapes (classes), however it exhibits large differences from one composite to another.
In what follows we are interested in the DIC prediction at the last time step (the number 200), that will consist of our quantify of interest –QoI– $ \mathcal O $, that for each surface results in the values $ \mathcal O^{(k)}, \ k = 1, \dots, 1359 $ depicted in Figure 8b.
Now, we are interested in constructing a regression for expressing the QoI, $ \mathcal O $, as a function of the considered surface, the geometry of the last expressed through its persistence image.
For that purpose we are considering two regression techniques: (ⅰ) the so-called Code2Vect [24] summarized in the Appendix, and (ⅱ) the random forest.
● Code2Vect maps the surfaces described by the $ 400 $ values related to the pixels of their associated persistence images into another low dimensional vector space where the distance between any two points (representing two surfaces) scales with the QoI difference, that is, with respect to the difference of their DIC. However, as for usual nonlinear regression techniques, the complexity scales with the number of parameters involved in the regression, and here $ 400 $ seems a bit excessive with respect to the available data.
For this reason, and prior to use de Code2Vect regression, the 1359 persistence images, each represented by $ 20 \times 20 $ pixels, are first analyzed by using the principal component analysis –PCA– to remove linear correlations [23] where the two most significant modes were retained, and each persistence image described by its projection on both models. Thus, the reduction is impressive, each persistence image, and in consequence each surface, is now described from only two parameters. Then, the Code2Vect was employed to establish the regression between these two parameters and the quantity of Interest $ \mathcal O $, the final DIC [24].
Again, to evaluate the regression performances, Code2Vect was trained by using $ 80\% $ of the data, and the remaining $ 20\% $ served for evaluating the prediction performances.
● As previously indicated a regression based on the use of Random Forest [23] (using 400 trees) was considered, with $ 65\% $ of the data used in the training and $ 35\% $ for evaluating the prediction performances.
3.5. Models evaluation
For evaluating the model performances we consider different procedures:
● Confusion matrix
The component $ (i, j) $ of the confusion matrix contains de number of surfaces that belonging to a class $ i $ are predicted belonging to class $ j $. Obviously the classification is perfect when this matrix becomes diagonal.
● Classification scoring. Evaluating a classification model is determining how often labels are correctly or wrongly predicted for the testing samples. In other words, it is counting how many times a sample is correctly or wrongly labelled into a particular class. We distinguish four qualities:
- TP (True Positive): the correct prediction of a sample into a class;
- TN (True Negative): the correct prediction of a sample out of a class;
- FP (False Positive): the incorrect prediction of a sample into a class;
- FN (False Negative): the incorrect prediction of a sample out of class.
These quantities are involved in the definition of different estimators of the model performances:
- The Precision (P) is the number of correct positive results divided by the number of all positive results, expressed by Eq 9:
- The Recall (R) is the number of correct positive results divided by the number of all relevant samples, expressed by Eq 10:
- The F1 score is the harmonic mean of precision and recall, expressed by Eq 11:
- The Accuracy (A) is the number of correct predictions over the number of all samples, expressed by Eq 12:
● Regression scoring
We evaluate our regression prediction using the $ \mathcal R^2 $ coefficient, defined in Eq 13:
We also use the mean absolute percentage error $ MAPE $, defined in Eq 14:
with best model having the closest MAPE to $ 0\% $.
● Features importance. In decision trees, every node is a condition on how to split values for a single feature, so that similar values of the dependent variable end up in the same set after the split. The condition is based on impurity, which in the case of classification problems is the Gini impurity or the information gain (entropy), while for regression trees it is the variance. So when training a tree, we can compute how much each feature contributes to decreasing the weighted impurity, and in the case of Random Forest, we are talking about averaging the decrease in impurity over all the trees [23]. Although this method is known to be statistically biased for categorical variables, it should not be affected in our case, as we only have homogeneous and continuous variables, $ 20 \times 20 $ pixels images.
4.
Results
In this section we provide the numerical results and evaluations associated to each of the previously introduced models: Random Forest classification, $ k $-means clustering, Code2Vect and Random Forest regression.
4.1. Classification results
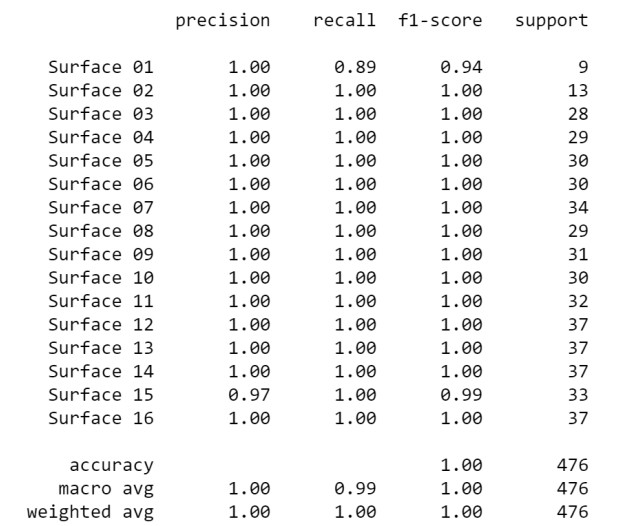
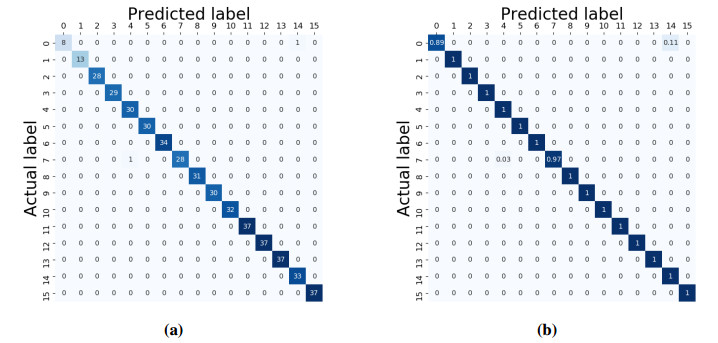
The trained random forest classifier for the persistence images shows high accuracy scores (over $ 99\% $), suggesting a strong differentiation of the images with respect to their generating surface profiles. The classification performance report shown in Figure 9 summarizes the precision, recall, f1-score estimators over each of the 16 classes (surface labels) from the test dataset. The number of samples for each class is also provided. The accuracy score estimator is computed over the complete test dataset, along with the macro and weighted averages of the previously cited estimators.
The confusion matrix given in Figure 10 shows that images are accurately labelled across all classes, reporting also the normalized scores. It was proved that these results are quite insensible to randomizing and changing the ratio between the training and testing samples.
4.2. Clustering results
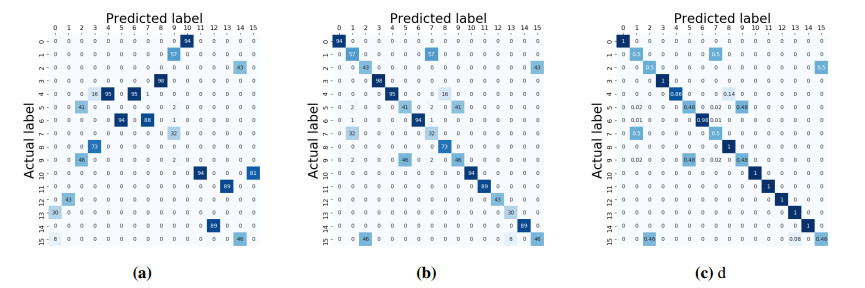
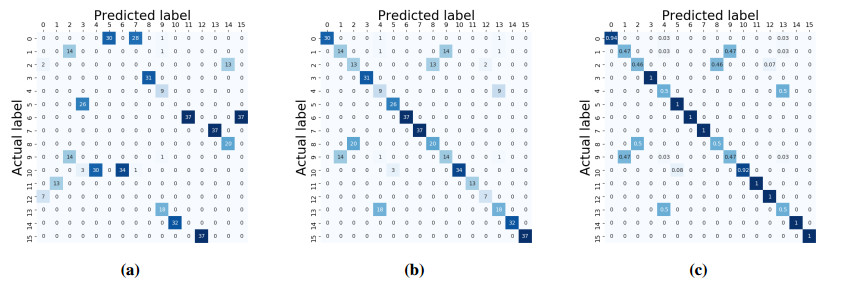
Given the disparity between clusters labels and original labels ($ k $-means algorithm assigns clusters labels arbitrarily), the confusion matrix is the best way to evaluate the model performance. It shows a majority of one-to-one classes correspondence, meaning that given a certain permutation of the columns (clusters labels), we can obtain a rearranged matrix. The permuted confusion matrix given in Figure 11b shows a good accuracy ($ 80\% $) for the clustering compared to the original profiles labels.
In order to evaluate the predictive performances of the trained model, we compare the predicted labels (clusters) of the test data against their actual labels. The labelling disparity still remains, with a majority of one-to-one classes correspondence. After reordering the confusion matrix, depicted in Figure 12b, we can observe a good enough accuracy of the clustering ($ 77\% $) for predicting labels. Thus, the model allows to identify the surface of new incoming profiles, when proceeding in an unsupervised way.
4.3. DIC prediction by regression
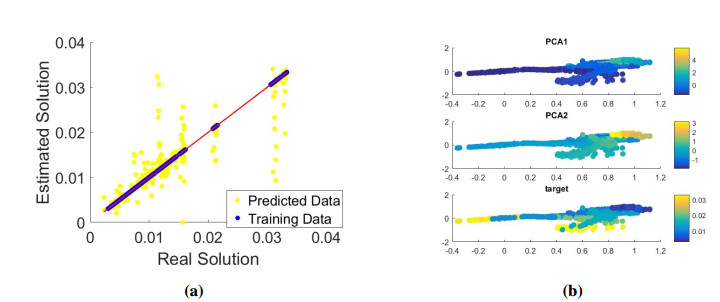
Code2Vect performs an accurate regression of the DIC, with a MAPE of $ 2.3\% $ when considering all the data and a MAPE of $ 12.86\% $ when applied on the points that were not used in training, as shown in Figure 13. Thus, it can be concluded that the reduction of the persistence images to only two quantities (the weights of the two most relevant modes extracted from the PCA applied on the persistence images) has not a significant impact in the regression performances, proving that the combination of Code2Vect and PCA constitutes an excellent nonlinear dimensionality reduction technique. The correlation between these two parameteres (PCA weights) and the QoI (DIC) is also shown in Figure 13b.
Similarly, the random forest regression shows a high reliability to accurately predict our quantity of interest, with an $ R^2 $ score over $ 96\% $.
5.
Conclusion
Composite tapes have been successfully classified using the persistence images related to their rough surfaces. Topological Data Analysis seems a very valuable way of describing accurately and concisely those surfaces, in particular its roughness that constitutes the main factor when evaluating the consolidation performances, from the time evolution of the DIC (degree of intimate contact).
Different classification (supervised) and clustering (unsupervised) were successfully applied for associating the different surfaces to the composites from which they were extracted. On the other hand, by using advanced regression techniques, the degree of intimate contact was associated to the surface topological content, with excellent and fast predictions of the expected DIC for a given surface.
These procedures open unimaginable possibilities in process control and the online adaptation of processing parameters for ensuring the adequate DIC at the end of the process.
5.1. Code2Vect
Code2Vect maps data, eventually heterogenous, discrete, categorial, ... into a vector space equipped of an euclidean metric allowing computing distances, and in which points with similar outputs $ \mathcal O $ remain close one to other as sketched in Figure 14.
We assume that points in the origin space (space of representation) consists of $ \mathtt P $ arrays composed on $ D $ entries, noted by $ {\bf y}_i $. Theirs images in the vector space are noted by $ {\bf x}_i \in \mathbb R^d $, with $ d \ll D $. The mapping is described by the $ d \times D $ matrix $ \bf W $, according to Eq 15:
where both, the components of $ \bf W $ and the images $ {\bf x}_i \in \mathbb R^d $, $ i = 1, \cdots, \mathtt P $, must be calculated. Each point $ {\bf x}_i $ keep the label (value of the output of interest) associated with is origin point $ {\bf y}_i $, denoted by $ \mathcal O_i $.
We would like placing points $ {\bf x}_i $, such that the Euclidian distance with each other point $ {\bf x}_j $ scales with their outputs difference, as expressed in Eq 16:
where the coordinates of one of the points can be arbitrarily chosen. Thus, there are $ \frac{\mathtt P^2}{2}-\mathtt P $ relations to determine the $ d \times D+\mathtt P\times d $ unknowns.
Linear mappings are limited and do not allow proceeding in nonlinear settings. Thus, a better choice consists of the nonlinear mapping $ {\bf W}({\bf y}) $ [24].
Acknowledgments
Authors acknowledge the ESI Chair ArtsetMétiersInstituteofTechnology,theESIChair Universidad Cardenal Herrera, the AWESOME E2S/Arkema/Canoe Chair and the French ANR through the DataBEST project.
Conflict of interests
There is no conflict of interests between authors.









 DownLoad:
DownLoad: