1 Department of Nanotechnology, Center for Post Graduate Studies, Bengaluru Region, VIAT, Muddenahalli, Chikkaballapur-562101 Visvesvaraya Technological University (VTU), Karnataka; 2 International advanced research centre for powdered metallurgy and new material (ARCI), Balapur, Hyderabad-500005, India
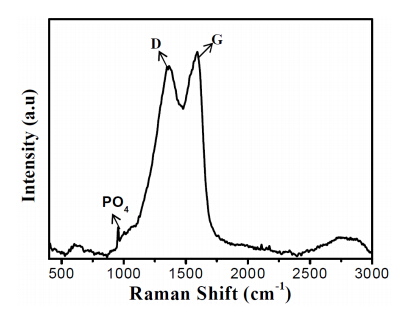
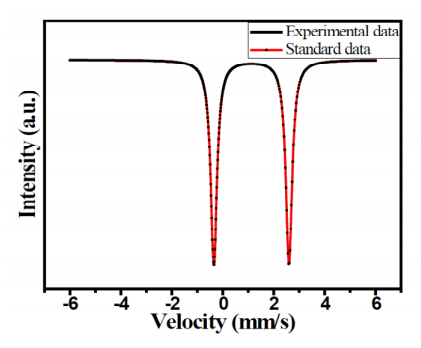
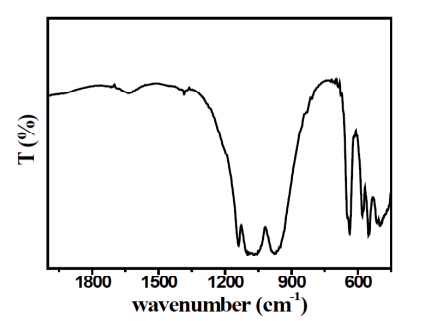
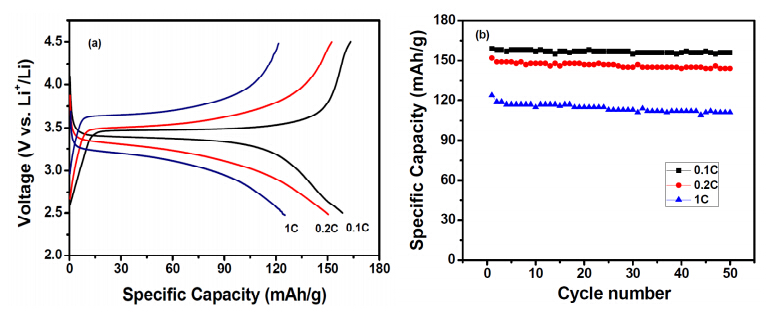
In this paper, we are reporting a combustion method to prepare carbon coated LiFePO4 nanoparticles using urea as fuel and sucrose as carbon source. The process involves exothermic decomposition of a viscous liquid, containing fuel to oxidizer molar ratio of 1:1 at 300 ℃, followed by heat treatment at 600 ℃ for 6 h, under Ar (95%) and H2 (5%) mixed gas atmosphere. The resultant products are characterized by Thermogravimetric analysis (TG-DSC), Field emission-scanning Electron microscopy (SEM), Transmission electron microscopy (TEM), X-Ray diffraction (XRD), Raman Spectroscopy, Fourier transformation infrared spectroscopy (FTIR), and Moss-Bauer spectroscopy. The investigation reveals that the prepared sample has ordered olivine structure|with average crystallite size in the range of 30-40 nm. The SEM and TEM images show porous network type morphology with the size of the individual particles in range of 30-40 nm with spherical and oval shape morphology. The cathode obtained by combustion method exhibits a high discharge capacity (~156 mAhg-1) with a good cyclic performance and rate capability.
