Geostatistical modelling of soil contamination with arsenic, cadmium, lead, and nickel: the Silesian voivodeship, Poland case study

Jolanta Kwiatkowska-Malina; Andrzej Szymon Borkowski

doi:10.3934/geosci.2020009

AIMS Geosciences, 2020, 6(2): 135-148. doi: 10.3934/geosci.2020009. Research article

Export file:

Format

RIS(for EndNote,Reference Manager,ProCite)
BibTex
Text

Content

Citation Only
Citation and Abstract

Geostatistical modelling of soil contamination with arsenic, cadmium, lead, and nickel: the Silesian voivodeship, Poland case study

Jolanta Kwiatkowska-Malina, Andrzej Szymon Borkowski

Department of Spatial Planning and Environmental Sciences, Faculty of Geodesy and Cartography, Warsaw University of Technology, Politechniki Sq. 1, 00-661 Warsaw, Poland

Received: , Accepted: , Published:

Abstract Full Text(HTML) Figure/Table Related pages

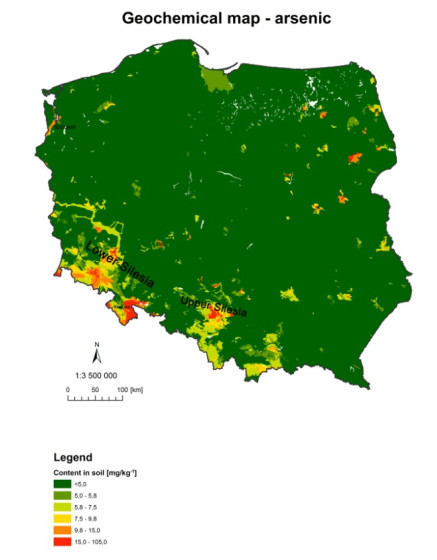
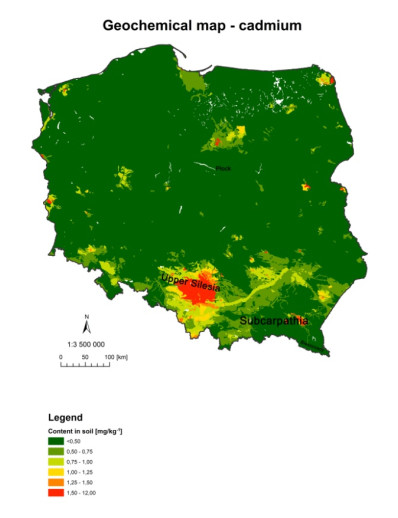
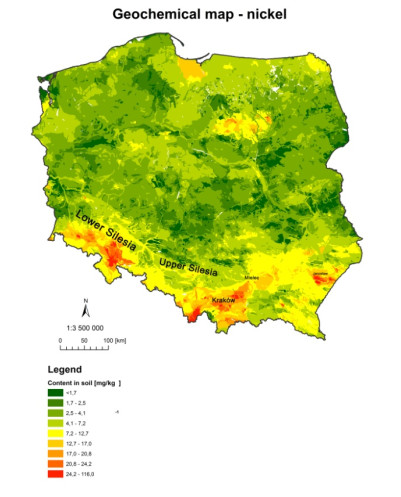
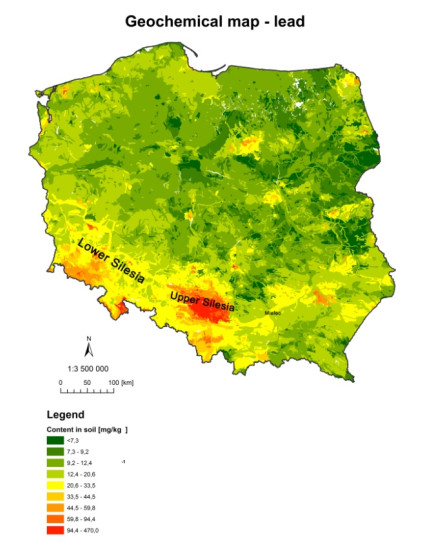
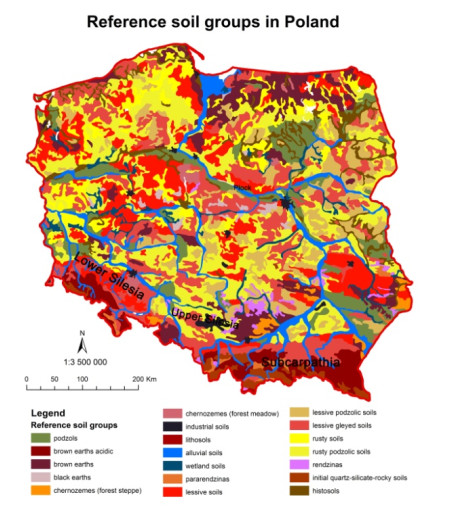
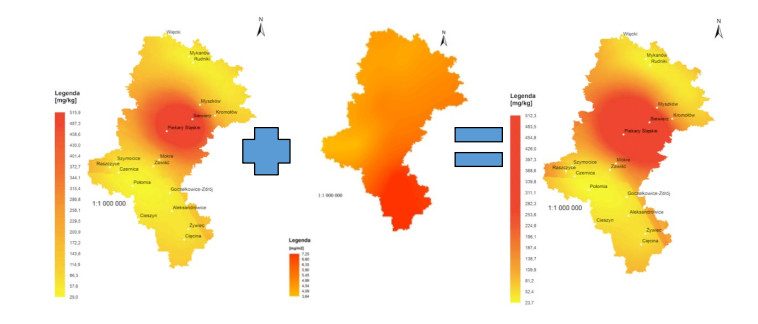
The increasing number of spatial data sets permits their application for minimising the duration and cost of such research. An example of such application is geostatistical modelling. Data on the quality of atmospheric air can be used for the assessment of the quality of soil in a given area. The objective of the study was an attempt to apply geostatistical methods in the estimation of the degree of soil contamination with selected heavy metals resulting from deposition from atmospheric air. This paper uses data obtained from the State Environmental Monitoring (data on the quality of atmospheric air) and other collections of publicly available spatial data for the purpose of analysis of the state of quality of soils in the province of Silesia in Poland. Conducted analyses revealing that contamination with lead in atmospheric air in the Silesian voivodeship considerably exceeds acceptable values, and the load of lead deposition is largely transferred to the soil. The paper also presents geochemical maps necessary to understand sources of soil contamination, including their natural content.

Figure/Table

Supplementary

Article Metrics

Keywords: soil contamination; heavy metals; geostatistical modelling; geochemical maps; lead deposition

Citation: Jolanta Kwiatkowska-Malina, Andrzej Szymon Borkowski. Geostatistical modelling of soil contamination with arsenic, cadmium, lead, and nickel: the Silesian voivodeship, Poland case study. AIMS Geosciences, 2020, 6(2): 135-148. doi: 10.3934/geosci.2020009

References:

1. Modrzewska B, Wyszkowski M (2014) Trace metals content in soils along the state road 51 (north-eastern Poland). Environ Monit Assess 186: 2589-2597.
2. Osakwe SA (2013) Chemical partitioning of iron, cadmium, nickel and chromium in contaminated soils of south-eastern Nigeria. Chem Speciation Bioavailability 25: 71-78.
3. Bień JD, Meer J, Rulkens WH, et al. (2005) A GIS-based approach for the long-term prediction of human health risks at contaminated sites. Environ Model Assess 9: 221-226.
4. Jalali M, Karami S, Marj AF (2016) Geostatistical Evaluation of Spatial Variation Related to Groundwater Quality Database: Case Study for Arak Plain Aquifer, Iran. Environ Model Assess 21: 707-719.
5. Krami LK, Amiri F, Sefiyanian A, et al. (2013) Spatial patterns of heavy metals in soil under different geological structures and land uses for assessing metal enrichments. Environ Monit Assess 185: 9871-9888.
6. Goovaerts P (1997) Geostatistics for natural resources evaluation. Oxford Uni. Press, New York, 483.
7. Lin WC, Lin YP, Wang YC (2016) A decision-making approach for delineating sites which are potentially contaminated by heavy metals via joint simulation. Environ Pollut 211: 98-110.
8. Shen F, Liao R, Ali A, et al. (2017) Spatial distribution and risk assessment of heavy metals in soil near a Pb/Zn smelter in Feng County, China. Ecotoxicol Environ Saf 139: 254-262.
9. Xie Y, Chen TB, Lei M, et al. (2011) Spatial distribution of soil heavy metal pollution estimated by different interpolation methods: Accuracy and uncertainty analysis. Chemosphere 82: 468-476.
10. Zawadzki J, Fabjańczyk P (2012) Geostatistical evaluation of lead and zinc concentration in soils of an old mining area with complex land management. Int J Environ Sci Technol 10: 729-742
11. Namysłowska-Wilczyńska B (2019) Application of Geostatistical Techniques for the Determining of an Anomalous Zone of Copper Ore Deposit in the Area of Polkowice Mine (Region of Lubin-Sieroszowice, SW Part of Poland). Geoinfor Geostat Overv 7: 1-22
12. Namysłowska-Wilczyńska B, Wilczyński A (2002) Multivariate estimation and simulationfor environmental data modelling: processing of heavy metals concentration data in soil. Data Sci J 1: 27-44
13. Ripin SNM, Hasan S, Kamal M (2014) Environmental Geochemical Mapping on Distribution of Metal Contamination in Topsoils Perlis, Malaysia. J Med Bioeng 3: 277-281.
14. Cai L, Xu Z, Bao P, et al. (2015). Multivariate and geostatistical analyses of the spatial distribution and source of arsenic and heavy metals in the agricultural soils in Shunde, Southeast China. J Geochem Explor 148: 189-195.
15. Salminen R, Tarvainen T, Demetriades A, et al. (1998) FOREGS Geochemical Mapping Field Manual. Geological Survey of Finland.
16. De Vivo B, Lima A, Bove AM, et al. (2006) Environmental Geochemical Atlas of Italy. European Congress on Regional Geoscientific Cartography and Earth Information and Systems Water, 126-127.
17. Guillén MT, Delgado J, Albanese S, et al. (2011) Environmental geochemical mapping of Huelva municipality soils (SW Spain) as a tool to determine background and baseline values. J Geochem Explor 109: 59-69.
18. Frentiu T, Ponta M, Levei E, et al. (2008) Preliminary study on heavy metals contamination of soil using solid phase speciation and the influence on groundwater in Bozanta-Baia Mare Area, Romania. Chem Speciation Bioavailability 20: 99-109.
19. Malina G (2004) Ecotoxicological and environmental problems associated with the former chemical plant in Tarnowskie Gory, Poland. Toxicology 205: 157-172.
20. Saito H, Goovaerts P (2000) Geostatistical Interpolation of Positively Skewed and Censored Data in a Dioxin-Contaminated Site. Environ Sci Technol 34: 4228-4235.
21. Fowler D, Skiba U, Nemitz E, et al. (2004). Measuring Aerosol and Heavy Metal Deposition on Urban Woodland and Grass Using Inventories of ²¹⁰Pb and Metal Concentrations in Soil. Water Air Soil Pollut Focus 4: 483-499.
22. Brunner PH, Rechberger H (2016) Practical Handbook of Material Flow Analysis. CRC Press, 173-178.
23. Pleim J, Venkatram A, Yamartino R (1984) ADOM/TADAM model development program. ERT P-b980-520, prepared for OME AES of Canada and the Umweltbundesamt, West Germany, 111.
24. Sportisse B (2007) A review of parameterizations for modelling dry deposition and scavenging of radionuclides, Atmos Environ 41: 2683-2698.
25. Hopenhayn C (2006) Arsenic in Drinking Water: Impact on Human Health. Elements 2: 103-107.
26. Kapaj S, Peterson H, Liber K, et al. (2006) Human Health Effects From Chronic Arsenic Poisoning-A Review. J Environ Sci Health Part A Toxic/Hazard Subst Environ Eng 41: 2399-2428.
27. Zawierucha I, Kozłowski C, Malina G (2016) Immobilized materials for removal of toxic metal ions from surface/groundwaters and aqueous waste streams. Environ Sci Processes Impacts 18: 429.
28. Kucharczak-Moryl E, Moryl A, Żmuda R (2014) Environment influence arsenic content in croplands in the zgorzelecki-bogatyński region. Ecological Engineering, No 37: 107-116. Available from: http://www.ineko.net.pl/Wplyw-srodowiska-na-zawartosc-arsenu-w-glebach-uprawnych-rejonu-zgorzelecko-bogatynskiego,283,0,1.html. Accessed 5 May 2016.
29. Mikulski S (2010) Gold, arsenic and dopeore. Polish Geological Institute-National Research Institute.
30. Kuys K, Ralston J, Sobieraj S, et al. (1989) Methods for the enrichment of bauxite ultrafines. Physicochem Metall Probl 21: 23-26.
31. Bernard A (2008) Cadmium & its adverse effects on human health. Indian J Med Res 128: 557-564.
32. Kabata-Pendias A, Piotrkowska M (1997) Transfer of cadmium, zinc and lead from soils to plants. The 5th international conference proceedings: transport, fate and effects of silver in the environment, 171-176.
33. Kwiatkowska-Malina J, Maciejewska A (2013) Uptake of heavy metals by darnel multifloral (Loliummultiflorum Lam.) at diverse soil reaction and organic matter content. Soil Sci Annu 64: 19-23.
34. Maciejewska A, Kwiatkowska J (2001) Contamination of soil with heavy metals along highways as well as in the city of Warsaw, In Obieg pierwiastków w przyrodzie (in Polish), Instytut Ochrony Środowiska: 49-54.
35. Maciejewska A, Ociepa E, Kwiatkowska J (2003) Changes in the availability of heavy metals and content of organic carbon in polluted soil after the application of an organic-mineral fertilizer obtained from brown coal. Pol J Soil Sci 36:129-136.
36. Duda-Chodak A, Błaszczyk U (2008) The impact of nickel on human health. J Elem 13: 685-696.
37. Cempel M, Nikel G (2006) Nickel: A Review of Its Sources and Environmental Toxicology. Pol J Environ Stud 15: 375-382.
38. Järup L, Åkesson A (2009) Current status of cadmium as an environmental health problem. Toxicol Appl Pharmacol 238: 201-208.
39. Mohammed AS, Kapri A, Goel R (2011) Heavy Metal Pollution: Source, Impact, and Remedies: Biomanagement of Metal-Contaminated Soils. Environ Pollut 20: 1-28.
40. Pistocchi A, Groenwold J, Lahr J, et al. (2011) Mapping Cumulative Environmental Risks: Examples from the EU NoMiracle Project. Environ Model Assess 16: 119-133.
41. Strzelecki R (2004) Directions and problems of abiotic environment research in Poland conducted by the State Geological Survey. Pol Geol Rev 52: 716-719.
42. Institute of Soil Science and Plant Cultivation-State Research Institute (2010) The assessment of soil contamination in Poland. Available from http://www.iung.pulawy.pl/index.php?option=com_content&view=article&id=147:zanieczyszczenia&catid=45:oferta&Itemid=115. Accessed 11 June 2016.

show all references

Reader Comments

your name: * your email: *

Download full text in PDF

Associated material

Metrics