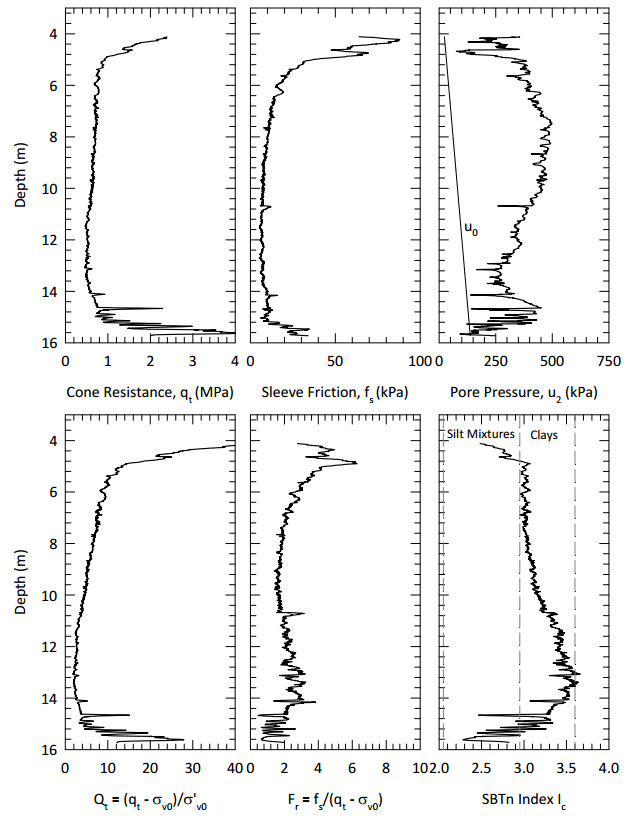
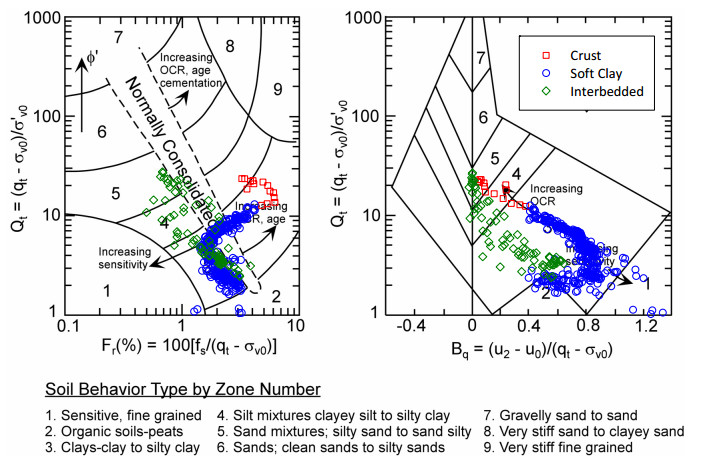
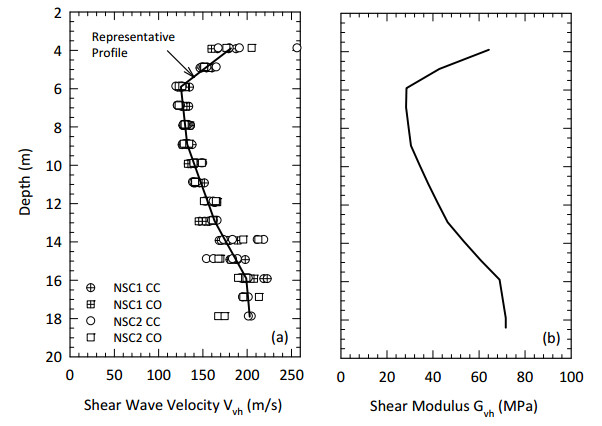
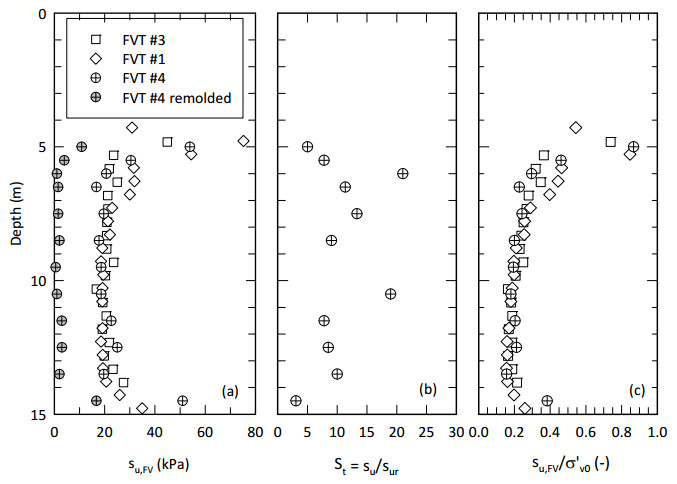
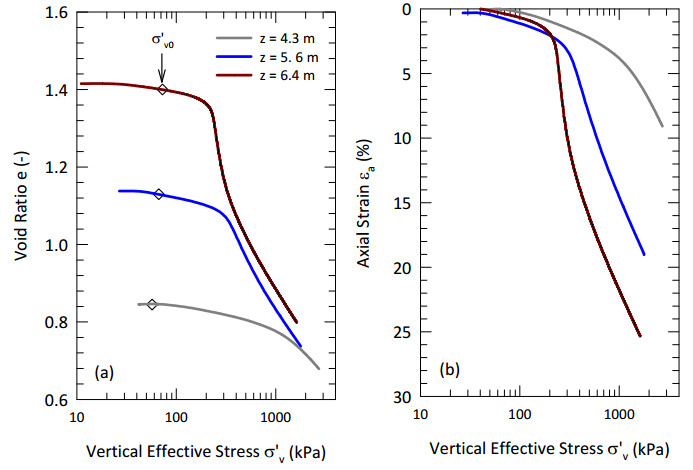
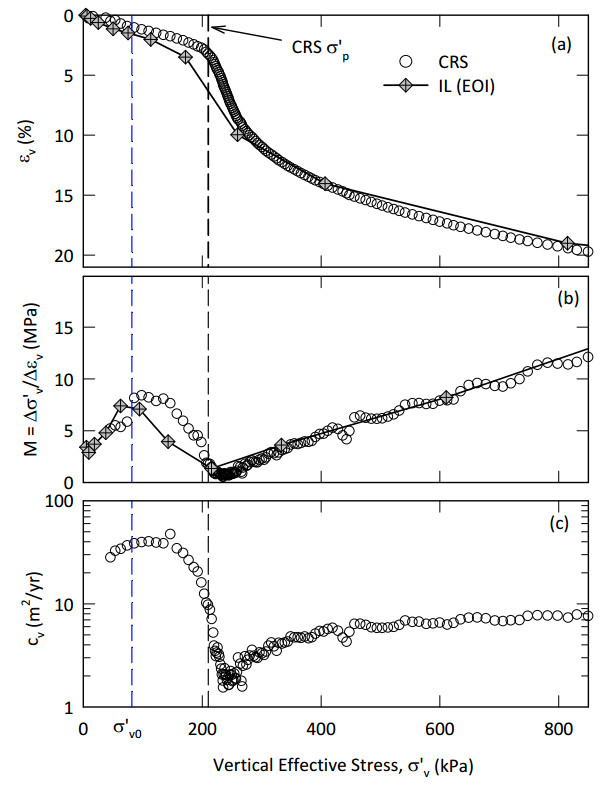
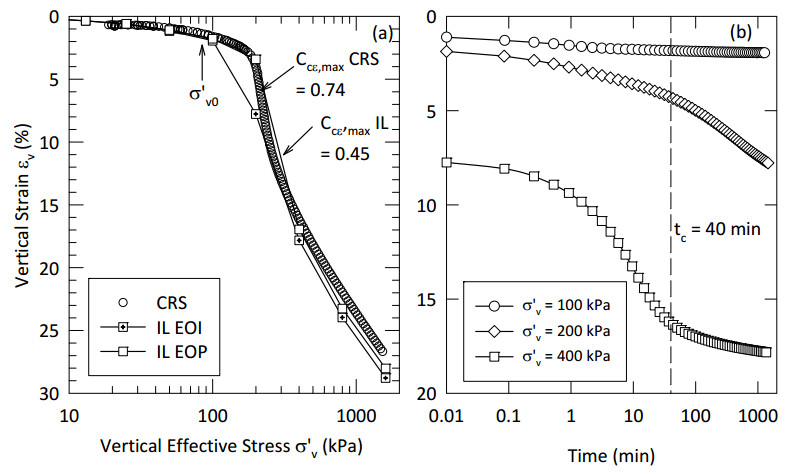
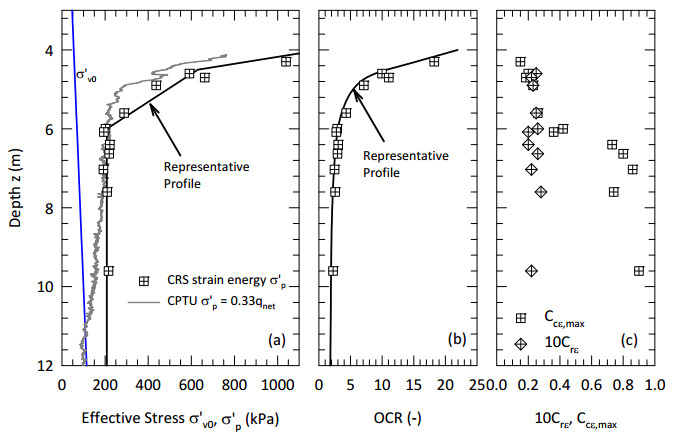
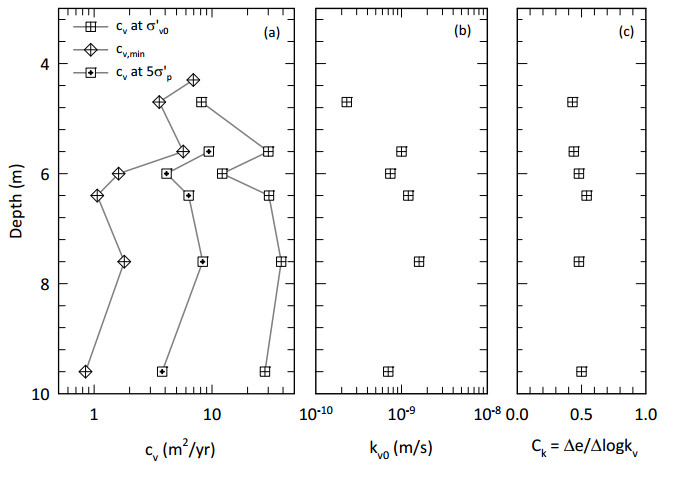
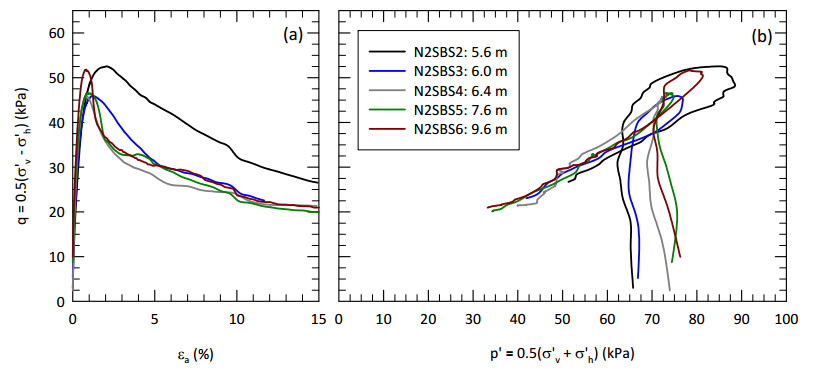
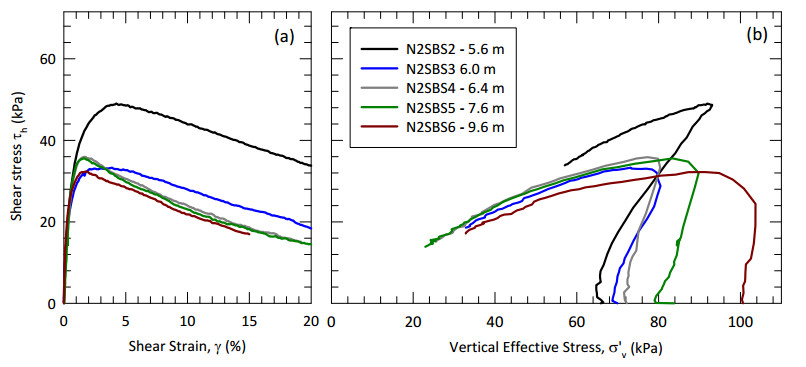
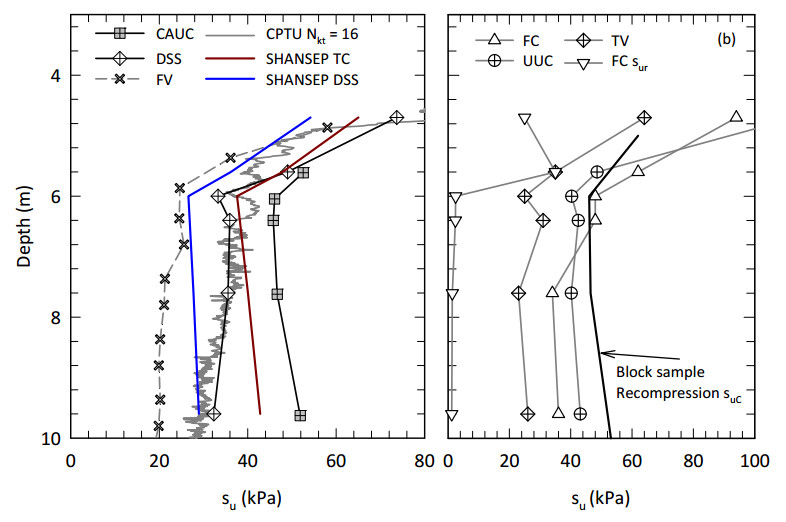
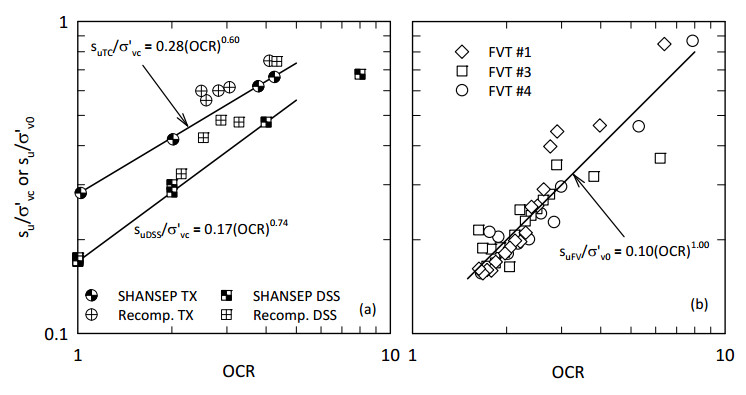
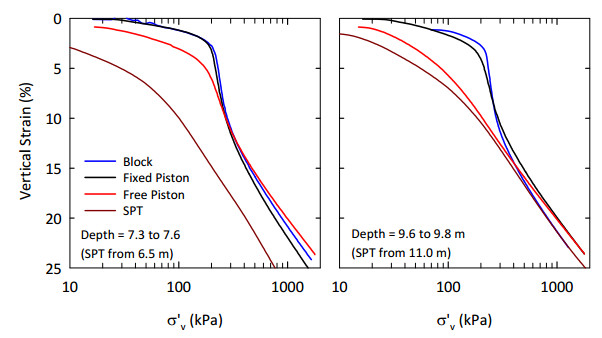
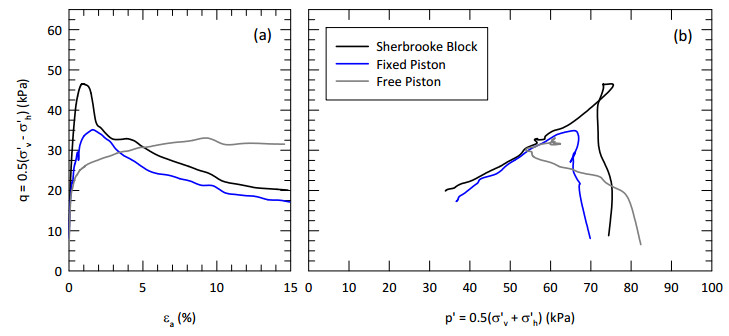
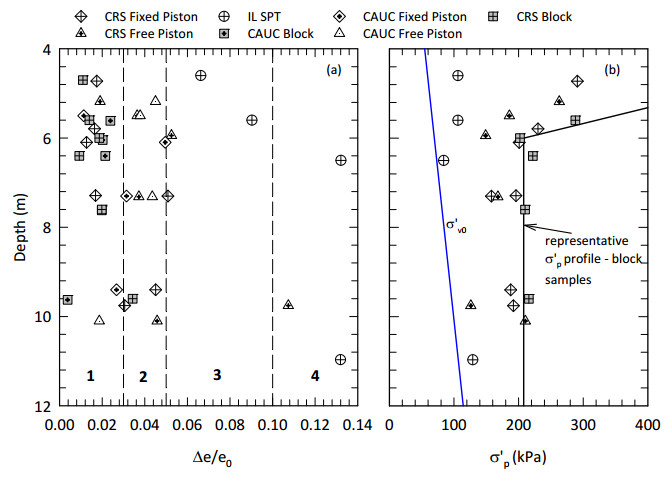
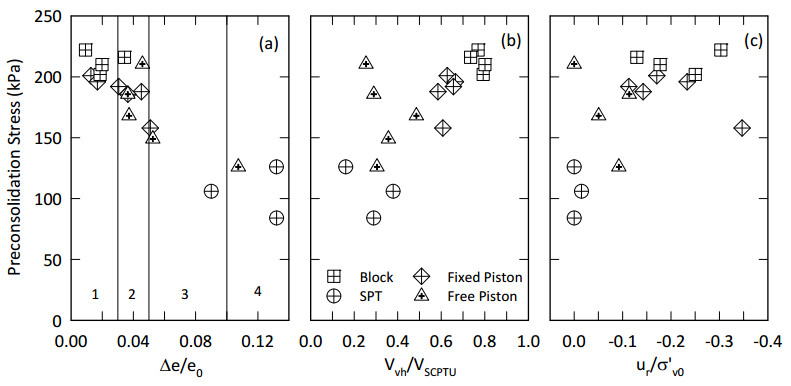
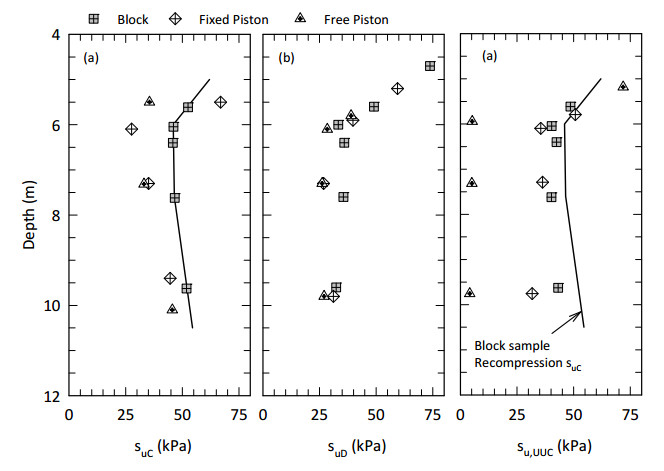
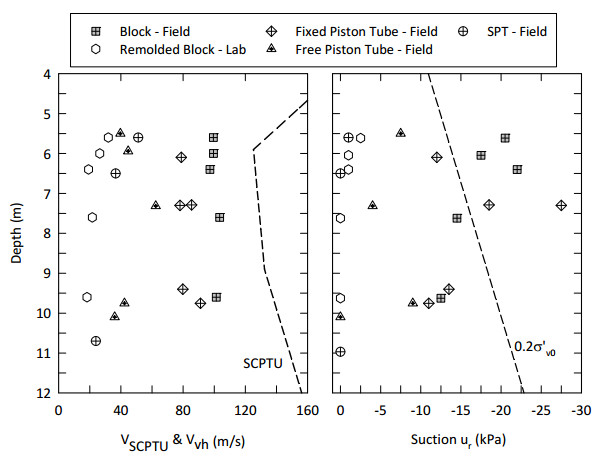
This paper describes the geology and geotechnical engineering properties of a sensitive marine clay deposit at a research site located in Newbury, Massachusetts (MA) in the northeast USA. Results from in situ testing, soil sampling, and laboratory testing are presented. The clay is locally known as Boston Blue Clay (BBC) which is a glacial marine clay that was deposited approximately 14,000 years ago in the greater Boston, MA area during retreat of the Laurentide Ice Sheet. The thickness, stress history, and soil properties of BBC can vary significantly depending on location. At the Newbury research site, the BBC deposit consists of a shallow thin desiccated crust underlain by a 12-meter thick low plasticity clay with an overconsolidation ratio ranging from 2 to 3. Sensitivity of the clay ranges from approximately 10 to 30, based on field vane and fall cone measurements. In situ testing performed at the site included seismic piezocone and field vane. Soil sampling was performed using a variety of samplers including Sherbrooke block, fixed piston thin-walled Shelby tube, and a thick-walled drive sampler. A full suite of advanced laboratory tests was performed on the various quality samples collected, which ranged from very poor (thick-walled drive sampler) to excellent (Sherbrooke block), including constant rate of strain consolidation, consolidated undrained triaxial and direct simple shear. The efficacy of the Recompression and SHANSEP procedures to mitigate sample disturbance was evaluated using results from the advanced laboratory test program. The paper presents data from these advanced tests as well as other soil classification, index, and engineering properties based on in situ measurements and laboratory test results. A synopsis of constructed facilities built on and in BBC within the greater Boston area is also presented.
1.
Introduction
Strategic decision-making tools, clustering analysis, medical diagnosis, pattern recognition, computer networking systems, and shortest path dilemmas are massive valuable fields of genuine scenarios where awkward sort of situations are involved. In such sort situations, the mathematical representation of the fuzzy set (FS) [1] has a massively valuable and beneficial tool as compared to crisp sets. In these ways, where there is ambiguity, there is the class for an FS and their expansions to address such dilemmas, to describe various genuine life troubles effectively, involved awkward data, the main theory of intuitionistic FS (IFS), diagnosed by Atanassov [2] in 1983. An IFS plays a beneficial role in the environment of different valuables fields. The fixed and basic tool of IFS is described: 0≤μ(t)+ν(t)≤1. If someone from group of experts gives (0.6,0.5) for truth and falsity grades, then using the tool of IFS, we get 0.6+0.5=1.1>1 has been unsuccessful. For this, the major idea of Pythagorean FS (PyFS), invented by Yager [3] by putting the mathematical tool: 0≤μ2(t)+ν2(t)≤1. Yet again situation are massive awkward, because various practical examples are existing, if a person give (0.9,0.8) for duplet, then the principles of Atanassov-IFS and Yager-PyFS have been neglected i.e., 0.9+0.8=1.7>1 and (0.9)2+(0.8)2=0.81+0.64=1.45>1. To completely and accurately illustrated the above dilemmas, the major scenario of q-rung orthopair FS (QROFS), exposed by Yager [4] suggested a new tool: 0≤μq(t)+νq(t)≤1,q≥1. In the presence of its powerful and effective structure, different scholars have employed the principle of QROFS in the environment of separated regions, for instance, Ali [5] diagnosed the well-known and dominant technique of complex QROFSs, Liu and Wang [6] invented the aggregation operators for QROFSs using t-norm and t-conorm, Wang et al. [7] stated the different from of measures using QROFSs, Wei et al. [8] explored the Heronian mean operators, Riaz and Hashmi [9] proved linear Diophantine FS, and the mathematical form of N-soft topology was invented by Riaz et al. [10]. QROF information is also utilized in strategic decision-making tools [11,12].
The principle of FS has to deal with only one-dimension information in the form of [0,1]. Ramot et al. [13] invented the complex FS (CFS) is to modify the TG by including the two-dimension information instead of one-dimension information in fuzzy TG to manage inconsistent information. Further, Alkouri and Salleh [14] tried to modify the major form of CFS, to diagnose the fundamental theory of complex IFS (CIFS) with 0≤μW(t)+νW(t)≤1 and 0≤θW(t)+ϑW(t)≤1. Additionally, Ullah et al. [15] diagnosed the complex PyFS (CPyFS) with 0≤μ2W(t)+ν2W(t)≤1 and 0≤θ2W(t)+ϑ2W(t)≤1. Still, there were certain troubles, if an experts give 0.9ei2π(0.9) for TG and 0.8ei2π(0.8) for FG, then the principle of CIFS and CPyFS have been neglected i.e., 0.9+0.8=1.7>1.0.9+0.8=1.7>1 and (0.9)2+(0.8)2=0.81+0.64=1.45>1,(0.9)2+(0.8)2=0.81+0.64=1.45>1. To completely and accurately illustrated the above dilemmas, the major scenario of complex QROFS (CQROFS), elaborated by Liu et al. [16,17]. The prominent characteristic of CQROFS is described: 0≤μqW(t)+νqW(t)≤1 and 0≤θqW(t)+ϑqW(t)≤1. Due to its structure, the different individual has employed the principle of CIFSs, CPyFSs, and CQROFS in the environment of decision-making tool [18], aggregation operators [19], complex intuitionistic fuzzy graph [20], complex interval-valued IFSs [21]. Further, [22] and [23] included the complex Pythagorean fuzzy planar graphs, [24] contained the competition graph for CPyFSs, [25] contained operators for CQROFSs, [26] diagnosed the complex q-rung orthopair fuzzy 2-tuple linguistic sets, and Maclaurin symmetric mean diagnosed in [27].
The mathematical shape of fuzzy graph (FG) [28] covers two basic terms, called nodes and edges in the shape of TGs. There were a few situations where the FG should be utilized alongside TG and the hypothesis of FG could not adapt to such issues. To manage such complicated sorts of troubles, the principle of the intuitionistic FG (IFG) [29] are massively modified than the FG, which includes the FG in the environment of FG. The hypothesis of IFGs is massively powerful and extensive flexible than FGs to survive with awkward and inconsistent information in practical dilemmas. Various implementations of the above existing work in the environment of decision-making are described in [30]. Davvaz et al. [31] utilized the idea of IFGs in n-type of IFGs and gave an application on the social network. Additionally, Akram et al. [32] again modified the rule of IFG is to initiate the Pythagorean FG (PyFG) with 0≤μɎ2(Λ,ζ)+νɎ2(Λ,ζ)≤1, θɎ(Λ,ζ), ϑɎ(Λ,ζ) ∈[0,2π] ∀,Λ,ζ∈Ŭ. Still, there were certain troubles, if an expert give 0.9 for TG and 0.8 for FG, then the principle of IFG and PyFG have been neglected i.e., 0.9+0.8=1.7>1 and (0.9)2+(0.8)2=0.81+0.64=1.45>1. For this, the principle of q-rung orthopair FGs (QROFGs), initiated by Habib et al. [33], by improving the rule: 0≤μɎq(Λ,ζ)+νɎq(Λ,ζ)≤1, θɎ(Λ,ζ), ϑɎ(Λ,ζ) ∈[0,2π] ∀,Λ,ζ∈Ŭ. Due to its structure, the different people has employed the principle of QROFG in the environment of separated regions [34].
Complex FG (CFG), explored by Thirunavukarasu et al. [35], covers the degrees of truth explained using complex numbers instead of real values from [0,1]. There were a few situations where the FG should be utilized alongside TG and the hypothesis of CFG could not adapt to such issues. To manage such complicated sorts of troubles, the principle of complex IFG (CIFG) was utilized by Anwar and Chaudhry [36]. Moreover, Akram and Naz [37] initiated the complex PyFG (CPyFG). Sahoo and Pal [38] utilized the concepts of CG in the framework of intuitionistic fuzzy sets (IFSs). Due to its structure, many researchers have employed the principle of CPyFG in the environment of separated regions [37,39,40]. Keeping the beneficial and valuable terms and conditions of prevailing theories, various scholars have diagnosed various theories, for instance, Samanta and Pal [41] initiated fuzzy planer graph, Pramanik et al. [42] developed the interval-valued fuzzy graph, Samanta et al. [43] proposed the new concept of fuzzy planer graph, Alshehri et al. [44] elaborated the intuitionistic fuzzy graphs, and Akram et al. [45] proposed the planer graph for PyFSs. The idea of planarity is likewise examined in a few different systems remembering CPyFGs for [46]. There are a few issues that cannot be settled by utilizing CPyFG, for example, if a leader gives data that cannot be taken care of by CPyFG because of its limitation the amount of the squares of the two grades can't surpass the unit span.
In the consideration of the above-cited data, we noticed that existing theories of FG, IFG, PyFS, CIFG, and CPyFG have a lot of weaknesses and complexities. Therefore, the main concept of complex QROFG (CQROFG) is more flexible and massive feasible for managing awkward data. The major consideration of this script is prearranged here:
1) To analyze the well-known and massive idea of CG in the presence of a new and dominant technique of CQROF setting. The mathematical form of the CQROF setting is more flexible and massive consistent for demonstrating the beneficial option from the collection of objectives during the decision-making process.
2) The major concept of in-neighbourhood and out-neighbourhood using CQROFDG are also invented to enhance the quality of the diagnosed approach.
3) The fundamental theory of CQROF k-competition, CQROF p-competition, CQROF neighbourhood and m-step CQROF neighbourhood graphs are also explored. In the availability of the above-described theories, the basic and significant results for the presented work are obtained to show the compatibility and worth of the invented approaches.
4) To show the practicality of the developed approach, we try to verify the proposed work with the help of various examples.
5) To describe the validity and practicality of the invented work, we diagnosed an application using presented approaches based on the CQROF setting is to enhance the major weakness of the existing approaches.
6) In the availability of the invented ideas, we discussed the sensitivity analysis of the described approaches.
The manuscript is organized as follows; In Section 2, we briefly also discuss CG, FCDG, CPyFS, CQROFS, CQROFR, CPyFG, CQROFG and CPyFDG. In Section 3, the CQROFCG and their examples are elaborated. Section 4 is based on generalized the concept of CQROFG in the CQROF k-competition graph (CQROF k-competition graph) and a few results which are related to the following graphs. In Section 5, we will increase the radius of CQROFCG and discussed it for p-competition of (CQROFPCG). In Section 6, the complex q- rung orthopair fuzzy open and close neighbourhood of nodes and explained with the help of examples. In Section 7, we define them-step (CQROFDG). So, we explain CQROF m- step out-neighborhood CQROF m-step in- neighbourhood of the nodes and m-step (CQROFCG). In Section 8, to show the practicality of the developed approach, we try to verify the proposed work with the help of various examples. To describe the validity and practicality of the invented work, we diagnosed an application using presented approaches based on the CQROF setting is to enhance the major weakness of the existing approaches. In the availability of the invented ideas, we discussed the sensitivity analysis of the described approaches. Finally, the concluding remarks are in Section 9.
2.
Preliminaries
In this Section, we comprehensively discuss basic definitions and notations that are more useful for further development.
A graph is a pair G=(Ҳ,Ɏ) in which Ҳ represent the vertices and Ɏ represent the edges. In a graph, every edge is incident with one or more vertices. A graph in which each edge has a specific direction is known as a digraph →Ģ and a diagraph is denoted by →Ģ=(Ҳ,→Ɏ). In which →Ɏ represent the edges →uv for all u,v∈Ҳ. A sequence of nodes and edges in a graph G is called a walk such as E=v0,e1,v1,e2,...,en,vn, for j=1,2,...,n the nodes vj−1 and vj are the endpoints of the edge ej. A walk-in which edge ej is directed from vj−1 to vj is called a directed walk.
A walk-in in which no edge occurs more than one time is called a trail. A trail in which no internal vertex is occur more than one time is known as a path. A closed path of length at least one known as a cycle. N+(u)={v∈Ҳ−{u}:→uv∈→Ɏ} and N−(u)={v∈Ҳ−{u}:→uv∈→Ɏ} represents the out-neighbourhood and in-neighbourhood [33] of a node u in →Ģ respectively.
Definition 1: [47] The CG of a digraph →Ģ=(Ҳ,→Ɏ) is unidirectional graph G=(Ҳ,Ɏ) which has the same vertex set Ҳ and has an edge between two distinct vertices Λ,ζ∈Ҳ if there exist a vertex x∈Ҳ and edges Λx,ζx∈→Ɏ in →Ģ,Λ,ζ∈Ŭ.
Definition 2: [42] Let a fuzzy diagraph (FDG) is →Ģ=(Ҳ,→Ɏ) and a fuzzy competition graph (FCG) C(→Ģ) of →Ģ is an undirected graph G=(Ҳ,Ɏ) that contains be the family of similar fuzzy node in →Ģ and an edge exists among two different vertices Λ,ζ∈Ŭ in C((→Ģ) if and only if (iff) N+(Λ)∩N+(ζ)≠∅ in →Ģ and the TG of the edge (Λ,ζ) in C(→Ģ) is in the form:
Definition 3: [23] A CPyFS on Ŭ is the form of:
where i=√−1, ∀,t∈Ŭ,0≤(μW(t))2+(νW(t))2≤1 and 0≤(θW(t))2+(ϑW(t))2≤1 ∀,t∈Ŭ.
Definition 4: [14] A CQROFS on Ŭ is the form of:
where i=√−1, ∀,t∈Ŭ,0≤(μW(t))q+(νW(t))q≤1 and 0≤(θW(t))q+(ϑW(t))q≤1 ∀,q∈Z+,t∈Ŭ.
Definition 5: [48] A CQROF relation R(A,B) is explained as the subset of A×B is characterized by the TG and FG such as:
That is i=√−1,μR(Λ,ζ),νR(Λ,ζ)∈[0,1],θR(Λ,ζ),ϑR(Λ,ζ)∈[0,2π] and 0≤μqR(Λ,ζ)+νqR(Λ,ζ)≤1, ∀,q∈Z+,(Λ,ζ)∈A×B.
Definition 6: [47] A CPyFG Ģ=(Ŭ,Ҳ,Ɏ) in which Ҳ and Ɏ are CQROFS and CQROFR on Ŭ respectively such that:
and
0≤μɎ2(Λ,ζ)+νɎ2(Λ,ζ)≤1, θɎ(Λ,ζ), ϑɎ(Λ,ζ) ∈[0,2π] ∀,Λ,ζ∈Ŭ.
Definition 7: [48] A CQROFG Ģ=(Ŭ,Ҳ,Ɏ) in which Ҳ and Ɏ are CQROFS and CQROFR on Ŭ respectively such that:
and
0≤μɎq(Λ,ζ)+νɎq(Λ,ζ)≤1, θɎ(Λ,ζ), ϑɎ(Λ,ζ) ∈[0,2π] ∀,Λ,ζ∈Ŭ,q∈Z+.
Definition 8: [24] A complex Pythagorean fuzzy diagraph →Ģ=(Ŭ,Ҳ,→Ɏ) in which Ҳ and Ɏ are CQROFS and CQROFR on Ŭ respectively such that:
and 0≤μɎ2→(Λ,ζ)+νɎ2→(Λ,ζ)≤1, θɎ→(Λ,ζ),ϑɎ→(Λ,ζ)∈[0,2π] ∀,Λ,ζ∈Ŭ.
Definition 9: A CQROFDG →Ģ=(Ŭ,Ҳ,→Ɏ) in which Ҳ and Ɏ are CQROFS and CQROFR on Ŭ respectively such that:
and 0≤μɎq→(Λ,ζ)+νɎq→(Λ,ζ)≤1, θɎ→(Λ,ζ),ϑɎ→(Λ,ζ)∈[0,2π] ∀,Λ,ζ∈Ŭ,q∈Z+.
3.
Materials and methods
First of all, we define CQROF-out-neighborhood of the node, CQROF-in-neighborhood of the node, intersection of two CQROFSs, height and cardinality of CQROFS which will be biased for the further devolvement. After this, we will discuss CQROFCGs.
Definition 10: A CQROF out-neighbourhood of a nodes Λ of a CQROFDG →Ģ=(Ŭ,Ҳ,→Ɏ) is a CQROFS explained by:
That is Sq={ζ:μɎ→(Λ,ζ)>0orνɎ→(Λ,ζ)>0} s.t μq:Sq→[0,1] explained by μq(ζ)=μɎ→(Λ,ζ),φq:Sq→[0,2π] explained by φq(ζ)=θ Ɏ→(Λ,ζ),νq:Sq→[0,1] explained by νq(ζ)=νɎ→(Λ,ζ) and ψq:Sq→[0,2π] defined by ψq(ζ)=ϑɎ→(Λ,ζ).
Definition 11: A CQROF in-neighbourhood of a nodes Λ of a CQROFDG →Ģ=(Ŭ,Ҳ,→Ɏ) is a CQROFS explained by:
That is Sƞ={ζ,μɎ→(ζ,Λ)>0orνɎ→(ζ,Λ)>0} Such that μƞ:Sƞ→[0,1] explained by μƞ(ζ)=μɎ→(ζ,Λ),φƞ:Sƞ→[0,2π] explained by φƞ(ζ)=θɎ→(ζ,Λ),νƞ:Sƞ→[0,1] explained by νƞ(ζ)=νɎ→(ζ,Λ) and ψƞ:Sƞ→[0,2π] defined by ψƞ(ζ)=ϑɎ→(ζ,Λ).
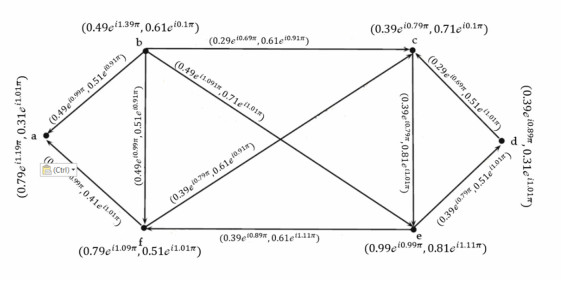
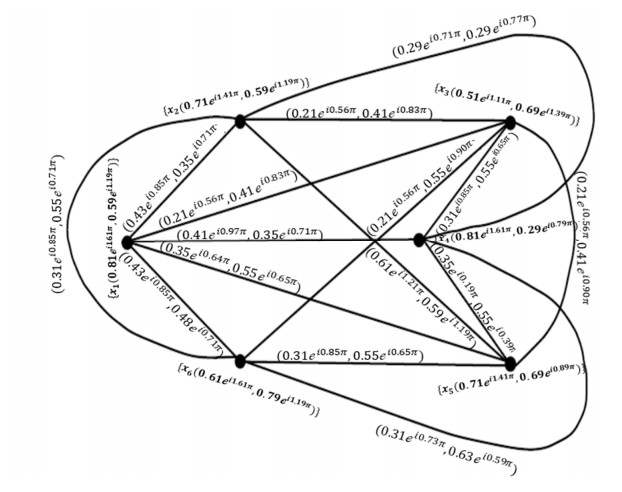
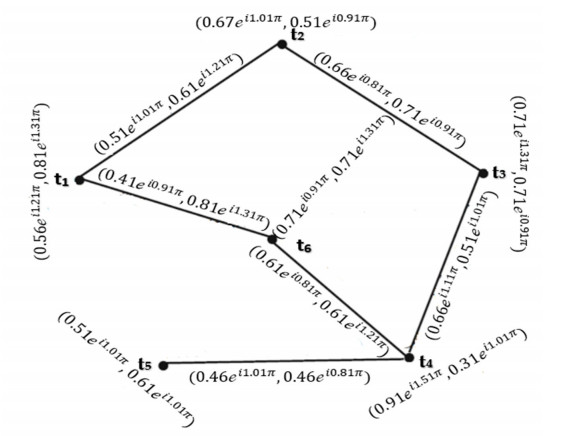
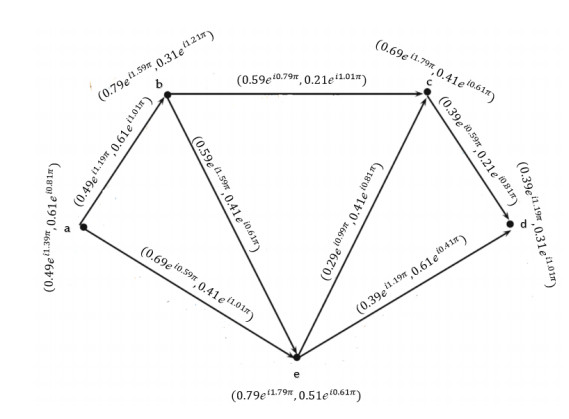
Example 1: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG for q=3 shown in following Figure 1.
Following Table 1 shows that CQROF out-neighborhood of the vertex and CQROF in-neighbourhood of the vertex.
Definition 12: Suppose that W1 and W2 are both CQROSs on Z that is:
W1∩W2, be the intersection of W1 and W2 of CQROF in the following specific way:
where:
Definition 13: Suppose that a CQROFS W={(t,μW(t)eiθW(t),νW(t)eiϑW(t):t∈Z)} and the cardinality of CQROFS W is represented by |W|=(|W|μei|W|θ,|W|νei|W|ϑ) is the sum of TG and FG value of objects of Z in the form of:
Definition 14: Suppose that a CQROFS W=(t,μW(t)eiθW(t),νW(t)eiϑW(t):t∈Z) and the height of CQROFS W is represented by ĥ(W)=(ĥμ(W)eiˆhθ(W),ĥν(W)eiˆhϑ(W)) is explained:
A (CQROFCG) is defined below.
Definition 15: Suppose that →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG. Then CQROFCG C(→Ģ) of a CQROFDG →Ģ is an undirected CQROFG Ģ=(Ŭ,Ҳ,Ɏ) in which set of nodes of C(→Ģ) is similar in →Ģ and a CQROF edge exists between two different vertices Λ,ζ∈Ҳ in C(→Ģ) iff the CQROFS Ξq(Λ)⋂Ξq(Λ)=∅ in →Ģ. The values of TG and FG of edges (Λ,ζ) in C(→Ģ) are explained in the form:
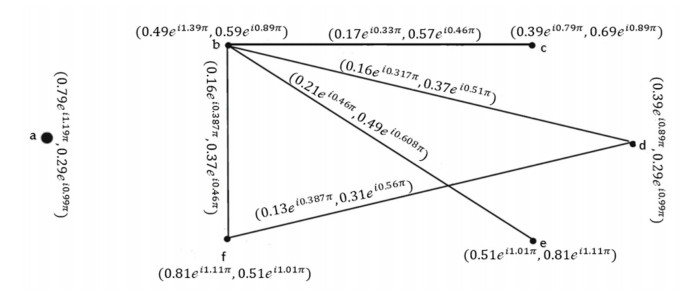
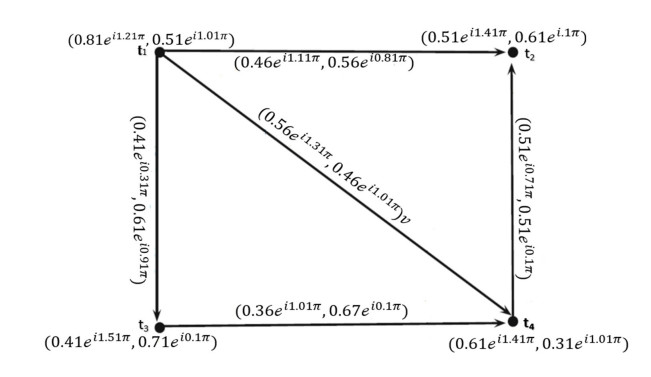
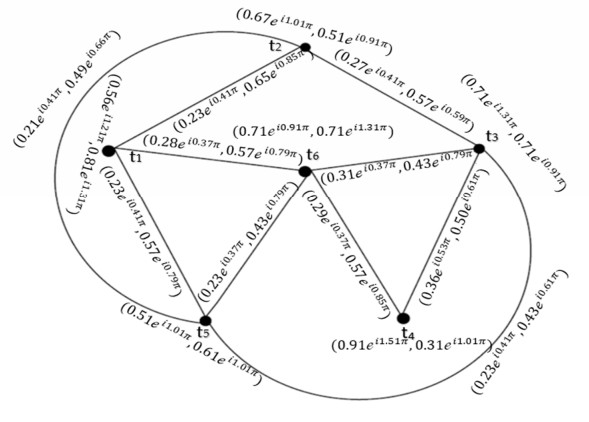
Example 2: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG for q=3 in the following Figure 2, explained as:
The CQROF out-neighbourhood of the vertices are shown in Table 2. The CQROFS Ξq(Λ)∩Ξq(ζ) and ˆh(Ξq(Λ)∩Ξq(ζ) evaluated in Table 3. We observe the edges b and c,b and f,b and a,b and f,b and e by using Table 3, which is an illustration of Figure 3 for the CQROFG.
Definition 16: Suppose that Ģ=(Ŭ,Ҳ,Ɏ) be a CQROFG. So, an edge (Λ,ζ) in a CQROFG be strong if it satisfies the following conditions:
∀,Λ,ζ∈Ŭ.
Theorem 1: Suppose that a CQROFDG →Ģ=(Ŭ,Ҳ,→Ɏ). A CQROFS having one element Ξq(Λ)∩Ξq(ζ) and the edge (Λ,ζ) of C(→Ģ) is strong if satisfy the following conditions:
Ⅰ. |Ξq(Λ)∩Ξq(ζ)|μ>12, and |Ξq(Λ)∩Ξq(ζ)|ν<12.
Ⅱ. |Ξq(Λ)∩Ξq(ζ)|θ>1π and |Ξq(Λ)∩Ξq(ζ)|ϑ<1π.
The proof of this Theorem 1, discussed in Appendix.
4.
Complex q-rung orthopair fuzzy k-competition graphs
In this section, we generalized the concept of (CQROFG) in the CQROF k-competition graph (CQROF k-competition graph) and a few results which are related to the following graphs.
Definition 17: Suppose that a complex number represented by k=aeiɣ and Ξq(Λ)∩Ξq(ζ)=(a′eiɣ′,b′eiη′). The CQROFKCG Ck(→Ģ) of →Ģ=(Ŭ,Ҳ,→Ɏ) is an undirected CQROFG Ģ=(Ŭ,Ҳ,Ɏ) i.e., CQRO the CQROF family of nodes is Ck(→Ģ) iff a′>a,ɣ′>ɣ for TG and b′>a,η′>ɣ for the FG. The TG and FG values of the edges (Λ,ζ) in Ck(→Ģ) in the following form:
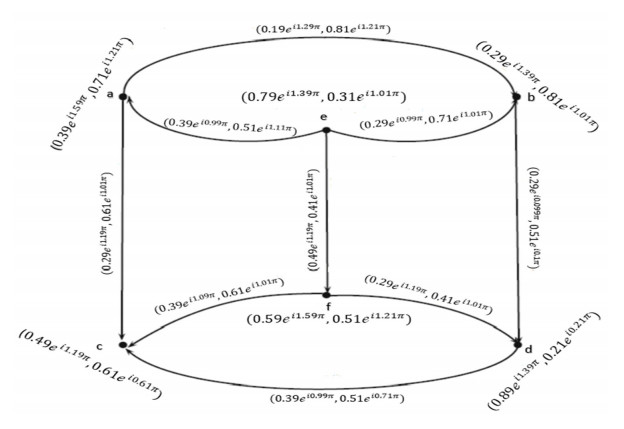
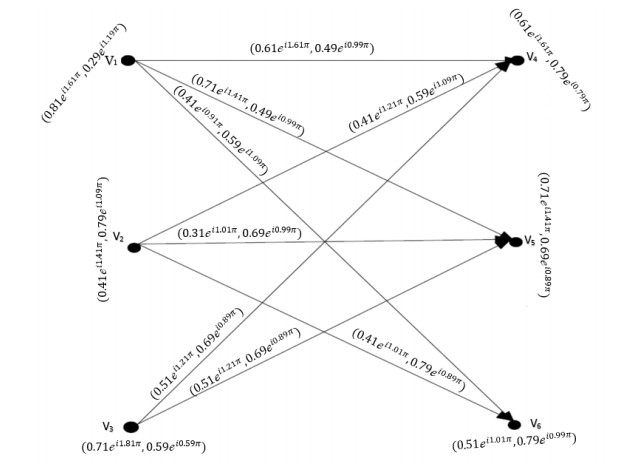
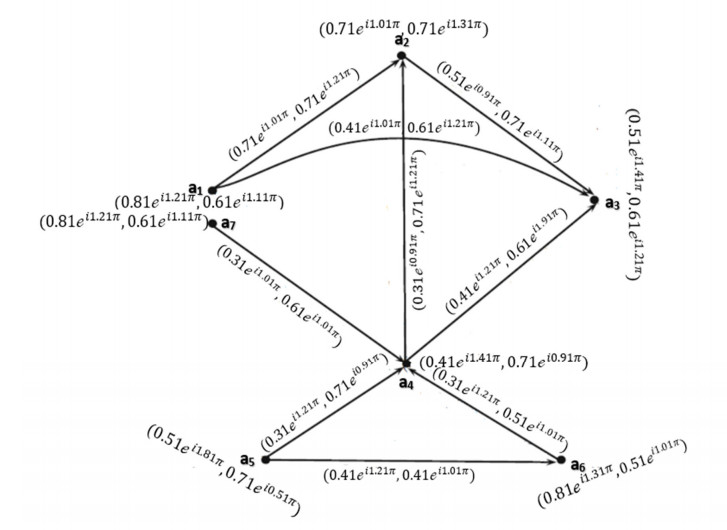
Example 3: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG for q=3 as in Figure 4 and explained as:
The CQROF out-neighbourhood of the nodes are shown in Table 4.
The CQROFSs Ξq(Λ)∩Ξq(ζ) and ˆh(Ξq(Λ)∩Ξq(ζ)) calculated in Table 5.
Let k=0.25ei0.70π then CQROFCG 0.25ei0.70π has edges.
The Complex q-rung orthopair fuzzy k=0.25ei0.70π-competition graph is displayed in Figure 5.
Theorem 2: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG. If ˆh(Ξq(Λ)∩Ξq(ζ))=(1ei2π,1ei2π) and a′>2a,ɣ′>2ɣ, b′<2a and η′<2ɣ. Then edges (Λ,ζ) is strong in Ck(→Ģ) such that:
The proof of this Theorem 2, discussed in Appendix.
5.
p-competition complex q-rung orthopair fuzzy graphs
Now we will increase the radius of CQROFCG and discussed it for p-competition of (CQROFPCG). Firstly, we will explain the support of CQROFS in the following form:
Definition 18: Considered that W={(t,μW(t)eiθW(t),νW(t)eiϑW(t):t∈Z)} be a CQROFS. So, support of CQROFS of W⊆Wo of Z.
Definition 19: Consider that →Ģ=(Ŭ,Ҳ,→Ɏ) a CQROFDG. The p- competition of CQROFG Cp(→Ģ) of the CQROFDG →Ģ is an undirected CQROFG Ģ=(Ŭ,Ҳ,Ɏ) that is the CQROF family of nodes Cp(→Ģ) is equal to →Ģ and CQROF edges exist between two different vertices (Λ,ζ)∈Ŭ in Cp→Ģ iff |supp(Ξq(Λ)∩Ξq(ζ))|≥p. The TG and FG values of the edges (Λ,ζ) are in the following form:
Since u=|Λupp(Ξq(Λ)∩Ξq(ζ))|.
Theorem 3: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG. If ˆh(Ξq(Λ)∩Ξq(ζ))=(1ei2π,0eiπ) in C|t|2(→Ģ) then the edges (Λ,ζ) is strong, in which t=|Λupp(Ξq(Λ)∩Ξq(ζ))|.
The proof of this Theorem 3, discussed in Appendix.
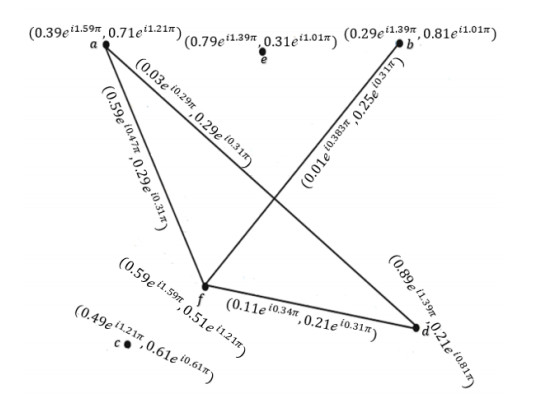
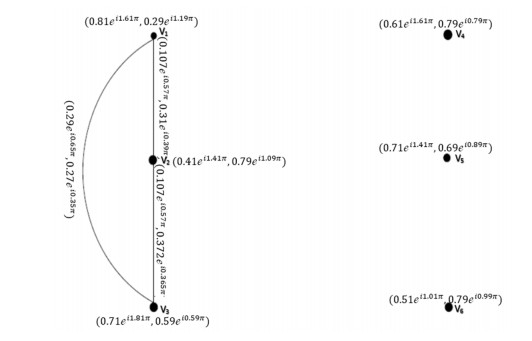
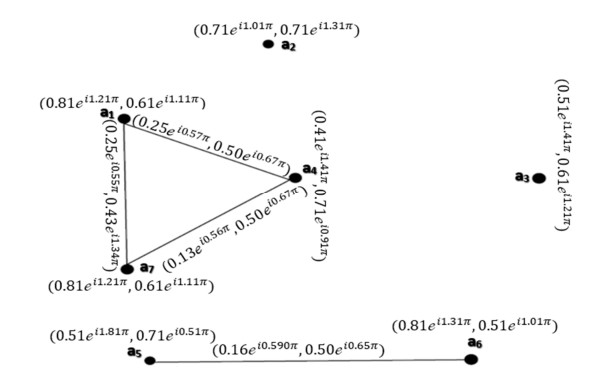
Example 4: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG for q=3 in the following Figure 6, explained as:
The CQROF out-neighbourhood of the nodes which are shown in Table 6. Table 7 shows that the height, support, and carnality of support of CQROFS (Ξq(Λ)∩Ξq(ζ)),∀Λ,ζ∈Ŭ. For p=2 the correspondence C2(Ģ) shown in Figure 7.
6.
Complex q-rung orthopair fuzzy neighborhood graphs
Now, will discuss the complex q- rung orthopair fuzzy open and close neighbourhood of nodes. After that CQROF open and close neighbourhood graph is explained in the following form:
Definition 20: CQROF open neighbourhood of a node v of a CQROFG Ģ=(Ŭ,Ҳ,Ɏ) is a CQROFS in the form:
where SΛ={ζ:μɎ(Λ,ζ)>0,orνɎ(Λ,ζ)>0}, Such that: tΛ:SΛ→[0,1] explain in the form tΛ(ζ)=μɎ(Λ,ζ),ϕΛ:SΛ→[0,2π] explain in the form ϕΛ(ζ)=θɎ(Λ,ζ),fΛ:SΛ→[0,1] explain by fΛ(ζ)=νɎ(Λ,ζ) and ωΛ:SΛ→[0,2π] explain by ωΛ=ϑɎ(Λ,ζ).
∀,Λ∈Ŭ. CQROF singleton set in the form:
Such that: μ′A:{Λ}→[0,1] explain in the form μ′A(Λ)=μA(Λ),θ′A:{Λ}→[0,2π] explain in the form θ′A(Λ)=θA,ν′A:{Λ}→[0,1] explain by ν′A(Λ)=νA(Λ) and ϑ′A:{Λ}→[0,2π] explain in the form ϑ′A(Λ)=ϑA(Λ). The complex fuzzy closed neighbourhood of a node Λ in the following form:
Definition 21: Consider that Ģ=(Ŭ,Ҳ,Ɏ) the CQROFG. The CQROFONG of Ģ is a CQROFG N(Ģ)=(Ŭ,Ҳ,D) in which family of nodes of CQROF is equal in Ģ and a CQROF edge exist between two different vertices Λ,ζ∈Ŭ in N(Ģ) iff the CQROFS Ξ(Λ)∩Ξ(ζ)≠∅ in Ģ. The TG and FG values of the edge (Λ,ζ) in NĢ in the following form:
Definition 22: Consider that Ģ=(Ŭ,Ҳ,Ɏ) the CQROFG. The CQROFCNG of Ģ is a CQROFG N[Ģ]=(Ŭ,Ҳ,D) in which family of nodes of CQROF is equal in Ģ and a CQROF edge exist between two different vertices Λ,ζ∈Ŭ in N[Ģ] iff the CQROFS Ξ[s]∩Ξ[w]≠∅ in Ģ. The TG and FG values of the edges (Λ,ζ) in N[Ģ] in the following form:
Theorem 4: Each edge of CQROFG Ģ in which there exists just one edge in N[Ģ].
The proof of this Theorem 4, discussed in Appendix.
Example 5: Consider Ģ=(Ŭ,Ҳ,Ɏ) be a CQROFG for q=3 in the following Figure 8, explained as:
Table 8 contains the family of open and close vertex of CQROF. Table 9 contained the CQROFS (Ξ(Λ)∩Ξ(ζ)) and ˆh(Ξ(Λ)∩Ξ(ζ)),∀Λ,ζ∈Ŭ and Figure 9 illustrates CQROFONG. Table 10 contains the CQROFS (Ξ[Λ]∩Ξ[ζ]) and ˆh(Ξ[Λ]∩Ξ[ζ]),∀Λ,ζ∈Ŭ and Figure 10 show the CQROFCNG.
7.
m-step complex q-rung orthopair fuzzy fompetition graphs
If prey is assailed by the predator c then the association between them can be represented by an edge →(c,d) in a CQROFDG. But if the predator needs the support of numerous mediators (c1,c2,c3,…,cm−1) then the connection among them is represented by CQROFDP →Pm(c,d) in a CQROFDG. In this segment, first, we define the m-step (CQROFDG). So, we explain CQROF m- step out-neighbourhood CQROF m-step in- neighbourhood of the nodes and m-step (CQROFCG).
Definition 23: Consider that →Ģ=(Ŭ,Ҳ,→Ɏ) the CQROFDG. The m- step CQROFDG of →Ģ is represented by →Ģm=(Ŭ,Ҳ,→Ɏ) which has an equal family of nodes →Ģm of CQROF and a CQROF edges among two different vertices Λ and ζ in →Ģm if there happen a CQROF directed path (CQROFDP) of interval m from Λ to ζ so →Pm(Λ,ζ) in →Ģ.
Definition 24: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be CQROFDG. The CQROFDG (m-step out neighbourhood) of a node Λ of a CQROFDG →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFS:
Such that: {SqΛ=ζ:∃ is a CQROFDP of distance m from Λ to ζ →Pm(Λ,ζ)}.
So, tqΛ:SqΛ→[0,1] explain in the form tqΛ(ζ)={minμҲ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ),ϕqΛ:SqΛ→[0,2π]} explain in the form ϕqΛ(ζ)={minθҲ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ)} fqΛ:SqΛ→[0,1] explain fqΛ(ζ)={maxυҲ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ),ωqΛ:SqΛ→[0,2π]} explain in the form ωqΛ(ζ)={maxϑҲ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ)}.
Definition 25: Consider that →Ģ=(Ŭ,Ҳ,→Ɏ) be CQROFDG. Then CQROF m-step in- neighbourhood of a node Λ of a CQROFDG →Ģ=(Ŭ,Ҳ,→Ɏ) is CQROFS:
Such that: SnΛ=ζ:∃ is a CQROFDP of length m from ζ to Λ →Pm(ζ,s).
So, tnΛ:SnΛ→[0,1] explain in the form tnΛ(ζ)={minμ Ҳ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ),ϕnΛ:SnΛ→[0,2π]} explain in the form ϕnΛ(ζ)={minθ Ҳ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ)} fnΛ:SnΛ→[0,1] explain fnΛ(ζ)={maxυ Ҳ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ)} and ωnΛ(ζ):SnΛ→[0,2π] explain in the form ωnΛ(ζ)={maxϑ Ҳ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ)}.
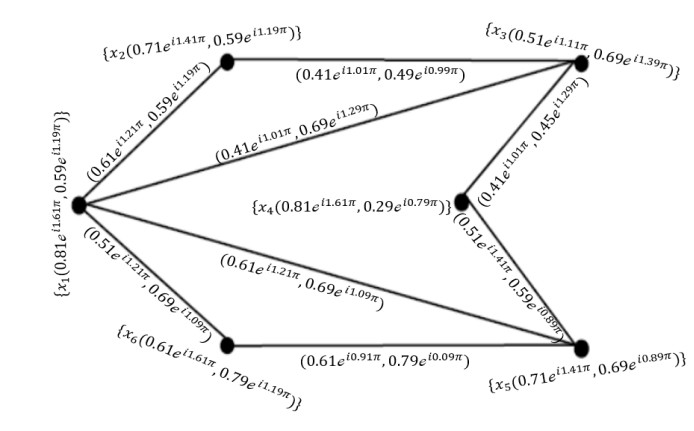
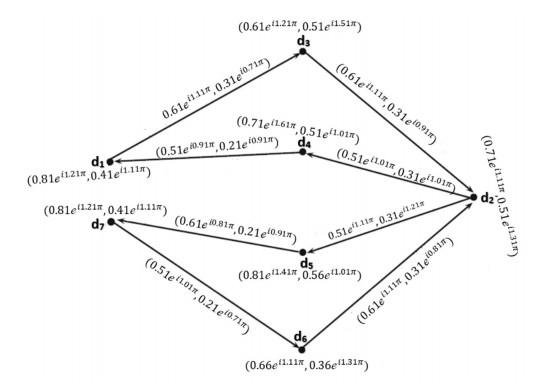
Example 6: Suppose →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG for q=3 in Figure 11, explained as:
Table 11 shows that out and in the neighbourhood of the nodes of CQROF.
Definition 26: Consider that →Ģ=(Ŭ,Ҳ,→Ɏ) be CQROFDG. Then m-step CQROFCG of Ģ is represented by Cm(→Ģ)=(Ŭ,Ҳ,D) i.e., The CQROF family of nodes of Cm(→Ģ) equal to →Ģ and a CQROF edge exists between two different vertices Λ and ζ in Cm(→Ģ) iff (Ξmq(Λ)∩Ξmq(ζ)≠0 in CQROFDG. The TG and FG values of (Λ,ζ) in the following form:
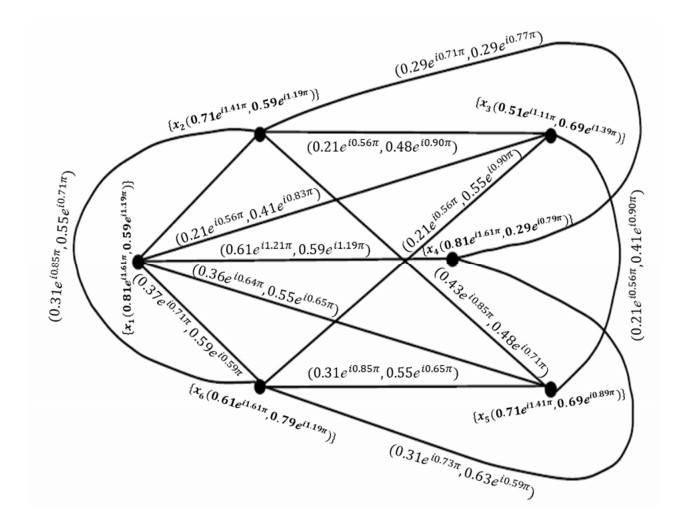
Example 7: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG for q=3 in the following Figure 12, explained as:
Table 12 contains the family of out- neighbourhood of nodes of CQROF 2-step.
Now
and
Therefore
and
By using this draw Figure 13. for 2-step CQROFCG.
Theorem 5: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be CQROFDG and if m>|Ŭ| then family of the edge of Cm(→Ģ) is empty.
The proof of this Theorem 5, discussed in Appendix.
Definition 27: Consider that Ģ=(Ŭ,Ҳ,Ɏ) be CQROFG. Then CQROF m-step neighbourhood of nodes Λ of a CQROFG Ģ=(Ŭ,Ҳ,Ɏ) is CQROFS:
Such that: SΛ=ζ:∃ is a CQROFDP of interval m from Λ to ζ →Pm(Λ,ζ).
So, tΛ:SΛ→[0,1] explain in the form tΛ(ζ)={minμҲ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ),ϕΛ:SΛ→[0,2π]} explain in the form ϕΛ(ζ)={minθҲ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ)} fΛ:SΛ→[0,1] explain fΛ(ζ)={maxυҲ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ),ωΛ:SΛ→[0,2π]} explain in the form of ωΛ(ζ)={maxϑҲ(d,g),(d,g)iΛanedgeof→Pm(Λ,ζ)}.
Definition 28: Consider that Ģ=(Ŭ,Ҳ,Ɏ) be CQROFG. Then m-step CQROFNG of Ģ is represented by Nm(Ģ)=(Ŭ,Ҳ,D) i.e., The CQROF family of nodes of Nm(Ģ) is equal to Ģ and a CQROF edge exist between two different nodes Λ and ζ in Nm(Ģ) iff (Ξm(Λ)∩Ξm(ζ)≠0 in CQROFG. We calculate the TG and FG values of the edges (Λ,ζ) in the following way:
Example 8: Consider Ģ=(Ŭ,Ҳ,Ɏ) be a CQROFG for q=3 in the following Figure 14, explained as:
The CQROF 2-step neighbourhood of the family of nodes which are shown in Table 13. The CQROFS (Ξ2(Λ)∩Ξ2(ζ)) and ˆh(Ξ2(Λ)∩Ξ2(ζ)) are shown in Table 14 and their graphical representation is shown in Figure 15.
Definition 29: Consider that →Ģ=(Ŭ,Ҳ,→Ɏ) be CQROFDG. Suppose that joint node of m-step out- neighbourhoods of nodes t1,t2,t3,…,tn∈r.
Consider μҲ→(q1,ζ1)eiθҲ→(q1,ζ1),μҲ→(q2,ζ2)eiθҲ→(q2,ζ2),μҲ→(q3,ζ3)eiθҲ→(q3,ζ3),…,μҲ→(qn,ζn)eiθҲ→(qn,ζn) show the lower TG values of the edge of a path →Pm(t1,r),→Pm(t2,r),→Pm(t3,r),…,→Pm(tn,r) and νҲ→(q1,ζ1)eiϑҲ→(q1,ζ1),νҲ→(q2,ζ2)eiϑҲ→(q2,ζ2),νҲ→(q3,ζ3)eiϑҲ→(q3,ζ3),…,νҲ→(qn,ζn)eiϑҲ→(qn,ζn) show that the high TG values of the edge of a path →Pm(t1,r),→Pm(t2,r),→Pm(t3,r),…,→Pm(tn,r) respectively.
The m-step nodes r∈Ŭ is heavy if μҲ→(qk,ζk)>12 and θҲ→(q2,ζ2)>1π for TG and νҲ→(qk,ζk)<12 and ϑҲ→(q2,ζ2)<1π for FG values ∀,k=1,2,3,…,n. (SŢ(r),SF(r)), represent the strength of prey r, s.t SŢ(r):Ŭ→{y:y∈C:|y|≤1} and SF(r):Ŭ→{y′:y′∈C:|y′|≤1} in the following form:
Example 9: Consider →Ģ=(Ŭ,Ҳ,→Ɏ) be a CQROFDG for q=3 as shown in Figure 16 and explained as:
Now we discuss the strength of the node d2 from Figure 16.
So, the node d2 is heavy for 2- steps if 0.56>12 and 1.06>1π for TG and 0.31<12 and 0.86<1π for FG values.
Theorem 6: If all the nodes in CQROFDG →Ģ are heavy. Then in Cm(→Ģ):
Ⅰ. μD(Λ,ζ)>12(μҲ(Λ)∧μҲ(ζ)) and θD(Λ,ζ)>12(θҲ(Λ)∧θҲ(ζ))
Ⅱ. νD(Λ,ζ)<12(νҲ(Λ)∨νҲ(ζ)) and ϑD(Λ,ζ)<12(ϑҲ(Λ)∨ϑҲ(ζ))
The proof of this Theorem 6, discussed in Appendix.
Theorem 7: Let r be the strong node of →Ģ then in strength of r:
Ⅰ. ∑nk=1μҲ→(qk,ζk)n>12, and ∑nk=1νҲ→(q3,ζ3)n>1π, ∀,Ţ,F,ϵ(r)
Ⅱ. ∑nk=1θҲ→(q3,ζ3)n<12 and ∑nk=1ϑҲ→(q3,ζ3)n<1π, ∀,Ţ,F,ϵ(r)
The proof of this Theorem 7, discussed in Appendix.
8.
Application
The FCGs have become considerable as they may be relevant to many regions in which there may be competition between different real global units. However, there are some competitions of actual international which can't be characterized through those graphs.
To characterize all the competitions, we endorse CPyFCGs that have the higher capability to show all of the competitions of real global. To fully appreciate the idea of CQROFCGs. We construct claim of competition graphs of CQROF surroundings with an algorithm underneath.
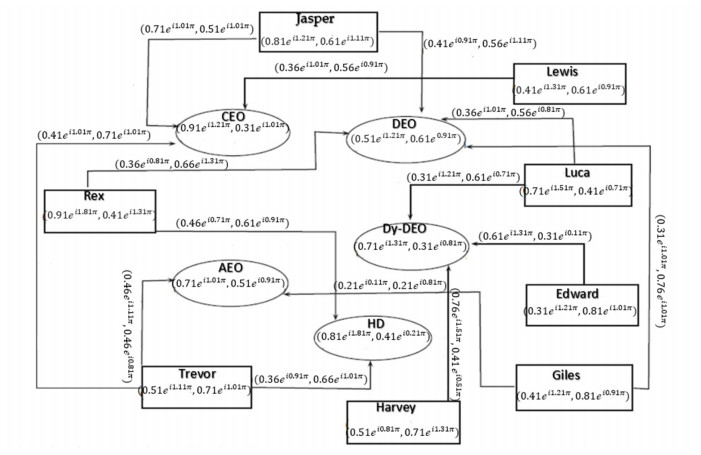
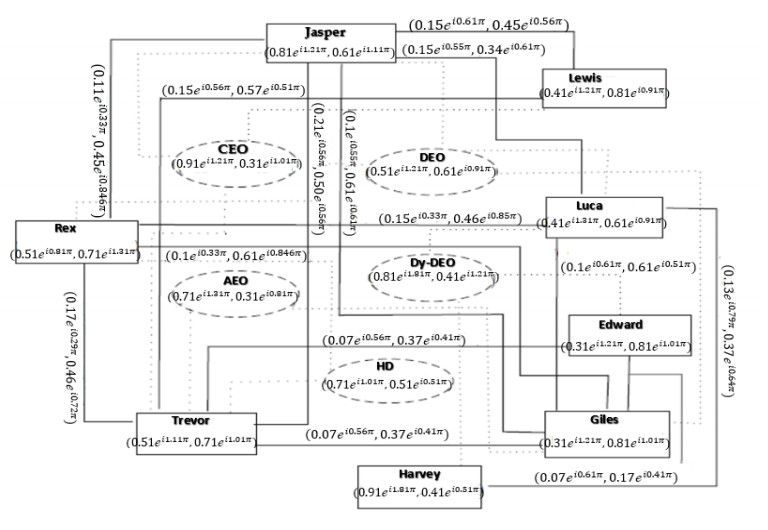
Now we explain through an example consider that eight candidates competing for designations in public institute School education department. Suppose that family of employees {Jasper, Lewis, Luca, Rex, Trevor, Edward, Giles, Harvey} and post filled according to a few certain designations in the education department {CEO, DEO, Dy-DEO, AEO, HD}. The real part of the TG and FG values of each person shows the value of honesty and dishonesty according to his designation. The imaginary part of the TG and FG values of each employee shows the value of satisfying and being unsatisfied with the work assigned from the higher authority and fulfilling their goals. In the same way, the TG and FG values for each post show the value of how much designation is appropriate and inappropriate for the employee. The imaginary part of the TG and FG values for each post shows the value for available and unavailable. So, the TG and FG values for employee and designation are shown in the following Table 15.
The real part of the TG function of each direct edge between employee and designation shows the verified and un-verified degrees of the employee for a certain post. In the same way, the imaginary part of the TG and FG of each direct edge between employee and designation shows the values of experience of his previous work and unexperienced having no past work according to his present post. The CQROFDG is shown in Figure 17. In this figure, we take employees and their designation as nodes and the relation between them show as a direct edge which is seen in Figure 17 and the CQROF out- neighbourhood of the nodes shown in Table 16. CQROFSs ( Ŋq(s)∩ Ŋq(w)) and h(( Ŋq(s)∩ Ŋq(w)) are shown in Table 17.
Figure 18 shows two sets of dotted and solid lines. Solid lines represent the competition between the person who has applied for a particular post and dotted lines represent competition between candidates and a particular post. We observe from the previous Figure in which seen that competition of 5-persons with Jasper, namely, Rex, Lewis, Trevor, Luca, and Giles. In the same way, competition four candidates have with Rex, namely, Trevor, Luca, Giles and Jasper, and Lewis having a competition with Trevor. Similarly, competition has between Trevor and Edward, Trevor and Giles, Harvey and Luca, Harvey and Giles, Luca and Giles and the last one are Edward with Giles. For this, we use Table 18. For explaining our application.
9.
Comparative analysis
Competition graphs are more effective in the field of competition in which different objects are compared with the different real-world objects. Sahoo and Pal [38] utilized the concepts of CG in the framework of intuitionistic fuzzy sets (IFSs). But some competitions have two-dimensional or periodic information for the objects. In 2019, Habib et al. [33] proposed work on QROFCGs which discuss how we deal with the uncertain and incomplete information about the nodes and edges. After this Akram et al. [47] worked on CG in the environment of complex PyF (CPyF) information. All previously existing research works have a large ability to deal with uncertain and vague information of a graph. To increase the ability to deal with uncertain data of graphs, we used the CG under the CQROF information and its several numerical examples in different fields of life. We also discussed an application of CQROFSs under CGs with the help of numerical example for q = 3 . Suppose that a family of employees {Jasper, Lewis, Luca, Rex, Trevor, Edward, Giles, Harvey} competing for a few certain designations in the public education department {CEO, DEO, Dy-DEO, AEO, HD}. Consider TG and FG of candidates denote the value of loyalty and disloyalty of candidates for particular designations while the TG and FG of designations show the availability and non-availability of designations. A lot of public and private offices may change our selection policy to fulfil their vacant posts based on experience according to the designations. So, the given information about the candidates and designations is not enough. In the same way, candidates are unable to know by using the given information that how much the job is suitable. We utilized a new model of CQROFCG to deal with two-dimensional data. CQROFCGs have larger potential and play an important role to deal with two-dimensional information. The capability of these graphs for addressing two-dimensional phenomena makes it better than handling vague and uncertain data. Finally, the statistical comparison of the invented work is described in the shape of Table 19.
In Table 19, the notation \surd , is used for hold and the symbol \times , is used for not holding. From the above table, it is clear that the suggested work based on CQROFG is more powerful than the existing approaches.
10.
Conclusions
This manuscript aims summarized below:
1) We analyzed the well-known and massive idea of CG in the presence of a new and dominant technique of CQROF setting. The mathematical from of CQROF setting is more flexible and massive consistent for demonstrating the beneficial option form the collection of objectives during decision-making process.
2) The major concept of in-neighbourhood and out-neighbourhood using CQROFDG are also invented to enhance the quality of the diagnosed approach.
3) The fundamental theory of CQROF k-competition, CQROF p-competition, CQROF neighbourhood and m-step CQROF neighbourhood graphs are also explored.
4) In the availability of the above-described theories, the basic and significant results for presented work are obtained to show the compatibility and worth of the invented approaches. To show the practicality of the developed approach, we try to verify the proposed work with the help of various examples.
5) We described the validity and practicality of the invented work; we diagnosed an application using presented approaches based on CQROF setting is to enhance the major weakness of the existing approaches. Finally, in the availability of the invented ideas, we discussed the sensitivity analysis of the described approaches.
10.1. Limitations of the proposed works
In the presence of various issues occurred in genuine life troubles, some limitations of the invented approaches are described below.
1) When expert suggested information \left(0.4{\mathcal{e}}^{i2\pi \left(0.3\right)}, 0.3{\mathcal{e}}^{i2\pi \left(0.2\right)}, 0.2{\mathcal{e}}^{i2\pi \left(0.1\right)}\right) for support, abstinence, and support against, then the scenario of CQROFG has been unreliable, for this, we have required to investigate the complex picture fuzzy graph.
2) When expert suggested information \left(0.6{\mathcal{e}}^{i2\pi \left(0.3\right)}, 0.5{\mathcal{e}}^{i2\pi \left(0.7\right)}, 0.2{\mathcal{e}}^{i2\pi \left(0.1\right)}\right) for support, abstinence, and support against, then the scenario of CQROFG has been unreliable, for this, we have required to investigate the complex spherical fuzzy graph.
3) When expert suggested information \left(0.9{\mathcal{e}}^{i2\pi \left(0.8\right)}, 0.8{\mathcal{e}}^{i2\pi \left(0.7\right)}, 0.7{\mathcal{e}}^{i2\pi \left(0.6\right)}\right) for support, abstinence, and support against, then the scenario of CQROFG has been unreliable, for this, we have required to investigate the complex T-spherical fuzzy graph.
10.2. Future works
In future we will extend our proposed in the environment of complex picture fuzzy graphs [49] and generalized our proposed work in the framework of interval valued fuzzy graph, neutrosophic graph [50] and decision-making techniques [51,52,53].
Acknowledgement
This research was supported by the Researchers Supporting Project number (RSP2022R476), King Saud University, Riyadh, Saudi Arabia. Data Availability: The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of interest
The authors declare no conflict of interest.
Appendix
Proof of Theorem 1: Since \overrightarrow{\mathrm{Ģ}} = \left(Ŭ, Ҳ, \overrightarrow{Ɏ}\right) be a CQROFDG. Let {{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right) = \left(c, r{e}^{i\alpha }, ş{e}^{i\beta }\right) i.e., r{e}^{i\alpha } and ş{e}^{i\beta } are TG and FG values ({\mathit{\Lambda}}, c) or (\zeta, c) . So {\widehat {\rm{h}}}({{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right) = \left(r{e}^{i\alpha }, {\mathit{\Lambda}} {e}^{i\beta }\right) = {{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right) .
So:
By using the previous definition 16. The TG and FG values of the edges \left({\mathit{\Lambda}}, \zeta \right) in CQROFCG in the following form:
So, \left({\mathit{\Lambda}}, \zeta \right) is a strong edge if satisfy \zeta > \frac{1}{2}, ş < \frac{1}{2}, \alpha > \pi and \beta < \pi .
Proof of Theorem 2: Suppose that \overrightarrow{\mathrm{Ģ}} = \left(Ŭ, Ҳ, \overrightarrow{Ɏ}\right) be a CQROFDG. Consider {\mathbb{C}}_{k}\left(\overrightarrow{\mathrm{Ģ}}\right) be the correlative k- competition graph. By the given condition if {{\widehat {\rm{h}}}}_{\mu }\left({{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right)\right) = 1 for real terms and {{\widehat {\rm{h}}}}_{\theta }\left({{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right)\right) = 2\pi for the imaginary terms of the TG values. Now if we see definition 17, then TG values of the edge \left({\mathit{\Lambda}}, \zeta \right) in correspondence CQROFKCG {\mathbb{C}}_{k}\left(\overrightarrow{\mathrm{Ģ}}\right) .
So, {\mu }_{Ɏ}\left({\mathit{\Lambda}}, \zeta \right) > \frac{1}{2}\left[2\pi \left({\mu }_{Ҳ}\left({\mathit{\Lambda}} \right)\wedge {\mu }_{Ҳ}\left(\zeta \right)\right)\right] as \frac{{a}^{'}-a}{{a}^{'}} > \frac{1}{2} and {\theta }_{Ɏ}\left({\mathit{\Lambda}}, \zeta \right) > \frac{1}{2}\left[2\pi \left({\theta }_{Ҳ}\left({\mathit{\Lambda}} \right)\wedge {\theta }_{Ҳ}\left(\zeta \right)\right)\right] as \frac{{ɣ}^{'}-ɣ}{{ɣ}^{'}} > \frac{1}{2} .
Similarly, if {{\widehat {\rm{h}}}}_{\nu }\left({{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right)\right) = 1 for real terms and {{\widehat {\rm{h}}}}_{\vartheta }\left({{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right)\right) = 2\pi for the imaginary terms of the TG values. Now if we see the definition 17, then TG values of the edge \left({\mathit{\Lambda}}, \zeta \right) in correspondence CQROFKCG {\mathbb{C}}_{k}\left(\overrightarrow{\mathrm{Ģ}}\right) .
So, {\nu }_{Ɏ}\left({\mathit{\Lambda}}, \zeta \right) < \frac{1}{2}\left({\nu }_{Ҳ}\left({\mathit{\Lambda}} \right)\vee {\nu }_{Ҳ}\left(\zeta \right)\right) as \frac{{b}^{'}-a}{{b}^{'}} < \frac{1}{2} and {\vartheta }_{Ɏ}\left({\mathit{\Lambda}}, \zeta \right) < \frac{1}{2}\left({\vartheta }_{Ҳ}\left({\mathit{\Lambda}} \right)\vee {\vartheta }_{Ҳ}\left(\zeta \right)\right) as \frac{{\eta }^{'}-ɣ}{{\eta }^{'}} < \frac{1}{2} .
Since the edges ({\mathit{\Lambda}}, \zeta) is strong
Proof of Theorem 3: Suppose that \overrightarrow{\mathrm{Ģ}} = \left(Ŭ, Ҳ, \overrightarrow{Ɏ}\right) be a CQROFDG and \mathrm{Ģ} = \left(Ŭ, Ҳ, Ɏ\right) be the corresponding \frac{\left|t\right|}{2} -competition CQROFG. By the given if {{\widehat {\rm{h}}}}_{\mu }\left({{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right)\right) = 1 and {{\widehat {\rm{h}}}}_{\theta }\left({{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right)\right) = 2\pi in {\mathbb{C}}^{\frac{\left|t\right|}{2}}\left(\overrightarrow{\mathrm{Ģ}}\right) then the TG values of the edge \left({\mathit{\Lambda}}, \zeta \right) in {\mathbb{C}}^{\frac{\left|t\right|}{2}}\left(\overrightarrow{\mathrm{Ģ}}\right) in the following form:
So {\mu }_{Ɏ}\left({\mathit{\Lambda}}, \zeta \right) > \frac{1}{2}\left({\mu }_{Ҳ}\left({\mathit{\Lambda}} \right)\wedge {\mu }_{Ҳ}\left(\zeta \right)\right) , {\theta }_{Ɏ}\left({\mathit{\Lambda}}, \zeta \right) > \frac{1}{2}\left[2\pi \left(\frac{{\theta }_{Ҳ}\left({\mathit{\Lambda}} \right)}{2\pi }\wedge \frac{{\theta }_{Ҳ}\left(\zeta \right)}{2\pi }\right)\right] and \frac{\left(u-p\right)+1}{u} > \frac{1}{2} . In the same way if {{\widehat {\rm{h}}}}_{\nu }\left({{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right)\right) = 0 and {{\widehat {\rm{h}}}}_{\vartheta }({{\mathit{\Xi}} }^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{\mathit{\Xi}} }^{\mathfrak{q}}\left(\zeta \right) = 0 in in {\mathbb{C}}^{\frac{\left|t\right|}{2}}\left(\overrightarrow{\mathrm{Ģ}}\right) then FG values of the edge \left({\mathit{\Lambda}}, \zeta \right) in {\mathbb{C}}^{\frac{\left|t\right|}{2}}\left(\overrightarrow{\mathrm{Ģ}}\right) in the following form:
{\nu }_{Ɏ}\left({\mathit{\Lambda}}, \zeta \right) < \frac{1}{2}\left[{\nu }_{Ҳ}\left({\mathit{\Lambda}} \right)\vee {\nu }_{Ҳ}\left(\zeta \right)\right] and {\vartheta }_{Ɏ}\left({\mathit{\Lambda}}, \zeta \right) < \frac{1}{2}\left[2\pi \left(\frac{{\vartheta }_{Ҳ}\left({\mathit{\Lambda}} \right)}{2\pi }\vee \frac{{\vartheta }_{Ҳ}\left(\zeta \right)}{2\pi }\right)\right], 0 < \frac{1}{2} .
Proof of Theorem 4: Consider that \mathrm{Ģ} = \left(Ŭ, Ҳ, Ɏ\right) the CQROFG and \mathbb{N}\left[\mathbb{Ģ}\right] = \left(\mathbb{Ŭ}, \mathbb{Ҳ}, \mathbb{Ɏ}\mathbb{'}\right) be the CQROFCNG. Suppose \left({\mathit{\Lambda}}, \zeta \right) be an edge of CQROFG \mathrm{Ģ} . Then {\mathit{\Lambda}}, \zeta \in {\mathit{\Xi}} \left[{\mathit{\Lambda}} \right] and {\mathit{\Lambda}}, \zeta \in {\mathit{\Xi}} \left[\mathrm{\zeta }\right] . Thus {\mathit{\Lambda}}, \zeta \in {\mathit{\Xi}} \left[{\mathit{\Lambda}} \right]\cap {\mathit{\Xi}} \left[\mathrm{\zeta }\right] . So, {{\widehat {\rm{h}}}}_{\mu }\left({\mathit{\Xi}} \left[\mathrm{s}\right]\cap {\mathit{\Xi}} \left[\mathrm{\zeta }\right]\right)\ne 0 and {{\widehat {\rm{h}}}}_{\theta }\left({\mathit{\Xi}} \left[\mathrm{s}\right]\cap {\mathit{\Xi}} \left[\mathrm{\zeta }\right]\right)\ne 0 . By using the definition 22, the TG value of the edges \left({\mathit{\Lambda}}, \zeta \right) in \mathbb{N}\left[\mathbb{Ģ}\right] in the following form:
In the same way {{\widehat {\rm{h}}}}_{\nu }\left({\mathit{\Xi}} \left[{\mathit{\Lambda}} \right]\cap {\mathit{\Xi}} \left[\mathrm{\zeta }\right]\right)\ne 0 and {{\widehat {\rm{h}}}}_{\vartheta }\left({\mathit{\Xi}} \left[{\mathit{\Lambda}} \right]\cap {\mathit{\Xi}} \left[\mathrm{\zeta }\right]\right)\ne 0 for the height of FG value of functions:
So, \forall, \left({\mathit{\Lambda}}, \zeta \right) in \mathrm{Ģ} therefore an edge \left({\mathit{\Lambda}}, \zeta \right) in \mathbb{N}\left[\mathbb{Ģ}\right] .
Proof of Theorem 5: Consider \overrightarrow{\mathbb{Ģ}} = \left(\mathbb{Ŭ}, \mathbb{Ҳ}, \overrightarrow{\mathbb{Ɏ}}\right) be CQROFDG and {\mathbb{C}}_{\mathrm{m}}\left(\overrightarrow{\mathrm{Ģ}}\right) = \left(Ŭ, Ҳ, D\right) be the corresponding m-step CQROFCG. By using definition 26, the TG and FG grades of the edge \left({\mathit{\Lambda}}, \zeta \right) in {\mathbb{C}}_{\mathrm{m}}\left(\overrightarrow{\mathrm{Ģ}}\right) form as:
\forall, ({\mathit{\Lambda}}, \zeta)\in Ŭ . If the \mathcal{m} > \left|\mathcal{Ŭ}\right| then there does not exist any CQROFDP of interval \mathcal{m} in \overrightarrow{\mathcal{Ģ}} . So the CQROFS \left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) = \varnothing . Therefore, {\mu }_{D}\left({\mathit{\Lambda}}, \zeta \right) = 0 , {\theta }_{Ɏ}\left({\mathit{\Lambda}}, \zeta \right) = 0 for the TG value and {\nu }_{D}\left({\mathit{\Lambda}}, \zeta \right) = 0, {\vartheta }_{D}\left({\mathit{\Lambda}}, \zeta \right) = 0 for the FG value. So {\mathbb{C}}_{\mathrm{m}}\left(\overrightarrow{\mathrm{Ģ}}\right) having without edge.
Proof of Theorem 6: Consider that \overrightarrow{\mathrm{Ģ}} = \left(Ŭ, Ҳ, \overrightarrow{Ɏ}\right) be CQROFDG and let all vertices of \overrightarrow{\mathrm{Ģ}} be the strong and {\mathbb{C}}_{\mathrm{m}}\left(\overrightarrow{\mathrm{Ģ}}\right) = \left(Ŭ, Ҳ, D\right) be the corresponding m-step CQROFCG. We explain it in two different steps.
Step 1: Consider \left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right)\ne 0 So that having no edge between two {\mathit{\Lambda}} and \zeta in {\mathbb{C}}_{\mathrm{m}}\left(\overrightarrow{\mathrm{Ģ}}\right) .
Step 2: Let a non-empty set \left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) . All the nodes are strong if there is {{\widehat {\rm{h}}}}_{\mu }\left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) > \frac{1}{2} and {{\widehat {\rm{h}}}}_{\theta }\left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) > \frac{1}{2} . So, the TG values of the edges ({\mathit{\Lambda}}, \zeta) in {\mathbb{C}}_{\mathrm{m}}\left(\overrightarrow{\mathrm{Ģ}}\right) in the following form:
So, {\mu }_{D}\left({\mathit{\Lambda}}, \zeta \right) > \frac{1}{2}\left({\mu }_{Ҳ}\left({\mathit{\Lambda}} \right)\wedge {\mu }_{Ҳ}\left(\zeta \right)\right) and {\theta }_{D}\left({\mathit{\Lambda}}, \zeta \right) > \frac{1}{2}\left[2\pi \left(\frac{{\theta }_{Ҳ}\left({\mathit{\Lambda}} \right)}{2\pi }\wedge \frac{{\theta }_{Ҳ}\left(\zeta \right)}{2\pi }\right)\right] as {{\widehat {\rm{h}}}}_{\mu }\left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) > \frac{1}{2} and {{\widehat {\rm{h}}}}_{\theta }\left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) > \frac{1}{2} . In the same way {{\widehat {\rm{h}}}}_{\nu }\left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) < \frac{1}{2} and {{\widehat {\rm{h}}}}_{\vartheta }\left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) < \frac{1}{2} . Therefore, FG values of the edge ({\mathit{\Lambda}}, \zeta) in the following form:
So, {\nu }_{D}\left({\mathit{\Lambda}}, \zeta \right) < \frac{1}{2}\left({\nu }_{Ҳ}\left({\mathit{\Lambda}} \right)\vee {\nu }_{Ҳ}\left(\zeta \right)\right) and {\vartheta }_{D}\left({\mathit{\Lambda}}, \zeta \right) < \frac{1}{2}\left[2\pi \left(\frac{{\vartheta }_{Ҳ}\left({\mathit{\Lambda}} \right)}{2\pi }\vee \frac{{\vartheta }_{Ҳ}\left(\zeta \right)}{2\pi }\right)\right] as {{\widehat {\rm{h}}}}_{\vartheta }\left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) < \frac{1}{2} and {{\widehat {\rm{h}}}}_{\vartheta }\left({{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left({\mathit{\Lambda}} \right)\cap {{{\mathit{\Xi}} }_{\mathcal{m}}}^{\mathfrak{q}}\left(\zeta \right)\right) < \frac{1}{2} .
Proof of Theorem 7: Consider that \overrightarrow{\mathrm{Ģ}} = \left(Ŭ, Ҳ, \overrightarrow{Ɏ}\right) be CQROFDG. Suppose that joint node of m-step out- neighbourhood of nodes {t}_{1}, {t}_{2}, {t}_{3}, \dots, {t}_{n}\in r .
Consider {\mu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{1}, {\mathrm{\zeta }}_{1}\right)}{e}^{i{\theta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{1}, {\mathrm{\zeta }}_{1}\right)}}, {\mu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{2}, {\mathrm{\zeta }}_{2}\right)}{e}^{i{\theta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{2}, {\mathrm{\zeta }}_{2}\right)}}, {\mu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{3}, {\mathrm{\zeta }}_{3}\right)}{e}^{i{\theta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{3}, {\mathrm{\zeta }}_{3}\right)}}, \dots, {\mu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{n}, {\mathrm{\zeta }}_{n}\right)}{e}^{i{\theta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{n}, {\mathrm{\zeta }}_{n}\right)}} show the lower TG values of the edge of a path {\overrightarrow{\mathcal{P}}}_{({t}_{1}, r)}^{\mathcal{m}}, {\overrightarrow{\mathcal{P}}}_{({t}_{2}, r)}^{\mathcal{m}}, {\overrightarrow{\mathcal{P}}}_{({t}_{3}, r)}^{\mathcal{m}}, \dots, {\overrightarrow{\mathcal{P}}}_{({t}_{n}, r)}^{\mathcal{m}} and {\nu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{1}, {\mathrm{\zeta }}_{1}\right)}{e}^{i{\vartheta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{1}, {\mathrm{\zeta }}_{1}\right)}}, {\nu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{2}, {\mathrm{\zeta }}_{2}\right)}{e}^{i{\vartheta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{2}, {\mathrm{\zeta }}_{2}\right)}}, {\nu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{3}, {\mathrm{\zeta }}_{3}\right)}{e}^{i{\vartheta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{3}, {\mathrm{\zeta }}_{3}\right)}}, \dots, {\nu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{n}, {\mathrm{\zeta }}_{n}\right)}{e}^{i{\vartheta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{n}, {\mathrm{\zeta }}_{n}\right)}} show that the high TG values of the edge of a path {\overrightarrow{\mathcal{P}}}_{({t}_{1}, r)}^{\mathcal{m}}, {\overrightarrow{\mathcal{P}}}_{({t}_{2}, r)}^{\mathcal{m}}, {\overrightarrow{\mathcal{P}}}_{({t}_{3}, r)}^{\mathcal{m}}, \dots, {\overrightarrow{\mathcal{P}}}_{({t}_{n}, r)}^{\mathcal{m}} respectively.
If node r\in Ŭ is heavy if {\mu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{k}, {\mathrm{\zeta }}_{k}\right)} > \frac{1}{2} and {\theta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{2}, {\mathrm{\zeta }}_{2}\right)} > 1\pi for TG and {\nu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{k}, {\mathrm{\zeta }}_{k}\right)} < \frac{1}{2} and {\vartheta }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{2}, {\mathrm{\zeta }}_{2}\right)} < 1\pi for FG values \forall, k = \mathrm{1, 2}, 3, \dots, n .
i.e., \frac{{\sum }_{k = 1}^{n}{\mu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{k}, {\mathrm{\zeta }}_{k}\right)}}{n} > \frac{\frac{1}{2}+\frac{1}{2}+\frac{1}{2}, \dots, \left(n-time\right)+\frac{1}{2}}{n} > \frac{1}{2},
In the same way,
i.e., \frac{{\sum }_{k = 1}^{n}{\nu }_{Ҳ}\overrightarrow{\left({\mathcal{q}}_{k}, {\mathrm{\zeta }}_{k}\right)}}{n} < \frac{\frac{1}{2}+\frac{1}{2}+\frac{1}{2}, \dots, \left(n-time\right)+\frac{1}{2}}{n} < \frac{1}{2}









 DownLoad:
DownLoad: