Alzheimer's disease is an important public concern with rising prevalence across the globe. While many therapeutic approaches for Alzheimer's disease have been developed, there are currently no validated disease-modifying treatments. Thus, in order to develop novel treatment strategies, there is a significant need to progress our understanding of the pathogenesis of Alzheimer's disease. Several large genome-wide association studies and whole genome and exome sequencing studies have identified novel genes associated with late-onset Alzheimer's disease. Interestingly, many of the genes are associated with inflammation and the immune system, including complement receptor 1, clusterin, CD33, EPH receptor A1, membrane-spanning 4-domains subfamily A, ATP-binding cassette sub-family A member 7, major histocompatibility complex class II, inositol polyphosphate-5-phosphatase, myocyte enhancer factor 2C, and triggering receptor expressed on myeloid cells 2. The pathogenetic contributions of immune reaction and neuroinflammation in Alzheimer's disease have been regarded largely as part of amyloid cascade hypothesis. The neurotoxic amyloid-β (Aβ) induces activation of immune cells, such as microglia, astrocytes, perivascular macrophages and lymphocytes and decreased capability of clearing Aβ by immune system and chronic inflammation caused by activated immune cells aggravate neuronal damage and eventually Alzheimer's disease. But the precise mechanism and hereditary impact on such process is largely unknown. The current findings in genetic studies suggest that the immunological mechanisms of Alzheimer's disease may extend beyond passive reaction of Aβ, including the development of Alzheimer's disease such as time of onset and rate of progression. In this article, we aimed to review the mechanisms of immune reaction and neuroinflammation in Alzheimer's disease, with an emphasis on the function of genes known to be associated with a risk of Alzheimer's disease in terms of neuroinflammation and immune function.
1.
Introduction
A hypoxic environment is a well-known sign of tumor cells growing in an uncontrolled manner. Since the growth rate of tumor cells outnumbers the rate of employment of new vessels, that is, angiogenesis formation speed, some tumor cells are deprived of oxygen. In addition, a heterogeneous vascular network, possibly attributed to the imbalanced secretion of proangiogenic factors by tumor cells, induces an environment with insufficient oxygen levels, namely hypoxia [1,2,3]. These reasons mainly account for the existence of a hypoxic environment in solid tumors.
The presence of hypoxia leads to several implications for tumor progression and aggressiveness. Through the expression of hypoxia-inducible factors and subsequently secretion of vascular endothelial growth factor, vessel density is promoted at tumor sites [4,5]. Also, the absence of oxygen in the tumor microenvironment causes tumor cells to be more aggressive, that is, more prone to metastasis and an increased invasive growth tendency [6,7]. More importantly, the presence of hypoxia in the tumor microenvironment promotes resistance to traditional anticancer treatments such as both radiotherapy and chemotherapy, resulting in poor outcomes [8,9,10]. Since hypoxic areas induce the formation of disorganized vascular structures, one of the consequences of impeded perfusion, namely, inefficiency exists in drug delivery, i.e., the transport of chemotherapy drugs, to tumor sites [11,12]. An oxygenated environment is required to achieve positive results, as aerobic tumor cells are more prone to be affected by therapies than hypoxic ones. Tumor cells in hypoxic regions tend to regenerate if they are not completely eliminated. Therefore, exploiting hypoxic areas is of crucial importance to attain the desired therapeutic results. In this context, benefiting from treatments that target the hypoxic fractions of tumors may offer advantages for killing tumor cells without affecting relatively healthy ones.
Hypoxia-activated prodrugs (HAPs) have the potential for the treatment of tumor hypoxia. These prodrugs are inactive at normal oxygen concentrations, which are typically in the range of 10–80 mmHg [13]. However, under hypoxic conditions in which the oxygen partial pressure (pO$ _{2} $) is below 10 mmHg, they become active to target hypoxic cells without increasing toxicity and side effects, making them an ideal therapeutic strategy to exploit tumor hypoxia. HAPs are required to be activated enzymatically in order to be used as a cytotoxic agent, commonly by one- or two-electron reductases. In one-electron reduction, a prodrug radical is produced, and this radical is either reduced further to its active cytotoxic form in hypoxic cells or oxidized again to the prodrug in oxygenated cells. In contrast, two-electron reductions convert the prodrug directly into its active form without forming a prodrug radical [14]. HAPs can selectively target tumor cells in the active form under low oxygen conditions [15]. Furthermore, activated HAPs can diffuse back into the normoxic region and exert cytotoxicity in non-hypoxic cells, which is called the bystander effect, a crucial factor in improving the antitumor activity of HAPs [8,16].
To be able to prevent the hypoxic barrier from leading to therapeutic resistance, these bioreductive prodrugs are preferably administered together with chemotherapy and radiotherapy to eradicate the resistance of hypoxic tumor cells to these anticancer treatments. Various experimental studies have been conducted on different tumor types to investigate the efficacy of HAPs. Studies using HAPs as a type of monotherapy have reported that HAPs show an antitumor activity profile that leads to significant tumor growth inhibition and growth delay, as well as hypoxic area reduction; additionally, the results are dependent on the dose of HAP and the level of hypoxia [15,17,18,19]. Several preclinical studies investigating the co-administration of HAPs with radiotherapy in various xenograft tumor models have demonstrated an enhanced efficacy profile with combination therapy as compared to either treatment alone [10,19,20,21].
Many in vitro and in vivo studies have observed additive or synergistic effects of HAPs when combined with chemotherapeutic drugs in a variety of solid tumors, including breast cancer [22,23,24], pancreatic cancer [20,25], sarcoma [11,26] and other tumor types [17,18]. These studies suggest that HAPs can increase the antitumor activity of chemotherapeutic drugs such as doxorubicin [12,26,27], gemcitabine [12,25], cisplatin [17,28] and docetaxel [12,22], leading to favorable results for tumor cell death and growth control. The application of HAPs in combination with chemotherapy appears to be complementary; while HAPs exhibit cytotoxicity in hypoxic regions of tumors, chemotherapy mostly exerts therapeutic effects on tumor cells in well-oxygenated areas so that targeting both regions can be achieved. In xenograft models of breast cancer, the efficiency of HAP TH-302 in combination with the chemotherapeutic drug paclitaxel has been examined, and combination therapy rather than monotherapies, elicits a significantly better response in terms of tumor growth delay and inhibition; the conclusion was that TH-302 cooperates with paclitaxel and shows antitumor activity [23]. In another preclinical study [25], the addition of HAP TH-302 to chemotherapy drugs gemcitabine and nab-paclitaxel improved the efficacy in human pancreatic ductal adenocarcinoma.
Despite the positive results of combination therapy, some studies have failed to show any benefit, and this has been mainly attributed to the failure to determine the optimal schedule and insufficient identification of the tumor hypoxia status in patients [8,29]. The dosing schedule and regimen often appear to be decisive, so they need to be carefully adjusted in combination therapies involving HAPs. In several preclinical studies with different xenograft models, the importance of scheduling and sequencing has been highlighted, suggesting that, in combination treatments, HAP-first administration (neoadjuvant) is optimal sequencing rather than adjuvant or concurrent administration to maximize the tumor response [12,21,30]. HAP application targets hypoxic cells and causes a decrease in the hypoxic area, which leaves tumor cells sensitive to chemotherapy or radiotherapy [10,12]. Moreover, hypoxia levels in tumors emerge as a factor that particularly affects the treatment results and the effectiveness of HAPs. Several xenograft models exposed to HAPs elicit different responses, and differences in treatment outcomes are attributed to the variations in tumor oxygenation levels [20]. Some HAPs are quite sensitive to highly hypoxic environments, thus exhibiting more significant cytotoxicity [12,15,19], while others are activated at moderate hypoxia [31], suggesting the behavior of HAPs in a hypoxia-dependent manner. In a preclinical study by Sun et al. [15], the antitumor efficacy of HAP TH-302 differs such that severe hypoxia provides enhanced therapeutic activity of TH-302 while activity decreases with an increasing oxygen level.
In addition to experimental and clinical studies, mathematical models are extensively exploited in cancer treatments since they are easier to use, more convenient and cost-effective. A number of in silico studies have been carried out to explore potential treatment strategies to combat tumor hypoxia. Stochastic modeling approaches have been developed to simulate radiotherapy dose fractions and examine the effects of different treatment schedules to determine the optimal one and to achieve the growth control for tumors with varying levels of oxygenation [32,33,34,35]. Moreover, tumor growth and behavior have been examined during hyperfractionated radiotherapy for tumors with different hypoxia levels; the tumor response to treatments has been shown to be strongly dependent on the growth kinetics [36]. In another in silico study by Lindblom et al. [37], a 3-D model of a hypoxic tumor has been used to investigate the tumor control probabilities with different radiotherapy schedules. In this study, the differences in the radiosensitivities of chronically and acutely hypoxic cells have also been taken into account, and the different forms of hypoxia have been observed to impact the effectiveness of treatments.
Several mathematical modeling studies have also been conducted to understand the mechanism of action and key properties of HAPs [38,39,40], as well as their interaction with other anticancer treatments [41,42,43,44,45]. In a study by Hicks et al. [46], a pharmacokinetic/pharmacodynamic (PK/PD) model was exploited to identify the analogues of the HAP tirapazamine, indicating that the resulting compounds exhibit enhanced therapeutic activity when administered in combination with radiation. A recent study in which a PK/PD model was developed using Green's function method has evaluated the impact of bystander effects on HAP TH-302 activity [47]. Agent-based modeling approaches are also utilized to study the bystander effects of HAPs [48]. Lindsay et al. [49] has proposed a stochastic mathematical model to investigate the combination of HAPs with standard therapies in order to optimize the drug schedules. Meaney et al. [42] has shown that HAP TH-302 combined with radiotherapy enhances therapeutic activity; they identified the optimal treatment scheduling for the tumor response. They further examined the effects of administering HAP TH-302 in combination with antiangiogenic agents, which indicated the increased efficacy of combination therapy.
Here, we have aimed to explore the potential benefit of administering HAPs in combination with chemotherapy from the perspective of the treatment response. To do this, we propose a mathematical model that is based on our previous in silico model and represents the changes in biological components in the tumor microenvironment [50]. HAPs and chemotherapy drugs were applied to the system to demonstrate their complementary antitumor effects. In addition, the importance of varying levels of hypoxia in tumors, as well as the sequencing and scheduling of combination therapy have been explored.
2.
Mathematical model
In this study, a mathematical model was developed with reference to our previously published study [50]; the biological parts in the tumor microenvironment were designed to change in time due to the coupled interactions of each part. The model captures the tumor cell growth, vasculature and oxygenation, along with the drug treatments. Nonlinear partial differential equations (PDEs) are utilized in a nondimensional form for each part of the developed framework. The governing equations have been solved by adopting a finite difference method for PDEs.
2.1. Tumor cells, vasculature and oxygen concentration
The spatial and temporal changes of tumor cells and the heterogeneous vasculature are described by using the reaction-diffusion equations for a growing tumor. Tumor cells and vasculature are represented by ($ c({\textbf{x}}, t) $) and ($ m({\textbf{x}}, t) $), respectively. The equation for tumor cells (Eq (1)) defines the evolution of tumor with diffusion and logistic growth. This form of tumor evolution has been adopted in previous modeling studies [42,50,51,52]. Equation (1) includes the diffusion of tumor cells and the growth of the cells up to a carrying capacity of the microenvironment. In the presence of only these two terms, Eq (1) has two fixed points: at $ c = 0 $, an unstable point at which there is not any cell population, and at $ c = c_{lim} $, a stable point where the cell population approaches its carrying capacity. The third term of Eq (1) describes the interaction of tumor cells with vasculature, where $ \alpha_{mc} $ is the proliferation rate of cells increasing with the high vascular network. The last two terms indicate the destruction of tumor cells by the activated HAP ($ h_a({\textbf{x}}, t) $) and chemotherapy drug ($ d({\textbf{x}}, t) $), respectively. Initially, tumor cells are set to have a Gaussian distribution.
To represent the heterogeneous structure of tumor vasculature that is functionally different from healthy vessels, a coarse-grained model is utilized and vessel islands are generated. To create vessel islands, Eq (2) was formed by utilizing the term $ m({\textbf{x}}, t)(\alpha+\beta m({\textbf{x}}, t)+\gamma m({\textbf{x}}, t)^{2}) $. Using this term, the equation is collapsed to the two stable points at $ m = 1 $ and $ m = 0 $, implying the regions in which vessels are present and not present. The evolution of the vascular structure in the model exhibits a similar behavior as in the studies of [50,51,53,54]. Tumor-induced angiogenesis is represented by the terms $ \alpha_{cm}c({\textbf{x}}, t)(1-{c({\textbf{x}}, t)}/{c_{lim}})m({\textbf{x}}, t) $ and $ \beta_{cm}\nabla.(m\nabla c) $, which enable the occurrence of overvascularization of the tumor ($ m > 1 $) and the directed movement of vessels from periphery to the interior regions of the tumor, respectively. The vascular network is initiated as a map of random numbers between 0 and 1.
The changes in oxygen concentration indicated by K(x, t), is described by the following reaction-diffusion equation below (Eq (3)). The equation consists of the terms for the diffusion of oxygen in the interstitium, the transport of oxygen through vessels, the consumption of oxygen by tumor cells, and the natural decay of oxygen, respectively. Here, the second term $ \Theta_{K}m({\textbf{x}}, t) exp(-{m({\textbf{x}}, t)}/{m_{lim}})^2 $ represents the impairment in the delivery of oxygen by abnormal tumor vessels as in [42,51], such that for large values of m, the formation of regions with less oxygen concentration occurs, which corresponds to the hypoxic regions.
In the simulations, the steady-state of oxygen concentration equation is solved because its evolution is faster than the time scales associated with tumor and vessel growth ($ \frac{\partial K({\textbf{x}}, t)}{\partial t} = 0 $). The experimental study by the authors of [55] that examined the glioblastoma xenografts growing in the mouse brain has been referenced in the model to simulate the kinetics of tumor growth, the vascular structure, and oxygenation; the relevant parameters for each part are listed in Table 1.
2.2. Hypoxia-activated prodrugs and chemotherapy drugs
The inactive and active forms of HAPs are defined by the Eqs (4) and (5), respectively. The HAPs, indicated by ($ h({\textbf{x}}, t) $), are inactive when they are administered to blood plasma. They extravasate and are distributed through the tumor interstitium via diffusion, as described by the second and first terms of Eq (4). The last term is responsible for the decay of the HAPs. The HAPs were assumed to be activated at oxygen concentrations below 5 mmHg [56]. The oxygen-dependent activation of HAPs is described by the term $ -\frac{q_h K_h^2}{K_h^2+K^2}h({\textbf{x}}, t) $, where $ q_h $ and $ K_h $ stand for the maximum activation rate of HAPs and the pO$ _2 $ for the half-maximal activation rate of HAPs, respectively. The activated HAPs ($ h_a({\textbf{x}}, t) $) diffuse farther and exert cytotoxic effects on hypoxic and normoxic tumor cells via a bystander effect.
The main modes of transport, as dictated by Peclet numbers, vary with the drug size used. For small-sized drugs, diffusion outweighs convection in the tumor microenvironment. In this study, we considered the delivery of a small-sized chemotherapy drug ($ d(x, t) $) and utilized the following reaction-diffusion equation:
In Eq (6), the terms on the right side includes the diffusion of the drug in the interstitium and the diffusion through the vessels. The remaining terms represent the lymphatic drainage of the drug, which assumes no drainage within the tumor, the reaction of the drug with tumor cells and the decay of the drug in tissue, respectively.
The time scale for the transport of drugs is shorter than the time scale of tumor growth, so the HAPs and chemotherapy drug equations are solved in a steady state ($ \frac{\partial h({\textbf{x}}, t)}{\partial t}, \frac{\partial d({\textbf{x}}, t)}{\partial t} = 0 $). For both equations, no-flux boundary conditions are used. Bolus injections in plasma are determined by the exponentially decaying functions $ h_{p}\!\left(t\right) = h_{0}e^{-t/t^{h}_{1/2}}, \label{equation7} $ and $ d_{p}\!\left(t\right) = d_{0}e^{-t/t^{d}_{1/2}}, \label{equation8} $ where $ h_{0} $ and $ d_{0} $ and $ t^{h}_{1/2} $ and $ t^{d}_{1/2} $, represent the initial plasma concentration and plasma half-life of the HAPs and chemotherapy drug, respectively. Parameters related to the transport of the HAPs and chemotherapy drug are indicated in Table 2; they were taken from the experimental studies and also from the mathematical modeling studies in which parameter estimations were based on experimental results [41,57,58,59,60].
3.
Results
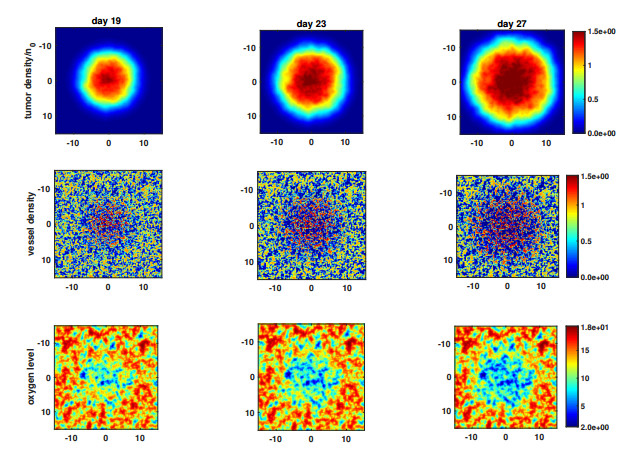
In the simulations, tumor cells started to be distributed as Gaussian with an initial radius of 0.2 mm, and they were allowed to reach a radius of approximately 13.5 mm for 30 days. Initially, vessels were set to be distributed randomly between 0 and 1 in the computational domain, but they evolved into heterogeneous vessel islands in the presence of tumor cells (Figure 1, vessel density). A decrease in oxygen concentration could also be observed at the tumor site due to increased tumor density in the inner parts of the tumor (Figure 1, oxygen level).
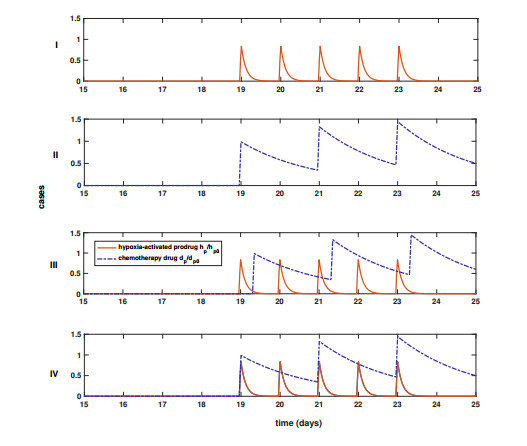
Various drug schedules were examined in the model to investigate the effect of the combination of HAPs and a chemotherapy drug on treatment efficacy. The simulated cases are presented in Figure 2. Dimensionless dose values for the drugs were adjusted to obtain a similar treatment response as in [12]. The HAP was administered in daily doses for 5 consecutive days starting from Day 19 (Days 19–23), while the chemotherapy drug was applied every other day for 3 pulses (Days 19, 21 and 23). In the simulations, each treatment case was initiated with the same tumor and vasculature to accurately observe the effect and make a fair comparison. Also, due to the random initial distribution of vessels, the simulations were conducted with 10 different vascular networks for each treatment case and the calculations were averaged. Here, we display four cases: only HAP administration starting on Day 19 (Ⅰ), only chemotherapy drug administration on Day 19 (Ⅱ), administration of the HAP before the chemotherapy drug (Ⅲ) and the simultaneous application of the HAP and chemotherapy drug (Ⅳ). In the cases of dosing sequencing, each drug was given at the same time, or the HAP was given eight hours before the chemotherapy drug for non-simultaneous application. The eight-hour interval yielded the optimal sequence in the simulations, though there was a slight difference with the other examined sequences.
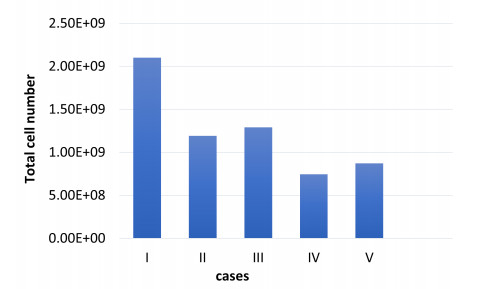
To understand whether adding HAPs in the presence of a chemotherapy drug enhances the therapeutic benefit as compared to cytotoxic treatment alone, several cases were examined in the simulations; the tumor response is presented as the final tumor cell number after each treatment. Figure 3 displays the total cell numbers for the cases of the control (Ⅰ), administration of the HAP alone (Ⅱ), chemotherapy alone (Ⅲ), HAP before chemotherapy (Ⅳ) and HAP administration with chemotherapy at the same time (Ⅴ), respectively. It can be seen that monotherapy with HAPs gives more effective results than the untreated control or chemotherapy alone (Figure 3). The HAPs alone treatment resulted in approximately 45% cell death (Case Ⅱ in Figure 3), whereas chemotherapy alone induced 37%, demonstrating higher antitumor activity of HAPs with the bystander effect [15]. However, increased cell death was observed for the combination of HAPs and chemotherapy drug relative to that for chemotherapy or HAPs as a single agent (Cases Ⅳ and Ⅴ in Figure 3), confirming qualitative agreement with the previous experimental studies [11,12,22]. In the simulations, the case of the HAP administered before chemotherapy resulted in more effective antitumor activity than that of the other sequences; particularly, a 64.5% reduction in total cell number was achieved in that case (Case Ⅳ in Figure 3). Moreover, the simultaneous administration of both drugs induces approximately 58% cell death (Case Ⅴ in Figure 3).
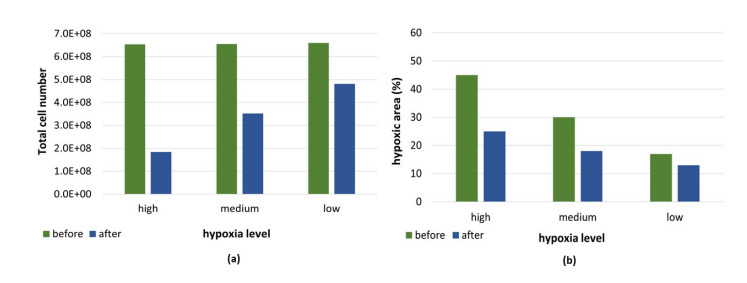
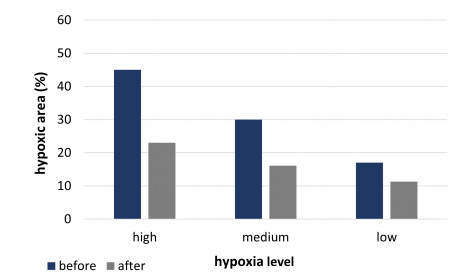
In order to investigate the oxygen dependence of the antitumor activity of HAPs, which have an effect on the hypoxic area of the tumor, varying hypoxia levels were examined. A HAPs alone treatment was carried out for the cases with high ($ O_2 < $ 5 mmHg), moderate (5 mmHg $ < O_2 < $ 10 mmHg) and low ($ O_2 > $ 10 mmHg) hypoxia levels. The ranges for hypoxia levels were taken from the studies in the literature [15,64]. Changes in the total cell number and hypoxic area before and after the treatment are presented in Figure 4. The results reveal that the treatment response shows variations depending on the level of hypoxia in the tumor. As can be seen in Figure 4: the most pronounced effect was observed for high hypoxic conditions.
In this case, there was a change in total cell number of approximately 68% before and after HAP administration, indicating that HAPs are more sensitive to highly hypoxic tumors and have improved efficacy profiles. On the contrary, low hypoxia levels induce less cell death, such that only about 27% change is observed after the treatment. According to these findings, it can be concluded that as the level of oxygenation increases, less favorable results may be obtained from treatment, as HAPs require highly hypoxic conditions to exert their therapeutic effects on tumors in agreement with previously published experimental studies [12,15,19,23]. Additionally, changes in the hypoxic area were investigated in the study for combination therapy with low, medium and high hypoxia levels. The HAP administered before chemotherapy case yielded more effective results in terms of killing cells as compared to the other cases, so changes in the hypoxic area were examined for this case; the results are displayed in Figure 5. This finding again demonstrates the significance of determining the level of tumor hypoxia, as the tumor response to combination therapy varies depending on the hypoxia level and accordingly affects the treatment outcomes.
We also performed a parameter sensitivity analysis on some model parameters, such as the diffusion coefficient for inactive HAPs in tissue ($ D_h $), the interaction terms for tumor cells with activated HAPs ($ h_r $) and the chemotherapy drug ($ d_r $), the diffusion coefficient for chemotherapy drug in tissue ($ D_d $), the supply rate of the inactive HAP ($ \theta_h $) and the decay rate of the inactive HAP ($ d_h $). By doing so, we aimed to examine the effects of changing both the estimated and referenced parameters on the total number of cells in the tumor. The value of each parameter was multiplied by factors of 0.5 and 2 separately for the analysis, and the simulations were repeated for each change in combination therapy. Percentage changes in the total number of cells in tumor were then calculated using the modified parameter set; the results are presented in Table 3. The baseline in Table 3 indicates the % change in total cell number, as obtained for the original parameter set.
Some parameters related to the HAPs were examined to observe their impacts on the HAP efficacy. In Table 3, it can be seen that a higher diffusion coefficient for the inactive HAPs facilitated diffusive transport of the drug to the hypoxic area, leading to increased cell death; conversely, a lower value resulted in a smaller change. The parameter $ h_r $, which describes the interaction of tumor cells with activated HAPs, was also explored to see how tumor cells are influenced by the cytotoxic effect of HAPs. In this case, the expected results are observed such that a decrease in the value of $ h_r $ induced lower cell death, whereas an increased value of $ h_r $ resulted in higher cell death. In addition, a similar analysis was carried out for the parameters $ d_r $ and $ {\theta_h} $ to understand the killing effect of the chemotherapy drug on tumor cells and the influence of the supply rate of inactive HAPs, respectively. Increasing the value of the parameter $ d_r $ led to higher efficacy and therefore more tumor cell death. Also, a smaller HAPs supply yielded a relatively minor effect on the outcome.
4.
Discussion
In this study, the cytotoxic effect and corresponding tumor response of combining HAPs with a chemotherapy drug were investigated by examining different administration times and sequences. In order to do this, our previously published in silico model of tumor cells and vascularization [50] was employed together with the results of experimental studies. The model incorporates tumor growth, vasculature and oxygenation and allows us to experiment with various drug regimens. In the mathematical model, the experimental study by Winkler et al. [55], which examined the glioblastoma xenografts growing in the mouse brain is used to simulate the kinetics of tumor growth, the vascular network and oxygen concentration; also, for combination therapy, treatment responses similar to those in the study of [12] were investigated, and the parameters were adjusted accordingly.
Tumor hypoxia is known to be resistant to radiotherapy and chemotherapy, so overcoming this phenomenon is critical for the treatment of cancer [9]. In this context, combined therapies with cytotoxic prodrugs targeting the hypoxic fractions of tumors have been extensively explored in many preclinical and clinical studies. HAPs have the potential to target tumor cells residing in hypoxic regions and exert cytotoxic effects, and chemotherapy drugs can then exploit the reoxygenation effects of HAPs. Therefore, integrating HAPs and chemotherapeutics may seem like a viable approach in which both hypoxic and normoxic tumor cells can be targeted and cytotoxicity can be achieved at these sites, which is not feasible via the monotherapy of each drug, which mainly targets only one region. Based on this, the addition of HAPs to chemotherapy was investigated using the model, and the combined therapy demonstrated a complementary effect with positive treatment outcomes. In the simulations, the cytotoxic effects of the HAPs and chemotherapy drug were examined both as a single agent and in combination. All treatments resulted in more cell death than the untreated control case, but higher tumor cell death was observed in the HAPs combined with chemotherapy cases, which is qualitatively consistent with the experimental studies [11,12,22].
The treatment schedule and the order of drug administration appear to be factors that affect the outcomes. Experimental studies have revealed that HAPs administration prior to conventional therapeutics provides a better tumor response, as HAPs selectively target hypoxic cells, inducing a reduction in the hypoxic fraction as well as total cell number, and leaving tumor cells sensitive to the chemotherapy drug in the oxygenated area [12,22,25,26]. After experimenting with several drug regimens throughout the simulations, optimal results were obtained in the case of HAPs administration before chemotherapy. The largest change in total cell number was achieved in that case compared to the cases of monotherapies of each drug and their simultaneous administration. HAPs reduce the cell density and thus the total cell number, complementing the efficacy of the companion drug [12,15]. Although, as compared to HAPs and chemotherapy drug as a single administration, simultaneous administration seems to be effective in terms of cell death according to the simulations, in preclinical studies, it has been reported to increase toxicity compared to other sequences [12]. Moreover, chemotherapy administered prior to HAPs is asserted to be less successful than that administered after HAPs, suggesting that the effects of the cytotoxic activity of the chemotherapy drug on normoxic cells leads to a decrease in the oxygen consumption and induces reoxygenation of the hypoxic parts in tumor. Thus, with reduced hypoxic areas, decreased therapeutic activity of the HAP might be observed [12,65,66].
The time interval between administration of HAPs and chemotherapy drugs is reported to influence treatment outcomes in terms of efficacy and toxicity [67,68]. In a study by Liu et al. [12], various conventional chemotherapy drugs, including doxorubicin, docetaxel, cisplatin, and gemcitabine, were applied together with HAP TH-302, in several xenograft tumor models to evaluate the effects of combination therapy according to different drug administration sequences. The time interval between the administration of both drugs was observed to affect the results, as HAP administration 2–8 hours before the conventional chemotherapeutic drug resulted in greater tumor growth inhibition than that resulting from administration 12, 24 or 48 hours before; although the underlying mechanism is not completely clear, it might be due to the pharmacokinetic properties or mechanism of action of the combined agents [12]. In this study, we experimented with several cases as well to determine the optimal dosing sequence; we observed that the administration of HAP 4–8 hours before the chemotherapy drug provides better efficacy and increased tumor cell death as compared to other sequences (12 and 24 hours before).
The level of tumor hypoxia stands as another point that needs to be taken into account to optimize the benefit of the treatments. In a preclinical study by Sun et al.[15], several human tumor xenograft models with varying hypoxic fractions were subjected to HAP TH-302 as a monotherapy. The results showed that there is a good correlation between the antitumor efficacy of TH-302 and the level of hypoxia; significant tumor growth inhibition was observed in the cases of the xenograft models holding higher hypoxic fractions. Furthermore, patients having tumors with high levels of hypoxia have been reported to have a poorer response to conventional anticancer therapies [69,70]. Using the model, low, moderate and high hypoxic cases were simulated to determine to which condition HAPs are more sensitive. The antitumor activity of the HAPs was reflected as changes in the total cell number and hypoxic area of the tumor according to different hypoxia levels. The results demonstrate that the hypoxia selectivity of HAPs plays an important role in their effectiveness, as a higher level of tumor hypoxia augments the antitumor activity of HAPs with enhanced cell killing ability and a reduced hypoxic area, which is in agreement with previously published experimental studies [12,15,23]. Moreover, changes in the hypoxic area that depend on tumor oxygenation have been explored in the study for the combination treatment of HAPs with a chemotherapy drug. A larger decrease was observed at the high hypoxia level, suggesting that the complementary effects of the two drugs begin to emerge at higher tumor hypoxia, which aligns with the results stated in [71]. These findings highlight the importance of determining tumor oxygenation levels before the treatment in terms of specifying the hypoxic prodrug to be used in therapy and predicting treatment outcomes. The assessment of tumor hypoxia can complement the monitoring of the response to HAPs [10,72], as well as imaging modalities like magnetic resonance imaging (MRI) and positron emission tomography [73,74]. Moreover, a recent study has incorporated a deep learning model that was developed with an MRI dataset to determine the hypoxic status of tumors and predict the response to HAP TH-302 prior to treatment [75]. The model demonstrated high accuracy in estimating the hypoxia fractions. In this context, benefiting from imaging approaches that provide additional necessary information about tumors and their hypoxic conditions may also facilitate the patient selection process by identifying those more likely to respond to hypoxia-targeted therapies.
As no mathematical model perfectly represents all of the complex biological interactions, our model has some limitations and simplifications regarding the underlying biology. In the study, 2-D tumor microenvironment maps were used, but a 3-D mathematical model would provide more detailed information about the spatial features of the tumor microenvironment. Since the cells characterized as chronically hypoxic and acutely hypoxic have been observed to display different response characteristics, the sensitivity of these hypoxic cells to therapies would affect the treatment results [37]. In this study, however, we adopted a general approach, considering that cells have the same cellular response and sensitivities. Still, it would be useful for a future study to examine the influence of different hypoxic cell types on treatment outcomes. The types of tumor cells, such as cancer stem cells and differentiated cells, were also not specified in the model. As with stochastic modeling studies in the literature that examined the effects of tumor growth in a hypoxic environment on treatment outcomes [33,34,76,77], incorporating a comprehensive tumor composition into the model and investigating the tumor response to treatments would be a helpful approach to observing the behavior of different cancer cells in therapies. The model uses a simulated vascular network, but implementing vascular images taken from clinical data would be interesting as a future study to make patient-specific response predictions.
The model predictions here provide qualitative insights into the effectiveness of the combination treatment and drug scheduling. That might be helpful when conducting an experiment to examine treatment scenarios that can produce better results and avoid unnecessary ones, as HAP-related studies are still in development. The proposed model was employed for glioblastoma, but other tumor models can be applied using appropriate parameter sets. Besides, with the support of experimental studies, detailing the model by incorporating the mechanism of activation and enzymatic reduction of prodrugs may be informative, and thus help to identify tumors that highly express activating enzymes. For the simulations, TH-302 and doxorubicin were selected as the HAP and chemotherapy drug, respectively, and the relevant parameters obtained from the experimental and theoretical studies in the literature were implemented into the model. However, the cytotoxic activity of different hypoxic prodrugs and chemotherapeutic agents could also be investigated with their respective transport parameters.
In the model, most parameters were taken from studies in the literature, but some were estimated to mimic the biological behavior of the tumor and cytotoxic drugs. Parameters for describing the cell-killing effects of the HAP and chemotherapy drug were adjusted to observe the treatment response similar to that observed in the experimental study presented in [12]. A sensitivity analysis was also performed for some parameters, including those estimated, to investigate the sensitiveness of the model results to changes in the parameters. The analysis findings revealed the robustness of the model against reasonable parameter changes. It should be noted again that the model makes qualitative predictions rather than quantitative ones, which provide more precise information about the treatment response.
Parameter values might differ from patient to patient, so making precise measurements could be challenging in a clinical setting. Also, determining the optimal timing and sequencing of the combined drugs would tend to be experimentally intensive work. In this context, mathematical modeling studies may assist in making qualitative and quantitative estimations about parameter values and appropriate treatment schedules and dosages. Moreover, in silico models that are appropriately analyzed and validated by experimental studies could be advantageous for optimizing patient-specific treatment plans or selecting patients for combination therapy trials of with HAPs and chemotherapeutic drugs.
5.
Conclusions
In this study, the therapeutic efficacy of HAPs together with a chemotherapeutic drug was explored by adopting a modeling approach. In this regard, a mathematical model was designed based on our previous in silico model that incorporates the biological features of the tumor microenvironment. The effects of combination therapy on tumor growth and the treatment response were examined under various drug treatment scenarios. The case of HAPs administration with chemotherapy induced more pronounced cell death for highly hypoxic tumors than the administration of chemotherapy or HAPs as a single agent; that is qualitatively in agreement with experimental observations. The order of drug administration also seems to influence the results, as HAP administration prior to chemotherapy was observed to yield more potent antitumor activity than the other examined sequences. Moreover, HAPs have been found to show effectiveness that varies with the level of tumor oxygenation.
Acknowledgements
This research was supported by the TUBITAK grant no. 117F047, the Republic of Turkey Ministry of Development grant (2009K120520), the Council of Higher Education (100/2000 Ph.D. fellowship) and the TUBITAK 2211/A National Ph.D. Scholarship Program.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: