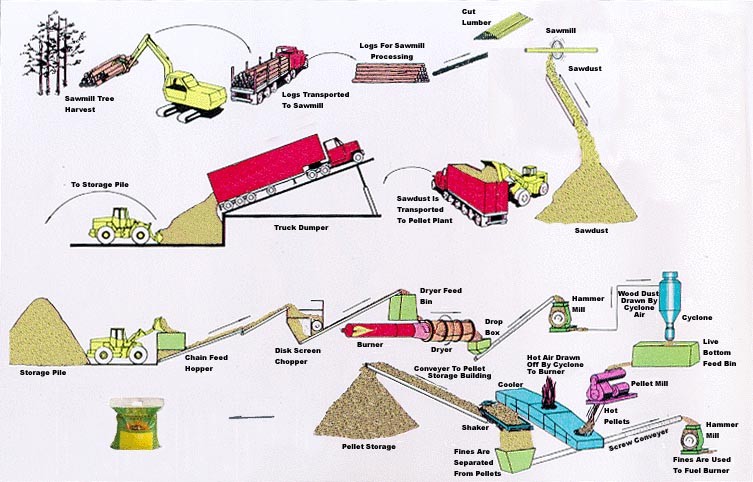
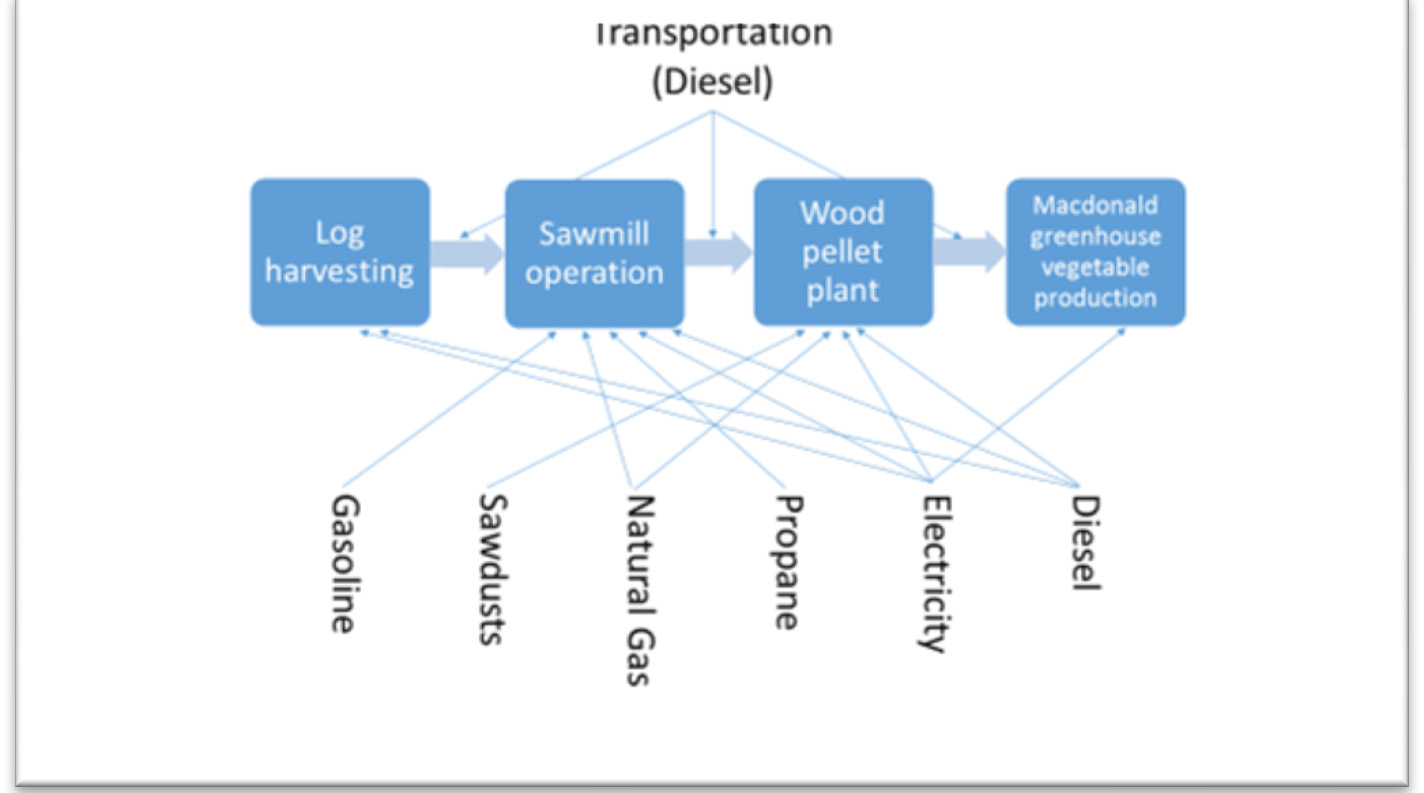
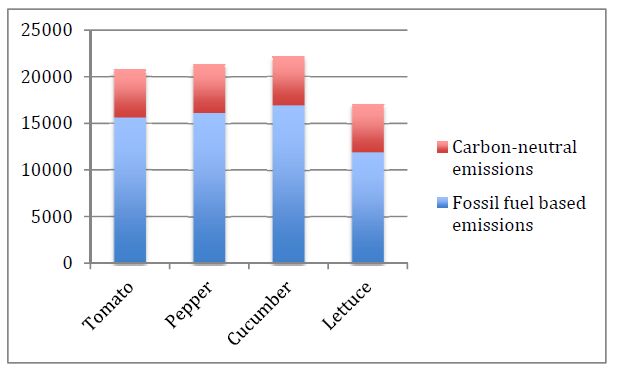
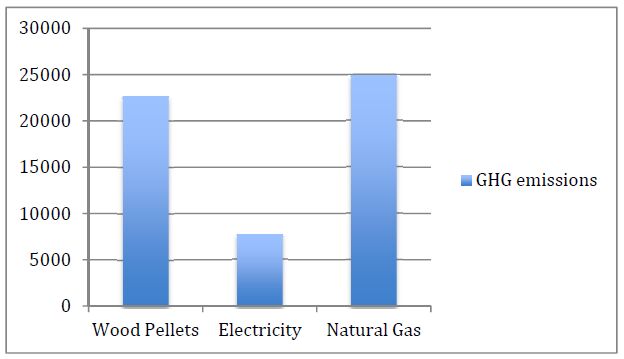
Wood pellets are one of the most promising alternatives to fossil fuel in Canada. Using wood pellets for heating allows saving on heating source expenses as compared to fossil fuels. Moreover, direct carbon emissions from wood pellets are regarded as carbon neutral since regrowth of vegetation captures and stores carbon that already exists in the atmosphere. Using wood pellets as a heating fuel for greenhouse vegetable production is expected to result in less greenhouse gas emissions than fossil fuels. Increasing the domestic consumption of wood pellets for greenhouse heating in Canada would reduce the environmental impact of energy consumption. This study investigates the potential of using wood pellets as an alternative fuel for commercial greenhouses in Quebec. This study applied a life-cycle analysis to demonstrate the energy flows and environmental consequences of using wood pellets for greenhouse vegetable production. The results found that greenhouse gas emissions from wood pellets are lower than natural gas in greenhouse operations.
1.
Introduction
We consider the initial boundary value problem of the following porous elastic system with nonlinear or linear weak damping terms and nonlinear source terms
where u(x,t) and ϕ(x,t) are the displacement of the solid elastic material and the volume fraction, respectively, μ, b, δ and ξ are coefficients with physical meaning satisfying
u0, u1,ϕ0 and ϕ1 are given initial data, and the assumptions of weak damping terms g1, g2 and nonlinear source terms f1, f2 will be given in Section 2 by Assumption 2.1 and Assumption 2.2, respectively.
In the physical view, elastic solid with voids is an important extension of the classical elasticity theory. It allows the processing of porous solids in which the matrix material is elastic and the interstices are void of material (see [8,20] and references therein). Porous media reflects the properties of many materials in the real world, including rocks, soil, wood, ceramics, pressed powder, bones, natural gas hydrates and so on. Due to the diversity of porous media and its special physical properties, such models were widely applied in the past few decades in the petroleum industry, engineering, etc (see [1,12,13,16,17,19]).
As mathematical efforts, Goodman and Cowin [2,8] established the continuum theory and the variational principle of granular materials. Then Nunziato and Cowin [3,18] developed the linear and nonlinear theories of porous elastic materials. In recent years, the study of the porous elastic system also attracted a lot of attention [5,6,7,21,22]. We particularly mention that Freitas et.al. in [5] studied the problem (1.1) and proved the global existence and finite time blowup of solutions. Especially, they built up the continuous dependence on initial data of the local solution in the following version
which can also be extended to the global solution with the same form. By denoting z=(u,ϕ) and ˜z=(˜u,˜ϕ) the global solutions to problem (1.1) corresponding to the initial data z0, z1 and ˜z0, ˜z1, respectively, ˆE(0) is the distance of two sets of different initial data
and
that is
and ˆE(t) is the distance of solutions induced by these two sets of different initial data
The growth estimate (1.2) indicates that the growth of the distance of solutions ˆE(t) is bounded by an exponential growth bound with time t. In other words, as the time t goes to infinity, the distance of solutions ˆE(t) of the system is bounded by a very large bound, by which it is hard to explain the solutions z and ˜z of such a dissipative system with the initial data z0,z1 and ˜z0,˜z1, respectively, as both of them are expected to decay to zero as the time t goes to infinity. Hence, the estimate on the growth of the distance of solutions ˆE(t) is proposed to be improved to reflect the decay properties with time t to be consistent with the dissipative behavior of the system. To achieve this, the efforts in the present paper are illustrated by two new continuous dependence results on the initial data for the global-in-time solution. Especially, it is found that the system with the linear damping term behaves differently from that with the nonlinear damping term. Hence in the present paper, we adopt two different estimate strategies to deal with the problem and derive two different conclusions:
(i) For the linear damping case, i.e., g1(ut) and g2(ϕt) take the linear form and satisfy Assumption 2.1, we have
where the positive constants C1,C2,C3,a,ρ are independent of initial data.
(ii) For the nonlinear damping case, i.e., g1(ut) and g2(ϕt) take the nonlinear form and satisfy Assumption 2.1, we have
where 0<κ<1, and the positive constants C5,C6,C7,b0 are dependent of initial data.
By observing (1.3) and (1.4), we find that these two continuous dependence results can reasonably reflect the decay property of the dissipative system (1.1). The difference between (1.3) and (1.4) is that the parameters in (1.3) do not depend on the initial data, while the parameters in (1.4) depend on the initial data. Hence although (1.3) and (1.4) are in the similar form, we present and prove them separately.
Additionally, to develop the finite time blowup of the solution to problem (1.1) at the arbitrary positive initial energy level derived in [22], we estimate the lower bound of the blowup time in the present paper for the nonlinear weak damping case by noticing that the linear weak damping case was discussed in [22]. For more relative works on the blowup of solutions to the hyperbolic equations at high initial energy, please refer to [10,11,14,15,25]. We can also refer to [9,23,24] for the works about the blowup of solutions to parabolic equations.
The rest of the present paper is organized as follows. In Section 2, we give some notations, assumptions about damping terms and source terms, and functionals and manifolds for the potential well theory. In Section 3, we deal with the continuous dependence on initial data of the global solution for the linear weak damping case. In Section 4, we establish the continuous dependence on initial data of the global solution for the nonlinear weak damping case. In Section 5, we estimate the lower bound of blowup time at the arbitrarily positive initial energy level for the nonlinear weak damping case.
2.
Preliminaries
2.1. Notations and assumptions
We denote the L2-inner product by
and the norm of Lp(0,L) by
As we are dealing with the system of two equations, for z=(u,ϕ) and ˆz=(ˆu,ˆϕ), we introduce
and
Further, we consider the Hilbert space
with inner products given by
for z=(u,ϕ), ˆz=(ˆu,ˆϕ), where μ, δ, ξ, b are the coefficients of the terms in the equations in problem (1.1). Therefore, we have
The norm ‖z‖V is equivalent to the corresponding usual norm on V, i.e., H10(0,L)×H10(0,L), introduced in [20]. For 1<q<+∞, we define
which means
for z∈V. Here, due to H10(0,L)↪Lq(0,L) for 1<q<+∞, we see 0<Rq<+∞. And we denote
and
where fj(u,ϕ), j=1,2, are the source terms, and g1(ut) and g2(ϕt) are the damping terms in the equations in problem (1.1).
We give the following assumptions about damping terms, i.e., g1(ut) and g2(ϕt), and source terms, i.e., fj(u,ϕ), j=1,2, in the equations in problem (1.1).
Assumption 2.1. (Damping terms) Let g1,g2:R→R be continuous, monotone increasing functions with g1(0)=g2(0)=0. In addition, there exist positive constants α>0 and β>0 such that
(i) for |s|≥1
and
(ii) for |s|<1
and
Assumption 2.2. (Source terms) For the functions fj∈C1(R2), j=1,2, there exists a positive constant C such that
where η=(η1,η2)∈R2, fj(η)=fj(η1,η2), j=1,2, and
There exists a nonnegative function F∈C2(R2) satisfying
and
for all λ>0, where F(η)=F(η1,η2) and
According to [5], Assumption 2.2 implies that there exists a constant M>0 such that
2.2. Potential well
Next, we recall some functionals and manifolds for the potential well theory. We recall the potential energy functional
and the Nehari functional
The energy functional is defined as
And the Nehari manifold is defined as
Then we can define the depth of the potential well
By above, we introduce the stable manifold
Next, since we need to apply the decay rate of the energy in investigating continuous dependence on the initial data of the solution, we recall the following notations used in the investigation of the decay rate of the energy in [5]
where
and M(s) attains the maximum value at
Here, Proposition 2.11 in [5] shows the fact ˆd≤d.
3.
Continuous dependence on initial data of the global solution for linear weak damping case
In this section, we consider the model equations in (1.1) with the linear weak damping terms, i.e., r=m=ˆr=ˆm=1. First, we need the following decay result of the energy.
Lemma 3.1. (Decay of the energy) Let Assumption 2.1 and Assumption 2.2 hold with r=m=ˆr=ˆm=1. For any 0<σ<1, if E(z0,z1)<σˆd and z0∈W, then one has
for t>0, where λ0 and K0 will be defined in the proof.
Proof. We define
where ε>0. Here, according to Cauchy-Schwartz inequality, Young inequality, and (2.5), we have
and
According to Theorem 2.12(ⅳ) in [5], we know
which means that (3.2) and (3.3) turn to
and
According to (3.5) and (3.6), we know
where
and
We calculate the derivative of the auxiliary functional H(t) with respect to time t as
In (3.8), we have
Here, the notation ∇F is defined by (2.13). Thus, according to (2.11), we know ∇F(z)=F(z), which means (3.9) turns to
Testing the both sides of the first equation in (1.1) by ut and integrating both sides over [0,L], we have
And testing the both sides of the second equation in (1.1) by ϕt and integrating both sides over [0,L], we have
By substituting (3.11) and (3.12) into (3.10), we have
Next, we use Assumption 2.1 to deal with (3.13). In Assumption 2.1, for |s|≥1, according to (2.6) with m=1 and (2.7) with r=1, we know that
Then taking the absolute value of (3.14) gives
For |s|<1, according to (2.8) with ˆm=1 and (2.9) with ˆr=1, we know that (3.15) also holds. Meanwhile, since g1(0)=g2(0)=0 and gj(s), j=1,2, are assumed to be the increasing functions, for j=1,2, we know gj(s)>0 for s>0 and gj(s)<0 for s<0, which gives gj(s)s≥0, j=1,2, for s∈R. Thus, we have
which makes (3.13) turn to
We deal with the term ε(ztt,z) in (3.8). Testing the both sides of the first equation in problem (1.1) by u and integrating both sides over [0,L], we have
And testing the both sides of the second equation in problem (1.1) by ϕ and integrating both sides over [0,L], we have
By (3.17) plus (3.18), we have
According to (3.16) and (3.19), we know that (3.8) turns to
Next, we deal with the term ε|(G(zt),z)| in (3.20). By using (3.15) and Hölder inequality, we know
Then, We deal with ε(F(z),z) in (3.20). Here, we first need to give
For all λ>0, taking the derivative of both sides of (2.12) with respect to λ, we know
where ∇F is defined by (2.13). By taking λ=1 in (3.23) and using (2.11), we obtain (3.22). According to (3.22) and (2.14), we have
By using (2.5), (3.24) turns to
Then, we estimate the term ‖z‖p−1V in (3.25). According to Theorem 2.12 (ⅱ) in [5], we know z(t)∈W for t>0. By using I(z(t))>0, i.e., z(t)∈W, we have
which means
Meanwhile, according to (3.16), i.e.,
we have E(z(t),zt(t))≤E(z0,z1). Thus, we know
i.e.,
for t>0, which implies that (3.25) turns to
Due to E(z0,z1)<σˆd being assumed, we know that (3.28) turns to
where ˆd is defined by (2.17). Substituting (3.21) and (3.29) into (3.20), we have
By using Young inequality for δ0>0 and inequality (2.5) for q=2, we know that (3.30) turns to
In (3.31), we choose δ0>0 to make 1−σp−12−βδ0R2>0 hold, where 1−σp−12>0 due to σ∈(0,1). Then, we select ε>0 such that α−ε−εβδ0>0 and
To deal with (3.31), we first have
According to Theorem 2.12 (ⅳ) in [5], (3.32) turns to
Due to (3.7), i.e., H(t)≤α2E(z(t),zt(t)), (3.33) turns to
Thus, we know that (3.31) implies
where
By using Gronwall's inequality, (3.35) gives
According to (3.7), (3.37), and the assumptions E(z0,z1)<σˆd and 0<σ<1, we have
where
Theorem 3.2. (Continuous dependence on initial data for linear weak damping case) Let Assumption 2.1 and Assumption 2.2 hold with r=m=ˆr=ˆm=1. For any 0<σ<1, suppose E(z0,z1)<σˆd, z0∈W, E(˜z0,˜z1)<σˆd and ˜z0∈W. Let z=(u,ϕ) and ˜z=(˜u,˜ϕ) be the global solutions to problem (1.1) with the initial data z0, z1, and ˜z0, ˜z1, respectively. Then one has
where
λ0 and K0 are defined by (3.36) and (3.39), respectively, R4(p−1) is the best embedding constant defined in (2.4) taking q=4(p−1),
and
Proof. We denote w:=z−˜z. According to the proof of Theorem 2.5 in [5], we notice that
holds by Assumption 2.1 and Assumption 2.2. In the following, we shall finish this proof by considering the following two steps. In Step I, we shall derive a similar estimate of the growth of ˆE(t) to (135) in [5]. As we build this estimate for the global solution instead of the local solution treated in [5], we have to rebuild all the necessary estimates based on the conditions for global existence theory.
Step Ⅰ: Global estimate of ˆE(t) for global solution.
We estimate the term ∫t0∫L0(F(z(τ))−F(˜z(τ)))wt(τ)dxdτ in (3.43) as follows
Here, according to the proof of Lemma 3.2 in [5], we notice that (2.10) in Assumption 2.2 gives
which means (3.44) turns to
Next, we deal with A1 and A2 separately. For A1, by Hölder inequality and Young inequality, we have
By the similar process, we can deal with A2 as
According to (3.47), (3.48) and Hölder inequality, we know that (3.46) turns to
In (3.49), by noticing z=(u,ϕ), ˜z=(˜u,˜ϕ), we see that
By using Hölder inequality and Young inequality, we know (3.50) turns to
Next, we deal with ∫L0(|u|p−1+|˜u|p−1+|ϕ|p−1+|˜ϕ|p−1+1)4dx in (3.49). For k1, k2, k3, k4, k5≥0, we have
From above observation, we have
According to (3.51) and (3.52), (3.49) turns to
By using (2.5), we know that (3.53) turns to
According to (3.27) and the assumptions E(z0,z1)<σˆd and E(˜z0,˜z1)<σˆd, we have
and
Substituting (3.55) and (3.56) into (3.54), we have
Due to (3.57), we know
Substituting (3.58) into (3.43), we have
Then, by a variation of Gronwall's inequality (see Appendix), we have
As the growth estimate (3.60) we derived in Step I does not reflect the decay of the solution, we shall deal with the decay terms and the non-decay terms separately in Step II to upgrade the results obtained in Step I, i.e., (3.60), by giving an improved estimate to reflect the dissipative property of the system (1.1).
Step Ⅱ: Decay estimate of ˆE(t).
According to (3.46), we have
By the similar process dealing with A1 and A2, we can treat A3 and A4 as
and
By the similar process of obtaining (3.54), i.e.,
we can use (3.62) and (3.63) to give
Due to (3.26), (2.16) and Lemma 3.1, we know
and
According to (3.65) and (3.66), we have
and
which mean
By substituting (3.67) into (3.64), we obtain
Substituting (3.68) into (3.61) and using Hölder inequality and (2.5), we have
According to (3.60), we know
i.e.,
for 0<a<1. Meanwhile, combining (3.65) and (3.66), we also have
i.e.,
and
Combining (3.70), (3.71) and (3.72), we have
We choose 0<a<min{2λ0ˉMC+λ0,1} such that
in (3.74). Meanwhile, according to (3.70), (3.72) and (3.73), we notice that
Due to (3.74) and (3.76), we see that (3.69) turns to
By substituting (3.77) into (3.43), we obtain
where
Here, according to (3.79), we notice that D≤Nλ1, which means that (3.78) turns to
i.e.,
We define
Thus, we can rewrite (3.81) as
By applying Gronwall's inequality, (3.83) gives
which means (3.80) turns to
For 0<ρ<1, according to (3.84), we have
Here, by using Young inequality, we know
According to (3.65) and (3.66), we know
and
By substituting (3.87) and (3.88) into (3.86), we have
which means that (3.85) turns to (3.40).
4.
Continuous dependence on initial data of the global solution for nonlinear weak damping case
In this section, we consider the continuous dependence of the global solution on the initial data for the nonlinear weak damping case of the model equations in problem (1.1) by supposing that m≥1, r≥1, and ˆm=ˆr=1 in Assumption 2.1, which means that the weak damping terms gj(s), j=1,2, take the nonlinear form for |s|≥1 and linear form for |s|<1. These conditions are applied to improve the estimate (1.2) and reflect the decay property of (1.1), which was clearly clarified in Corollary 2.14 in [5], that is, the condition ˆm=ˆr=1 is necessary to obtain the exponential decay of the energy, which helps to get the exponential decay, and the absence of such linear condition can only lead to the polynomial decay of the energy. Hence although we discuss the nonlinear weak damping case here, we still need to assume that the terms gj(s), j=1,2, take the linear form for |s|<1.
Theorem 4.1. (Continuous dependence on initial data for nonlinear weak damping case) Let Assumption 2.1 and Assumption 2.2 hold with ˆr=ˆm=1, E(z0,z1)<M(s0−ν), E(˜z0,˜z1)<M(s0−ν), ‖z0‖V≤s0−ν, and ‖˜z0‖V≤s0−ν for some ν>0. Let z=(u,ϕ) and ˜z=(˜u,˜ϕ) are the global solutions to the problem (1.1) with the initial data z0, z1, and ˜z0, ˜z1, respectively, where M and s0 are defined in (2.18) and (2.19), respectively. Then one has
where
and θ>0, ˜θ>0, and T>0 satisfy
and
ˉM is defined in (3.42),
and
Proof. Due to Corollary 2.14 in [5], for any T>0, we know that there exist θ and ˜θ to make (4.3) and (4.4) hold, where θ is dependent on E(z0,z1) and T, and ˜θ is dependent on E(˜z0,˜z1) and T. According to Proposition 2.11 in [5], the assumptions E(z0,z1)<M(s0−ν), ‖z0‖V≤s0−ν, and E(˜z0,˜z1)<M(s0−ν), ‖˜z0‖V≤s0−ν give z0∈W and ˜z0∈W, respectively. Here M(s0−ν)<ˆd can be observed according to (2.17). Thus, we know (3.26) also holds. According to these facts and (2.16), we have
and
Due to (4.2), we know that (4.6) and (4.7) turn to
and
respectively. According to (4.8) and (4.9), we have
and
which mean
Next, we need to use the estimate (3.64) to continue this proof. More precisely, by substituting (4.10) into (3.64), we obtain
By substituting (4.11) into (3.61) and the similar process of obtaining (3.69), we have
According to (3.60), we know
i.e.,
where b0 is defined by (4.5). Meanwhile, combining (4.8) and (4.9), we know
i.e.,
and
where b0>0 and 1−b0>0 are ensured by (4.5). According to (4.13), (4.14) and (4.15), we have
According to (4.5), we have
i.e.,
in (4.17). Meanwhile, according to (4.13), (4.15) and (4.16), we notice that
Due to (4.17) and (4.19), we know that (4.12) turns to
By substituting (4.20) into (3.43), we obtain
where
Here, according to (4.22), we notice that D1≤N1λ2, which means that (4.21) turns to
i.e.,
By similar process of obtaining (3.84), we have
For 0<κ<1, according to (4.25), we know
By the similar process of obtaining (3.86), we have
According to (4.8) and (4.9), we know
and
By substituting (4.28) and (4.29) into (4.27), we have
which means that (4.26) turns to (4.1).
5.
Lower bound estimate of blowup time for positive initial energy and nonlinear weak damping case
The finite time blowup at the positive initial energy level was established for the linear weak damping case and nonlinear weak damping case in [22], and for the linear weak damping case, the lower and upper bounds of the blowup time were also estimated there. Hence in this section, we shall estimate the lower bound of the blowup time at the positive initial energy level for the nonlinear weak damping case.
Theorem 5.1. (Lower bound of blowup time for positive initial energy and nonlinear weak damping case) Let Assumption 2.1 and Assumption 2.2 hold, and E(z0,z1)≥0. Suppose z(x,t) is the solution to problem (1.1). If z(x,t) blows up at a finite time T0, then we have the estimate of blowup time
where
and
Proof. Let z=(u,ϕ) be a weak solution to problem (1.1). We suppose that such solution blows up at a finite time T0. Our goal is to obtain an estimate of the lower bound of T0.
For t∈[0,T0), we define
then, by Hölder inequality and Young inequality, we have
Next task is to estimate the terms in the last line of (5.2). By (2.14) and (2.16), we obtain
According to (3.16), we know
where E(z0,z1)≥0. We notice that (5.3) and (5.4) give
which means
and
Combining (2.5) and (5.6), we see
By substituting (5.7) and (5.8) into (5.2), we have
We consider the function h(x):=xp,x>0,p>1. Since h″(x)=p(p−1)xp−2>0, h(x) is a convex function. Thus it gives that
that is to say
Then, due to E(z0,z1)≥0 and G(t)≥0, we can get
which means that (5.9) turns to
i.e.,
Recalling the assumption that the solution of problem (1.1) blows up in finite time T0, we have
Then, integrating both sides of (5.11) on (0,T0) and combining (5.12), we get
Thus, the proof of Theorem 5.1 is completed.
6.
Appendix: a variation of Gronwall's inequality
In Sept Ⅰ of the proofs of Theorem 3.2, by the classical form of Gronwall's inequality (integral form) shown in Appendix B.2 of [4], we know that (3.59) gives
In (6.1), the growth order of the distance of the solutions, i.e., ˆE(t), is controlled by the product of an exponential function and a polynomial function, which is higher than that in (1.2) established for the local solution. In Sept Ⅱ of the proofs of Theorem 3.2, in order to build the growth estimate of ˆE(t) in the same form as (1.2) for the global solution, i.e., (3.60), we need the following variation of Gronwall's inequality.
Proposition 6.1. For a nonnegative, summable function ζ(t) on [0,ˉT] with satisfying
for the constants ˉC1,ˉC2≥0, one has
for a.e. 0≤t≤ˉT.
Proof. We use the similar idea of proving the classical form of Gronwall's inequality shown by Appendix B in [4] to give the proofs. We first define the auxiliary function
By direct calculation, we have
Substituting (6.2) into (6.5), we have
which means
i.e.,
According to (6.4) and (6.6), we have
Substituting (6.7) into (6.2), we obtain (6.3).
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
Runzhang Xu was supported by the National Natural Science Foundation of China (12271122) and the Fundamental Research Funds for the Central Universities. Chao Yang was supported by the Ph.D. Student Research and Innovation Fund of the Fundamental Research Funds for the Central Universities (3072022GIP2403).
Conflict of interest
The authors declare there is no conflict of interest.













 DownLoad:
DownLoad: