1. Introduction
Systems that harvest the energy from ocean waves, tidaland ocean flows, along with more exotic technologies like salinity gradient engines and ocean thermal energy conversion (OTEC), collectively known as Ocean Renewable Energy (ORE), are attracting increasing interest in Australia as a potentially viable source of renewable energy. The Australian Commonwealth Scientific and Industrial Research Organisation (CSIRO) was commissioned to produce maps of wave, tidaland non-tidal ocean flow energy distributions around the Australian coastline. These preliminary energy distribution maps, produced from the best available existing information, provide evidence of substantial, potentially extractable energy [1,2] . Several Australian and overseas companies have initiated ventures to use ORE for grid-connected electricity generation and /or related uses, such as desalination.
This paper considers ocean energy conversion devices and their characteristics with specific examples of devices for which performance data is available. In addition issues in setting up “farms” of multiple devices are described. The analysis concentrates particularly on wave and tidal flow energy as the most likely form of significant ORE in Australia.
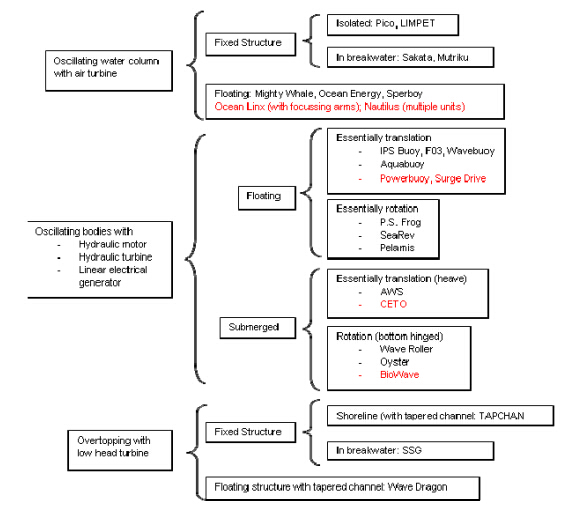
Over 200 devices have been proposed for the extraction of ORE. Of these, only a few have actually been constructed and are anywhere near demonstration or at commercial size, and more importantly, have been tested in actual operating conditions. Wave energy extraction devices largely fall into three categories-oscillating water columns that drive air turbines, oscillating bodies (floats, buoys) that drive generators or produce pressurized water and overtopping systems that drive water turbines. Tidaland ocean flow devices consist of turbines placed in either constricted or unrestricted water flows. Other types of extraction devices that draw energy from ocean thermaland salinity gradients are available, but there are few locations in Australia where they would be applicable at a reasonable scale and cost.
Wave power is potentially the single greatest ORE source for Australia. For commercial operation, wave devices will need to be built in “wave farms”; collections of devices in specific areas. Ocean current is widely available, but few devices, and even fewer economic devices, presently exist to exploit it. Ocean thermal, salinity gradient and tidal power are all available in significant quantity within restricted areas of Australia and have the potential to supply a useful niche market. The machinery required to access tidal power is the most developed of all the technologies; however, its environmental impact may be the least understood. Wave power in Australia is ubiquitous to the south west, south and south east coasts and provides potentially the greatest resource of energy with a preliminary estimate [3] of the extractable energy suggesting that it could supply up to ten percent of Australia’s electricity needs by 2050 [1,4] . For a more technical discussion of the wave resource of the southern seaboard see [3] .
The solar energy that creates freshwater streams by evaporating water from the oceans can be retrieved by remixing that freshwater with sea water. This salinity difference between sea water and the relatively fresh water returned to the sea, by the world’s rivers and flood pumping stations, represents 2 to 3 TW of resource and 150 GW of extractable power [5] . This is not likely to be relevant to Australia except perhaps as a means of energy storage in remote, reversible desalination plants.
Ocean Thermal Energy Conversion (OTEC) supplies energy by taking advantage of the difference in temperature between an ocean’s surface and depths greater than a kilometer. The surface temperature varies seasonally with solar intensity while temperatures at 1km depth are relatively constant at about 4 °C.
Although the authors acknowledge the interesting science behind both these technology areas, unfortunately they are outside the scope of this report, principally for brevity but also because there is no current plan to utilize this technology in Australia.
2. Wave energy devices
The classification of wave energy converters (WECs) is not harmonized; there are many systems in use and each share subsets of techniques and nomenclature. Two commonly used broad classifications are described here, together with their associated techniques [6,7,8,9,10,11,12] :
· collector surface orientations: (point absorber, attenuator and terminator), and
· wave energy transfer mechanism: (oscillating water column, overtopping and oscillating bodies).
2.1. Classification by collector surface orientation
2.1.1. Point absorber
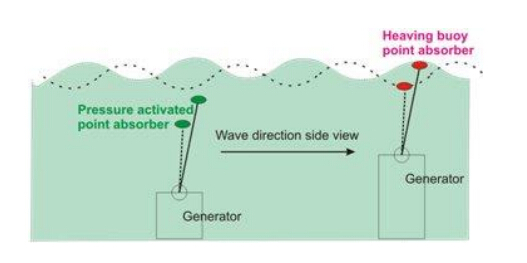
The term point absorber refers to devices that most commonly incorporate a float that is small compared to the swell wavelength. The device is able to accept wave energy from any direction, and energy output is dependent on wave frequency. It can be tethered so that it is submerged, or it can float near the surface and “surge” or “heave” with the movement of the water, as shown in Figure 1.
2.1.2. Linear absorber or attenuator
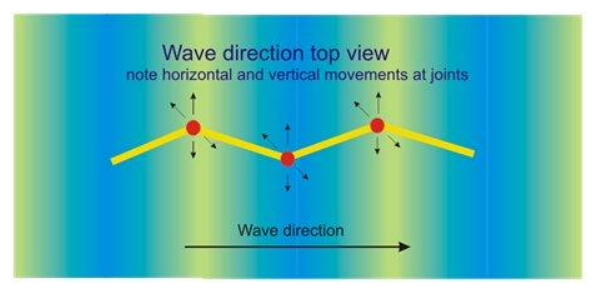
These devices incorporate a float, or a number of floats that are shaped or distributed to be aligned in the direction of wave travel. Their overall length may be of the same order as the swell wavelength. However, they are also wavelength dependent. Unlike a point absorber they need to be slack moored so that they can turn to maintain their principal axis normal to the incoming wave crests, see Figure 2.
2.1.3. Terminator
Terminators are designed to collect energy from waves by directly facing them. They may include passive devices such as a tapered channel to focus energy from a wide section of wave front. Examples of terminators include oscillating water column and overtopping classes of device, see Figure 3.
2.2. Classification by wave energy transfer mechanism
2.2.1. Overtopping
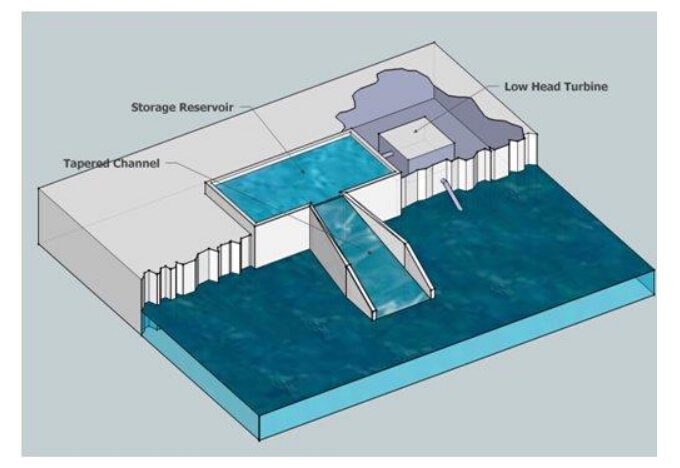
Overtopping devices are terminators. They face into the wave direction and direct waves up a ramp and into a catchment tank. These devices are designed to concentrate wave energy from a wide area to the narrow collecting ramp to effectively increase the wave height at the ramp. The ramp converts the waves horizontally directed energy flux into vertically directed potential energy by “focusing” and lifting the incoming water, which can rise high enough to pass over a walland into the catchment tank where it forms a head of several meters of water pressure. The water then flows down through a bank of “low head” turbines to turn a generator. These devices can be attached to the sea bed or shoreline, as shown in Figure 3, or be designed to float. The Wave Dragon is an example of a floating overtopping WEC.
2.2.2. Oscillating water column (OWC)
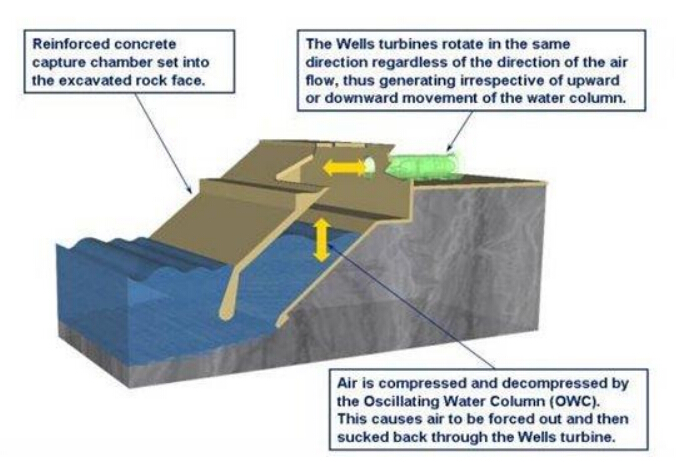
These devices are nearly always terminators in which energy transfers from the wave to the converter via a pneumatic intermediate stage. The principle is analogous to a blow hole and is shown in Figure 4. Waves enter a chamber with a horizontal opening facing the sea. The wave front traps a volume of air and pushes it through a funnel or chimney containing a turbine. The turbine is designed to rotate in one direction only independent of the direction of the air flow. Two designs for this are the Wells turbine that uses symmetric airfoils to allow unidirectional rotation and the Denniss-Auld turbine which uses blade pitch control to achieve unidirectional rotation with a higher efficiency than the Wells turbine. These devices are usually fixed to the seabed or coastline. However, they can be built such that the whole of the device floats on the ocean and is moored away from shore. Examples of such converters are:
· Shore-based fixed installations such as the European OWC Wave Power Plant on the island of Pico, Portugaland the LIMPET, deployed on the Isle of Islay, Scotland .
· Offshore floating oscillating WEC such as the Oceanlinx devices developed in Australia and the Mighty Whale developed in Japan [14] .
2.2.3. Oscillating body
The oscillating body classification outlines how wave energy that is harvested using floating or submerged barriers or buoys can be transferred to the energy converter using mechanical levers or pistons. There are a number of sub classifications presented below.
· Single-body: fixed frame
A buoy or other floating body (wave-buoy) on the sea surface picks up wave energy and transfers it to a converter that turns it into electrical or hydraulic energy as shown in Figure 1. The converter is set in a fixed frame of reference such as the sea bed or a point on a nearby shore. The mechanical connection between the buoy and converter is often a taut cable connected to a moving actuator in the converter. The converter may also include technology to allow active control of the dynamics so that performance can be maximized for any given wave environment encountered. Examples of such converters are the Sea Based linear electrical generator developed at Uppsala University [15] .
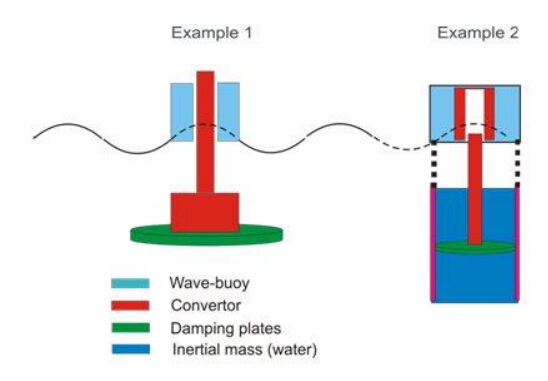
· Two-body: inertial
The principal difference between a single-body and two-body WEC (Figure 5) is that the converter is contained within or adjacent to the wave-buoy instead of being attached to a fixed frame on land or the sea floor. The two bodies considered here are the wave-buoy and a converter component. They are arranged so that they move differentially in response to waves. This can be achieved by arranging for a local mass of water to react against a damping plate attached to the converter. The resulting differential movement allows the transfer of mechanical energy from the wave-buoy to the converter.
The wave float and converter may be arranged coaxially as in the L-10 linear electrical generator, developed at Oregon State University. They may also be connected by a mechanism such as a piston and inertial mass (water) as in the IPS buoy developed by Uppsala University. As with the single body fixed frame devices the connection may be associated with an elastic component to assist in load matching between the wave-buoy and the generator and there is a consequent need for tuning the converter to match the spectrum of the wave environment.
· Multi-body: inertialand fixed frame
The two-body systems described above can be combined to include multiple sets of generators and wave harvesting floats connected together. For example the Wave Rider (Figure 6) with 20 floats connected to hydraulic pistons set in a fixed frame converter [16] ; or the Pelamis, which has four floating cylindrical hollow steel tubes, linked via hinges coupled to hydraulic generators, forming a multi-body inertial converter [17] .
· Pitching devices
These devices are tethered buoys designed to rock back and forth in the waves picking up energy from the movement of the wave. One of the earliest examples is the Salter Duck. Due to the variability in the direction from which waves come, there is some difficulty to adapting tether arrangements to cope. This means that these devices are best used where the direction the wave comes from does not vary significantly.
· Hinged systems - pendulum - oscillating wave surge converters
The pendulum category of WEC describes devices which form a wall in the water, arranged to hinge around a horizontal axis located either near the surface (for example the Pendulor), or near the sea floor (for example in an inverted pendulum configuration such as Aquamarine Power’s Oyster). These devices capture energy from the horizontal movement of the wave as it surges near the shore. Some are designed to attach to a floating platform so that they can self align to the direction of the wave.
2.3. Summary of WEC energy transfer mechanisms
Inevitably there are a few WECs that operate on principles that cannot be covered by the classifications described here. One such example is the Ocean WaveMaster converter, a submerged device that uses the differential pressures below wave peaks and troughs to drive submerged turbines. A classification scheme by wave energy transfer mechanism is illustrated in Figure 7.
3. Ocean and tidal current
3.1. General approaches to tidal power conversion
Tidal power conversion is achieved by the placement of turbines in a tidal current. The placement can be as part of a dam wall in which sluice gates are opened to fill the dam and closed to divert flow through a turbine. Or they can be part of an open wall that traverses a tidal flow gradient, or supported on a bridge like structure so that only the turbine and bridge supports are in the tidal stream, or the turbines can be individually supported in the tidal stream.
3.1.1. Barrages
The dam wall approach is known as a barrage and has the dual advantage of providing energy storage and intensifying flow rates so that energy can be extracted with fewer turbines and /or smaller turbine blades. Well known examples are the La Rance Tidal Power Station in France which generates 240MW and the Sihwa scheme in South Korea, where an artificial lake intended to supply fresh water became polluted and was ab and oned. Turbines are now built into the dam wall to allow sea water to exchange with the lake water and improve its quality while supplying an estimated 254 MW of power generation capacity. Issues with barrage tidal power converters include the significant environmental impacts caused by restricting tidal flow rates and extent. This together with cost has seen the cancellation of the 8 GW AUD$15 billion Severn tidal barrage project in the United Kingdom.
3.1.2. Free Stream Tidal Turbine
Free stream turbines are st and -alone, self supporting devices. Their advantages are reduced infrastructure cost and reduced environmental impact. However, they operate in a relatively limited range of tidal velocities with a lower economic limit of 2 m/s and an engineering limit of 3 m/s due to stresses on the turbine blade. At present there is a strong research focus on optimizing turbine shrouds to increase the turbine’s capture width and flow velocity. A number of units (tens of kilowatts up to 1.2 MW) are being installed and assessed in Canada, China, Norway and the United Kingdom.
3.1.3. Tidal Fences
A trade-off between the “free stream” and “barrage” methods is the use of a bridge-like structure known as a “fence” or “caisson”, which supports a set of turbines across the flow of sea water. This approach provides some freedom for marine life to pass between the turbines and less restriction on tidal flow and area. It can also serve the dual function of a bridge and a tidal power plant. There are no examples of large scale tidal fences in use today, although a substantial number of proposals have been made with one of the largest advanced being for a 2.2 GW, AUD$2.8 billion across the San Bernardino Strait in the Philippines.
3.1.4. Dynamic Tidal Power
A new concept in tidal power energy involves constructing a long wall from the coast into the ocean so that it traverses a tidal flow gradient at an angle that does not excessively compromise tidal influx to a bay or estuary. The wall may be “T”-shaped, terminating on the sea wards side in a shorter wall at right angles. A pressure differential “head” forms across the wall to provide current flow through a turbine.
3.2. Hydraulic Turbines
Hydraulic turbines are usually either vertical axis or horizontal axis devices. Each has advantages and disadvantages and is used for different conditions and locations.
3.2.1. Horizontal Axis Turbines (Axis parallel to flow)
Horizontal axis turbines spin around an axis parallel to a horizontal fluid flow. They are generally the most efficient method for converting the energy from a unidirectional fluid flow. These devices are generally used where the direction of flow is well known. Some devices are able to automatically align to cope with slow changes in flow direction. The Atlantis Resources Corporation “AK” device is an example, and is illustrated in Figure 8. A shroud or duct can be used to increase the turbines’ capture area and efficiency. The largest operating free stream turbine is the SeaGen device, which produces up to 1.2 MW of power and is located in Strangford Lough, in Northern Ireland [18] .
3.2.2. Vertical Axis Turbines (Axis orthogonal to flow)
Vertical axis turbines are so named as the axis of rotation of the turbine is generally vertical, in relation to a horizontal fluid flow. It should be noted that a vertical axis device could be arranged with its axis horizontaland still operate successfully so long as the axis was orthogonal to the direction of the flow. One of the advantages of a vertical axis is that there is no requirement for a separate support pole, post or structure on which the turbine is supported, as it can be supported on its own axis from the sea floor, or suspended from above the surface of the water. In the vertical orientation such turbines are insensitive to flow direction, and this can be a significant advantage where the flow may be turbulent, or where the flow direction changes are unpredictable or occur frequently.
A key disadvantage is the relatively lower efficiency compared to horizontal axis turbines. This is mainly due to the additional drag on the non-working blade or blades.
3.2.3. Other Turbines and Devices
Not all designs operate by rotating around an axis. Several companies have conceived and tested oscillating hydrofoil devices. Two known examples include the BioPower “bioStream” and the “Stingray” from IHC Engineering. These systems act as unstable hydrofoils which oscillate about an axis in the stream flow. With appropriate design and control systems they can be made to assume a streamlined arrangement in extreme flow conditions. The movement is a swimming motion, similar to a fish tail, except energy is being generated rather than expended. BioPower state on their
website [20] that a 250 kW pilot plant is under construction and installation is planned at Port Fairy, Victoria, Australia in 2015. The device is shown in Figure 9.
4. Desalination
In addition to electricity production, wave power can supply energy as high pressure brine for specific processes, thus removing load from electricity generators. Desalination is a particularly useful example. Desalination plants are becoming more common globally. Within Australia alone there are six operating desalination plants (Victoria, Queensland , South Australia, New South Wales and two in Western Australia) and at least one other planned. The reverse osmosis process is currently considered the most energy efficient method for desalination and is used by most modern plants. The energy requirements for various options are:
· pumping energy with no desalination, to supply fresh water in Newcastle, Australia on average, typically 0.4 Wh/L [21] ,
· run a reverse osmosis desalination plant between 3 to 6 Wh/L [22,23,24,25] ,
· run a vapor compression desalination plant 6 to 16 Wh/L [26] , and
· run a distillation-type desalination plant 22 Wh/L [27] .
A number of state governments are purchasing renewable energy to offset the carbon footprint of their desalination plants. For example, Sydney’s desalination plant is indirectly powered by 100% renewable energy from Capital Wind Farm at Bungendore.
As an alternative to providing a carbon offset, wave energy could contribute to desalination directly by supplying high pressure sea water for the reverse osmosis desalination technique, or indirectly by supplying hydraulic or electrical power to transport groundwater or treated water from a sewage plant for desalination or purification. Whether it is more efficient to use a WEC to provide hydraulic pressure or electricity depends on the plant’s elevation and distance from the converter. It is significantly more expensive to transport hydraulic pressure than electricity over long distances. Pumping pressures for typical reverse osmosis desalination plants include:
· Hadera, Israel, pumping 275 ML per day and requiring a pressure of 67 to 75 Bar (6.7 to 7.5 MPa) [28] , and
· Tampa Bay, USA, pumping 95 ML per day and requiring a pressure of 625 to 1050 psi (4.3 to 7.2 MPa) [29] .
Such pressures may be considered “high”, but if an existing ocean energy converter is unable to generate these pressures directly, due to design or to a low energy ocean state, a “pressure intensifier” can be utilized. Such a system has been proposed to allow an Oyster WEC to be used to pump water to a reverse osmosis desalination process [30] .
There are currently two operational examples of WECs used to desalinate water. In one case an oscillating water column is used to create electrical energy for powering the electric pumps in a reverse osmosis desalination system (Vizhinjam, India, 2004 [31] ). In the other case, a device was developed and commercialized for using wave energy to directly pump sea water through a reverse osmosis desalination system (The DELBUOY™, by ISTS Delaware Inc [32] ).
5. Key design constraints
5.1. Geographic location
Ocean WECs and current flow converters can be designed for most ocean and estuarine environments. However, the location makes a considerable impact on the cost effectiveness of a design approach. Some of the key design considerations are briefly described below.
Deep Ocean (greater than 500 m depth) : Ocean waves at these depths have lost very little energy. The difficulties of anchorage, the limitations on design imposed by longer wavelengths and smaller wave heights, and logistical costs are all likely to preclude this option, except where there may be a local need for power such as for island communities or drilling rigs.
Off Shore (greater than 50 to 70 m depth) : As waves reach the continental shelf a small amount of wave energy is lost and the wave lengths decrease. The relative proximity to land reduces capital, operations and maintenance costs, and shallower depths increase the range of anchorage options, and therefore WEC designs, compared to deep ocean installations.
Near Shore (less than 50 m) : A WEC located near shore trades off the advantages and disadvantages of off shore and on shore systems. The power and consistency of wave energy may have been lost by the time a wave is close to shore. However, the capital, operation and maintenance costs are likely to be lower and design options are increased. For example these might include mounting a wave buoy in the sea and mechanically coupling it to a land based generator. An ocean current system would typically be located near shore. This decision would be resource based and some reasonable ocean currents may exist further from shore. The decision on near shore location becomes a trade-off between choosing a depth that offers a good resource, but is not so deep as to incur large maintenance costs (for example decompression divers), or expensive engineering solutions (to float the mechanism for maintenance).
On Shore: Locating a WEC onshore has the advantages of accessibility for maintenance, limited power transmission costs and the potential for designers to use the land as part of the structure of the device. However, wave energy decreases in magnitude the closer to the shoreline the wave gets. There may also be difficulty in finding suitable on shore sites for WECs, due to competing land uses as well as correct land profile, access to reasonable waves, environmental impact, proximity to necessary infrastructure etc.
In Shore (estuarine) : Where a tidal current system is harvesting a river’s tidal flow the system would be placed within the river system. This may be a barrage or dam that captures some or all of the river’s flow.
5.2. Power Transmission
To provide electrical energy to the main power grid, a water based system must transport energy to the shore either as electrical energy, or as some other form which can be converted on shore. Examples of energy transportation methods include direct current electrical energy, alternating current electrical energy, or hydraulic power (as pumped sea water). Using pumped sea water as a method of transmitting power provides further potential for storing energy, or alternative uses of the energy, as outlined below. In general if a significant distance is involved such as for off shore installations, the option of transmitting electrical energy is likely to be the most cost effective.
Although there are some examples of WEC systems that transmit hydraulic power, for onshore desalination or power production, the authors are unaware of any current/tidal systems that transmit hydraulic power. In principle there is no reason why this could not be done and in the case of off-shore systems there may be distinct advantages in minimizing the level of electrification in the deployed system.
5.3. Energy Storage
For smooth delivery of power from a water based system, some amount of energy storage or “capacitance” is required to help offset the cyclic nature of wave energy. Such devices could potentially take the form of flywheels, hydraulic accumulators, a head of water, batteries, mechanical or pneumatic springs, salinity gradient systems etc. It seems that most WECs include some form of capacitance for short term power smoothing, while some could potentially use capacitance for the long term storage of energy.
As mentioned above, some wave energy generators have the ability to pump water directly to shore (for example Carnegie CETO). This not only provides the ability to smooth the power output, but also the potential to store energy during times when the electrical energy is not needed. This might be achieved by simply pumping sea water into an elevated reservoir or accumulator, which can then be released at some point later to generate electricity at a time when it is required.
In the case of a tidal system that partially or fully dams a river system, the basis of the energy storage can be as a head of water which is then converted to power over a more convenient time period.
5.4. Directional Dependency/Independency
Some types of WEC work equally well in waves from any direction, including, by definition, any Point Absorber. Other types of WEC work best when wave energy is from a given direction. Pendulums, pitching devices and terminator style converters are commonly directionally dependent. With suitable anchorage, some directionally dependent WECs, such as the Pelamis and the Wave Dragon, are able to realign their orientation to the wave direction for optimal energy conversion.
As tidaland most ocean current resources are predominantly mono- or bi-directional systems, designs for capture of this energy do not particularly need to consider directional dependency. Consideration needs to be given to correctly setting the device’s orientation. In addition a few systems are capable of swiveling to harvest variable ocean current direction.
5.5. Strategies for Coping with Extreme Sea States
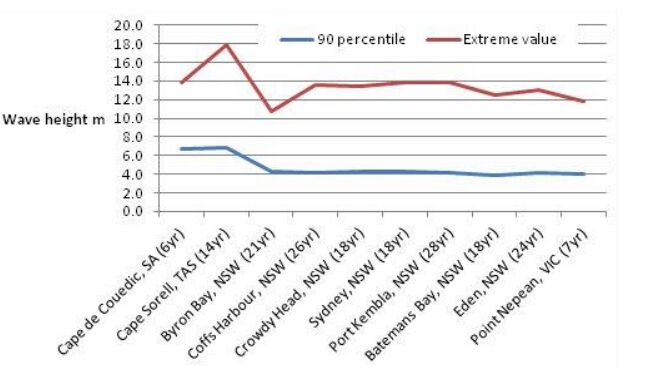
A key issue for Wave Farms and WECs, which may comprise a hundred or more converters of similar size to a bulk carrier, has been the need to withst and storms and extreme wave conditions, while remaining cost effective. However, WECs are usually designed for best performance in average or predominant wave conditions, and are sized and manufactured accordingly. The devices are therefore not necessarily designed to work optimally in high wave energy sea states, but they must be designed to survive extreme wave heights that may occur only once in twenty years [33] .
Wave buoy measurements at eight sites around the southern coast of Australia show that a maximum wave height of between 15 to 17 m has been observed at least once over a twenty year period at each of these sites. The latest was an 18 m wave on 16 September 2010, 10 km off Cape Sorrell on the west coast of Tasmania (Figure 10).
Strategies for coping with such extreme waves include:
· providing protection mechanisms such as automated lowering of expensive components to the sea floor when extreme conditions are forecast,
· the device and the farm could be made large enough or sufficiently sea worthy to cope with the extreme conditions,
· shutting down the devices so that they are not operating, and simply “ride the waves”, and
· if a device or components of that device were cheap enough for their energy and economic costs to be paid back between extreme wave events, then it could be an acceptable strategy to design them as potentially disposable or recyclable elements. This approach has been adopted by The Wave Power Project at Lysekil where a relatively low cost and easily replaced wave buoy is deemed sacrificial, while the high cost generation equipment is located on the sea floor so that it is not exposed to damaging wave energy [34] .
Extreme wave conditions may be a consideration for near shore and off shore deployment of ocean current systems. Tidaland current systems are substantially, if not completely, below the surface and thus are utilizing the strategy noted above: placement of the device to the sea floor to survive extreme events.
6. Environmental Impact
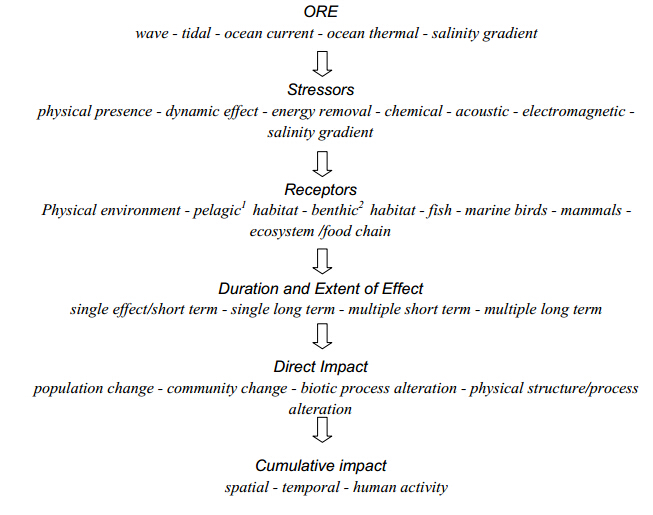
The development of ORE is generally perceived as having a minimal risk of environmental degradation and on occasion a net positive environmental outcome, for example the recent construction of a 254 MW tidal power station at Sihwa Lake North Korea that will supply 254 MW of power and remediate stagnation caused by the construction of a sea wall in 1994 [35] ; or the provision of shelter and potential for seeding artificial reefs. While such instances do show the potential for creative and positive solutions arising from careful planning the slow pace of development of ORE has been matched by an even slower pace of research into its environmental consequences [36,37] . This deficit will be evident in the following discussion, which suggests a great need for research linked to the development of ORE in Australia.
The potential for environmental impacts, their range and interdependencies can be more readily appreciated by presenting them as classifications in a framework of: technologies, stressors, receptors and impacts [37] . Figure 11 shows the framework used here to review the environmental risks associated with wave, tidal, current, and ocean thermal sources of renewable energy and to highlight, both the known impact and those potential impacts that remain unresearched.
6.1. Wave Power
Off shore wave devices have the potential for low visibility and noise level from a shore line perspective and minimal construction site impact. However, the impact of off shore ORE devices will depend non-linearly on scale. While small developments are unlikely to have much effect, as the size increases a range of environmental impacts will need research. These include the impacts of i) extracting energy from the sea and ii) the presence of a large distributed structure with some of the characteristics of an artificial reef or fish aggregation device. Both features can have positive and negative impacts.
6.1.1. Sea Calming Effects (taking energy from the sea)
The effects of diffraction and the small size of low power (less than 100 MW) installations a kilometer or more off shore could, by design, avoid appreciably reducing the energy flux that reaches the shore, by limiting the extraction of energy. For example a large scale (500 MW) wave farm that reduces an average energy flux of 50 kW/m by 20%, would extend along 50 km of shore line. Limiting the extraction to 10% would increase the extension proportionately. The trade off is between the impact of taking up long lengths of shore line vs. the need to limit the extraction of energy from waves. The balance between detrimentaland beneficial effects would need specific research for each location; and ongoing research is essential if wave farm technology develops and expands [37] . Typical effects might include:
· A wave farm might be expected to shelter beaches and prevent erosion. However, it might also encourage the accretion of s and over a sea bed and this in turn could alter the growth of plant life for example reducing kelp forests and changing the associated fauna, for example rock lobsters and abalone might be critically affected. Movement of s and towards beaches might also result in the denuding of some beaches and accumulation of s and in others [37,38] .
· Changes in sediment transport, could impact a wide range of species which rely on the presence of a certain distribution or particle sizes in sediments, a distribution which could be affected by the physical presence of structures and /or the removal of some of the wave energy which would naturally be present [37] .
· Alteration of verticaland lateral currents may change the transport of food and larvae from the surface to the sea bed or between feeding and spawning grounds [37] .
6.1.2. Artificial Reefs or Fish Aggregation Devices
Floating structures and artificial reefs are thought to attract juvenile and adult fish byproviding [36,37] ;
· no take zones and protection against predation,
· the opportunity for new food sources to develop,
· opportunities for spawning, and
· stations for resting or cleaning.
The above effects may improve or degrade a local environment. For example account should be taken of the potential to [37] :
· divert marine life from their well established natural habitat,
· favor more opportunistic species that do not reflect the populations of the local natural habitat,
· interfere with the normal feeding patterns and movement of fish, sea birds and marine mammals by creating obstacles to passage, and
· provide misleading sensory data through the generation of electromagnetic signals, noise and lighting that may either repel or attract marine life. For example the electromagnetic fields associated with power cables may interfere with the ability of sharks and rays to navigate and find prey; while buoy warning lights may interfere with the behavior of sea birds, diverting them from normal activities or causing disorientation and collision [36,37] .
Whether such interfering factors have a net positive or negative effect on marine life and diversity is likely to be locale dependent and to require a strategic program of research associated with the ongoing development of ORE.
6.2. Tidal
The degree to which tidal renewable energy devices impact the environment depends strongly on the class of device employed: Barrage, tidal fence, tidal current or dynamic tidal power as described in Section 3.
6.2.1. Barrages
Barrages are essentially dams with turbines incorporated into their outlets. While each site would need to be assessed on its own merits [39] , they can have significant environmental impacts including reducing the intertidal area, slowing down currents, changing sediment transport, reducing the salinity range and changing bottom water characteristics. Each and all of these effects can lead to significant changes in the composition of estuarine flora and fauna [40,41] . This, together with their high capital cost and their potential impact on shipping, limits the range of suitable sites in Australia and makes them unlikely c and idates for renewable energy supply, except, perhaps, for the regions near King Sound in the Kimberley region of WA.
6.2.2. Tidal Fences and Turbines
Tidal fences and turbines are likely to be less damaging to the environment than a barrage as they allow water to flow relatively freely through the caisson support structure. The rotating blades do pose a risk to fish and marine mammals but this can be reduced by gearing turbines to turn slowly (25-50 rpm), providing fences or acoustic warnings to direct larger animals away from the turbines and possibly providing detection mechanisms that can slow or stop the turbines in the presence of animals. In the relatively small scale installations constructed to date the timing and amplitude of the tide remains substantially unchanged, reducing the impact on the estuarine tidal area, salinity, and sediment transport. However, for larger scale systems, the effect of changes in tidal velocity on sediment transport will need to be assessed [40,42,43,44] .
6.3. Ocean Thermal Energy Conversion
Environmental impacts from Ocean Thermal Energy Conversion (OTEC) include those associated with the construction, maintenance and decommissioning of any large marine structure.
Apart from this there is a potential impact related to the transference of nutrient and chemical rich cooling water from the deep ocean and its discharge as nutrient rich warmer water near the sea surface. This may alter the food web, changing the quantity, size and species of marine organisms. Larvae or juveniles, small fish, jellyfish, and invertebrates attracted to the nutrient rich waters could become entrained in the OTEC warm water intake. The degree to which this has a positive or negative impact on fisheries and the ecosystem is unknown [45,46] , and would require study at each site as has been carried out for the Hawaii OTEC site [47] .
In addition a relatively small amount of CO2 could be released due to out-gassing from water drawn from the abyss. This has been estimated at about 1% of the CO2 released from fuel oil combustion for energy production equivalent to the OTEC installation. These issues are thought to be controllable by arranging for the subsurface discharge of cooling water below the ocean surface mixed layers and photic zone, an action that will also improve the efficiency of the plant by reducing the cooling of surface water [40] .
The remaining potential impacts are due to possible release of the chemicals ammonia and chlorine. Chlorine if released has been estimated at levels of 0.02 ppm. Ammonia could be used in a closed cycle system and would have a significantly toxic impact if released in the event of a catastrophic accident or extreme event [40,48] .
6.4. Marine Protected Areas
A Marine Protected Area (MPA) [49] is “an area of land and /or sea especially dedicated to the protection and maintenance of biological diversity and of naturaland associated cultural resources, and managed through legal or other effective means”. It can include:
· Seabeds in deep water. · Mangroves.
· Reefs. · Rock platforms.
· Seagrass beds. · Shipwrecks.
· Tidal lagoons. · Archaeological sites.
· Mudflats. · Underwater areas on the coast.
· Salt marshes.
The types of MPA protection in Australia are formally described using the International Union for Conservation of Nature (IUCN) categories [49,50] , as shown in Table 1.
Table 1. Classification of Marine Protected Areas.
| Type of area | IUCN | Explanation |
| Strict nature reserve | Ia | Managed primarily for scientific research or environmental monitoring. |
| Wilderness area | Ib | Protected and managed to preserve its unmodified condition. |
| National park | II | Protected and managed to preserve its natural condition. |
| Natural monument | III | Protected and managed to preserve its natural or cultural features |
| Habitat/species management area | IV | Managed primarily, including (if necessary) through active intervention, to ensure the maintenance of habitats or to meet the requirements of specific species |
| Protected land scape/seascape | V | Managed to safeguard the integrity of the traditional interactions between people and nature. |
| Managed resource protected area | VI | Managed to ensure long-term protection and maintenance of biological diversity with a sustainable flow of natural products and services to meet community needs |
Less formal categorizations, more oriented to describing levels of protection, are sometimes used in State Government or privately managed MPA’s. These may include terms describing high levels of protection such as “no take zone” or “sanctuary” to the relatively low level of protection described as “multiple use”.
Currently there are more than 200 MPA’s in Australia, covering 64.8 million hectares. They include marine parks, such as the Great Barrier Reef, fish habitat reserves and sanctuaries, aquatic reserves, conservation areas, and marine and coastal parks.
MPAs may be managed either by Federal State or Territory Governments. In 1991 the Australian Government initiated the development of a National Representative System of Marine Protected Areas (NRSMPA). The intent is to increase the resilience of MPAs and more comprehensively reflect the biodiversity of Australia’s marine ecosystems by developing networks of MPA’s that bring together Federal, State and Territory Governments.
6.5. Tourism, Recreation and Fishing
The principal questions regarding the impact of wave farms on tourism, recreation and fishing might be expected to include: noise, visual amenity, safety, effects on surfing, boating, the environment, recreational fishing and local employment. Wave farms of from 50 MW to 250 MW located offshore could extend along 5 km to 35 km of coastline and take up about 5 km2 to 50 km2 of area. They would typically be located from 1 km to 10 km off shore. However, it is unlikely that wave farms greater than 50 MW would prove acceptable where these impacts are of concern.
6.5.1. Noise and Visual Amenity
On shore wave farms would have significant impacts on both noise and visual amenity both during the construction phase and during operation [51,52,53,54,55] . Likewise some forms of wave farm may produce significant levels of underwater noise. However, there is insufficient research to answer the question of what level of subsurface noise is acceptable. With regard to visual amenity and noise above water, most wave farms would not be easily visible from the shore depending on the method of providing navigational hazard warnings and most of the noise generated would be sub surface.
6.5.2. Safety and Boating
The key issues for safety and boating are likely to be navigational hazards and accidental damage to the farm. It will be necessary to ensure that the presence of a wave farm is included on charts and in navigational systems available to small boat users as well as being signaled appropriately. Broken moorings and electrical cabling may bring the possibility of collision or electrical hazards. It would be expected that such issues could be addressed using inbuilt fault detection and buoy location technology.
6.5.3. Surfing
Whereas for single devices and small scale installations the impact on surfing has been shown to be minimal, the same might not be true for a large scale wave farm. There is an economic imperative to concentrate devices in a confined region to reduce capital costs and operations and maintenance expenditure. A trade-off exists between the number of farms, their size and the length of coast line they operate in to achieve a competitive wave energy supply with no undesirable impacts on wave height and period. A 500 MW farm could be designed to extract as much as 50% of the wave power from coast lines that might be expected to extend along 20 km of coast. However, only 10 such farms would be needed to supply 10% of Australia’s electricity in 2050. The same energy could be provided by 50 MW wave farms each taking up 5 km of coast line and extracting 20% of the energy. This would greatly reduce the local impact but require 100 such farms. These are very tentative estimates and it will be essential as wave technology develops to measure and assess the impact of wave energy devices on wave height and period. Projects conducted overseas have benefited in this regard from early engagement with the affected communities.
In areas that rely on fishing, boating and environmental quality to attract tourists it is unlikely that large on shore installations will prove acceptable. Very large off shore installations (500 MW) are also problematic. However, medium scale (less than 50 MW) offshore wave farms that are carefully designed and located may prove usefuland work well in some locations. It is worth emphasizing here that this is a very preliminary review and the impact of wave farms on tourism will depend on the results of environmental research that has yet to be carried out as well as the m and atory environmental assessment and community consultation [56,57,58,59,60,61] .
6.5.4. Reduction in Sea Lanes for Fishing Vessels
This is primarily an issue for off shore wave energy farms. These may be located from 1 km to 10 km off shore, extend up to 30 km along the coast and cover areas from up to 50 km2. Australia has extensive fishing boat operations from virtually all coastal regions and there is clearly a need for careful assessment of the size and distribution of wave farms in regions with well developed fishing industries.
6.5.5. Alteration of the Fishery Environment
All three of the ORE resources: wave power, tidal power and ocean thermal energy can alter the habitat in their vicinity in ways that impact significantly on fisheries. Wave farms may alter the distribution of s and along a coast by reducing the energy and changing the distribution of waves. This has the potential to change the s and coverage of rocks and reefs that host lobster and abalone. Tidal barrages and to a much lesser extent tidal fences and tidal current turbines may reduce intertidal areas, alter sediment transport, salinity range and bottom water characteristics, all of which could change the composition of fish species. Depending on the design, ocean thermal systems may disrupt ecosystems, either by bringing nutrient-rich water to the euphotic zone, triggering algal blooms (some open cycle designs) or causing potentially unwanted cooling or heating [56,57,58,59,60,61] .
7. Conclusion
Ocean energy conversion devices were classified as Wave Energy Conversion devices or Ocean and Tidal Current devices, and sub categorized by method of operation. Wave energy conversion devices were categorized by surface orientation and by energy transfer mechanism. The various operating methodologies were described and matching examples provided with a summary diagram. Ocean and tidal current devices were categorized by energy capture methodology. Descriptions of each methodology have been provided, including some of the advantages and disadvantages of each methodology. The significant environmental impact of the Barrage methodology was highlighted.
A further benefit of production of desalinated water by some forms of ocean energy converters was outlined. This capability was discussed as an alternative to other forms of renewable energy which currently provide electrical energy to desalination plants in Australia: the production and use of high pressure seawater directly in a desalination plant eliminates a conversion step, and its associated efficiency loss, compared to generating electricity to run a seawater pump.
Key design constraints for the installation and operation of ocean energy conversion devices were outlined, with some design trade-offs highlighted. The effects of geographical location in relation to land and ocean depth, methods of power transmission and the potential benefits of some energy storage techniques were summarized. Further design constraints were discussed regarding the directional dependency of some forms of ocean energy conversion devices, and the importance of strategies that allow devices to survive extreme states (particularly for wave energy devices).
Off shore farms are not likely to produce visual or auditory impacts on land owners or shore based businesses. However, sub surface noise may be a problem for divers and for naval operations. The most significant impacts could arise where the size of a wave farm has the potential to interfere with sea lanes, or obstruct fishing areas.
Interference with sea lanes can be mitigated by appropriate selection of device types that can alter wave farm size and shape by as much as a factor of 5 to 10. Likewise it may be possible to use sub surface devices to allow smaller boats to pass over the farm.
It is unlikely that fishing would be allowable over a wave farm; on the other h and there is a reasonable prospect that the farms based on larger devices will serve also as shelters for sea life and promote fishery stocks. In terms of fish production the level of extraction of energy from a wave farm may in some areas need to be researched to ensure that there is no migration of s and that might interfere with rock lobster and abalone fisheries.
Wave farms may also be synergistic with other ocean use. They have the potential for sea calming which could be useful if a farm were combined with an off shore oil or gas well, or wind turbine, or to protect a vulnerable section of coast. They also have the potential to provide significant levels of employment to coastal communities.
Detailed research is required prior to the design of a wave farm and ongoing throughout its development and operation. This is to ensure that its benefits can be optimized and the impacts mitigated, for other users in its vicinity.
Wave farms may have both positive and negative environmentaland competing use impacts and there is likely to be sufficient flexibility in the design parameters for a farm that the benefits can be optimized and the impacts mitigated. However, this will require a detailed level of research specific to each location. This is both to avoid environmental damage and to avoid damage to the farm and to minimize capital, operations and maintenance costs, by building in a program of assessment considerations at each stage of the wave farm design and development.
Conflict of Interest
All authors declare no conflicts of interest in this paper.
Acknowledgements
This work was jointly funded by the CSIRO Energy Transformed and Wealth from Oceans National Research Flagships.









 DownLoad:
DownLoad: