1. Introduction
Forecasting accurately photovoltaic (PV) power output is not only based on climatic conditions but large variation of the power output is also observed due to several factors such as solar irradiance, temperature, wind speed and humidity. Actually PV nominal specifications such as power output or energy yield of recent modules are evaluated by manufacturers under standard conditions (STC) by a flashing technology and these nominal specifications are hand out to customers. Under real outdoor conditions theses specifications are not always valid. Meanwhile, an economical solar simulator based on micro-channel solar cell thermal (MCSCT) [1,2,3] has been designed and tested in indoor condition. Yet, the PV measured data from indoor and outdoor conditions are decorrelated. Since late 70 s the simplest explicit equation [4] for the steady-state operating temperature of a solar module links with the ambient temperature and the incident solar radiation flux had been studied. It is difficult to effectively assess the impact of PV output variability [5,6] on the power grid stability without a clear understanding of the factors that influence this variability.
Many factors have become redundant in the presence of other factors, and their value in the forecasting framework may vary under different prediction horizons and error measurements. Nevertheless, many studies conducted to date have shown that temperature [7,8,9] is the most important parameter that influences the PV output, although the latter is largely dependent on solar irradiance. Comparative studies of different models have been used to predict the PV module temperature in a mathematically [10] explicit and several empirical models [6,11,12] for estimation of PV module temperature have been proposed based on solid state physics of PV or thermal radiation and convection contributions [13,14,15] to the PV operating temperature as well as for PV technologies such as thin film PV system under Mediterranean climate conditions [16]. More implicit in form or experimental results have validated temperature effect on electrical model [17] in outdoor conditions. In the past few years, many statistical techniques [18,19,20,21] have also been proposed to forecast energy output of PV system or others have shown either how to improve confidence intervals of PV data from estimator's variance [22] or modeling solar forecasting through Artificial Neural Network [23,24,25,26] as an alternative to conventional approaches. Also a novel contribution of fault detection algorithm [27] has been proposed using a statistical analysis of real-time long term measured data and theoretical thresholds.
Some studies have used classical regression methods that took advantage of correlation nature of meteorological variables which are used prediction model as inputs. However, regression between non-stationary series may lead to conclude on the existence of a relationship between two variables even though there is no meaningful linear relationship between them. The novelty of this paper is to show that if PV explanatory variables are non stationary then a study of first difference must be determined. An incidental advantage of the first-difference transformation is that it may make a nonstationary time series stationary to reach the final PV equation taking into account the temporal relations between the PV explanatory variables in a moderate zone.
We compared measurements and prediction of energy output [28] in real outdoor conditions as a function of location and environmental conditions mainly solar irradiance φ (W/m2). The goal of the present work carried out is to develop an operational forecasting framework zone. An accurate PV output forecasting method would be of great help to grid operators and would minimize costs while enabling more integration of variable renewable energy (RE) in the grid. The resulting statistical model should then be applied in future works on collected datasets at several particular temperate climatic sites for validation. A mathematical model [29] using satellite data has also been proposed to determine PV performance in continental scale. The two models should be compared in a future work.
Statistically we studied a linear relation analysis of time series data collected over a period of time and investigated mainly the dependent variable of power output P on explanatory variables such as solar irradiance G and temperature T. For that we first determined the stationary character or not of each time series of solar irradiance and temperature as this will set the statistical method to be used. Testing the stationarity of a series would be able to understand autocorrelation function and its statistical significance. Dickey Fuller (DF) have developed a test called Augmented Dickey & Fuller (ADF) [30,31] which is a unit root test for stationarity.
The ADF test is used to determine the method of regression estimation between PV variables such as P, G and T. Then we show that these variables are not stationary at level and an ordinary least square (OLS) regression is only possible at difference level for each variable including a constant in the regression. First results of the study show that temperature at first difference level and the constant are not very significant as the OLS coefficients are well estimated. Then we analyze residual hypotheses.
Analysis of residuals is a powerful diagnostic tool and it helps to assess whether some of underlying assumptions of regression have been violated. Ideally all residuals should be small and unstructured meaning that the regression analysis has been successful in explaining the essential part variation of the dependent variable. We first apply the Goldfeld-Quandt (GQ) test when heteroscedastic variance is related to variables in the regression model then the Durbin Watson (DW) test to detect serial correlation in the residuals. In this present study, the GQ test is well verified but DW test is still doubtful and not very conclusive. Outliers are suspected in the model. Therefore, a more recent procedure such as the Engle & Granger (EG) method is suggested to determine the most appropriate model. Our model is formulated on the basis of PV real conditions statistical approach and is more realistic than steady approach models.
For this study, the small samples of one year daily means data is retrieved among the 7 years measurements from the GREEN lab of Physics department of University of Lorraine in Metz. The PV design of the GREEN lab is an on grid connected system. Six polycrystallinemodules of SCHÜCO technologies are connected in a series wiring pattern and mounted on the south-south east vertical wall of the platform building. Each module has a peak power of 205 WP, at tilt angle of 60°, low ventilation and connected to a SCHÜCO inverter for a power level up to 1 kWP.
This paper is organized as follows. Section 2 is an introduction to the methodology explaining the ADF stationary test and Engle Granger tests for cointegration. In Section 3, we describe the input solar irradiance distribution of this peculiar zone to predetermine if a frequency distribution such as Weibull distribution is expected. In Section 4, we use informal tools such correlograms and Q-statistic to test whether each variable such as solar irradiance G, power output P and temperature T is stationary or non-stationary. The ADF test is applied to each variable and results are presented and analyzed in table form. If a time series has a unit root then first differences of such time series are assume to become stationary. In that section, we apply the ADF test to first difference series transforming non-stationary time series to yield stationary series, we propose a probable estimates difference equation regression model. In section 5, we propose the OLS regression equation and identify outliers before analyzing residuals from the propose regression using the GQ test then the DW-d stat test with its corresponding tabulated bound. We discuss and highlight the proposed regression equation with residuals and introduction to EG method. In section 6, we apply the EG correction mechanism reconciling the short-run behavior with its long-run behavior and a final relationship without suspicious heteroscedasticity is proposed. Finally, conclusion and future work are indicated in Section 7.
2. Methodology
Let us consider a dependent variable Y and a number of explanatory variables such as X's (X1,
X2, ..., Xk). Xk, being the kth explanatory variable. These (k+1) variables will denote the ith observation on explanatory variable Xk. In order to determine the linear relationship between variables, for example, Y = a0 + a1X1 +... + ajXj+... + akXk, the well-known least squares linear regression technique is used. This technique provides an estimate of each of the coefficients for ai, giving a measure of the quality of the linear fit of the correlation coefficient Rand provides confidence intervals for the predictions, etc. The interpretation of R in a multiple regression model is of dubious value and this technique can only be used when observations of one explanatory variable is independent one to each other.
However, and in this study, this hypothesis of independency is not necessarily verified, due to time series: there exists a relationship between the y(t) series and y(t–1), y(t–2) series and so on, there may be an autocorrelation phenomenon for Xk variables as well.
In this context, it is then necessary to check whether the series are stationary or not. Indeed, performing a regression between non-stationary series leads to what is known as spurious results or regression [29] for R2 determination as well as for the regression coefficients. This can lead to conclude the existence of a relationship between two variables when in fact there is no linear relationship between them. Regressions involving time series data include the possibility of obtaining spurious or dubious results [29] in the sense that superficially results look good but on further probing they look suspect.
If variables are non stationary which is the case of this study, then the first difference (or upper orders if needed) must be studied. If these first differences are stationary then the multiple regression technique is used to determine linear relationships between theses first differences. An incidental advantage of the first-difference transformation is that it may make a nonstationary time series stationary.
A linear combination of variables at a non stationary level may become stationary which is given as the co-integration equation also known as the Engel Granger (EG) method [32,33]. Highlighting of such a relationship should allow improving the estimation of the linear relationship between the variables in difference that should also lead to reach the final equation, first by taking into account the temporal relations between the variables, then by introducing explanatory variables as variables measured in the previous period.
2.1. Dickey-Fuller stationary test
The principle of DF [9] in statistics stationary test is based on null hypothesis or test for the existence of a unit root in an autoregressive model. Unit root test is explained in appendix A. DF have shown that under the null hypothesis that is if π = 0 then the estimated t value of the coefficient of Xt–1 follows the τ (tau) statistic. The tau statistic or test is known as the DF test. DF has computed critical tau values and can be obtained in a tabulated form.
The DF test is usually estimated on three models with their corresponding equation under three different null hypotheses. But we should consider only one random walk equation for the model as others are mainly used by economists in a financial field.
Model: Xt is a random walk, where there is no constant or drift component and no trend:
|
Xt=ρXt−1+utorΔXt=πXt−1+ut
|
(1)
|
In each case, the null hypothesis is given for π = 0, that is there is a unit root and the time series is non-stationary. The alternative hypothesis is that π is less than zero and the time series is stationary.
In this paper, the following indication for different hypotheses will be used:
Hypothesis H0 π = 0 means ρ = 1 then such series is a non-stationary series.
Hypothesis H1 π < 0 means ρ < 1 then such series is a stationary series.
It is extremely important to note that the critical values of the tau test to test the hypothesis that π = 0, are different for each of the preceding three specifications of the DF test. The estimation procedure of tau will be explained later from experimental data table. However, if the computed absolute value of the tau statistic (τ) less than the DF critical tau values from tables, hypothesis that π = 0 is rejected in which case the time series is stationary. On the other hand, if the computed τ is less than the critical tau value the null hypothesis is not rejected in which case the time series is non-stationary.
In conducting the DF test it was assumed that the white noise error term ut was uncorrelated. But in case the ut are correlated then DF have developed a test, known as the Augmented Dickey-Fuller (ADF) test which is explained in the next section.
2.2. Augmented Dickey-Fuller stationary test
To tackle autocorrelation problems DF have developed a test called Augmented Dickey-Fuller (ADF) which is still a unit root test for stationarity. This test is conducted by augmenting the above equation by adding the lagged values of the dependent variable ΔXt. This equation is given as follows:
|
Model(1):Xt=ρXt−1+∑pj=1ψjΔXt−j+utorΔXt=πXt−1+∑pj=1ψjΔXt−j+ut
|
(2)
|
Where ΔXt−1=(Xt−1−Xt−2),ΔXt−2=(Xt−2−Xt−3), etc.
The number of lagged difference terms to include is often determined empirically, the goal is to include enough terms so that the error is serially uncorrelated. In ADF still test whether π = 0 and the ADF test follows the same asymptotic distribution as the DF statistic so the same critical values can be used.
2.3. Spurious regression
Let us consider a random walk model given by Eq 3a:
|
Zt=Zt−1+vtandXt=Xt−1+ut
|
(3a)
|
And the same number of observations generated from vt et ut and also assumed that the initial values of both Z and X were zero. Il is also assumed that ut and vt are serially uncorrelated as well as mutually uncorrelated. Suppose Zt is regressed on Xt as both are uncorrelated processes the R2 from the regression of Z on X should be close to zero; that is, there should not be any relationship between the two variables. However, it may happen that the R2 value is significant but there is no linear relationship between the variables. This is the phenomenon of spurious regression and spurious model is not desirable [33].
To avoid spurious regression problem that may arise from regressing a non-stationary time series on one or more non-stationary time series, we have to transform non-stationary time series to make them stationary. If a linear combination of non-stationary variables is stationary, the variables are said to be cointegrated [33]. Their fluctuations are concomitant. But the regression model is not appropriate for highlighting linear relationships between non-stationary variables, this is the problem of spurious regression, so other procedures such as Engle & Granger must be used as described in the next section.
2.4. Engle-Granger tests for cointegration
A linear combination of non stationary variables can be stationary, the variables are then cointegrated and their fluctuations are related. But the OLS regression model is not appropriate for highlighting linear relationships between non stationary variables, this is the problem of spurious regression as discussed earlier. Another procedure such as EG [34,35] is then applied. The EG test for cointegration is a three-step procedure.
The first step: it is necessary to ensure that the first differences of the corresponding Zt and Xt series are stationary series.
The second step: let vt be the residual of the regression of Zt with respect to Xt given as follows:
then if vt is stationary then Zt and Xt series are cointegreted and the relationship is usually called long run equilibrium. Practically it's not possible to do a stationary test on the unknown zt series but the test can be applied to the following series:
ˆvt=Zt−ˆaXt−ˆb where hat a and hat b are determined by regressing Zt with respect to Xt. The critical values of DF test and ADF test are then modified.
The third step: Error Correction Model (ECM)
The model is as follows:
|
ΔZt=γˆvt−1+βΔXt−1+δ+εtandΔZt=γ(Zt−1−ˆaXt−1−ˆb)+βΔXt−1+δ+εt
|
(3c)
|
The three variables of this equation ΔZt,
γt–1 and ΔXt–1 are stationary so that all estimations of this equation are given by the least squares method. If γ is a negative value, vt–1 acts as spring force and thus when vt–1 is a positive value the Zt value has a higher value than it should be given the long run relationship, Zt–1 > aXt–1 + b. As γ has negative value the vt–1 effect on ΔZt gives a negative value and thus Zt < Zt–1 that tends to balance the long run relationship. For those interested on that topic may refer to a more specialized books in econometrics.
3. Solar irradiance frequency distribution test
Solar energy is harnessed with solar PV converting sunlight directly into electricity. Thus the energy output of PV system depends on the input solar irradiance distribution. In this section, the solar data of a peculiar site is systematically recorded and analyzed to determine whether the distribution of solar irradiance frequency distribution follows a predetermined distribution such as Weibull distribution which is then used to predict performance and energy output as for wind turbine [34]. Although 8 years of solar irradiance data have been recorded from the GREEN Platform of University of Lorraine and due to data similarities between years, only one year data is used for the test. Otherwise the 8 years data that is being sampled every 10 minutes would need huge processing time.
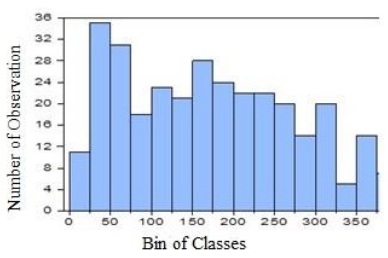
These long term irradiance data are used to calculate the probability density function of the irradiance for different hours of a typical day in a month. The frequency distribution of solar irradiation of the study series is displayed as a histogram in Figure 1. The histogram divides the series range (the distance between the maximum and minimum values) into a number of equal length intervals or bins and displays a count of the number of observations that fall into each bin. Figure 1 indicates the number of observation against 15 bins of classes and each class is an interval of values of the irradiance variable G (W/m2). For example, the fourth bin between 75 to 100 indicate the corresponding number of 17 observations. The visual examination does not seem to identify any appropriate functional form of a Weibull distribution curve that may be superimposed on the histogram pattern. We therefore proceed by a statistical test as indicated in Table 1.
Table 1. Rejecting the normal distribution of solar irradiance.
| Method |
Value |
Adj. Value |
Probability |
| Cramer-von Mises |
0.159053 |
0.160722 |
(0.01, 0.025) |
| Watson |
0.157972 |
0.159630 |
(0.01, 0.025) |
| Anderson-Darling |
1.250903 |
1.264034 |
< 0.01 |
| Hypothesis Weibull; Sample: 363; Observation: 363. |
The statistical hypothesis testing framework is as follows, the null hypothesis H0 is Weibull distribution and H1 is non Weibull distribution. The statistical test is based on the likelihood ratio that gives the number of times data is more likely under one model than the other.
This likelihood ratio is then used to determine the probability or p-value or compared to a critical value to decide whether or not to reject the null hypothesis. Table 2 is the second part of the output of Table 4. The p-value is less than the required significance level then we say the null hypothesis is rejected at the given level of significance. But at the same time the z-statistic value is so great compared to test critical values.
Table 2. The likelihood table.
| Parameter |
Value |
Std. Error |
z-statistic |
Probability |
| M |
0.000000 |
- |
NA |
NA |
| S |
234.2153 |
8.624198 |
27.15477 |
0.0000 |
| A |
1.500020 |
0.062977 |
23.81856 |
0.0000 |
| Log likelihood |
–2267.794 |
Mean dependent var |
211.5373 |
| No. of coefficients |
2 |
S.D dependent var |
141.4750 |
Table 3. Correlogram solar irradiance series.
Table 4. Correlogram first difference solar.
Therefore, the null hypothesis of a Weibull distribution cannot be retained but seems to be very unlikely.
4. From pattern recognition to stationary assumption
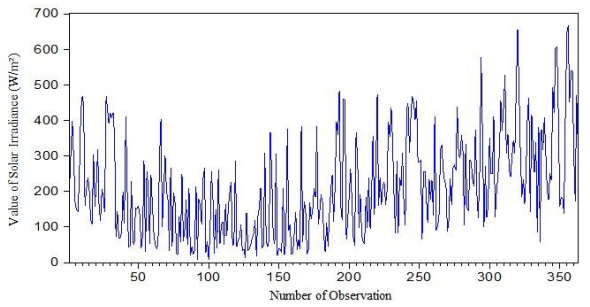
Figure 2 represents 363 observations of the solar irradiance G evolution to demonstrate the application of ADF test on variable.
Before we go to the ADF model, we draw the graph of the study series for an eye examination of any pattern that might be important in our future assumption. In the next sections, we should verify whether the series are stationary or not.
4.1. Correlograms & Q-Statistics
In that part the two alternative hypothesis are considered, H0: series X is stationary; H1: series X is not stationary.
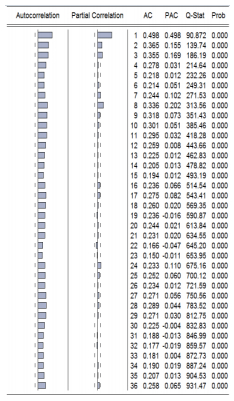
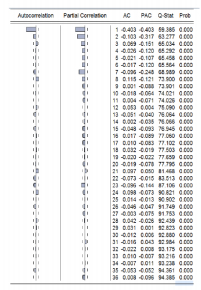
We shall be using correlograms or Ljung box statistics to test whether the series is stationary or not. The following tables show pictures of correlograms of a time series. Autocorrelation and partial autocorrelation functions characterize the pattern of temporal dependence in the series and typically make sense only for time series data. This is applied to solar irradiance data and is displayed in Table 3. The first column is the autocorrelation column represented as spikes between vertical lines.
The autocorrelation of a series Z at lag k is estimated by the following Eq 4:
|
τk=∑Tt=k+1(Zt−ˉZ)(Zt−k−ˉZ)∑Tt=1(Zt−ˉZ)
|
(4)
|
where Z is the sample mean of Z. This is the correlation coefficient for values of the series k periods apart. If τ1 is non zero, it means that the series is first order serially correlated. If τk dies off more or less geometrically with increasing lag k it is a sign that the series obeys a low-order autoregressive (AR) process. If τk drops to zero after a small number of lags it is a sign that the series obeys a low order moving-average (MA) process.
Normally, when the spikes are outside the two lines we suspect that the data is not stationary and this is for example one sign among others. From the AC column in Table 3, the estimated values at lag k that are usually noted as hat symbol ˆρk is gradually going down which means that probably data is non-stationary and is lagged from 1 to 36.
The partial autocorrelation at lag k is the regression coefficient on Zt–k when Zt is regressed on a constant and Zt–1, ..., Zt–k. This is a partial correlation since it measures the correlation of Z values that are k periods apart after removing the correlation from the intervening lags. When the pattern of autocorrelation is one that can be captured by an autoregression of order less than k then the partial autocorrelation at lag k will be close to zero that is indicated by the PAC (Partial AutoCorrelation) column in Table 3.
Finally, the last value of the Q-stat (Q-Statistic) column in Table 3 are significant at all lags indicating significant serial correlation in the residuals. The last value of the Q-stat column which 931.47 is a high value and the corresponding probability or p-value is zero which less that 5% meaning that the null hypothesis H0 is rejected.
We note that equation for Q-stat is given as follows:
where T is the total number of observations et m is the lag length.
The stationary test of the solar irradiance series seems to be a non-stationary data so OLS between these series could not be applied. The slow linear decay of the AC coefficients in Table 3 can be observed which indicates the need to differentiate. An advantage of the first-difference transformation is that it may make a non stationary time series stationary.
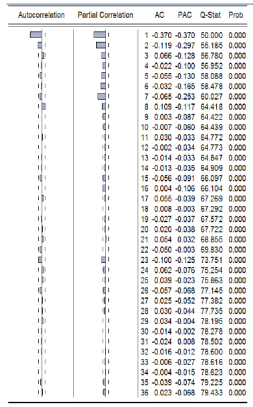
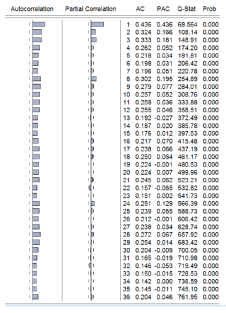
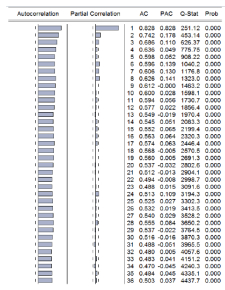
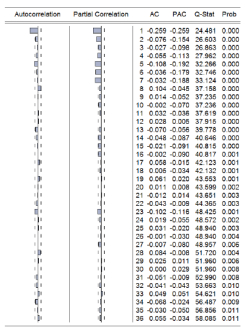
Correlogram of the first difference for solar irradiance is given in Table 4, the autocorrelations at various lags hover around zero which is a picture of the correlogram of a stationary time series. We repeated the procedure for power output and temperature data. Tables 5 & 7 respectively, show each correlogram of power and temperature series with the corresponding correlogram of the first difference series given in Tables 6 & 8. These correlograms show similarities to the solar irradiance series. The null hypothesis is thus rejected and all series are non-stationary series but not for the first difference series.
Table 5. Correlogram of power series.
Table 6. Correlogram of difference power series.
Table 7. Correlogram of temperature series.
Table 8. Correlogram of difference temperature.
The ADF is discussed in the next section to determine the functional form of the regression model with the first difference as variables.
4.2. Augmented dickey fuller solar irradiance test
To tackle the autocorrelation problem, the augmented Dickey-Fuller (ADF) is applied to test the null hypothesis of whether a unit root unit is present in a time series test. The test is applied to the three series solar irradiance series (G), power output series (P) and temperature series (T) with the following assumption, H0: series has a unit root; H1: series has no unit root.
The ADF test results are divided into two distinct sections. The first portion displays the test of the unit root output provides information about the form of the test that is, the type of test, the exogenous variables and lag length used and contains the test output associated critical values such as the probability p-value. The second part of the output shows the intermediate test equation computed to calculate the ADF statistic. In this section, the unit root test is applied to the solar irradiance and the results are explained. In the following sections, the same procedure is then applied to the power and temperature series.
The first portion of the ADF test is given in Table 8a, where the none exogenous estimate the test that does not include a constant and linear trend in the test regression and the variable is E that is lagged once as displayed by the correlogram of Table 3.
Table 8a. Testing solar irradiance.
|
|
t-Statistic |
Probability* |
| Augmented Dickey-Fuller test statistic |
|
–0.778035 |
0.3786 |
| Test critical values: |
1% level |
–2.571511 |
|
|
5% level |
–1.941721 |
|
|
10% level |
–1.616099 |
|
| Null Hypothesis: G has a unit root; Exogenous: None; Lag Length: 8 (Automatic: based on SIC, maxlag = 16). |
ADF statistic absolute value in Table 8a is –0.778035 and the associated one-sided p-value is –0.3786 for a number of observations specified in Table 8b. In addition, the critical values at the 1%, 5% and 10% levels are also reported. We notice here that the t-statistic value is greater than the critical values which is higher than 5% so that we do not reject the null hypothesis at conventional test sizes.
Table 8b. Second output of ADF solar equation.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| E (–1) |
–0.021473 |
0.027599 |
–0.778035 |
0.4371 |
| D (E (–1)) |
–0.632395 |
0.058947 |
–10.72823 |
0.0000 |
| D (E (–2)) |
–0.525921 |
0.064797 |
–8.116418 |
0.0000 |
| D (E (–3)) |
–0.354483 |
0.067566 |
–5.246454 |
0.0000 |
| D (E (–4)) |
–0.328680 |
0.067350 |
–4.880199 |
0.0000 |
| D (E (–5)) |
–0.366181 |
0.066697 |
–5.490251 |
0.0000 |
| D (E (–6)) |
–0.374641 |
0.066079 |
–5.669598 |
0.0000 |
| D (E (–7)) |
–0.337516 |
0.062371 |
–5.411434 |
0.0000 |
| D (E (–8)) |
–0.124641 |
0.054153 |
–2.301633 |
0.0220 |
| R-squared |
0.335576 |
Mean dependent var |
–0.290650 |
| Adjusted R-squared |
0.320169 |
S.D. dependent var |
142.5432 |
| S.E. of regression |
117.5296 |
Akaike info criterion |
12.39635 |
| Sum squared resid |
4765554. |
Schwarz criterion |
12.49472 |
| Log likelihood |
–2185.154 |
Hannan-Quinn criter |
12.43549 |
| Durbin-Watson stat |
2.028671 |
|
|
| Augmented Dickey-Fuller Test Equation; Dependent Variable: D (E); Method: Least Squares; Sample: (adjusted 363); Included observations: 354 after adjustments. |
Second part of the output is displayed in Table 8b and shows the intermediate test equation that has been used to calculate the ADF statistic upon 363 observations and the dependent variable is D (G) which is regressed first lag.
In Table 8b, the column labeled coefficient depicts the estimated coefficients or estimates and should not be viewed as being deterministic. It's a kind of indication upon the variable precision. The absolute t-statistic value associated to the G (–1), that is 0.778035 is defined as the ratio coefficient to the standard error and given as follows:
|
CoefficientvalueStd.Errorvalue=ˆmˆσm=−0.0214730.027599=−0.778035
|
The t-stat value of the coefficient value should be compared to critical values tabulated by DF. This value is less than those indicated in Table 2, given as 2.58, 1.95, 1.61 for the corresponding threshold 1%. This comparison indicates that the solar irradiance series is not stationary. In this test we ignored the probability value from Table 8b because the coefficient value of G (–1) is not distributed that is it does not follow the student distribution. The t-statistic value and corresponding probability value of the first difference term lagged one are highly significant so we did not make any mistake from earlier analysis in considering this variable.
In the following sections, only results of the first part of the ADF test corresponding to power output and temperature data are presented as the second parts have similar characteristics to the first difference lagged at different levels to the second part of solar irradiance ADF test.
4.3. Augmented dickey fuller power & temperature test
Similar ADF test is applied to the variable power (P) and temperature (T) and each first part is given in appendix C. Examination of these tables reveals that the observed p-value in each case given respectively as 0.3459 and 0.6907 is not significant as it is a very high value compare to 5%. Also t-stat value of the variable power (P) equal to –0.853089 is again higher than all the critical values. The t value of the temperature coefficient is 0.026823 but this value is greater than even the 10 percent critical τ value of –1.616101 suggesting that even after taking care of possible autocorrelation in the error term, both power and temperature series is a non-stationary series. However, the both dependent variable D (P) and D (T) first difference lagged one shows significant characteristics values of a stationary series.
The next section is concerned with the ADF test applied to difference series.
4.4. ADF test to difference series of irradiance, power and temperature
To avoid the spurious regression problem that may arise from regressing a non stationary time series on one or more non stationary time series, we have to transform non stationary time series to make them stationary. If a time series has a unit root then the first differences of such time series may be stationary. Therefore, the solution here is to take the first differences of the time series.
Table 9a. First part difference solar irradiance G.
|
|
t-Statistic |
Probability* |
| Augmented Dickey-Fuller test statistic |
|
–12.22837 |
0.0000 |
| Test critical values: |
1% level |
–2.571511 |
|
|
5% level |
–1.941721 |
|
|
10% level |
–1.616099 |
|
| Null Hypothesis: D (G) has a unit root; Exogenous: None; Lag length: 7 (Automatic-based on SIC, mawlag = 16). |
Table 9b. Second part difference solar irradiance G.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| D (G (–1)) |
–4.145076 |
0.338972 |
–12.22837 |
0.0000 |
| D (G (–1), 2) |
2.492967 |
0.311017 |
8.015532 |
0.0000 |
| D (G (–2), 2) |
1.949729 |
0.275106 |
7.087194 |
0.0000 |
| D (G (–3), 2) |
1.579856 |
0.234643 |
6.733011 |
0.0000 |
| D (G (–4), 2) |
1.237359 |
0.192906 |
6.414317 |
0.0000 |
| D (G (–5), 2) |
0.859116 |
0.149072 |
5.763101 |
0.0000 |
| D (G (–6), 2) |
0.474450 |
0.101222 |
4.687212 |
0.0000 |
| D (G (–7), 2) |
0.129271 |
0.053794 |
2.403044 |
0.0168 |
| R-squared |
0.758759 |
Mean dependent var |
–0.900650 |
|
| Adjusted R-squared |
0.753878 |
S.D. dependent var |
236.7688 |
|
| S.E. of regression |
117.4625 |
Akaike info criterion |
12.39246 |
|
| Sum squared resid |
4773916 |
Schwarz criterion |
12.47990 |
|
| Log likelihood |
–2185.465 |
Hannan-Quinn criter |
12.42725 |
|
| Durbin-Watson stat |
2.029534 |
|
|
|
| Augmented Dickey-Fuller Test Equation; Dependent Variable: D (G, 2); Method: Least Squares; Sample: (adjusted 363); Included observations: 354 after adjustments. |
D operator is used to specify differences of series. To specify first differencing, we simply include the series name in parentheses after D with the corresponding lagged. The number of lagged difference terms to include is often determined empirically, the idea being to include enough terms so that the white noise error term in is serially uncorrelated. The difference solar irradiance table of the ADF test is illustrated in following tables. The similar tables of each dependent variable P and T are given in appendix C.
The lag length is being checked with the corresponding correlogram of the series to determine and to re-estimate with one less round of differencing.
4.5. Conclusion
The time series of variable P, G, T are not stationary series but differencing may yield stationary series. We can therefore use the regression test between the 3 variables in difference. This is discussed in the next section.
5. Difference regression equation
We computed the regression as each variable is stationary in difference. Table 10, is the regression difference where the explanatory variables ΔG and ΔT are used including a constant C. The dependent variable is ΔP (Delta P) for 363 samples and 362 included observations after adjustments. Let's just turn to interpreting the results. From Table 14, firstly we deduce the expected regression equation referring to the corresponding explanatory coefficient.
Table 10. The regression difference data.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| ΔG |
0.969868 |
0.027980 |
34.66231 |
0.0000 |
| ΔT |
0.500517 |
0.603774 |
0.828980 |
0.4077 |
| C |
–0.010523 |
1.778432 |
–0.005917 |
0.9953 |
| R-squared |
0.945447 |
Mean dependent Var |
0.284254 |
|
| Adjusted R-Squared |
0.945143 |
S.D dependent var |
144.4618 |
|
| S.E of regression |
33.83531 |
Akaike Info criterion |
9.889140 |
|
| Sum squared resid |
410993.4 |
Schwarz criterion |
9.921391 |
|
| Log Likelihood |
–1786.934 |
Hannan-Quinn criter |
9.901961 |
|
| F-statistic |
3110.855 |
Durbin-Watson stat |
2.799248 |
|
| Prob (F-Statistic) |
0.000000 |
|
|
|
| Dependent Variable: ΔP; Method: Least Squares; Sample: (adjusted 363); Included observations 362 after adjustments. |
Table 11. Regression difference data without outliers.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| C |
0.024771 |
1.338098 |
0.018512 |
0.9852 |
| ΔG |
0.996329 |
0.021519 |
46.29970 |
0.0000 |
| ΔT |
–0.389609 |
0.461854 |
–0.843577 |
0.3995 |
| R-squared |
0.967559 |
Mean dependent Var |
0.949972 |
|
| Adjusted R-Squared |
0.967376 |
S.D dependent var |
140.1690 |
|
| S.E of regression |
25.31743 |
Akaike Info criterion |
9.309208 |
|
| Sum squared resid |
227545.1 |
Schwarz criterion |
9.341726 |
|
| Log Likelihood |
–1663.348 |
Hannan-Quinn criter |
9.322140 |
|
| F-statistic |
5293.958 |
Durbin-Watson stat |
2.732836 |
|
| Prob (F-Statistic) |
0.000000 |
|
|
|
| Dependent Variable: ΔP; Method: Least Squares; Sample: (adjusted 359); Included observations: 358. |
Table 12. Final regression difference data.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| ΔG |
0.980052 |
0.009507 |
103.0827 |
0.0000 |
| S.E of regression |
25.27172 |
Akaike Info criterion |
9.300038 |
|
| Sum squared resid |
228001.5 |
Schwarz criterion |
9.310878 |
|
| Log Likelihood |
–1663.707 |
Hannan-Quinn criter |
9.304349 |
|
| F-statistic |
10595.79 |
Durbin-Watson stat |
2.722380 |
|
| Prob (F-Statistic) |
0.000000 |
Mean dependent var |
0.949972 |
|
| Dependent Variable: ΔP; Method: Least Squares; Sample: (adjusted 359); Included observations: 358. |
Table 13a. Regression based on the first 100 observations.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| ΔG |
0.980428 |
0.017402 |
56.33851 |
0.0000 |
| S.E of regression |
31.99997 |
Akaike Info criterion |
9.779297 |
|
| Sum squared resid |
101375.8 |
Schwarz criterion |
9.805349 |
|
| Log Likelihood |
–487.9648 |
Hannan-Quinn criter |
9.789840 |
|
| Durbin-Watson stat |
1.901483 |
S.D dependent var |
75.58948 |
|
| Mean dependent var |
–166.9105 |
|
|
|
| Dependent Variable: ΔP; Method: Least Squares; Sample: 260359; Included observations: 100. |
Table 13b. Regression based on the last 100 observations.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| ΔG |
0.978710 |
0.015881 |
61.62793 |
0.0000 |
| S.E of regression |
29.54568 |
Akaike Info criterion |
9.619702 |
|
| Sum squared resid |
86421.76 |
Schwarz criterion |
9.645753 |
|
| Log Likelihood |
–479.9851 |
Hannan-Quinn criter |
9.630245 |
|
| Durbin-Watson stat |
1.754791 |
S.D dependent var |
72.19141 |
|
| Mean dependent var |
169.8802 |
|
|
|
| Dependent Variable: ΔP; Method: Least Squares; Sample: 260359; Included observations: 100. |
Table 14a. Long term data for regression.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| G |
0.93982 |
0.010494 |
89.55454 |
0.0000 |
| C |
16.67559 |
2.669565 |
6.246557 |
0.0000 |
| R-squared |
0.956926 |
Adjusted R-squared |
0.956807 |
|
| S.E of regression |
28.24849 |
Akaike Info criterion |
9.525451 |
|
| Sum squared resid |
228069.7 |
Adjusted R-squared Akaike Info criterion |
0.956807 9.525451 |
|
| Log Likelihood |
–1726.869 |
Schwarz criterion |
9.546908 |
|
| F-statistic |
8020.015 |
Hannan-Quinn criter |
9.533980 |
|
| Prob (F-Statistic) |
0.000000 |
Durbin-Watson stat |
1.494379 |
|
|
|
Mean dependent var |
215.4845 |
|
|
|
S.D dependent var |
135.9218 |
|
| Dependent Variable: P; Method: Least Squares; Sample: 363; Included observations: 363. |
Table 14b. EG residcoint data.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| ResidCoint (–1) |
–0.747317 |
0.050917 |
–14.67710 |
0.0000 |
| R-squared |
0.373717 |
Mean dependent var |
0.0181680 |
0.0000 |
| Adjusted R-squared |
0.373717 |
S.D. dependent var |
34.53230 |
|
| S.E. of regression |
27.32818 |
Akaike info criterion |
9.4564721 |
|
| Sum squared resid |
269605.4 |
Schwarz criterion |
9.4672335 |
|
| Log likelihood |
–1710.622 |
Hannan-Quinn criter |
9.4607460 |
|
| Durbin-Watson stat |
2.045377 |
|
|
|
| Dependent Variable: D (ResidCoint); Method: Least Squares; Sample: (adjusted 363); Included observations: 362 after adjustments. |
Table 14c. EG critical values.
|
|
t-Statistic |
Probability* |
| Augmented Dickey-Fuller test statistic |
|
–14.67710 |
0.0000 |
| Test critical values: |
1% level |
–2.571336 |
|
|
5% level |
–1.941701 |
|
|
10% level |
–1.616113 |
|
| Null Hypothesis: ResidCoint has a unit root; Exogenous: None; Lag Length: 0 (Automatic-based on SIC, maxlag = 16). |
This is given as Eq 6a below:
|
ΔP=0.969ΔG+0.500ΔT−0.105
|
(6a)
|
It is a standard practice to use the coefficient p-values to decide whether to include variables in the final model. Yet, the corresponding p-value of ΔT and constant term C are not statistically significant because their corresponding p-value (0.4077, 0.9953) are greater than the usual significance level of 1%, 5%, 10% and can be removed from Eq 6a. Whereas the t-statistic value of ΔG is highly significant as well as the corresponding probability that is less than 5%, expecting good regression between ΔP and ΔG.
The overall regression fit as measured by the R2 value is more than 94% indicating a very tight fit. Obviously we'll focus on R-squared (R2) suggesting that solar irradiance alone can explain over nearly 95% of the variation of power output and it will have only 1% impact on the variable power P. Although this regression seems to be very significant however, both the constant and temperature difference are not significant as is revealed by the corresponding probability p-value 0.99 and 0.40. Indeed, the p-value given just below the F-statistic in Table 10 denoted as Prob (F-statistic) is the marginal significance level of the F-test. If the p-value is less than the significance level that is 5% the hypothesis that all slope coefficients are equal to zero are rejected.
For example, in Table 10, the p-value is essentially zero for ΔG. Note that the F-test is a joint test so that even if all the t-statistics are insignificant the F-statistic can be highly significant. However, we can propose the apparent estimate equation using least squares given as follows by Eq 6b.
The proposed regression equation is still not satisfactory because other data in the table seem to indicate differences between the predicted value (based on the regression equation) and the actual observed value. This is discussed in the next section.
5.1. Outliers & analyzing residuals from regression
One problem with least squares occurs when there are one or more large deviations for example, cases whose values differ substantially from the other observations. These points are called outliers. They may represent important information about the relationship between variables. Robust regression might be a good strategy since it is a compromise between excluding these points entirely from the analysis and including all the data points and treating all them equally in ordinary least squared (OLS) regression. In linear regression, an outlier is an observation with large residual.
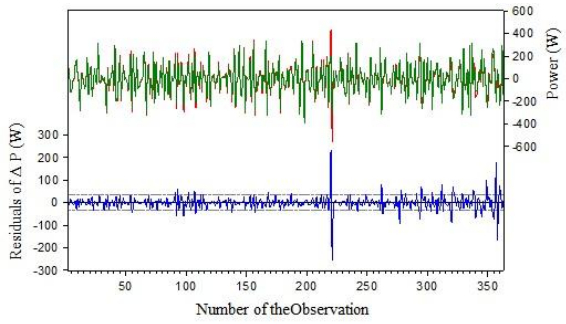
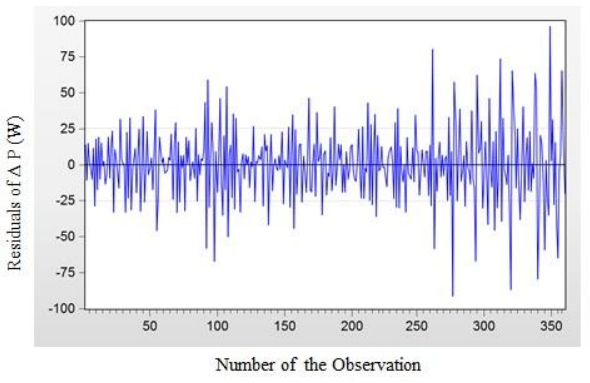
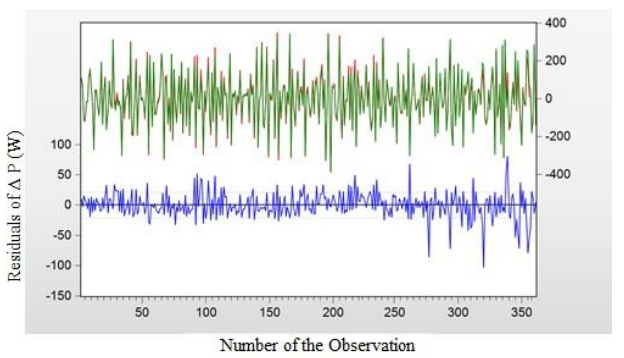
Figure 3, represents the residual graph where the blue curve is the residuals from the regression provided by a residual table. The green and red curves are respectively the real or actual and fitted curves of power output against the number of observations. We see that the regression seems to be going rather well from the point of view of predicting power output evolution. However, the residual graph shows 4 outliers diagnosing failures of the above assumptions of the regression model. The 4 outliers do appear on one side at 220 and 221 observations with amplitude around 100 and on the other side at 357 and 358 with amplitude around 170.
Given the existence of outliers, we re-estimate the regression without these 4 points as given in Table 11 with the corresponding residual curve of ΔP as illustrated in Figure 4.
From the residual graph of ΔP in Figure 4, we can see that there is no longer any spurious residual but we can suspect a little heteroscedasticity, that is to say a variance of the residual values varying with the level of the variables. This is discussed in the next section.
5.2. Heteroscedasticity & autocorrelation
When using some statistical techniques such as OLS, a number of assumptions are typically made. In a linear regression model in which the errors have expectation zero and are uncorrelated as well as having equal variances then the best linear unbiased estimator (BLUE) of the coefficients is given by the OLS estimator. If the variance of the error term εi is not the same across all observations i = 1, ..., n, then the disturbances are said to be heteroscedastic.
Heteroscedasticity tends to produce p-values that are smaller than they should be. This effect occurs because heteroscedasticity increases the variance of the coefficient estimates but the OLS procedure does not detect this increase. Consequently, OLS calculates the t-values and F-values using an underestimated amount of variance.
This problem can lead to conclude that a model term is statistically significant when it is actually not significant as the coefficients are biased. In our case, as the t-test for each coefficient examines them individually the t-test of ΔG in Table 11 is higher than that in Table 10 with the F-value very significant in Table 11. The overall F-test is significant and the R-squared value has been improved therefore correlation between the model and dependent variable is statistically significant.
We thus identified the single significant explanatory variable which is ΔG with heteroscedastic disturbance and therefore the kind of heteroscedasticity must be identified. In the next section we propose more in-depth studies in order to propose a regression equation closer to real experimental conditions.
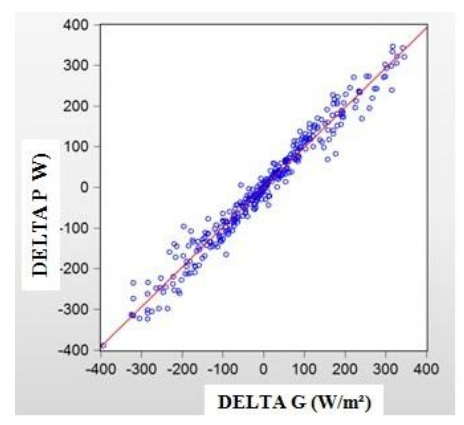
The corresponding graph of first difference of power output ΔP against first difference of solar irradiance ΔG is illustrated in Figure 5. However, some scattered values do not fit the regression line reasonably and although the constant term has been removed, the very slight intercept on the delta P axis are indications to pursue further studies.
We then test that the residual is an increasing function of the explanatory variable and the Goldfeld Quandt (GQ) test is proposed. This is discussed in the next section.
5.3. The goldfeld quandt test
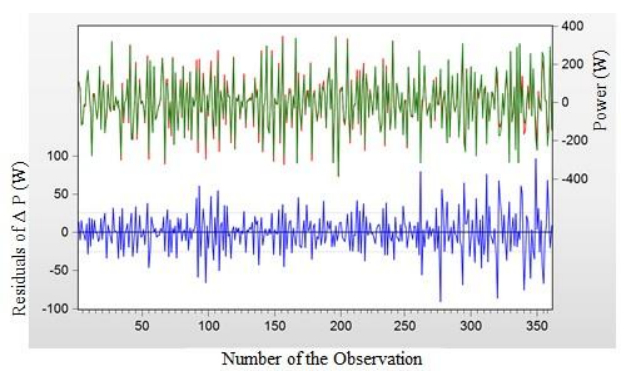
The blue curve of Figure 6 is the residual of ΔP with no outliers and is oscillating in a range of values that act as good estimates. This range is also known as the confidence interval and is represented by the dotted blue lines. GQ have argued that the error term may not satisfy the ordinary least squares assumptions and may itself be heteroscedastic.
The GQ test is accomplished by undertaking separate least squares analyses on two subsets of the original dataset: these subsets are specified so that the observations for which the pre-identified explanatory variable takes the lowest values are in one subset, with higher values in the other. The test statistic or F-test used is the ratio of the mean square residual (MSR) errors for the regressions on the two subsets given by Eq 7 where MSRmax is the highest value in a subset and MSRmin is the lowest value.
In our study, the OLS regressions of the GQ test is based on the first 100 and the last 100 observations and their associated residual sums of squares are given respectively in Tables 13a and 13b.
From Tables 13a and 13b, the corresponding sum squared residuals values are MSRmax = 101375 and MSRmin = 86421. The F ratio as indicated above is determined and is equal to 1.17 so we can reject the hypothesis of heteroscedasticity.
However, this value from the GQ method is a non-zero value for the error term and a further study on the DW d-stat test is proposed in the next section.
5.4. Durbin Watson D-Stat test
The corresponding residual graph is displayed in Figure 6, the colored curves have the same defintion as defined in Figure 3 where the blue curve indicates that no outliers values are blatant for the residuals but does not explain the DW statistic value. The conventional DW tables are not applicable when a constant term does not exist in the regression and instead an appropriate set of Durbin-Watson tables is used as reference table.
The DW is a test that the residuals from a linear regression or multiple regression are independent and makes it possible to detect a first order autocorrelation errors that is an equation given as follows:
Because most regression problems involving time series data exhibit positive autocorrelation the hypotheses usually considered in the DW test are H0: ρ = 0 and H1:
ρ > 0.
The test statistic is given as follows:
|
d=T∑t=2(ut−ut−1)2T∑t=2(u2t)
|
(9)
|
For ut=yt−ˆyt where y and hat y are respectively, the observed and predicted values of the response variable for individual t. d becomes smaller as the serial correlations increase. Upper and lower critical values d2 and d1 have been tabulated for different values of the number of explanatory variables and T. If a test for negative autocorrelation is desired, then the 4-d statistic is used. The decision rules for H0, ρ = 0 versus H1
ρ < 0 are the same as those used in testing for positive autocorrelation.
The DW table at 5% level d1 = 1.664 and d2 = 1.779. The tabulated bound is summarized as follows:
0 < d < d1: positive autocorrelation of residuals
d1 < d < 4-d2: no autocorrelation
4-d2 < d < 4-d1: undefined
4-d1 < d < 4: negative autocorrelation of residuals
The DW statistic from Table 16 is 2.72 which is between 2.336 and 4 therefore a negative autocorrelation is expected.
Table 15. ECM regression data.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| ResidCoint (–1) |
–0.725527 |
0.051027 |
–14.21850 |
0.00000 |
| ΔG |
0.969314 |
0.010166 |
95.35067 |
0.00000 |
| C |
0.013603 |
1.423750 |
0.009554 |
0.99244 |
| R-squared |
0.965033 |
Mean dependent var |
0.284254 |
|
| Adjusted R-squared |
0.964836 |
S.D. dependent var |
144.4618 |
|
| S.E. of regression |
27.08863 |
Akaike info criterion |
9.444358 |
|
| Sum squared resid |
263432 |
Schwarz criterion |
9.476610 |
|
| Log likelihood |
–1706.429 |
Hannan-Quinn criter |
9.457179 |
|
| Durbin-Watson stat |
2.045261 |
F-statistic |
4953.946 |
|
| Prob (F-statistic) |
0.000000 |
|
|
|
| Dependent Variable: ΔP; Method: Least Squares; Sample: (adjusted 363); Included observations: 362 after adjustments. |
Table 16. Error term regression without constant.
| Variable |
Coefficient |
Std. Error |
t-Statistic |
Probability |
| ResidCoint (–1) |
–0.601050 |
0.049178 |
–12.22193 |
0.0000 |
| ΔG |
0.966657 |
0.008066 |
119.8493 |
0.0000 |
| R-squared |
0.977102 |
Mean dependent var |
0.949972 |
|
| Adjusted R-squared |
0.977037 |
S.D. dependent var |
140.1690 |
|
| S.E. of regression |
21.24035 |
Akaike info criterion |
8.955253 |
|
| Sum squared resid |
160610.3 |
Schwarz criterion |
8.976932 |
|
| Log likelihood |
–1600.990 |
Hannan-Quinn criter |
8.963875 |
|
| Durbin-Watson stat |
2.062846 |
F-statistic |
7578.573 |
|
| Prob (F-statistic) |
0.000000 |
|
|
|
| Dependent Variable: ΔP; Method: Least Squares; Sample: (adjusted 363); Included observations: 362 after adjustments. |
However, a more rigorous method such as Cochrane Orcutt method [29] can be applied if required but this is beyond the scope of this study.
5.5. Discussion
Regression of a non stationary series on another non stationary series may cause spurious regression which is not desirable. In our case, we have two variables P and G and they have unit root at level meaning non stationary. They are stationary after first difference. Nevertheless the regression model is not appropriate for highlighting linear relationships between non stationary variables and suppose P is regressed on G as follows:
where et has a unit root and is stationary as explained in the previous section. It is then proposed to estimate the regression of equation (10) and obtain the residuals.
However, there is one precaution to exercise. Since the estimated et are based on the estimated cointegrating parameter γ, ADF critical significance values are not quite appropriate and other values are used and determined from Engle and Granger method. This is discussed in the next section.
6. Engle and granger method
The outline of Engle & Granger (EG)
[30] method is explained in section 2.4, still we can simply resume the principle. EG note that a linear combination of two or more series may be stationary, in which case we say the series are cointegrated. Such a linear combination defines a cointegrating equation between variables with cointegrating vector of weights characterizing the long-run relationship between the variables. Therefore, from Eq 10 is deduced the following relationship:
This is computed and the results are given in distinct tables.
Table 14a shows result of regression between variables at level, that is long term relationship. The dependent variable is P and the explanatory variables are solar irradiance G and a constant term C.
When the dependent variable Pt is regressed on Gt the following regression is obtained
|
Pt=0,9398Gt+16,6755+et
|
(11b)
|
So we focus on stationarity or not of the residual of Table 14c. The residual is noted as ResidCoint.
Since the computed t value (–14.677) is very significant and much more negative than –2.5713 [30,33,36], our conclusion is that the residuals from the regression of P on G are stationary.
Hence, Eq 17b is a cointegrating equation and is called the long run function and interprets its parameters as long run parameters. Thus, 0.9398 represents the long-run or equilibrium. Obviously, in the short run there may be disequilibrium. Therefore, the error term in Eq 11a must be processed as the equilibrium error and this error term is used to link the short-run behavior of PCE to its long-run value.
The error correction mechanism (ECM) which is the third step of the EG test as described in section 2.4 is applied and the similar Eq to (3b) is given as follows:
|
ΔPt=α0+αΔGt+βet−1+εt
|
(12)
|
Where, Δ as usual denotes the first difference operator, εt is a random error term, and
that is the one lagged value of the error from the cointegrating regression of Eq 11b.
ECM equation, that is Eq 12, states that ΔP depends on ΔG and also on the equilibrium error term et–1. If the latter is non zero, then the model is out of equilibrium. Suppose ΔG is zero and et–1 is positive this means ΔPt–1 is too high to be in equilibrium. Since β is expected to be negative the term βet–1 is negative and therefore ΔPt will be negative to restore the equilibrium. That is, if Pt is above its equilibrium value it will start falling in the next period to correct the equilibrium error. As well as if et–1 is negative that is P is below its equilibrium value βet–1 will be positive which will cause ΔPt to be positive leading Pt to rise in period t. Thus, the absolute value of β decides how quickly the equilibrium is restored.
Eq 13 is computed the corresponding results are given in Table 15. The coefficient β tells us at what rate it corrects the previous period disequilibrium of the system. When β is significant and contains a negative sign it validates that there exists a long run equilibrium relationship among the variables.
The coefficient value β of ResidCoint (–1) or (et–1) = –0.7255 that validate the long run relationship between P and G.
Therefore, from Table 19 we can deduce that the model is very significant as the R squared value is very high thus the Fisher statistic value is high. The two explanatory variables that is, first difference stationary solar irradiance DG, ResidCont lagged one (et–1) are very significant whereas the constant term C = α0 is not significant as indicated by its p-value.
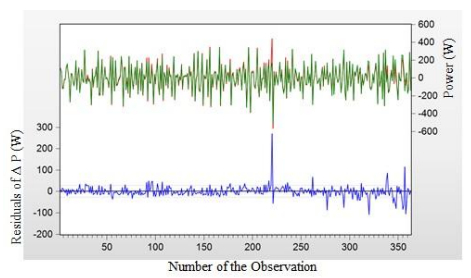
Still, we plot the residual graph and this is displayed in Figure 7.
The colored curves have the same defintion as defined in Figure 3 and where two outliers are identified respectively at position 320 and 357. Thus we applied the EG test for difference regression and the dependent variable is ΔP.
Results are given in Table 16 for the coefficient of the equilibrium error term and the short run term (coefficient of ΔG).
The R-squared value is very significant as well as the DW statistic close to 2 there is no more heteroscedasticity as represented in Figure 8.
Thus, the relationship between the variables is given as
|
ΔP=0.966ΔG−0.601(Pt−1−0.939Gt−1−16.67)
|
(14)
|
where ΔP = Pt – Pt–1 and ΔG = (Gt – Gt–1) and by substituting ΔP and ΔG in Eq 14 the final relationship for Pt is written as follows
|
Pt=0,966Gt−0.402Gt−1+1,601Pt−1+10.019
|
(15)
|
Hence, Eq 15 is the full equation not only with variables P and G in difference but also with P and G with one period lagged.
7. Conclusion and future work
It is difficult to effectively assess the impact of PV output variability on the power grid stability without a clear understanding of the factors that influence this variability. Many factors can become redundant in the presence of other factors and their value in the forecasting framework may vary under different prediction horizons and error measurements. One of the objectives of this paper consisted of applying a statistical method of time series data to identify the most important on-site climatic and environmental parameters that influence PV output variability. Various estimation technique to estimate a linear relationship between PV variables have been proposed in the literature but these OLS regression techniques had lead to spurious results as these techniques were based on the assumption that the variables involved are stationary. Regressions involving time series data include the possibility of obtaining spurious or dubious results in the sense that superficially results look good but on further probing they look suspect.
The originality of this paper is that a technique of cointegration has been introduced known as the EG method according to which models containing nonstationary stochastic variables have been constructed in such a way that the results are statistically meaningful. Through this technique a linear relationship is obtained including not only the dependent variable P(t) and explanatory variable Gk(t), but also their one time lagged variables P(t–1) and Gk(t–1), thus a temporal link between the variables in small samples, that is daily mean data upon one year.
For that, the EG method requires testing whether variables are integrated of the same order. This is done using the ADF unit root test. We then used the error correction model to test whether the residuals of the long run relationship between P and G are stationary. All these conditions are satisfied and the two variables under investigation cointegrate.
The advantage of the Engle-Granger method over the other techniques is its ease of implementation. However, its results are dependent on how the long-run equilibrium equation is specified. In some cases, it might not be easy to identify which variable enters as the dependent variable.
This study was conducted in a temperate region and temperature had been eliminated in the final PV relationship. However, the latter cannot be readily adopted by other countries as both the methodologies employed depend on several site-dependent features. The PV output also is heavily reliant on numerous local meteorological and environmental factors. Therefore, future work has been proposed in a South West Indian Ocean project to improve this PV model.
Acknowledgements
The authors wish to acknowledge the GREEN platform industrial partners.
Conflict of interest
The authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: