1. Introduction
1.1. Inflammatory bowel disease associated colorectal cancer
Inflammatory bowel disease (IBD) is a chronic relapsing inflammation of the intestine that affects either all or some parts of the gastrointestinal tract (GIT). Prolonged activation of the intestinal mucosal immune system promotes the release of biological markers associated with IBD, causing persistent inflammation [1]. The incidence and prevalence of IBD are known to be the highest in western industrialized nations. Europe and the United States of America being the countries with highest prevalence of IBD, with an estimated 2.2 and 1.4 million people affected respectively [2,3]. IBD is differentiated into two broad categories; ulcerative colitis (UC) and Crohn’s disease (CD). UC is limited to the colon or rectum, while inflammation during CD can affect any part of the GIT from the oesophagus to the anus [4]. UC is mainly characterized by the formation of continuous superficial lesions along the proximal or distal colon. On the other hand, CD results in the formation of deep-fissured ulcers, fistulae, and perforations in the bowel [1,4].
The aetiology of IBD has not been fully explored and still on its way to have a clear picture; however, dysregulation of the immune response via luminal, genetic and environmental factors are considered to increase the risk of IBD [5]. The onset of IBD can occur at any stages of life. Although, it is more frequently seen in the elderly population, 20% of IBD cases are diagnosed during childhood or adolescence [6]. Atypical symptoms and extraintestinal manifestations of IBD cause major difficulties for the identification and diagnosis of the disease in paediatric patients. Comparatively, the incidence rate of CD in children is nearly double (0.2 to 8.5 per 100, 000) than UC [7]. Overall, the impact of UC predominates as 7 to 12 per 100, 000 cases diagnosed annually compared to 5 to 7 cases of CD [8]. Currently, there is no cure for IBD. Moreover, there are no specific biomarkers for the identification of IBD disorders, and therefore, endoscopic, clinical, radiologic and other therapeutic measures remain the core source for their diagnosis.
The connection between IBD and colorectal cancer (CRC) is well established. IBD is known to play a substantial role in sustaining and promoting CRC development [9]. Long-term chronic inflammation of the colon, as observed in IBD patients, is correlated with an enhanced risk of developing colorectal cancer. An association between IBD and CRC was first reported by Crohn and Rosenberg in 1925 [9]. The accumulating preclinical and clinical data suggest an increased risk of developing intestinal carcinogenesis in patients suffering from IBD [10,11]. In a meta-analysis by Eaden et al., patients with UC were reported to have a 9-fold increase in the cumulative incidence of CRC development 20 years after initial UC diagnosis [12]. Among IBD patients, UC-driven CRC has been a focal point of interest inthe majority of preclinical and clinical studies. However, a 2.5 to 4.5-fold increased risk of developing CRC has also been reported in patients with CD [13]. The chances of developing CRC in patients with CD are up to 33 times higher than in the general population. The majority of risk factors associated with IBD-CRC are yet to be fully elucidated. Nevertheless, the major contributory factors, which are known to enhance the likelihood of IBD-CRC progression, include the duration and extent of colonic inflammation or other existing IBD-related inflammatory conditions like sclerosing cholangitis etc. [14,15].
Chemoprevention with anti-inflammatory agents and immunomodulators have been shown to reduce the risk of developing IBD-CRC. However, their effects remain conflicting [16,17]. Newer technologies such as chromo-endoscopy for the early detection of dysplasia needs to be established [18]. An animal model of a particular disease state is critical to unravelling the pathological mechanisms behind a disease. However, we currently lack a suitable animal model to recapitulate the pathogenesis of IBD-CRC as in humans. Nevertheless, there are animal models to study IBD and CRC and combining such models could help us in improving the understanding on IBD-CRC. The various models of IBD-CRC, the molecular pathways associated with this disease and various potential novel therapies that can be used for the management of IBD-CRC are discussed below.
2. Experimental Models to Study IBD Associated Colorectal Cancer
2.1. In-vitro models
In-vitro models represent the first critical step towards elucidating the mechanism(s) responsible in the complex pathophysiology of IBD-CRC. Moreover, these models remain a primary and fundamental tool for the identification of novel therapeutic interventions. Several studies documented the use of cell lines representing colon-associated CRC. These cell lines include HCT116, SW620, HCT15, DLD1, HT29, LOVO, SW408, Caco2, Isreco1, SNU1033 or SNU407 [19,20,21,22]. Such studies have provided an essential information towards the recognition and involvement of various inflammatory biomarker(s) involved in IBD-CRC, with a view towards understanding the specific aspects of tumor biology, assessment of endogenous inflammatory mediators and expression of relevant genes. The identified biomarkers in IBD-CRC include various cytokines and chemokines, like interleukin (IL)-6 and IL-8, transcription factors, such as nuclear factor kappa-light-chain-enhancer of activated B cells (NF-κB) and runt-related transcription factor (RUNX).
In-vitro organoid culture is a breakthrough that facilitates an accurate study of characteristic pathophysiological features of many biological disorders including IBD and CRC [23]. For instance, the establishment of intestinal and CRC organoids provides an opportunity to study the underlying mechanisms involved in IBD and CRC, and thereby contribute to improved treatments for these disorders [24,25,26]. Organoid culture has emerging trends which can help in overcoming the current shortcomings that hinder us from studying the development and pathobiology of IBD-CRC. Although, in-vitro analysis is critical and permits faster and simpler assessment of biological phenomena, these models are restricted to investigate specific stages of tumor development. Importantly, the loss of tissue context is one of the major limitations of these models. Comparatively, in-vivo models provide comprehensive insight of the factors that affect tumor development, as well as attributing processes, such as proliferation, invasion, angiogenesis and metastasis. A number of strategies have been employed to develop murine models of IBD, to evaluate the pathogenesis behind IBD, as well as IBD-CRC. Some of the most widely used murine models that represent human IBD, include dextran sodium sulphate (DSS) and Winnie [27,28]. These models are briefly discussed below.
2.2. In-vivo mouse models: Pivotal tools in understanding IBD-CRC
2.2.1. Genetically engineered mice models
The germline mutation in the adenomatous polyposis coli gene (APC) gives rise to familial adenomatous polyposis (FAP) syndrome and is associated with the development of polyps in the colon and rectal regions during CRC [29]. Various attempts have been made to generate mouse models that recapitulate the human FAP syndrome. The Min mouse model has been utilized to investigate the risk factors and clinical application of chemoprotective drugs such as piroxicam and acarbose during CRC [30,31]. This Min mouse model carries a heterozygous germline mutation in APC genethat resembles the progressive and developmental phase of polyps formation as observed in patients with FAP syndrome. However, the formation of polyps in small intestine remains one of the major limitations of this model since polyps are usually confined to colon and rectum in patients suffering from FAP [32].
Nevertheless, certain modifications in the APC gene resulted in a double mutant mouse model where the formation of polyps is confined to colon region [33]. Moreover, homozygous deletion of mismatch repair gene such as MSH1, MSH2, and MSH6 in this model produced a robust mouse model that mimics the features related to hereditary nonpolyposis colorectal cancer (HNPCC) [34]. These genetically modified models have their own limitations and continued advancements might make these models more efficient for CRC research.
Other genetically engineered mice model utilized to study IBD-CRC focused on homozygous deletion of Mucin2 (MUC2-/-) gene [35]. Depletion of this gene was not only associated with morphological alterations in the intestinal epithelium leading to inflammation of the colon but also gave rise to invasive colon adenocarcinoma [36]. Such models help us better understand the protective role of MUC2 in IBD and IBD-CRC. Mice deficient in mothers against decapentaplegic homolog 3 (Smad3-/-) gene are known to develop colonic lesions, mucosal hyperplasia, polyploid tumors, metastatic carcinoma and increases infiltration of inflammatory cells [37]. However, this model lacks the information regarding the role of microflora in pathogenesis of tumor generation [38].
2.2.2. Chemically induced mice models
Several chemically induced murine models of intestinal inflammation have been established. Among them, DSS model of IBD remains one of the most extensively used models in the study of IBD. DSS is a polysulphated polysaccharide having molecular weights ranging from 5 KDa to 500 KDa [39]. The molecular weight of DSS and the degree of induced colonic inflammation are known to be directly proportional to each other. This model has proved highly valuable, due to its ease of development, reliability, reproducibility and wide availability of the agent.
Alternative models employing carcinogenic agents like azoxymethane (AOM) have been established to imitate IBD-CRC. One such widely accepted murine models representing IBD-CRC is AOM/DSS. AOM, a chemical carcinogen and a metabolite of 1, 2-dimethylhydrazine, is known to induce CRC in rodents. Metabolic activation of AOM via hydroxylation results in the formation of methylazoxymethanol (MAM), a reactive metabolite that causes pro-mutagenic lesions [40]. Numerous enzymes are associated with the metabolic activation of AOM. However, CYP2E1, an isoform of cytochrome P450 enzymes, is known to play a vital role in the conversion of AOM to MAM [41]. Corresponding to DSS, some of the top benefits of applying AOM to study IBD-CRC include stability, reproducibility, potency, simple mode of application and cost effectiveness [42].
A single hit of AOM in combination with repeated cycles of DSS has proven to shorten the duration required for the induction of IBD-CRC [43]. Different AOM/DSS administration protocols, for the induction of colorectal tumors, have been tested and are summarized in a review by Robertis et al. [44]. Till date, AOM/DSS model remain one the best prototypes in the study of human IBD-CRC. For instance, AOM/DSS induced tumors are formed in the distal colon, together with the formation of pre-cancerous lesions and foci of aberrant crypts (ACF). Consistent to human CRC, other abnormalities induced by AOM/DSS, include deregulation of APC/beta-catenin-signaling pathway and regulation of correlated genes, such as myelocytomatosis oncogene (c-Myc), cyclin D1 and cyclin-dependent kinase 4 (cdk4). Mutation of Kristen rat sarcoma (K-RAS) viral oncogene, increased expression of inducible nitrogen synthase (iNOS) and cyclooxygenase-2 (COX-2) has also been reported [44].
Another widely accepted class of chemical carcinogen include the use of heterocyclic aromatic amines and alkylnitrosamide to induce colonic lesions in rodents [45,46]. Repeated bouts of heterocyclic amine (PhIP) for 104 weeks develops tumor in rodents [46]. Additionally, a combination of high doses of PhIP together with AOM was shown to enhance the tumorigenic and mutagenic effect [47]. Contrariwise, no such effect was observed with low doses of PhIP [47]. Compared to AOM/DSS model, this model is not correlated with P53 and KRAS mutations, which is known to play a key role during early stage transition from IBD to CRC. However, induction of APC mutation and microsatellite instability make this model more relevant to study sporadic CRC [48].
Administration of 3, 2’-dimethyl-4-aminobiphenyl (DMBA) or intra-rectal injection of methylnitrosourea (MNU) are also used to induce lesions (colonic or rectal) and epithelial neoplasms in rodents respectively [45,49]. However, repeated injections and infiltration of the neoplasm to adjacent tissues make DMBA, a less potent carcinogen [45]. Although, no biochemical activation is required for MNU however, intra-rectal administration limits its use in comprehensive studies [49].
2.2.3. Combination models
The intestinal mucus is well known to play a pivotal role in limiting the extent of inflammation and infection. Gel-forming mucins, especially Mucin2 (MUC2), is one of the major components of the mucus system [50]. Defective colonic mucus formation, mainly MUC2, is implicated in the pathogenesis of IBD and related disorders [36]. Winnie model of IBD is derived from N-ethyl-N-Nitrosourea (ENU) mutagenesis. This model possesses missense mutation in D3 and D4 domains of MUC2. Disruption of MUC2 secretory function leads to the activation of unfolded protein response (UPR), and endoplasmic reticulum (ER) stress, resulting in a spontaneous and severe model of IBD [28].
Recently, Winnie and DSS model of IBD were merged together and trailed for the characterization of molecular and cellular pathways linking IBD and CRC [51]. After the completion of DSS protocol in Winnie model, glandular morphological abnormalities, resembling pre-cancerous evolution was observed. Other pre-cancerous changes include architectural derangement consistent to high-grade dysplasia, and penetration of crypts beyond muscularis mucosae. A pattern of altered expression of pro-inflammatory cytokines and other inflammatory markers was also noticed [51]. Nevertheless, there is still a need for further research attempts to strengthen the effectiveness of this model in exploring the progression of IBD-CRC. Identical to AOM/DSS, development of AOM/Winnie model to correlate IBD and CRC will help us to obtain meaningful and comprehensive etiological data on IBD-CRC and hence, the opportunities for the treatment of such malignancies.
3. Insight into the Molecular Mechanisms of IBD-CRC
The mechanisms responsible for the transformation of chronically inflamed tissue to early pre-cancerous lesion remain largely unknown. The various proposed molecular mechanisms that may account for IBD-CRC include-
3.1. Oxidative stress, genetic and epigenetic alterations
Oxidative stress is a key component responsible for the progression of various inflammatory disorders, including IBD and CRC [52,53]. An imbalance in the production and elimination of reactive oxygen species (ROS), and reactive nitrogen species (RNS), are hallmark features of oxidative stress. Various types of ROS and RNS released into the tissue microenvironment include nitrogen, hydrogen peroxide, superoxide, hydroxyl radicals, and singlet oxygen [52,53] which brings the tissue damage. Numerous studies have documented the increased expression and detrimental effects of ROS/RNS in human IBD [54,55,56]. ROS has been implicated in human IBD and CRC. Nanoparticle(s)-mediated suppression of ROS has shown to reduce the symptoms of IBD [57]. DNA damage-dependent interaction between the ROS/RNS is one the major contributory factors influencing the growth of the tumor. Oxidative stress induced disruption of DNA methylation patterns leads to genomic instability and mutations. For instance, oxidative stress induced DNA damage of tumor suppressor (p53) and proto-oncogenes (Ras) during tumorigenesis by inactivating p53 and by activating the Ras, drives UC to CRC [58,59].
Recent reports have shown the pathogenic role of oxidative stress in mice model of IBD-CRC [60,61,62,63,64]. However, the role of ROS/RNS in IBD-CRC is still unclear. Using preclinical murine models of IBD-CRC, the direct and indirect function of ROS/RNS, and resulting epigenetic changes during the early transition from IBD to dysplasia should be clearly defined.
The epigenetic abnormalities involved in IBD-CRC are not yet fully understood. However, inflammation-driven heritable changes in the expression of genes and associated regulatory pathways have been recognized to play a substantial part in IBD and CRC. Various genetic and epigenetic deformities that may influence the transition from IBD to CRC include changes in DNA methylation through chromosomal and microsatellite instability, mutations in tumor suppressor genes, such as TP53, APC, and INK4, as well as alterations in genes like MLH that control DNA stability [65,66,67,68,69,70]. Activation and up-regulation of DNA methyltransferase (Dnmt1 and Dnmt3) genes have also been reported [71,72]. Importantly, the expression of these genes has a broad impact on DNA methylation profile and hence, been positively correlated with IBD-CRC.
Post-translational histone modifications are also one of the epigenetic irregularities which are known to be associated with CRC [73]. Histones are the proteins that regulate normal functioning of genes in healthy cells. During cancer, the lysine and arginine residues of unstructured N-terminal tail of histones get modified by various chemical reactions including phosphorylation, acetylation, ubiquitination and methylation [73]. However, histone modification due acetylation and methylation are predominantly characterized in CRC pathogenesis [73,74,75,76]. The functioning of histone acetylation modification is regulated by histone deacetylases (HDACs)/histone acetyltransferases (HATs) whereas, histone methylation is controlled by histone methyltransferases (HTMs)/histone demethylases (HDMs), in a reversible manner [76,77]. During CRC, lysine-9 residues gets modified by deacetylation and methylation in histone H3, lysine- 16 gets monoacetylated while lysine-20 residues in histone H4 undergoes trimethylation [78,79]. Several studies have been conducted to identify the possible link between histone deacetylation and IBD-CRC using HDAC inhibitors in DSS and AOM/DSS models of IBD and IBD-CRC [80,81]. For instance, HDAC inhibitors like valproic acid suppress the release of pro-inflammatory cytokines (IL-6, TNF-aand INF-g), increases the apoptosis and histone H3 acetylation in DSS model of IBD [80]. Another HDAC inhibitor (ITF2357) attenuated the inflammation, growth and number of tumors by increasing histone H3 acetylation, inhibiting HDAC enzyme as well as NF-kB signaling, enhancing apoptosis in lamina propria and IL-10 release [81].
Other most prominent epigenetic modifications involve the action of microRNAs (miRNAs), which holds potential for the study of IBD-CRC. miRNAs belong to multiple gene families and are a class of small, endogenous non-coding RNA molecules having 18-24 nucleotide. These molecules are known to directly bind the messenger RNAs (mRNAs), causing their degradation or translation repression and thereby, regulate the process of gene expression [82]. Expression of several miRNAs have been reported to be elevated in patients with IBD or progressive IBD-CRC such as miR-26b, miR-17, miR-21, miR-126, miR-155, miR-143, miR-192 etc. [83,84,85,86,87,88,89]. miRNAs are known to regulate the expression of multiple genes and inflammatory mediators that are imperative in the development of IBD and IBD-CRC [90,91]. For instance, miR-126 was observed to increase the inflammatory response via the activation of NF- κB signaling [92]. Likewise, miR-155 was shown to be involved in the activation of JAK/STAT signaling during IBD [93]. As a proof of concept, inhibition of miRNAs was found to reduce the severity of IBD and IBD-CRC [85,87]. Additional research is still required to fully understand the regulatory relationship between miRNAs and their targeted genes during IBD-CRC, to progress towards miRNA therapeutics.
3.2. Innate/Adaptive immune related mechanism
Like several other chronic inflammatory conditions, dysregulation of the immune response in patients with IBD or IBD-CRC, triggers infiltration and accumulation of immune cells; that provokes the release of several pro-inflammatory cytokines and chemokines. These cells comprise, neutrophils, tumor-associated macrophages, cluster of differentiation (CD)4 and CD8 cells, endothelial cells, natural killer (NK) cells, dendritic cells, as well as mesenchymal cells [94,95]. The release of pro-inflammatory cytokines/chemokines plays an essential role as a predictive marker for the early identification of inflammation. However, spontaneous hyper-production of pro-inflammatory mediators counteracts their effector functions, contributing to aberrant immune responses, as seen in IBD-CRC [95]. The release of various other inflammatory cytokines/chemokines, such as IL-1β, IL-6, IL-8, IL-17, IL-18, IL-21, IL-23, interferon-gamma (INF-γ), CCL22, CCL12 and tumor necrosis factor-alpha (TNF-α), have been reported during IBD [94,96,97,98,99,100]. Each of these mediators, notably IL-6, TNF-α, IL-17 and IL-23, is implicated in IBD associated tumor development [101,102,103]. Suppression of these cytokines was found to ameliorate the symptoms of IBD-CRC progression [102,104,105].
Dysregulation of novel innate immune mechanism nucleotide oligomerization domain (NOD)-like receptor proteins (NLRPs) has been linked to IBD and IBD-CRC. Various anti-tumorigenic activities of NOD in the gut, include inhibition of Toll-like receptor (TLR) signaling, balancing T cell-mediated immune responses, alleviates production of anti-inflammatory cytokines, like IL-10, and inhibition of potent inducers of inflammation (inflammasomes) [106,107]. It is still contraversial whether IBD-CRC is fully dependent on NOD or NLRPs. However, dampened production of NOD/NLRPs in mouse model of IBD-CRC has shown to increase IBD severity and rapid progression towards tumor development [108,109,110].
3.3. Immune signaling pathways
Several immune signaling pathways are known to be involved in IBD and CRC. Nonetheless, the activation of two major oncogenic transcription factors/pathways, NF-κB and signal transducer and activator of transcription 3 (STAT3) drives the process of chronic inflammation and carcinogenesis. These pathways are mostly activated via pro-inflammatory stimuli. Several lines of evidence indicate, that activation of NF-κB and STAT3 pathways, lead to the production of a myriad of inflammatory mediators contributing to inflammation-induced CRC [111,112,113]. Inhibition of these transcription factors/pathways thought to play a significant role in limiting the extent of tumorigenic processes, like cell proliferation, apoptosis, metastasis and angiogenesis, occurring during IBD-CRC [111,113,114]. The process of activation of NF-ĸB via canonical pathway consist of dimers of RelA, p50 and RelC subunits. During unstimulated state, these dimers remain bound to specific inhibitors, IkB proteins, in the cytoplasm. However, stimulus from microbial infections, IL-1, TNF-α and lipopolysaccharide (LPS) activates the IkB kinase complex (IKKa and IKKb) and triggers the proteosomal degradation of IkB. Consequently, unbound subunits RelA/p50 translocate to the nucleus and begins the transcription of target genes. An alternative pathway for NF-kB stimulation requires the IkB-Kinase-alpha (IKKα) subunit-mediated proteosomal degradation. The unbound p52/RelB dimers translocate and start the transcription of target genes in the nucleus. During inflammation, persistent activation of NF-kB leads to cancer [115,116]. A preclinical study by Greten et al., has also shown the role of IKKbin activation NF-kB signaling and linking inflammation and tumorigenesis in AOM/DSS model of IBD-CRC [117].
Activation of NF-kB liberates IL-6 from myeloid, macrophages, lymphocytes, monocytes and other cancerous cells. IL-6 forms a complex by binding to its soluble IL-6R receptors, that further engages with glycoprotein gp130 subunit and results in the activation of various downstream signaling pathways involving STAT3, Janus Kinase (JAK) and phosphatidylinositol 3 kinase (PI3K-Akt) [118]. STAT3 is a transcription factor which assist cell proliferation and survival by inhibiting apoptosis, metastases, cell adhesion, angiogenesis and inflammation [119]. Not only IL-6, but other inflammatory mediators such as IL-11, hepatocyte growth factor (HGF), IL-22 and vascular endothelial growth factor (VEGF) activates STAT3 during IBD and IBD-CRC [119,120,121]. IL-6 promotes tumor development via activation of STAT3 mediated intestinal epithelial cell proliferation and survival in mouse model of IBD-CRC [113]. In addition, persistent activation of NF-kB in tumor cells is mediated by STAT3 which prompts the retention of RelA into nucleus and hence, amplify the effect of NF-kB during malignant transformation [114].
3.4. Role of host microbiota in IBD-CRC
The intestinal tract is a home to diverse species of microorganisms, including microbes, viruses, and fungi, that contribute towards maintaining the homeostasis. Recently, however, there have been reports on the role of intestinal microbiota in IBD and CRC development [122,123,124,125]. Multiple mechanisms have been postulated regarding the action of intestinal microbiota in the pathogenesis of IBD and CRC. An imbalance of the normal microbiota (dysbiosis) is thought to be one of the key mechanisms linked to the development of IBD-CRC [126]. Dysbiosis is associated with the production of carcinogenetic genotoxins, the release of pro-inflammatory mediators and activation of critical cellular inflammatory signaling pathways, and hence, implicated in the causation of IBD-CRC [107,127,128]. For instance, toxins released from bacteria such as Escherichia coli, Bacteroides fragilis, Citrobacter rodentium andClostridium defficile are shown to directly influence the growth of tumor in the colon [128]. Moreover, the role of bacteria like H. hepaticus was found to be critical during inflammation and initiation of carcinogenesis in murine models of IBD [14].
Dysbiosis leads to the activation of pattern recognition receptors (PRRs) including TLRs. During inflammation, entry of pathogens into lamina propria triggers the activation of TLRs resulting in the release of pro-inflammatory cytokines and subsequent stimulation of the innate immune system cells that binds to microbe-associated molecular patterns (MAMP), ending in uncontrolled NF-kB signaling [127]. Among 13 TLRs, TLR2 and TLR4 are gaining wide attention for their role in the progression of IBD-CRC. TLR2 is reported to have a protective role in AOM/DSS model of IBD-CRC [129]. Contrastingly, mice deficient in TLR4 was found to have reduced number of tumors and COX-2 expression [130]. Differences in the microbiota in different mice models of IBD-CRC might contribute to these conflicting findings. Further studies are warranted to strengthen such observations.
4. Current and Future Management Strategies
The most common types treatments of CRC or IBD-CRC include surgery, chemo- and radiation therapy. Surgical resection is usually recommended when patients are unresponsive to pharmacological interventions or radiation therapies [131]. Cytocidal drugs and biological agents are administered to the patients in conjunction with surgery, chemo- or radiation therapy [132]. However, these approaches are reported to have a number of drawbacks and may cause severe and potentially life-threatening complications. Most importantly, these approaches are also associated with higher rates of tumor recurrence.
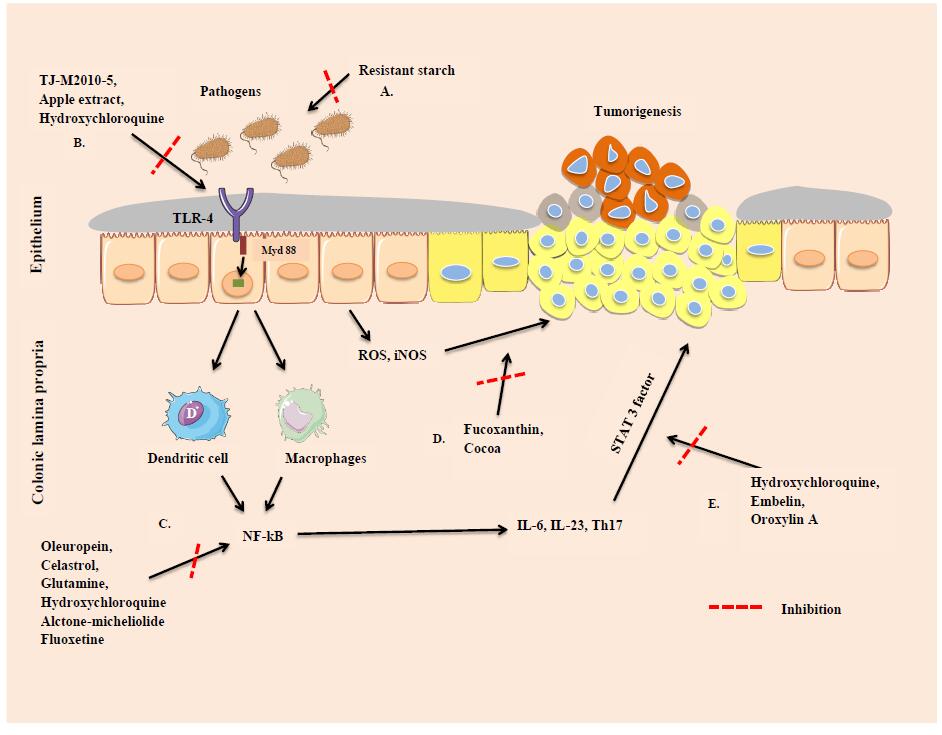
The generation of in-vitro attempts and various animal models of IBD, CRC, as well as IBD-CRC, have been pivotal in testing many biological molecules, as an anti-tumor agent. For instance, the anti-inflammatory and anti-tumorigenic potential of monoclonal antibodies and anti-cytokine agents, such as TNF-αinhibitors, has been tested in patients with IBD and IBD-CRC [105]. However, as seen with other chemotherapeutic agents, their prolonged use is associated with significant side effects. Moreover, these agents are quite expensive, and importantly, many patients do not respond to these therapies leading to remission of chronic inflammation and tumor formation that require surgical intervention. Nevertheless, there are studies suggesting the potential role of several natural and synthetic compounds in the management of IBD, CRC, and potentially IBD-CRC, by targeting the release of inflammatory markers associated with such disorders. These compounds are summarized in Table 1. together with their role and potential mode of action (Figure 1). Herein, we have briefly described below the novel therapeutic agents that might play a key role in discontinuing the inflammatory/tumorigenic response during IBD-CRC.
Table 1. Classification of novel therapeutic compounds and their role and mechanism of action in ameliorating IBD-CRC
| Compound | Class | Inhibitory Effect | Potential Mode of Action | References |
| Oleuropein | Natural Product | INF-g, TNF-a, IL-6, COX-2 and IL-17A | Blockade of immune signaling pathways, such as STAT3 and NF-kB | [137] |
| GNDPs2 | Natural Product | TNF-a, IL-6 and IL-1b | Inhibition of pro-inflammatory cytokine release | [138] |
| Celastrol | Natural Product | TNF-a, IL-6 and IL-1b, COX-2 and iNOS | Downregulation of NF-kB pathway | [139] |
| Resistant Starch | Natural Product | COX-2, IL-1b and TNF-a | Decreased NF-kB expression and altered gut microbiota | [142] |
| Fucoxanthin | Natural Product | TNF-a, IL-6 and iNOS | Suppression of oxidative stress | [143] |
| Cocaine | Natural Product | COX-2 and iNOS | Suppression of oxidative stress | [144] |
| Apple extract (AP) | Natural Product | IL-6, TNF-a and INF-b | Suppression of NF-kB signaling | [173] |
| Digitoflavone | Natural Product | IL-6, TNF-a and IL-1b | Suppression of oxidative stress | [174] |
| Oroxylin A | Natural Product | IL-6 and IL-1b | Attenuation of IL-6/STAT3 signaling | [150] |
| TJ-M2010-5 | Synthetic analogue | TNF-a, IL-6, IL-11, IL-17A, IL-22, COX-2 and IL-23 | Downregulation TLR signaling | [155] |
| Glutamine supplements | Synthetic/pre-existing drugs | TNF-a, IL-6, COX-2 and iNOS | Downregulation of NF-kB signaling | [175,176] |
| Tropisetron | Synthetic/pre-existing drugs | TNF-a, IL-6 and IL-1b, TLR4, COX-2 and b-catenin | Inhibition of pro-inflammatory cytokine release | [156] |
| Fluoxetine | Synthetic/pre-existing drug | TNF-a | Inhibition of TNF-a-mediated NF-kB signaling | [158] |
| Cimetidine and clobenpropit | Synthetic/pre-existing drug | IL-6, TNF-a, IL-1b, COX-2 and iNOS | Modulation of oxidation and antioxidant ratio | [159] |
| Hydroxychloroquine | Synthetic/pre-existing drug | IL-6, TNF-a, COX-2 and IL-1b | Attenuation of TLR4 activation, STAT3 and NF-kB pathway | [162] |
| Embelin | Synthetic analogue | IL-6, IL-17A, IL-23A and IL-1b, | Attenuation of IL-6/STAT3 signaling | [163] |
| ITF2357 | Synthetic analogue | INF-g | Inhibition of NF-kB activation | [81] |
5. Naturally-occurring Compounds
5.1. Oleuropein
Oleuropein is a natural phenolic secoiridoid obtained from olive leaves and is known to have anti-inflammatory, anti-tumorigenic and anti-proliferative properties. It has been tested in several inflammatory models such as DSS-colitis and also in prostate and breast cancer cells [133,134,135,136]. In a recent study by Giner et. al., the anti-cancer potential of oleuropein was investigated in AOM/DSS model of IBD-CRC [137]. Oleuropein treatment reduced the colonic neoplasms by 64% as compared to control (100%) by downregulating the level of cytokines, enhancing the expression of apoptosis genes and limiting the activation of signaling pathway associated with IBD-CRC [137].
5.2. GDNPs2
GDNPs2 is a naturally occurring nanoparticle, extracted from edible ginger, identified as one of the most effective novel nanoparticles for the management of IBD-CRC. Oral administration of GDNPs2 attenuated the symptoms associated with IBD-CRC, raised the production of anti-inflammatory cytokines such as IL-10 and IL-22, and enhanced the proliferation of intestinal epithelial cells in mice model of IBD-CRC [138]. They have also shown merits like overcoming potential toxicity and limiting the production scale which is essential to prepare synthetic nanoparticles.
5.3. Celastrol
Celastrol (tripterine) is a compound isolated from a Chinese herb and is known to possess anti-tumorigenic and anti-inflammatory properties. Recent, in-vitro and in-vivo experiments explored the anti-tumorigenic and anti-inflammatory potential of celastrol in IBD-CRC. The compound was observed to downregulate the production of inflammatory markers, oncogenes, p53 mutated genes that are involved in the process of IBD associated carcinogenesis [139,140].
5.4. Resistant starch
Resistant Starch (RS) is among the dietary components which were tested against IBD-CRC. RS fermentation is known to produce short-chain fatty acids (SCFAs). These fatty acids are a contributing factor towards the maintenance of the intestinal homeostasis, as well as, attenuation of carcinogenesis [141]. Recently, Hu et al. evaluated the potential of RS in AOM/DSS model of IBD-CRC. Interestingly, RS was found to prevent the further progression of IBD-CRC mostly via encouraging the production of SCFAs and altering the gut microbiota [142].
5.5. Fucoxanthin and cocoa
Fucoxanthin is isolated from edible brown algae and is considered as one of the ROS/RNS scavengers. The anti-cancer potential of fucoxanthin was tested using mice model of IBD-CRC. It was reported that fucoxanthin ameliorated the progression of IBD-CRC development by reducing the occurrence of neoplasms. Fucoxanthin-induced upregulation of superoxide dismutase (endogenous anti-oxidative enzyme), as well as, downregulation of malondialdehyde (endogenous oxidant) prevents the cells from DNA damage and therefore, capable of impeding the process of carcinogenesis [143]. Similarly, cocoa, a naturally occurring polyphenolic compound suppressed the progression of IBD-CRC in AOM/DSS model. The anti-oxidative nature of this compound was found to downregulate the concentrations of malondialdehyde, COX-2, and iNOS and create an upsurge in the levels of antioxidant enzymes like superoxide dismutase [144].
5.6. Konjac glucomannan and inulin
One of the fibrous substances “inulin and Konjac Glucomannan”, diminished the progression of IBD-CRC via recovering the leukocyte phagocytic capacity, reducing the extent of tumor invasion and attenuating the production of pro-inflammatory mediators like TNF-a and IL-1b [145]. Further reduction in hyperplasia-dysplasia transition in IBD-CRC mice model was initiated after dietary consumption of fruit “Ziziphus jujuba”, enriched with polysaccharides, flavonoids, oleamide, and triterpenoids [146].
5.7. Sesquiterpene and fisetin
Sesquiterpene is one of the promising molecules which is considered to be a potent inhibitor of NF-kB signaling pathway and therefore, attenuated IBD-CRC progression in AOM/DSS model [147]. Likewise, another dietary flavonoid, fisetin, was shown to ameliorate IBD-CRC development via a reduction in enzymatic and non-enzymatic antioxidant levels including superoxide dismutase [148].
5.8. Astaxanthin and oroxylin A
Astaxanthin, a natural carotenoid, inhibited IBD-CRC in AOM/DSS model by downregulating the expression of inflammatory mediators such as NF-kB, IL-1b, COX-2, and IL-6 [149]. Similarly, oroxylin A, a flavone obtained from medicinal plants, was reported to be effective in in-vitro and in-vivo models of IBD-CRC by inactivating the IL-6/STAT3 pathway [150].
5.9. Bio-active peptides
Recently, a melanocortin-derived tripeptide, KVP has been depicted as an anti-inflammatory and anti-carcinogenic agent in murine models of IBD-CRC [151]. KVP was found to obstruct the development of CRC by reducing the tumor burden in AOM/DSS model. However, studies are warranted to decipher the exact mechanism via which KVP reduces the tumor load to act against the advancement of IBD-CRC [152].
6. Synthetic/Pre-Existing Drugs
There is an increasingly expanding array of synthetic/pre-existing molecules aimed at reducing the extent of inflammatory responses during IBD-CRC. These agents are briefly discussed below.
6.1. Ursodeoxycholic acid
Ursodeoxycholic acid drops the release of excessive bile acids and hence, reduces the risk of developing CRC [153,154]. Excessive release of secondary bile acids in the lumen of colon is considered as one of the risk factors causing IBD-CRC. Correspondingly, “TJ-M2010-5”, a novel synthetic inhibitor of TLR/MyD88 signaling restricts the development of IBD-CRC in AOM/DSS model. Apart from reducing the levels of pro-inflammatory cytokines, TJ-M2010-5, also promotes the dimerization of MyD88 and alters its configuration, hence negatively regulates the tumorigenesis process [155].
6.2. Tropisetron
Serotonin, a neurotransmitter, and its associated receptors are found to be overexpressed in IBD and promoted CRC. Inhibition of serotonin receptors by antagonist tropisetron proved to be protective in AOM/DSS model. Tropisetron is used as an antiemetic in chemotherapy, inhibited the IBD-CRC and significantly reduced the inflammatory mechanisms in colitis [156,157]. Another drug “fluoxetine” is an antidepressant from the class of serotonin reuptake inhibitors also attenuated DSS-induced inflammation and IBD-CRC in DSS and AOM/DSS mice models, respectively. The major mechanism involved was the inhibition of TNF-a mediated NF-kB signaling in COLO-205 cells, as well as in mouse models of IBD-CRC. It also inhibited the production of myeloperoxidase (MPO) and macrophage inflammatory protein 2 (MIP2) secretion [158].
6.3. Cimetidine and clobenpropit
The antagonist of histamine receptors such as cimetidine (histamine receptor 2 inhibitor) and clobenpropit (histamine receptor 3 inhibitor) exhibited the chemopreventive efficacy in IBD-CRC. Clobenpropit is also known to inhibit histamine receptor 4. These inhibitors modulate the oxidative and anti-oxidative status and enhance apoptosis of cells due to an increase in the levels of histamine as reported in UC, CD, and CRC patients [159,160]. These studies also reported a potential role of histamine receptors in causing IBD-CRC.
6.4. GAP, hydroxychloroquine and embelin
“GAP [3-(4-geranyloxy-3-methoxyphenyl)-2-trans-propenoic acid] or (4-geranyloxy-ferulic acid)”, a synthetic prodrug ameliorates the IBD-CRC via a reduction in oxidative stress by lowering the 8-OHdG levels (oxidative stress biomarker) in mice and proliferation of cells in-vivo [161]. Anti-inflammatory potential of antimalarial drugs such as hydroxychloroquine (HCQ) might make this medication useful for the treatment of IBD-CRC. HCQ ameliorates IBD-CRC by reducing the release of ROS in lamina propria and inactivation of TLR4 in macrophages [162]. “Embelin” is a small molecule inhibitor, enriched with various properties such as antioxidant, anti-cancer and anti-inflammatory. It exerts its action by reducing the infiltration of macrophages, CD4+ T cells, proliferation of the tumor epithelial cells and inactivation of STAT3 pathway [163].
6.5. FTY720
S1P (metabolite) produced from sphingokinases (SphK1) are the proteins involved in various cellular processes (cell growth, invasion, cytokine and chemokine production). This metabolite is implicated in UC and CRC and is known to be a vital player for the persistent activation of the STAT3 signaling pathway. Inhibition of S1P by prodrug “FTY720” reduces the expression of S1P receptor S1PR and SphK1 and hence ameliorates the activation of NF-kB and IL-6/STAT3 pathways in IBD-CRC model [164,165,166].
6.6. Nimesulide, troglitazone and celecoxib
The role of COX-2 inhibitors in the treatment of CRC and intestinal inflammation has already been identified [167]. A study reported the chemopreventive effectiveness of nimesulide (selective COX-2 inhibitor) in AOM/DSS model. It suppressed the proliferation of cells, induce apoptosis and downregulate the levels of b-catenin, COX-2, and iNOS, and therefore, was found to be effective in sporadic as well as IBD associated carcinomas [168]. In the same study, PPAR ligands such as troglitazone exerted similar anti-cancer effects [168]. Another selective COX-2 inhibitor “celecoxib” act as a chemopreventive agent in IBD-CRC mice model by inhibiting the PI3K/Akt pathway [169].
6.7. Statin hydroxamate and ITF2357
Inhibition of histone deacetylase by statin hydroxamate and ITF2357 is another therapeutic approach which is currently tested in clinical trials. These compounds modulate the acetylation of NF-kB and inhibit the apoptosis of cells. Statin hydroxamate and ITF2357 also inhibit the release of bacterial endotoxins, suppress the production of pro-inflammatory cytokines, decrease the infiltration of macrophages and neutrophils in cancerous regions and elevate the apoptosis of mononuclear cells in lamina propria [81,170,171].
Considering, the present scenario and trends, there is an urgent need to identify and develop novel chemotherapeutic agents, which are cost effective, safe, patient compliant and free from adverse effects. Several novel classes of compounds, such as naturally occurring agents, pre-existing drugs, synthetic analogues, and dietary composites, have shown considerable promise in the management of inflammation associated CRC. A new technique named “photodynamic therapy” was developed for the treatment of IBD-CRC. It involves the treatment with liposomal formulation (metatetra hydroxyphenyl chlorine also called foslip), which in low doses lowers the influx of neutrophils and prevents the dysbiosis of gut microbiota and hence was found to be effective in IBD-CRC [172]. Furthermore, Vong et al. developed a novel oral nanotherapy by designing redox nanoparticles, which can be considered as a promising treatment for IBD-CRC [57].
Discovery of an active, multi-target mono-therapeutic agent, for patients with CRC, would change the course of cancer research. However, the complexity of such disorders makes it hard to implement such therapies. Nevertheless, in conjunction with currently used surgical and pharmacological interventions, prospective randomized controlled trials should focus on evaluating the long-term efficacy, and side-effect profiles of the promising anti-cancer agents to pave the way towards eradicating inflammation-related carcinogenesis.
7. Conclusion
Various scientific findings evidence a functional link between IBD and CRC. The molecular mechanisms behind IBD-CRC progression are still not fully revealed and need attention. However, recent findings from animal studies implicate the potential role of various immune cells, signaling pathways, pro-inflammatory cytokines and other inflammatory markers in IBD-CRC development. Continued research in this field especially the discovery of various new natural and synthetic therapeutic moieties would help us decode the underlying mechanisms involved with IBD-CRC and would eventually lead to new therapeutic interventions which can significantly contribute in IBD-CRC clinics.
Acknowledgements
This work was supported by Early-Career Fellowship awarded to Dr Madhur D. Shastri by the Faculty of Health, University of Tasmania and Tasmanian Post-Graduate Research Scholarship (TGRS) awarded to Sonia Shastri.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: 



