1. Introduction
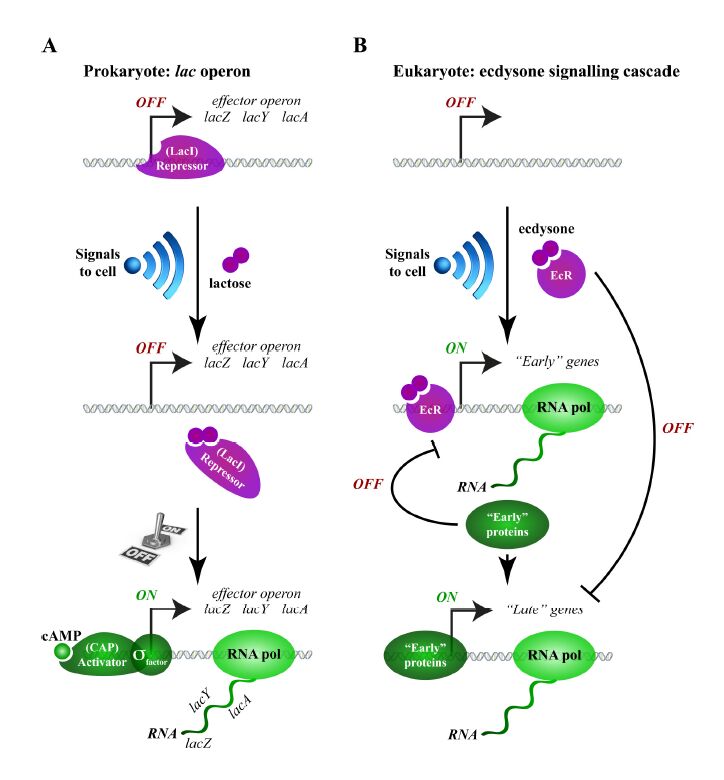
Before eukaryotes, the life of DNA was somewhat simpler. Bacterial genomes are compact, ranging in size from 1 to 10 Mb, and they contain very little non-coding DNA (on average, less than 15%) [1]. Most of the bacterial DNA is readily accessible for sequence-specific DNA binding proteins making gene regulation transparent [2,3,4]. Genes are switched “ON” or “OFF” in response to environmental signals through unperturbed binding of transcription activators or repressors respectively. The logic of bacterial gene control can be effectively described knowing the affinities of regulatory proteins to DNA and their concentrations under the framework of François Jacob and Jacques Monod model [5,6,7,8]. In brief, following the classic Jacob and Monod example of Escherichia coli lactose (lac) operon gene switch, it has been shown that in the absence of lactose, a lac repressor protein (LacI) binds DNA sequence located downstream of lac operon promoter. When lactose is available, it binds to the LacI repressor resulting in LacI displacement from DNA. Following LacI removal, RNA polymerase is free to bind to lac operon promoter sequence initiating the transcription of lacZ, lacY and lacA effector genes. The activation of lac operon is aided by the sigma factor and CAP (Catabolite Activator Protein) in complex with cAMP (Figure 1A). The proteins translated from lac operon mRNA are used then by E. coli to metabolize lactose [5,9]. Thus, a simple allosteric modulation of repressor affinity to DNA triggered by environmental/metabolic signal
s can switch bacterial gene circuitries “ON”/”OFF” to guarantee adequate cellular response to new conditions.
By large, since its inception in 1961, the paradigm of Jacob and Monod remains instrumental in the dissection of regulatory mechanisms of gene activation and repression. This model led to the establishment of common principles of gene regulation not only for prokaryotes, but also for eukaryotes [10]. In eukaryotes, one of the first demonstrations of Jacob-Monod model came from pioneering studies of Michael Ashburner on regulation of Drosophila melanogaster ecdysone inducible genes. During Drosophila development, pulses of ecdysone hormone trigger sequential activation of a number of genes required for developmental transitions from embryo to larvae, to pupae and to adult. Ligand-bound ecdysone receptor (EcR) induces the expression of “early” but inhibits “late” genes. The products of “early” ecdysone inducible genes activate the expression of “late” genes leading to a cascade of genetic switches (Figure 1B) [11,12]. In essence, quoting Jacques Monod this shows that “what is true for E. coli is also true for the elephant”. However, there are a number of aspects unique for eukaryotes, where the standard Jacob-Monod model is limited. In this review, I will highlight the parallels and differences between prokaryote and eukaryote gene regulation, and I will attempt to illustrate the limitations of gene-centric view imposed by Jacob-Monod interpretation.
2. DNA Packaging Problem
To begin, let’s firstly note that the size of eukaryotic genomes is orders of magnitude larger than that of bacteria, which ranges from about 10 Mb to 100 Gb [1]. Secondly, eukaryotic DNA is split into many linear chromosomes confined within a nucleus. If we take all chromosomes from a single human diploid cell and stretch them, the resulting length of DNA will be enormous totalling about 2 meters. This is 200’000 times longer than average diameter of cell nuclei. Thus, these initial conditions necessitate to keep DNA molecules compact enough—to fit into the nucleus, and ordered—to ensure the fidelity of replication, segregation and expression. But how can it be achieved?
There are several imaginable strategies to solve DNA packaging problem. Firstly, DNA can be randomly coiled into a globule within the nuclear interior. In a simplistic model, DNA can be described as a chain consisting of freely joint stiff links with Kuhn length (lk) of ~ 100 nm (two times the persistence length of DNA) [13,14,15]. Then, given an average length for human chromosomes of ~ 120 Mb (~ 40 mm), the average radius of randomly compacted DNA globule would be ~ 60 µm (r= N1/2lk; where N is the number of Kuhn segments). This already provides a good level of compaction, but it still exceeds the nuclear diameter 6 times and there are 46 of such DNA coils that have to be packaged within a single nucleus. Fortunately, given a rather low density of Gaussian coils, they can, in principle, be squeezed into the nuclear volume before incurring insurmountable energy costs [16].
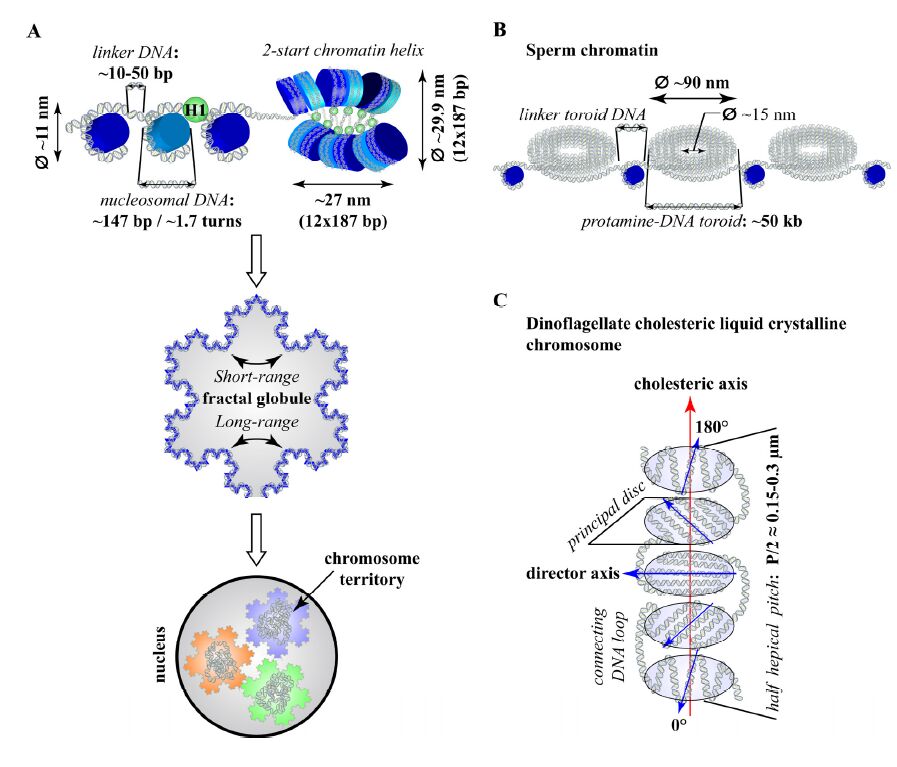
Although simple and energetically attractive, Gaussian coils formed by random walk are expected to be in a disordered state, in which DNA threads are mixed and tangled [17]. Intuitively, this does not seem to be compatible with cellular demands for organized control over genetic material. To address the needs of keeping DNA packaged inside the nucleus but yet ordered, nucleosome emerged in evolution of eukaryotes. Nucleosome, a term coined by Pierre Chambon [18], defines a protein-DNA complex, in which a 147 bp of DNA is wrapped in ~ 1.7 left-handed superhelical turns around a positively-charged protein spool comprising one tetramer of histones H3 and H4, and two dimers of histones H2A and H2B [19,20,21]. On the exit, adjacent stretch of DNA wraps around another histone spool separated from the previous by 10-50 bp of linker DNA, and this wrapping process is repeated until all DNA is packaged (Figure 2A) [22]. When visualised by electron microscopy, at a low ionic strength the resulting structure resembles a collection of beads (histone octamers) on a DNA string, and, hence, it is known as “beads on a string” [18,23,24]. In total, depending on the organism and cell type, 75-90% of eukaryotic DNA is wrapped onto histone spools [25], which corresponds to 20-25 million nucleosomes per diploid human genome.
“Beads on a string” is the most basal and fundamental level of DNA packaging into chromatin found in most of the species from Eukaryota domain. Of note, however, there are several exceptions to that. 1) In many sexually reproducing animal species, sperm DNA is tightly packaged into a compact, needle-shaped nucleus by protamines, a diverse group of fast-evolving basic (positively-charged) proteins distinct from core histones [27,28]. Protamines coil DNA into toroids, each containing ~ 50 kb of DNA and scaling ~ 90 nm in outer diameter with a hole of ~ 15 nm. Toroids are separated by nuclease-sensitive DNA linkers, which are assembled into remaining nucleosomes and are attached to sperm nuclear matrix (Figure 2B) [28,29,30,31,32]. Such extreme packaging enhances sperm hydrodynamicity and protects paternal genome from damage while it is on its way to oocyte. DNA often assumes toroidal shape in vitro in the presence of multivalent (+3 or greater) cations, such as spermidine3+, spermine4+, Co3+, etc., and, in many viruses, DNA is packaged into viral capsid as toroid [30,33,34,35,36]. 2) In dinoflagellates, a group of mixotrophic flagellate protists, DNA is packaged in the absence of core histones into a cholesteric liquid crystalline chromosomes with the help of bivalent counterions, such as Ca2+ and Mg2+ [37,38,39,40]. In cholesteric liquid crystalline phase, DNA molecules are ordered into the stacks of highly condensed discs, in which DNA strands are aligned along director axes, connected by DNA loops. Director axes twist along the cholesteric axis with half the helical pitch (P/2) ranging from 0.15 to 0.3 mm depending on the species (Figure 2C) [41]. Dinoflagellate genomes are among the largest known eukaryotic genomes reaching in size ~ 100-150 Gb [42]. The nuclear concentration of DNA in dinoflagellates is up to 80 times higher than that in human cells (~ 200 mg/ml), while protein to DNA ratio is 10 times less (~ 1:10) than for the typical nucleosome-based chromatin [43,44]. Interestingly, at such extreme concentrations, DNA naturally transits to cholesteric liquid crystalline phase [45,46]. Although beyond the scope of this review, these non-canonical DNA condensation approaches emphasize the diversity of possible solutions to DNA packaging problem explored by nature.
Upon assembly of DNA into array of nucleosome, in vitro, the resulting 10-nm chromatin fiber tends to coil into a more compact 30-nm fiber due to stacking interactions between neighbouring nucleosome core particles. Since the discovery of the 30-nm chromatin fiber, there were two major competing models of how nucleosomes can be arranged within the fiber [47,48]. In the first model, nucleosome array is thought to coil into a one-start solenoid helix [47,49]. In the second model, nucleosomes are arranged into two stacks separated by the linker DNA zigzagging back and forth between the stacks [26,48,50,51]. Although the exact geometry of 30-nm fiber and whether it even exists in living cells is actively debated [52,53,54,55,56,57], recent cryo-EM studies of in vitro assembled chromatin fibers support the latter two-start model with the linker histone H1 zipped between two stacks (Figure 2A) [26,58]. However, it has to be noted that in most of these studies nucleosome arrays with fixed nucleosome repeat length are often used to reconstitute a 30 nm fiber; a condition difficult to expect in living cells.
Assembly of DNA into nucleosome arrays achieves the packaging ratio of ~ 5-10 for 10 nm chromatin fiber and ~ 50 for 30 nm chromatin fiber [59], but the resulting fibers are still too long to fit into nuclear dimensions. If we coil 30 nm chromatin fiber randomly, the expected globule radius for average human chromosome (~ 120 Mb) would be ~ 20 µm (r = (Lclk)1/2; where Lc is the contour length—1333.33 µm at mass density of 90 bp/nm and lk is the Kuhn length— ~ 0.3 µm for 30 nm fiber) [60]. This globule is already 3 times more compact than that formed by the “naked” DNA (~ 60 µm for 120 Mb), but it exceeds nuclear diameter (~ 10 µm), necessitating an additional level of compaction. This is achieved through a combination of short- and long-range interactions on chromatin fiber mediated by non-histone proteins. A wealth of data has been accumulated recently on pair-wise associations between distinct chromosomal loci by 3C (Chromatin Conformation Capture) related techniques, such as 4C, 5C, Hi-C, etc., on genome-wide scale [61,62,63,64]. These studies reveal that 1) the majority of interactions are intra-chromosomal substantiating earlier observations that chromosomes are confined within chromosome territories; and 2) the probability of contacts depends on genomic distance (s) as power low with exponent −1 or so (P(s)~ s-1) suggesting that chromatin fiber is folded into fractal globule (Figure 2A) [63,64,65,66]. Fractal globule (FG) has a number of useful implications for eukaryotic genome organization and regulation: 1) folding of chromatin fiber into FG ensures separation of chromosomes into distinct territories; 2) FG is demixed (unknotted) at all length scales allowing for rapid unfolding of any region to make it accessible for regulatory proteins [17,67,68,69]. However, the precise configuration and dynamics of chromatin globule remains an actively investigated issue and alternative models have been proposed including Dynamic Loop model [70,71] and Strings and Binders Switch model [72,73]. For more detailed overview of current approaches to modelling of chromatin fiber folding please refer to the studies by Moscalets A.P. et al., and Caré B.R. et al. appearing in this issue of AIMS Biophysics [74,75].
Being tightly wrapped around the histone core, 147 bp of nucleosomal DNA is inaccessible for most of the DNA binding proteins unless nucleosome is moved or removed. At the same time, however, N-terminal tails of the core histones protrude from nucleosome particle creating an accessible binding surface on a nucleosome. Histone tails are subjected to various combinations of post-translational modifications (PTMs) comprising “histone code”. These PTMs allow for specific tethering of various transcription regulators to selective promoters at selective genomic loci [76,77,78,79,80,81]. Thus, modulation of nucleosome positioning and PTMs comprise a whole new layer of eukaryotic genome regulation, which is absent in prokaryotes. Consequently, this raises the question of how eukaryotic gene regulation is realised on chromatin templates, and how and whether does it fit into Jacob-Monod model.
3. Pioneers—Setting the Stage for Execution of Eukaryotic Gene Circuitries on Chromatin
None of the gene switches would be ever possible without sequence-specific DNA binding transcription factors [82]. In recent years, it has been recognized that, in eukaryotes, there are two types transcription factors: pioneers and non-pioneers [for detailed review see [83]]. Although it is commonly believed that DNA wrapped around a core histone octamer is inaccessible for DNA-binding proteins, it is only true for non-pioneer factors. Pioneer factors can recognize their sites on nucleosomal DNA and initiate transcription on nucleosome arrays [83]. In fact, several studies indicate that pioneer transcription factors preferentially target motifs occluded by nucleosomes rather than nucleosome-free sites [84,85,86]. However, their binding depends on rotational settings of the target motif embedded in the core nucleosome particle [87]. For example, a tumor suppressor protein p53 binds to response elements in cell cycle arrest genes (CCA-sites) with high affinity, while its binding affinity to sites in apoptosis-associated genes (Apo-sites) is low. CCA-sites often locate at ~ 5 bp from nucleosome dyad and are exposed in conformation favourable for p53. In contrast, Apo-sites are separated by ~10 bp from nucleosome dyad. This little, half helical turn shift rotates the site by 180° inhibiting p53-DNA interaction [87].
Upon binding to nucleosome-occluded sites, pioneers mediate nucleosome repositioning and displacement in the absence of any enzymatic activities facilitating the recruitment of other non-pioneer transcription factors [88,89]. Interestingly, pioneers are represented by early factors, which act upstream of many developmental gene cascades [83,88,90,91,92,93,94]. For example, Oct4, Sox2 and Klf4 transcription factors are not intimidated by nucleosome and recognize their respective sites on the histone core. Along with the c-Myc (a non-pioneer transcription factor), they trigger cellular reprogramming, converting differentiated cells into induced pluripotent cells [94,95,96]. Thus, it is rational to place pioneers on top of eukaryotic gene hierarchy, while most of the chromatin transactions, which will be discussed further, occur downstream.
4. “Histone Code” Hypothesis—Extension of the Jacob-Monod Model to Chromatin
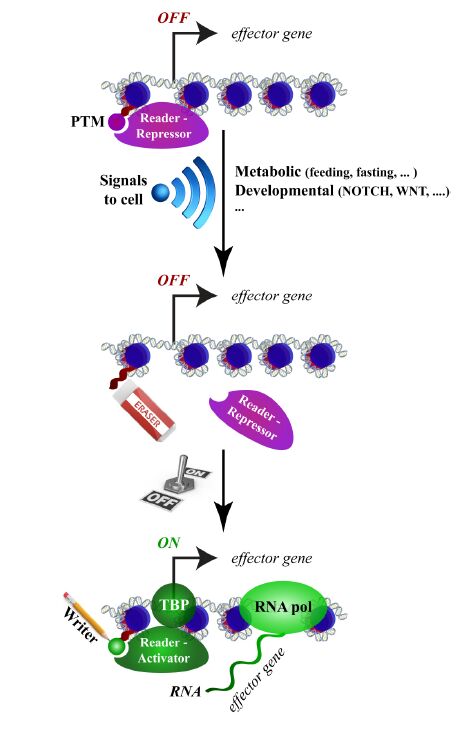
Before diving into the histone core, let’s take a look into the tails. Approximately 1/3 of core histones protein mass consists of structurally undefined, but evolutionary conserved N-terminal tail domains, which are subjected to PTMs. Numerous of such PTMs have been identified up to date and their combinations constitute the “histone code” [for the detailed catalog of histone modifications see 81]. In its original formulation, the “histone code” hypothesis asserts that “multiple histone modifications, acting in a combinatorial or sequential fashion on one or multiple histone tails, specify unique downstream functions” [77]. In essence, this hypothesis parallels the Jacob-Monod logic of gene control [97].
Leaving nuances aside, PTMs are installed on histone tails by a diverse set of enzymes known as “writers”, and they are removed by enzymes with opposite activities—“erasers” [98]. For example, histone acetyltransferases (HATs), which were among the first histone modifying enzymes to be discovered, add acetyl group to Lysine residues in histone tails, whereas histone deacetylases (HDACs) erase such acetyl marks [99,100,101,102,103]. Likewise, pairs of “writers” and “erasers” have been identified for many other PTMs: methylation, phosphorylation, ubiquitination and so on [104]. Existence of “writers” and “erasers” pairs ensures PTMs dynamics in response to diverse cellular signals. PTMs are recognized and interpreted by yet another group of proteins, known as “readers” [26,105]. “Readers” may act as effectors by executing specific regulatory functions themselves, or as presenters by recruiting other effector proteins (activators or repressors) [98]. Thus, combined actions of “writers”, “readers” and “erasers” orchestrate gene switches on nucleosomes at selective genomic loci. Importantly, however, the pioneer transcription factors, which trigger cellular reprogramming Oct4, Sox2, Klf4 and c-Myc, induce marked changes in histone PTMs landscape [106]. This indicates that “histone code” acts downstream of the transcription factors to reinforce and maintain a gene switch. Of course the quest for mechanisms coupling a vast number of PTMs along with their combinations to gene regulation is far from being over, it is already clear that “histone code” hypothesis extents the Jacob-Monod model to chromatin (Figure 3).
5. Nucleosome Array—a Buffer for Eukaryotic Genome
The Jacob-Monod model and “histone code” hypothesis are purely gene-centric. In other words, all sequences of regulatory events considered by these models unfold on a specific gene ignoring global parameters of DNA topology and nucleosome arrays configuration.
Starting again from E. coli, it has to be noted that global DNA supercoiling plays an important role in regulation of transcription. Bacterial chromosome is circular and it is maintained in a negatively supercoiled state. The supercoiling is controlled by DNA gyrase, which generates negative supercoils, and topoisomerases I and IV, which relax negatively supercoiled DNA. DNA gyrase is sensitive to cellular energy charge expressed as [ATP/ADP] ratio coupling supercoiling to cell growth and metabolism [107,108,109,110,111]. In growing cells, a total DNA superhelicity (superhelical density) s is about −0.05; where s is the number of turns added (+) or removed (−) relative to the total number of turns in а relaxed DNA molecule. In stationary phase, however, the cellular energy charge is reduced and superhelicity is lowered (s ~ −0.03) [109,112]. Upon osmotic stress, the ratio of [ATP] to [ADP] is raised and the total superhelicity is increased (s ~ 40.09) [108,110]. Such changes are perceived by every gene and are expected to impact the functioning of all genes [107,113]. Interestingly, however, the transcriptional response to total superhelical density alterations turns to be specific [114,115,116], and there are several reasons for this. Firstly, initiation of transcription of many bacterial genes relies on sigma factor, which recognizes two consensus motifs located at ~ −35 bp and ~ −10 bp relative to the transcription start site (TSS). The ability of sigma factor to bind to DNA depends on spacing and rotational orientation between these two sites. Thus, depending on the initial promoter settings, the effect of superhelicity on transcription will vary. Secondly, G+C-rich sequences require more energy to melt due to higher duplex stability as compared to A+T-rich sequences. Negative supercoiling supplies the energy needed for opening of DNA duplex facilitating activation of G+C-rich genes. A+T-rich genes appear to be less sensitive to the changes in total superhelicity. There are, of course, some other factors to consider, but what is important here is that global modulation of DNA topology provides a pervasive mean of gene regulation in bacteria [for detailed reviews see [107], [113], [113]].
In eukaryotes, topological domains are formed within DNA loops attached to nuclear matrix or other scaffolding proteins. Variations in superhelicity between these domains are correlated with gene activity, but precise relations between DNA topology and gene regulation remain poorly understood [118,119]. However, there is one other parameter to consider, which may have a similar role in eukaryotic gene control as total superhelicity in bacteria. This parameter is represented by configuration of nucleosome arrays with respect to spacing, positioning and turnover rates. Nucleosomes impose a significant barrier for general transcription factors, RNA polymerase and other proteins to access DNA. Thus, global modulation of nucleosome arrays configuration is expected to interfere with all aspects of eukaryotic genome functions.
5.1. Determinants of nucleosome positioning
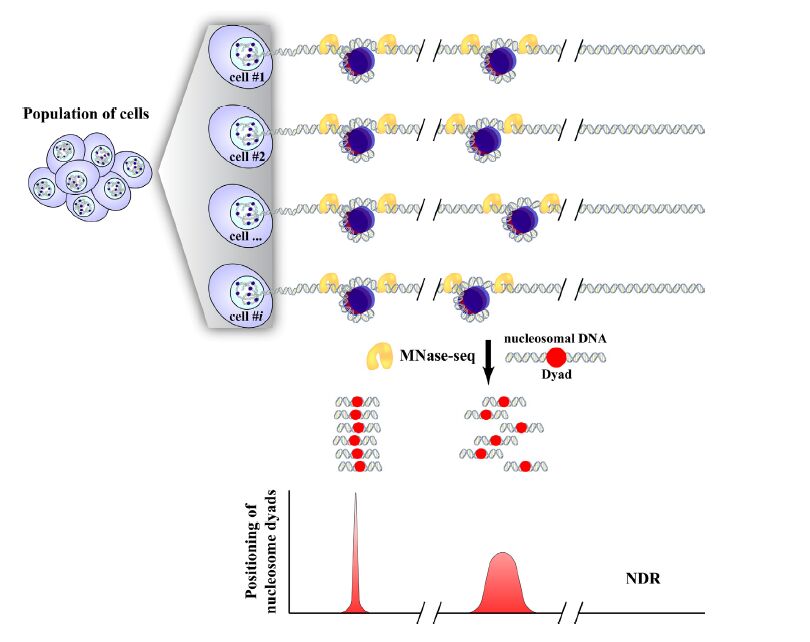
Before entering into further discussion on the role of nucleosome arrays configuration in gene control, we, first, have to address the question of what determines nucleosome positioning in living cells. Nucleosome positions are commonly assessed by digestion of chromatin with Micrococcal Nuclease (MNase), which cuts linker DNA releasing mono-, di-, tri-, etc. nucleosomes [120]. Followed by high-throughput paired-end sequencing of mono-nucleosomal DNA fragments (MNase-seq), nucleosome positioning can be estimated (Figure 4). If, in a population of cells, nucleosomes were positioned in a random phase (from cell to cell), then the resulting MNase-seq profile would be uniform. However, all high-resolution nucleosome maps are distinctly waveform. This indicates that nucleosome arrays are assembled in phase and thus, there must be a mechanism controlling nucleosome positioning in vivo.
To understand the rules behind nucleosome positioning, it is important to note that within nucleosome core particle 147 bp DNA endures aggregate bend of ~ 600° [19]. Thus, it is reasonable to assume that DNA sequences with higher propensity for anisotropic bending or increased flexibility will be favoured for nucleosome formation [121,122,123,124]. DNA flexibility is determined by a set of fundamental physical and chemical properties of dinucleotides, such as inter-base pairs translational (shift, slide, rise) and rotational (tilt, roll, twist) displacements. By large, energetics of these displacements is determined by base-stacking energy between adjacent base pairs [125]. On average, it is stronger for G:C containing dinucleotides, and weaker for A:T containing dinucleotides. Hence, no wonder that most of the correlations between DNA sequence and nucleosome placement emerging from genome-wide nucleosome mapping can be effectively described by relative enrichment of G:C and A:T dinucleotides. Well positioned nucleosomes tend to occupy DNA sequences enriched in G:C dinucleotides, while linker DNA and nucleosome depleted regions (NDRs) tend to locate within A:T rich sequences [126,127].
In addition to this, sequences with helical periodicity (10-11 bp) in dinucleotides show increased propensity to circularize [123] making them susceptible for optimal wrapping around a histone core. Indeed, a number of observations indicate that efficient nucleosome formation sites are characterized by ~ 10-11 bp periodic distribution of WW (W: A or T) dinucleotides followed in ~ 5-6 bp by SS (S: G or C) dinucleotides [127,128,129,130,131]. WW dinucleotides are most flexible and are located at “pressure” points within nucleosomal DNA, where the double helix endures maximum distortions, with minor grove facing the histone octamer [132,133]. Short runs of G:C nucleotides tend to bend towards the major groove [134], and within nucleosomal DNA SS dinucleotides are located 5-6 bp away from WW dinucleotides, where the major groove is bent towards the histone octamer [132,133]. Thus, a combination of dinucleotide content and fundamental 10-11 bp periodicities define intrinsic sequence preferences for nucleosome formation [for an excellent review on nucleosome structure see [20]].
These sequence rules, however, do not always apply. Several recent studies have indicated that so called NDRs, are, in fact, assembled into “labile” or “fragile” nucleosomes, which are sensitive to MNase digestion [135,136,137]. Comparingnucleosome maps generated by digestion of chromatin with varying concentrations of MNase revealed that “canonical” nucleosomes (resistant to MNase) are assembled on the sequences with relatively high G:C dinucleotides content. In contrast, “labile” nucleosomes (sensitive to MNase) occupy sequences with increased A:T content (unpublished results). These results argue that in vivo DNA sequence preferences for nucleosome formation might be significantly relaxed, in contrast to what was proposed earlier [128,129]. Substantiating this idea, it can be noted that affinity of the core histone octamer to DNA sequences depends in vitro on nucleosome assembly reaction conditions, such as temperature and histone to DNA ratio [138]. Thus, to what extent the underlying DNA sequence influences in living cells nucleosome array configuration remains to be an open issue.
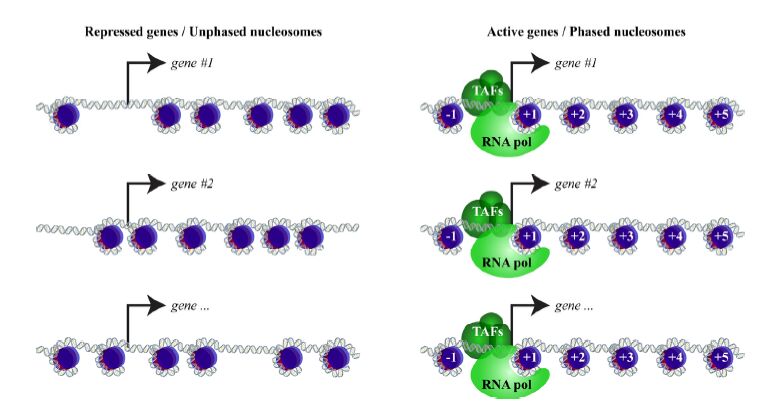
Besides DNA sequence, positioning of multiple nucleosomes along the DNA is dictated by steric exclusions. In other words, nucleosomes can not invade each others’ territories, which brings statistical nucleosome positioning in scope [139,140]. Statistical positioning causes nucleosomes to phase off the potential barriers represented by DNA bound protein complexes or off the wells formed by nucleosomes clamped to the precise position (Figure 5) [141,142,143]. Statistical nucleosome positioning immediately becomes evident from the comparison of nucleosome arrays in the vicinity to transcription start sites (TSS) of active and repressed genes. Nucleosome maps aligned to TSS show a clear phasing of nucleosomes up- and down-stream of TSS for actively transcribed genes, and the lack of so for repressed genes (Figure 5). Promoters of active genes recruit multiple regulatory proteins to DNA along with RNA polymerase, which might act as nucleosome organizing barriers or clamp the +1 nucleosome creating a potential well.
These are not the only barriers present in eukaryotic genomes. Nucleosome phasing is found in the vicinity to Ori Recognition Complex sites (ORC), CCCTC-binding factor (CTCF) sites and so on [144,145,146,147]. The phasing of nucleosomes off the barriers can be effectively described by the methods borrowed from statistical physics. Interestingly, in such models nucleosome phasing at TSS of active genes can be well recapitulatedwithout any DNA sequence information [141,142]. Combined, these observations indicate that configuration of nucleosome arrays sums up from sequence-dependent and statistical positioning of nucleosomes.
5.2. Configuration of nucleosome arrays by ATP-dependent chromatin remodelers
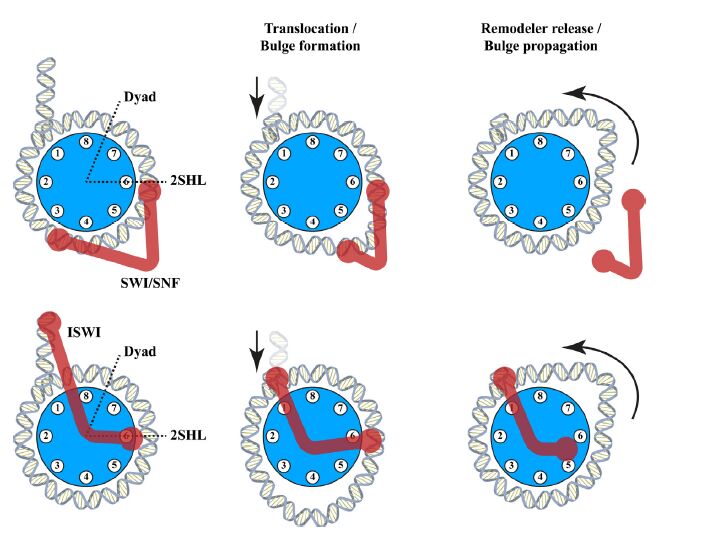
The phasing of nucleosomes off the barriers or wells occurs in a short range as moving away from a barrier anchoring potential decays. However, under various physiological conditions (cell differentiation, aging, etc.) nucleosome arrays and chromatin fiber undergo through genome-scale rearrangements [148,149,150,151]. There are several means for modulation of entire nucleosome array configuration. Firstly, a trivial change in core histones concentration, such as that found in replicative aging of yeast, or in linker histone H1 concentration will alter nucleosome spacing across entire DNA thread [149,152]. Secondly, there is a potent machinery capable of global modulation of nucleosome positioning represented by a family of ATP-dependent chromatin remodelling enzymes (remodelers). In most cases remodelers utilize the energy of ATP to translocate DNA along nucleosome. This leads to local DNA distortion and formation of DNA loops (bulges), which propagate around the surface of nucleosome exiting on the other side. As a result, nucleosome is repositioned or evicted by remodelers (Figure 6) [153,154,155,156,157,158,159].
There are several classes of remodelling ATPases, such as SWI/SNF, ISWI, MI2/CHD, INO80, etc., which are characterized by unique domain compositions. In addition to that, these ATPases are incorporated into large macromolecular assemblages, which define the exact remodelling reaction mechanism, kinetics and biological functions [153,154,155,156,160,161,162]. For example, ISWI ATPase incorporated into ACF (ATP-utilizing Chromatin assembly and remodelling Factor), CHRAC (CHRomatin Accessibility Complex), RSF (Remodelling and Spacing Factor) or ToRC (Toutatis-containing chromatin Remodelling Complex) complexes catalyzes the formation of regularly spaced nucleosome arrays [163,164,165,166,167,168]. In contrast, NURF (NUcleosome Remodelling Factor) complex powered by ISWI disrupts nucleosome periodicity [169,170]. Remodelers also show distinct selectivity to nucleosome substrates depending on the linker length and PTMs on histone tails. ISWI ATPase requires longer linkers and recognizes unmodified histone H4 tail to produce regularly spaced nucleosome arrays [157,171,172,173]. SWI/SNF ATPase activity does not depend on DNA linkers and it preferentially targets acetylated nucleosome arrays for remodelling [157,174]. The paper by Ralf Blossey in this issue of AIMS Biophysics [175] and other studies suggest that coupling of a recognition step to a kinetic step ensures high specificity of remodelling reactions, which overall can be described by a kinetic proofreading mechanism [176,177,178,179].
Remodelers are ubiquitous in the nucleus and their concentration is estimated to be about one remodeler per every 10 nucleosomes [16,160,180]. Assuming nucleosome repeat length of ~200 bp, this indicates that there are ~ 3 × 106 remodelling ATPases per diploid human cell. This number is an order of magnitude larger than the number of RNA polymerase II molecules, which is estimated to be ~ 1 × 105 per cell [181,182]. The precise localization of remodelling ATPases in genome remains a debated issue [183], but just based on their estimated concentrations the remodelers impact on nucleosome positioning is expected to be large. Indeed, depletion of remodelling ATPases leads to global repositioning of nucleosomes in various species from yeast to mammals [126,160,184,185,186,187,188,189,190,191,192]. Besides global reconfiguration of nucleosome arrays, loss of remodelers often results in the disruption of higher-order chromatin fiber organization. This is most evident from the analysis of Drosophila polytene chromosomes. Polytene chromosomes are formed in insects’ salivary glands due to the multiple rounds of endoreplication in the absence of newly-replicated DNA strands separation. Chromatin fibers in polytene chromosomes are folded into densely compacted units (bands) followed by decondensed units (interbands). Mutations in ISWI, MI2 and CHD1 ATPases result in global decondensation of polytene chromosomes suggesting a link between nucleosome positioning and higher-order chromatin structure [193,194,195]. Combined, from these observations it can be concluded that 1) ATP-dependent chromatin remodelers are capable of reconfiguring entire nucleosome array; and 2) nucleosome positioning may impact chromatin fiber folding and, thus, the density of DNA packaging.
5.3. ATP-dependent chromatin remodelers in gene control
Given these genome-wide effects of ATP-dependent chromatin remodelers on nucleosome positioning and chromatin fiber formation, it becomes difficult to reconcile all aspects of their function in the frame of classical Jacob-Monod model. Similarly to superhelicity in bacterial chromosome, reconfiguration of nucleosome arrays is expected to interfere with the expression of every gene. Indeed, in yeast, loss of the RSC remodelling ATPase results in global repositioning of nucleosomes followed by a decline in expression of many genes [189,190]. Strikingly, however, depletion of ISWI and CHD remodelling ATPases has little effect on total gene expression despite having pronounced effects on nucleosome array. Instead, loss of these two remodelers leads to initiation of transcription from cryptic promoters located within coding regions of active genes [186,191]. The reason for such differences comes from the fact that nucleosome array has a number of degrees of freedom, in which it may be reconfigured. For example, RSC widens nucleosome-depleted regions at TSS by pushing nucleosomes away from it, thus facilitating the transcription initiation. In contrast, ISWI and CHD recognize nucleosomes in gene bodies, which are partially unwrapped by RNA polymerase, and they act in stabilizing of such nucleosome arrays. This, in turn, blocks recruitment of transcription factors to cryptic promoters and suppress the unwanted noise [186,189,190,191].
In multicellular eukaryotes, the functions of remodelers turn to be more complex, because 1) each class of remodelling ATPase is commonly represented by several paralogs, which are included into distinct complexes, and 2) these complexes are developmentally regulated and express in tissue-specific manner [162,196,197,198]. In addition, increased genomic sizes and delegation of a bulk of gene control to distant regulatory elements add to the complexity [1]. Nonetheless, remodelers may drive entire nucleosome array out of equilibrium facilitating the gene switches by pioneer transcription factors. This can again be illustrated by cellular reprogramming induced by Oct4, Sox2, Klf4 and c-Myc transcription factors. Alone, these factors do suffice to trigger undifferentiation of fibroblasts, but the efficiency of such reprogramming is low [94,95,96]. Interestingly, it is increased significantly when ATP-dependent chromatin remodeler SWI/SNF is added to the system [199]. Likewise, SWI/SNF ATPase BRG1 extracted from amphibian eggs facilitates the nuclear reprogramming of human somatic cells [200]. Although the precise mechanism for SWI/SNF function in reprogramming is unclear, in principle it does not have to be specific. Global modulation of nucleosome arrays configuration and dynamics would already affect access of all transcription factors present to DNA, and once bound these factors “know” what to do next.
6. Conclusions
In conclusion, on the one hand, nucleosomes act as regulatory units transducing cellular signals to selective genes through “histone code”. On the other hand, nucleosome arrays act as a buffer system adjusting all eukaryotic genome functions. Nucleosome arrays are dynamically configured with respect to spacing, positioning and turnover rates by ATP-dependent chromatin remodelers. Although global changes in nucleosome arrays are perceived by every gene, the precise transcriptional output will depend on a new nucleosome array configuration and on a number of initial settings characteristic to a given gene in a given cell type, such as availability of appropriate transcription factors. Thus, the effects of ATP-dependent chromatin remodelers on gene expression may appear as specific, even though the underlying mechanism is not. However, our quest for understanding of the principles of eukaryotic gene regulation by nucleosome positioning in combination with other epigenetic signals is far from being over and there is a growing need to bridge the gap between biology and biophysics of chromatin.
Acknowledgments
I would like to thank Olga Derkatch for help in preparation of this review, and Mikhail and Matvey Moshkin for comments and discussion. This work was supported by the Russian Science Foundation [RNF 14-14-00934, RNF 141-14-0021] and Transregional Collaborative Research Centre TRR81.
Conflict of Interest
The author declares that there are no conflicts of interest.









 DownLoad:
DownLoad: