1. Introduction
Epigenetics, the inheritable change of gene expression programs without altering the underlying DNA sequence, is most commonly associated with mechanisms that change the packaging of DNA and the landscape of chromatin associated proteins and RNAs. Regulation is correlated with changes in DNA and histone modifications and the specific recognition of these modifications by effector molecules.
Modifications to DNA and histones are dynamically set and removed by chromatin-modifying enzymes in a highly regulated manner. Currently there are four different DNA modifications and a plethory of different histone modifications [1,2,3,4,5]. The DNA and histone code is set by so called writer molecules (methylases, kinases, acetylases and others) that modify histones and DNA. These chromatin marks are specifically recognized by so called reader molecules that were shown to alter chromatin structure by non-covalent interactions with and between nucleosomes. The type and combination of sequestered protein/RNA readers determine the function of the underlying chromatin domain. In a regulated fashion the activity of such chromatin domains is changed by the recruitment of eraser molecules that remove and change local DNA and histone marks (deacetylases, demethylases and others) [6]. Metastable epigenetic regulation relies on a complex re
gulatory network specifically binding to modified chromatin by many weak but combinatorial interactions. An understanding of the regulatory processes requires detailed knowledge about the specific binding parameters, with MicroScale Thermophoresis being a novel and versatile method to accelerate their identification.
The epigenetic network is build up by the combinatorial interaction between the recognition domains in Proteins, RNAs and DNAs with their associated modifications. Methods based on high throughput sequencing or mass spectrometry, present a correlative picture of epigenetic coding but fail to provide a dynamic and functional description of the underlying mechanisms. The quantitative description of interactions is absolutely essential to understand the regulatory basis of these networks. On the bi-molecular level binding parameters, such as binding affinities, stoichiometries, thermodynamics and kinetics, have to be unraveled, requiring easy and fast methodologies to study the interactions in a higher throughput.
Currently, researchers in the field of epigenetics use mainly semi-quantitative methods such as electrophoretic mobility shift assays (EMSA) and classical pull down assays. Binding kinetics and binding affinities are measured by surface based Surface Plasmon Resonance (SPR) and labelfree calorimetric approaches that measure the enthalpy of the binding event (Isothermal titration calorimetry, ITC). Fluorescence correlation spectroscopy (FCS) determines binding dependent changes in diffusion times to characterize molecular interactions. FCS measures changes in the translational diffusion, whereas fluorescence anisotropy (FA) is based on measurement of changes in rotational diffusion. MicroScale Thermophoresis (MST) is a rather new technology combining different aspects of the methods mentioned above. The technology provides significant experimental advantages, is easy in setup and requires low amounts of material, as such having the potential to develop into the first choice method to study regulatory/interaction networks in epigenetics.
1.1. MicroScale Thermophoresis
MicroScale Thermophoresis is based on a physical phenomenon called thermophoresis, which describes the movement of molecules through temperature gradients. This directed movement is dependent on three molecular parameters: i) size; ii) charge; iii) hydration shell. Upon bi-molecular interaction of ligand and target molecule, at least one of these parameters will be altered, resulting in a change of the thermophoretic mobility of the complex, which is used to access binding parameters of the molecular interaction [7,8,9,10,11,12,13].
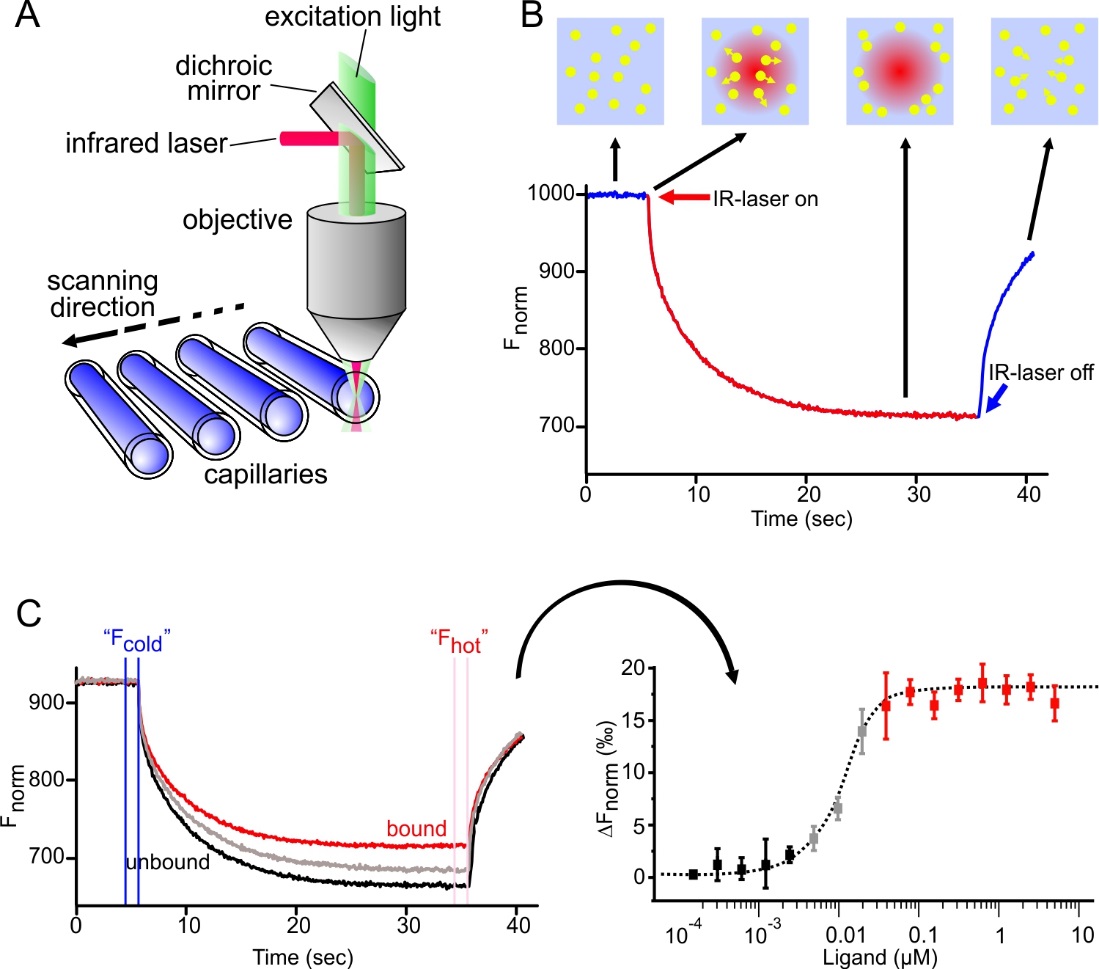
The changes in thermophoretic movement of one molecule is monitored with an optical system, detecting either the intrinsic fluorescence of tryptophanes within proteins, or the fluorescence signal of a fluorophore, attached to one of the interaction partners. The immobilization-free MicroScale Thermophoresis method records the directed movement of the fluorescent molecules in a µm-sized temperature gradient. The binding parameters are determined by the changing thermophoretic properties of the sample with increasing concentrations of the potential binding partner. The technical setup of the MST device (Monolith NT.115, NanoTemper Technologies GmbH, Munich, Germany) is represented in Figure 1A. The optics focuses in the center of thin glass capillaries, holding 4-6 µl of sample. The microscopic temperature gradient with a diameter of ~50 µm and a temperature difference ΔT of 2-6 °C, is established by an infrared laser, also focusing in the observation window. Upon activation of the laser, thermophoretic depletion or accumulation of molecules can be observed in the region of elevated temperature, which is quantified by the Soret coefficient: ST: chot/ccold = exp(−ST ΔT).
Figure 1B represents a typical MST experiment. The initial fluorescence in the sample is recorded and serves as a base line in the absence of the temperature gradient. After 5 seconds, the IR-laser is activated, which leads to the establishment of the temperature gradient. As a result of this, an initial steep drop of the fluorescence signal—the so-called Temperature- or T-Jump—reflecting the temperature dependence of the fluorophore quantum yield is observed. A slower thermophoresis-driven depletion of fluorophores follows the T-Jump. Once the IR-laser is deactivated, a reverse T-Jump and concomitant back diffusion of fluorescent molecules can be observed.
As mentioned above, the thermophoresis of a molecule is highly sensitive with respect to changes in size, charge and hydration shell. Hence, the binding of a ligand to the molecule will alter the thermophoretic behaviour, which can be used to study equilibrium constants, such as the dissociation constant Kd. To get this information, a serial dilution of the ligand is prepared, mixed with a constant concentration of labelled target molecule, loaded into capillaries and analyzed in the instrument by subsequent scanning of each capillary. The results of a typical binding experiment are illustrated in Figure 1C.
1.2. Advantages of the MST
The strengths of the MicroScale Thermophoresis in speed, quality and costs are summarized in Figure 2. The MST system allows a fast and flexible setup and optimization of the assays. Very helpful to obtain high quality data-in short time-with internal quality controls, allowing to detect sticking and aggregation/precipitation effects in real time. Upon detection of these effects, technical conditions and buffers can be easily optimized to ensure ideal binding conditions. Besides the rapid measurements (Kd in 15 min), the immobilization free MicroScale Thermophoresis offers free choice of buffers, with the possibility to measure in lysates and sera. Due to the fact, that the thermophoresis of molecules depends on the charge and hydration shell, besides size, there are no limitations in the size of the measured interaction partners. Additional strengths of MST are the wide dynamic range, from pM to mM, to reveal binding affinities and the low sample consumption required to allow measurements.
1.3. Applications of the MST to study epigenetic systems
The quantification of transcription factor binding affinities is an ideal application of MST. Besides others [14,15,16,17,18], the study of Pham and colleagues [19] on the hematopoietic master transcription factor PU.1 nicely demonstrates the accuracy of MST in the characterization of TF binding site affinities. Binding site selection of the transcription factor PU.1 was analyzed during human macrophage differentiation by ChIP-Seq. Bioinformatic analysis of the ChIP-Seq data, allowed to identify bound Pu.1 sites and to predict binding site motifs with high Pu.1 occupancy in the cells. A score list with binding motifs exhibiting best binding was derived and these sites were used for binding site affinity measurements by MST. Studying the binding affinity of 75 individual DNA sequence motifs revealed an inverse correlation between the ChIP-Seq score list and the Kd values determined in vitro. This demonstrates that motif log-odds scores represent a good measure for motif binding site affinity, implying that binding site selection in vivo is in part driven by the affinity of the transcription factor to its site [19]. This study
identified three major categories of consensus sites for PU.1 binding. (i) non-bound sites within inaccessible chromatin domains exhibiting low binding affinity, (ii) PU.1 bound, autonomous binding sites with high affinity which are DNase I inaccessible, (iii) PU.1 bound, autonomous binding sites with intermediate / low affinity which are DNase I accessible. Here binding is likely stabilized by cooperativeness with neighboring transcription factor binding sites [19].
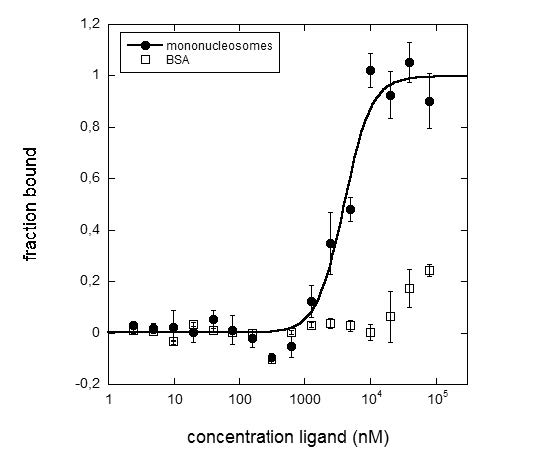
Besides the binding affinity of an interaction, its specificity and selectivity can be determined using the MicroScale Thermophoresis. Using the MST, the study of Schubert and colleagues demonstrated, that the effector protein Df31 (Decondensation factor 31), which plays a role as RNP complex in the decondensation of Drosophila chromatin, is able to bind specifically to Cy5 labelled ssRNA but not to ssDNA [20]. Furthermore, the study identified specific RNAs (snoRNAs), enriched at open, accessible chromatin, which do preferentially interact with Df31. MST competition assays using differentially labelled RNAs revealed the specificity of the interaction, which were later validated by Df31 pull down assays and RT PCR. In addition, MicroScale Thermophoresis revealed an additional interaction surface in Df31, targeting the histones. Df31-EGFP interacts with the core histones H3 and H4, but not with H2A and H2B.
Histone interactions allow the specific binding of Df31 to nucleosomes, as depicted in Figure 3. Mononucleosomes were reconstituted on a 601 positioning sequence carrying a Cy5 label on the DNA and incubated with increasing amounts of Df31 to analyse the binding affinity (Figure 3).
Histone tails are known to be modified post-translationally, with these modifications serving as epigenetic marks. Modifications such as methylation, acetylation, phosphorylation or ubiquitinylation are set and recognized by a large number of proteins-domains that have been named “reader” domains. Lysine methylation at positions 4 and 36 of histone 3 do correlate with transcriptional activity, whereas methylation of Lysine at positions 9 and 27 on the same histone tail correlate with transcriptional repression. The acetylation of lysine residues in histones is known to correlate with accessible chromatin and active transcription [4,21,22,23]. The histone code hypothesis suggests a modification landscape that enables the recruitment of specific effector proteins that in turn determine the chromatin structure and the activity of the underlying DNA. As indicated by several studies, the MST is perfectly suited to characterize protein-histone and protein-histone tail interactions [24,25,26,27].
Alpatov and colleagues studied the role of the fragile X mental retardation protein (FMRP) in the fragile X syndrome [28]. FMRP was identified as a chromatin binding protein that uses its tandem tudor domain for binding. MST experiments using MLA nucleosomes (methyl-lysine analogs) showed that the protein has a preference towards K3Kc79me (Kd = 135 ± 28 nM) and H3Kc27me1 (Kd = 102 ± 11 nM) modified nucleosomes. Unmodified H3 nucleosomes were bound with an affinity of about 1 mM. The study describes an important role of FMRP in DNA damage response (DDR), which is mediated in a chromatin-dependent manner. FMRP regulates genomic stability at the chromatin interface and potentially impacts on gametogenesis and some other developmental aspects of the fragile X syndrome [28].
The study of Josling and colleagues using the malaria parasite Plasmodium falciparum, demonstrates how the parasite specific Bromodomain protein PfBDP1 is involved in the transcriptional regulation of invasion-related genes [29]. Knockdown of the protein results in a drastic inhibition of growth and caused defects in erythrocyte invasion. The study identified 186 downregulated genes affecting different time points of the parasites live cycle. Interestingly, invasion related genes were predominantly found to be downregulated, strengthening the hypothesis that PfBDP1 is involved in the transcriptional regulation these genes. ChIP experiments revealed that the protein binds to 5xintergenic regions of invasion-related genes in schizonts, but not in the ring stages of the parasite. Label-free MST analyses demonstrated that the bromodomain protein PfBDP1 binds specifically to H3K9Ac and H3K14Ac peptides with a Kd = 110.79 ± 10.31 µM (R2 = 0.995) and Kd = 126.17 ± 14.39 µM
(R2 = 0.993) respectively. These reported affinities are nicely in line with previously published affinities for bromodomain-histone tail interactions. Furthermore, BDP1 bound to unmodified H3 and H3K16Ac peptides much reduced affinity and did not bind to H3K9me2 and H3K4me2 peptides.
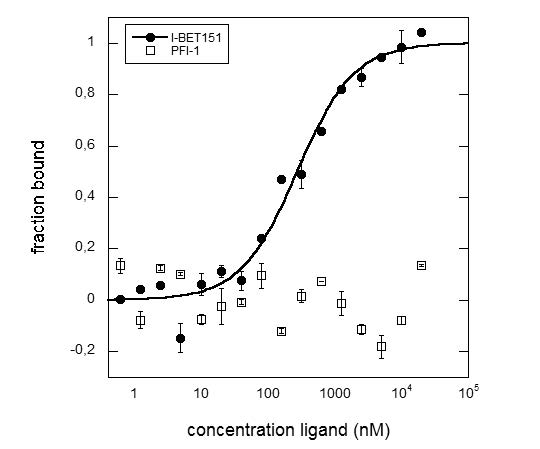
As demonstrated in different studies, the MST can be used in the development of small compound drugs binding to epigenetic proteins [30,31]. Due to the specific role of PfBDP1 in the parasite it presents an interesting drug target. Two known bromodomain inhibitors were tested for binding to the protein in our laboratory at the 2bind GmbH, Regensburg, Germany. The compound PFl-1, which is a selective BET (bromodomain containing protein) inhibitor for BRD4 with a described IC50 of 0.22 mM was shown not to bind to the PfBDP1. However, the compound I-BET151 (GSK1210151A), which is a selective inhibitor for BRD2 (IC50 = 0.5 mM), BRD3 (IC50 = 0.25 mM) and BRD4 (IC50 = 0.79 mM), was identified to bind to PfBDP1 in vitro with an affinity of 260 ± 53 nM (R2 = 0.978) (Figure 4).
The study of Tan and colleagues on the proliferation cell nuclear antigen (PCNA), which takes part in various cellular processes, demonstrates that the MST is a useful tool to characterize the interaction between an epigenetic effector protein and a small compound [30]. Initially, an in silico screen of a compound library using the crystal structure of PCNA revealed a set of 200 compounds that could potentially inhibit PCNA. Two compounds (PCNA-I1 and 2) showed an IC50 value in the low mM range in tumor cell proliferation assays. A subsequent similarity search in the ZINC chemical data base based on the PCNA-I1 compound identified in total 8 additional candidates (PCNA-I3-10). MicroScale Thermophoresis was used to directly determine the binding affinity between recombinant, fluorescently labelled PCNA and the compound PCNA-I1. The Kd of this interaction was determined to be 0.41 ± 0.17 mM. Rabbit IgG was not bound by the compound. Surface plasmon resonance experiments strengthened the MST data, as the affinity was calculated to be 0.17 mM. Native gel electrophoresis indicated that the compound was binding to the trimeric form of PCNA, potentially stabilizing this state. Additionally the compound was shown to release PCNA from
chromatin in a dose and time dependent manner. Growth assays using different tumor types and non-transformed cells indicated that the growth of tumor cells is affected at lower compound concentrations than the non-transformed cells. A cell cycle arrest was identified to be the major reason of the growth deficiency upon treatment with the PCNA-inhibitor 1 [30].
2. Conclusion
Beginning 2014 more than 500 publications using the MicroScale Thermophoresis (MST) could be found in literature, characterizing different kinds of molecular interactions in terms of binding affinity (pM to mM range), stoichiometry and thermodynamics. The MST represents a versatile and precise technology with a broad application range from screening assays, binding assays, competition assays, assays with multiple binding partners, buffer optimization assays to stability assays. The high information content of these assays is widely used in drug development, antibody characterization and aptamer development. This review summarized recent studies demonstrating the suitability of this technology to characterize epigenetic networks. The fast and flexible MST assay setup is strengthened by integrated quality controls detecting sticking effects and aggregation/precipitation effects allowing for fast optimization of reaction conditions to ensure high quality data. Freedom of reaction buffer enables the user to work under previously challenging conditions (sera, lysates). The technology is perfectly suited to study protein-protein, protein-nucleic acids, which are characteristic for interaction within chromatin environment. In addition, the method allows for fast quantification of protein-small compound interactions, making it the perfect tool for the characterization of drugs targeting epigenetic players.
Conflict of Interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: