1. Introduction
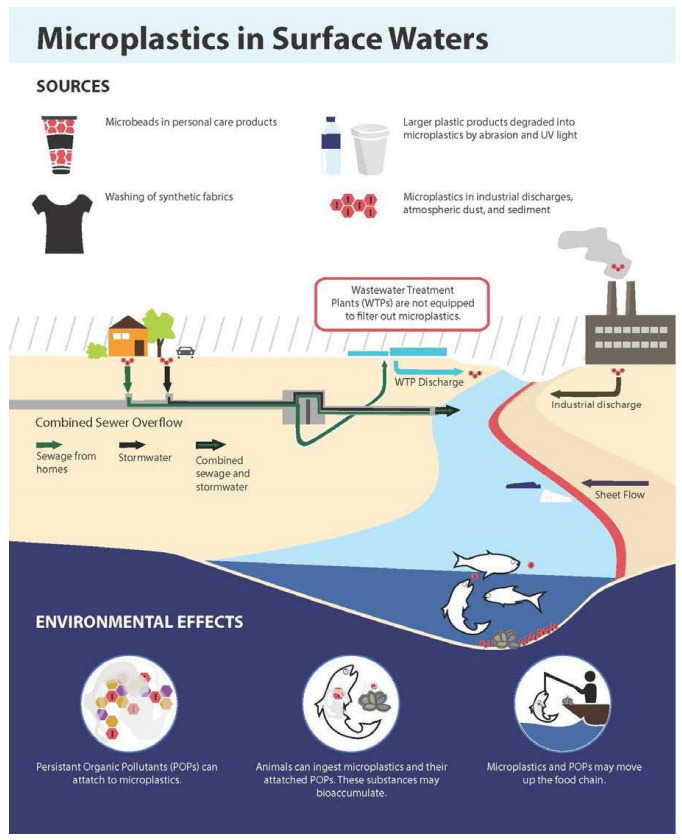
The presence of plastics in marine waters is extensively documented [1,2,3,4]. Recent research shows that plastic pollution is also present in freshwater systems at concentrations equal to or greater than those documented in the world's oceans [5,6,7,8,9]. Napper et al. [10] estimated that thousands of microplastic beads are released by using as little as 5 mL of facial scrub exfoliants once each day; Rochman et al. [11] estimated that total daily microbead release into aquatic environments may be as high as 8 trillion microbeads day–1. Wastewater treatment plants were not designed to remove this pollution during treatment [7,12]. When microplastics are transported through treatment facilities via industrial effluent or wastewaters they discharge into receiving waters [13,14]. New studies suggest atmospheric deposition may also be a significant source of microplastic fibers [15].
Urban rivers may be an important component of microplastic transport, contributing to the global microplastic lifecycle [16,17], and urban populations (human and aquatic species) may be subject to adverse health effects associated with this pollution. Identified sources of freshwater microplastic pollution include discharges from wastewater treatment plants [12], atmospheric deposition [18], and non-point sources such as combined sewer overflows (CSOs) and urban runoff [9,19]. However, research documenting microplastics in freshwaters is recent, and so the full extent of environmental impacts associated with this pollution are not well understood [20].
There are multiple environmental concerns associated with microplastics in surface waters. Evidence is accumulating that microplastic pollution can move through natural food webs [21,22,23,24]. Microplastics have been documented in fin fish and shellfish tissues [21,25,26,27,28], which means microplastics and associated pollutants have the potential to move into human food chains. In addition to the chemical composition of the various types of microplastics and/or compounds resulting from environmental breakdown of plastics, there is also the potential for persistent organic pollutants (POPs), particularly those that are hydrophobic, to attach themselves to plastic particles [29,30,31]. POP transport via microplastic adsorption is most probably a function of POP concentrations, local environmental conditions, and the microplastic composition [31]. However, data describing the risk to biota from chemical and physical properties associated with microplastic particles is currently lacking [32].
This proof of concept study links the presence of microplastic pollution to potential impacts on aquatic environmental health. In order to evaluate the environmental risks associated with microplastic pollution, there are a number of factors that must be considered (Figure 1): the size, composition, age, and physio-chemical properties of the microplastic particle; the composition of compounds adsorbed to the particle, potentially soluble in the water column; the source of the microplastic (surface water discharge, atmospheric deposition, sediment resuspension) and the route(s) of exposure to the particle (physical contact, ingestion, inhalation); and hydrologic characteristics, such as surface water flow and depth, and channel bathymetry.
The goals of this study were to determine whether urban New Jersey freshwaters contained microplastic pollutants, and if so, to test analytic techniques that could potentially identify chemical compounds associated with this pollution. A third objective was to test whether identified associated compounds might have physiological effects on an aquatic organism. In order to assess potential effects associated with microplastic pollution in urban New Jersey (NJ) surface waters, we collected water samples and quantified microplastic densities, identified potential environmental breakdown products associated with three types of recovered microplastics, identified potentially mobile adsorbed organic compounds associated with the recovered microplastic particles, and exposed embryonic zebrafish to field recovered and pure microplastic samples.
2. Materials and methods
2.1. Density calculations
Three replicate surface water samples were collected at each sampling location (N = 45) between May 12 and August 6,2016 (Table 1, Figure 2) to determine: (1) microplastic densities, (2) adsorbed compounds and plastic polymer composition(s), and (3) for toxicity testing. The Raritan and Passaic River watersheds were selected because they encompass some of the most densely developed urban and suburban areas in NJ, containing both residential and industrial properties. There are numerous permitted point sources discharging into both rivers within a 5-mile radius of the sampling locations, including personal care product producers, companies with "plastic" in their name, and wastewater treatment plants (Figure 2).
Table 1. Urban NJ Surface Water Sampling Locations.
| Municipality |
North |
West |
River |
| Sayreville |
40.47429 |
–74.3574 |
Raritan |
| Edison |
40.48746 |
–74.3840 |
Raritan |
| New Brunswick |
40.48884 |
–74.4335 |
Raritan |
| Piscataway |
40.54078 |
–74.5124 |
Raritan |
| Bridgewater |
40.54995 |
–74.6687 |
Raritan |
| Newark |
40.7129 |
–74.119 |
Passaic |
| Newark |
40.7333 |
–74.1521 |
Passaic |
| Kearny |
40.76401 |
–74.1590 |
Passaic |
| Lyndhurst |
40.8180 |
–74.1350 |
Passaic |
| Rutherford |
40.8300 |
–74.1211 |
Passaic |
| Elmwood Park |
40.9096 |
–74.1320 |
Passaic |
| Fairfield |
40.8979 |
–74.2800 |
Passaic |
| Livingston |
40.77899 |
–74.3689 |
Passaic |
| Chatham |
40.7387 |
–74.3720 |
Passaic |
| Berkeley Hts. |
40.6897 |
–74.4390 |
Passaic |
The Raritan River watershed is the largest contained within NJ, draining approximately 2862 km2 (see [33,34] for watershed descriptions pre-and post-urbanization, respectively). Samples were collected upriver (Bridgewater) and downriver of the North Branch/Lamington River, Millstone, and South Branch confluences (Piscataway, New Brunswick, Edison, Sayreville). The Passaic River Basin, home to over 2 million residents, is the third largest drainage basin within NJ, encompassing 2460 km2 [35]. Samples were collected under dry weather conditions (defined as a period without rain for at least 48 hours). Five Passaic River locations were also sampled under wet weather conditions (24 hours or less after a rain event of 2.2 cm). Sample collection from the urbanized lower river tidal reaches was conducted on an outgoing tide.
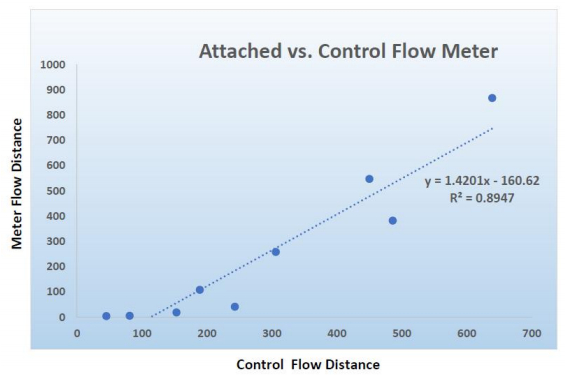
Water samples were collected using a manta trawl with attached flow meter (Model 315, OceanTest, Inc.). Accurate flow calculation is critical because flow rate determines the water volume used to calculate microplastic density. Due to low flow conditions outside the 0.20 m sec–1 accuracy range of the attached meter, flow was measured using a second flow meter (Marsh McBirney Flomatic Model 2000A) placed just downstream of the manta trawl net. Samples were collected through a rectangular opening 16 cm high × 61 cm wide, attached to a 333 μm mesh collection net 3 m long and 30 × 10 cm2 [19]. The net was held perpendicular to the current flow at the surface for 15 min. Flow distance was calculated using the attached flow meter count multiplied by the Impellor Constant (a factor of 0.245); the flow measurement from the second meter was read from the Marsh McBirney screen. Flow rates were compared using a Regression Analysis, which yielded an R2 of 0.89 (Figure 3). In order to compare sampling locations, we converted all attached flow meter values using Equation 1:
|
FlowRate=(Attachedflowmeterdistance+160.62)/1.4201
|
(1)
|
After sample collection, the outside of the net was washed down with filtered site water to force collected material into a cod piece attached to the end of the trawl net, and the cod piece sample transferred to a glass collection jar. Isopropyl alcohol was added to one of the 3 replicates as a preservative; the other 2 samples were placed on ice for transport back to the laboratory.
Following protocols of Ericson et al. [19], one of each replicate sample was digested using the Fenton Reaction (20 mL of 0.05 M iron sulfate and 20 mL 30% hydrogen peroxide) to remove remaining organic material. Large organic particles were rinsed with DI to collect any attached plastic particles and the organic material discarded. To verify efficiency of microplastic recovery, 10 blue microbeads (0.330 mm diameter) were added to the Passaic samples. Reagent additions were repeated until the solution turned a pale yellow color and visible remnants of organic material were completely oxidized. This reaction does not digest the plastic particles. Recovered microplastics were placed under a dissecting microscope and separated into one of three size categories (0.355–0.999 mm, 1–4.749 mm, > 4.75 mm), and the type of plastic (fragment, pellet, fiber, film, or foam) within each size category determined. Total microplastic density was calculated using the formula:
|
Plasticdensitykm−2=#microplasticsrecovered(netopeningxflowdistance)
|
(2)
|
2.2. Chemical analyses
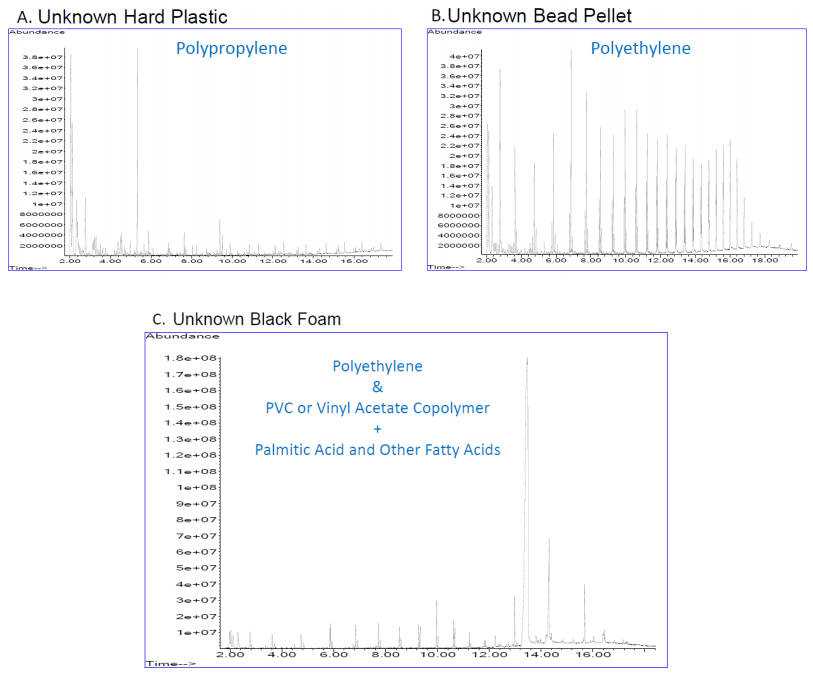
Different polymers exert various toxicities and adsorb other compounds in different quantities, and so knowledge of polymer composition is important in a microplastic environmental risk assessment. In a novel method of pyrolysis GC-MS, a very small piece of microplastic sample less than 1 mg in size was placed in a narrow quartz tube, which was then placed in a platinum coil and heated to 750 ℃. The intense heat breaks down large polymer chains into smaller fragments that are then analyzed by GS/MS to identify specific compounds. The fragmentation patterns have been reported to be reproducible and unique to a given polymer type [36]. Pure plastic samples (polyethylene high density, medium density and low density (HD, MD, and LD, respectively), polyethylene-co-vinyl acetate, polystyrene, polystyrene-co-acrylonitrile, polyvinylchloride, poly-methyl-methacrylate, sodium polyacrylate, polyurethane, polyethylene terephthalate, and polyamide) were purchased from Sigma Aldrich and analyzed by pyrolysis coupled with gas chromatography (Pyr-GC/MS) to create a "fingerprint" for comparison with three field collected microplastic samples (Figure 4).
To determine the presence of organic compounds sorbed to the microplastic particles, headspace solid phase micro extraction coupled with gas chromatography/ion trap mass spectrometry (HS-SPME/GC-ITMS) was employed. Microplastic solids and overlying site water were processed for organic contaminant analysis using A CTC Analytics Combi PAL system with SPME agitator attachment (Zwingen, Switzerland). This system combines headspace extraction of organics and injection. The Combi PAL HS-SPME and injection program run was: extraction time of 30 min. at 55 ℃ (water samples) or 75 ℃ (solid plastics), followed by pre-incubation time of 2.58 min., agitation speed of 350 rpm, agitation for 5 sec., agitation off for 2 sec., SPME fiber vial penetration of 25.0 mm, desorption time of 10 min., and injection penetration of 54.0 mm at 290 ℃ into a septum programmable injector (Varian 1079) operated in the splitless mode. Pre-and post-each sample injection, control blank runs with the SPME fiber (60 µm polydimethylsiloxane/divinylbenzene StableFlex fiber, Supelco, Bellefonte, PA, USA) were performed according to manufacturer instructions.
A Varian CP-3800 gas chromatography system (Walnut Creek, CA) equipped with A DBXLB 30 m column with a 0.18 mm ID and 0.18 μm film thickness (Agilent Technologies, Santa Clara, CA, USA) was used for chromatographic separation. Helium carrier gas flow was constantly maintained at 0.9 mL/min. Analyte elution from the GC column occurred using a temperature program that ranged from 35 ℃ to 320 ℃ over 40 min. Eluted compounds were analyzed by a Saturn 2200 ion trap mass spectrometer (Walnut Creek, CA), operated in EI positive mode and tuned with perfluorotributlyamine (FC-43) according to manufacturer's instructions. The electron multiplier voltage, emission current, multiplier offset, and modulation amplitude were set at 1750 V, 40 μA, +/–100, and 7.5 V, respectively. The ion trap was set at 225 ℃ and the transfer line at 275 ℃. Saturn GC/MS workstation (version 6.6 software) was used for data acquisition and integration. After background subtraction, unknown peaks were qualitatively identified by spectra comparison to the vendor's library and NIST/EPA/NIH 2012 mass spectral library. Identified compounds showing a correlation of > 70% fit to the library spectrum were defined as Tentatively Identified Compounds (TICs).
2.3. Larval fish exposure
Recovered Fenton treated microplastics and pure polymers found in three microplastic field samples, identified using Pyr-GC/MS, were used in the larval fish experiments. The three samples (bead, pellet, and foam) were composed of polyethylene, polypropylene, and polyethylene-vinyl acetate copolymer, respectively (Figure 4). Larger particles of these pure plastics (Sigma Aldrich) and Fenton treated unknown plastics from a previously acquired field sample were pulverized using a dremel with a diamond tip followed by glass homogenization in 95% ethanol. The slurry was poured through a U.S.A Standard testing 2 mm sieve #10 (Fisher Scientific). The filtrate was collected and centrifuged in 95% ethanol for 15 min. at 8000 rpm. The supernatant was discarded and the pellet was completely dried by air pump for 24 hr. The dried pulverized plastic was weighed and re-suspended in autoclaved and aerated egg water to make microplastic concentrations of 1 or 10 μg/mL.
All fish studies were carried out using an approved IACUC approved protocol 08-025. AB strain zebrafish (Danio rerio) embryos were exposed to one type of microplastic per embryo at 3 hours post fertilization (hpf) and sacrificed at 96 hpf. Twenty embryos were randomly placed in individual glass vials and treated with 1.0 μg/mL or 10.0 μg/mL concentrations of pure microplastic. Autoclaved aerated egg-water was used as a control. Embryos were also exposed to field-collected microplastics in 1 or 10 μg/mL concentrations suspended in egg-water with methylene blue; controls were pure egg water and egg water with methylene blue. The embryos were incubated at 26 ℃ for 96 hpf in a static non-renewal protocol. Daily observations were made and observable lesions recorded. Upon endpoint of treatment, the sac fry were fixed in 10% buffered formalin and stained with Alcian Blue-Alizaran Red dye. Photographs and measurements (N = 20) were taken on an Olympus SZ-PT microscope with Scion camera and Adobe Photoshop CC 2015. Statistics were determined via Sigma Plot 11 software, used to calculate statistical significance with T tests and One Way ANOVA. Box plots were generated using the data and represent the mean plus and minus standard deviation with 75 and 25% boxes.
3. Results
Microplastics, whose densities ranged from ~28,000 to over 3,000,000 particles km–2, were observed in all sampled locations (Figure 5); the types and quantities of microplastics were site specific (Tables 2 and 3). The most frequently recovered (38%) microplastic was fragment (broken off from a larger plastic item), followed by foam (breakdown of polystyrene items) > line (fiber, filament) > film (breakdown from bags, wrappers) > pellet (microbeads, nurdles). Recovered microplastic sizes were predominately (71%) in the larger 1 to > 4.5 mm size ranges. Passaic River densities were an order of magnitude greater than densities observed in the Raritan River (Figure 5; Table 2), which may be due to the population density in this highly urbanized watershed. The highest concentration of microplastics was observed during wet weather sampling (Figure 6). Raritan River microplastic density was highest at the two sites closest to Raritan Bay (Figures 2 and 5a). Conversely, downriver Passaic microplastic density was lower in the heavily urbanized locations (Figures 2 and 5b), although under wet weather conditions upriver Passaic densities decreased and the downriver Lyndhurst density increased (Figure 6).
Table 2. Recovered microplastic units by type and location under 2 sampling conditions (dry, wet).
| Location |
Collection Conditions |
Microplastic Type |
Total |
| Fragment |
Pellet |
Line |
Film |
Foam |
| Bridgewater |
Dry |
6 |
0 |
1 |
0 |
0 |
7 |
| Piscataway |
Dry |
0 |
8 |
9 |
23 |
0 |
40 |
| New Brunswick |
Dry |
7 |
1 |
6 |
0 |
0 |
14 |
| Edison |
Dry |
13 |
1 |
39 |
11 |
5 |
69 |
| Sayreville |
Dry |
8 |
0 |
2 |
5 |
34 |
49 |
| Berkeley Heights |
Dry |
31 |
0 |
4 |
3 |
14 |
52 |
| Berkeley Heights |
Wet |
6 |
0 |
1 |
1 |
1 |
9 |
| Chatham |
Dry |
163 |
16 |
206 |
33 |
65 |
483 |
| Chatham |
Wet |
30 |
1 |
57 |
19 |
36 |
143 |
| Livingston |
Dry |
94 |
3 |
56 |
22 |
54 |
229 |
| Livingston |
Wet |
2 |
0 |
3 |
0 |
0 |
5 |
| Fairfield |
Dry |
5 |
0 |
14 |
8 |
46 |
73 |
| Elmwood Park |
Dry |
2 |
21 |
5 |
2 |
0 |
30 |
| Rutherford |
Dry |
34 |
0 |
3 |
9 |
28 |
74 |
| Lyndhurst |
Dry |
6 |
0 |
2 |
2 |
7 |
17 |
| Lyndhurst |
Wet |
308 |
17 |
59 |
212 |
565 |
1161 |
| Kearny |
Dry |
297 |
1 |
23 |
37 |
43 |
401 |
| Kearny |
Wet |
176 |
3 |
3 |
11 |
32 |
225 |
| Newark |
Dry |
14 |
2 |
4 |
14 |
21 |
55 |
| Newark |
Dry |
1 |
0 |
1 |
0 |
1 |
3 |
| Total Recovered |
|
1203 |
74 |
498 |
412 |
952 |
3139 |
| Total Recovered |
|
38.32% |
2.36% |
15.86% |
13.13% |
30.33% |
|
Table 3. Recovered microplastic units by size and location under 2 sampling conditions (dry, wet).
| Location |
Collection Conditions |
Microplastic Type |
Total |
Recovery % |
| 0.3–0.99 mm |
1–4.75 mm |
> 4.75 mm |
| Bridgewater Raritan |
Dry |
2 |
4 |
1 |
7 |
N/A |
| Piscataway-Raritan |
Dry |
16 |
15 |
9 |
40 |
N/A |
| New Brunswick-Raritan |
Dry |
5 |
9 |
0 |
14 |
N/A |
| Edison-Raritan |
Dry |
19 |
22 |
28 |
69 |
N/A |
| Sayreville-Raritan |
Dry |
7 |
30 |
12 |
49 |
N/A |
| Berkeley Hts-Passaic |
Dry |
24 |
25 |
3 |
52 |
100% |
| Berkeley Hts-Passaic |
Wet |
0 |
7 |
2 |
9 |
10% |
| Chatham-Passaic |
Dry |
167 |
207 |
109 |
483 |
100% |
| Chatham-Passaic |
Wet |
22 |
65 |
56 |
143 |
80% |
| Livingston-Passaic |
Dry |
128 |
77 |
24 |
229 |
20% |
| Livingston-Passaic |
Wet |
0 |
3 |
2 |
5 |
40% |
| Fairfield-Passaic |
Dry |
12 |
36 |
25 |
73 |
N/A |
| Elmwood Park-Passaic |
Dry |
30 |
0 |
0 |
30 |
100% |
| Rutherford-Passaic |
Dry |
26 |
38 |
10 |
74 |
100% |
| Lyndhurst-Passaic |
Dry |
3 |
8 |
6 |
17 |
N/A |
| Lyndhurst-Passaic |
Wet |
173 |
387 |
601 |
1161 |
60% |
| Kearny-Passaic |
Dry |
165 |
188 |
48 |
401 |
80% |
| Kearny-Passaic |
Wet |
97 |
113 |
15 |
225 |
50% |
| Newark-Passaic |
Dry |
1 |
23 |
31 |
55 |
100% |
| Newark-Passaic |
Dry |
2 |
1 |
0 |
3 |
60% |
| Total Recovered |
|
899 |
1258 |
982 |
3139 |
|
| % Total Recovered |
|
28.64% |
40.08% |
31.28% |
|
|
3.1. Chemical analyses
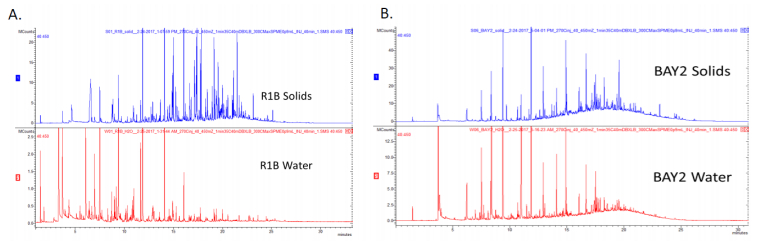
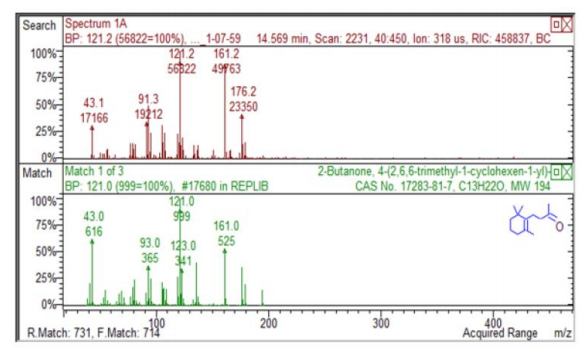
The HS-SPME GC/ITMS method allowed comparison of compounds identified/associated with the solid plastic particles, and demonstrates that the lower retention time compounds were also present in the water fraction (Figure 7). As shown, the TIC patterns observed for the different recovered microplastics have similar patterns to those of the pyrolysis coupled GC (Pyr-GC/MS) of pure plastic standards (Figure 8). In addition, individual peaks of interest can be further probed by examining the mass spectral flagged peaks of interest (Figure 8). Peaks with similar elution times and the same mass fragment patterns in both the solid plastic particles and in the water are strongly suggestive of plastic degradants/leachates contaminating the water. Using the fragmentation pattern, a library match can be determined as shown in Figure 9 for 2-Butanone, 4-(2, 6-trimethyl-1-cyclohexen-1yl.
3.2. Larval fish exposure
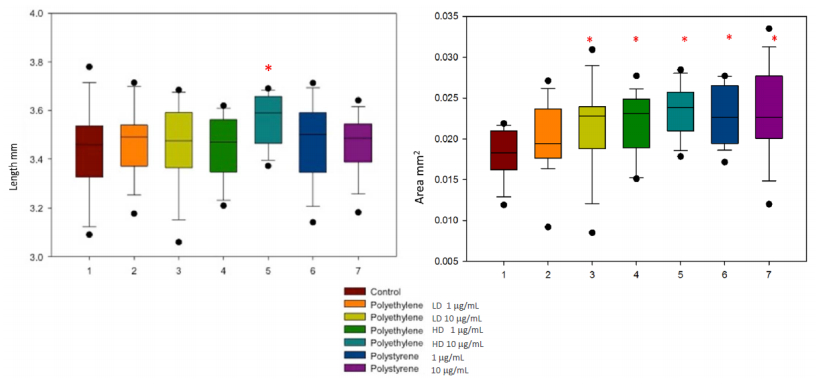
Exposure to the pure individual plastic compounds led to significant changes in zebrafish morphometrics. A significant increase in total body length was seen in polyethylene high density (HD) 10 μg/mL treatment exposure. Significant increase in the pericardial sack size was seen in polyethylene low density (LD) 10 μg/mL, polyethylene HD 1 μg/mL and 10 μg/mL, and polystyrene 1 μg/mL and 10 μg/mL treatment exposures (Figure 10). Conversely, exposure to microplastics recovered from the field samples after treatment with a Fenton reagent did not show any abnormalities (data not shown).
4. Discussion
This research demonstrates that microplastics are present in northern NJ surface waters, that POP are associated with these particles, and that these pollutants are mobile, found in both the water column and associated with the solid microplastics. Identical retention times for GC peaks found in both fractions indicated compounds can move between the two phases, making them potentially available for uptake by aquatic biota in the dissolved phase. Larval fish exhibited morphologic abnormalities when exposed to the polymers comprising microplastic fragment, bead, and foam particles recovered from the field samples. These abnormalities were not observed when the fish were exposed to microplastics that had been processed using the Fenton reagents that oxidize organic material. Our initial results indicate that lower molecular weight compounds are mobile, and may be carried in the water column beyond the location of the microplastic particles.
Using two methods (SPME GC/MS and Pyr-GC/MS) allows for the unambiguous identification of the compound(s) associated with microplastic debris and characterization of the major plastic type(s). By combining these two methods there is much greater confidence in identifying compounds that are derived from plastic versus non-plastic sources. In the future, specific "fingerprint" patterns can be used to categorize the class of plastics present in a waterbody and identify compounds that are associated with the particles. The GC/MS technique can be used for specific identification of compounds of environmental concern that are entering the waterway. This technique can also be used to identify compounds detected in biota that may be the result of ingesting or coming into contact with plastics or plastic-associated compounds. These analytical methods may be expanded into assessing pyrolysis of plastics and atmospheric contributions that are likely to occur when plastics are incinerated or sewage sludge contaminated with microplastics is used for energy production at sewage treatment facilities.
Density calculations, combined with identification of the polymer(s) and POPs associated with specific types of microplastic, can aide in calculating loadings of microplastic-associated pollution in a surface water body. The site specific amounts and types of plastic particles are potentially influenced by proximity to point source microplastic discharges, water flow rates, tributary connections, and river bathymetry. However, the data collected in these initial studies is not sufficient to identify specific pollution sources, and so further investigations that incorporate hydrologic flow patterns and bathymetry are needed.
Although previous samples (data not shown) indicate high microplastic densities in the NY/NJ harbor estuary, the heavily urbanized lower sections of the Passaic River did not exhibit the highest microplastic densities. This may be the result of tidally influenced flushing that dilutes plastic concentrations and moves the pollution out of the river and into the harbor. Tidal waters do not reach the Piscataway, Chatham, Livingston, or Fairfield upriver locations. The higher densities observed at these sites may be a function of the number of permitted discharges upriver of the sampling locations, inputs via tributary connections, or low flow conditions that allow plastics to accumulate. Because the downriver sites are tidally influenced, although samples were collected on outgoing tides it is possible that microplastic particles moved upriver from Newark (Lyndhurst, Kearny) or Raritan (Edison, Sayreville) Bays. Further research is needed to aide in microplastic source tracking.
Embryonic zebrafish exposed to plastic polymers identified by Pyr-GC/MS from field collected samples exhibited significant morphologic abnormalities (Figure 10). Field samples treated with the Fenton reagent did not result in alterations in growth or pericardial enlargement in the zebrafish embryos and yolk sac larvae. The Fenton reagent treatment, which oxidizes organic components and non-bound plasticizers, would leave only the polymerized plastic matrix. The plastic matrix scaffold would not be available for uptake into the embryo and likely explains the lack of toxic effects observed in these samples. This explanation is partially supported by the SPME-GCMS method, which demonstrated the same compounds on both the plastic particle and in the overlying water (Figures 7 and 8). Future studies will use both Fenton and non-Fenton treated samples, and will add exposure of juvenile fish, which would likely ingest the microplastic particles. The development of the analytical tools discussed above will enable us to determine the bioaccumulation of different compounds into aquatic organisms, both from the field and in laboratory studies.
There are a number of factors that make quantification of microplastic densities challenging [37]. In this study, density estimates could be affected by the limited number of samples, as well as temporal variations in microplastic inputs (i.e., post-precipitation sampling events, or conversely, drought conditions). Experimental bias may occur because the process for separating microplastics from organic material is labor intensive, and so there is the possibility of human error. Microbead spikes in the Passaic samples averaged 80% recovery, ranging from 20% (one sample) to 100% (5 samples), and so the density estimates may be understated. There is also potential experimental bias because the net mesh was 330 μm, and so smaller microplastics and any associated compounds are not captured in this dataset. In spite of these quantification challenges, our results demonstrate that there is a significant amount of microplastic in two of New Jersey's largest watersheds, and that potentially problematic organic compounds are associated with these particles.
5. Conclusions
This study demonstrates that urban New Jersey freshwaters contain microplastic pollutants that may have physiological effects on aquatic organisms. This proof of concept study demonstrates the ability to identify compounds associated with surface water microplastic pollution through a combination of SPME-GC and Pyr-GC/MS analytic methods. These methods can also determine which plastic-associated POPs are dissolved in the overlying water column. Once specific compounds are identified and microplastic densities are calculated, pollutant loadings, toxicological effects, and potential environmental risk can be assessed. These techniques may also be useful in identifying potential input sources based on the chemical "fingerprint" signatures of particle polymers and particle-associated compounds.
Acknowledgements
This work was carried out at the NJ Agricultural Experiment Station with funding support through Cooperative State Research, Education, and Extension Services Multi State 01201 and the National Institute of Environmental Health Sciences K99 ES025280. Funding for this research was also provided by the New Jersey Water Resources Research Institute FY2016 Program—Project ID 2016NJ378B (USGS Grant Award Number G16AP00071 and a grant from USEPA Urban Waters (EPA-OW-IO-15-01). We thank student interns Gabriella Bonaccorsi and Juan Carlos Ortega from East Side High School, Newark, NJ for their assistance with field sampling and laboratory analysis. We thank Anna Erickson and Angela Johnsen for providing assistance in preparing Figures.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: