Investigating the impact of biomass quality on near-infrared models for switchgrass feedstocks

Lindsey M. Kline; Nicole Labbé; Christopher Boyer; T. Edward Yu; Burton C. English; James A. Larson

doi:10.3934/bioeng.2016.1.1

AIMS Bioengineering, 2016, 3(1): 1-22. doi: 10.3934/bioeng.2016.1.1. Research article Topical Section

Export file:

Format

RIS(for EndNote,Reference Manager,ProCite)
BibTex
Text

Content

Citation Only
Citation and Abstract

Investigating the impact of biomass quality on near-infrared models for switchgrass feedstocks

Lindsey M. Kline, Nicole Labbé, Christopher Boyer, T. Edward Yu, Burton C. English, James A. Larson

1 Center for Renewable Carbon, University of Tennessee, 2506 Jacob Drive, Knoxville, TN 37996 USA
2 Department of Agricultural and Resource Economics, University of Tennessee, Knoxville, TN USA

Received: , Accepted: , Published:

Topical Section: Bioenergy and Biofuels

Abstract Full Text(HTML) Figure/Table Related pages

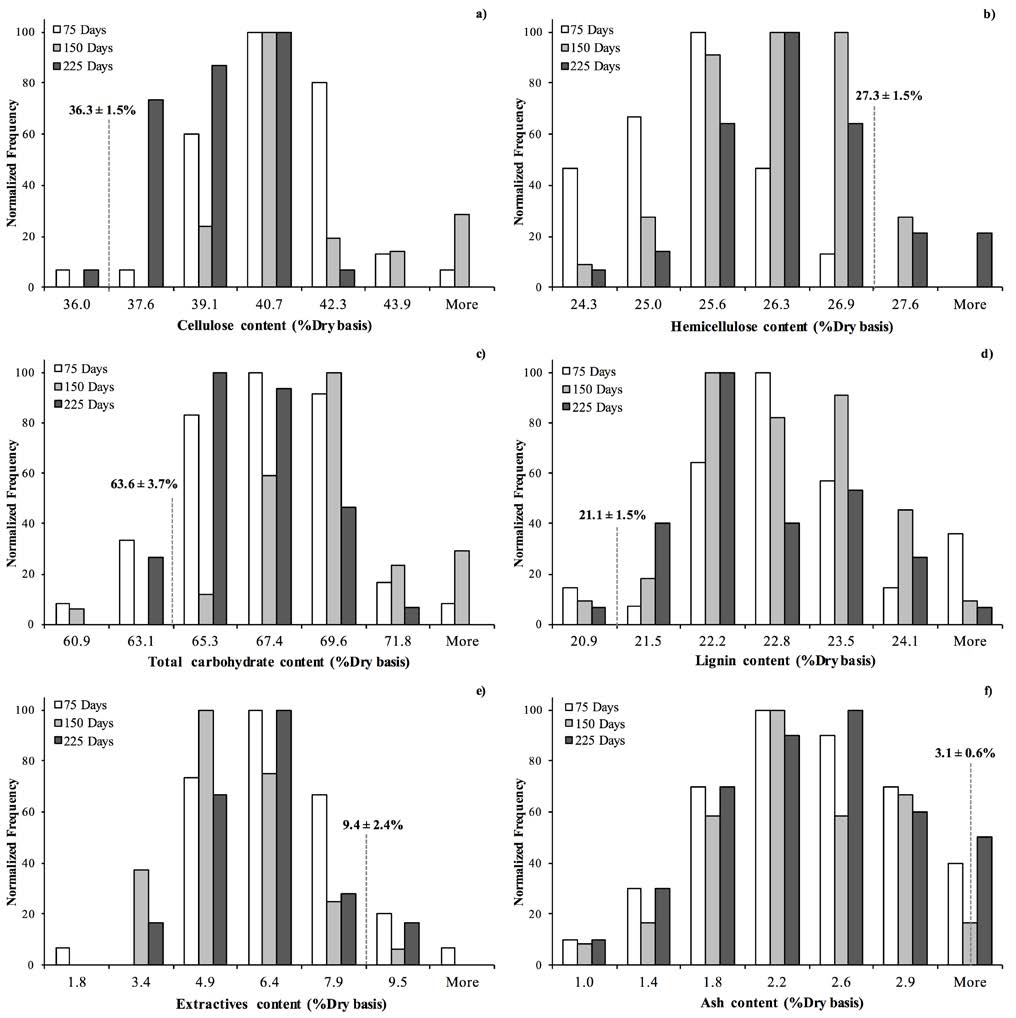
The aim of this study was to determine the impact of incorporating switchgrass samples that have been in long term storage on the development of near-infrared (NIR) multivariate calibration models and their predictive capabilities. Stored material contains more variation in their respective spectral signatures due to chemical changes in the bales with storage time. Partial least squares (PLS) regression models constructed using NIR spectra of stored switchgrass possessed an instability that interfered with the correlation between the spectral data and measured chemical composition. The models were improved using calibration sample sets of equal parts stored and fresh switchgrass to more accurately predict the chemical composition of stored switchgrass. Acceptable correlation values (r_calibration) were obtained using a calibration sample set composed of 25 stored samples and 25 samples of fresh switchgrass for cellulose (0.91), hemicellulose (0.74), total carbohydrates (0.76), lignin (0.98), extractives (0.92), and ash (0.87). Increasing the calibration sample set to 100 samples of equal parts stored to senesced material resulted in statistically increased (p = 0.05) correlations for total carbohydrates (0.89) and ash (0.96). When these models were applied to a separate validation set (equal to 10% of the calibration sample set), high correlation coefficients (r) for predicted versus measured constituent content were observed for cellulose (0.94), total carbohydrates (0.98), lignin (0.91), extractives (0.97), and ash (0.90). For optimization of processing economics, the impact of feedstock storage must be investigated for implementation in conversion processes. While NIR is a well-known high-throughput technique for characterization of senesced switchgrass, the selection of appropriate calibration samples and consequent multivariate models must be taken into careful consideration for NIR application in a biomass storage facility for rapid chemical compositional determination.

Figure/Table

Supplementary

Article Metrics

Keywords: switchgrass; feedstock quality; chemical composition; storage; near-infrared spectroscopy; partial least squares regression

Citation: Lindsey M. Kline, Nicole Labbé, Christopher Boyer, T. Edward Yu, Burton C. English, James A. Larson. Investigating the impact of biomass quality on near-infrared models for switchgrass feedstocks. AIMS Bioengineering, 2016, 3(1): 1-22. doi: 10.3934/bioeng.2016.1.1

References:

1.Sanderson MA, Agblevor F, Collins M, et al. (1996) Compositional analysis of biomass feedstocks by near infrared reflectance spectroscopy. Biomass Bioenerg 11: 365–370.
2.Moore KA, Owen NL (2001) Infrared spectroscopy studies of solid wood. Appl Spectros Rev 36: 65–86.
3.Kelly SS, Jellison J, Goodell B (2002) Use of NIR and MBMS coupled with multivariate analysis for detecting the chemical changes associated with brown-rot biodegradation of spruce wood. FEMS Microbiol Lett 209: 107–111.
4.Hames BR, Thomas SR, Sluiter AD, et al. (2003) Rapid biomass analysis : new tools for compositional analysis of corn stover feedstocks and process intermediates from ethanol production. Appl Biochem Biotech 105–108: 5–16.
5.Starks JP, Zuli D, Phillips WA, et al. (2006) Development of canopy reflectance algorithms for real-time prediction of bermudagrass pasture biomass and nutritive values. Crop Sci 46: 927–934.
6.Labbé N, Ye XP, Franklin JA, et al. (2008) Analysis of switchgrass characteristic using near-infrared spectroscopy. BioResources 3: 1329–1348.
7.Vogel KP, Dien BS, Jung HG, et al. (2011) Quantifying actual and theoretical ethanol yields for switchgrass strains using NIRS analyses. Bioenerg Res 4: 96–110.
8.Shenk JS, Workman JJ, Westerhaus MO (2001) Application of NIR spectroscopy to agricultural products, In Handbook of Near-infrared Analysis, 2eds., DA Burns, and EW Ciurczak, New York : Marcel Dekker, Inc., 383–431.
9.Wolfrum EJ, Sluiter AD (2009) Improved multivariate calibration models for corn stover feedstock and dilute-acid pretreated corn stover. Cellulose 16: 567–576.
10.Nkansah K, Dawson-Andoh B, Slahor J (2010) Rapid characterization of biomas using near infrared spectroscopy coupled with multivariate data analysis: Part 1 yellow-poplar (Liriodendron tulipifera L.). Bioresource Tech 101: 4570–4576.
11.Monono EM, Haagenson DM, Pryor SW (2012) Developing and evaluating NIR calibration models for multi-species herbaceous perennials. Industrial Biotech 8: 285–292.
12.Templeton DW, Scarlata CJ, Sluiter JB, et al (2010) Compositional analysis of lignocellulosic feedstocks. 2. Method uncertainties. J Agric Food Chem 58: 9054–9062.
13.English BC, De La Torre Ugarte DG, Walsh ME, et al. (2006) Economic competitiveness of bioenergy production and effects on agriculture of the southern region. J Agric Appl Econ 38: 389–402.
14.Mooney DF, Larson JA, English BC, et al. (2012) Effect of dry matter loss of profitability of outdoor storage of switcghrass. Biomass Bioenerg 44: 33–41.
15.Yu TE, English BC, Larson JA, et al. (2015) Influence of particle size and packaging on storage dry matter losses for switchgrass. Biomass Bioenerg 73: 735–144.
16.Chaoui H, Eckhoff SR (2014) Biomass feedstock storage for quantity and quality preservation, In: Engineering and science of biomass feedstock production and provision, 1ed. New York: Springer Science+Business Media, 165–193.
17.Kenney KL, Smith WA, Gresham GL, et al. (2013) Understanding biomass feedstock variability. Biofuels 4: 111–127.
18.Shinners KJ, Boettcher GC, Much RE, et al. (2010) Harvest and storage of two perennial grasses as biomass feedstocks. Trans ASABE 53: 359–370.
19.Shah A, Darr MJ, Webster K, et al. (2011) Outdor storage characteristics of single-pass large square corn stover bales in Iowa. Energies 4: 1687–1695.
20.Smith WA, Bonner IJ, Kenney KL, et al. (2013) Practical considerations of moisture in baled biomass feedstocks. Biofuels 4: 95–110.
21.Darr MJ, Shah A (2012) Biomass storage: An update on industrial solutions for baled biomass feedstocks. Biofuels 3: 321–332.
22.Larson JA, Yu TE, Boyer CN, et al. (2010) Cost evaluation of alternative switchgrass producing, harvesting, storing, and transporting systems and their logistics in the southeastern USA. Agric Fin Rev 70: 184–200.
23.Larson JA, Yu TE, English BC, et al. (2015) Effect of particle size and bale wrap on storage losses and quality of switchgrass. SunGrant Conference, Auburn, AL.
24.American Society of Testing Materials (ASTM), ASTM in West Conshohocken, PA: From Standard practices for infrared multivariate quantitative analysis. Available from: http://enterprise.astm.org/filtrexx40.cgi?+REDLINE_PAGES/E1655.htm. Accessed 15 December 2014.
25.National Renewable Energy Laboratory (NREL). (2008) Determination of extractives in biomass. National Renewable Energy Lab. NREL/TP-510-42619.
26.National Renewable Energy Laboratory (NREL). (2008) Determination of total solids in biomass and total dissolved solids in liquid process samples. National Renewable Energy Lab. NREL/TP-510-42621.
27.National Renewable Energy Laboratory (NREL). (2008) Determination of structural carbohydrates and lignin in biomass, National Renewable Energy Lab. NREL/TP-510-42618.
28.National Renewable Energy Laboratory (NREL). (2008) Determination of sugars, byproducts, and degradation products in liquid fraction process samples. National Renewable Energy Lab. NREL/TP-510-42623.
29.Labbé N, Ye XP, Franklin JA, et al. (2008) Analysis of switchgrass characteristics using near infrared spectroscopy. Bioresources 3: 1329–1348.
30.Çelen İ, Harper D, Labbé N (2008) A multivariate approach to the acetylated poplar wood samples by near infrared spectroscopy. Holzforschung 62: 189–196.
31.Taylor A, Labbé N, Noehmer A (2011) NIR-based prediction of extractives in American white oak hardwood. Holzforschung 65: 185–190.
32.Martens H, Naes T (1989) Multivariate calibration. Chichester: Wiley.
33.Esbensen KH (2002) Multivariate data analysis in practice: An introduction to multivariate data analysis and experimental design, 5 eds. Oslo, Norway: CAMO Process AS.
34.Rials TG, Kelley SS, So CL (2002) Use of advanced spectroscopic techniques for predicting the mechanical properties of wood composites. Wood Fiber Sci 34: 398–404.
35.Wold S, Sjöström M, Eriksson L (2001) PLS-regression: A basic tool of chemometrics. Chemometr Intell Lab. 58: 109–130.
36.Tsuchikawa S, Siesler HW (2003) Near-infrared spectroscopic monitoring of the diffusion process of deuterium-labeled molecules in wood. Part I: softwood. Appl Spectrosc 57: 667–674.
37.Goulden CH (1952) Methods of statistical analysis, 2eds. New York: John Wiley.
38.Garde-Cerdán T, Lorenzo C, Alonso GL, et al. (2010) Employment of near infrared spectroscopy to determine oak volatile compounds and ethylphenols in aged red wines. Food Chem 119: 823–828.
39.Arvelakis S, Koukios EG (2013) Critical factors for high temperature processing of biomass from agriculture and energy crops to biofuels and bioenergy. WIREs Energy Environ 2: 441–455.
40.Evans RJ, Milne TA (1987) Molecular characterization of the pyrolysis of biomass. 1. Fundamentals. Energ Fuel 1: 123–137.
41.Everard CD, Fagan CC, McDonnell KP (2012) Visible-near infrared spectral sensing coupled with chemometric analysis as a method for on-line prediction of milled biomass composition pre-pelletising. J Near Infrared Spectrosc 20: 361–369.
42.Lestander TA, Johnsson B, Grothage M (2009) NIR techniques create added values for the pellet and biofuel industry. Bioresource Tech 100: 1589–1594.
43.Hayes DJM (2012) Development of near infrared spectroscopy models for the quantitative prediction of the lignocellulosic components of wet Miscanthus samples. Bioresource Tech 119:393–405.
44.Sluiter A, Wolfrum E (2013) Near infrared calibration models for pretreated corn stover slurry solids, isolated and in situ. J Near Infrared Spectrosc 21: 249–257.

show all references

This article has been cited by:

1. Mario Aboytes-Ojeda, Krystel Castillo-Villar, Tun-hsiang Yu, Christopher Boyer, Burton English, James Larson, Lindsey Kline, Nicole Labbé, A Principal Component Analysis in Switchgrass Chemical Composition, Energies, 2016, 9, 11, 913, 10.3390/en9110913
2. Arturo Gonzalez-Quiroga, Kevin M. Van Geem, Guy B. Marin, Towards first-principles based kinetic modeling of biomass fast pyrolysis, Biomass Conversion and Biorefinery, 2017, 10.1007/s13399-017-0251-0
3. Pyoungchung Kim, Choo Hamilton, Thomas Elder, Nicole Labbé, Effect of Non-Structural Organics and Inorganics Constituents of Switchgrass During Pyrolysis, Frontiers in Energy Research, 2018, 6, 10.3389/fenrg.2018.00096

Reader Comments

your name: * your email: *

Copyright Info: 2016, Lindsey M. Kline, et al., licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution Licese (http://creativecommons.org/licenses/by/4.0)

Download full text in PDF

Associated material

Metrics