We propose and analyse a mathematical model for cholera considering vaccination. We show that the model is epidemiologically and mathematically well posed and prove the existence and uniqueness of disease-free and endemic equilibrium points. The basic reproduction number is determined and the local asymptotic stability of equilibria is studied. The biggest cholera outbreak of world's history began on 27th April 2017, in Yemen. Between 27th April 2017 and 15th April 2018 there were 2 275 deaths due to this epidemic. A vaccination campaign began on 6th May 2018 and ended on 15th May 2018. We show that our model is able to describe well this outbreak. Moreover, we prove that the number of infected individuals would have been much lower provided the vaccination campaign had begun earlier.
Abbreviations: CAS: coffee agroforestry system; GE: green economy; UNEP: the United Nations Environment Programme
1.
Introduction
The concept of green economy (GE) is closely tied to the 2012 United Nations Conference on Sustainable Development (UNCSD or Rio+20), where GE as a framework for sustainable development and poverty alleviation was explored [1,2,3]. For decades, scholars have discussed GE as a way to internalize the values of environmental impacts on economic activity, particularly through government intervention [4]. With increasing awareness of the negative ecological consequences of economic development, discussions of a green economy have reemerged [5]. The United Nations Environment Programme (UNEP) defines GE as increasing human well-being and social equality while significantly reducing environmental risks and ecological scarcity. GE is a low-carbon, resource-efficient, and inclusive of social groups closely tied to economic activity [3,6].
In the context of natural resource management, GE is a pathway to long-term resource management to meet the demands of current and future generations [7], also to be aligned with Sustainable Development Goals (SDGs) [3,7,8]. In defining human welfare through economic and social growth, natural resources are crucial. However unsustainable usage of natural resources has resulted in environmental quality decline and resource depletion. Natural resource management is, therefore, essential for ensuring that human welfare, economic growth, and environmental development are all sustained over the long term [7].
Agriculture, forestry, fishery, food industry, aquaculture, chemical, pharmaceutical, cosmetics, textile, and energy production sectors that use biomass as a primary raw material are GE implementation channels [7,9]. Sustainable agricultural and forestry systems are crucial for achieving sustainable development through a land-based green economy [2,7,10]. Managing multiple crops on a single plot of land is one example of an integrated and sustainable agricultural system. With the consideration of respect towards traditional community beliefs, this method can support food security and become a sustainable source of income for the community [11,12], minimizing environmental degradation [12,13]. Coffee is an increasingly popular agroforestry practice, as it offers multiple benefits to the environment and farmers' income. By combining coffee production with sustainable agriculture and forestry practices, farmers are able to preserve the natural environment while producing coffee under a canopy of shade trees, which helps preserve biodiversity, protects soils from erosion, and sequesters carbon [14]. In Colombia, coffee agroforestry aged between 1 and 40 years has been observed to have a consistent positive relationship between carbon stocks, erosion control, and epiphyte richness [15]. The benefits of agroforestry include reducing soil erosion, maintaining soil fertility, conserving water, reducing the use of fertilizers, and providing a habitat for wildlife.
Forests provide a habitat for various species and a means of survival for the communities that rely on them [10,16,17]. Throughout history, many cultures have revered forests and used them to guide a way of life [10]. Sustainable forest management systems and reduced deforestation align with the GE concept. In Indonesia, community-based sustainable forest management is manifested through social forestry programs [18]. According to the Minister of Environment and Forestry Regulation No. 9 of 2021 on Social Forestry Management, Social Forestry is a sustainable forest management system carried out by local communities or Customary Law Communities as the main actors to improve their welfare, environmental balance, and socio-cultural dynamics in the form of Village Forests, Community Forests, or Community Plantation Forests.
Agroforestry is one alternative to GE practices implemented in Indonesia through community-based sustainable forest management. As a sustainable agricultural system widely adopted by communities living near forests, agroforestry has been acknowledged for its potential to act as a catalyst for the rehabilitation of degraded lands and the provision of ecosystem services [11,15,19]. The practice of agroforestry not only helps to mitigate the negative effects of climate change [20,21] but also contributes to climate change adaptation through carbon sequestration in trees and soil [21,22].
In Indonesia, coffee agroforestry is commonly found as part of the implementation of social forestry and Community Base Forest Management (CBFM) [23,24]. Coffee agroforestry also has economic benefits, such as diversifying farmers' income streams by incorporating other crops and products. Indonesia can contribute to the global effort to achieve a green economy and SDGs by promoting coffee agroforestry [3,7,8].
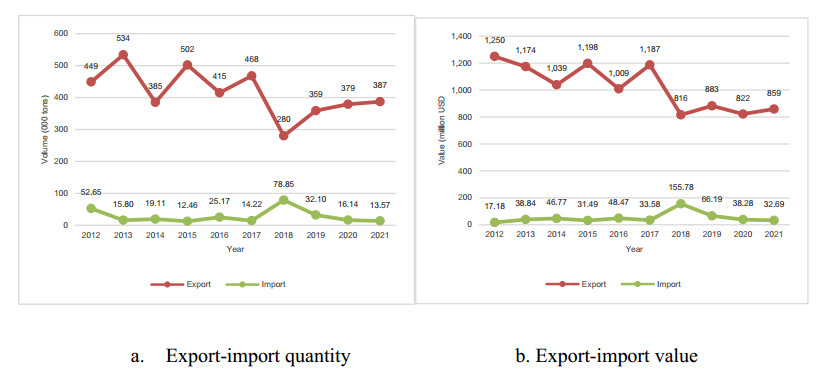
Indonesia is one of the world's largest coffee-producing and exporting countries, along with Vietnam, Brazil, Colombia, India, and Honduras. Indonesia has always been in the top ten world coffee exporters in the last decade, contributing to around 3.69%–8.34% of the total world coffee exports [25]. Indonesia's coffee exports in the 2012–2021 period were above 280,000 tons per year, with an average of 416,000 tons per year, which generated about USD 1.024 billion per year (Figure 1). Moreover, Indonesia's coffee import during the same period was an average of 28,000 tons per year, valued at USD 50.93 million. However, Indonesian coffee exports are now less than 10% of global coffee demand until 2021. Thus, there is potential to boost them.
Indonesian coffee production is supplied by three business entities, namely state plantations, private plantations, and smallholder plantations, with an area of 1,279,570 hectares in 2021. The area of the state plantation is only 13,315 hectares (1.04%), with a production of 4,125 tons (0.52%). Private plantations totaled 8,464 hectares (0.66%) with the production of 1,197 tonnes (0.15%). Smallholder plantations have dominated the coffee plantation area for the last ten years, with an area of 1,257,791 ha (98.30%) which produced 780,869 tonnes of coffee (99.9%) [26]. Smallholder coffee plantations are generally managed by farmers in the form of yards located around their houses [27,28] and agroforestry systems [27,29,30,31].
GE is one of the economic approaches that can address the challenges of sustainable economic activity in various commodities around the world, including coffee [2,32]. The GE approach emphasizes the use of natural resources and the provision of environmental services in a sustainable manner. The coffee agroforestry system (CAS) can provide income without depleting natural resources, making it an ideal practice for a green economy. As one of the world's main coffee producers, Indonesia faces the degradation of natural resources, including forests. While smallholder coffee plantations are generally located around forests, the implementation of CAS has the opportunity to be a solution for sustainable coffee production that is environmentally sound.
However, some challenges should be addressed for CAS to fully realize its potential as a GE practice in Indonesia. One major challenge is farmers' lack of knowledge and awareness about the benefits of agroforestry and the potential for income generation from environmental services. Another challenge is the lack of government support and policies to promote coffee agroforestry as a GE practice. To address these challenges, therefore, it is important to provide a systematic review of the social, economic and environmental benefits of CAS to be used as a reference in order to support the implementation of CAS as a GE practice in Indonesia. This could include providing financial incentives for farmers to adopt agroforestry practices, also technical assistance and support for research and development of sustainable coffee agroforestry systems.
2.
Materials and methods
2.1. Research framework
GE is a path to achieve sustainable development and response to three global challenges: environmental degradation, poverty and inequality. Environmental quality is a major concern for Indonesia's economic development. CAS can benefit smallholder farmers in Indonesia economically and socially by reducing environmental risks and improving soil quality.
CAS is an approach to forest resource management by providing access to communities around forests to use them for livelihoods. CAS also focused on the benefits that could accrue to the farmer due to the beneficial effects of coffee plantations, crops, and forests on food and agricultural production. Besides that, CAS incorporate both agriculture and forestry into their farming system. Faced with the problems of deforestation and environmental degradation, farmers and other institutions focused their search for appropriate land-use approaches that would be socially acceptable, ensure the sustainability of the production base, and meet the need to produce multiple outputs.
Agroforestry practices in Indonesia still largely prioritize farmers' income rather than environmental interests in the short term. For example, agroforestry practices in areas with steep land slopes cultivate horticultural crops. In the long run, the area will become an open area so that it will have an impact on the loss of forest ecosystems and landslides. Therefore, the implementation of CAS in areas with high environmental risk requires strong support from several aspects such as financial, marketing, regulatory, human resources development. In the end, CAS is expected to be a practice to realize socially inclusive, low-carbon, and resource-efficient economic development (Figure 2).
2.2. Systematic literature review method
This review is aimed to assess the opportunities for developing CAS as a GE practice in Indonesia, as well as the challenges in its development. To provide comprehensive and exhaustive research, a systematic review approach has been used as the method. Steps of systematic review are presented in Figure 3 [33,34].
The scoping stage formulates several key issues as the scope of the systematic review [34]. At the planning stage, research questions are formulated and broken down into individual concepts to create search terms [33,34]. A comprehensive literature search is carried out in the identification or searching stage. The access to a range of literature sources is made as wide as possible to obtain various information [33,34]. Reviews are carried out on global and national indexed scientific publications, books, laws, and regulations relevant to the topic. The screening step is conducted to select the eligible studies. Essential data were extracted and synthesized from eligible papers to respond to the research questions [33,34,35].
Figure 4 depicts the process of selecting articles for the literature review. The main topic of this research is the concept of green economy and coffee agroforestry with a focus on studies in Indonesia. These three things are then used to determine the electronic database used. Considering that the discussion will start from the global level which will eventually focus on the national level (Indonesia), an electronic database is selected to accommodates these needs. Then determine the keywords used to find articles that match your needs. Keywords are formulated based on proximity to the main topic. After obtaining articles that match the keywords, select eligible papers are carried out which are then used in writing articles.
3.
Results
3.1. Dynamics of green economy and agroforestry
3.1.1. Green economy concept
The industrialization era brought about technological advancements and economic growth but also caused environmental degradation due to the release of materials from the production process. This has led to the concurrent emergence of several crises, including climate, biodiversity, fuel, food, water, financial systems, and economic crises. The main reason for these crises is dirty and inefficient capital allocation [3,36], where the majority of the capital has been invested in real estate, fossil fuels, and structured financial assets. A green industrial revolution with investments in clean technologies, renewable energy, waste management, sustainable agriculture, green cities, and ecosystem management is seen as the solution to climate change and the financial crisis, as proposed by the UNEP [3].
The GE concept, rooted in sustainable development, has evolved over time and received increasing political endorsement from governments and international bodies, such as the UNEP, Organization for Economic Co-operation and Development (OECD), United Nations Conference on Trade and Development (UNCTAD), International Chamber of Commerce (ICC) and European Economic Area (EEA). The GE model aims to address environmental degradation post the industrialization and inefficient capital allocation by directing public and private capital toward green economic activities. The rural poor in developing countries, who rely heavily on ecosystem services [7], would benefit from a green economy as it would improve human well-being and reduce poverty [16,37]. The GE model is also a pathway to new opportunities for trade, growth, and sustainable development [38], especially in developing countries [39].
However, there are certain issues with the GE model. Some contend that the concept's breadth is excessively broad and lacks social imperatives. There are also concerns about the burden of regulation on businesses and the focus on green growth without a critical examination of development itself [40]. Implementing the green economy model also faces economic and ecological challenges, particularly regarding the circularity dimension in environmental and ecological protection. According to general EU statistics, the EU generates more than 2.5 billion tons of garbage annually. Capital equipment manufacturing consumes 7.2 billion tons of raw materials globally every year [41]. Moreover, several international agreements to combat global climate change still need to be made more powerful to respond to a temperature increase of less than 1.5 CO2, as highlighted in the Paris Agreement and worldwide political decisions [42]. Thus, it is the challenge for GE to contribute significantly to achieve the 2030 agenda for sustainable development and eliminating poverty by protecting the ecological threshold that supports human health, welfare, and development.
3.1.2. Agroforestry concept
Agroforestry dates back several thousand years, when humans first practiced slash-and-burn agriculture for shifting cultivation. After several cropping cycles, the forest will be allowed to fallow for a period of time. It was customary at the time to plant and sow seeds of food crops while keeping a few trees, resulting in a mix of timber tree and crops on a piece of land [43]. Agroforestry is broadly defined as a land unit that combines the cultivation of timber crops or a forest with agriculture crops, fisheries, and animal husbandry [43,44]. There are four essences or keywords of agroforestry, they are intentional, intensive, interactive, and integrated. Agroforestry systems are designed and managed as a unit to maximize productivity and protect the environment in which there are interactions between biological and physical components. Agroforestry is defined by three basic sets of characteristics, which are productivity (production of specific commodities and land resources), sustainability (conservation of the resource base's production potential), and adoption (acceptance of practices by farming communities and other users) [43].
Since the late 1970s, significant progress has been made in the science of agroforestry, including its role in land use issues. Agroforestry is regarded as a promising and long-term land-use strategy [43]. Some scientists consider agroforestry an innovative and beneficial land use option and environmental model [44]. Agroforestry systems are a comprehensive approach to addressing land use issues, combining trees with crops or livestock sequentially and simultaneously [11,19,43].
Crop diversification within a single land unit promotes a more balanced cropping system, preserving soil fertility and agroecosystems, diversifying production systems, and increasing the sustainability of smallholder farming systems. The incorporation of trees into land-use practices demonstrates the importance of tree-based agroforestry and land-use practices in smallholder livelihoods [11,21]. For decades, agroforestry has been important in improving smallholder livelihoods and modernizing agriculture [21] with a favorable environmental impact [21,45,46].
Agroforestry can be viewed as a climate change mitigation and provides ecosystem services such as carbon sequestration, biodiversity conservation, water quantity and quality improvement, and land degradation [13,21,43,45]. Benefits of ecosystem services can be produced in agroforestry and can be the source of income for the community and the government. In agroforestry practices, forest products such as timber, conservation, amenities, and environmental services become a source of income for the agroforestry system [46].
3.1.3. The linkages between green economy and coffee agroforestry
Implementing GE concept to ensure sustainable development requires the consideration of political, economic, and cultural factors [47]. The transition to GE implementation requires a combination of short and long-term policies with different combinations of policies and instruments for developed and developing countries [1]. Implementation of GE comprises investment or divestment, taxes or incentives, payments, compensation, voluntary approaches (e.g. certification and standards), and other regulatory and policy instruments [1,48]. Applying GE concept through traditional cultural practices can produce environmental services and provide a source of income [12,13].
The example of GE practice in the forestry sector is agroforestry. As most sectors contribute to greenhouse gas emissions from land-use change and forestry [49], agroforestry is one of the strategies to mitigate carbon dioxide emissions and contribute to increasing income as the core of GE concept. Agroforestry can be recognized as a GE practice because it has an impact on increasing farmer productivity and income as well as contributing to environmental sustainability [50,51,52]. Agroforestry is a land use system that intentionally integrates trees (woody plants), crops, and livestock [53]. Agroforestry is one of the best land use strategies because it contributes to increasing food security while reducing environmental degradation [52]. Agroforestry recognized as a sustainable agricultural practice, can also solve environmental and economic problems and provide benefits to society [54,55,56,57,58]. Agroforestry is promoted as a strategy to stop deforestation [59]. In addition, agroforestry provides agroecological services by increasing soil fertility, controlling erosion, mitigating climate change, and preserving biodiversity [53,60].
Agroforestry as an integrated farming system [43,44] is one of GE's implementations because it improves human welfare and social justice while reducing environmental risk and scarcity [3]. Agroforestry can play a role in implementing GE towards green economic growth at various utility and political levels, from local to global [1]. CAS provides more local and immediate benefits than global and long-term benefits. Local and direct benefits from coffee agroforestry are closely related to land use policies and carbon sequestration. At the same time, the relationship between CAS as a GE practice and payments for ecosystem services, large-scale water management projects, natural resource management and pricing, and global carbon taxes has global and long-term benefits [61,62,63].
Coffee cultivation in forest areas implements the concept of GE, particularly in providing environmental impact, generating added value, and creating social equality. Coffee agroforestry provides ecosystem services similar to forests while also achieving social, economic, and ecological or conservation interests [23,64]. The system is adopted globally [50,51,53], including in Indonesia [23,62,64]. Coffee agroforestry alleviates political implementation difficulties by moderating potential disputes, so it has been widely practiced in Indonesian land-use planning policies and social forestry schemes.
3.2. Green economy policy, social forestry, and coffee agroforestry implementations in Indonesia
3.2.1. Green economy practices in agriculture
Indonesia leads the world in green growth, green economy transformation, and new ideas [65]. President Joko Widodo listed three Indonesian GE initiatives during the World Economic Forum on January 20, 2022. First, the medium and long-term development plans prioritize low-carbon development. Second, by 2030, Indonesia will implement a net zero emission strategy, including net sinks in the forestry and land sectors, and publish a plan to reach zero emissions by 2060. Third, green stimuli boost GE development.
Implementing GE, particularly in developing countries like Indonesia, has its own complexities and challenges. In the agricultural sector, whereby GE is most implemented in Indonesia, it is found that the ecosystem services have not met sufficient promotion for GE development [66]. Based on the Aceh Green Program, the initial implementation of GE in Indonesia concluded that less engagement with the private sector for investing in GE made the program unsustainable. The investors focused on the short incentive received during the programs neglecting the environmental impacts of GE. This is due to the unavailability of market incentives for GE in Indonesia, including the certified palm oil and timber price premiums. Swainson and Mahanti in 2018 mentioned that the only favorable incentive is the coffee industry [67]. Another challenge is the lack of coordination between the political economy and the different scales of governance [68], including corruption and lack of trust from the investors.
The agricultural sector is dominated by GE criteria in Indonesia [69]. Organic farming is one of the common implementations of GE that started since the green revolution campaign in the 1980s. Environmental issues are the main reason for developing these agricultural systems [70]. Organic agriculture does not only focus on high production in a short time but also on more sustainable production by paying more attention to land quality and environmental sustainability while producing safe products for consumption [71,72]. Organic farming practices in Indonesia can be classified into fully organic and semi-organic cultivation, for example, using certain organic inputs such as organic fertilizers or pesticides. This practice can be found in various commodities such as rice [71,73,74,75,76], chili [77], cocoa [78], shallots [79], and coffee [80,81].
Another GE practice in the agricultural sector is crop-livestock integration. It is an example of an agricultural system model that can be developed to increase agricultural productivity while reducing environmental impacts because waste from one business activity can be an input for other activities. This system also applies the zero-waste concept and supports environmental conservation [82]. Crop-livestock integration patterns that can be found in Indonesia include oil palm-beef cattle [83,84], coconut-cocoa-cow [82], citronella-beef [85], potato-beef [86], and vegetables-beef-duck-fish [87]. As a GE practice, the integration of oil palm-cow is proven to provide benefits for cattle farmers from an environmental, social, and economic perspectives [84]. Weeds from oil palm plantations can be used as feed for cattle, thereby reducing the use of herbicides, while cow dung can be used as organic fertilizer for oil palm plantations. Moreover, cow-potato integration contributes to reducing production costs because organic fertilizer for potato plants is obtained from cow dung, also using organic fertilizer has an impact on increasing potato production [86].
GE practice is also found in forestry as part of the agricultural sector. In Indonesia, this type of GE practice includes swamp buffalo, paludiculture, and agroforestry. The cultivation of swamp buffalo has the potential to be developed as a livelihood for communities around peatland forests because it is profitable and financially feasible [88]. Whereas paludiculture, an application of GE thought to be capable of restoring biophysical conditions and biological functions as well as the ability to restore the economic role of the peat ecosystem, is one of the restoration and cultivation techniques on peatlands, [89,90]. Paludiculture involves rewetting of peatlands, revegetation, and revitalizing community livelihoods [91]. Paludiculture should be a solution for restoring degraded peatlands, reducing emissions, and at the same time also increasing food security and reducing poverty levels and even being an option for cost-effective management that can reduce fires on peatlands [92].
In Indonesia, agroforestry has developed for a long time and is a source of income for households living near forests [93]. Agroforestry patterns that develop in Indonesia are widely diverse, including agro silviculture (forestry-agriculture), silvopasture (forestry-livestock), agro silvopasture (forestry-agriculture-livestock), and various other practices [93,94,95,96].
Certification is an important aspect to be developed in Indonesia to identify GE practices, particularly in farming systems. Plantation of export-oriented crops have been used for several certifications to show GE practices. Certification can be found in palm oil [97,98] and coffee [81,99,100,101,102]. Certifications on palm commodities that are commonly used in Indonesia are the Roundtable Sustainable Palm Oil (RSPO) and Indonesian Sustainable Palm Oil (ISPO). These certifications typically aim for sustainable production with minimal social and environmental impacts and improved natural resource management [98]. In addition, the certification includes good cultivation standards (Good Agriculture Practices or GAP), which, if fulfilled and implemented in an integrated manner, will be able to overcome sustainability problems as well as increase productivity.
For coffee farming in Indonesia, the sustainability certifications applied include C.A.F.E Practices, Indonesian Organic Farm Certification (INOFICE), Rainforest Alliance (RA), and Common Code for Coffee Community (4C). From the economic aspect, RA certification contributes to improving coffee quality and controlling production costs; while from the environmental side, it supports wildlife protection, integrated plantation, and waste management for better ecosystem and water and soil conservation [100]. The application of C.A.F.E Practices certification in coffee farming also has an impact on better coffee cultivation practices; so, it enhances coffee productivity, quality, and selling prices [102]. In addition to contributing to increased income, 4C certification also produces environmental benefits in the form of biodiversity conservation by planting shade plants, using organic fertilizers, and not driving wild animals into farmers' coffee plantations [81].
3.2.2. Coffee agroforestry
Coffee agroforestry is one of the agroforestry patterns that has been developed in Indonesia. Typically, coffee agroforestry is a multi-cropped pattern, the cultivation of coffee alongside horticultural crops such as vegetables, bananas, durian, stinky bean, mangosteen, dog fruit (Archidendron pauciflorum), lanzones (Lansium domesticum), chempedak (Artocarpus integer), rambutan (Nephelium lappaceum), plantation crops (cocoa, areca nut, cloves, candlenut, pepper), woody plants (pine, champaca, mahogany, sengon, randu (Ceiba pentandra), suren (Toona sureni), and calliandra [103,104,105,106,107]. For shading plants, those plants are usually placed at the border of the field [103,108,109,110,111]. The spacing between those plants in the coffee plantation is adjusted accordingly to the land conditions and farmer preferences, including the number of mixing plants is vary based on farmers' experience and knowledge exchange. The selection of these types of plants is based on complex considerations, including high selling value, market availability, ease of cultivation, or short harvest life, and government programs [103,106,110].The development of coffee agroforestry in Indonesia is primarily driven by social forestry programs, which aim to correct the previous timber-focused economic model. These programs, such as Community Forestry (Hutan Kemasyarakatan or HKm) and Village Forests, allow farmers to reclaim control of forest areas and plant cash-producing crops, including coffee. Historically, before 1998, coffee farmers faced forced eviction from forested regions, leading to the destruction of their crops [61,63,112,113,114,115]. Consequently, the government took charge and initiated the cultivation of forest plants. However, with the massive Government Reformation in 1998, the local community regained authority over the forest area and embarked on the cultivation of profitable crops, such as coffee.
Since the government issued the HKm policy, there has been an increase in the number of HKm groups beginning around 2000. The HKm groups are required to plant trees in an agroforestry pattern as coffee shading crops [61]. For example, members of the HKm group in the West Lampung District Head's Decree No. 11 of 2004 are required by the District Head to plant a minimum of 400 stems per Ha of timber and fruit tree species other than coffee plants [29], but the type of coffee plant is specifically mentioned. Government and NGO programs, particularly forest or watershed rehabilitation programs, make it easier for HKm groups to fulfill their obligation to plant tree species other than coffee plants. However, intercropping patterns are only suitable for relatively flat land. Therefore, coffee plantation is uncommon in protected forests dominated by hilly land. Village Forests policy is also a social forest policy that is suitable for coffee cultivation (see [27,116,117]). The first Village Forests policy was issued in 2008, and it has since expanded to cover an area of 2,013,017.21 Ha, while HKm has reached 916,414.60 Ha [118]. Unlike HKm, which is based on farmer group institutions, the Village Forest scheme promotes a village government-established institution to manage a forest area.
Social Forestry in Indonesia is in line with the national land rehabilitation program both as individuals and as a group that later evolved into a social forestry group [119]. Both HKm and village forests are expected to participate in rehabilitating forest areas. The term agroforestry is not mentioned in the regulation, but rather intercropping with a composition of 60% for wood-base plants and 40% for multipurposes tree species. These policies have been successful in reducing deforestation [113] and contributing to various forms of capital [120], including human, physical, natural, and financial capital.
However, the recent regulations have further emphasized the development of social forestry businesses without specific mentions of agroforestry patterns, including the Social Forestry regulation, No. P.9 of 2021. Unlike the regulations on the implementation of forest and land rehabilitation, No. 23 of 2021, which mentions agroforestry as one of the patterns in reforestation and regulates the number of timber and/or NTFP trees of at least 400 stems/Ha, or at least 200 stems/Ha if there are at least 500/Ha of intercrops, the number of agroforestry plants in social forestry can be adjusted to the type of plants. Agroforestry is defined in this regulation as a pattern or type of forest area utilization, both in protection and production forests, as part of the development of social forestry businesses. Technical regulations governing forest and land rehabilitation activities provide guidelines for agroforestry implementation, such as The Ministry of Environment and Forestry's Director General for Watershed and Protected Forest Control issued Special Regulation No. P.7 of 2017 concerning Agroforestry Implementation Guidelines.
The implementation of the Social Forestry Program is one of the conflict solutions offered by the government for the management of community crops, including coffee in forest areas [121], and has contributed to increasing income. The turning point for social forestry policy changes in Java, like elsewhere, occurred after the political reform era. Perhutani, a state-owned enterprise, manages most of the state forest area on the island of Java. Perhutani launched the community forest management named Pengelolaan Hutan Bersama Masyarakat (PHBM), or Managing Forest with the Company program, in 2001 [122]. Despite being viewed as the state's attempt to reclaim control of its forests (see [123]), PHBM is also considered to have contributed to increasing the income of participants and local communities [124,125]. Coffee-based agroforestry is a PHBM model effort that has been shown to be effective in resolving conflicts and increasing community income [124,126,127].
The practice of coffee agroforestry, particularly in Harjomulyo Village, Jember, East Java, is an option to solve the conflicts between the community and PT. Perhutani, where farmers are allowed to grow coffee with CAS in forest areas with the Community-Based Forest Management (PHBM) program [128]. Coffee agroforestry in the Protected Forest Management Unit (KPHL) Batutegi is an example of a development intended as a solution for forest utilization while maintaining forest functions [129]. The community is given the right to manage the forest through the HKm program on the condition that they do not develop monoculture plant species. Coffee production and forest protection are also commonly found in Lampung Province, especially in water catchment areas for the Way Seputih Sekampung Watersheds which were later developed in agroforestry [130]. Concerning the social forestry program, [31] report that the Sarimukti Forest Village Community Institution (LMDH) in Ciamis, West Java benefits financially from the production of coffee and other crops in coffee agroforestry through a forestry partnership scheme. With a social forestry permit, the community does not feel threatened or afraid of managing the forest.
However, the change process at the site level is complex, and farmers have expressed concerns about the interference of woody trees with coffee productivity. Wulandari and Kurniasih [131] describe the desires of HKm participants in order for the government adjusts current policies in response to societal changes. The main complaint of HKm coffee farmers is the presence of woody trees that have shaded the coffee plants but cannot be cut down, despite the fact that they are interfering with coffee plant productivity. This complex issue has happened in Semende. The Social Forestry Program is undergoing a process of change and improvement, both within Java and outside Java. However, the change process at the site level is also fast and complex. Another barrier to implementing coffee-plant-based HKm is the growing population [120]. For HKm participating coffee farmers in protected forests outside Java, facilitation in the form of entrepreneurship training is highly prioritized, especially when the coffee reaches five years old and beyond ten years old [131].
3.2.3. Contribution of coffee agroforestry to the green economy
As mentioned previously in the theoretical framework (Figure 2), GE stands on three pillars, namely increasing societies' welfare, improving social justice and minimizing environmental impacts [3,132]. In the implemented GE, coffee agroforestry practices balance economic and environmental benefits [121]. Coffee agroforestry is an alternative or primary source of income for villagers in Indonesia, especially people who live around the forests [93]. For example, the Binawana HKm in West Lampung [133], Bandung Highlands [28], and Way Besai Watershed, Lampung West [134]. In some cases, this system generates higher income than those not practicing agroforestry [104,135]. In another report, it is found that coffee agroforestry in KPH Malang provides an average of 33% of the households' total income [111] and 20-41% of the farmer income in the Waybesai Watershed, West Lampung [134].
The technique of mixing coffee plants with other plants in coffee agroforestry has proven to be capable of generating higher economic income, such as in the Samosir community forest, North Sumatra [136], Sesaot HKm in West Lombok [106], and Sarimukti LMDH (Forest Village Community Institution) in Ciamis [31]. Profits are obtained from coffee beans, multipurpose tree species (MPTS) and other plants [130]. The farmers allocate the income to meet household needs [133], garden maintenance, developing non-agricultural businesses, creating partnerships between farmers and forest managers, supporting credit guarantees, and savings for education [128]. Farmers' economic benefits from implementing agroforestry are influenced by land area because land is the primary production factor in coffee agroforestry [129].
Diversifying farmers' income sources from various plants grown in an area of coffee agroforestry can minimize the risk of crop failure or declining yield of one commodity [60,111,137]. Another additional income opportunity is through agro-tourism in agroforestry coffee plantations, for example, based on the observed rise of coffee cafes and coffee lovers in Indonesia [31,138]. Education and recreation in coffee agroforestry areas are also supported by the landscape comprising various types of plants [105] and the historical existence of coffee plantations, most of which have been built since the colonial era in Indonesia [139].
Coffee agroforestry also contributes to the environment and ecosystem protection. For example, coffee agroforestry in Tanggamus, Lampung has an impact on protecting spring water [107], reducing the deforestation rate, and contributing to the restoration of damaged watersheds [104]. The conversion of shrubland and dry land into coffee agroforestry has improved the watershed quality in Maros, South Sulawesi [137]. The same system also supports biodiversity conservation by providing a habitat for small mammals, birds, and insects in East Java [138] and the Javan slow loris in Central Java [127]. Other contributions are improving ecosystem balance, including water regulation and microclimate, reducing erosion risk, oxygen production, increasing flora diversity, and providing animal habitat [93,105,133,134,140].
The coffee plantation also increases community participation in the agricultural business [141]. In contrast to state and private coffee plantations, coffee agroforestry is managed on a small-scale area [99,141,142]. However, even though it is managed in a small area of land, the aggregate of small-scale coffee plantations has reached 1,257,791 ha or 98.30% of Indonesia's total coffee plantations in 2021 [26]. Coffee agroforestry plantations provide employment opportunities for villagers through direct management rights on the planting land [93,133]. Another advantage of the availability of these jobs is sustainability which can occur throughout the year because commodities are harvested at various times [137]. Communities participating in agroforestry schemes gain more secure access rights and knowledge development through farmer groups [28,135]. Government programs often involve farmer groups with regular assistance and training. The involvement of institutions also provides investment guarantees for farmers and, at the same time, guarantees for the implementation of protected area management objectives by the government [130,139].
To summarize, coffee agroforestry practices in Indonesia have generated economic, social, and environmental contributions, parallel with GE concept developed by [3]. Coffee agroforestry in various regions of Indonesia creates a better ecosystem and provides a more significant portion of community involvement. The contribution of CAS to the GE is presented in Table 1. Agroforestry also has the potential for climate change mitigation and adaptation strategy [142,143,144]. Multi-strata agroforestry allows for the management of the seasonal variability of rainfall and extreme temperatures [142]. This practice is used as a conflict mitigation strategy between farmers and forest managers in several regions in Indonesia.
Coffee agroforestry in Indonesia has the potential to be developed in the form of a social forestry program that synergizes the management and protection of natural resources with a better livelihood system [30]. Coffee agroforestry also has the potential to be developed as organic farming to increase product value. The demand for organic agricultural products in Indonesia is expected to increase along with an increase in per capita income and a better level of education [70].
The application of agroforestry still faces the challenges of limited resources such as land, human resources and finance [53,57]. Rachman et al. [145] underlined the importance of the farmer's knowledge as the most critical dimension in developing agroforestry. Another challenge is farmers' growing perception that trees will interfere with the coffee crops' growth [146]. While actually, combining many species of trees in coffee agroforestry in the highlands of South Sumatra is common to minimize risk [110]. Another challenge is contesting options between coffee and high-value crops such as oil palm, which also occurs in Ethiopia by introducing exotic trees instead of indigenous trees in the agroforestry system [146]. As a developing country, some agroforestry practices in Indonesia are still traditional, although the sustainability of the new technology introduced is still questionable.
4.
Discussion
CAS practice allows for the implementation of GE in Indonesia. Referring to the definition of GE by UNEP [3], it is indicated that CAS can play a role in social, economic, and environmental frameworks. CAS practices (Table 1) may involve the community actively, contribute to people's income and livelihoods, as well as maintain and improve environmental quality. Nonetheless, its development has various opportunities and challenges for GE implementation. Most of Indonesia's coffee is produced from smallholder coffee plantations, which are usually managed traditionally on a small scale. Coffee processing and marketing have also been done traditionally, causing the implementation of coffee agroforestry as a green economy practice in Indonesia to face various opportunities and challenges (Figure 5).
On the bright side, coffee agroforestry as a green economy practice has various strengths. Coffee agroforestry involves coffee farmers living around forests on a large scale, the activities of which are carried out both outside and inside forest areas. Coffee-based agroforestry practices in forest areas in Indonesia are a part of the social forestry program of the Ministry of Environment and Forestry (MoEF). CAS is a forest management practice with the community that is considered successful in overcoming conflicts, involving the community to actively participate and contribute significantly to community income and livelihood. CAS increases income and provides income continuity thanks to product diversification. Coffee agroforestry is a strategy to implement GE for the community through the production of various coffee products while maintaining environmental quality.
In addition, CAS in Indonesia also has some opportunities. The agroforestry coffee production system is in line with Good Agriculture Practices (GAP) on Coffee (Regulation of the Minister of Agriculture of the Republic of Indonesia No. 49/Permentan/OT.140/4/2014). GAP on coffee suggests permanent shade trees with great economic value to provide woody plants with long-term cover. Policies from both the Ministry of Environment and Forestry and the Ministry of Agriculture support the development of coffee-based agroforestry as a channel for GE development. Government support also enables the availability of financial institutions to support the quality of agroforestry coffee cultivation and production, overcome limited land for cultivation through authorized access, and support farmers' capacity building. Various relevant NGOs also play an active role from cultivation, post-harvest to marketing.
Although the development of agroforestry coffee has good opportunities, several internal factors weaken its effect. Generally, the capacity of farmers is still low, especially in post-harvest processing and marketing. Agroforestry coffee produced by smallholders has various qualities and is usually still low. Farmers who are faced with limited income tend to produce random quality coffee which is sold under a cash economy scheme to middlemen. Farmers who intend to sell products for certain markets produce high-quality coffee, both domestically and abroad [147]. Quality-based coffee activists, the coffee industry and NGOs have the potential to become major partners in improving the quality of agroforestry coffee produced by farmers.
Institutions related to marketing products from coffee agroforestry at the farmer level are also still an obstacle [147]. Coffee farmers are generally price takers and have not been able to access markets outside the existing markets. Institutional strengthening is needed related to marketing in order to overcome limited (asymmetric) information and determination of selling prices. Partnerships with marketing agencies at other levels and locations are important so that farmers are more empowered in marketing coffee from agroforestry gardens. Farmers need assistance from the government, NGOs and coffee activists to access wider markets.
Product certification is both an opportunity and a challenge for coffee agroforestry. Certification is important concerning coffee quality, strategies for agroforestry sustainability, and the creation of new markets. Eco-certification is a trust incentive given by consumers for the application of green economy practiced in coffee agroforestry. This obstacle can be overcome by assisting farmers in producing good quality coffee products. NGOs, governments, and coffee-related business entities are expected to provide assistance to farmers in implementing environmentally friendly farming systems, for instance, in agroforestry patterns, minimizing the use of chemicals, reducing forest and environmental damage. With the help of various parties, both technical and funding, the agroforestry coffee production system will be oriented towards sustainability, paying attention to quality and environmental sustainability while yielding products that are safe for consumption as a result of GE practices [70,71,72].
Government policies can also be both an opportunity and a challenge in developing coffee agroforestry as a GE practice. Coffee agroforestry can create effective political implementation by moderating potential disputes in Indonesia. However, it was also found that policies related to social forestry, i.e., agroforestry coffee production areas, are not always aligned with the process of change at the site level [131]. In addition, there is also a lack of coordination between government agencies at various levels [68]. The development of coffee agroforestry must be facilitated with synergy between Ministries and local governments, adjusting conditions at the site level, starting from production to marketing aspects.
Government support can be provided in the form of programs and policies. Regulations, infrastructure, management access and incentive mechanisms are issued and facilitated by the government so that farmers, NGOs, coffee activists and industries, and financial institutions can be actively involved. The government becomes an enabler and guarantor in the availability of accessible financial institutions to support the quality of agroforestry coffee cultivation and production. NGOs, activists, and the coffee industry provide support in the form of assistance and facilities that increase farmer capacity and market access.
5.
Conclusions
As a GE practice, CAS has the potential to become a thriving economic business. Global and national market demand for agroforestry coffee is increasing, creating an opportunity for its development. Despite the numerous opportunities, there are several challenges in developing CAS and producing high-quality coffee agroforestry products. Coffee quality, which is generally erratic, needs to be improved with the help of product certification in order for GE practices to be sustainable. Collaboration with NGOs and business entities must be established to enhance the quality of coffee agroforestry products and realize a more sustainable CAS in Indonesia. Government policies must be coordinated for concurrent implementation at the site level. Additionally, training and education programs must be implemented for farmers and other stakeholders in the coffee agroforestry system to increase their knowledge and skills in sustainable coffee production practices.
Research and development efforts should also focus on improving the productivity and profitability of coffee agroforestry systems and addressing the challenges of climate change as well as other environmental factors. Developing and implementing coffee agroforestry as a green economic practice in Indonesia requires a multifaceted approach, including collaboration between various stakeholders, government policies and regulations, including the support of research and development efforts. With these efforts, the coffee agroforestry system in Indonesia will become a sustainable and profitable business.
Acknowledgments
This research was funded by Rumah Program OR TKPEKM BRIN. N.A.U., A.H.H., A.L.S., A.Y., D.D., E.M., H., J.W., L.R.E.M., M.R.T.M, and S.A. had an equal role as main contributors who equally discussed the conceptual ideas and the outline, provided critical feedback on each section, and helped shape and write the manuscript. All authors have read and agreed to the published version of the manuscript.
Use of AI declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: