On the Caginalp phase-field system based on the Cattaneo law with nonlinear coupling

1.   Introduction

COVID-19 primarily affects the respiratory system and lungs ^[1,2,3,4]. The rapid and timely diagnosis of COVID-19 prevents severe damage to the lungs and prevents morbidity and mortality ^[5,6,7,8].

One of the most common methods of COVID-19 diagnosis is Reverse Transcriptase-Polymerase Chain Reaction (RT-PCR), which is expensive and time-consuming ^[9,12]. On the other hand, the chest X-ray is among the most accessible and cheapest ways of diagnosis ^[13,14,15] but it is challenging ^[9].

Many studies investigated the accuracy of the rapid antigen test for COVID-19 and reported a maximum accuracy of 75.9% ^[16,17,18].

One of the most widely used methods in the diagnosis of COVID-19 is the use of Computed Tomography (CT), which is significantly more accurate. A number of studies ^[19,20,21] have reported an accuracy rate higher than 94%. The algorithm for diagnosing COVID-19 with the help of CT images is as follows: The COVID-19 virus infection level is checked using a CT scan, and based on that level of lung involvement, the treatment plan and whether or not the patient needs to be hospitalized are decided. Additionally, during hospitalization, CT scan images are frequently taken from the patient so the specialist can determine whether the lung involvement has progressed or if the patient is recovering ^[22].

The studies have demonstrated that lung ultrasound has generated more accuracy in diagnosing pneumonia than chest X-ray ^[23]. Hence, it can be said that CT imaging is among the best tools for detecting and classifying COVID-19 ^[24,25], with a sensitivity of up to 98%, which is about 27% higher in comparison with the RT-PCR ^[26]. According to the growth in worldwide cases, to diagnose and manage the COVID-19 pandemic, CT imaging is probably going to become popular. Recent studies indicate a pathological road that could be tractable to early CT detection, especially if the patient's scanning is two or more days after the emergence of symptoms ^[25].

In many countries, due to the high growth rate and rapid transmission of coronavirus, social solutions have been considered to prevent the spread of this disease, which include: global lockdown, social distancing, closure of schools, universities, shopping malls, travel restrictions, closing borders, etc. These solutions have been caused to reduce disease transmission and mortality ^{[14,27,28,29]}.

In general, to follow up with the patient and check the healing process of the lung organ, specialists request consecutive CT images of the lungs of patients in the ward and Intensive Care Unit (ICU) ^[30]. Currently, image-gaining and testing kits are relatively fast and stress-free, but analysis of the options can be challenging, costly and time-consuming for medical professionals in Low-income countries. Hence, academic researchers have studied automatic diagnosis methods for the analysis of COVID-19 images based on Artificial intelligence ^[31].

Despite the advances in the field of diagnosing COVID-19 using neural network-based models, it has been challenged in terms of the high computation rate and the complexity of the network. Hence, in this paper, we presented a lightweight deep-learning model that has been generated with six layers for automatic COVID-19 diagnosis on CT scan images. The structure of this model is such that no dropping out has occurred of neurons in the network layers. It is the first time that the modeling has been conducted using the Rapidminer tool on the images of COVID-19. Specifically, we used the Global Feature Extractor (GFE) operator for preprocessing the images. In addition, the classification models include Decision Tree (DT), RF and standard Neural Network (NN). We have evaluated the efficiency of the generated methods in terms of accuracy, precision, F1-score, specificity and area under the curve. The proposed 6-layer deep model has obtained a high accuracy of 96.71% for COVID-19 diagnosis. Therefore, the performance of the proposed model outperformed the current models for detecting COVID-19.

The rest of the paper is structured as follows. In section 2, we reviewed the related works. Section 3 depicts the methods, and Section 4 is devoted to the results. Section 5 represents the discussion. Section 6 concludes with the results.

2.   Related works

In the study ^[19], the authors suggested deep-learning techniques to detect COVID-19. All three methods—DenseNet, InceptionV3 and New-DenseNet—were cited in the literature. New-DenseNet was created by placing a convolutional layer onto the DenseNet design. These three techniques were used on a dataset of 2482 CT scans as well as 1130 X-ray images. The CT scan dataset had a reported accuracy of 95.98%, while the X-ray dataset had the highest accuracy at 92.35%.

Another study employed X-ray scans to identify patients with coronavirus infection ^[32]. Three groups of X-ray scans were used in their research: COVID-19, pneumonia and healthy cases. To begin, fully connected layers from 13 different Convolutional Neural Network (CNN) models were used to extract the deep features of X-ray images. Each sample is then sent into the Support Vector Machine (SVM) for classification by one of the three groups mentioned above. ResNet50, together with SVM, had the highest accuracy (95.33%) of all the models.

To classify COVID-19 and healthy X-ray chest images, ^[33] provided a fine-tuned CNN model together with an SVM classifier used with a wide range of different kernels, such as Linear, Quadratic, Cubic and Gaussian. Nearly equal numbers of COVID-19 (180 instances) and healthy (200 cases) X-ray chest images were included in the dataset used for the study. Among the models used, the ResNet50 model and the SVM classifier's linear kernel had the highest accuracy (94.7%).

Two public datasets totaling 1300 images of bacterial, viral and healthy chest X-rays were taken into consideration in the study ^[34]. The Xception architecture, a 71-layer deep convolutional neural network upon which the authors based their CoroNet model, is a 71-layer deep convolutional neural network. The approach was employed in three different circumstances, using two alternative methodologies as modifications in addition to the 4-fold CoroNet as the primary model. The findings of this investigation indicate an average accuracy of 89.60%.

738 CT scan images were employed as a dataset by ^[35] to diagnose COVID-19. The authors' study included various models that were all based on CNN. First, a self-made model named CTnet-10 was applied to the data, and it produced an accuracy of 82.1%. Second, five other CNN methodologies were trained on the dataset to boost performance. With a 94.52% accuracy rate, the VGG-19 model exhibited the best capability to distinguish between COVID-19 findings that were positive and negative.

The literature ^[36] identified COVID-19 using two distinct CT scan datasets. On each dataset, they trained CNN models using SqueezeNet, tested the effectiveness of data augmentation and examined transfer learning. Each of the 30 attempts in each trial consisted of 20 epochs and had a unique set of hyperparameters. The findings show the highest sensitivity of 87.55% and accuracy of 85.03%.

The study ^[37] used data from 2617 patients and 2724 chest CT images, in which the authors used a 3D anisotropic hybrid network to segment the lung regions of the CT data (abbreviated AH-Net). Following that, the CT scans were categorized using both hybrid 3D and full 3D models. Finally, a pre-trained DenseNet 121 method was implemented to detect the 3D segmented lung areas with the best accuracy possible of 90.8%.

In ^[38], the authors investigated 742 CT scan images, including 345 COVID-19 patients and 397 healthy ones. This study proposed several deep CNN models, including AlexNet, VGGNet16, VGGNet19, GoogleNet and ResNet50, to diagnose COVID-19 patients. The performance of the models was further enhanced by combining data augmentation methods and Conditional Generative Adversarial Nets. The findings indicate that ResNet50, with an accuracy of 82.91%, performs the best of all models. ^[39]

Singh et al. in ^[39] used 344 COVID images and 358 non-COVID images from three independent datasets to diagnose coronavirus infection in patients. Deep CNN, Extreme Learning Machine (ELM), online sequential ELM and bagging ensemble with SVM was trained as different classifiers on the data following PCA that was already applied as a feature selector. According to the outcomes, the bagging ensemble, together with an SVM classifier, had the highest accuracy at 95.70%.

The research study ^[40] uses Bayes optimization-based MobilNetv2 and ResNet-50 models, as well as SVM and K-nearest Neighbors (KNN) methods, to propose a novel approach. This methodology achieved an accuracy of 99.37 on datasets, including both COVID and non-COVID samples. Examining the developed method's performance findings led to the prediction that it might be applied as a high-classification-success decision support mechanism regarding the use of CT scans in the detection of COVID-19.

Chieregato et al. in ^[41] examined 558 patients who were admitted to a hospital in northern Italy between February and May 2020 to create a hybrid method to classify patient categories based on critical care unit admissions or death. On baseline CT scans, a fully 3D patient-level CNN classifier was employed as a feature extractor. The collected features are supplied into a Boruta feature selection method using SHapley Additive exPlanations (SHAP) game-theoretical values for selection, coupled with laboratory and clinical data. The CatBoost gradient boosting algorithm is proposed to develop a classifier on the condensed feature space, and it achieves an AUC score of 0.949.

A large-scale learning strategy for COVID-19 classification employing stacked ensemble meta-classifiers and feature fusion based on deep learning was proposed by Ravi et al. in ^[42]. Using the Principal Component Analysis (PCA) method ^[43,44], the dimensionality of the features extracted from the penultimate layer of EfficientNet-based pre-trained models was reduced. The obtained features were then combined using a feature fusion approach. Finally, a two-step stacked ensemble meta-classifier-based technique was applied for classification. The initial predictions were made using SVM and Random Forest (RF), which were then combined and supplied to the next step. The CT scans, and X-ray image data samples were categorized into COVID-19 and non-COVID-19 groups in the second stage by a logistic regression classifier.

A novel methodology for improving COVID-19 patient classification according to their chest X-ray images was given in ^[45], which reduces the deep learning models' strong dependence on massive datasets. Using the various filter banks, including the Sobel, Laplacian of Gaussian and Gabor filters, the method allowed for deeper data extraction. The authors employed 4560 X-ray images of patients, 360 of which were in the COVID-19 category, and the remaining images belonged to the non-COVID-19 disorders, to assess the effectiveness of the implemented approach. The results show that the defined evaluation metrics have the most significant growth with the Gabor filter bank, resulting in the best accuracy of 98.5% when combined with the DenseNet-201 model.

The study ^[46] set up a variety of methods that have been improved upon by replacing the head of the network with an additional set of layers. Two different data were analyzed for this research project. The first one has X-ray images from the three classes Normal, COVID and Pneumonia. In contrast, Dataset-2 has the same types but places a stronger emphasis on the two main types of bacterial pneumonia and viral pneumonia. The investigation involved 959 X-ray images, with DenseNet121 achieving the maximum accuracy of 97%.

Nadler et al. presented an epidemiological model that integrates new data in real-time through variational data assimilation, facilitating forecasting and policy evaluation ^[47]. Also, a bespoke compartmental Susceptible-Infected Recovered (SIR) model was developed that accommodates variables about the pandemic's available data, termed the susceptible-infected-treatment-recovered (SITR) model. This model enables a more detailed inference of the infection numbers, thereby allowing for a more granular analysis. The application of a hybrid data assimilation approach serves to enhance the robustness of results in the presence of both initial condition variability and measurement error within the data. Their findings indicate that in Italy, the pinnacle of infections has already been attained, evidenced by the number of patients being treated reaching its peak in the middle of April. However, the trajectories of the United States and the United Kingdom are less discernible, with a probable rise in the medium term. This can be attributed to both countries exhibiting a strong increase in transmissibility rates after an initial decrease as a result of lockdown measures.

A fuzzy classifier was designed by Song et al, with the objective of identifying individuals with infections by means of scrutinizing and examining the CT images of patients suspected to be afflicted ^[48]. First of all, a deep learning algorithm is utilized to derive the low-level features of CT images. Afterward, the extracted feature information is analyzed using an attribute reduction algorithm to obtain features with superior recognition. Subsequently, a few crucial features are chosen to serve as input for the fuzzy diagnosis model in the training model. Lastly, a selection of images in the dataset is employed as the test set to evaluate the trained fuzzy classifier. The experimental findings indicate that the deep fuzzy model enhances the accuracy by 94.2% when compared to the deep learning diagnosis methods commonly employed in medical images.

In the study conducted by Wen et al., a novel attention capsule sampling network (ACSN) was introduced with the aim of diagnosing COVID-19 through the analysis of chest CT scans ^[49]. A method for enhancing key slices was implemented through attention enhancement to obtain crucial information from numerous slices. The authors employed the utilization of a key pooling sampling method, highlighting the representational capacity of the proposed approach to amalgamate the advantages of both max pooling and average pooling sampling methods. The outcomes of the experiments on a CT scan dataset of 35,000 slices have demonstrated that the ACSN model has achieved remarkable results, with an accuracy of 96.3% and an AUC of 98.3% when compared to the most advanced models currently available in diagnosing COVID-19.

In another study, Cheng et al. suggested an approach for updating a sequential network utilizing data assimilation techniques with the aim of merging a variety of temporal information sources ^[50]. The effectiveness of vaccination in a SIR model is compared among the assimilation-based approach, the standard method based on partially observed networks, and a random selection strategy. The initial step in the analysis involves conducting a numerical comparison of real-world face-to-face dynamic networks that were obtained from a high school. This is then followed by the generation of sequential multi-layer networks, which rely on the Barabasi-Albert model to emulate large-scale social networks that are comprised of multiple communities. In general, the vaccination strategy based on assimilation displays a competitive performance in this multi-layer modeling, even though the probabilities of the assimilated layers are mere approximations.

3.   Methods

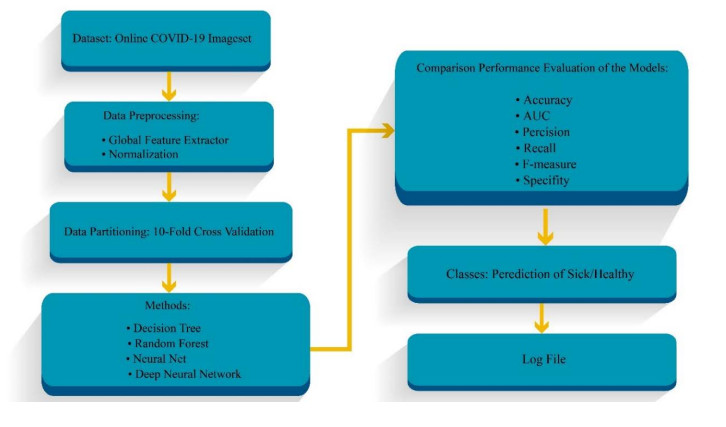
This study presents the 6-layer DNN model to diagnose COVID-19 using CT scan images. Besides, other models are generated, such as decision trees, random forests and neural networks. The proposed framework methodology is shown in Figure 1.

We used RapidMiner Studio version 9.9¹, which is open-source software for the COVID-19 diagnosis and classification process. The proposed methodology comprises data description, data preprocessing, data partitioning and definition of the models.

¹ https://docs.rapidminer.com/latest/studio/installation/

3.1.   Data Description

We utilized online COVID-19 X-ray images for the prediction of sick/healthy cases. This dataset contains 1252 unhealthy images and 1229 healthy ones and was extracted from an online source². Figures 2 and 3 show the two CT scan images from the dataset. Note that the dimensions of the images were different.

² https://www.kaggle.com/plameneduardo/sarscov2-ctscan-dataset

Regarding Figures 2 and 3, the non-specific hazy opacification of the lung in X-ray and CT scan images with no total annihilation of bronchial or vascular marks is known as ground glass opacity (GGO). A partial fluid filling of the lung alveoli, interstitial thickening, or a partial collapse of the lung alveoli is among the presumptive pathologies ^[51].

The most frequent findings on a chest CT in COVID-19 pneumonia patients are GGO, which is typically characterized as patchy, peripheral, bilateral and sub-pleural ^[52]. In a systematic review of 13 research, Bao et al. ^[53] discovered that GGO was the most prevalent manifestation, being recorded in 83.31% of patients.

3.2.   Data preprocessing

In the preprocessing data stage, the operators such as Multiple Color Image Opener (MCIO), GFE, global statistics, histogram, logarithmic distance (d-log distance), Border/Interior Classification (BIC) and Order-Based Block Color Feature (OBCF) have been implemented. Data normalization is conducted following the usage of these operators.

At first, the images of sick and healthy cases were selected. The first operator, MCIO, is illustrated in Figure 4.

3.2.1.   MCIO

According to Figure 4, in the first step, the MCIO operator was used to select a folder containing healthy and sick images. Since this operator handles data management, we chose the double_array option for the data management parameter. Moreover, to distinguish sick cases from healthy ones, a label is assigned to the images. Following this, the MCIO operator has a subprocess called GFE which is shown in Figure 5.

3.2.2.   GFE

Figure 5 shows how to extract features from a single image using the GFE operator along with a subprocess. Several operators were implemented in the subprocess, including global statistics, histogram, d-log distance, BIC and OBCF. Figure 6 depicts the relationship between the operators as mentioned above.

1) Global Statistics

According to Figure 6, every descriptive statistics information was extracted and represented from the relevant images using the global statistics operator. Statistical information such as mean, median, standard deviation, skewness, kurtosis, peak, min gray value, max gray value, the normalized center of mass, area fraction and edginess were extracted from the images.

2) Histogram

The number of features is specified in the next step based on the histogram operator by determining the number of bins. When the bin count is set to 128,128 features are typically generated.

3) BIC and d-log

Then, BIC Operator generates the pixel classification of the image's interior space and image border. This operator divides the image space into two parts and produces two inputs that describe the edges, border pixels and internal pixels of the image. Following these classifications, the d-log distance operator is applied to calculate the distance between the interior space and the image border. It was added to the dataset as a feature.

4) OBCF

The OBCF, as the final operator, extracts color features from images based on rows, columns and computations performed on them. The rows and columns were set to 12 and 16, respectively. The analyses also include average, minimum and maximum values. The prediction becomes more accurate as the number of rows and columns increases.

5) Data normalization

Finally, an image normalization process was applied to map the intensity of image pixels to the interval [0, 1]. In this regard, Figures 4-6 are generated by RapidMiner version 9.9.0 software.

3.3.   Data Partitioning

The 10-Fold Cross-Validation (FCV) technique was used for dataset partitioning and executed in each fold by applying 90% (9 bins) of the training data and the remaining data for testing ^[54,55]. To handle the training process, avoid data overfitting, improve the generalization and increase the accuracy, 80% of data was considered for training and 20% for validation from comprehensive training data. The process is performed in 10 rounds (folds). In addition, stratified sampling was chosen as the sampling method. The partitioning process on the dataset is shown in Figure 7.

3.4.   The methods used

3.4.1.   C5.0 Decision tree

The Decision Tree (DT) is one of the most common methods of generating a classification model in machine learning. The main idea of the decision tree is to get rules that can aid the specialists in diagnosing the data given by the system. In this paper, we proposed the decision tree of the C5.0 method. The C5.0 is less time-consuming than the equivalent versions such as CHAID, ID3 and C4.5 ^[56,57], but it requires a large amount of memory. The decision tree is composed of several nodes and edges so that the leaves demonstrate healthy and COVID-19 classes. Additionally, using the internal nodes, decisions about one or more features are made. Therefore, the C5.0 decision tree is a suitable method due to its simplicity and comprehensibility. Based on the image set, the graphical diagram of the C5.0 decision tree is shown in Figure 8.

The setting up of the parameters of the created DT model is described in Table 1.

2) Random Forest

One of the robust predictive methods in supervised learning is Random Forest (RF) which can improve accuracy and speed ^[56]. This method generates various trees and selects the highest votes. Also, to improve accuracy, it evaluates multiple features and combines functions and it assigns one input vector to each tree in the forest for classification. The structure of the RF on the image set is shown in Figure 9.

According to Figure 9, the RF model outperforms the C5.0 decision tree in terms of data management, computing accuracy and obtaining more information by pruning fewer features, operating with more data and extracting better rules. As a result, this model is better suited for disease diagnosis than the C5.0 decision tree. Table 2 describes how the parameters of the implemented RF model were set up in this study.

3) Neural Network

The Neural Network (NN) has been generated based on human neuron cells. The neural network contains input and output nodes joined by weighted links. In other words, a multi-layer neural network ^[58] is specified with three layers; input layer, hidden layer and output layer. In the input layer, each node is one of the predictive variables, the hidden layer involves the weights of nodes and the output layer represents healthy and sick classes. In general, the input neurons sum and multiply the specified weights of the individually input edge. By exploiting the bias, the outcome is transformed into an activation function, and its output continues to the subsequent layer ^[56,58]. The standard neural network is illustrated in Figure 10.

Table 3 demonstrates how the parameters for the proposed standard NN model were configured in this study.

4) Deep Neural Network

The Deep Neural Network (DNN) is an improved form of the neural network ^[57]. In the DNN model, one encounters multi-layered DNNs, which present multi-layered learning features such as the essential representative. The layers are titled hidden layers in the NN, and a network is considered a DNN when it contains more than two hidden layers ^[56]. For instance, a DNN model with three hidden layers is shown in Figure 11.

Based on Figure 11, in a 3-level model (low, middle and high), more complex features are extracted in the higher layers. The class type of the input data is specified in the model output. Hence, the objective of DNN is to realize some levels of distributed representations of the data by generating features in the lower layers. It can differentiate the options of the data variations and then compound these representations in the higher layers. One of the crucial advantages of a DNN model is that this model acts very well on image data and has higher accuracy than classification models. Another significant ability of a DNN is the action to extract features automatically and it has a high generalization ability to deal with new data.

In this paper, a lightweight deep neural network, namely a 6-layer DNN model with four hidden layers, is sized 50×30×25×50 in the 50 epochs. Furthermore, the utilized nonlinear activation function, which determines the activity of neurons in the middle layers, is determined by Maxout. The Maxout function chooses the maximum coordinates for the input vector and is used to avoid data overfitting and improve the model's training. Also, the sigmoid function is utilized to classify the output layer of the model. Moreover, the lightweight DNN model is structured without dropping out of neurons in the layers of the network during training.

Table 4 describes how the DNN model parameters were set up in our study.

4.   Results

The results of the methods are presented in this section, which includes the DT, RF, NN and DNN. These methods have been evaluated using performance metrics such as Accuracy (ACC), Precision (Pre), F1-score, Specificity (Spe) and Area Under the Curve (AUC). The metrics are calculated through a confusion matrix. The confusion matrix is clarified in Table 5.

In Table 5, the factors of the False Positive (FP), False Negative (FN), True Positive (TP) and True Negative (TN) are determined to obtain the following formula (1–4) ^[58].

(1) $ Specificity = \frac{{TN}}{{TN + FP}} $

(2) $Accuracy = \frac{{TP + TN}}{{TP + TN + FP + FN}}$

(3) $precision = \frac{{TP}}{{TP + FP}}$

(4) $F - measure = \frac{{2TP}}{{2TP + FP + FN}}$

The performance of the models in terms of accuracy demonstrates that the proposed DNN model, with 96.71%, has the best performance compared to the DT, RF and NN models reaching 84.57%, 85.62% and 91.43%, respectively. The precision of the proposed DNN, DT, RF and NN is obtained as 97.64%, 77.23%, 78.47% and 90.89%, respectively. Also, using the proposed DNN model, the F1-score and specificity are achieved at 96.67% and 97.65%, respectively, and the value of these criteria using the other methods has been less estimated. These results have been gained through 10-FCV on 2481 CT scan images. The experimental results based on the evaluation criteria are assigned in Table 6.

Moreover, another important measure used to determine the performance of the methods is the AUC criterion. This criterion is obtained via the surface area under Receiver Operating Characteristic (ROC) curve. The performance of binary classifier algorithms is usually measured by some factors such as "Sensitivity" and "Specificity." In the ROC diagram, both of these factors are combined and displayed as a curve. To draw the ROC curve, the TPR and the FPR is only needed. TPR determines how much the correct prediction has been made. That is, the number of accurate predictions is divided by the number of actual positive results, and the correct positive prediction rate is calculated. On the other hand, FPR indicates the number of identifications among negative observations. This ratio is also used as a false positive rate in the ROC curve ^[59]. Indeed, the ROC is formed by these two indicators, namely FPR on the horizontal axis and TPR on the vertical axis. As a result, a balance between benefit (TP) and cost (FP) is formed on the ROC curve, which is called AUC. The ROC curve of the DT, RF, NN and DNN is illustrated in Figures 12–15, respectively.

Based on Figures 12–15, it can be founded that the proposed DNN model has the best AUC rate of 99.5% than the DT, RF and NN, reaching 84.3%, 94.6% and 96.6%, respectively.

5.   Discussion

In this paper, we used the 6-layer DNN for COVID-19 diagnosis on the CT scan images. For the first time, the RapidMiner software was used for the modeling. First, the online COVID-19 image set was extracted. After that, data preprocessing using GFE and normalization was implemented. Following this, the image set has been divided by a 10-fold cross-validation technique. Finally, the methods such as decision trees, random forests, neural networks and deep neural networks were applied to the image set. To evaluate the proposed methods, the performance metrics such as accuracy, AUC, precision, F1-score and specificity have been conducted. The developed DNN has the best performance in terms of the above metrics.

A comparison between the current study and related studies regarding the accuracy achieved on the CT scan images is demonstrated in Table 7.

Table 7 shows that the proposed DNN model outperforms other methods in terms of accuracy, precision, F1-score, specificity and AUC. In addition, the 6-layer DNN model has been performed as a lightweight model without dropping out of neurons in the layers of the network that can be influenced for COVID-19 diagnosis on small datasets.

Our study has some limitations. First, in the case of using images with a large volume, the time complexity for processing images using software increases. Second, there is a need for high-powerful GPU and CPU hardware when using large datasets in the training process.

Third, there is a limit to the use of operators related to advanced algorithms based on neural networks, including CNN and autoencoder, for image classification.

6.   Conclusion

The COVID-19 pandemic has changed people's lives, resulting in a negative impact on the public health systems, especially the international economy. Computer-aided decision-making can help in the diagnosis of COVID-19. Since the outbreak of this virus, artificial intelligence models, including machine learning and deep learning, have been generated for the diagnosis of COVID-19 on medical images. Hence, in this study, we developed a deep neural network model for COVID-19 diagnosis on the CT scan images. First, the dataset is preprocessed based on global feature extractor and normalization approaches. Then, data partitioning is performed using a K-fold cross-validation (10-fold) technique to avoid overfitting and the better evaluation of models. In the following, the processed images were fed to the four algorithms such as decision tree, random forest, neural net and lightweight deep neural network. Among these generated models, the 6-layer deep learning model has the best performance in terms of accuracy, precision, specificity, F1-score and AUC metrics. The result of the classification accuracy of the proposed deep model is obtained as 96.71%. Also, regarding the area under the curve value, the proposed model has reached a high score (99.5%) compared to the other models.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Funding Statement

Associate Professor Shariful Islam is funded by the National Heart Foundation of Australia (102112) and a National Health and Medical Research Council (NHMRC) Emerging Leadership Fellowship (APP1195406).

Availability of Data and Materials

Publicly available datasets were analyzed in this study. This data can be found here: https://www.kaggle.com/plameneduardo/sarscov2-ctscan-dataset

Conflicts of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.