1. Introduction

Because of supply security and price fluctuations of rare-earth materials, some countries such as the USA, UK, Germany and Japan are making efforts on developing non-rare earth material and even non-permanent magnet machines for electric vehicles ^[1]. Over the past decades, due to its simple and robust structure and low cost, switched reluctance machines (SRMs) have received some attention ^[2]. However, vibration, noise and torque ripples of SRMs are potential disadvantages ^[3]. Furthermore, switched reluctance machines need unconventional drives and complex control strategies. In ^[4] a new type of synchronous machine (SM), with doubly salient structure, named "flux-modulating SM" was proposed. It also does not need permanent magnets but promises fewer technical problems than SRMs. This machine has two sets of stator windings: one field winding and an armature winding. Both are non-overlapped concentrated windings. Since there are neither permanent magnets nor field windings on the rotor, the new machine is well suited for high-speed operation. By regulating the field current, the machine can operate at a wider constant power region. In ^[4] the working principle of this machine was introduced, and in ^[5] the core losses were assessed. In ^[6] the effect of changing the rotor pole shape was investigated. The machine was also considered as variable flux reluctance machine and has been studied intensively ^{[7,8,9,10,11]}. In ^[10] the stator/rotor pole combinations such as 12/8, 12/10, 12/11, 12/12 and 12/14 are compared. It is found that 12/10 and 12/14 combinations can eliminate the inherent unbalanced magnetic force and exhibit more sinusoidal back-EMF. Compared with switched reluctance machine, variable flux reluctance machine can significantly reduce torque ripple and acoustic noise and vibration ^[11]. In ^[12] the torque variations along DC and AC currents were investigated through FEA and experiment methods. However, the slot assignment strategy for this type of machines with more than one set of winding is still missing. Since the two sets of windings are installed together in the same stator, the slot space allocation will influence the torque and the copper losses of the machine. Hence, this paper presents a detail derivation of torque equation through analytical methods. The methods described in this paper are also applicative for other machine types, which has more excitation sources on the stator.

This paper focuses on the slot space allocation and is organized as follows: Firstly, the structure and operation principle of DC-excited flux-modulated (DCEFM) are introduced in Section 2. Then, the methods and detailed derivation of torque equation are illustrated in Section 3. To verify the analysis, FEA method is used and the comparison of FEA and analytical results are shown in Section 4. Finally, the conclusion is drawn in Section 5.

---

2. Structure and principle

---

2.1. Structure evolution

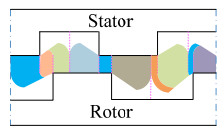
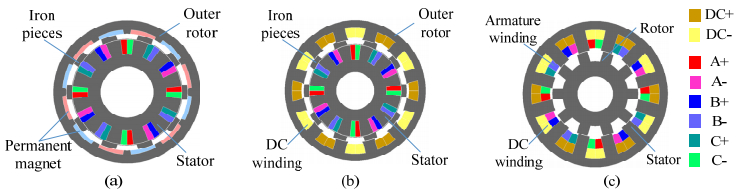
The structure of a basic flux-modulated machine with 12 slots and 10 poles is shown in Figure 1(a). Based on the equation p_r = p_f + p_a, this machine has p_a = 4, p_f = 6, p_r = 10. Of course, there are still many other slots/poles combinations following this rule, such as 12 slots 8 poles (p_r = 8, p_f = 6, p_a = 2), 12 slots 11 poles (p_r = 11, p_f = 6, p_a = 5), 12 slots 13 poles (p_r = 13, p_f = 6, p_a = 7), 12 slots 14 poles (p_r = 14, p_f = 6, p_a = 8). For this special configuration, the stator slots number is equal to the pole number of the outer rotor. If the permanent magnets (PMs) on the outer rotor were replaced by the field excitation, the structure of the machine is changed to Figure 1(b). Further on, by keeping the outer rotor stationary and combining the outer rotor with the inner stator, a new DCEFM machine is created as shown in Figure 1(c).

Since the DC winding and the armature winding are both installed on the stator, the machine does not need brushes. This arrangement also improves heat dissipation. A drawback is the additional DC winding. It decreases the fill factor of the armature winding and adds additional copper losses. Moreover, as the machine contains high harmonic field due to its working principle, it also causes high core losses.

---

2.2. DC field

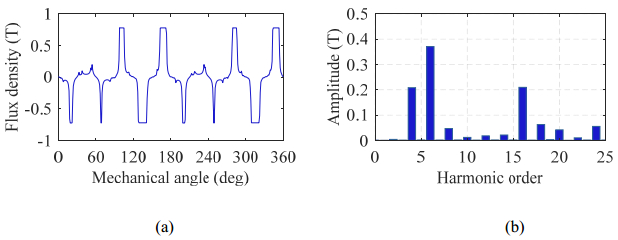
In this paper, a 12 slots 10 poles motor is analyzed. For this motor, the p_r = 10, p_f = 6 and p_a = 4. When only DC winding is excited and the DC current is equal to 10 A, the air gap flux consists high 6^th because p_f is equal to 6 as shown in Figure 2(b). In addition, the air gap flux consists high 4^th and 16^th components due to the interaction of rotor pole number 10 and pole-pair number of DC field winding which is equal to 6.

---

2.3. Armature field

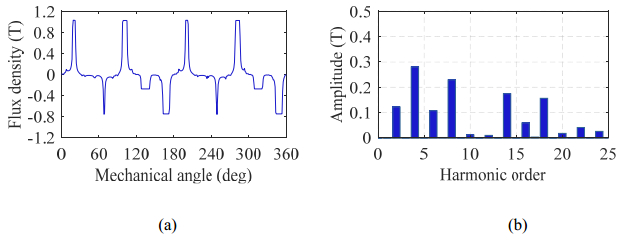
The air-gap flux density excited by armature winding is shown in Figure 3(a). To generate effective torque in the machine, the armature field must contain 4^th order harmonic, which interacts with the DC field to yield the torque. Due to the modulating rotor, the armature field also contains high frequencies harmonic field, which causes core losses.

---

2.4. Back EMF

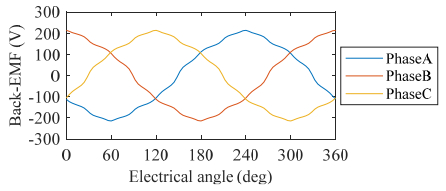
Although the structure of this machine is similar to the SRM, the control strategy and the power electronics are very different. This machine can use conventional three-phase half-bridges and the currents of it are sinusoidal. The back-EMF on the armature winding at 3000 rpm is shown in Figure 4 (with excited DC winding and DC current is equal to 10 A).

---

3. Analytical calculation

---

3.1. Maxwell stress tensor

According to the Maxwell stress tensor, the force on the rotor tooth contour can be described as (3.1) ^[13].

$F = \frac{l}{{2{\mu _0}}}\int_0^d {B_0^2dy}$

(3.1)

where, F is the force on the rotor tooth contour, µ₀ is the permeability of the air, d is the integral depth of the rotor tooth, l is the axial length of the rotor tooth, and B₀ is the flux density on the contour of the rotor tooth. This formula disregards the saturation of the iron.

It can be seen from (3.1) that in order to calculate the forces on the rotor teeth, the flux densities along the rotor teeth contours must be calculated firstly.

---

3.2. Schwarz-Christoffel mapping

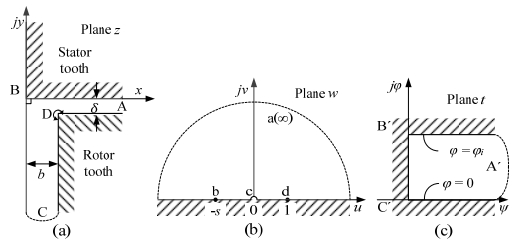
The following assumptions are made: The permeability of the iron core is infinitely large; rotor and the stator slots are infinitely deep and the teeth of the stator and rotor are infinitely wide. In order to eliminate the influence of adjacent teeth and slots, the slot opening of the stator and rotor are assumed to be infinitely wide. The equivalent model of a stator and a rotor tooth of the DCEFM are shown in Figure 5 ^[13,14,15].

Based on the Schwarz-Christoffel mapping, the relationship between Figure 5(a) and (b) can be expressed as (3.2), and the relationship between Figure 5(b) and (c) is expressed as (3.3) ^[13,14].

$dz = \frac{\delta }{\pi }\frac{1}{w}\sqrt {\frac{{w - 1}}{{w + s}}} dw$

(3.2)

$\frac{{dt}}{{dw}} = \frac{{{\varphi _i}}}{\pi }\sqrt {\frac{1}{{w(w + s)}}}$

(3.3)

where, s = (δ/b)², δ is the air-gap length and b is the distance between the rotor and stator tooth as shown in Figure 5(a).

The flux density and the force on the contour CD are expressed as (3.4) and (3.5), respectively ^[13,14].

${B_0} = {\mu _0}\left| {\frac{{dt}}{{dz}}} \right| = {\mu _0}\left| {\frac{{dt}}{{dw}}\frac{{dw}}{{dz}}} \right| = {\mu _0}\frac{{Ni}}{\delta }\left| {\sqrt {\frac{w}{{w - 1}}} } \right|$

(3.4)

$F = \frac{l}{{2{\mu _0}}}\int_{ - \delta }^{ - \infty } {B_0^2} dy = \frac{{{\mu _0}\varphi _i^2l}}{{2\delta \pi }}\left[ {\arcsin \left( {\frac{{s - 1}}{{s + 1}}} \right) - \frac{\pi }{2}} \right]$

(3.5)

where, φ_i is the magnetic potential on the contour BA, and the magnetic potential on the contour CDA is assumed to be 0.

---

3.3. Active belts

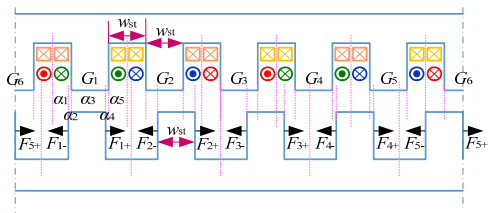
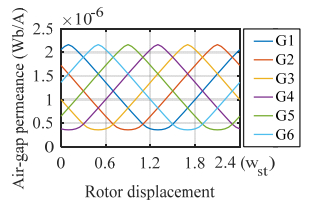
According to (3.5), if the magnetic potential φ_i on each stator tooth contour is known, the force on each rotor tooth can be easily calculated, and then the torque equation can be derived. By using the magnetic circuit method, the magnetic potential can be calculated. However, the air-gap permeance for the magnetic circuit is still unknown. Thus, a method named "active belts" is used to solve the air-gap permeance ^[16]. In this method, the air-gap region under each stator slot pitch can be divided into many belts. For example, the air-gap shown in Figure 6 is divided into 10 belts.

By using active belts method, the division of the air-gap under a module machine with 5-poles and 6-slots is shown in Figure 7. At this moment, it can be considered as rotor displacement α = 0. When the rotor displacement 0 ≤ α ≤ 0.1w_st, the width of each belt under G₁ region can be described as (3.6). The permeance of each belt can be expressed in (3.7). Then the air-gap permeance G₁ is equal to (3.8).

$\left\{ {\begin{array}{*{20}{c}} {{\alpha _1} = 0.4{w_{st}} + \alpha }\\ {{\alpha _2} = 0.1{w_{st}} - \alpha }\\ {{\alpha _3} = 0.9{w_{st}} + \alpha } \end{array}\begin{array}{*{20}{c}} {}&{\left\{ {\begin{array}{*{20}{l}} {{\alpha _4} = 0.1{w_{st}} - \alpha }\\ {{\alpha _5} = 0.5{w_{st}}} \end{array}} \right.} \end{array}} \right.$

(3.6)

$\begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{l}} {{G_{11}} = \frac{{{\mu _0}l}}{{2\beta }}\ln (1 + \frac{{2\beta {\alpha _1}}}{{\delta + \beta {\alpha _2}}})}\\ {{G_{12}} = \frac{{{\mu _0}l}}{\beta }\ln (1 + \frac{{\beta {\alpha _2}}}{\delta })}\\ {{G_{13}} = \frac{{{\mu _0}l{\alpha _3}}}{\delta }} \end{array}} \right.}&{\begin{array}{*{20}{c}} {}&{\left\{ {\begin{array}{*{20}{l}} {{G_{14}} = \frac{{{\mu _0}l}}{\beta }\ln (1 + \frac{{\beta {\alpha _4}}}{\delta })}\\ {{G_{15}} = \frac{{{\mu _0}l}}{{2\beta }}\ln (1 + \frac{{2\beta {\alpha _5}}}{{\delta + \beta {\alpha _4}}})} \end{array}} \right.} \end{array}} \end{array}$

(3.7)

${G_1} = {G_{11}} + {G_{12}} + {G_{13}} + {G_{14}} + {G_{15}}$

(3.8)

where, β is a coefficient. When w_st/δ ≤ 10, β = 1; when w_st/δ > 10, β = 1.1 ^[16].

By following this method, the air-gap permeance of each stator slot pitch region along with the rotor rotation can be calculated and drawn as shown in Figure 8.

---

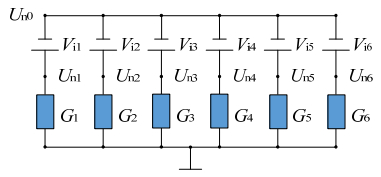
3.4. Magnetic circuit

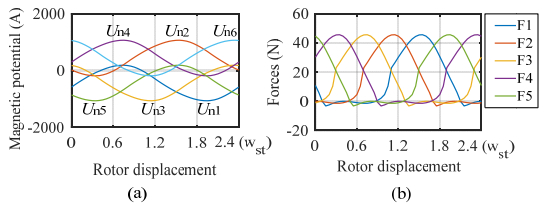
The equivalent magnetic circuit of the module machine in Figure 7 is shown in Figure 9. In the circuit, U_n1 to U_n6 are the magnetic potential of each stator tooth contour, respectively. V_i1 to V_i6 are the MMF of the coil on each tooth. They can be expressed as given in (3.9).

$\left\{ {\begin{array}{*{20}{l}} {{V_{{\rm{i}}1}} = - {N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{i_B}}\\ {{V_{{\rm{i2}}}} = {N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{i_C}}\\ {{V_{{\rm{i3}}}} = - {N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{i_A}} \end{array}\begin{array}{*{20}{c}} {}&{} \end{array}} \right.\left\{ {\begin{array}{*{20}{l}} {{V_{{\rm{i4}}}} = {N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{i_B}}\\ {{V_{{\rm{i5}}}} = - {N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{i_C}}\\ {{V_{{\rm{i6}}}} = {N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{i_A}} \end{array}} \right.$

(3.9)

where, N_dc and N_ac are the turns number of the DC winding and armature winding on each tooth, respectively; i_dc is the DC current, i_A, i_B and i_C are the three-phase AC current, and they can be written as (3.10).

$\left\{ {\begin{array}{*{20}{l}} {{i_A}(\alpha ) = {I_{{\rm{sp}}}}\sqrt 2 \sin (\frac{{\alpha + 0.7{w_{{\rm{st}}}}}}{{2.4{w_{{\rm{st}}}}}}2\pi )}\\ {{i_B}(\alpha ) = {I_{{\rm{sp}}}}\sqrt 2 \sin (\frac{{\alpha + 0.7{w_{{\rm{st}}}}}}{{2.4{w_{{\rm{st}}}}}}2\pi - \frac{{2\pi }}{3})}\\ {{i_C}(\alpha ) = {I_{{\rm{sp}}}}\sqrt 2 \sin (\frac{{\alpha + 0.7{w_{{\rm{st}}}}}}{{2.4{w_{{\rm{st}}}}}}2\pi + \frac{{2\pi }}{3})} \end{array}} \right.$

(3.10)

where, I_sp is the phase RMS current.

As a result, the magnetic potential U_n1 to U_n6 can be expressed in (3.11).

$\begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{c}} {{U_{{\rm{n}}1}} = {U_{{\rm{n0}}}} + {V_{{\rm{i}}1}}}\\ {{U_{{\rm{n4}}}} = {U_{{\rm{n0}}}} + {V_{{\rm{i4}}}}} \end{array}} \right.}&{\left\{ {\begin{array}{*{20}{c}} {{U_{{\rm{n2}}}} = {U_{{\rm{n0}}}} + {V_{{\rm{i2}}}}}\\ {{U_{{\rm{n5}}}} = {U_{{\rm{n0}}}} + {V_{{\rm{i5}}}}} \end{array}} \right.}&{\left\{ {\begin{array}{*{20}{c}} {{U_{{\rm{n3}}}} = {U_{{\rm{n0}}}} + {V_{{\rm{i3}}}}}\\ {{U_{{\rm{n6}}}} = {U_{{\rm{n0}}}} + {V_{{\rm{i6}}}}} \end{array}} \right.} \end{array}$

(3.11)

With

${U_{{\rm{n}}0}} = - \frac{{{G_1}{V_{{\rm{i}}1}} + {G_{\rm{2}}}{V_{{\rm{i2}}}} + {G_{\rm{3}}}{V_{{\rm{i3}}}} + {G_{\rm{4}}}{V_{{\rm{i4}}}} + {G_{\rm{5}}}{V_{{\rm{i5}}}} + {G_6}{V_{{\rm{i6}}}}}}{{{G_1} + {G_{\rm{2}}} + {G_{\rm{3}}} + {G_{\rm{4}}} + {G_{\rm{5}}} + {G_6}}} \approx 0$

(3.12)

---

3.5. Force and torque equations

By substituting (3.11) and (3.12) to (3.5), the forces variation with the rotor rotation can be expressed. For example, when the rotor displacement is: 0 ≤ α ≤ 0.1w_st, the forces on the rotor tooth 1 shown in Figure 7 can be expressed as (3.13) and (3.14).

${F_{1 + }} = \frac{{{\mu _0}U_{{\rm{n}}1}^2l}}{{2\delta \pi }}\left[ {\arcsin \left( {\frac{{s - 1}}{{s + 1}}} \right) - \frac{\pi }{2}} \right]$

(3.13)

${F_{1 - }} = \frac{{{\mu _0}U_{{\rm{n6}}}^2l}}{{2{\delta _{11}}\pi }}\left[ {\arcsin \left( {\frac{{{s_{11}} - 1}}{{{s_{11}} + 1}}} \right) - \frac{\pi }{2}} \right]$

(3.14)

where, ${\delta _{11}} = \sqrt {{\delta ^{\rm{2}}}{\rm{ + (}}\alpha {\rm{ + 0}}{\rm{.9}}{w_{st}}{{\rm{)}}^2}}$, ${s_{11}} = {\left( {{\delta _{11}}/{w_{{\rm{st}}}}} \right)^2}$ and $s = {\left( {\delta /0.1{w_{{\rm{st}}}} - \alpha } \right)^2}$.

When the rotor displacement is: 0.1w_st ≤ α ≤ 1.1w_st, the forces on the rotor tooth 1 shown in Figure 7 can be obtained as (3.15) and (3.16).

${F_{1 + }} = \frac{{{\mu _0}U_{{\rm{n2}}}^2l}}{{2{\delta _{12}}\pi }}\left[ {\arcsin \left( {\frac{{{s_{12}} - 1}}{{{s_{12}} + 1}}} \right) - \frac{\pi }{2}} \right]$

(3.15)

${F_{1 - }} = \frac{{{\mu _0}U_{{\rm{n1}}}^2l}}{{2\delta \pi }}\left[ {\arcsin \left( {\frac{{s - 1}}{{s + 1}}} \right) - \frac{\pi }{2}} \right]$

(3.16)

where, ${\delta _{12}} = \sqrt {{\delta ^{\rm{2}}}{\rm{ + (1}}{\rm{.1}}{w_{st}} -\alpha {{\rm{)}}^2}}$ and ${s_{12}} = {\left( {{\delta _{12}}/{w_{{\rm{st}}}}} \right)^2}$.

By analogy, all the forces can be expressed in the similar form. Because the force on a rotor tooth can be considered to be on the top of it, the torque equation of the machine can be expressed as (3.17).

$T = 2({F_{1 + }} - {F_{1 - }} + {F_{2 + }} - {F_{2 - }} + {F_{3 + }} - {F_{3 - }} + {F_{4 + }} - {F_{4 - }} + {F_{5 + }} - {F_{5 - }})R$

(3.17)

where, R is the radius of the rotor.

---

4. Verification by finite element analysis

To verify the analyses above, FEA method is used. The main parameters and size of the FEA model are listed in Table 1.

---

4.1. DC excitation only

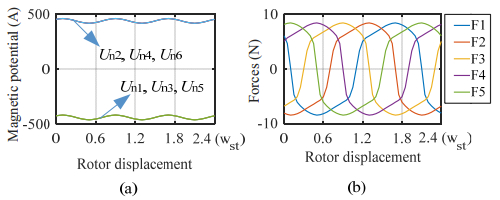
In the analyzed machine, N_dc is equal to N_ac. When there is only DC excitation on the stator and i_dc = 10 A, based on (3.11) the magnetic potential U_n1 to U_n6 are illustrated in Figure 10(a). The forces variation with the rotor rotation is shown in Figure 10(b).

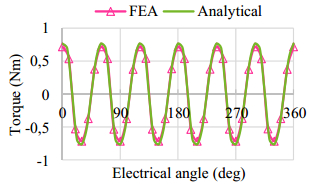
To verify the results, a FEA model was built. The comparison between FEA and analytical result is shown in Figure 11. Obviously, the analytical method has a high accuracy. If there is only DC excitation, the magnetic potential of the stator teeth contours is almost flat along with the rotor rotation. Under this circumstance, the effective torque is equal to 0.

---

4.2. Armature current only

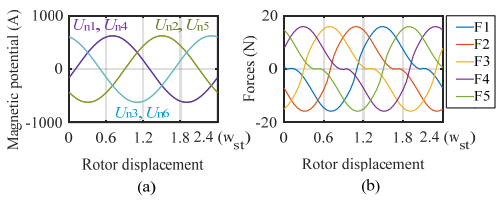
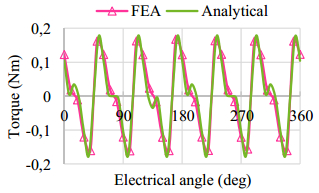
When the armature winding is excited with three-phase sinusoidal current and I_sp = 10 A, while the DC current is 0, according to the principle of the flux-modulated machine, the effective torque is also 0. The magnetic potential on the stator teeth contours is shown in Figure 12(a). The forces variation and the torque comparison are illustrated in Figure 12(b) and Figure 13, respectively.

---

4.3. Optimal currents

To maximize the torque, both DC and AC windings on each tooth must have the same current density. If the effective slot area is A_s, the areas for DC winding A_sdc and AC winding A_sac have a relationship as expressed in (4.1).

$\left\{ {\begin{array}{*{20}{c}} {{A_{{\rm{sdc}}}} = \frac{{{N_{dc}}{i_{{\rm{dc}}}}}}{{{N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{I_{{\rm{sp}}}}}}{A_{\rm{s}}}}\\ {{A_{{\rm{sac}}}} = \frac{{{N_{ac}}{I_{{\rm{sp}}}}}}{{{N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{I_{{\rm{sp}}}}}}{A_{\rm{s}}}} \end{array}} \right.$

(4.1)

Then the resistances of DC and AC windings on each tooth are equal to (4.2).

$\left\{ {\begin{array}{*{20}{c}} {{R_{{\rm{dc}}}} = 2k\frac{{N_{{\rm{dc}}}^2\rho l}}{{{A_{{\rm{sdc}}}}}} = 2k\frac{{{N_{{\rm{dc}}}}\rho l}}{{{i_{{\rm{dc}}}}{A_{\rm{s}}}}}({N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{I_{{\rm{sp}}}})}\\ {{R_{{\rm{ac}}}} = 2k\frac{{N_{{\rm{ac}}}^2\rho l}}{{{A_{{\rm{sac}}}}}} = 2k\frac{{{N_{{\rm{ac}}}}\rho l}}{{{I_{{\rm{sp}}}}{A_{\rm{s}}}}}({N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{I_{{\rm{sp}}}})} \end{array}} \right.$

(4.2)

where, ρ is the resistivity of copper, k is the coefficient considering the end-winding. As both windings are single-tooth concentrated, they have the same coefficient.

The copper losses of each tooth P_copper are equal to (4.3).

${P_{{\rm{copper}}}} = I_{{\rm{sp}}}^2{R_{{\rm{ac}}}} + i_{{\rm{dc}}}^2{R_{{\rm{dc}}}} = \frac{{2k\rho l}}{{{A_{\rm{s}}}}}{({N_{{\rm{dc}}}}{i_{{\rm{dc}}}} + {N_{{\rm{ac}}}}{I_{{\rm{sp}}}})^2}$

(4.3)

It can be seen from (4.3) that for a certain stator, the slot area and the effective length of the stator are constant. If the MMFs of the two windings on each tooth are constant, the copper losses is constant.

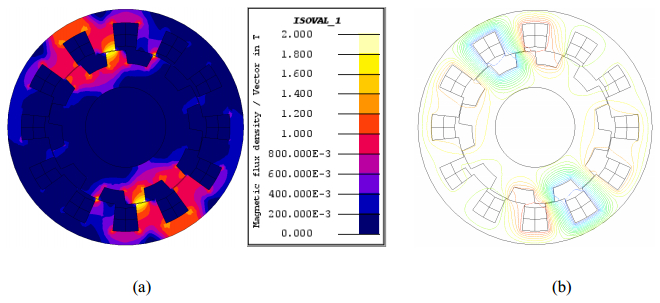
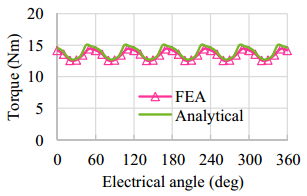
When the MMFs of both the DC excitation and the AC excitation on each stator tooth are equal: i_dc = 10 A and I_sp = 10 A, the magnetic flux density and flux line of the motor is shown in Figure 14. Figure 14 shows that under load condition, the flux densities of each tooth are much different. Because of the iron saturation, this type of motor cannot reach a very high torque density. The magnetic potential, forces and torques comparison are presented from Figure 15 and 16, respectively. By comparing Figure 10, 12 and 15, it can be found that in order to generate highest effective torque, at any moment all the forces need to be greater than or equal to 0. For example, when the rotor displacement is: 0 ≤ α ≤ 0.6w_st, the force F₂ is negative and is mainly generated by the square of U_n2. To generate zero force F₂ during this time, U_n2 is need to be 0. According to (3.9), (3.10) and (3.11) it can be known that the armature AC current (RMS) is required to be approximately equal to the DC current.

The analytical results compared with FEA results are shown in Table 2. Since the analytical method does not consider the non-linear of the iron and the fringe influence, there are small difference between analytical and FEA results. However, the analytical method is sufficient to quickly determine the slot area assignment to the two windings.

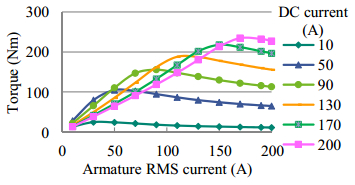
To confirm the analytical conclusion, FEA method is used. The FEA torque variation with DC and AC currents is shown in Figure 17. At constant DC excitation and increasing AC current, the torque firstly increases to a maximum and then gradually falls off again. The reason is if the MMFs of the DC and AC excitation are unequal, the absolute value of the minimum magnetic potential will be larger than 0, and this can result in negative forces on the rotor. As seen in (3.17), the effective torque may decrease. Because of the saturation of the iron steel, the highest torque occurs when the MMFs of the two sets of windings are approximately equal instead of the exact equal point.

Based on this analysis, to obtain the highest torque at the lowest MMFs of the windings, the MMFs of the two sets of windings need to be approximately equal.

---

5. Conclusion

A detail analysis of the torque calculation of a DC-excited flux-modulated machine has been performed. By using the FEA method, the validity of the analytical result was validated. The analysis shows that in order to obtain the highest torque at the admissible copper losses, the MMFs of the two sets of stator windings need to be approximately equal. Since the three-phase winding is excited with sinusoidal current, the armature AC current (RMS) is required to be approximately equal to the DC current. In other words, the slot space is required to be equally assigned to the two windings. The analytical methods and progress described in this paper can also be referred to analyze other machines with salient stators and rotors such as variable flux reluctance machine, field excited flux-switching machine.

---

Acknowledgments

This work was supported in part by the China Scholarship Council under Grant 201608080024.

---

Conflict of Interest

The authors declare no conflict of interests in this paper.

---