Finite-time stability of elastoplastic lattice spring systems under simultaneous displacement-controlled and stress-controlled loadings

1.   Introduction

Finite-time stability in differential equations with nonsmooth right-hand-sides is addressed in Bernuau et al. ^[4], Bhat-Bernstein ^[5], Oza et al. ^[16], Sanchez et al. ^[19] over the Lyapunov function $V$ that solves

where $\varepsilon > 0$ and $x$ is a solution. Adly et al. ^[1] extended the Lyapunov function approach to differential inclusions with a subdifferential of a convex function $\Phi:\mathbb{R}\to\mathbb{R}^n$ (given by a cone, see Rockafellar ^[18])

and derived an inequality of form (1.1) (and corresponding finite-time stability) from a cone-type condition

where $B_\varepsilon(0)$ is the ball of $\mathbb{R}^n$ of radius $\varepsilon$ centered at 0.

More recently, a significant interest in the study of finite-time stability of differential inclusions has been due to new applications in elastoplasticity (see e.g., Gudoshnikov et al. ^[8]). We remind the reader that according to the pioneering work by Moreau ^[15] (see also Gudoshnikov and Makarenkov ^[9]), the stresses in a network of $m$ elastoplastic springs with time-varying displacement-controlled loadings are governed by

where $A$ is a positive diagonal $m\times m$-matrix, and $N_{C(t)}^A(y)$ is a normal cone to the set

at a point $y$, with appropriate $d, c_j^-,$ $c_j^+,$ $g(t)$, $h(t)$ that define mechanical parameters of the network of elastoplastic springs, displacement-controlled loadings and stress-controlled loadings (to be discussed in Section 4 in details), and where $e_j\in\mathbb{R}^m$ is the vector with 1 in the $j$-th component and zeros elsewhere. The solutions $y(t)$ of differential inclusion (1.4) never escape from $C(t)$ (i.e., $y(t)$ is swept by $C(t)$) for which reason (1.4) is called sweeping process. Spring $j$ undergoes plastic deformation when the inequality $c_j^- < \left < e_j, Ay(t)-Ah(t)+Ag(t)\right > < c_j^+$ is violated. Therefore, knowledge of the evolution of $y(t)$ allows to make conclusions about the regions of plastic deformation (that lead to low-cycle fatigue or incremental failure, see Yu [20, §4.6]).

Krejci ^[13] proved that if $C(t)$ is $T$-periodic then any solution $y(t)$ of (1.4) always converges to a $T$-periodic solution. Colombo et al. ^[7] proved the existence of the attractor in the case when $C(t)$ is a parallelepiped (of potentially changing dimensions). Extending their earlier two-dimensional version ^[8], Gudoshnikov et al. ^[11] offered a rule to compute the $T$-periodic attractor of (1.4) in the case where $h(t)\equiv 0$, i.e., when just displacement-controlled loading is present (meaning that the shape of the moving polytop doesn't change). Details of geometry of the attractor of (1.4) are addressed in Gudoshnikov et al. ^[12]. The goal of the present work is to investigate finite-time convergence of (1.4) in the case of displacement-controlled loading and stress-controlled loading present simultaneously.

As also mentioned in Gudoshnikov et al. ^[11], predicting the behavior of solutions of sweeping process (1.4) within a guaranteed time is of crucial importance for materials science. Current methods of computing the asymptotic response of networks of elastoplastic springs (see e.g., Boudy et al. ^[6], Zouain-SantAnna ^[21]) run the numeric routine until the difference between the responses corresponding to two successive cycles of loading get smaller than a prescribed tolerance (without any estimate as for how soon such a desired accuracy will be reached).

The approach of the present paper is a suitable generalization of Gudoshnikov et al. ^[11] (pioneered by Adly et al. ^[1]). Specifically, let $y_*(t)$ be a vertex of $C(t)$. We prove that if $y_*(t)$ can be expressed as

where

and if

where $B_ \varepsilon^A(0)$ is a ball in the norm induced by the scalar product (1.4), then, for any solution $y(t)$ of (1.4), the function

satisfies the estimate (1.1) on $[0, \tau_d]$ for a suitable Lyapunov function $V$ that measures the distance from $x(t)$ to $y_*.$ In the earlier work ^[11], the difference $C(t)-c(t)$ is independent of $t$ due to the lack of the stress-controlled loading. Accordingly, ^[11] assumes

instead of (1.9), where $F$ is however allowed to be a face, not just a vertex of $C$. The complication we encounter when adding a stress-controlled loading is that $C(t)-c(t)$ is no longer constant, but we discover that, for applications to lattice spring models, $y_*(t)-c(t)$ can still be assumed to be constant thanks to an appropriate construction of $c(t)$ (Lemma 4.2), which is the main result of the paper.

The paper is organized as follows: In Section 2, we adjust the proof of [11, Theorem 3.1] for the case where assumption (1.11) is replaced by (1.9). The corresponding theorem (Theorem 2.1) provides an estimate for the time it takes for any solution of (1.4) to reach $y_*(t)$. A corollary of Theorem 2.1 for the case where $c(t)$ is $T$-periodic is given in Section 3. Section 4 links the entries of Theorem 2.1 to parameters of a lattice spring model, which allows to specify the structure of $C(t)$ and $c(t)$ and to prove the main result of the paper (Lemma 4.2) about the existence of representation (1.6)-(1.7) for the case where sweeping process (1.4) comes as a model of an elastoplastic lattice spring model (as introduced in Moreau ^[15] and adapted to lattice spring models in Gudoshnikov et al. ^[9]). Section 5 combines Sections 2 and 4 in order to provide a step-by-step guide for computation of the entries of Theorem 2.1 in terms of mechanical parameters of elastoplastic lattice spring models. Section 6 follows the guide of Section 5 in order to investigate several instructional cases of a benchmark model of 5 springs on 4 nodes (Rachinskiy ^[17], Gudoshnikov et al. ^[11]) that allows us to clarify (Section 6.4) the role of the stress-controlled loading in the diversity of possible attractors of sweeping process (1.4) and, accordingly, in the diversity of different destributions of plastic deformations in elastoplastic lattice spring models. Conclusions section concludes the paper.

2.   A sufficient condition for finite-time stability of sweeping process with a moving constraint of changing shape

We remind the reader that the normal cone $N_C^A(y)$ to the set $C$ at a point $y\in C$ in a scalar product space $V$ with the scalar product

is defined as (see Bauschke and Combettes [3, §6.4])

In what follows (see Bauschke and Combettes [3, §3.2])

Definition 2.1. (see e.g., ^[14]) A set-valued function $C(t)$ (acting from $\mathbb{R}$ to a vector space $V\subset\mathbb{R}^m$) is called Lipschitz continuous, if, for any $T > 0$, there exists $L > 0$ such that

where $d_H(C_1, C_2)$ is Hausdorff distance between closed bounded sets $C_1, C_2\in\mathbb{R}^m.$

We remind the reader that solution of an initial-value problem for sweeping processes (1.4) with Lipschitz continuous moving constraint $C(t)$ exists, unique and features continuous dependence on initial conditions (see e.g., Kunze and Monteiro Marques [14, Theorems 1–3]).

The statement of the following theorem and its proof follow the corresponding statement and proof of [11, Theorem 3.1], but we still rewrite the proof for completeness because [11, Theorem 3.1] uses condition (1.9) with $C(t)-c(t)$ replaced by $C$, i.e., $C(t)-c(t)$ is assumed totally constant in ^[11]. It turns out that replacing $C$ by $C(t)-c(t)$ requires almost no changes in the proof.

Theorem 2.1. Let $V$ be a $d$-dimensional linear subspace of $\mathbb{R}^m$ with scalar product (2.1), $t\mapsto C(t)$ be a Lipschitz continuous multi-valued function with closed convex values, and $c:[0, \infty)\to V$ be Lipschitz continuous, and

Assume that there exists an $\varepsilon > 0$ such that condition (1.9) holds on an interval $[0, \tau_d]$ with

Then, every solution $y$ of (1.4) with the initial condition $y(0)\in C(0)$ satisfies $y(\tau_d) = y_*+c(\tau_d).$

The proof of Theorem 2.1 follows the lines of ^[11]. The idea is based on observing that

is a Lyapunov function for the sweeping process

which is related to (1.4) through the change of the variables (1.10). Accordingly, $V(x(t_1)) = 0$ will imply $y(t_1) = y_*+c(t_1).$ For completeness, the proof of Theorem 2.1 is included in Appendix.

The supremum in (2.4) of Theorem 2.1 can be estimated using the following proposition (which extends [9, Proposition 3.14]).

Proposition 2.1. For any $y\in C(t)-c(t)$, it holds that

Proof. We have

which can be estimated from above by $\|A^{-1}c^+-A^{-1}c^-\|^A$ according to [9, Proposition 3.14]. The proof of the proposition is complete. □

3.   The existence of a globally one-period stable periodic attractor

Corollary 3.1. If, in the settings of Theorem 2.1, we additionally have that $c(t)$ is $T$-periodic with $T\ge\tau_d$, then $y_*$ is a globally one-period stable $T$-periodic solution of (1.4).

Corollary 3.1 follows by observing that

4.   Application to a general elastoplastic system with displacement-controlled loading and stress-controlled loading present simultaneously

We remind the reader that according to Moreau ^[15] a network of $m$ elastoplastic springs on $n$ nodes with 1 displacement-controlled loading and subjected to a stress-controlled loading at all nodes is fully defined by an $m\times n$ kinematic matrix $D$ of the topology of the network, $m\times m$ matrix of stiffnesses (Hooke's coefficients) $A = {\rm diag}(a_1, ..., a_m)$, an $m$-dimensional hyperrectangle $C = \prod_{j = 1}^m [c_j^-, c_j^+]$ of the achievable stresses of springs (beyond which plastic deformation begins), a vector $R\in\mathbb{R}^m$ of the location of the displacement-controlled loading, a scalar function $l(t)$ that defines the magnitude of the displacement-controlled loading, and a function $\bar h(t)\in \mathbb{R}^m$ such that

defines the forces applied at the $n$ nodes of the network. When all springs are connected (form a connected graph), we have (see Bapat [2, Lemma 2.2])

We furthermore assume that

To formulate the Moreau sweeping process corresponding to the elastoplastic system $(D, A, C, R, l(t), f(t))$, we first follow the 3 steps described in Gudoshnikov and Makarenkov [10, §5]:

$(1)$ Find an $n\times (n-2)-$matrix $M$ of ${\rm rank}(DM) = n-2$ that solves $R^T DM = 0$ and use $M$ to introduce $U_{basis} = DM.$

$(2)$ Find a matrix $V_{basis}$ of $m-n+2$ linearly independent column vectors of $\mathbb{R}^m$ that solves

$(3)$ Find an $m\times(m-n+1)-$matrix $D^\perp$ that solves $(D^\perp)^T D = 0_{(m-n+1)\times n}$ and such that

With the new matrices introduced, the moving constraint $C(t)$ of sweeping process (1.4) corresponding to the elastoplastic system $(D, A, C, R, l(t), f(t))$ is given by

where, for each $j\in\overline{1, m},$

with $e_j$ being the basis vectors of $\mathbb{R}^m$, i.e., $e_j = (\underbrace{0, ..., 0}_{j-1}, 1, 0, ..., 0)^T,$ and where $h(t)$ is found from $\bar h(t)$ according to a formula given by the following proposition (^[11] focused on $h(t) = 0$ and didn't derive explicit formula for $h$). The existence of $W^{-1}$ is proved in Gudoshnikov et al. ^[11].

Lemma 4.1. If the stress-controlled loading $f(t)$ verifies the representation (4.1), then the corresponding function $h(t)$ in (4.6) is given by

or, equivalently,

In particular, the $(n-2)\times(n-2)$-matrix $(U_{basis})^TAU_{basis}$ is invertible.

Proof. First of all, we observe that the $(n-2)\times (n-2)$ matrix $(U_{basis})^TAU_{basis}$ is invertible. Indeed, if $(U_{basis})^TAU_{basis}x = 0$, then $(U_{basis}\ x)^TA(U_{basis} \ x) = 0$. But since the stiffness matrix $A$ is positive definite, then $U_{basis}\ x = 0$. This means that $\text{Ker} (U_{basis}) = \text{Ker} ((U_{basis})^TAU_{basis})$ and hence, $\text{Rank}(U_{basis}) = \text{Rank} ((U_{basis})^TAU_{basis}) = n-2$.

According to [9, formula (16)],

where $P_U$ is a linear (orthogonal in sense of scalar product (2.1)) projection map on $U$ along $V$. To compute $P_U$ we decompose $x$ as

and compute $u\in\mathbb{R}^{\dim U}$ from (4.10). Applying $(U_{basis})^TA$ to both sides of (4.10), using (4.4), and solving for $u$, we get

which implies

The statement of the proposition is obtained by substituting (4.11) to (4.9). The proof of the proposition is complete. □

Using Lemma 4.1 and [9, Theorem 3.1], the solution $y(t)$ of sweeping process (1.4) is related to the vector $s(t) = (s_1(t), ..., s_m(t))^T$ of the stresses of springs via

provided that $f(t)$ admits representation (4.1) or, equivalently (see [9, Remark 3.5]),

In contrast with Gudoshnikov et al. ^[11], the function $c(t)$, that we need to verify condition (1.9) for, depends on the choice of the vertex $y_*$, i.e., on the choice of $I_0$ in (1.7).

Definition 4.1. A set of indices $I_0\subset\{-1, 1\}\times\overline{1, m}$ with $|I_0| = d$ will be called non-singular, if the matrix

is invertible.

Remark 4.1. [11, formula (7.9)] If $I_0\subset\{-1, 1\}\times\overline{1, m}$ with $|I_0| = d$ is non-singular then $\bigcap\limits_{(\alpha, j)\in I_0} \overline{\overline{L}}(\alpha, j)$ is a singleton and $y_*$ in (1.7) is well defined.

Lemma 4.2. Let $I_0\subset\{-1, 1\}\times\overline{1, m}$ be non-singular and let $y_*$ be given by (1.7). Then, $y_*(t)$ given by (1.6) belongs to $C(t)$, if $c(t)$ is defined by

and if the feasibility condition

holds.

Remark 4.2. Equation (4.16) is equivalent to

Proof of Lemma 4.2. Introduce

Since $C_{*}(t) \subset C(t)$, the problem of finding $y_{*}(t)$ with (1.6)-(1.7) reduces to finding $y_{*}(t)$ that satisfies

By (4.20), $C_{0}(t)$ can be rewritten in the form

To solve (4.20) we rewrite (4.20) as

Observe that if $y \in \{ y\in V : F(y+k) = 0 \}$ for some $k\in V$, then letting $x = y+k$, we have $x \in V$ and $F(x) = 0$, meaning that $y$ can be represented as $y = x-k\in \{x\in V:F(x) = 0\}-k$.

Therefore, with formula (4.23), the expression for $C_{0}(t)$ can be written as

where

and where $c(t)$ is given by (4.15). Therefore, $C_{0}(t)$ is a singleton given by

where $y_*(t)$ is defined by (1.6)-(1.7), i.e., (4.21) is established.

The inclusion (4.22) follows from (4.19). The proof of the lemma is complete.□

To understand what the conclusion

of Theorem 2.1 says about the dynamics of the elastoplastic system $(D, A, C, R, l(t), f(t))$, recall that by [9, Theorem 3.1 and §3.2],

or, by combining with (4.24) and (4.15),

i.e.,

5.   A step-by-step guide for analytic computations

The following lemma from Rockafellar-Wets [18, Theorem 6.46] (see also [11, Lemma 5.1]) gives a computational recipe to check condition (1.9). Recall that ${\rm cone}\{\xi_1, ..., \xi_K\}$ stays for the cone formed by vectors $\xi_1, ..., \xi_K.$

Lemma 5.1. Let $V$ be a $d$-dimensional linear subspace of $\mathbb{R}^m$ with scalar product (2.1). Consider

where $\widetilde n_k\in V$, $c_k\in\mathbb{R},$ $K\in\mathbb{N}.$ If $\widetilde I(y) = \left\{k\in\overline{1, K}:\left < \widetilde n_k, Ay\right > = c_k\right\}$, then

Corollary 5.1. If $y_*(t)\in C(t)$ satisfies (1.6)-(1.7) for suitable $c(t)$ and $y_*$, then

where $n_j\in V$, $j\in\overline{1, \dim V}$ are the vectors that solve the equality

Proof. First note that

To apply Lemma 5.1, we rewrite (4.6) as follows:

Therefore, we want to compute $\tilde I(y_*+c(t))$ given by

By successively using (4.19), (4.20), and (1.7) the above equality rewrites as

which provides the required statetment. The proof of the Corollary is complete. □

Using (5.2), condition (1.9) can be rewritten as

Therefore, when $c'(t)$ is $T$-periodic, the required $\varepsilon > 0$ exists, if

where ${\rm rb}(B)$ denotes the relative boundary of a set $B$ of a linear subspace $V\subset\mathbb{R}^m.$ The irreducibility condition can be further rewritten as

In other words, (5.5) says that $I_0$ is irreducible, if any $\tilde I_0\subset I_0$ with $\tilde I_0\not = I_0$ makes

According to [10, formula (27)], $n_j$ can be taken as

and substitution of (5.2), (4.7), and (4.15) to (5.4) gives

or

Based on Lemma 4.2 and formula (5.8) we can now split verification of conditions of Theorem 2.1 into the following steps.

Step 1. Fix appropriate indexes $I_0$ (springs that will reach plastic deformation). Spot a non-singular $I_0$ that is admissible and irreducible (i.e., solves (5.8) and such that $\tilde I_0$ doesn't satisfy (5.8) for any $\tilde I_0\subset I_0,$ $\tilde I_0\not = I_0$).

Combination of Theorem 2.1 and Lemma 4.2 lead to the following qualitative description of the asymptotic behavior of elastoplastic system $(D, A, C, R, l(t), f(t))$ and of the associated sweeping process (1.4). Here the quantities $y_*$, $c(\cdot),$ $I_0$, $\Delta_{I_0}$, $h(\cdot)$ are those referred to in the statement of Lemma 4.2.

Proposition 5.1. (Conclusion of Step 1). If

1) both $l'(t)$ and $f'(t)$ are constant,

2) $f(t)$ satisfies the static balance condition (4.13),

3) there exists a non-singular and irreducible $I_0$ satisfying (5.8),

then there exist $c_j^\alpha$, $(\alpha, j)\not\in I_0$, such that the solution $y$ of sweeping process (1.4) with initial condition $y(0)\in C(0)$ satisfies

for an appropriate $\tau_d > 0$, and the stress vector $s(t)$ of the elastoplastic system $(D, A, C, R, l(t), f(t))$ satisfies

Indeed, conditions of Proposition 5.1 imply that condition (1.9) of Theorem 2.1 is satisfied on $[0, \tau_d]$, where

with suitable $\varepsilon > 0$, which gives $\tau_d$ used in the statement. Relation (5.11) follows from (5.10) by Remark 4.2.

Remark 5.1. Relation (5.11) means that springs with indices $I_0$ get to plastic mode (i.e., capable to deform plastically) by the time $\tau_d.$

One has to proceed to Steps 2 and 3 to come up with an explicit version of Proposition 5.1 where conditions for $c_i^\alpha$ and formulas for $\varepsilon$ and $\tau_d$ are given in closed form.

Step 2. Compute $y_*$ and impose the feasibility condition. By [11, formula (7.9)] the formula for $y_*$ of (1.7) reads as

Substitution of $y_*$, $\Delta_{I_0}$, $h(t)$ as defined by (5.13), (4.16), (4.8) to (4.19) yields feasibility condition in terms of mechanical parameters of the lattice-spring model.

Note, function $f(t)$ must additionally satisfy (4.13) for formula (4.8) to be valid.

Step 3. Compute $\varepsilon_0$. This step is devoted to finding $\varepsilon$ for which assumption (5.3) holds. Assumption (5.3) requires computation of the distance from $-c'(t)$ to the boundary of cone ${\rm cone}\{\alpha n_j:(\alpha, j)\in I_0\}$. The required boundary is $\partial {\rm cone}\left\{\alpha n_j:(\alpha, j)\in I_0\right\}$.

Using formula (5.2), we compute

According to [11, formula (7.18)] and [11, Lemma 7.7], the quantity

computes as (see [11, formula (7.20)])

where

Choose $\varepsilon_0 > 0$ such that $\varepsilon_0\le \bar \varepsilon_0(t)$ for all $t\in[0, \tau_d].$ Theorem 2.1, Proposition 2.1, and Lemma 4.2 then lead to the following conclusion.

Proposition 5.2. (Conclusion of Steps 1–3). If assumptions 1)–3) of Proposition 5.1 hold, then condition (1.9) holds on $[0, \tau_d]$ for any $\tau_d\ge \tau$, where

If, additionally,

4) condition (4.19) holds on some $[0, \tau_d]$ with $\tau_d\ge\tau$,

then conclusions (5.9)–(5.11) of Proposition 5.1 hold with $\tau_d$ replaced by $t$, $t\in[\tau, \tau_d].$

6.   A benchmark example

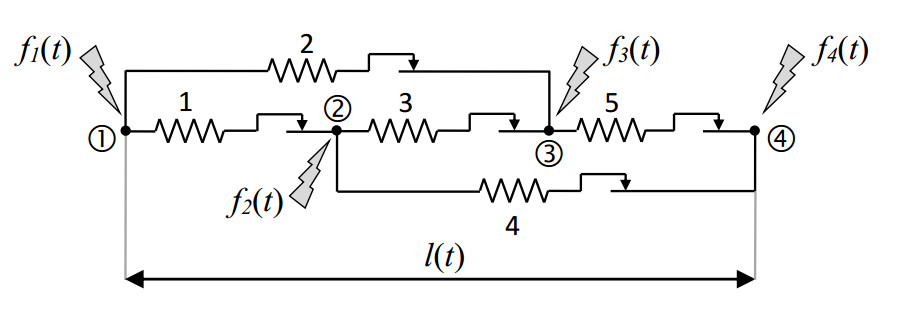
The focus of the present section is on the elastoplastic model shown in Figure 1 (earlier introduced in Rachinskiy ^[17]), which allows to fully illustrate the practical implementation of Theorem 2.1.

According to Gudoshnikov et al. ^[11], the elastoplastic system of Figure 1 leads to the following expressions for $D$ and $R$

We now follow Gudoshnikov et al. ^[11] to formulate the quantities used in Section 5.

First of all, based on [10, formula (17)], we compute the dimension of sweeping process (1.4) as

According to [10, §5,Step 1], we then look for an $4\times 2$ matrix $M$ such that $R^TDM = 0$ and such that the matrix $DM$ is full rank. Such a matrix $M$ can be taken as

The next step is determining $V_{basis}$ which consists of $d = 3$ linearly independent columns of $\mathbb{R}^m = \mathbb{R}^5$ and solves $(DM)^TA V_{basis} = 0$. Such a $V_{basis}$ can be takes as

Finally, a $5\times 2$ full rank matrix $D^\perp$ satisfying $(D^\perp)^TD = 0$ can be taken as

Formula (5.6) then yields

with

In what follows, we consider

where $l_0, l_1 > 0$, $b_1, b_2, b_3, b_4, d_1, d_2, d_3, d_4\in\mathbb{R}$, which leads to

with $k$ given by (6.3).

We now illustrate computations of Steps 1–3 of Section 5 and statements of Propositions 5.1 and 5.2 through three instructive cases of $I_0.$

6.1.   Case $I_0 = \{ (+, 2), (+, 3), (+, 4) \}$

This case was addressed in ^[11] without stress-controlled loading.

Step 1. Computation of matrix $\Delta_{I_0}$ gives

Substituting to (5.8) gives

The vector in the left-hand-side won't belong to the boundary of the right-hand-side (i.e., $I_0$ will be admissible and irreducible), if

Remark 6.1. Conditions (6.7) can be viewed as a condition for $l_1$ to be sufficiently large or as a condition for $|b_2|+|b_3|$ to be sufficiently small.

Proposition 6.1. (Conclusion of Step 1). Assume that stress-controlled loading $f(t)$ and displacement-controlled loading $l(t)$ of elastoplastic system of Figure 1 are given by (6.4) and satisfy (6.7). Then $c_j^\alpha$, $(\alpha, j)\not\in I_0$, can be amended in such a way that the stress vector $s(t)$ of the elastoplastic system $(D, A, C, R, l(t), f(t))$ satisfies

Step 2. Formula (5.13) yields

and substitution to (4.19) returns

Step 3. Since $|I_0| = 3,$ for any $(\alpha_*, j_*)\in I_0$, the set $I_0\backslash\{(\alpha_*, j_*)\}$ consists of two elements $\{(\alpha_1, j_1), (\alpha_2, j_2)\}$, and formulas (5.15) and (5.16) can be rewritten as

Substituting $n_j$ and $c'(t)$ given by (6.2) and (5.7) to (6.12), we get

Proposition 6.2. (Conclusion of Steps 1–3). Assume that assumptions of Proposition 6.1 hold. Let $\varepsilon_0$ be given by (6.13) and assume that

Then the stress vector $s(t)$ of the elastoplastic system $(D, A, C, R, l(t), f(t))$ satisfies

for all $t\ge\tau$ that satisfy (6.11).

Remark 6.2. When $b_2 = d_2 = b_3 = d_3 = 0$ (e.g., in the absence of the stress-controlled loading), condition (6.11) is the standard feasibility condition of vertex $y_*$ ([11, formula (8.5)]). Therefore, condition (6.11) can be viewed as a condition for the stress-controlled loading to not be too big.

6.2.   Case $I_{0}= \{ (+, 2), (-, 3), (+, 4) \}$

Formula (6.5) stays because computation of $\Delta_{I_0}$ is independent of the signs of $\alpha$ in $(\alpha, j)\in I_0.$ The relations (6.6) and (6.10) take the form

Admissibility and irreducibility condition (6.7), feasibility condition (6.11), and convergence time (6.11) now compute as follows.

Admissibility and irreducibility condition:

Feasibility condition:

Convergence time:

Proposition 6.2 can now be concisely formulated as follows.

Proposition 6.3. Assume that condition (6.17) holds. Then, for any $t\ge 0$ that satisfies simultaneously (6.18) and (6.19) the stress vector $s(t)$ of elastoplastic system $(D, A, C, R, l(t), f(t))$ obeys properties (6.8) and (6.9). In particular, for these values of $t$, spring $j$ plastically expands if $(+, j)\in I_0$ and spring $j$ plastically contracts if $(-, j)\in I_0$.

6.3.   Case $I_{0}= \{ (+, 1), (+, 2), (-, 3) \}$

Relations (6.5), (6.6) and (6.10) take the form

Admissibility and irreducibility condition (6.7), feasibility condition (6.11), and convergence time (6.11) now compute as follows.

Admissibility and irreducibility condition:

Feasibility condition:

Convergence time:

A statement about convergence of the stress vector and about the terminal distribution of plastic deformations given by $I_0$ comes in direct analogy with the statement of Proposition 6.3.

6.4.   Comparison of the cases considered

While the admissibility and irreducibility condition (6.6) for the case $I_0 = \{ (+, 2), (+, 3), (+, 4) \}$ does hold when the stress-controlled loading is absent, this no longer the case for the cases $I_{0} = \{ (+, 2), (-, 3), (+, 4) \}$ and $I_{0} = \{ (+, 1), (+, 2), (-, 3) \}$ meaning that the latter two cases are possible only when stress-controlled loading is forcing the model of Figure 1. However, the requirements for the stress-controlled loading in cases $I_{0} = \{ (+, 2), (-, 3), (+, 4) \}$ and $I_{0} = \{ (+, 1), (+, 2), (-, 3) \}$ are qualitatively opposite. Indeed, we can see that arbitrary small amount of stress-controlled loading is sufficient to realize the case of $I_{0} = \{ (+, 1), (+, 2), (-, 3) \}$. In this case, the role of stress-controlled loading is to make admissible and reducible $I_{0} = \{ (+, 1), (+, 2), (-, 3) \}$ irreducible (because in the absence of the stress-controlled loading $I_{0} = \{ (+, 1), (+, 2), (-, 3) \}$ reduces to $I_{0} = \{ (+, 1), (+, 2)\}$). The case of $I_{0} = \{ (+, 2), (-, 3), (+, 4) \}$, in contrast, requires a significant amount of stress-controlled loading to make $I_0$ admissible (see e.g., the second inequality of (6.17) saying that stress-controlled loading should surpass the displacement-controlled loading). The elastic limits of the remaining springs 1 and 5 should be large enough to accommodate such a large stress-controlled loading, see feasibility condition (6.18).

6.5.   Remaining cases of $|I_0|=3$

We recall the reader that in the case where the model of Figure 1 is forced by just displacement-controlled loading, all admissible irreducible $I_0$ are ^[11] $I_0 = \{(+, 1), (+, 2)\}$, $I_0 = \{(+, 4), (+, 5)\}$, $I_0 = \{(+, 1), (-, 3), (+, 5)\}$, $I_0 = \{(+, 2), (+, 3), (+, 4)\}$, see formulas (5.4) and (5.5) for the definitions of admissibility and irreducibility. Addition of stress-controlled loading enlarges this list substantially even in this case of $|I_0| = 3$ that this work sticks to. Indeed, the only $|I_0| = 3$ that are singular (Definition 4.1) are

with all possible combinations of pluses and minuses. And, additionally,

are not admissible, i.e., do not satisfy (5.4).

7.   Conclusions

We developed an algorithm to determine finite-time convergence of sweeping processes with moving and shape changing polytope to a vertex of the polytope. The earlier results either considered special shapes of polytopes (parallelepipedal) or didn't allow change of shape. As an application we were able to understand the influence of stress-controlled loading on asymptotic (finite-time) elastoplastic behavior of lattice spring model. In particular, we discovered that addition of a small stress-controlled loading can reduce the dimension of attractor that is present in the system otherwise (i.e., add more plastically deforming springs to the springs that deform plastically already), while addition of a larger stress-controlled loading can create such combinations of plastically deforming springs $I_0$ that none of $I\subset I_0$ constitute an eligible (i.e., admissible and irreducible) set of plastically deforming springs in the absence of stress-controlled loading.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflicts of interest.

Appendix

Proof of Theorem 2.1. This proof follows the proof of [11, Theorem 3.1] with $C$ replaced by $C(t)-c(t)$.

Let $y(t)$ be an arbitrary solution of (1.4). For the function $x(t)$ given by (1.10) consider

Note, that $x(t)$ is differentiable almost everywhere on $[0, \infty)$ because $c(t)$ is Lipschitz continuous. Let us fix some $t\ge 0$ such that $x(t)$ is differentiable at $t$. Without loss of generality we can assume that $t\ge 0$ is chosen also so that $V(x(t))$ is differentiable at $t.$ Then

By the definition of normal cone, (2.6) implies

Therefore, taking $\xi = y_*$ we conclude from (7.1) that

Now we use assumption (1.9), which is equivalent to

or, using the definition of the normal cone,

Therefore, letting $\xi = x(t)$ and $\zeta = x(t)-y_*,$ we get

which allows to further rewrite inequality (7.2) as

Therefore, the Lyapunov function (2.5) satisfies estimate (1.1). The proof is complete. □