It is known that long waves in spatially periodic polymer Fermi-Pasta-Ulam-Tsingou lattices are well-approximated for long, but not infinite, times by suitably scaled solutions of Korteweg-de Vries equations. It is also known that dimer FPUT lattices possess nanopteron solutions, i.e., traveling wave solutions which are the superposition of a KdV-like solitary wave and a very small amplitude ripple. Such solutions have infinite mechanical energy. In this article we investigate numerically what happens over very long time scales (longer than the time of validity for the KdV approximation) to solutions of diatomic FPUT which are initially suitably scaled (finite energy) KdV solitary waves. That is we omit the ripple. What we find is that the solitary wave continuously leaves behind a very small amplitude "oscillatory wake." This periodic tail saps energy from the solitary wave at a very slow (numerically sub-exponential) rate. We take this as evidence that the diatomic FPUT "solitary wave" is in fact quasi-stationary or metastable.
1.
Introduction
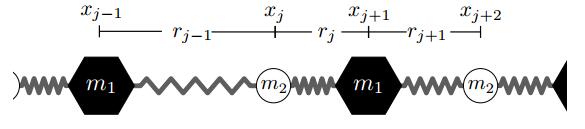
We consider a diatomic Fermi-Pasta-Ulam-Tsingou (FPUT) lattice as depicted in Figure 1 below. Newton's second law gives the equations of motion:
To be clear, here xn(t) is the position of the nth (with n∈Z) particle at time t. We assume that the masses satisfy
and the spring force is
That is to say the lattice is a so-called "mass dimer, " as studied in [1,2,3,4,5,6,7,8,9,10,11,12]. It is convenient and technically advantageous to rewrite the system in terms of the relative displacements rn:=xn+1−xn and velocities pn:=˙xn:
We are principally interested in the long time dynamics of finite energy* solutions r(t):=(r(t),p(t)) which are of long wavelength and small amplitude. This situation is sometimes called "the KdV limit" for, as shown in [4,7,13], such solutions of (1.1) are well-approximated for long, but finite, times by suitably scaled solutions of Korteweg-de Vries equations. KdV equations famously possess solitary wave solutions and as such the approximation results indicate that (1.1) has a solution which is "solitary wave-like, " at least for very long times. In particular, for 0<ε≪1, there is a solution of (1.1) of the form
*Naturally the system conserves energy. Specifically E(t):=∑n∈Z(12mnp2n(t)+12r2n(t)+13r3n(t)) is constant so long as it is initially finite. It is straightforward to show that, so long as ‖r‖ℓ2 is not too big, √E is equivalent to ‖(r,p)‖ℓ2×ℓ2.
where
The quantity cε is the wave-speed and c0 is called "the speed of sound." The error† function z(t) is less than Oℓ2×ℓ2(ε5/2) for |t|≤T0/ε3. In this article we take z(0)=0, though the results in [4,7] allow a fair bit of latitude for its initial value. The key question of this article is this: What happens to Ψm1,m2,ε(t) for times much greater than O(1/ε3)? In the monatomic problem, i.e., when m1=m2=m>0, the system (1.1) possesses a family of supersonic (that is, with speeds c>c0) solitary wave solutions which are asymptotically stable with respect to perturbations initially small in ℓ2×ℓ2 ([14,15,16,17,18]). This solitary wave is given by
†If m1=m2 the error estimate is stronger: z(t) is Oℓ2×ℓ2(ε7/2).
The constants β, cε and v are exactly as in (1.2). The function ηε(y) is small and spatially localized in the sense that there exists ˜β>0 such that cosh(˜βy)ηε(y/ε)=OHs×Hs(ε4). As such we can divine the ultimate fate of the solution Ψm,m,ε(t) in the monatomic case:
for some ε′∼ε and t′∼0. Note that the convergence is not in ℓ2×ℓ2, but in a somewhat more complicated space. See [18] for the details.
On the other hand, the recent work in [1,2,11,12] demonstrates that for a mass dimer the natural analog of the monatomic solitary wave is a "generalized solitary wave", i.e., a traveling wave which is the superposition of a core which is qualitatively a solitary wave and a very small amplitude periodic "ripple." Such solutions are sometimes called "nanopterons" [19]. Specifically, when m1≠m2 and ε>0 is not too large, there is a solution of (1.1) of the form
In the above, β, cε and v are as in (1.2). The functions ηn,ε(y) and ϕn,ε(y) satisfy:
Which is to say that, with respect to the subscript n, they have the same periodicity as the lattice. Moreover there exists a constant ˜β>0 such that cosh(˜βy)ηn,ε(y/ε)=OHs×Hs(ε3), i.e., the ηn,ε are small and go to zero exponentially fast at spatial infinity. The functions ϕn,ε(y) are spatially periodic. Their frequency is ξε=ξ0+O(ε) where ξ0=ξ0(m1,m2) is the unique positive solution of the "phase resonance" condition
The amplitudes of ϕn,ε(y) are small beyond all orders of ε; for all n∈N,
Without being too technical, in the diatomic problem the dispersion relation for (1.1) has two branches whereas the monatomic problem has a single branch. The first of the diatomic problem's branches is called the "acoustic branch" and it is qualitatively similar to the dispersion relation for the monatomic problem. Roughly speaking, the acoustic part of the diatomic problem can, in isolation, support a solitary wave at speeds slightly above the speed of sound c0. The second branch is called the "optical branch." As it happens, this branch has plane wave solutions which can propagate with any phase speed. As such, the nonlinearity in the problem causes the acoustic branch solitary wave to resonate weakly with plane waves with the speed of sound, ultimately generating the ripple. The spatial frequency at which this resonance occurs is ξ0 in (1.3). See [1,11,20] for a more in depth treatment.
Despite the fact that it is so small, the presence of the ripple precludes membership of Γm1,m2,ε in ℓ2×ℓ2, since this solution does not converge‡ to zero as |j|→∞. Thus the generalized solitary wave has infinite energy and as such it is categorically impossible for the finite energy solution Ψm1,m2,ε(t) to converge to Γm1,m2,ε as t→∞. And so something else must happen, something which is quite different than the convergence to the solitary wave which takes place in the monatomic problem.
‡It is worth pointing out that the results in [1,11] do not prove that the amplitude of the ripple is nonzero and thus one might wonder if the ripple is really there or if its presence is a technical crutch. While there is some compelling formal evidence that for special values of m1, m2 and ε the ripple may in fact vanish [2,12], our expectation is that in all but a set of measure zero in parameter space the ripple is nonzero. After all, this is the case for generalized solitary waves in the gravity-capillary problem [21,22], a problem which, at a technical level, is rather similar to the FPUT problem considered here.
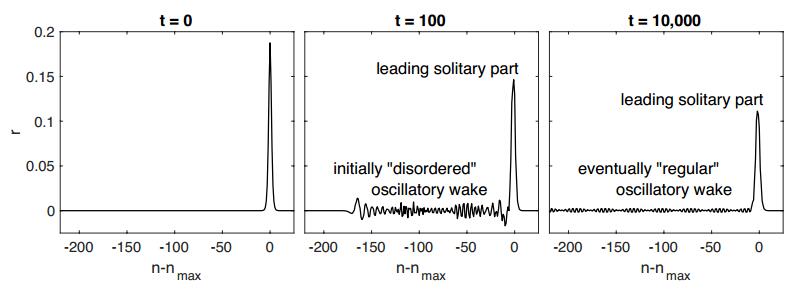
We study this by carefully simulating the solitary wave-like solution Ψm1,m2,ε(t) over very long times. The results are unambiguous: as Ψm1,m2,ε(t) propagates, it leaves behind a small amplitude, relatively high frequency "oscillatory wake." Initially somewhat disordered in appearance, the wake eventually settles into a rather regular periodic structure. Figure 2 contains a visualization of the simulations.
While it is not atypical for small perturbations of solitary waves in nonlinear dispersive systems such as KdV or monatomic FPUT to leave a "dispersive tail" behind early on in their evolution, in those cases the tail "disconnects" from the main solitary wave and eventually falls far behind it. But in these diatomic FPUT problems, the oscillatory wake is generated during the entirety of the simulation, always immediately trailing the leading solitary wave and inexorably increasing in width.
The oscillatory wake was not unexpected—simulations for the "small mass ratio problem" (that is, ε>0 is fixed and m1/m2 is taken to be very small) in [10] and [9] exhibit similar behavior. Those results were somewhat hobbled by the lack of computing power available at the time of their execution and as such the time scales of their runs were rather short. Also worth pointing out are the simulations of waves through lattices whose material properties randomly vary (as opposed to periodically vary) with respect to n. In this situation a "superdiffusive" effect is observed wherein the leading part of the pulse deteriorates very rapidly into "noise" [23], an effect similar too, but rather more pronounced, than what we see here.
Our simulations run for times substantially longer than 1/ε3. An interesting finding: The frequency of the wake is largely independent of the leading wave's size and is not particularly close to the frequency ξε of the ripple in the associated nanopteron. Moreover, as the width of the wake grows it slowly saps energy from the leading wave. In this way, the amplitude of the leading solitary wave slowly erodes during the evolution. The numerics indicate that the rate of this erosion is at most algebraic in t, much slower than the exponential rate one would expect were there a genuine linear instability. For these reasons, the solution Ψm1,m2,ε(t) is viewed as a metastable solitary wave.
2.
The numerical method
Our numerical method for computing Ψm1,m2,ε(t), implemented in MATLAB, is rather straightforward. First we restrict the size of the domain to be N=210. Specifically we take n∈[−N/2+1,N/2]∩Z and enforce periodic boundary conditions in (1.1), that is rN/2(t)=r−N/2+1(t) for all t. In this way we have converted the original infinite-dimensional system into a large finite-dimensional first-order system of differential equations. After picking m1, m2 and ε, we take the initial condition to be rn(0)=3ε2sech2(βεj)v with β and v as in (1.2). Then we simulate this system with a standard RK4 method. The time step is fixed at h=1/10.
Because our simulations are to run for long periods and the oscillatory wake is relatively motionless in comparison to the leading solitary wave, we enforce a "windowing" on the numerically computed solution, lest the solitary wave interact with its wake after wrapping around the periodic box§. Specifically, at each time step tl we compute the location nmax of the maximum of √r2n(tl)+p2n(tl); this gives us the position of the leading solitary wave. Then we multiply rn(tl) by the function W(j−nmax+N/8) where W is the N-periodic function which, for k∈[−N/2+1,N/2], is given by:
§Another way to avoid this problem would be to make the domain extremely large, on the order of N=107. Such a remedy is obviously computationally expensive and hence we took another route
Consequently our numerical method will not come close to conserving energy: Energy leaves the leading solitary wave, goes into the wake and is eventually "zeroed out" by the window¶. Note, however, that our simulations indicate that anything that falls behind the solitary pulse has no further discernible effect on it (this is consistent with aspects of the stability theory for the monatomic solitary wave, which is known to "outrun" all disturbances [14,15,16,17]). Moreover, the size of the window is sufficiently large that the oscillatory wake is given enough time to settle down into a regular and consistent configuration. In this way, we are able to run our simulations for very long times in a way which focuses on the leading solitary wave and a very large part of the oscillatory wake. Since our main interest is on the formation of the wake immediately behind the solitary wave, the windowing is large enough to adequately resolve this phenomenon||.
¶That the method as described will not conserve energy is one reason why we use an RK4 time stepping method, as opposed to, say, a more complicated symplectic structure preserving method (as in [24]).
||An interesting project would be to carry out the rigorous numerical analysis of this method. As pointed out by one of the referees, the method as described has features in common with the "freezing" method in [25,26] and as such those articles point towards a strategy for such an analysis.
3.
Results
With our numerical method, we performed the following runs:
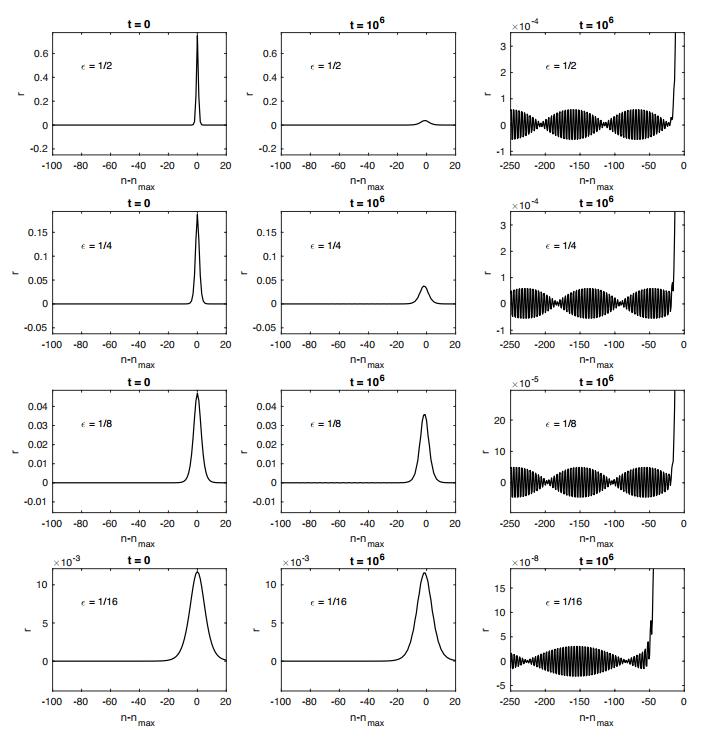
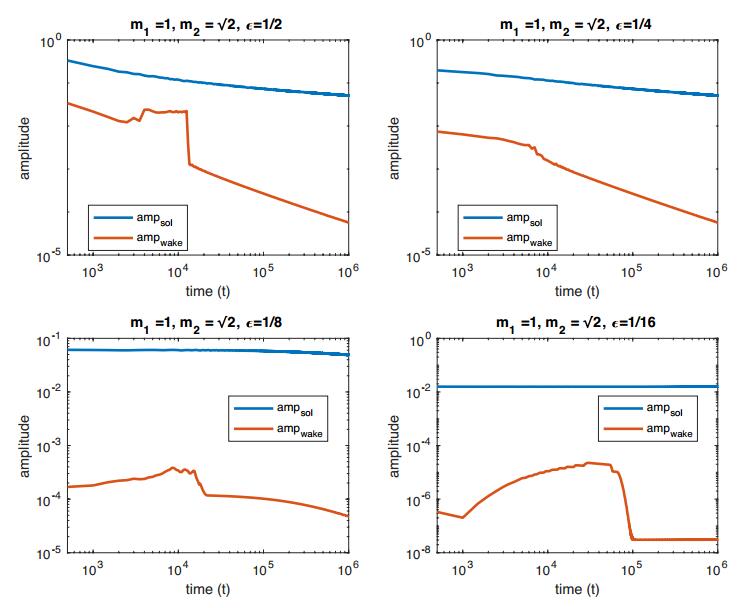
● Fixed m1=1, m2=√2 and took ε=1/2,1/4,1/8,1/16.
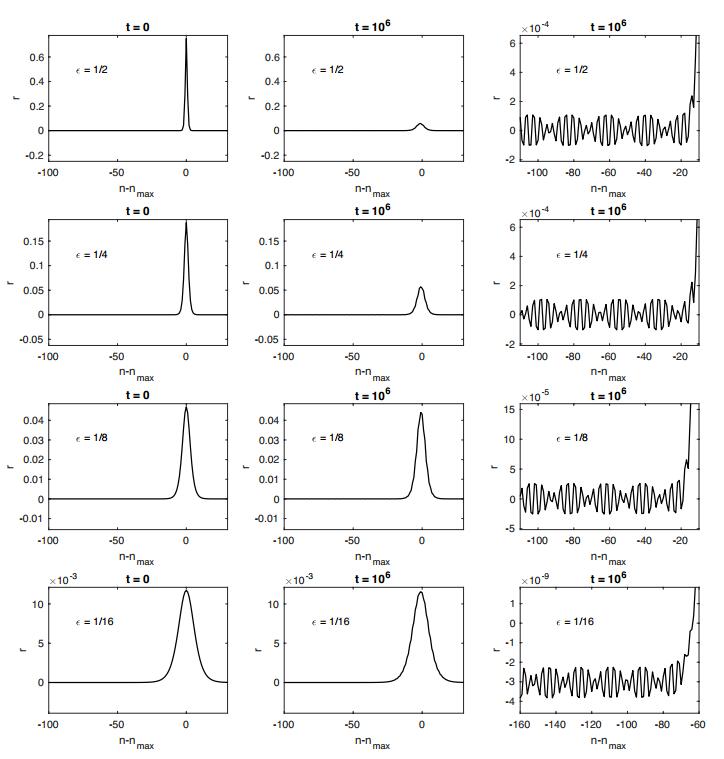
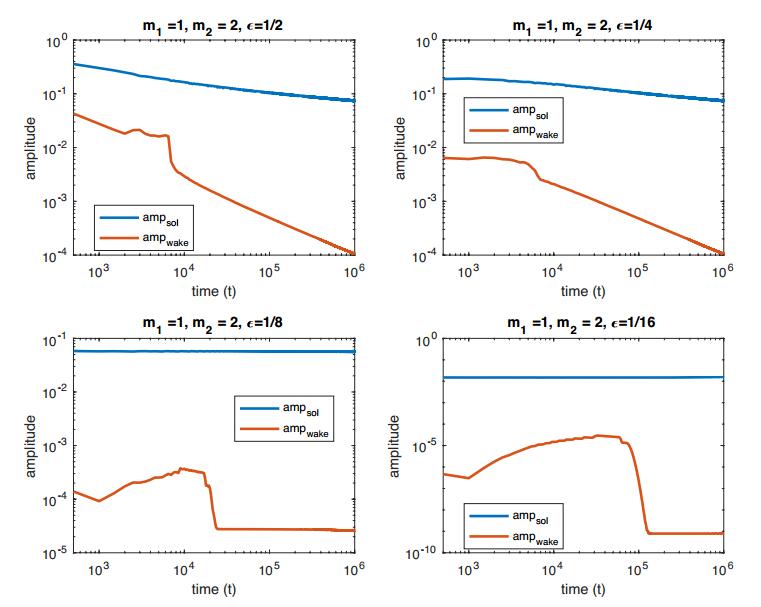
● Fixed m1=1, m2=2 and took ε=1/2,1/4,1/8,1/16.
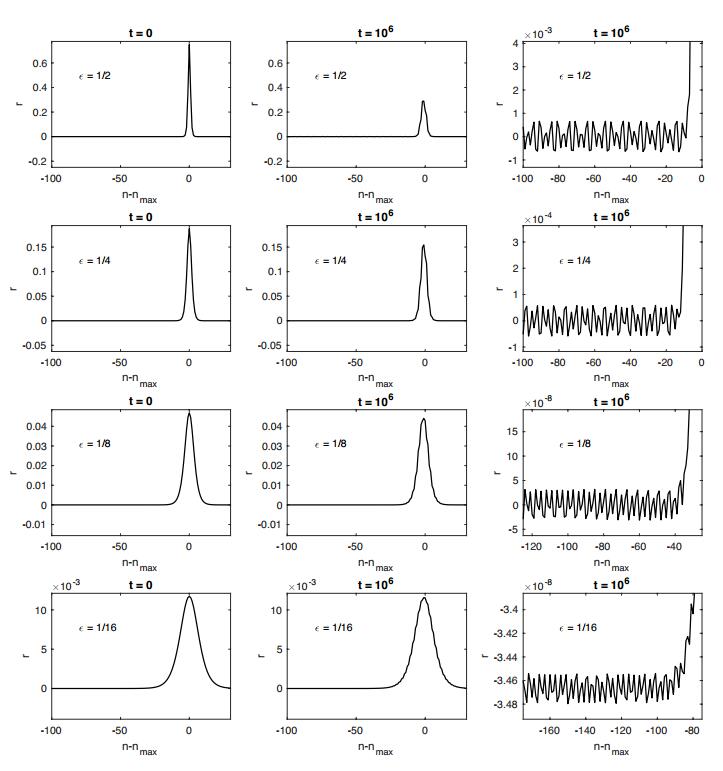
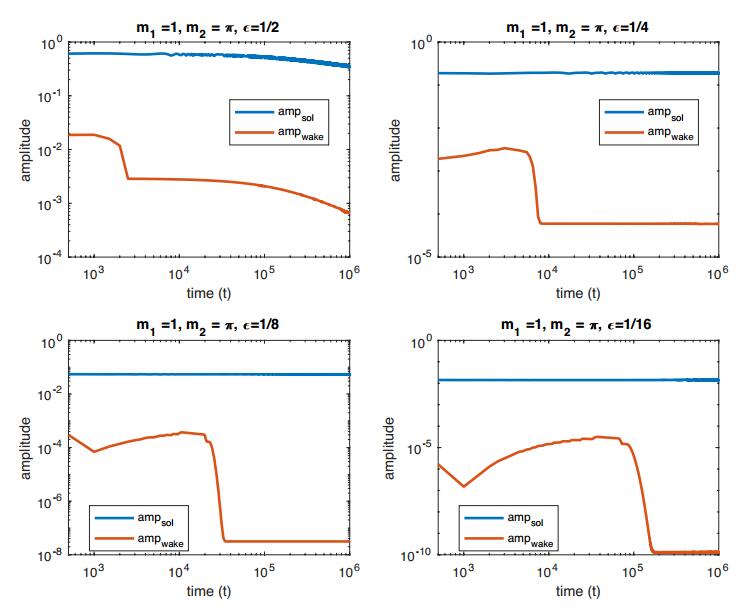
● Fixed m1=1, m2=π and took ε=1/2,1/4,1/8,1/16.
We picked these choices of masses so that we would have a mix of rational/irrational mass ratios as well as mass ratios which were large, small and close to one. Each run ran from t=0 to t=106. For each run, at each time step tl we compute the amplitude of the main pulse:
Then we compute the amplitude of the solution at a fixed distance behind the location of the main pulse. This quantity gives us the size of the wake right after its formation. Specifically we use a "peak to trough" measure of the amplitude:
3.1. Profile snapshots
In Figures 3–5 we present snapshots of the of r−component of the numerical computation of Ψm1,m2,ε(t) vs. n at t=0 and t=106. That is, at the beginning and end of the run. Since the runs are so long, by the end of the run the amplitude of the oscillatory wake is quite small indeed and as such we provide "zooms" of these. Here are our observations:
1. The attenuation of the ampsol is quite pronounced when ε is large, but when ε is small is barely discernible.
2. It is visible in these figures that, for fixed mass ratio, the spatial frequency of the wake is more or less constant across all simulated values of ε. The only variation from this is in in Figure 3 where the frequency when ε=1/16 is notably different than for the other values of ε. We do not present this, but numerical computation of the frequency of the wake is all but constant (for fixed mass ratio and ε) in time once the disordered transient period has elapsed and the solution settles into the regular "wake plus solitary wave" form.
3. Note that in Figures 4 and 5 the wake at ε=1/16 oscillates about a non-zero value. Note also that the amplitude of the wake in these cases is extremely small: O(10−9) and O(10−10), respectively. In these cases we are at the limit of the precise quantitative accuracy of our method. We include these principally because the qualitative dynamics are in line with the other simulations.
3.2. Amplitudes vs. time
In Figures 6–8 we present plots of ampsol and ampwake vs. time for our runs. We present these on log−log plots. Here are our observations:
1. In each case, it is plain that there is an initial transient phase (corresponding to the initial disordered wake) followed by a longer period where the dynamics are more regular.
2. In situations where ε is relatively large, the graphs follow a distinctly linear decay following the transient phase. Since the plots are log−log this indicates that these quantities are decaying at an algebraic rate.
3. When ε is smaller, the ampsol and ampwake settle into seemingly constant values.
4. Using a best fit approximation, we compute the rates of decay of ampsol and ampwake for those where the decay appears to algebraic. See Table 1. In this table, we denote the cases where the ultimate fate is seemingly constant by writing "∼cst".
4.
Conclusions
These simulations indicate that "solitary wave plus oscillatory wake" is the generic structure of Ψm1,m2,ε(t) when t≫1. This appears to be true over a range of mass ratios and values of ε. The general trend is that the amplitude of the wake is much smaller than that of the leading solitary wave but with a frequency seemingly fixed by the mass ratio. The likely cause of the oscillatory wake is a resonance between the acoustic and optical parts of the solution, though the precise mechanism is as yet unknown.
Since the problem conserves energy, it is impossible that both ampsol and ampwake are ultimately constant and nonzero, although some of our simulations seem to indicate that this is what is taking place. However, we conjecture that the rate of decay in these cases is actually so slow, slower even than algebraic, that it is undetectable using the methodology presented here. Given that the nanopterons from [1] and [11] have ripples which are small beyond all orders of ε, it seems within the realm of possibility that a truly rigorous treatment of the oscillatory wake will likewise involve a beyond all orders sort of analysis [19]. Such a treatment is beyond the scope of this investigation, but we feel our results demonstrate that such an analysis would be of great interest.
Acknowledgements
This work was supported by the National Science Foundation through grant DMS-1511488.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: