Compact structures as true non-linear phenomena

1.   Introduction

Traveling waves of permanent form are typical in hyperbolic linear systems. In nonlinear systems it is usual that the permanent form of the wave is lost and in finite-time a gradient catastrophe occurs ^[17]. Only in special, but remarkable, situations nonlinear hyperbolic systems admits global existence of solutions. An example is given by transverse waves in nonlinear elasticity: Transverse waves of fixed amplitude are globally defined in time, transverse waves of fixed polarization are subject to gradient catastrophe ^[28].

When nonlinearity is coupled with dispersive and/or dissipative effects and an ad hoc balance between these effects occurs then a solitary wave can emerge. In our discussion we consider only $1+1$ problems, but it is important to remark that $2+1$ and $3+1$ situations are, to our knowledge, still beyond rigorous treatments. Solitary waves are non trivial solutions of nonlinear equations, which are invariant under translation in time $t$ and space $x$ and they are defined on all the real line. In some situations, for special classes of equations, solitary waves can behave as solitons. Typically solitons are solutions of nonlinear equations that interacts in a very special way emerging unchanged from collsions, except for a phase shift. All solitons have infinite tails.

In some nonlinear problems it is possible to have solitary waves with compact support. This phenomena has been pointed out by Rosenau and Hyman in ^[22]. In this seminal paper based on a generalization of the KdV, the $K(m, n)$ equation, the idea of a compact wave is introduced. Moreover, it has been noticed, by numerical evidence, that sometimes a compact wave preserves its shape after interacting with another compact wave: These solutions are denoted compactons ^[21]. Recently a topical review paper by Rosenau and Zilburg ^[24] has been published on the subject. We refer to this paper for a detailed survey of the seminal results obtained by Rosenau and his coworkers.

From a physical point of view compactification is mainly possible along two pathways. One is via a nonlinearity in the higher order gradient terms of the phenomena. This happens, for example, in dispersive elasticity if we consider nonlinear dispersion coupled with nonlinear elasticity or in slender structures (as rods), if we consider fully nonlinear constitutive equations for the relationship among angular momenta and curvature ^[14]. This happens also in nonlinear viscoelasticity if we add nonlinear viscosity functions to nonlinear elasticity ^[11]. Another way has been obtained in phase field models describing physical systems that can exhibit different homogeneous phases ^[2]. Diffuse interfaces in phase-field models are derived by solving the Euler equations which minimize a suitable energy functional, which is usually constructed by summing a bulk term to an interface contribution penalizing field gradients. The interface contribution is usually chosen proportionally to the square of the norm of the field gradient with the proportionality constant called stiffness. In ^[8] it has been proven that non-constant stiffness can induce the appearance of compact interfaces in the framework of a model connected to the porous material description ^[4,5,6,7].

Compacton-like configurations have been also experimentally observed by ^[15]. A simple experience of compacton-like structures can also be led pushing the end points of a sheet of paper to obtain a kind of Euler instability, where the out-of-plane deformed shape necessarily has a compact support, see e.g., ^[14].

In this paper we study the possibility of compact interfaces in a more general model in which powers larger than two are considered for the norm of the field gradient.

From a mathematical point of view the compactification is related to a degeneration of the evolution equation driving the phenomena. In $1+1$ dimension this means that the ordinary differential equation we deduce to determine the traveling waves stop enjoying the Lipschitz condition ^[16]. In this case uniqueness is lost and patch-work weak solutions are possible. This phenomenon is peculiar of a fully nonlinear theory.

In the present note we shall first investigate the problem from an abstract point of view and then we shall consider some physical examples. In some of these examples we focus on a Cauchy problem in other examples on different kind of boundary conditions.

The next step is to extend our analysis to a multi-dimensional framework. Multidimensional compact solutions have been studied for a special equation ^[23] but always with a reduction to an ordinary differential equation. The crucial problem is to obtain a general criteria based on the degeneration of the multidimensional partial differential equation for example considering the pathway of ^[1].

2.   The compact interface problem

The mathematical issues that we analyze in our note are relevant in several applications. First of all, consider a $1D$ phase field system admitting two pure phases for the field derived as the two local minima of a double-well potential. The field profile connecting the two phases is described by some ordinary differential equation to be solved with the two pure phases as boundary conditions.

A typical situation is the one where the field $u(x)$ is the solution of the second order ordinary differential equation

where $m$ and $V$ are sufficiently regular functions, respectively called stiffness coefficient and bulk energy. The prime denotes the derivative and $x$ is the space coordinate. The bulk energy, has two local minima, i.e., the pure phases, and diverges at infinity. See for instance the gas-liquid interface model proposed in ^[9] and studied in detail in [8, Section 3(a)].

The solutions of (2.1) are such that the quantity $m(u)u_x^2/2-V(u)$ is constant with respect to $x$. This constant is called the energy level of the solution. A connection or interface is a profile connecting the two phases with energy level equal to the value of the minimum of the bulk energy, namely, the value of the bulk energy corresponding to the pure phases. Profiles connecting the two phase with energy level smaller than such a critical value are possible, but have a finite prescribed length.

Provided the coefficient $m(u)$ is larger than a positive constant in the interval between the two pure phases, it is easy to show that the connection has an infinite length, i.e., the solution of (2.1) tends the the two pure phases for $x\to\pm\infty$. On the other hand, if the coefficient $m(u)$ vanishes at the two pure phases and is positive between them, then the situation is intriguing and in some cases finite length connections, called compact interfaces or connections, can exist. The length of such compact interfaces is prescribed a priori by the property of the model, but, fixed a sufficiently large length of the sample (larger of the compact interface length), it is possible to construct a compact connection by adding constant solution of (2.1) constantly equal to the two phases. Indeed, these constant solutions of (2.1) have the same energy level of the compact connection.

A related problem emerges in different contexts, for instance, starting from the dispersive wave equation

which is suggested by the wave equation obtained by Destrade and Saccomandi ^[12,13]. Dispersive waves have been studied in different frameworks, but the theory proposed by Destrade and Saccomandi based on the Gottlieb, Rosenau, and Rubin idea ^[25] allows to consider nonlinear dispersive terms that can be also function of the strain $v_x$. Considering the traveling wave $v = w(x-ct)$ ansatz, by integrating we get the ordinary differential equation

where $\alpha$ is a real. Letting $w' = u$, we get the equation

Solutions of (2.2) in terms of $w$ can be constructed from the solution of the last second order equation as weak patch-work solutions requiring continuity of $w$ and leaving free its derivative to exhibit jumps. It is clear that as we are patching classical solutions in a finite number of points internal to the domain the obtained solution is a weak solution ^[19].

A similar situation is also obtained if we consider a nonlinear Klein-Gordon equation ^[20,27]. Compact waves may have an important role in our understanding of DNA denaturation ^[27].

Another interesting application is obtained if we consider the diffusive wave equation ^[11]

whose reduced wave equation is the first order ODE

Clearly the physical meaning of the term $H$ is different for the dispersive and diffusive case. In the diffusive case $H$ is the internal viscosity. It is simple to find several example or real polymeric and solids materials where the viscosity is a function of the strain and the strain rate ^[18]. On the other hand in the dispersive case $H$ is the dispersion coefficient which is a constitutive function that depends on the internal structure of the material.

Here we propose a rather general framework, and we shall discuss which hypotheses must be satisfied by the constitutive coefficient so that the compact interface does exist. We are able to do that summarizing the mathematical properties of a dynamical system and this with a low level of technical sophistication but in a clear and rigorous way.

3.   A general model

The problem described in the Section 2 can be encoded in the following general model. The state of the system on the volume $\Omega = [a, b]\subset{\mathbb{{R}}}$, with $a < b$ such that $a\in\{-\infty\}\cup{\mathbb{{R}}}$ and $b\in\{+\infty\}\cup{\mathbb{{R}}}$, is coded into a so called phase-field $u(x)$ depending on the space variable $x\in\Omega$. Two values of the phase-field, say $-1$ and $1$, represent the two homogeneous phases and the bulk energy^* is $U(u) = (1-u)^2(u+1)^2$ having the minima at the homogeneous phases $\pm1$; note that $U(u)\stackrel{u\to\pm1}{\sim}(u\mp1)^2$. The energy functional is

^* For definitness we assume that the two phases are $\pm1$ and, for simplicity, we choose a specific form of the bulk energy $U$, but all the results discussed below can be easily rephrased for different choices for the potential energy, for example, for those sharing the property to have two local minima in $\pm1$ with a single local maximum between them.

where $N\subset{\mathbb{{N}}}\setminus\{0\}$ is a finite and arbitrary set of positive integers, $c_{2k}$ (called $2k$-order stiffness) are positive regular real functions (at least $C^1({\mathbb{{R}}})$) possibly vanishing only at $\pm1$, and the subscript $x$ denotes the space derivative. We shall write

for any $k\in N$ with $\beta_{2k}^\pm\ge0$, where $\beta_{2k}^\pm = 0$ means that the corresponding stiffness coefficient does not vanish at the phases. The gas-liquid interface model in ^[8] discussed in Section 2 is obtained in the case $N = \{1\}$ for a special choice of the function $c_2(u)$. On the other hand, the problem (2.3) in the case $H(c^2(u')^2, u^2) = c(u')^2$ provides an equation in the form (3.3) with $N = \{2\}$ and $c_4(u)$ constant and in the case $H(c^2(u')^2, u^2) = H(u^2)$ provides an equation in the form (3.3) with $N = \{1\}$ and $c_2(u)$ constant.

By a standard variational computation, assuming Dirichlet or Neumann boundary conditions, the Euler equation

is derived, where the prime denotes the derivative with respect to the natural argument of the considered function.

A standard computation shows that the equation admits the constant of motion

where

3.1.   Compact interfaces

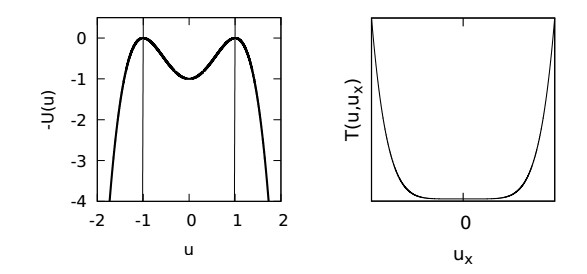
The structure of the solutions of the Euler equation (3.3) can be fully exploited via a Weierstrass argument ^[3,8,10]. We shall then use the typical language of classical mechanics: $x$ will be called time, $u$ position, $u_x$ velocity, $-U$ potential energy, $T$ kinetic energy, and $E$ total energy. Indeed, the trajectories on the phase space $u$–$u_x$ can be deduced by the knowledge of the level curves of the energy function $E$, whose algebraic equation is $E(u, u_x) = W$.

The graph of the potential energy $-U$ is depicted on the left in Figure 1. The qualitative graph of $T(u, u_x)$ as function of $u_x$ at any given $u\in(-1, 1)$ is shown on the right in Figure 1. Hence, for any fixed value $W > -U(0) = -1$ of the total energy and any $u\in(-1, 1)$ such that $|u|$ is sufficiently small, the equation $W = T(u, u_x)-U(u)$ can be solved with respect to $u_x$ and it admits two opposite solutions that will be denoted by $\pm f(u)$, with $f(u) > 0$ and continuous in $(-1, +1)$.

3.2.   The phase portrait

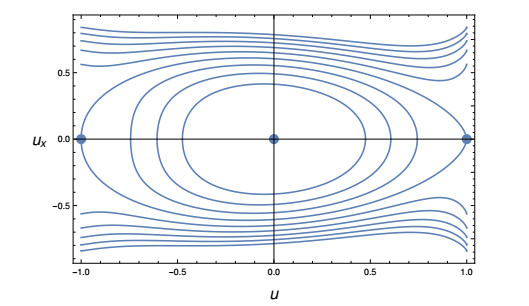
For any $-1 < W < 0$ the trajectory on the phase plane $u$–$u_x$ of the solution of (3.3) is a closed orbit (periodic motion) around the stable fixed point $(u, u_x) = (0, 0)$ symmetric with respect to both the coordinate axes.

For any $W > 0$ the discussion is more delicate, since the motion extends to $u = \pm1$ where the stiffness coefficients can vanish. For simplicity consider the phase $u = -1$ (the discussion in $+1$ is similar). Since $T = W+U$ and $W+U(-1) > 0$, we have the following: If all the stiffness coefficients vanish at $-1$, then $u_x(-1)$ must be infinite so that the kinetic energy stays finite at the phase. On the other hand, if there exists at least one not vanishing stiffness coefficient then the phase orbit stays finite (and different from zero) at $-1$, otherwise the kinetic energy would diverge at the phase.

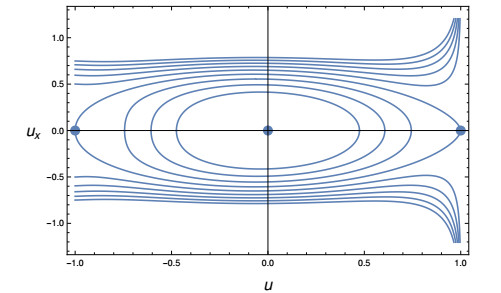
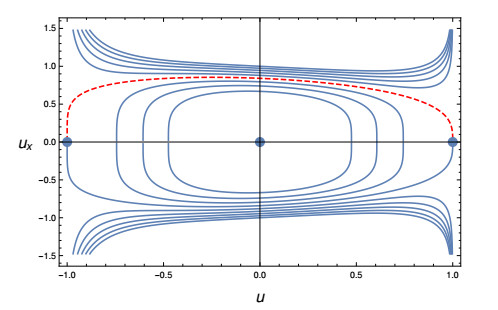
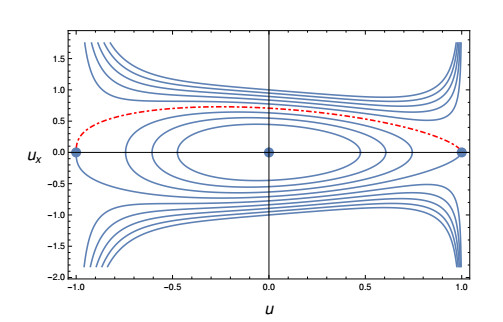
In ^[8] it has been studied the case $N = \{1\}$ with $c_2(u)$ vanishing at both phases. The phase portraits in [8, Figures 1 and 2] show that the orbits corresponding to energy larger than zero diverge at the phases. In Figures 2 and 3 the phase portraits of two models with $N = \{1, 2\}$ are depicted. The model accounted for in Figure 2 has coefficient $c_4$ different from zero at the phases, in particular we have chosen it constant, hence, the orbits corresponding to positive total energy stay finite and not zero at the two phases. On the other hand, the coefficient $c_4$ of the model described in Figure 3 tends to zero at $+1$ and to one at $-1$, since the coefficient $c_2$ tends to zero to both phases, we have that the orbits corresponding to total positive energy stay finite at $-1$ and diverge at $+1$.

The case $W = 0$ is peculiar and the orbit connecting the two phases is called heteroclinic. Since $T = U$, we have that the phase trajectory must be such that $f(u)\stackrel{u\to\pm1}{\sim}(1\mp u)^{\gamma^\pm}$ for some $\gamma^\pm$ such that $\beta_{2k}^\pm+2k\gamma^\pm\ge2$ for all $k\in N$ with the equality which holds for at least one value of $k\in N$. The heteroclinic orbit can then tend to zero, have finite limit or diverge at the phases.

In [8, Figure 2] it is shown an example in which the orbit tends to zero at one phase and diverges at the other. In the two examples depicted in figures 2 and 3, on the other hand, the heteroclinic orbits tend to zero at the phases since $\gamma^+ = 5/8$ and $\gamma^- = 1/2$ in both cases. Indeed, consider the case in Figures 2, to compute $\gamma^+$ we first note that looking at the degree two term of the kinetic energy we have $3/4+2\gamma^+ = 2$, yielding $\gamma^+ = 5/8$, and find that the corresponding behavior of the fourth degree term is $4\gamma^+ = 5/2 > 2$. On the other hand, if we computed $\gamma^+$ considering the fourth degree term we would have $4\gamma^+ = 2$ which implies $\gamma^+ = 1/2$ and the corresponding behavior of the second degree term would be $3/4+2(1/2) = 7/4 < 2$. Hence, we conclude $\gamma^+ = 5/8$.

To compute $\gamma^-$ we note that looking at the degree two term of the kinetic energy we have $5/4+2\gamma^- = 2$, yielding $\gamma^+ = 3/8$, and find that the corresponding behavior of the fourth degree term is $4\gamma^- = 3/2 < 2$. On the other hand, if we computed $\gamma^-$ considering the fourth degree term we would have $4\gamma^- = 2$ which implies $\gamma^- = 1/2$ and the corresponding behavior of the second degree term would be $5/4+2(1/2) = 9/4 > 2$. Hence, we conclude $\gamma^- = 1/2$.

The exponents for the case in Figure 3 can be computed similarly.

3.3.   Compact solitary waves

The flight time $K$ from $-1$ to $+1$ along the orbits corresponding to total energy $W\ge0$ can be formally expressed via the definite integral

If $W > 0$, then $f(u) > 0$ for any $u\in[-1, +1]$, hence the integral defining $K$ is convergent and the flight time from $-1$ to $+1$ is finite. If $W = 0$, namely, if we are interested to the flight time measured along the heteroclinic orbit, the integral in (3.6) can be not convergent, since the exponent $\gamma^\pm$ can be positive. If the time of flight is finite, following ^[8,9], we say that the heteroclinic is compact or that it is a compact solitary wave.

The existence of the compact solitary waves mainly depends on the second degree term in (3.1). In particular, if the coefficient of the second degree term does not vanish at the phases, then the compact wave does not exist. Indeed, since $\beta_{2}^\pm = 0$, we have that $\gamma^\pm = 1$, since $\beta_{2}^\pm+2\cdot1\gamma^\pm = 2$ and $\beta_{2k}^\pm+2\cdot k\gamma^\pm > 2$ for any $k > 1$, where we used that $\beta_{2m}^\pm\ge0$. Finally, since $\gamma^\pm = 1$, the integral (3.6) is divergent. On the contrary, if the second degree term is such that $\beta_{2}^\pm > 0$ (it vanishes at the phases at least as a power), then the compact solitary wave exists. Indeed, we have that $\gamma^\pm < 1$, which proves that the integral (3.6) is convergent. The fact that $\gamma^\pm < 1$ is rather trivial, indeed, if it were $\gamma^\pm\ge1$ we would have $\beta_{2k}^\pm+2k\gamma^\pm > 2$ for all $k$.

On the other hand, if the second degree term is not present in (3.1), namely, $N\not\ni 1$, then the compact solitary wave exists whatever is the behavior of the higher order stiffness coefficients. Indeed, $\gamma^\pm\le1/2$ proves that the integral (3.6) is convergent.

Although the existence of the compact solitary wave depends strongly on the properties of the second degree term, the behavior of the heteroclinic orbit at the phase can be controlled by higher degree terms. This fact is illustrated, for instance, in the example discussed in Figure 2. The heteroclinic orbit is compact, indeed we found $\gamma^+ = 5/8$ and $\gamma^- = 1/2$. The existence of the compact wave is strictly connected to the fact that the second degree coefficient vanishes at the phases, but as we have seen at the end of the Section 3.2, the behavior of the heteroclinic at $-1$ is controlled by the fourth degree term of the kinetic energy.

We have discussed the existence of compact solitary waves in a very general setup. In particular, we have proven that for the compact solitary wave to exist it is necessary that the second order stiffness coefficient vanishes at the phases. As a consequence, even in presence of terms of degree larger or equal to four in (3.1), compactification is not possible if the second degree term (if present) does not vanish at the phases. This is in other words a sufficient condition for non-existence of compact solitary waves. It is useful to prove this fact with a different approach. Suppose $1\in N$ and consider the heteroclinic motion corresponding to total energy $W = 0$ connecting the two phases $-1$ and $+1$ for $x\in[x_{-1}, x_{+1}]$. As above we can write $u_x^2 = G(u)$ (we are letting, here, $G = f^2$). Deriving with respect to $x$ we get $2u_xu_{xx} = G'(u)u_x$, yielding $u_{xx} = G'(u)/2$ at any point of the orbit except for the two end points where it can be $u_x = 0$. Indeed, let us assume that $u_x = 0$ at least at one of the two end points (say at the phase $+1$), otherwise the flight time would necessarily finite so that the compact wave would exist. In order to understand if the compact wave exists, one has to find the order of the zero $+1$ for the function $G$. Hence, we have to compute $G'$: Deriving the integral of the energy $T-U = W$, we get

At any $x$ different from the ending points, since $u_x\neq0$, we have that

Thus,

where we used that we have assumed $u_x\to0$ for $x\to x_{+1}$. Thus, if $c_2(+1)\neq0$, then it must be $\lim_{x\to x_{+1}}u_{xx} = 0$, which implies that $G'(+1) = 0$. We can then conclude that, if $c_2(+1)\neq0$ then the phase $+1$ is necessarily at least a zero of order two for $G$, which implies that the compact wave does not exist.

It is possible to shed some light on this point by performing a direct computation in the very particular case $N = \{1, 2\}$, namely, when only the second and the fourth degree terms are present in the energy functional. We shall also assume $c_4(\pm1)\neq0$. The energy conservation reads $3c_4u_x^4+c_2u_x^2-U = 0$. Solving with respect to $u_x^2$ we find

and note that $\pm1$ are zeros of $G$, indeed, one has

In order to understand the order of the zero, we have to compute $G'(\pm1)$. We first note that

If $c_2(\pm1)\neq0$, by simply computing the expression above at $u = \pm1$ one finds $G'(\pm1) = 0$, hence the phases are zeros of order at least equal to two for $G$ so that the compact solitary wave does not exist. On the other hand, if $c_2(\pm1) = 0$, we get

Assuming $c_2$ is analytic, we write $c_2(u) = (u\pm1)^n \bar{c_2}(u)$, with $n\ge1$ and $\bar{c_2}(\pm1)\neq0$. We find

for $n = 1$ and $G'(\pm1) = \sqrt{48c_4(\pm1)}/(6c_4(\pm1))$ for $n\ge2$. In both cases, since $c_4, U > 0$, we have that $G'(\pm1) > 0$. Hence the phases are zeros of order one for $G$ and thus the compact solitary wave does exist.

3.4.   Inflection point

In some applications a relevant property of compact solitary waves is the presence of inflection points where the interface changes its convexity. This cannot be studied at the level of generality we adopted in this section, but in some particular cases, by using the conservation of the total energy and the equation of motion, it is possible to express the second derivative of the interface in terms of the parameters defining the model, namely, the bulk energy and the stiffness coefficients. We discuss two cases. Suppose first $N = \{1\}$, see also [8, Section 3(b)]. The equation of motion and the energy conservation law (recall the total energy is equal to zero) read

which, combined, yield

Now, consider the case $N = \{2\}$. The equation of motion and the energy conservation law (recall the total energy is equal to zero) read

which, combined, yield

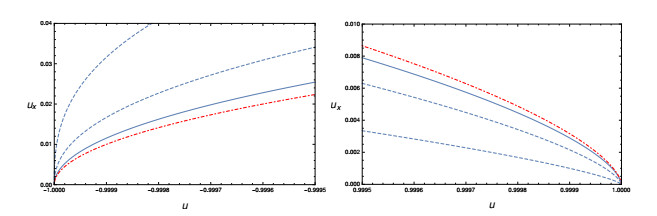
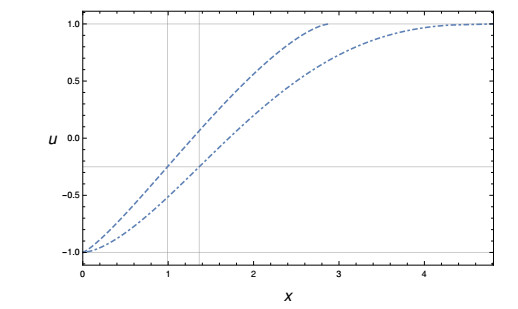
These last results are illustrated in Figure 5 where the compact solitary wave profiles are depicted for the two models described in the caption. Note that for the model represented by the dot-dashed line in the picture, equating the right hand side of (3.8) to zero we get that the inflection point corresponds to the value $u = -1/4$ of the profile, indeed a direct computation yields $U'/U-c'_2/c_2 = -(1+4u)/[2(1-u)(1+u)]$. In the case referring to the dashed line, on the other hand, equating the right hand side of (3.9) to zero we get that the inflection point corresponds to the value $u = -1/4$ of the profile, indeed a direct computation yields $U'/U-c'_4/c_4 = -(1+4u)/[2(1-u)(1+u)]$.

For completeness, we report in Figures 6 and 7 the phase portraits of these two models. Note that, since in both models the stiffness coefficients vanishes at the phases, the orbit corresponding to total energy larger than zero diverges both at $-1$ and at $+1$. Moreover, since in each model a single stiffness term is present, it is immediate to deduce that for the model in Figure 6 $\gamma^+ = 5/16$ and $\gamma^- = 3/16$, whereas for the model in Figure 7 $\gamma^+ = 5/8$ and $\gamma^- = 3/8$. The fact that all these exponents are positive explains why the heteroclinic orbits tends to zero at the phases in both models.

4.   Concluding remarks

Using simple arguments of analytical mechanics we have discussed the showing up of weak compact traveling wave interfaces for a class of problems where powers larger than two are considered for the norm of the field gradient. The use of elementary arguments allowed to provide in a simple, clear and rigorous setting a proof of compactification. Obviously this discussion has been developed in $1+1$ dimension, further developments will be devoted to extend the adopted approach to the multidimensional case, starting once again from the simplest one, say the compact solutions of an axisymmetric problem.

Conflict of interest

The authors declare no conflict of interest.