Energy transmission in Hamiltonian systems of globally interacting particles with Klein-Gordon on-site potentials

1.   Introduction

Nonlinear partial differential equations of the sine-Gordon type appear in many physical applications. For instance, a damped sine-Gordon equation occurs in the study of long Josephson junctions when dissipative effects are taken into account ^[1]. A similar partial differential equation with different nonlinear terms appears in the study of fluxons in Josephson transmission lines ^[2], while a modified Klein-Gordon equation appears in the statistical mechanics of nonlinear coherent structures, in the form of a Langevin equation ^[3]. On the other hand, the spatially discrete version of the sine-Gordon equation also has many important applications. For example, a coupled system of discrete sine-Gordon equations describes a chain of harmonic oscillators coupled through Hookean springs ^[4], or a system of Josephson junctions attached through superconducting wires ^[5]. In these cases, the system is initially at rest with zero initial velocities and a sinusoidal Dirichlet boundary condition is applied at one end to study the phenomenon of supratransmission of energy ^[4,6]. Supratransmission is a nonlinear process characterized by a sudden increase in the amplitude of wave signals generated at the periodically perturbed boundary. This phenomenon is also present in the investigation of energy transmission in chains of Josephson junctions except that, in this case, a Neumann boundary condition needs to be imposed for reasons of physical meaningfulness ^[5].

It is important to point out that several bounded nonlinear systems exhibit the phenomenon of supratransmission when they are harmonically perturbed at one end, provided the driving frequency belongs to a "forbidden" band lying outside the linear frequency spectrum of the system. This is the case e.g. with Klein-Gordon arrays ^[4], Fermi-Pasta-Ulam-Tsingou ^[7], Bragg media in the nonlinear Kerr regime ^[8], and even spatially continuous bounded media described by sine-Gordon-like equations ^[9]. Moreover, nonlinear supratransmission has been observed in discrete double sine-Gordon chains ^[6], forced linear arrays of anharmonic oscillators ^[10] and two-dimensional lattices with nearest-neighbor interactions ^[11]. It is worth noting that it has also been detected experimentally in many physical media, including electronic networks described by Klein-Gordon equations ^[12], in nonlinear quantum systems with saturable nonlinearities ^[13], discrete optical wave-guide arrays ^[14] and electrical transmission lines which present a chameleon-like behavior ^[15].

In recent years, the investigation of systems consisting of oscillators with global interactions has witnessed a remarkable development in view of its various applications to physical sciences ^[16]. Indeed, beyond the classical examples of point masses in gravitational fields, or systems of charged particles in space ^[17], many other physical systems of particles with long-range interactions (LRI) have been investigated ^[18]. For instance, the nonlinear interactions of vortices in two dimensions, elasticity phenomena arising in the study of planar stress, systems that consider dipolar forces ^[19] and the activation/repression of transcription in chromosomal and gene regulation ^[20] are some well known problems involving globally interacting particles.

Fermi-Pasta-Ulam-Tsingou (FPUT) 1-dimensional Hamiltonian lattices have also been studied under various LRI schemes and found to exhibit weakly chaotic dynamics for strong LRI especially in the thermodynamic limit ^[21,22]. In fact, it has already been established that supratransmission in FPUT lattices occurs at higher and higher threshold amplitudes as the "length" of the interactions increases ^[23]. Finally, it is worth pointing out that the mathematical investigation of some models with global interactions has been extended to the continuous scenario (based on a continuous-limit process involving the transformation into Fourier series, the inverse Fourier transform and the limit when the interparticle distance tends to zero), obtaining thus models with anomalous diffusion ^[24].

In view of these facts, a natural direction of investigation is the study of nonlinear supratransmission in arrays of oscillators with varying ranges of particle interactions in the presence of on-site potentials. The goal of this paper is to study the properties of this phenomenon employing suitable computational techniques. The main numerical method employed is a convergent and stable finite-difference scheme which considers discrete forms of the local energy and the total energy of the system ^[25]. This method is capable of exploiting the conservation properties of the continuous medium, and is ideal for the investigation of nonlinear supratransmission. It may thus be possible to propose applications to the design of amplifiers of weak signals, or the fabrication of detectors of ultra weak pulses, as has been done for the Klein-Gordon equation ^[5]. In the present work, we explore numerically the occurrence of supratransmission in discrete systems of globally interacting particles and on-site potentials of the Klein-Gordon type, and conjecture that similar effects may be present in other systems of the same form.

Our paper is structured as follows: In Section 2, we introduce the mathematical model under investigation. The linear dispersion relation of the system is calculated and its importance is also discussed. Section 3 is devoted to the numerical method employed to approximate the solutions. In Section 4, we confirm the presence of nonlinear supratransmission in a Hamiltonian system with quadratic particle interactions and on-site potential $V(x) = 1-cosx$. More specifically, we measure using a parameter $0\leq\alpha < \infty$ the length of particle interactions and establish that supratransmission occurs at larger thresholds the longer the range of particle interactions, as $\alpha$ decreases from infinity. Interestingly, however, this trend is reversed in the strong LRI regime $0\leq \alpha \lesssim 1.5$ where the thresholds decrease to values lower than their nearest neighbor ($\alpha = \infty$) limits. Finally, we close this work with a section on concluding remarks and various directions for future investigation.

2.   Preliminaries

Throughout this work, we will consider a one-dimensional system consisting of $N + 2$ unit mass particles interacting via long-range forces that decay with distance as $1/r^{\alpha }$, for $\alpha \geq 0$. Our model incorporates both an on-site potential $V(u)$ and a potential of the form $W(u) = 1/2 a^2 u^2$ for some constant $a$, which involves all coupling terms. Our system is described by the Hamiltonian

where $p _n$ and $x _n$ are the canonical conjugate pairs of momentum and position variables, respectively, assigned to the $n$th particle, with $n = 0, 1, \ldots, N + 1$.

Here, the number $\alpha$ governs the "length" of the particle interactions, with $\alpha = \infty$ denoting the shortest possible range of nearest neighbor interactions. Thus, we shall say that the system possesses long-range interactions if $\alpha < \infty$, with the strongest LRI corresponding to $0\leq\alpha\leq1$. The scaling factor

is used to make the last term at the right-hand side of (2.1) extensive, that is, proportional to $N$ (see ^[21,22]).

The respective energy densities are given by ${H} _n + {P} _n$, where

It is worth noting that (2.1) extends various well known models of mathematical physics to account for LRI. In this paper, we have treated the classical sine-Gordon chain when $V (u) = 1 - \cos (u)$ and have numerically checked that the solutions and phenomena observed are very similar with what one finds for other potentials like $V (u) = \frac {1} {2!} u ^2 - \frac {1} {4!} u ^4 + \frac {1} {6!} u ^6$, and the double sine-Gordon chain with $V (u) = \frac {1} {2} - \frac {1} {6} [2 \cos u + \cos (2 u)]$. This is perhaps to be expected since the first terms in an expansion of all these potentials around $u = 0$ coincide.

We therefore consider a system of unit mass particles whose positions satisfy the initial-boundary-value problem

where $1 \leq n \leq N$ and $A$, $\Omega$ are positive. Thus, our system is initially at rest, and is perturbed harmonically at the left end, with a free boundary at the last particle on the right. Moreover, to model a long chain we let $N$ be relatively large, and use damping coefficients, $\gamma_n \in \mathbb {R} ^+ \cup \{ 0 \}$ to simulate an absorbing boundary at the right ^[6]. Now, let $N _0$ be a positive integer such that $N _0 < N$, and define

for each $n \in \{ 1, \ldots, N \}$. Note that the physical reason for the above choice of $\gamma _n$ is to avoid waves bouncing back and returning to the medium.

Recall that the sine-Gordon, the Klein-Gordon and the double sine-Gordon chains exhibit the phenomenon of supratransmission ^[4,6], which is a process characterized by a sudden increase in the amplitude of wave signals propagated into a nonlinear medium by a periodically driven boundary. Consider, therefore, any of these systems and apply a sinusoidal perturbation at one end. Assume that the frequency $\Omega$ belongs to a "forbidden" band-gap that lies (together with its harmonics) outside the phonon spectrum of the system and is hence unable to drive normal mode resonances at low energies.

However, as the driving amplitude is increased, a critical value $A_s$ is reached above which the system suddenly absorbs great amounts of energy from the oscillating boundary. The number $A _s$ is called the supratransmission threshold, and in the case of Klein-Gordon type systems an analytical approximation of its value at $\alpha = \infty$ and $\gamma _n = 0$ for each $n \in \{ 1, \ldots, N \}$, is known ^[4]

for each $\Omega \in (0, 1)$, and $c = 1 / \sqrt {M}$. It is worth noting that this approximation is valid for relatively large values of $c$, and for values of $\Omega < 1$ which are close to $1$.

Let us now use a formulation based on fractional derivatives to obtain an approximate linear dispersion relation and hence a phonon band estimate for an infinite system of interacting particles whose equations of motion of are

where the $a^2$ factor before the sum will be explained below. Let $\mathcal {F} _h : x _n (t) \rightarrow \hat {x} (k, t)$ denote the Fourier series transform, let $\mathcal {L} : \hat {x} (k, t) \rightarrow \tilde {x} (k, t)$ be the passage to the limit when the distance between consecutive oscillators tends to zero, and let $\mathcal {F} ^{- 1} : \tilde {x} (k, t) \rightarrow x (s, t)$ be the inverse Fourier transform. Let $\circ$ represent the operation of composition of functions and $\mathcal {T} = \mathcal {F} ^{- 1} \circ \mathcal {L} \circ \mathcal {F} _h$. Using this notation, the infinite set of equations is transformed into the fractional partial differential equation

Here,

and $\Gamma$ is the usual Gamma function. Meanwhile, the new variable $s$ physically represents position, and the fractional partial derivative with respect to $s$ is understood in the sense of Riesz. Specifically, the derivative is the well-known Riesz fractional partial derivative of $x$ of order $\nu - 1$ with respect to $x$.

Recall in general that if $\beta \in \mathbb {R} ^+ \cup \{ 0 \}$, $(s, t) \in \mathbb {R} \times \mathbb {R} ^+$ and $n \in \mathbb {Z}$ satisfy $n - 1 < \beta \leq n$, then the Riesz partial derivative of $x$ of order $\beta$ with respect to $s$ is defined as

where $_a D _s ^\beta$ and $_s D _b ^\beta$ are, respectively, the left and the right Riemann-Liouville fractional derivatives in space of order $\beta$. More concretely,

for each $(s, t) \in \mathbb {R} \times \mathbb {R} ^+$. Here, $c _n = 1 / \Gamma (n - \beta)$.

Considering the linearization of (2.9) and using plane wave solutions of the form $x (s, t) = A e ^{i (\omega t + k s)}$ for each $k \in \mathbb {Z}$, we obtain the linear dispersion relation identity $\omega ^2 (k) = 1 + D |k| ^{\alpha - 1}$ for $\alpha \in (1, 3]$. The fact that $D$ is positive suggests a forbidden band-gap of the form $0 < \Omega < 1$, within which to select our driving frequency. Indeed, it is very interesting that these results are in agreement with those obtained very recently in ^[26], where the following dispersion relation was derived for a similar system of particles with long-range interactions

In fact, graphs of this relation given in ^[26], for $\alpha > 1$, show that the above $\omega^2(k)$ does not reach values much bigger than 1, which explains why the driving frequencies $\Omega$ used below to observe supratransmission truly belong to a forbidden gap of the system.

3.   Computational model

From a practical point of view, we shall employ here a full discretization of the system (2.5) in the form of an explicit finite-difference scheme. To describe it, let $T$ be a positive number that physically represent a temporal period, and fix a uniform partition $0 = t _0 < t _1 < \ldots < t _K = T$ of the interval $[0, T]$, of norm equal to $\tau$. Use $x _n ^j = x _n (t _j)$ for each $n \in \{0, 1, \ldots, N + 1 \}$ and $j \in \{ 0, 1, \ldots, K \}$, and introduce

The finite-difference method we use to approximate the solution of (2.5) is given by

Equations (3.5) are valid for $n \in \{ 1, \ldots, N \}$ and $j \in \{ 1, \ldots, K - 2 \}$. This method is an explicit four-step technique that has been successfully applied recently to approximate the solution of Riesz space-fractional nonlinear multidimensional wave equations with damping ^[25]. Moreover, the method is stable and convergent and is described by the following discrete form of (2.1):

for each $j \in \{ 1, \ldots, K - 2 \}$.

Clearly, the local energy density of the $n$th particle at the time $t _j$ is given by $H _n ^j + P _n ^j$, with the local kinetic and potential energies being, respectively,

Thus, the total kinetic energy of the system over $[0, T]$ is

The above method is an adaptation of the one employed in ^[25]. Thus, the discrete Hamiltonian (20) is conserved when the damping coefficients are all equal to zero and homogeneous Dirichlet boundary data are imposed on the first and last particles. In the damped case, this methodology is also capable of incorporating the dissipation of energy. An interesting feature of the numerical approach adopted in this work is that it is valid for both continuous fractional equations and spatially discrete systems with any type of global interactions. Our technique is consistent, of second order, stable and quadratically convergent.

4.   Results

In this section, we shall demonstrate that system (2.5) does exhibit nonlinear supratransmission when the potentials are those of a sine-Gordon, Klein-Gordon or double sine-Gordon equation. At first, we test thoroughly our computational method on the model described in Section 3, for $\alpha = \infty$. This corresponds to the classical sine-Gordon, Klein-Gordon and double sine-Gordon discrete chains, and comparisons are made against supratransmission results already available in the literature ^[27,28].

To investigate the system (2.5) with sine-Gordon potential, we consider a system with $N = 100$ particles, and let $a = 4$ and $N _0 = 25$ (in this way, the last $25$ particles of the system are damped to simulate the absorbing boundary). Following the results of Section 2, we consider various experiments in which the value of $\alpha$ will be changed. Computationally, for satisfactory accuracy we let $\tau = 0.05$.

4.1.   Nearest-neighbor interactions

Throughout this stage, we fix $\alpha = \infty$. In this case, the system reduces to the classical FPUT model, and we compare against the analytical predictions available in the literature to check the accuracy of our calculations.

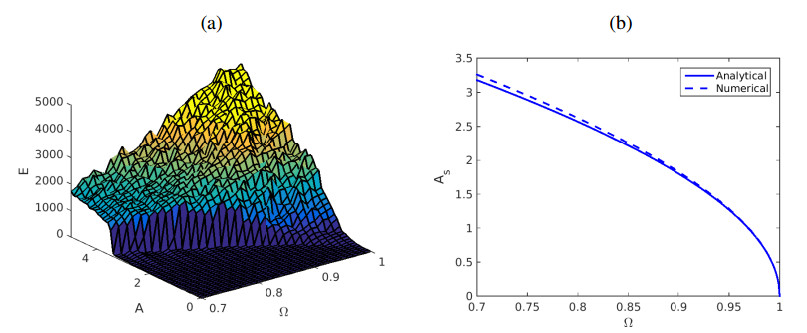
Example 1. Note that if $\alpha = \infty$ then the initial-boundary-value problem becomes

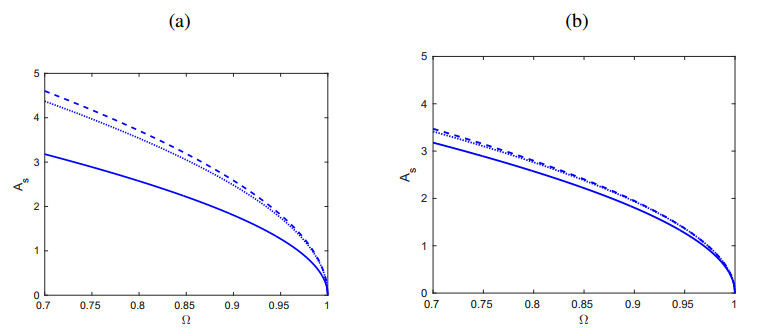
which describes a system of harmonic oscillators with nearest-neighbor interactions that exhibits the presence of supratransmission. More precisely, for values of $c = a$ relatively large, the supratransmission threshold is related to the driving frequency $\Omega$ via the expression (2.7). We have calculated the total kinetic energy absorbed by the system (4.1) over a period of time $T = 200$, using various values of $\Omega \in (0.7, 1)$ and $A \in [0, 5]$. A typical graph of the total kinetic energy versus $\Omega$ and $A$ is shown in Figure 1(a). This figure shows that, for each value of the driving frequency, there exists a critical amplitude $A _s$ above which the boundary of (4.1) starts to transmit energy into the system. On the other hand, in Figure 1(b), where we show only the dependence of $A _s$ on $\Omega$, it is clear that the dashed line of our numerical results is, as expected, very close to the solid curve in the figure showing the analytical prediction first derived in (2.7).

Figure 1.  (a) Graph of total kinetic energy of (2.5) versus $\Omega$ and $A$, using with $\alpha = \infty$, $N = 100$, $T = 200$ and $V (x) = 1 - \cos (x)$. Computationally, we used $\tau = 0.05$. (b) Graph of the approximate critical amplitude at which supratransmission is triggered versus $\Omega$. The solid line is the graph of the function (2.7), while the dashed line is the numerical approximation obtained from the graph (a).

DownLoad: Full-Size Img PowerPoint

4.2.   Long-range interactions

Let us now investigate the occurrence of nonlinear supratransmission in (2.5) when $\alpha < \infty$. To this end, we will employ the model and parameters used in Section 4.1.

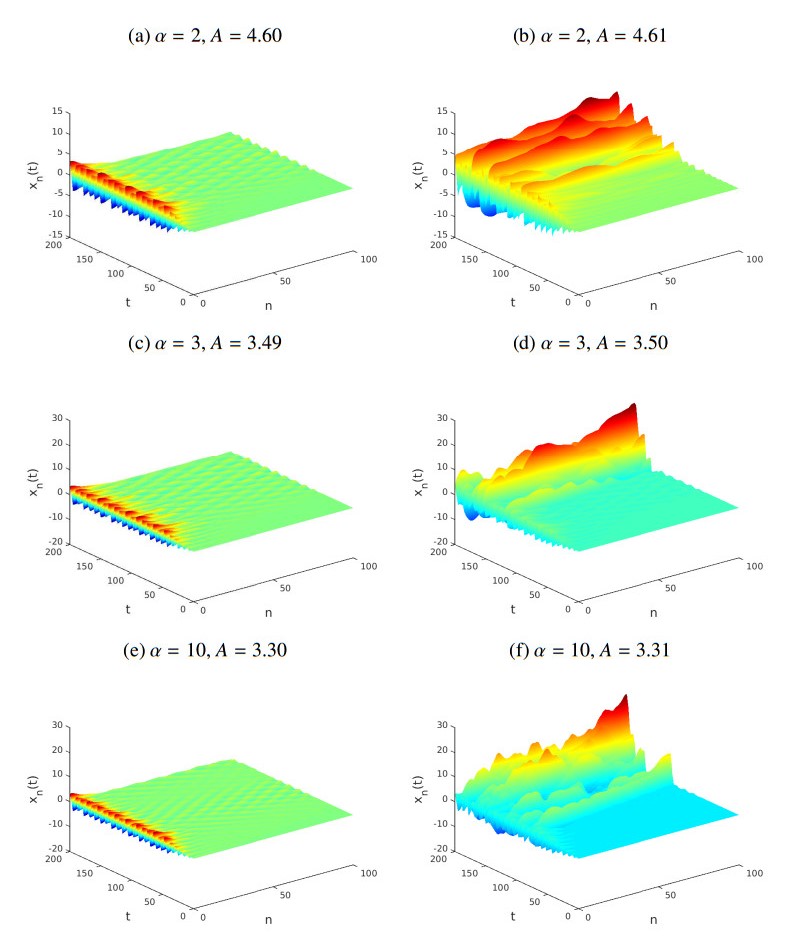
Example 2. Let us fix $\Omega = 0.7$, and consider the system (2.5). Under these circumstances, Figure 2 shows the behavior of the solution of the model versus $n$ and $t$, for different $A$ and various LRI values of $\alpha$. We have chosen systems with interaction exponents $\alpha = 2$ (top row), $\alpha = 3$ (middle row) and $\alpha = 10$ (bottom row). As in Example 1, we fix two driving amplitudes to exhibit the sudden "bifurcation" observed in the behavior of the solutions: one for which there is no transmission of energy into the medium, and one slightly larger, under which a large amount of energy is suddenly transmitted from the driving boundary. The graphs show clear evidence of supratransmission at thresholds $A _s$ which depend on $\alpha$ as follows: $A _s (2) \approx 4.60$, $A _s (3) \approx 3.49$ and $A _s (10) \approx 3.30$. Interestingly, $A _s (10) \approx A _s (\infty)$, as was evident also from the results of Example 1. Additionally, the simulations show that $A _s (\alpha)$ is a decreasing function for $\alpha > 1$, while $\lim _{\alpha \rightarrow \infty} A _s (\alpha) = A _s (\infty)$.

Figure 2.  Graphs of the solutions of (2.5) versus $n$ and $t$, using the parameters $\Omega = 0.7$, $a = 4$, $N = 100$, $T = 200$ and $V (x) = 1 - \cos x$. Various values of $\alpha$ and $A$ were used in each case, while $\tau = 0.05$.

DownLoad: Full-Size Img PowerPoint

Example 3. We have repeated Example 2 using $\Omega = 0.8$ and $\Omega = 0.9$ and found evidence of supratransmission in these cases also. The results (not shown here) are qualitatively very similar to what we saw in Figure 2 and exhibit supratransmission with threshold amplitudes: for $\Omega = 0.8$, $A _s (2) \approx 3.42$, $A _s (3) \approx 2.70$ and $A _s (10) \approx 2.59$, and for $\Omega = 0.9$, $A _s (2) \approx 1.95$, $A _s (3) \approx 1.86$ and $A _s (10) \approx 1.77$. These simulations verify our earlier conclusions that $A _s (10) \approx A _s (\infty)$, and that $A _s (\alpha)$ is a decreasing function of $\alpha$.

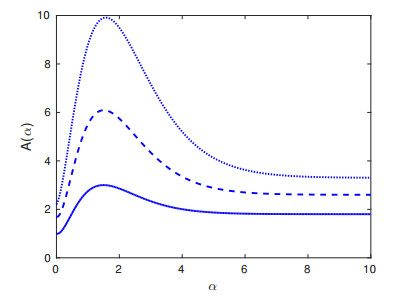
Unfortunately, there is as yet no analytical approximation for the occurrence of supratransmission in the system (2.5) when $\alpha < \infty$. Clearly, such a formula must be a function of $\alpha$ that incorporates (2.7) as $\alpha\rightarrow\infty$. Based on all our results thus far, we propose the following approximate formula

and plot it in Figure 3 for suitable $k, r \in \mathbb {R} ^+$. Here, $A _s(\Omega)$ is given in terms of $\Omega$ by (2.7), and $\Omega$ is a value in $(0.5, 1)$. Indeed, note that if $k = 6$ and $r = 4$ the function (4.2) yields a good approximation of the numerical results shown in Figure 3 for $\alpha = 2, 3$. The numerical findings are shown as dashed lines, (2.7) appears as a solid line, while the empirical formula is shown as a dotted curve which reproduces rather accurately the computational data down to $\alpha\approxeq 2$.

Figure 3.  Graphs of the approximate critical amplitude at which supratransmission is triggered versus $\Omega$, for (a) $\alpha = 2$ and (b) $\alpha = 3$. The parameters are as in previous figures. The solid curve is the short range interaction function (2.7), the dashed lines are the numerical approximations, and the dotted curve is the plot of the empirical formula (4.2).

DownLoad: Full-Size Img PowerPoint

However, as we will show in the next subsection, (4.2) does not provide a good approximation for $\alpha\lesssim 2$ because the dependence of $A_{th}(\alpha)$ ceases to be monotonic and starts to decrease sharply as $\alpha$ tends to zero. This is unexpected in view of the fact that in Hamiltonian lattices without on-site potentials, the monotonic increase of r supratransmission threshold amplitudes continues all the way to the strongest possible LRI case $0\leq \alpha \leq 1$ ^[23].

Before we leave this subsection, however, it is important to remark the following: At the end of Section 2 we alluded to the fact that $\Omega\in(0, 1)$ might be the forbidden band for our system. Yet, in all our results so far we have been using driving frequencies in the upper half of the $(0, 1)$ interval! This is because our supratransmission findings are much clearer and sharper in that range and the reason for this, we believe, is the following: As mentioned at the end of Section 2, the dispersion relation of our system yields a phonon band of the form $1 < \omega < B$, where $B$ is slightly greater than 1. It may, therefore, be the case that driving frequencies in the regime $\Omega\leq0.5$ possess low harmonics that lie in the phonon band, while $\Omega\in(0.6, 1)$ yields no such harmonics and thus constitutes the true forbidden band for our system.

4.3.   The strong LRI case

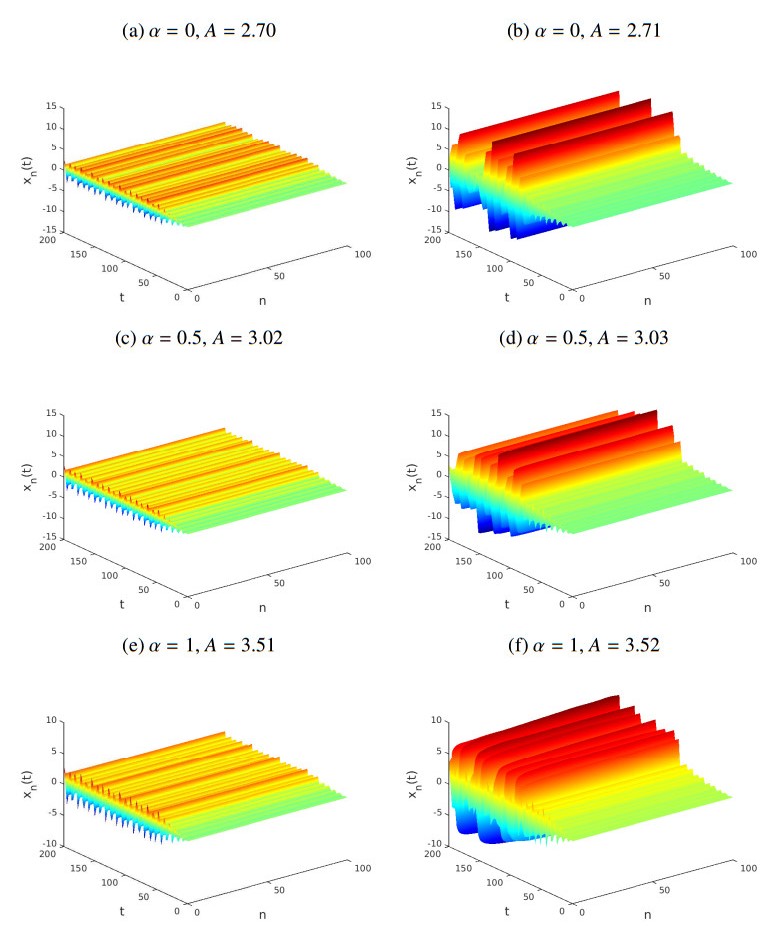
Example 4. Now let us start again with $\Omega = 0.7$. Figure 4 shows the behavior of the solution of (2.5) versus $n$ and $t$, for various values of $\alpha$ and $A$. To study the strong LRI case, we have chosen $\alpha = 0$ (top row), $\alpha = 0.5$ (middle row) and $\alpha = 1$ (bottom row). These plots present clear evidence of supratransmission at threshold amplitudes $A _s$: $A _s (0) \approx 2.70$, $A _s (0.5) \approx 3.02$ and $A _s (2.1) \approx 3.51$, and show that these amplitudes decrease as $\alpha$ decreases. In fact, this holds for all other values of $\Omega > 0.7$ we tried.

Figure 4.  Graphs of the solutions of (2.5) versus $n$ and $t$, using the parameters $\Omega = 0.7$, $a = 4$, $N = 100$, $T = 200$ and $V (x) = 1 - \cos x$. Various values of $\alpha$ and $A$ were used in each case, with $\tau = 0.05$.

DownLoad: Full-Size Img PowerPoint

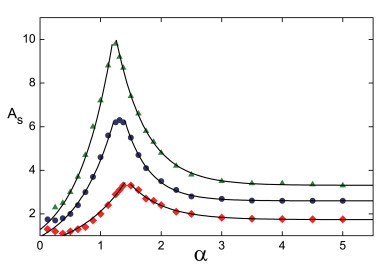
This aspect of our results suggests a complex relationship between the driving frequency and the critical amplitude at which supratransmission is triggered in the regime of strong LRI. In Figure 5 we have plotted the supratransmission threshold $A_s(\alpha)$ for the full range of $\alpha$ LRI values for three values of the driving frequency: $\Omega = 0.9$ (red diamonds), $\Omega = 0.8$ (blue circles) and $\Omega = 0.7$ (green triangles).

Figure 5.  The supertransmission threshold $A_s$ as a function of $\alpha$ for $\Omega = 0.9$ (red diamonds), $\Omega = 0.8$ (blue circles) and $\Omega = 0.7$ (green triangles).

DownLoad: Full-Size Img PowerPoint

We suggest the following explanation for this sudden decrease of $A_s$ as $\alpha$ goes to zero: As two of the authors have observed in their recent study of Klein-Gordon type systems ^[29], in the limit of $\alpha\rightarrow 0$ the phonon band shrinks to a line and all particles become so strongly correlated that energy transmission can occur for very small driving amplitudes, as shown in Figure 5. Now, what happens exactly in that limit is not clear, since the very nature of supratransmission becomes doubtful in the strong LRI regime $\alpha < 0.5$.

We, therefore, prefer to postpone this topic for a future publication and limit ourselves to presenting an empirical formula that captures the main features of the behavior of $A_s$ vs. $\alpha$ shown in Figure 5, in the hope that it may serve as a motivation for a deeper study of this phenomenon:

In this expression, the parameters $\lambda > 0$ and $\kappa_i, i = 1, 2, 3$ are meant to fit the particular features of the curves of Figure 5, while $A_s(\Omega)$ is taken from the known behavior of the thresholds at $\alpha = \infty$. Figure 6 shows some plots of the function (4.3) for various values of $\Omega$, which are in qualitative agreement with the actual numerical results shown in Figure 5.

Figure 6.  Graph of the threshold amplitudes given by the empirical formula (4.3) for $\Omega = 0.9$ (lower solid curve), $\Omega = 0.8$ (middle dashed curve) and $\Omega = 0.7$ (upper dotted curve).

DownLoad: Full-Size Img PowerPoint

We are currently studying the relation of the coefficients $\kappa_i, \lambda$ in Eq. (4.3) with $\Omega$, aiming to better understand the behavior of the supratransmission thresholds as $\alpha\longrightarrow 0$. However, since the comparison with numerical results in this region is quite delicate, we plan to pursue this analysis in a future paper.

5.   Conclusions and discussion

In the present work, we have explored the phenomenon of supratransmission in a Hamiltonian 1-dimensional lattice of $N = 100$ particles with global interactions and on-site potentials of sine-Gordon type $V(x) = 1-cos(x)$, or more general Klein Gordon cases of the form $V(x) = x^2/2!-x^4/4!+x^6/6!$. The system is initially at rest, and we apply a sinusoidal perturbation at the left boundary, treating the right end as absorbing, so that energy is not reflected back.

Using a stable and convergent finite-difference scheme ^[25], we drive the left end particle by $Asin\Omega t$ and record the threshold value $A = A_s$ at which there is a sudden flow of energy into the system via the effect of supratransmission ^{[4,6,7,8,9,10,11]}, which has so far been studied mainly in systems involving short range interactions of the nearest neighbor type.

We emphasize, of course, that for supratransmission the driving frequency must lie within the so-called forbidden gap, so that $\Omega$ and its harmonics do not excite the linear normal modes determined by the system's dispersion relation. Introducing in our potential a parameter $0\leq \alpha < \infty$ measuring the "length" of particle interactions we vary its value from infinity to the small $\alpha$ regime of long range interactions (LRI). We thus discover that supratransmission occurs at higher and higher $A_s(\alpha)$ thresholds, until they reach a maximum at about $\alpha\lesssim 1.5$ and then suddenly drop to values lower than their $\alpha = \infty$ value. As we have yet no analytical expression for these thresholds, we have proposed an empirical formula containing $\Omega$ and 5 parameters, which provides simple graphs that describe well the observed numerical results.

We conclude, therefore, that in Hamiltonian lattices of the Klein Gordon type with global interactions and on-site potentials, supratransmission is far more complex in the strong LRI case if it occurs there at all. Indeed, as $\alpha$ becomes smaller, the particles become more easily synchronized, oscillating in an in-phase manner. This has already been explained in ^[29], where it was shown that as $\alpha\rightarrow 0$, this in-phase oscillation becomes more pronounced, making the very nature of supratransmission highly questionable. We believe that similar results may be present in systems with global interactions and on-site potentials of the sine-Gordon, Klein-Gordon and double sine-Gordon types.

It would be interesting to test whether supratransmission effects occur as described above in real experiments involving arrays of Josephson junctions, electrical lattices with nonlinear dispersion, or discrete waveguide arrays with saturable nonlinearities ^[13]. Moreover, a rigorous justification of the mechanism that governs these phenomena under LRI is still lacking. Thus, the full explanation of the suppression of supratransmission in globally interacting systems, with or without on-site potentials ^[23], remains still an interesting problem that merits further investigation.

Acknowledgements

We thank the referees for their very valuable comments. A. Bountis acknowledges partial support for this research by an ORAU grant from Nazarbayev University, 2017–2020. Meanwhile, J. E. Macías-Díaz acknowledges support from the same research project for his visits at Nazarbayev University in May and October 2018, where some of the work presented here was performed. He thanks Prof. A. Bountis and his colleagues at Nazarbayev University for their hospitality and collaboration during this visit. H. Christodoulidi acknowledges support from the State Scholarship Foundation (IKY) operational Program: `Education and Lifelong Learning-Supporting Postdoctoral Researchers' 2014–2020, and is co-financed by the European Union and Greek national funds.

Conflict of interest

The authors declare no conflict of interest.