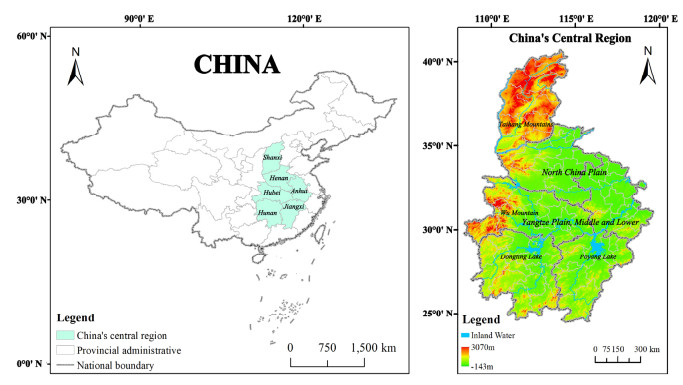
Under the influence of global climate change, the climatic conditions of China's major agricultural regions have changed significantly over the last half-century, affecting regional grain production levels. With its favorable conditions for agricultural activities, China's central region has been a strategic location for grain production since ancient times and has assumed an essential responsibility for maintaining national grain security. However, the key concerns of this study are whether the national grain security pattern is stable and whether it might be affected by global climate change (especially climate instability and increased risks in recent years). Therefore, the present study collected grain production data and used descriptive statistical and geospatial analyses to reveal the trend and spatiotemporal pattern of grain production in China's central region from 2010 to 2020. Then, a further analysis was conducted by combining meteorological data with a geographically weighted regression (GWR) model to investigate the relationship between spatial differences in the output per unit of the grain sown area (OPUGSA). The findings were as follows: (1) The overall development trend of grain production in China's central region from 2010 to 2020 revealed a positive overall trend in grain production, with notable differences in growth rates between northern and southern provinces. (2) Most regions in the southern part of the central region from 2015 to 2020 showed varying degrees of total output of grain (TOG) and OPUGSA reduction, possibly affected by the effects of the anomalies for global climate change and a strong El Niño effect in 2015. (3) Low-low (L-L) clusters of TOG and OPUGSA indicators were consistently in the northwest part (Shanxi) of the central region, and high-high (H-H) clusters of TOG were consistently in the central part (Henan and Anhui) of the central region, but H-H clusters of OPUGSA were not stably distributed. (4) The fitting results of the GWR model showed a better fit compared to the ordinary least squares (OLS) model; it was found that the annual average temperature (AAT) had the greatest impact on OPUGSA, followed by annual sunshine hours (ASH) and annual precipitation (AP) last. The spatiotemporal analysis identified distinct clusters of productivity indicators. It suggested an expanding range of climate impact possibilities, particularly in exploring climate-resilient models of grain production, emphasizing the need for targeted adaptation strategies to bolster resilience and ensure agricultural security.
1.
Introduction
Moving bottleneck models have been introduced in the engineering literature starting from the end of the last century to describe the interaction of slow moving vehicles, such as buses or trucks, with bulk traffic, see [9,28,30]. Further approaches have then be proposed in the applied mathematics community [1,15,27,39,41], always following the underlying idea of using multi-scale models consisting of Partial Differential Equations (PDEs) to model the overall traffic flow evolution, coupled with Ordinary Differential Equations (ODEs) accounting for the moving bottlenecks trajectories. Despite the intrinsic difficulties arising as a result of the flux constraint induced by the presence of the slow vehicles, corresponding existence and stability results have been provided, see also [17,20,31,32], together with numerical schemes to compute approximate solutions capturing the emerging non-classical phenomena [2,3,11,14,16].
More recently, moving bottleneck models have been applied to traffic flow regulation by means of Autonomous Vehicles (AVs), see e.g., [4,5,6,7,8,34]. Indeed, AVs can act as endogenous actuators of moving variable speed limits, improving throughput by hindering upstream traffic. This possibility has already been the object of several theoretical studies (see e.g., [13,24,26,35,40,42] and [19,Chapter 11]), but also artificial [25] and real world [38] experiments. In particular, it has been demonstrated that even low AV penetration rates can have a significant impact on reducing congestion phenomena and the associated energy consumption. In this context, macroscopic approaches are needed to address the curse of dimensionality in control design for microscopic models [18].
Even if some of the above works account for the presence of multiple AVs on the road, very few of them allow for AV interactions, and only in very specific modeling frameworks [21,37]. In this paper, we aim at generalizing the control framework designed in [20,34] for the Lighthill-Whitham-Richards model [33,36] to multiple, possibly interacting, moving bottlenecks, as if they were distributed on several lanes and they were allowed both to merge (if on the same lane) and to overtake (if on different lanes). This can be achieved by a careful study of the corresponding Riemann-type problems, and a natural generalization of the numerical reconstruction technique presented in [3].
The proposed model can be used to develop a general simulation environment accounting for several AVs interacting with the surrounding traffic flow and among themselves, which in turns allows to design optimization-based control strategies having fleets of AVs as actuators.
The paper is organized as follows: Section 2 details the model framework, providing a mathematical description of the fully coupled PDE-ODE model and the interactions among AVs at the level of Riemann problems. Section 3 describes the numerical scheme and Section 4 shows the results of the numerical experiments.
2.
PDE-ODE model with interacting moving bottlenecks
Following [15,20], we consider the following strongly coupled PDE-ODEs system
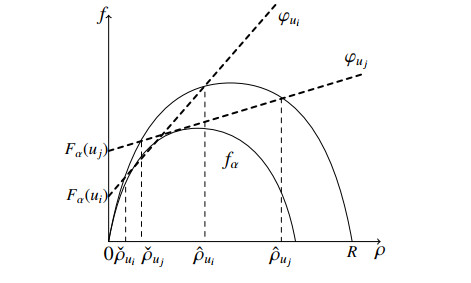
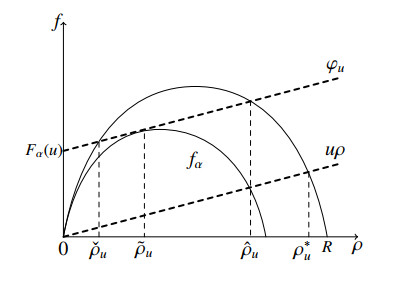
for ℓ=1,…,N and t>0,x∈R, where ρ=ρ(t,x)∈[0,R] denotes the macroscopic traffic density at time t≥0 and at position x∈R, f=f(ρ)=ρv(ρ) is the (strictly convex) flux and v∈C2([0,R];[0,V]) is a strictly decreasing function such that v(0)=V and v(R)=0, which represents the average speed of cars (R being the maximal vehicle density attainable on the considered road section). Above, ρ0∈[0,R] and y0ℓ∈R, ℓ=1,…,N, are respectively the initial traffic density and AV positions, while the function Fα in Eq (2.1c), α∈ [0,1], represents the road capacity reduction rate due to the presence of the AV at x=yℓ(t), ℓ=1,…,N, acting as a moving bottleneck which imposes a unilateral flux constraint at its position. For simplicity, we assume that this parameter is the same for all AVs, and it is a function of the number of lanes: α=(M−1)/M, where M∈N denotes the number of lanes. (The extension to a more general framework would follow the same lines detailed in this work.) To determine the function Fα, we consider the rescaled flux function
which is strictly concave function and such that fα(0)=fα(αR)=0. For every u∈[0,V], we define the point ˜ρu as the unique solution to the equation f′α(ρ)=u. Moreover, for every u∈[0,V], we define the function
Hence, if ˙y(t)=u, the function Fα in Eq (2.1c) is defined by
If ˙y(t)=v(ρ(t,y(t)+)), the inequality (2.1c) is trivially satisfied since the left-hand side is zero. Finally, the points 0≤ˇρu≤˜ρu≤ˆρu≤ρ∗u≤R are uniquely defined by
see [15,20] and Figure 1. We remark that ˇρV=˜ρV=ˆρV=ρ∗V=0.
Solutions to Eq (2.1) are defined as follows (see [20,Definition 3.1]):
Definition 2.1. The N+1-tuple (ρ,y1,…,yN) provides a solution to (2.1) if the following conditions hold.
1. ρ∈C0(R+;L1loc(R;[0,R])) and TV(ρ(t))<+∞ for all t∈R+;
2. yℓ∈W1,1loc(R+;R) for ℓ=1,…,N;
3. For every κ∈R and for all φ∈C1c(R2;R+) it holds
4. For a.e. t>0, f(ρ(t,yℓ(t)±))−˙yℓ(t)ρ(t,yℓ(t)±)≤Fα(˙yℓ(t)) for ℓ=1,…,N;
5. For a.e. t>0, ˙yℓ(t)=min{uℓ(t),v(ρ(t,yℓ(t)+))} for ℓ=1,…,N.
As long as AV trajectories do not intersect, one can apply the theory and the numerical schemes developed in [3,14,15,16,20]. In particular, we recall that the Constrained Riemann Solver is defined as follows.
Definition 2.2. The Constrained Riemann Solver Rα for
is the map Rα:[0,R]2×[0,V]→L1loc(R,[0,R]) defined as follows.
1. If f(R(ρL,ρR)(u))>Fα(u)+uR(ρL,ρR)(u), then
2. If f(R(ρL,ρR)(u))≤Fα(u)+uR(ρL,ρR)(u), then
Above, R denotes the standard (i.e., without the constraint (2.2c)) Riemann solver for Eqs (2.2a)–(2.2d), i.e., the (right continuous) map (t,x)↦R(ρL,ρR)(x/t) given by the standard weak entropy solution to Eqs (2.2a)–(2.2d).
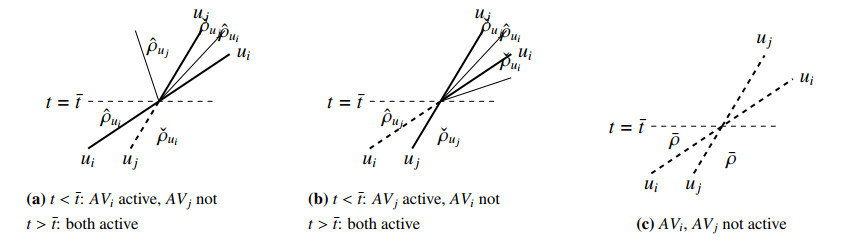
In this paper, we are interested in describing what happens when two vehicles AVi and AVj, with i,j∈{1,…,N}, i≠j, interact. Let us assume yi(t)<yj(t) with constant speeds ui(t)=ui>uj(t)=uj for t∈]ˉt−ε,ˉt[, so that yi(ˉt)=yj(ˉt) for some ˉt>0, see Figure 2. Depending on the surrounding traffic density conditions, only three situations may occur in a Riemann-like setting (piece-wise constant density with at most one jump discontinuity):
● The constraint (2.1c) is enforced for ℓ=i (we will say that AVi is active), so that ρ(t,x)=ˆρui for x<yi(t) and ρ(t,x)=ˇρui for x>yi(t). Since, at x=yj(t), it holds f(ˇρui)−ujˇρui≤Fα(uj) (see Figure 2), the constraint is not enforced for ℓ=j (AVj is then inactive).
● If AVj is active, we have ρ(t,x)=ˆρuj for x<yj(t) and ρ(t,x)=ˇρuj for x>yj(t). At x=yi(t), it therefore holds f(ˆρuj)−uiˆρuj≤Fα(ui), thus AVi is inactive.
● If both AVi and AVj are inactive, we may have either a constant density or a classical shock coinciding with one of the AV trajectories. In any case, the density must satisfy ρ(t,x)∈[0,ˇρui]∪[ˆρuj,R].
We remark that AVi and AVj cannot be both active at the same time, unless other waves are present between them.
To detail the problem evolution after the interaction (at t>ˉt), we distinguish if AVs are moving in different lanes or if they are located on the same lane.
Same lane interactions.
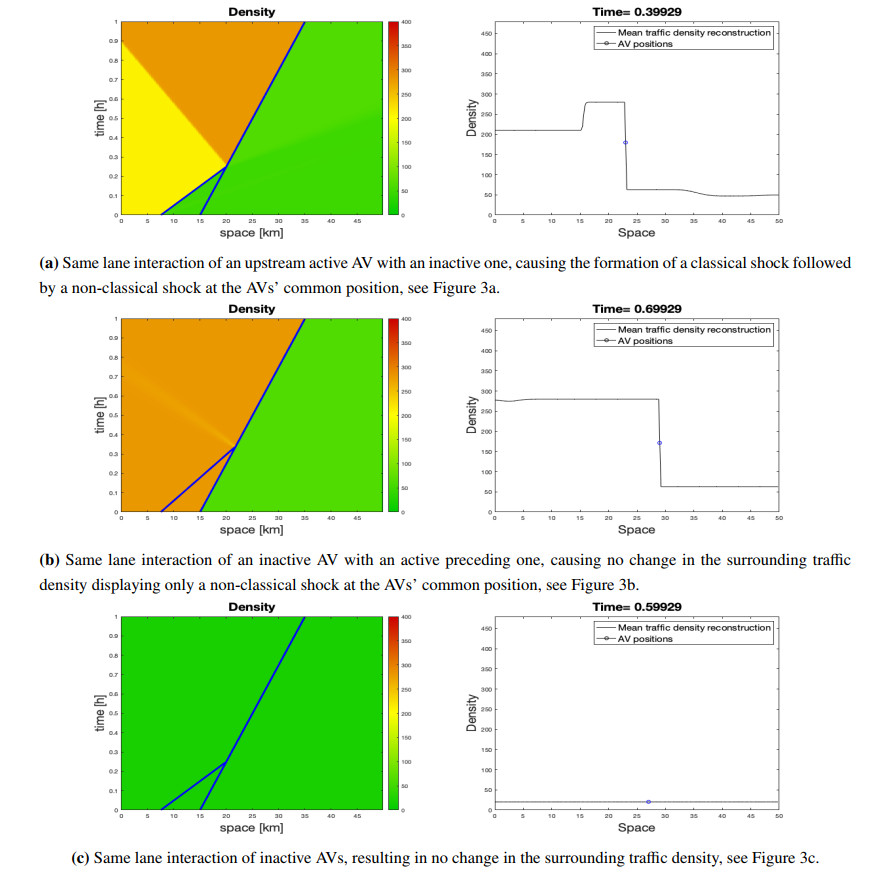
Let us assume that the two vehicles are in the same lane, so for t>ˉt the upstream vehicle must adapt to the downstream vehicle speed: we will have yi(t)=yj(t) with ui(t)=uj(t) for t≥ˉt. Three situations may occur, see Figure 3:
● If, before the interaction, AVi was active and AVj inactive, at t>ˉt the solution will consists of a classical shock joining ˆρui to ˆρuj, followed by a non-classical shock at x=yj(t)=yi(t) between ˆρuj and ˇρuj and a rarefaction wave from ˇρuj to ˇρui, see Figure 3a. In particular, after the interaction, both AVs will be active.
● If, before the interaction, AVi was inactive and AVj active, at t>ˉt the solution will consists only of a non-classical shock joining ˆρuj to ˇρuj, see Figure 3b. Again, after the interaction, both AVs will be active.
● If, before the interaction, AVi and AVj were both inactive, at t>ˉt the solution will consists at most of the classical shock that was already present before the interaction, see Figure 3c. After the interaction, both AVs will still be inactive.
In any case, after the interaction, the two vehicles behave as AVj.
Different lane interactions.
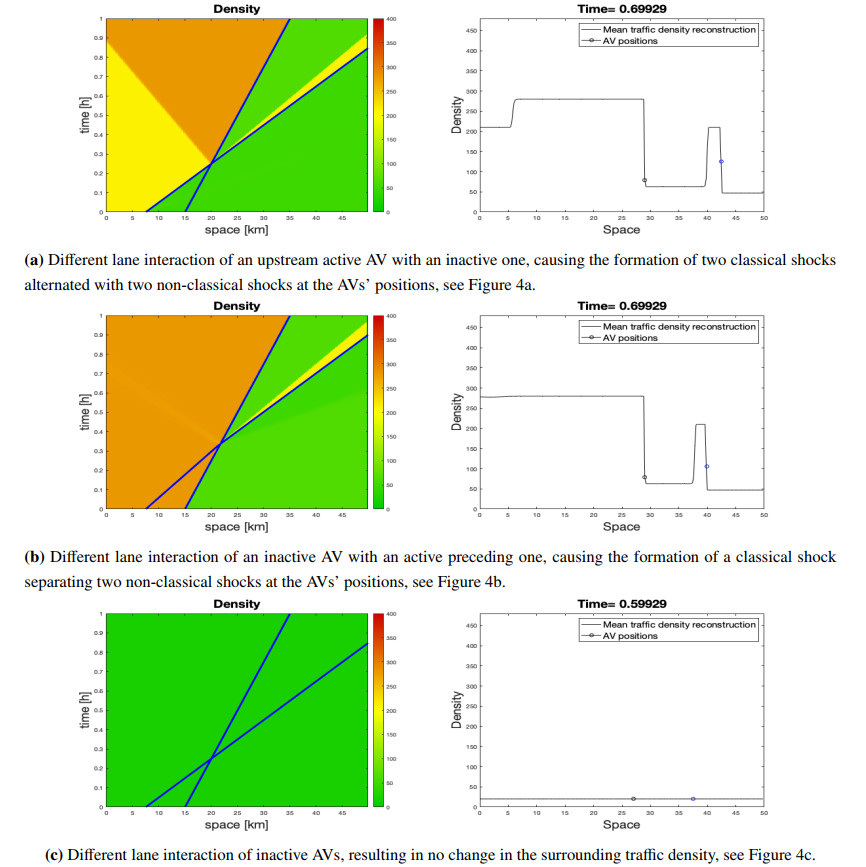
If the two interacting vehicles travel in different lanes, for t>ˉt they will follow their own trajectory and AVi will overtake AVj: we will have yi(t)≥yj(t) with ui(t)≥uj(t) for t≥ˉt. Three situations may occur, see Figure 4:
● If, before the interaction, AVi was active and AVj inactive, at t>ˉt the solution will consists of a classical shock joining ˆρui to ˆρuj, followed by a non-classical shock at x=yj(t) from ˆρuj to ˇρuj, a classical shock from ˇρuj to ˆρui and a non-classical shock at x=yi(t) from ˆρui to ˇρui, see Figure 4a. In particular, after the interaction, both AVs will be active.
● If, before the interaction, AVi was inactive and AVj active, at t>ˉt the solution will consists of a non-classical shock at x=yj(t) from ˆρuj to ˇρuj, followed by a classical shock from ˇρuj to ˆρui, a non-classical shock at x=yi(t) from ˆρui to ˇρui and a classical shock from ˇρui to ˇρuj, see Figure 4b. In particular, after the interaction, both AVs will be active.
● If, before the interaction, AVi and AVj were both inactive, at t>ˉt the solution will consists at most of the classical shock that was already present before the interaction, see Figure 4c. After the interaction, both AVs will still be inactive.
3.
Numerical scheme
We extend the reconstruction strategy introduced in [3] to include moving bottleneck interactions. The scheme is composed of two parts:
Numerical approximation of Eqs (2.1a)–(2.1c).
To approximate the conservation equation (2.1a), we use a conservative finite volume scheme for the constrained hyperbolic PDE using a flux reconstruction technique at the constraint locations, which allows to capture the non-classical shocks sharply. Let Δx and Δt be the fixed space and time steps satisfying the standard Courant-Friedrichs-Lewy (CFL) condition [10]:
and set xj−1/2=jΔx, xj=(j+1/2)Δx for j∈Z, and tn=nΔt for n∈N. The initial data ρ0 is approximated by the piece-wise constant function obtained by averaging it on the discretization cells Cj=[xj−1/2,xj+1/2], namely
Away from AV positions, Eq (2.1a) is approximated by the standard Godunov scheme [22], whose numerical fluxes at cell interfaces Fnj+12=F(ρnj,ρnj+1) can in this case be derived using the supply-demand formula [29]
where
ρcr=argminρ∈[0,R]f(ρ) being the point of maximum of the flux function f.
Let now the approximate ℓ-th AV position be ynℓ∈Cmℓ for some mℓ∈Z, ℓ=1,…,N. If
we assume a moving bottleneck at ˉxmℓ=xmℓ−1/2+dnmℓΔx with dnmℓ=ˇρunℓ−ρnmℓˇρunℓ−ˆρunℓ. If 0≤dnmℓ≤1, then ˉxmℓ∈Cmℓ and we set
We can then update the density by means of the conservative formula
Above, we set unℓ=uℓ(tn). If two or more AVs are located in the same cell, the moving bottlenecks are treated sequentially one after the other, starting from those which are not active (i.e., satisfy Eq (2.1c)), then processing those which are active (violating Eq (2.1c)).
Remark 1. For better resolution, we also apply the above reconstruction technique to classical shocks, as described in [3,Section 3.1].
Numerical approximation of Eq (2.1b).
To track the AV trajectories, at each time step, we update the positions ynℓ using an explicit Euler scheme
If two AVs are in the same lane and in the same cell, and the upstream AVℓ1 moves faster than the downstream AVℓ2, i.e., unℓ1>unℓ2, then we set
(A more accurate computation of the interaction point could be implemented to improve simulation accuracy.)
Remark 2. The above procedure seems not coherent with the observation that two vehicles travelling at close speeds ui≈uj would act as a single bottleneck with αij=αi+αj−1. In this perspective, another option could be to reconstruct a single front moving at speed uij=(ui+uj)/2 with α=αij whenever two vehicles are in the same cell on two different lanes. In this case, the procedure should be the following:
If f(R(ρnm−1,ρnm+1)(uij))>Fαij(uij)+uijR(ρnm−1,ρnm+1)(uij),
we replace ρnm by ˆρuij and ˇρuij, with the jump located at
where dnm∈[0,1] is given by
To reconstruct the numerical flux at the cell interface xm+12, we compute
and we set
4.
Numerical tests
In this section we illustrate the performances of the numerical scheme described in the previous Section 3 in capturing AV interactions correctly. We first analyze the Riemann-like cases described in Section 2, to conclude with a more general test case.
We consider a three lane stretch of road of length 50 km, parametrized by the interval [0,50] with absorbing boundary conditions. We consider the quadratic flux function proposed by Greenshields [23] that assumes a linear decreasing dependence of the speed on the traffic density
where V=140 km/h denotes the maximal speed and R=400 veh/km the maximal (bump-to-bump) density on the road. The capacity reduction ratio is set to α=0.6. In all simulations, we set Δx=0.2 and Δt=0.9Δx/V.
For the Riemann-like cases, we consider the following initial data:
The results are depicted in Figures 5 and 6. Except small spurious oscillations emerging from AV interactions in some cases, the solutions, and in particular non-classical shocks, are accurately reproduced.
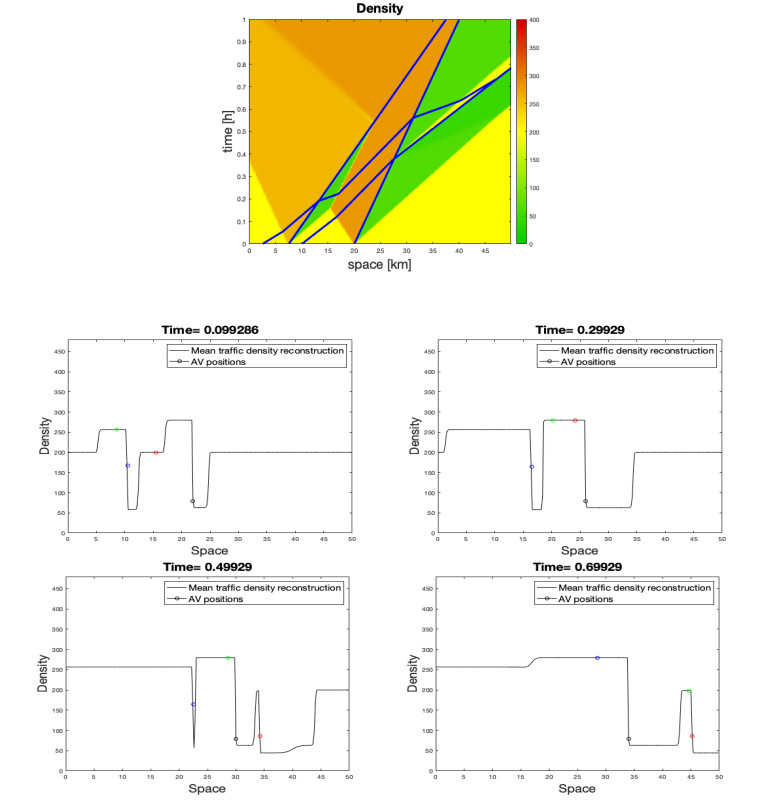
To give a more general example, we consider the following initial data: ρ0(x)≡200 and
Moreover, AV1 and AV3 are on the same lane.
Figure 7 displays the solution, accounting for the different interaction types (queuing and overtaking). We observe that AV1 and AV3 are initially inactive while AV2 and AV4 are active. Moreover, AV1 and AV3 overtake the preceding vehicles and finally merge. Also, AV1 is always inactive until it merges with AV3, which becomes active after the interaction with AV4, while AV4 is always active. On the contrary, AV2 becomes inactive when it reaches an high traffic density region.
5.
Conclusion
We have presented a strongly coupled PDE-ODE model describing the interaction of a small number of autonomous vehicles with bulk traffic on a multi-lane highway. The model allows for AV queuing and overtaking, expanding the range of traffic control applications of previous works [4,5,6,7,8,34]. A first study on traffic management opportunities offered by this framework is presented in [12], showing that low penetration rates are sufficient to reach nearly optimal improvements of a selected performance index.
Acknowledgements
The second author was partially supported by ERASMUS+/KA1 "NORTH SOUTH TRAINEESHIP" academic year 2020/21.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: